Towards Efficient Disaster Response via Cost-effective Unbiased Class Rate Estimation through Neyman Allocation Stratified Sampling Active Learning

Yanbing Bai Center for Applied Statistics and School of Statistics, Renmin University of ChinaBeijingChina ybbai@ruc.edu.cn , Xinyi Wu Center for Applied Statistics and School of Statistics, Renmin University of ChinaBeijingChina 2021103789@ruc.edu.cn , Lai Xu Independent ResearcherBeijingChina pkusimon@gmail.com , Jihan Pei Center for Applied Statistics and School of Statistics, Renmin University of ChinaBeijingChina 2021201671@ruc.edu.cn , Erick MAS Disaster Geo-informatics Laboratory, International Research Institute of Disaster Science, Tohoku UniversitySendaiMiyagiJapan mas@irides.tohoku.ac.jp and Shunichi Koshimura Disaster Geo-informatics Laboratory, International Research Institute of Disaster Science, Tohoku UniversitySendaiMiyagiJapan koshimura@irides.tohoku.ac.jp

(2024)

Abstract.

With the rapid development of earth observation technology, we have entered an era of massively available satellite remote-sensing data. However, a large amount of satellite remote sensing data lacks a label or the label cost is too high to hinder the potential of AI technology mining satellite data. Especially in such an emergency response scenario that uses satellite data to evaluate the degree of disaster damage. Disaster damage assessment encountered bottlenecks due to excessive focus on the damage of a certain building in a specific geographical space or a certain area on a larger scale. In fact, in the early days of disaster emergency response, government departments were more concerned about the overall damage rate of the disaster area instead of single-building damage, because this helps the government decide the level of emergency response. We present an innovative algorithm that constructs Neyman stratified random sampling trees for binary classification and extends this approach to multiclass problems. Through extensive experimentation on various datasets and model structures, our findings demonstrate that our method surpasses both passive and conventional active learning techniques in terms of class rate estimation and model enhancement with only 30%-60% of the annotation cost of simple sampling. It effectively addresses the ’sampling bias’ challenge in traditional active learning strategies and mitigates the ’cold start’ dilemma. The efficacy of our approach is further substantiated through application to disaster evaluation tasks using Xview2 Satellite imagery, showcasing its practical utility in real-world contexts.

Active Learning, xBD satellite imagery dataset, Disaster Response, Neyman Allocation Stratified Sampling, Class Rate Estimation

^†^†copyright: acmlicensed^†^†journalyear: 2024^†^†doi: XXXXXXX.XXXXXXX^†^†conference: Make sure to enter the correct conference title from your rights confirmation emai; October 21–-25,2024; Boise, Idaho, USA^†^†isbn: 978-1-4503-XXXX-X/18/06^†^†ccs: Active Learning^†^†ccs: Class Rate Estimation Disaster Response

1. Introduction

With the rapid development of earth observation technology, we have entered an era of massively available satellite remote-sensing data. However, a large amount of satellite remote sensing data lacks a label (Xu et al., 2019a; Rudner et al., 2019) or the label cost is too high (Van Etten et al., 2018; Bonafilia et al., 2020) to hinder the potential of AI technology mining satellite data. Especially in such an emergency response scenario that uses satellite data to evaluate the degree of disaster damage, the lack of labeled data (Lee et al., 2020) has seriously hindered the research and development of the AI model for supporting efficient disaster response. In the past, disaster damage assessment encountered bottlenecks due to excessive focus on the damage of a certain building (Bai et al., 2023; Xia et al., 2022) in a specific geographical space or a certain area (Bai et al., 2017) on a larger scale. This is a challenging problem given the limitations of satellite remote sensing resolution and the development level of AI technology. Indeed, in numerous scenarios, the precision of overall class rate estimations precedes the model’s classification accuracy. In fact, in the early days of disaster emergency response, government departments were more concerned about the overall damage rate of the disaster area instead of single-building damage, because this helps the government decide the level of emergency response (Xu et al., 2019b).

Although it is difficult to train a classification model with good robustness and high accuracy with limited samples, it is possible to achieve a high confidence class rate estimation (estimating the class rate of population unbiasedly ) result. In settings where labeled data is scarce, the efficient annotation of data poses a substantial challenge. Active learning rises to this challenge by selecting the most informative instances for annotation to reduce total labeling costs. Active learning is an effective method for performing class rate estimation. Active learning methods’ mainstream query strategies are rule-based non-probabilistic sampling methods. However, samples obtained cannot be directly used for class rate estimation tasks. Using probability sampling allows for an unbiased estimate of the class rate, with sampling errors decreasing as the magnitude of labeled samples increases. However, traditional probability sampling, equivalent to a ”passive learning” process without utilizing model information, cannot effectively guide model learning.

Refer to caption — Figure 1. Framework of the proposed approach

Figure 1 shows the research framework of this paper. In this study, We propose an active learning method based on Neyman stratified random sampling as the query strategy which combines the ideas of probability sampling and active learning, leveraging their respective strengths in class rate estimation and model training tasks. It efficiently utilizes labeling costs for annotation, allowing the obtained labeled samples to simultaneously serve model training and class rate estimation tasks. The proposed method is of practical value for many application scenarios that require both model training and high-confidence class rate estimation.

The paper conducts experimental evaluations on multiple public datasets and model structures to validate the effectiveness of the proposed approach. Our method surpasses both passive and conventional active learning techniques in terms of class rate estimation and model enhancement with only 30%-60% of the annotation cost of simple sampling. Finally, an application example in the context of building damage assessment based on Xview2 satellite remote sensing images in xBD dataset illustrates its practical application in rapid disaster response.

2. Related Work

Previous research on building damage assessment mainly focused on classification models of single buildings or regional buildings (Gupta et al., 2019; Xu et al., 2019b, a), and will not be introduced in detail here. Concerning the commonly employed uncertainty-based query strategy in active learning, numerous studies have pinpointed sampling bias as a prevalent issue. In response, there is an increasing inclination towards the fusion of diverse query strategies. Yang et al. (2015) have synthesized uncertainty with diversity strategies, evaluating data uncertainty across the full spectrum of the active pool. Meanwhile, Chu et al. (2016)have been exploring the transferability of active learning, devising a model that integrates various strategies, thereby quantifying the extent of active learning using linear weights.

The field of active learning is increasingly exploring interdisciplinary combinations with other fields. Both active learning and semi-supervised learning share the common objective of improving learning with limited labeled data. Gao et al. (2020)introduced a comprehensive framework that integrates both approaches. In the context of transfer learning, Xie et al. (2021) introduced an active learning strategy known as ”active domain adaptation.” This approach utilizes a straightforward energy-based sampling strategy, selecting data based on domain-specific characteristics and model prediction uncertainty.

In active learning, cold-start problem arises if the initial labeled sample set is not large enough. When the cold-start problem occurs, samples based on active learning do not perform better than simple random sampling (Wang and Shang, 2014). Therefore, the cold-start problem has always been a crucial research direction in the field of active learning. Gao et al. (2020) adopted a combination of semi-supervised learning and active learning methods to alleviate the issue to some extent.

In the context of class rate estimation, active learning aims to improve the accuracy of probability model predictions for unlabeled samples. Saar-Tsechansky et al. (2004) proposed BOOTSTRAP-LV, an active learning approach that selects samples with high variance in model output class rate estimates. This method incorporates the accuracy measure of class rate estimates into the active learning query strategy, enhancing both model training accuracy and class rate estimation precision. Melville et al. (2005) further improved BOOTSTRAP-LV by using Jensen-Shannon divergence to measure high information content.

However, relying solely on model-predicted probabilities for overall class rate estimation may not be useful for certain applications, such as disaster assessment based on remote sensing images and internet monitoring scenarios. In these scenarios, exploring how to directly utilize labeled samples acquired through iterative sampling in active learning is a valuable direction. However, due to this perspective not being mainstream in the active learning field, relevant works in this area are limited, and we take this research perspective as our starting point.

3. Method

3.1. Active Learning Ideas in Stratified Sampling

Stratified Random Sampling with Neyman’s allocation, is a probabilistic sampling method that embodies the uncertainty in active learning. It allocates sample sizes among strata by considering inter-stratum uncertainties. Additionally, it ensures coverage of the entire population distribution, providing every sample in the population a probability of being selected. This aligns with the diversity concept in active learning, helping mitigate the ”sampling bias” issue in the uncertain query strategy.

The following will further compare it with the uncertainty query strategy in active learning, thereby further illustrating the active learning ideas inherent in stratified random sampling with Neyman’s allocation.

For the uncertainty entropy sampling strategy in active learning, it selects a batch of samples with the highest entropy in each iteration. In binary classification, this means collecting more samples with model predictions around 0.5, near the decision boundary.Assuming a well-calibrated model, the Neyman Stratified Random Sampling strategy allocates fewer samples to extreme model predictions (close to 0 or 1) and more samples to around 0.5. This reflects a similar principle between Neyman Stratified Random Sampling and uncertainty entropy sampling, focusing on allocating more samples around the model’s decision boundary.

Simultaneously, it can be directly observed from the data that the two share similar ideas. Figure 2 shows a similar distribution pattern of sample entropy and estimated variance along the model predicted scores dimension. The ideal variance distribution forms a perfect parabolic shape in a well-calibrated model. Despite practical deviations, the basic trend of variance distribution adheres to a parabolic distribution.

Furthermore, in practice, sample allocation will be performed using the following formula:

(1)

n_{h}=\min\left(\max\left(n_{\text{threshold }},n\frac{W_{h}S_{h}}{\sum_{k=1}^{L}W_{k}S_{k}}\right),N_{h}\right)

Where the inner max function introduces a minimum threshold for sample allocation to ensure each layer receives a minimum sample allocation. This Neyman stratified random sampling considers both within-layer variance and overall distribution, incorporating the diversity idea from active learning. It prevents samples from being concentrated solely near the decision boundary, addressing the ”sampling bias” issue in the uncertainty query strategy. The outer min function ensures that Neyman sample allocation does not exceed the total population within the layer.

3.2. Main Algorithm

The proposed approach incorporates Neyman stratified random sampling as the query strategy into the iterative training process of active learning(details in Algorithm 1).

Algorithm 1 Main Algorithm of the Proposed Approach

Input::: Total number of iterations $T$ ; Initial unlabeled pool size $N$ ; Initial sampling size $n_{init}$ ; Sampling size at iteration $t$ $n_{roundt}$ ; In iteration round t, number of layers $L_{t}$ , Population size in layer h $N_{th}$ , Weight of layer h $W_{th}$ , Sample mean within layer h $\overline{y_{th}}$ , sample variance within layer h ${s_{th}^{2}}$
Initialize (Iteration $t=0$ )::: Initial simple random sampling $n_{init}$ as the initialization of the labeled training sample pool; Train the initial iteration $Model_{0}$ based on the initialized labeled training sample pool

Output: Estimated overall class rate

1: while the current unlabeled pool is not empty: do

2: Infer the total sample pool (including labeled and unlabeled) using the

Model_{t-1}

to obtain a sample pool with

Model_{t-1}

estimated scores.

3: Perform Neyman stratified random sampling on the sample pool using model estimated scores, obtaining the sample selection results for the current iteration.

4: Manually label the selected samples

5: Based on the labeled results in the current iteration t, provide an unbiased estimate for the overall class rate.

\widehat{\overline{Y}_{t}}=\sum_{h=1}^{L_{t}}W_{th}\overline{y_{th}}=\frac{1}{N}\sum_{\mathrm{h=1}}^{L_{t}}N_{\mathrm{th}}\overline{y_{th}}

6: Update the labeled training sample pool with the newly obtained labeled samples for model training

Model_{t}

7: end while

8: return:

\widehat{\overline{Y}}=\frac{1}{T}\sum_{t=1}^{T}\widehat{\overline{Y}_{t}}

It’s important to highlight that, unlike typical active learning , our query strategy samples from the overall pool in each iteration, including both labeled and unlabeled samples. This ensures that Neyman stratified random sampling in each iteration provides an unbiased estimate of the overall class rate. However, a challenge arises as the samples selected by Neyman stratified random sampling may include already labeled ones. To avoid redundant annotations, in step 2 of the Algorithm 1’s iteration, selected samples are deduplicated with the labeled pool before annotation. Afterward, the deduplicated samples are annotated and merged into the labeled training sample pool.

3.3. Tree Based Routine Stratification

During the model iteration process in active learning, the distribution of samples on the model estimated scores is continuously updated. Therefore, the stratified sampling scheme should also be iteratively updated. The following provides a routine implementation of Neyman stratified random sampling based on tree models in the iterative process, which allows for the routine determination of ”good” stratification schemes for each iteration. We view Neyman’s stratified random sampling as an optimization problem, aiming to minimize the variance of class rate estimation. Since Neyman allocation is not inherently suitable for multi-class problems, we’ll first illustrate the optimization problem with a binary classification example, as defined in Equation:

(2)

\begin{cases}x=[x_{0}=0,x_{1},x_{2},...,x_{L-1},x_{L}=1],\\ bucket_{h}=\{i;x_{h}\leq model(i)\leq x_{h+1}\},\\ W_{h}=\frac{N_{h}}{N},s_{h}^{2}=p_{h}*(1-p_{h}),\\ ST\quad\forall x_{k}\in[0,1],\\ MIN(\sum_{h=1}^{L}\frac{1}{n_{h}}W_{h}^{2}s_{h}^{2})\end{cases}

Where $[x_{0}=0,x_{1},x_{2},...,x_{L-1},x_{L}=1]$ is the stratification threshold points for each layer, $bucket_{h}$ is the overall set of layer h, $bucket_{h}$ is the layer weights within layer h, $p_{h}$ is the sample class rate within layer h, and $p_{h}$ is the sample variance within layer h. In practical, a binary tree, referred to as a stratified tree, is used for stratified random sampling whose time complexity is $O(logn)$ . The process is specifically explained for binary classification inAlgorithm 2.

Algorithm 2 Stratified Tree Algorithm(iteration round t)

Initialize: Total sample pool (including labeled and unlabeled samples in iteration round t) as the root node of the tree
Input: Total sample pool as the training set D; $Model_{t-1}$ ’s predicted scores as the feature set A
Stopping Condition: Set tree depth as k so the maximum expected number of layers is $2^{k-1}$
Output: Stratified Tree

1: Procedure GenerateStratifiedTree(

D,A

2: if all instances in

D

belong to the same class then

3: return tree T

4: else if

A

is an empty set then

5: return tree T

6: else

7: Calculate the target function for splitting

8: Choose the split threshold for features A based on the target function

9: Split the dataset D into two leaf nodes based on the feature A’s split threshold

10: Construct tree

T

with the current node and new leaf nodes

11: end if

12: for each child node i in the tree

T

: do

13: Call GenerateStratifiedTree(

D_{\text{i}},A_{\text{i}}

) to get the subtree

T_{i}

14: end for

15: return tree

T

Note that unlike standard CART trees, the split in Neyman stratified random sampling tree minimizes the sampling error estimate across the entire stratified result, considering both local and global changes in leaf nodes.

3.4. Solution for Multiclass Classification

In binary classification, the feature A is a single-dimensional feature, i.e., the $Model_{t-1}$ ’s estimated probability of positive instances for the samples. The allocation principle in Neyman allocation is optimized for a single class rate estimation target. In the case of multiple classes and objectives, the optimal allocation for one specific target may not necessarily be optimal for other targets. For multi-class problems (like K classification), this paper also provide an corresponding applicable solution:

In multi-class problems, the feature set A is composed of the vector of estimated positive probabilities of samples by the . Firstly, select M classes from the total of K classes, focusing on those more relevant in practical scenarios, as positive classes. The remaining K-M classes are considered negative classes, thus transforming the multi-class problem into a binary classification problem.

However, the obtained optimal Neyman allocation scheme may still not be applicable to each of the M classes. Therefore, specific guardrail determination rules are established for each of these M classes to ensure that the final sample allocation plan is suitable for each positive class(that is, adding a new decision condition in steps 3 and 4 of the stratified tree algorithm described in Algorithm 2). The specific condition is presented as follows:

(3)

\sum_{h=1}^{L}\frac{1}{n_{h}}W_{h}^{2}s_{hm}^{2}\geq\frac{1}{n}s_{m}^{2}

Where the positive class m = 1,…, M. If this decision condition is satisfied, then the node will not split at this threshold point split, and the algorithm returns a single-node tree T with this node as the root; otherwise, the algorithm proceeds to step 4.

The condition ensures that if the final stratified sampling result has a larger sampling error for positive class m compared to simple random sampling based on the current threshold point split, no stratification will be performed for that threshold point. This ”guardrail condition” guarantees optimization for each positive class among M, with sampling errors smaller than simple random sampling. Validation of the solution for multiclass classification will be discussed in Section 4.5.

4. Experiments

We conduct extensive experiments across multiple datasets and model structures to compare the effectiveness of our proposed active learning method based on stratified random sampling with Neyman’s optimum allocation(NSRS) against passive learning method with simple random sampling (SRS) and the traditional active learning method with uncertainty entropy sampling (UES). We use open computer vision datasets, including MNIST, CIFAR-10, and CINIC-10. The model structures include logistic regression, M1 (a custom simple convolutional neural network), Lenet5, Alexnet8, VGG16, and RESNET50. Training parameters involve using the Adam optimizer with an initial learning rate of 0.001 and decay mechanism, along with a batch size of 100.

4.1. Class Rate Estimation Results

Table 1 displays class rate estimates(the overall category rate is 0.1) and variances for three query strategies on the CIFAR-10 dataset, assuming a sampling size of 10,000. Neyman Stratified Random Sampling, based on model predictions, is affected by the quality of model predictions. Results are presented for logistic regression, M1, and Alexnet8 models, with variations based on model complexity and training iterations(represented as cumulative training sets).

	Cumulative Training Volume
	Query	Statistics	20%	40%	60%	80%
LR	SRS	Estimate	0.1	0.1	0.1	0.1
		V( $10^{-6}$ )	9.00	9.00	9.00	9.00
	NSRS	Estimate	0.097	0.098	0.101	0.099
		V( $10^{-6}$ )	6.17	6.02	5.79	5.51
	UES	Estimate	0.268	0.201	0.152	0.121
M1	SRS	Estimate	0.1	0.1	0.1	0.1
		V( $10^{-6}$ )	9.00	9.00	9.00	9.00
	NSRS	Estimate	0.1	0.1	0.098	0.1
		V( $10^{-6}$ )	5.28	2.76	1.92	1.70
	UES	Estimate	0.372	0.192	0.124	0.09
A8	SRS	Estimate	0.1	0.1	0.1	0.1
		V( $10^{-6}$ )	9.00	9.00	9.00	9.00
	NSRS	Estimate	0.098	0.104	0.1	0.1
		V( $10^{-6}$ )	2.65	3.64	1.95	1.40
	UES	Estimate	0.375	0.246	0.166	0.125

Table 1. Comparison of Class Rate Estimation Results. Where LR represents logistic regression model, M1 represents M1 model, A8 represents Alexnet8 model, V represents variance of estimate

In Table 1, we can find that both Simple Random Sampling and Neyman Stratified Random Sampling yield unbiased estimates around the true value of 0.1, whereas uncertainty entropy sampling does not. Neyman Stratified Random Sampling shows 30%-60% lower variance compared to simple random sampling. The variance decreases with increased model complexity and cumulative training volume, indicating improved performance. This indicates that the quality of model predictions influences the effectiveness of stratification. Better model prediction results in improved performance of the proposed approach based on the estimated model scores.

In summary, the proposed approach allows unbiased overall class rate estimation through iterative sampling, a capability lacking in traditional uncertainty entropy sampling. Additionally, it achieves lower variance, requiring only 30%-60% of the labeling cost compared to simple random sampling for equivalent sampling error. This holds practical value for applications relying on sampling annotation for class rate estimation.

4.2. Model Training Results

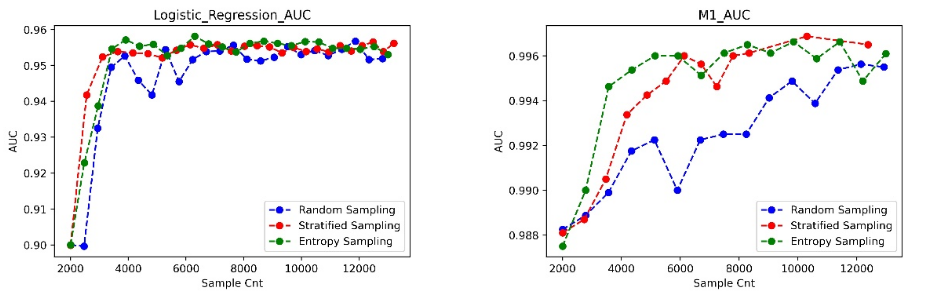
Figure 3, 4, and 5 depict AUC curve results for model iteration and training across three datasets (MNIST, CIFAR-10, CINIC-10) using three query strategies (Neyman stratified random sampling, simple random sampling, uncertainty entropy sampling) on six model structures (logistic regression, M1, Lenet5, Alnex8, Vgg16, Resnet50). The x-axis represents training sample size, and the y-axis represents model AUC results. Notably, due to MNIST’s simplicity, experiments focused on logistic regression and M1 models with a smaller sample size.

Neyman stratified random sampling outperforms simple random sampling across datasets and models, reflecting its active learning ideas. This emphasizes its ability to choose good samples based on model information during iteration. Neyman stratified random sampling and uncertainty entropy sampling show comparable results on high-complexity models. On low-complexity models, Neyman stratified random sampling slightly falls behind uncertainty entropy sampling, attributed to its dual focus on class rate estimation and model training compared to the latter’s emphasis on model training. The performance gap diminishes with increasing model complexity, with Neyman stratified random sampling slightly outperforming on Resnet50. This is because Neyman stratified random sampling alleviates the ”sampling bias” issue caused by uncertainty entropy sampling, leveraging overall distribution information.

4.3. Sampling Distribution

For a more visual comparison of the three sampling strategies, Figure 6 illustrates the distribution of samples based on the model’s estimated scores in the current round.

From the figure, Neyman stratified random sampling shows a distribution similar to simple random sampling, closely aligning with the overall sample distribution. Notably, Neyman stratified random sampling samples more around the model’s estimated score of 0.5 and less in areas close to 0 or 1. This aligns with the active learning ideas discussed in Section 3.1.

In contrast, uncertainty entropy sampling concentrates samples around the model’s estimated score of 0.5, indicating a reliance on the current model’s estimation . Neyman stratified random sampling and uncertainty entropy sampling share similar principles and Neyman stratified random sampling can mitigate the ”sampling bias” issue of uncertainty entropy sampling to some extent.

4.4. Cold-start problem

To some extent, Neyman stratified random sampling can mitigate the cold-start problem observed in uncertainty entropy sampling. In contrast to uncertainty entropy sampling, the query strategy based on Neyman stratified random sampling exhibits better robustness to the initial set size, as illustrated in Figure 7 on the CIFAR-10 dataset using two different model structures (M1, Alexnet8) with different initial set sizes (100 and 1000).

Uncertainty entropy sampling exhibits a cold-start problem, particularly in more complex networks. When the initial set size is 100, there is a notable drop in the improvement of model AUC after first iteration, a trend that becomes more pronounced in deeper network structures. On the Alexnet8 network, the model’s iterative training performance with an initial set of 100 is significantly inferior to that with an set of 1000. As the network complexity increases, Neyman stratified random sampling also encounters a cold-start problem. In the Alexnet8 network structure, Neyman stratified random sampling demonstrates a similar pattern where the improvement in model AUC in the first iteration is noticeably higher than in subsequent iterations. However, overall, Neyman stratified random sampling query strategy proves more effective than uncertainty entropy sampling in addressing the cold-start problem.

4.5. Multiclass Classification Problem

This section validates the effectiveness of Neyman stratified random sampling for multi-class classification, comparing three query strategies on CIFAR-10. The dataset focuses on ”motorcycle” and ”airplane” as positive instances (M=2), merging the remaining eight classes into a single category for a three-class dataset (K=3). Training is performed using the Alexnet8 model.

	Cumulative Training Volume
	Query	Statistics	20%	40%	60%	80%
M	SRS	Estimate	0.1	0.1	0.1	0.1
		V( $10^{-6}$ )	9.00	9.00	9.00	9.00
	NSRS	Estimate	0.102	0.102	0.101	0.101
		V( $10^{-6}$ )	5.30	4.19	4.24	4.18
	UES	Estimate	0.20	0.18	0.16	0.12
A	SRS	Estimate	0.1	0.1	0.1	0.1
		V( $10^{-6}$ )	9.00	9.00	9.00	9.00
	NSRS	Estimate	0.102	0.101	0.10	0.10
		V( $10^{-6}$ )	7.04	5.61	5.58	5.05
	UES	Estimate	0.16	0.19	0.16	0.12

Table 2. Comparison of Class Rate Estimation in Multiclass Classification Experiments. Where M represents motorcycle, A represents airplane, V represents variance of estimate.

Table 2 summarizes class rate estimation in multi-class classification problems, echoing Section 4.1. Simple random sampling and Neyman stratified sampling yield unbiased estimates around 0.1, while uncertainty entropy sampling lacks unbiasedness. Neyman stratified sampling shows lower variances on positive classes. Its optimization effect improves with cumulative training volume increasing. In multi-class problems, Neyman stratified sampling’s optimization effect is slightly lower than in binary classification. These results affirm the effectiveness of Neyman stratified random sampling for multi-class classification, aligning with Section 3.4’s theory—it optimizes each positive class target individually but doesn’t guarantee optimal results for every target.

4.6. Application

In this section, we illustrate the practical application of the proposed approach in disaster assessment using real xBD dataset. The dataset consists of 22,068 color images labeled with 19 events, suitable for disaster localization and assessment (Gupta et al., 2019). We use the Train dataset, dividing it into a 4:1 ratio for training and testing. We extract building polygons from each original image, resizing them to 32 pixels * 32 pixels for the training set. Focusing on Hurricane Harvey and Hurricane Matthew data, we perform a 4-class disaster assessment using Alexnet8 as the base model (K=4). The positive classes (M=3) include Minor damage, Major damage, and Destroyed.

Figure 8 shows a notable improvement with Neyman stratified random sampling compared to the baseline of simple random sampling. It also slightly outperforms uncertainty entropy sampling.

The result shows the proposed approach’s sample selection during model training provides unbiased estimates of true damage rates, with estimated variance 80%-90% lower than simple random sampling. Although the optimization degree is slightly lower than on open datasets, attributed to the greater difficulty and lower accuracy of real datasets. In Figure 9, the proposed approach significantly outperforms passive learning with simple random sampling and slightly surpasses the traditional active learning method with uncertainty entropy strategy in two disaster events.

Overall, the proposed approach has practical value. It enables rapid acquisition of unbiased estimates with high confidence, aiding rescue personnel in promptly making initial plans. Moreover, collected samples swiftly enhance model performance for more extensive disaster assessments, supporting further rescue planning.

5. Conclusion

This paper introduces an active learning method that combines active learning and probability sampling, using stratified random sampling with Neyman allocation, minimizing the annotation costs while addressing class rate estimation and model training tasks .

In class rate estimation, the proposed approach provides unbiased estimation of the overall class rate with lower variance compared to simple random sampling. This allows for equivalent results with only 30%-60% of the annotation cost, whcih has great application value in scenarios that rely on sample labeling. The proposed method shows notable improvement in model training compared to passive learning with simple random sampling. However, it slightly falls behind the traditional active learning strategy (uncertainty entropy sampling), as the proposed method addresses both class rate estimation and model training. As model complexity increases, the performance gap narrows . The paper shows, both theoretically and through experiments, that the proposed method, with its inclusion of overall distribution information, can alleviate ”sampling bias.” In practical scenarios, the method performs well in the cold-start problem. Its real-world applicability is evident in maintaining great performance on the xBD dataset.

The study identified limitations and future prospects of the proposed method. The implementation of the Neyman stratified random sampling query strategy relies on model prediction scores as the stratification dimension in each iteration. Therefore, the proposed approach is only suitable for explicit classification models that output model probabilities. The study acknowledges that the proposed approach and traditional uncertainty-based active learning methods each have their advantages, suggesting future research directions that explore the fusion of these two approaches.

References

(1)
Angluin (1988) Dana Angluin. 1988. Queries and Concept Learning. Machine Learning 2, 4 (1988), 319–342.
Bai et al. (2017) Yanbing Bai, Chang Gao, Sameer Singh, Magaly Koch, Bruno Adriano, Erick Mas, and Shunichi Koshimura. 2017. A framework of rapid regional tsunami damage recognition from post-event TerraSAR-X imagery using deep neural networks. IEEE Geoscience and Remote Sensing Letters 15, 1 (2017), 43–47.
Bai et al. (2023) Yanbing Bai, Jinhua Su, Yulong Zou, and Bruno Adriano. 2023. Knowledge distillation based lightweight building damage assessment using satellite imagery of natural disasters. GeoInformatica 27, 2 (2023), 237–261.
Balcan et al. (2007) Maria Florina Balcan, Andrei Z. Broder, and Tong Zhang. 2007. Margin Based Active Learning. lecture notes in computer science (2007).
Bonafilia et al. (2020) Derrick Bonafilia, Beth Tellman, Tyler Anderson, and Erica Issenberg. 2020. Sen1Floods11: A georeferenced dataset to train and test deep learning flood algorithms for sentinel-1. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. 210–211.
Chu and Lin (2016) Hong-Min Chu and Hsuan-Tien Lin. 2016. Can Active Learning Experience Be Transferred?. In 2016 IEEE 16th International Conference on Data Mining (ICDM). 841–846. https://doi.org/10.1109/ICDM.2016.0100
Cohn et al. (1994) David Cohn, Les Atlas, and Richard Ladner. 1994. Improving generalization with active learning. Machine Learning 15-2 (1994).
Cohn et al. (1996) David A. Cohn, Zoubin Ghahramani, and Michael I. Jordan. 1996. Active learning with statistical models. J. Artif. Int. Res. 4, 1 (mar 1996), 129–145.
Dasgupta and Hsu (2008) Sanjoy Dasgupta and Daniel Hsu. 2008. Hierarchical sampling for active learning. In Machine Learning, Proceedings of the Twenty-Fifth International Conference (ICML 2008), Helsinki, Finland, June 5-9, 2008.
Gao et al. (2020) Mingfei Gao, Zizhao Zhang, Guo Yu, Sercan Ö. Arık, Larry S. Davis, and Tomas Pfister. 2020. Consistency-Based Semi-Supervised Active Learning: Towards Minimizing Labeling Cost. In Computer Vision – ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part X (Glasgow, United Kingdom). Springer-Verlag, Berlin, Heidelberg, 510–526. https://doi.org/10.1007/978-3-030-58607-2_30
Geng et al. (2008) Bo Geng, Linjun Yang, Zheng Jun Zha, Chao Xu, and Xian Sheng Hua. 2008. Unbiased active learning for image retrieval. IEEE Computer Society (2008).
Guo et al. (2017) Chuan Guo, Geoff Pleiss, Yu Sun, and Kilian Q. Weinberger. 2017. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning - Volume 70 (Sydney, NSW, Australia) (ICML’17). JMLR.org, 1321–1330.
Gupta et al. (2019) Ritwik Gupta, Richard Hosfelt, Sandra Sajeev, Nirav Patel, Bryce Goodman, Jigar Doshi, Eric Heim, Howie Choset, and Matthew Gaston. 2019. xBD: A Dataset for Assessing Building Damage from Satellite Imagery. (2019).
Hauptmann et al. (2006) Alexander G. Hauptmann, Wei Hao Lin, Rong Yan, Jun Yang, and Ming Yu Chen. 2006. Extreme video retrieval: joint maximization of human and computer performance. In Acm International Conference on Multimedia.
He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep Residual Learning for Image Recognition. In IEEE Conference on Computer Vision and Pattern Recognition.
Hoi et al. (2006) Steven C. H. Hoi, Rong Jin, Jianke Zhu, and Michael R. Lyu. 2006. Batch Mode Active Learning and Its Application to Medical Image Classiflcation. In Machine Learning, Twenty-third International Conference, Pittsburgh, Pennsylvania, Usa, June.
Joshi et al. (2009) Ajay J. Joshi, Fatih Porikli, and Nikolaos Papanikolopoulos. 2009. Multi-class active learning for image classification. In 2009 IEEE Conference on Computer Vision and Pattern Recognition. 2372–2379. https://doi.org/10.1109/CVPR.2009.5206627
Klidbary et al. (2017) Sajad Haghzad Klidbary, Saeed Bagheri Shouraki, Aboozar Ghaffari, and Soroush Sheikhpour Kourabbaslou. 2017. Outlier robust fuzzy active learning method (ALM). In 2017 7th International Conference on Computer and Knowledge Engineering (ICCKE).
Konyushkova et al. (2017) Ksenia Konyushkova, Sznitman Raphael, and Pascal Fua. 2017. Learning Active Learning from Data. In Proceedings of the 31st International Conference on Neural Information Processing Systems (Long Beach, California, USA) (NIPS’17). Curran Associates Inc., Red Hook, NY, USA, 4228–4238.
Krizhevsky et al. (2017) Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. 2017. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 60, 6 (may 2017), 84–90. https://doi.org/10.1145/3065386
Lecun et al. (1998) Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner. 1998. Gradient-based learning applied to document recognition. Proc. IEEE 86, 11 (1998), 2278–2324. https://doi.org/10.1109/5.726791
Lee et al. (2020) Jihyeon Lee, Joseph Z. Xu, Kihyuk Sohn, Wenhan Lu, David Berthelot, Izzeddin Gur, Pranav Khaitan, Ke Huang, Kyriacos M. Koupparis, and Bernhard Kowatsch. 2020. Assessing Post-Disaster Damage from Satellite Imagery using Semi-Supervised Learning Techniques. ArXiv abs/2011.14004 (2020). https://api.semanticscholar.org/CorpusID:227227614
Lewis and Gale (1994) David D. Lewis and William A. Gale. 1994. A Sequential Algorithm for Training Text Classifiers. In Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (Dublin, Ireland) (SIGIR ’94). Springer-Verlag, Berlin, Heidelberg, 3–12.
Melville et al. (2005) Prem Melville, Stewart M. Yang, Maytal Saar-Tsechansky, and Raymond Mooney. 2005. Active Learning for Probability Estimation Using Jensen-Shannon Divergence. In Proceedings of the 16th European Conference on Machine Learning (Porto, Portugal) (ECML’05). Springer-Verlag, Berlin, Heidelberg, 268–279. https://doi.org/10.1007/11564096_28
Nguyen and Smeulders (2004) Hieu T. Nguyen and Arnold Smeulders. 2004. Active learning using pre-clustering. (2004).
Pan and Yang (2010) Sinno Jialin Pan and Qiang Yang. 2010. A Survey on Transfer Learning. IEEE Transactions on Knowledge and Data Engineering 22, 10 (2010), 1345–1359. https://doi.org/10.1109/TKDE.2009.191
Ren et al. (2021) Pengzhen Ren, Yun Xiao, Xiaojun Chang, Po-Yao Huang, Zhihui Li, Brij B. Gupta, Xiaojiang Chen, and Xin Wang. 2021. A Survey of Deep Active Learning. ACM Comput. Surv. 54, 9, Article 180 (oct 2021), 40 pages. https://doi.org/10.1145/3472291
Roth and Small (2006) Dan Roth and Kevin Small. 2006. Margin-Based Active Learning for Structured Output Spaces. lecture notes in computer science (2006).
Rudner et al. (2019) Tim GJ Rudner, Marc Rußwurm, Jakub Fil, Ramona Pelich, Benjamin Bischke, Veronika Kopačková, and Piotr Biliński. 2019. Multi3net: segmenting flooded buildings via fusion of multiresolution, multisensor, and multitemporal satellite imagery. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 33. 702–709.
Saar-Tsechansky and Provost (2004) Maytal Saar-Tsechansky and Foster Provost. 2004. Active Sampling for Class Probability Estimation and Ranking. Mach. Learn. 54, 2 (feb 2004), 153–178. https://doi.org/10.1023/B:MACH.0000011806.12374.c3
Settles (2010) Burr Settles. 2010. Active Learning Literature Survey. University of Wisconsinmadison (2010).
Settles and Craven (2008) Burr Settles and Mark Craven. 2008. An Analysis of Active Learning Strategies for Sequence Labeling Tasks. In 2008 Conference on Empirical Methods in Natural Language Processing, EMNLP 2008, Proceedings of the Conference, 25-27 October 2008, Honolulu, Hawaii, USA, A meeting of SIGDAT, a Special Interest Group of the ACL.
Shannon (1948) C E Shannon, A. 1948. mathematical theory of communication. mathematical theory of communication.
Simonyan and Zisserman (2014) Karen Simonyan and Andrew Zisserman. 2014. Very Deep Convolutional Networks for Large-Scale Image Recognition. Computer Science (2014).
Tang and Huang (2019) Ying-Peng Tang and Sheng-Jun Huang. 2019. Self-Paced Active Learning: Query the Right Thing at the Right Time. Proceedings of the AAAI Conference on Artificial Intelligence 33, 01 (Jul. 2019), 5117–5124. https://doi.org/10.1609/aaai.v33i01.33015117
Van Etten et al. (2018) Adam Van Etten, Dave Lindenbaum, and Todd M Bacastow. 2018. Spacenet: A remote sensing dataset and challenge series. arXiv preprint arXiv:1807.01232 (2018).
Wang and Shang (2014) Dan Wang and Yi Shang. 2014. A new active labeling method for deep learning. In 2014 International Joint Conference on Neural Networks (IJCNN). 112–119. https://doi.org/10.1109/IJCNN.2014.6889457
Xia et al. (2022) Zaishuo Xia, Zelin Li, Yanbing Bai, Jinze Yu, and Bruno Adriano. 2022. Self-supervised learning for building damage assessment from large-scale xBD satellite imagery benchmark datasets. In International Conference on Database and Expert Systems Applications. Springer, 373–386.
Xie et al. (2021) Binhui Xie, Longhui Yuan, Shuang Li, Chi Harold Liu, Xinjing Cheng, and Guoren Wang. 2021. Active Learning for Domain Adaptation: An Energy-based Approach. CoRR abs/2112.01406 (2021). arXiv:2112.01406 https://arxiv.org/abs/2112.01406
Xu et al. (2019a) Joseph Z Xu, Wenhan Lu, Zebo Li, Pranav Khaitan, and Valeriya Zaytseva. 2019a. Building damage detection in satellite imagery using convolutional neural networks. arXiv preprint arXiv:1910.06444 (2019).
Xu et al. (2019b) Joseph Z Xu, Wenhan Lu, Zebo Li, Pranav Khaitan, and Valeriya Zaytseva. 2019b. Building Damage Detection in Satellite Imagery Using Convolutional Neural Networks. arXiv (2019).
Yang et al. (2015) Yi Yang, Zhigang Ma, Feiping Nie, Xiaojun Chang, and Alexander G. Hauptmann. 2015. Multi-Class Active Learning by Uncertainty Sampling with Diversity Maximization. Int. J. Comput. Vision 113, 2 (jun 2015), 113–127. https://doi.org/10.1007/s11263-014-0781-x
Yoo and Kweon (2019) Donggeun Yoo and In So Kweon. 2019. Learning Loss for Active Learning. In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 93–102. https://doi.org/10.1109/CVPR.2019.00018
Zhang and Chen (2002) Cha Zhang and Tsuhan Chen. 2002. An active learning framework for content-based information retrieval. IEEE Transactions on Multimedia 4, 2 (2002), 260–268. https://doi.org/10.1109/TMM.2002.1017738
Zhang et al. (2022) Wenqiao Zhang, Lei Zhu, James Hallinan, Andrew Makmur, Shengyu Zhang, Qingpeng Cai, and Beng Chin Ooi. 2022. BoostMIS: Boosting Medical Image Semi-supervised Learning with Adaptive Pseudo Labeling and Informative Active Annotation. arXiv e-prints (2022).
Zhou et al. (2017) Zongwei Zhou, Jae Shin, Lei Zhang, Suryakanth Gurudu, Michael Gotway, and Jianming Liang. 2017. Fine-Tuning Convolutional Neural Networks for Biomedical Image Analysis: Actively and Incrementally. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 4761–4772. https://doi.org/10.1109/CVPR.2017.506