Towards Faithful Neural Table-to-Text Generation with
Content-Matching Constraints
Abstract
Text generation from a knowledge base aims to translate knowledge triples to natural-language descriptions. Most existing methods ignore the faithfulness between a generated text description and the original table, leading to generated information that goes beyond the content of the table. In this paper, for the first time, we propose a novel Transformer-based generation framework to achieve the goal. The core techniques in our method to enforce faithfulness include a new table-text optimal-transport matching loss and a table-text embedding similarity loss based on the Transformer model. Furthermore, to evaluate faithfulness, we propose a new automatic metric specialized to the table-to-text generation problem. We also provide detailed analysis on each component of our model in our experiments. Automatic and human evaluations show that our framework can significantly outperform state-of-the-art by a large margin.
1 Introduction

Understanding structured knowledge, e.g., information encoded in tables, and automatically generating natural-language descriptions is an important task in the area of Natural Language Generation. Table-to-text generation helps making knowledge elements and their connections in tables easier to comprehend by human. There have been a number of practical application scenarios in this field, for example, weather report generation, NBA news generation, biography generation and medical-record description generation Liang et al. (2009); Barzilay and Lapata (2005); Lebret et al. (2016a); Cawsey et al. (1997).
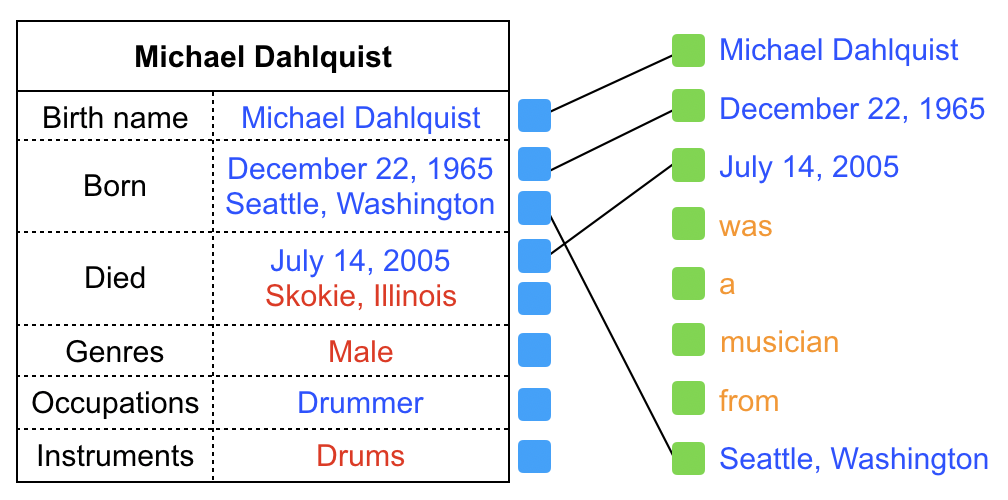
Most existing methods for table-to-text generation are based on an encoder-decoder framework Sutskever et al. (2014); Bahdanau et al. (2015), most of which are RNN-based Sequence-to-Sequence (Seq2Seq) models Lebret et al. (2016b); Liu et al. (2018); Wiseman et al. (2018); Ma et al. (2019); Wang et al. (2018); Liu et al. (2019a). Though significant progress has been achieved, we advocate two key problems in existing methods. Firstly, because of the intrinsic shortage of RNN, RNN-based models are not able to capture long-term dependencies, which would lose important information reflected in a table. This drawback prevents them from being applied to larger tables, for example, a table describing a large Knowledge Base Wang et al. (2018). Secondly, little work has focused on generating faithful text descriptions, which is defined, in this paper, as the level of matching between a generated text sequence and the corresponding table content. An unfaithful generation example is illustrated in Figure 1. The training objectives and evaluation metrics of existing methods encourage generating texts to be as similar as possible to reference texts. One problem with this is that the reference text often contains extra information that is not presented in the table because human beings have external knowledge beyond the input table when writing the text, or it even misses some important information in the table Dhingra et al. (2019) due to the noise from the dataset collection process. As a result, unconstrained training with such mis-matching information usually leads to hallucinated words or phrases in generated texts, making them unfaithful to the table and thus harmful in practical uses.
In this paper, we aim to overcome the above problems to automatically generate faithful texts from tables. In other words, we aim to produce the writing that a human without any external knowledge would do given the same table data as input. In contrast to existing RNN-based models, we leverage the powerful attention-based Transformer model to capture long-term dependencies and generate more informative paragraph-level texts. To generate descriptions faithful to tables, two content-matching constraints are proposed. The first one is a latent-representation-level matching constraint encouraging the latent semantics of the whole text to be consistent with that of the whole table. The second one is an explicit entity-level matching scheme, which utilizes Optimal-Transport (OT) techniques to constrain key words of a table and the corresponding text to be as identical as possible. To evaluate the faithfulness, we also propose a new PARENT-T metric evaluating the content matching between texts and tables, based on the recently proposed PARENT Dhingra et al. (2019) metric. We train and evaluate our model on a large-scale knowledge base dataset Wang et al. (2018). Automatic and human evaluations both show that our method achieve the state-of-the-art performance, and can generates paragraph-level descriptions much more informative and faithful to input tables.
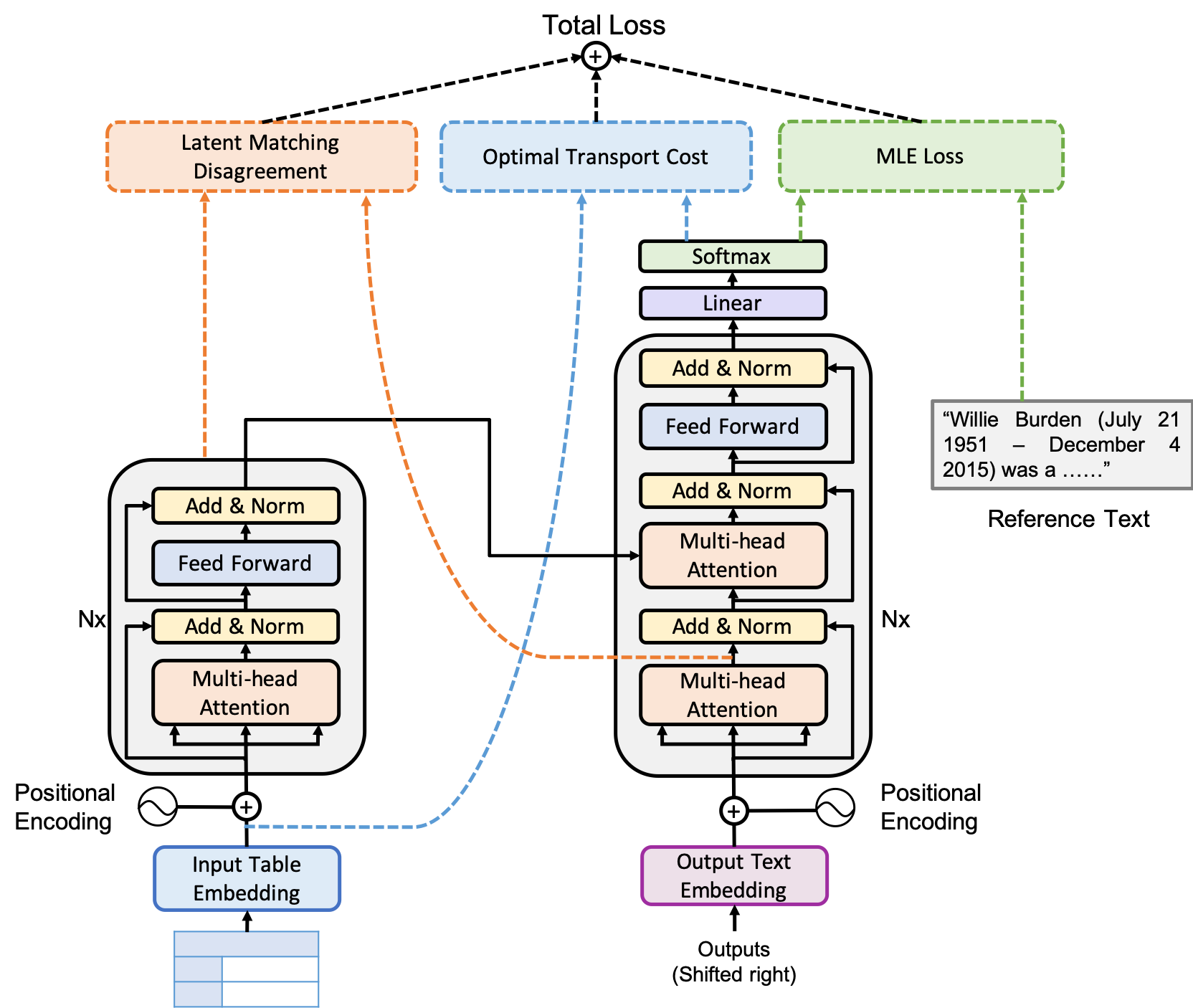
2 The Proposed Method
The task of text generation for a knowledge base is to take the structured table, , as input, and outputs a natural-language description consisting of a sequence of words that is faithful to the input table. Here, denotes the slot type for the row, and denotes the slot value for the row in a table.
Our model adopts the powerful Transformer model Vaswani et al. (2017) to translate a table to a text sequence. Specifically, the Transformer is a Seq2Seq model, consisting of an encoder and a decoder. Our proposed encoder-to-decoder Transformer model learns to estimate the conditional probability of a text sequence from a source table input in an autoregressive way:
| (1) |
where is the Transformer parameters and denotes the decoded words from previous steps.
Existing models for table-to-text generation either only focus on generating text to match the reference text Liu et al. (2018); Ma et al. (2019), or only require a generated text sequence to be able to cover the input table Wang et al. (2018). However, as the only input information is the table, the generated text should be faithful to the input table as much as possible. Therefore, we propose two constraint losses, including a table-text disagreement constraint loss and a constrained content matching loss with optimal transport, to encourage the model to learn to match between the generated text and the input table faithfully. Figure 2 illustrates the overall architecture of our model. In summary, our model loss contains three parts: 1) a maximum likelihood loss (green) that measures the matching between a model prediction and the reference text sequence; 2) a latent feature matching disagreement loss (orange) that measures the disagreement between a table encoding and the corresponding reference-text encoding; and 3) an optimal-transport loss (blue) matching the key words of an input table and the corresponding generated text.
2.1 Table Representation
The entities of a table simply consists of Slot Type and Slot Value pairs. To apply the Transformer model, we first linearize input tables into sequences. Slot types and slot values are separated by special tokens “” and “”. As an example, the table in Figure 1 is converted into a sequence: . We note that encoding a table in this way might lose some high-order structure information presented in the original knowledge graph. However, our knowledge graph is relatively simple. According to our preliminary studies, a naive combination of feature extracted with graph neural networks Beck et al. (2018) does not seem helpful. As a result, we only rely on the sequence representation in this paper.
2.2 The Base Objective
Our base objective comes from the standard Transformer model, which is defined as the negative log-likelihood loss of a target sentence given its input , i.e.,
| (2) |
with defined in (1).
2.3 Faithfulness Modeling with a Table-Text Disagreement Constraint Loss
One key element of our model is to enforce a generated text sequence to be consistent with (or faithful to) the table input. To achieve this, we propose to add some constraints so that a generated text sequence only contains information from the table. Our first idea is inspired by related work in machine translation Yang et al. (2019). Specifically, we propose to constrain a table embedding to be close to the corresponding target sentence embedding. Since the embedding of a text sequence (or the table) in our model is also represented as a sequence, we propose to match the mean embeddings of both sequences. In fact, the mean embedding has been proved to be an effective representation for the whole sequence in machine translation Yang et al. (2019); Wang et al. (2017). Let and be the mean embeddings of a table and the target text embeddings in our Transformer-based model, respectively. A table-target sentence disagreement loss is then defined as
| (3) |
2.4 Faithfulness Modeling with Constrained Content Matching via Optimal Transport
Our second strategy is to explicitly match the key words in a table and the corresponding generated text. In our case, key words are defined as nouns, which can be easily extracted with existing tools such as NLTK Loper and Bird (2002). To match key words, a mis-matching loss should be defined. Such a mis-matching loss could be non-differentiable, e.g., when the loss is defined as the number of matched entities. In order to still be able to learn by gradient descent, one can adopt the policy gradient algorithm to deal with the non-differentiability. However, policy gradient is known to exhibit high variance. To overcome this issue, we instead propose to perform optimization via optimal transport (OT), inspired by the recent techniques in Chen et al. (2019a).
Optimal-Transport Distance
In the context of text generation, a generated text sequence, , can be represented as a discrete distribution , where and , denotes a spike distribution located at . Given two discrete distributions and , written as and , respectively, the OT distance between and is defined as the solution of the following maximum network-flow problem:
| (4) |
where is the cost of moving to (matching and ). In this paper, we use the cosine distance between the two word-embedding vectors of and , defined as . is the set of joint distributions such that the two marginal distributions equal to and , respectively.
Exact minimization over in the above problem is in general computational intractable Genevay et al. (2018). Therefore, we adopt the recently proposed Inexact Proximal point method for Optimal Transport (IPOT) Xie et al. (2018) as an approximation. The details of the IPOT algorithm are shown in Appendix C.
Constrained Content Matching via OT
To apply the OT distance to our setting, we need to first specify the atoms in the discrete distributions. Since nouns typically are more informative, we propose to match the nouns in both an input table and the decoded target sequence. We use NLTK Loper and Bird (2002) to extract the nouns that are then used for computing the OT loss. In this way, the computational cost can also be significantly reduced comparing to matching all words.
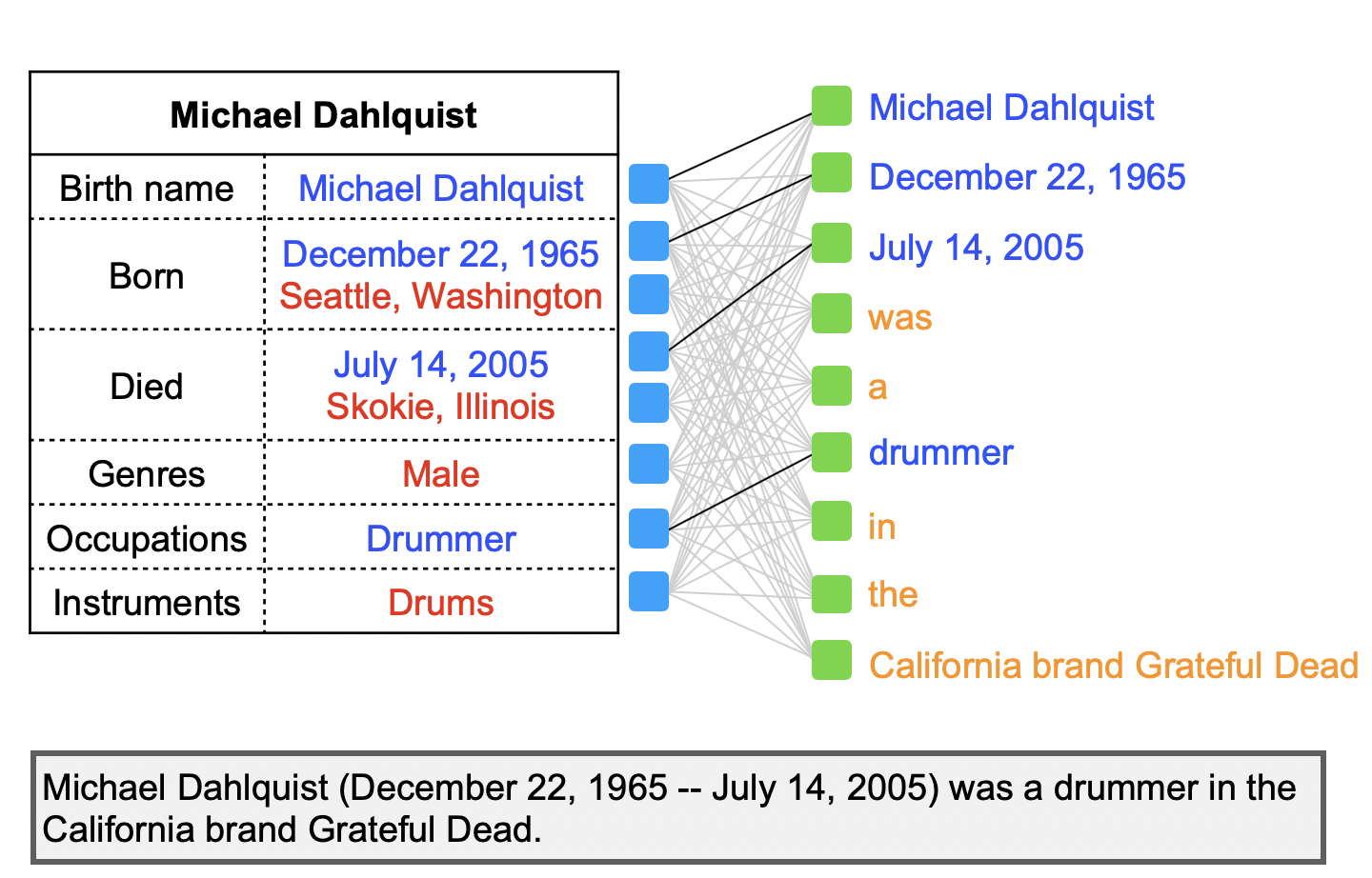
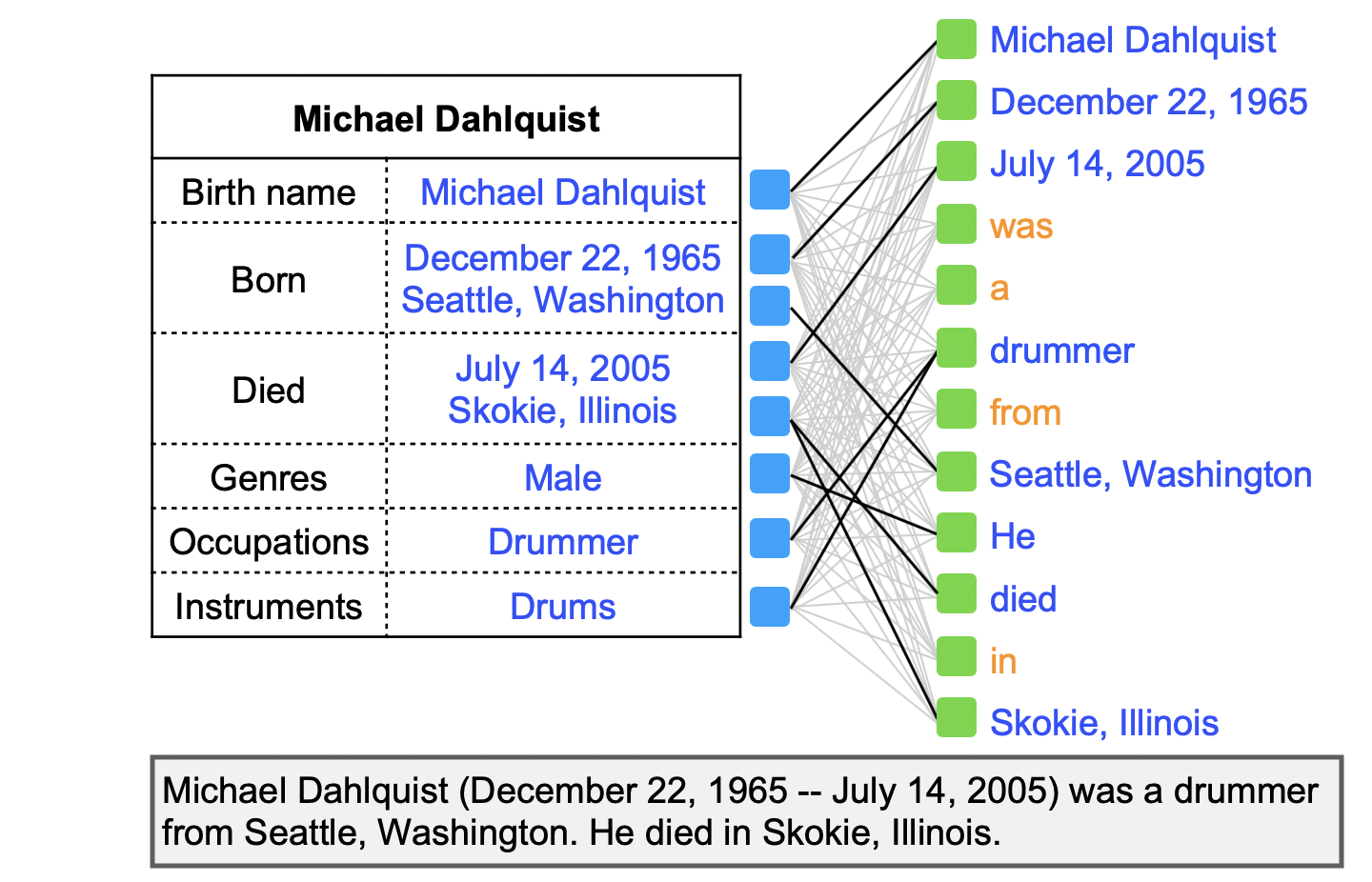
The OT loss can be used as a metric to measure the goodness of the match between two sequences. To illustrate the motivation of applying the OT loss to our setting, we provide an example illustrated in Figure 3, where we try to match the table with the two generated text sequences. On the left plot, the generated text sequence contains “California brand Grateful Dead”, which is not presented in the input table. Similarly, and the phrases ”Seattle, Washington” and “Skokie Illinois” in the table are not covered by the generated text. Consequently, the resulting OT loss will be high. By contrast, on the right plot, the table contains all information in the text, and all the phrases in the table are also covered well by the generated text, leading to a low OT loss. As a result, optimizing over the OT loss in (4) would enforce faithful matching between a table and its generated text.
Optimization via OT
When optimizing the OT loss with the IPOT algorithm, the gradients of the OT loss is required to be able to propagate back to the Transformer component. In other words, this requires gradients to flow back from a generated sentence. Note that a sentence is generated by sampling from a multinomial distribution, whose parameter is the Transformer decoder output represented as a logit vector for each word in the vocabulary. This sampling process is unfortunately non-differentiable. To enable back-propagation, we follow Chen et al. (2019a) and use the Soft-argmax trick to approximate each word with the corresponding soft-max output.
To further reduce the number of parameters and improve the computational efficiency, we adopt the factorized embedding parameterization proposed recently Lan et al. (2019). Specifically, we decompose a word embedding matrix of size into the product of two matrices of sizes and , respectively. In this way, the parameter number of the embedding matrices could be significantly reduced as long as is to be much smaller than .
2.5 The Final Objective
Combing all the above components, the final training loss of our model is defined as:
| (5) |
where and controls the relative importance of each component of the loss function.
2.6 Decoder with a Copy Mechanism
To enforce a generated sentence to stick to the words presented in the table as much as possible, we follow See et al. (2017) to employ a copy mechanism when generating an output sequence. Specifically, let be the output of the Transformer decoder. is a discrete distribution over the vocabulary words and denotes the probabilities of generating the next word. The standard methods typically generate the next word by directly sampling from . In the copy mechanism, we instead generate the next word with the following discrete distribution:
where is the probability of switching sampling between and , with learnable parameters and as the hidden state from the Transformer decoder for the -th word. is the attention weights (probability) returned from the encoder-decoder attention module in the Transformer. Specifically, when generating the current word , the encoder-decoder attention module calculates the probability vector denoting the probabilities of attending to each word in the input table. Note that the probabilities of the words not presented in the table are set to zero.
3 Experiments
We conduct experiments to verify the effectiveness and superiority of our proposed approach against related methods.
3.1 Dataset
Our model is evaluated on the large-scale knowledge-base Wikiperson dataset released by Wang et al. (2018). It contains 250,186, 30,487, and 29,982 table-text pairs for training, validation, and testing, respectively. Compared to the WikiBio dataset used in previous studies Lebret et al. (2016b); Liu et al. (2018); Wiseman et al. (2018); Ma et al. (2019) whose reference text only contains one-sentence descriptions, this dataset contains multiple sentences for each table to cover as many facts encoded in the input structured knowledge base as possible.
3.2 Evaluation Metrics
For automatic evaluation, we apply the widely used evaluation metrics including the standard BLEU-4 Papineni et al. (2002), METEOR Denkowski and Lavie (2014) and ROUGE Lin (2004) scores to evaluate the generation quality. Since these metrics rely solely on the reference texts, they usually show poor correlations with human judgments when the references deviate too much from the table. To this end, we also apply the PARENT Dhingra et al. (2019) metric that considers both the reference texts and table content in evaluations. To evaluate the faithfulness of the generated texts, we further modify the PARENT metric to measure the level of matching between generated texts and the corresponding tables. We denote this new metric as PARENT-T. Please see Appendix A for details. Note that the precision in PARENT-T corresponds to the percentage of words in a text sequence that co-occur in the table; and the recall corresponds to the percentage of words in a table that co-occur in the text.
| BLEU | METEOR | ROUGE | PARENT | PARENT-T | |
|---|---|---|---|---|---|
| Wang et al. (2018) | 16.20 | 19.01 | 40.10 | 51.03 | 54.22 |
| Seq2Seq Bahdanau et al. (2015) | 22.24 | 19.50 | 39.49 | 43.41 | 44.55 |
| Pointer-Generator See et al. (2017) | 19.32 | 19.88 | 40.68 | 49.52 | 52.62 |
| Structure-Aware Seq2Seq Liu et al. (2018) | 22.76 | 20.27 | 39.32 | 46.47 | 48.47 |
| Ours | 24.56 | 22.37 | 42.40 | 53.06 | 56.10 |
| P-recall | P-precision | PT-recall | PT-precision | |
|---|---|---|---|---|
| Wang et al. (2018) | 44.83 | 63.92 | 84.34 | 41.10 |
| Seq2Seq Bahdanau et al. (2015) | 41.80 | 49.09 | 76.07 | 33.13 |
| Pointer-Generator See et al. (2017) | 44.09 | 61.73 | 81.65 | 42.03 |
| Structure-Aware Seq2Seq Liu et al. (2018) | 46.34 | 51.18 | 83.84 | 35.99 |
| Ours | 48.83 | 62.86 | 85.21 | 43.52 |
| Copy | EF | OT (N/W) | latent | BLEU | METEOR | ROUGE | PARENT | PARENT-T | params |
| ✗ | ✗ | ✗ | ✗ | 24.49 | 22.01 | 40.98 | 48.31 | 49.89 | 98.92M |
| ✓ | ✗ | ✗ | ✗ | 24.57 | 22.43 | 42.26 | 51.87 | 54.29 | 98.92M |
| ✓ | ✓ | ✗ | ✗ | 25.07 | 22.38 | 42.37 | 51.76 | 54.36 | 45.94M |
| ✓ | ✓ | ✗ | ✓ | 23.86 | 22.08 | 42.65 | 52.72 | 55.30 | 45.94M |
| ✓ | ✓ | W | ✗ | 24.64 | 22.39 | 42.52 | 52.77 | 55.46 | 45.94M |
| ✓ | ✓ | N | ✗ | 25.29 | 22.60 | 42.25 | 52.74 | 55.80 | 45.94M |
| ✓ | ✓ | N | ✓ | 24.56 | 22.37 | 42.40 | 53.06 | 56.10 | 45.94M |
| Precision | Recall | F-1 measure | Fluency | Grammar | |
|---|---|---|---|---|---|
| Wang et al. (2018) | 76.3 | 62.1 | 68.02 | 2.98 | 3.06 |
| Seq2Seq Bahdanau et al. (2015) | 70.3 | 60.8 | 66.16 | 2.86 | 2.88 |
| Pointer-Generator See et al. (2017) | 76.6 | 61.5 | 67.95 | 3.03 | 3.02 |
| Structure-Aware Seq2Seq Liu et al. (2018) | 75.2 | 61.7 | 67.69 | 2.92 | 2.83 |
| Ours | 79.8 | 65.3 | 71.56 | 3.01 | 3.10 |
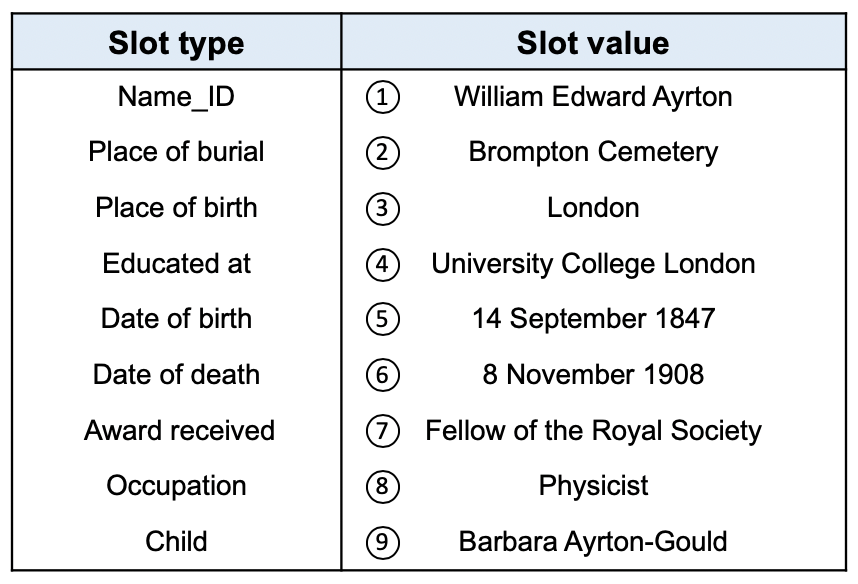
| Model | Miss | Generated texts |
|---|---|---|
| Wang et al. (2018) | 9 | William Edward Ayrton Fellow of the Royal Society ( 14 September 1847 – 8 November 1908 ) was a British Physicist . Brompton Cemetery he was born in London the son of Sir Thomas and his wife Mary ( née Fleming ) . he was educated at University College School and University College London . |
| Pointer generator | 2, 9 | William Edward Ayrton-Gould Fellow of the Royal Society (14 September 1847 – 8 November 1908) was an English Physicist who was born in London and was educated at Brompton College and University College London . he died in London on 8 November 1908 . William was elected a Fellow of the Royal Society in 1902. |
| Seq2Seq | 1, 2, 3, 9 | William Edward Sandys Fellow of the Royal Society (14 September 1847 – 8 November 1908) was a British Physicist . he was educated at the University College London and the University College London . he was a Fellow of the Royal Society and a Fellow of the Royal Society. |
| Structure-Aware | 1, 2, 9 | William Edward Keeler Fellow of the Royal Society (14 September 1847 – 8 November 1908) was a British Physicist and Physicist . he was elected a Fellow of the Royal Society in 1889 and was a member of the Royal Society of London and the Royal Society of London and the Royal Society of London . he was educated at the University College London and at the University College London where he was a pupil of the chemist William. |
| Ours | None | William Edward Ayrton Fellow of the Royal Society (14 September 1847 – 8 November 1908) was an English Physicist . William was born in London and educated at University College London. he is buried in Brompton Cemetery London . he was elected a Fellow of the Royal Society in 1901. he was the father of Barbara Ayrton-Gould . |
3.3 Baseline Models
We compare our model with several strong baselines, including
-
•
The vanilla Seq2Seq attention model Bahdanau et al. (2015).
-
•
The method in Wang et al. (2018): The state-of-art model on the Wikiperson dataset.
-
•
The method in Liu et al. (2018): The state-of-the-art method on the WikiBio dataset.
-
•
The pointer-generator See et al. (2017): A Seq2Seq model with attention, copying and coverage mechanism.
3.4 Implementation Details
Our implementation is based on OpenNMT Klein et al. (2017). We train our models end-to-end to minimize our objective function with/without the copy mechanism. The vocabulary is limited to the 50, 000 most common words in the training dataset. The hidden units of the multi-head component and the feed-forward layer are set to 2048. The baseline embedding size is 512. Following Lan et al. (2019), the embedding size with embedding factorization is set to be 128. The number of heads is set to 8, and the number of Transformer blocks is 3. Beam size is set to be 5. Label smoothing is set to 0.1.
For the optimal-transport based regularizer, we first train the model without OT for about 20,000 steps, then fine tune the network with OT for about 10,000 steps. We use the Adam Kingma and Ba (2015) optimizer to train the models. We set the hyper-parameters of Adam optimizer accordingly, including the learning rate = 0.00001, and the two momentum parameters, batch size = 4096 (tokens) and .
3.5 Results
Table 1 and 2 show the experiment results in terms of different evaluation metrics compared with different baselines. “Ours” means our proposed model with components of copy mechanism, embedding factorization, OT-matching with nouns, and latent similarity loss111The result of the method by Wang et al. (2018) is different from the score reported in their paper, as we use their publicly released code https://github.com/EagleW/Describing_a_Knowledge_Base and data that is three times larger than the original 106,216 table-text pair data used in the paper. We have confirmed the correctness of our results with the author.. We can see that our model outperforms existing models in all of the automatic evaluation scores, indicating high quality of the generated texts. The superiority of the PARENT-T scores (in terms of precision and recall) indicates that the generated text from our model is more faithful than others. Example outputs from different models are shown in Table 5 with an input table shown in Figure 4. In this example, our model covers all the entities in the input, while all other models miss some entities. Furthermore, other models hallucinate some information that does not appear in the input, while our model generates almost no extra information other than that in the input. These results indicate the faithfulness of our model. More examples are shown in Appendix E.
3.6 Ablation Study
We also conduct extensive ablation studies to better understand each component of our model, including the copy mechanism, embedding factorization, optimal transport constraint loss, and latent similarity loss. Table 3 shows the results in different evaluation metrics.
Effect of copy mechanism
The first and second rows in Table 3 demonstrate the impacts of the copy mechanism. It is observed that with the copy mechanism, one can significantly improve the performance in all of the automatic metrics, especially on the faithfulness reflected by the PARENT-T score.
Effect of embedding factorization
We compare our model with the one without embedding factorization. The comparisons are shown in the second and third rows of Table 3. We can see that with embedding factorization, around half of the parameters can be reduced, while comparable performance can still be maintained.
Effect of table-text embedding similarity loss
We also test the model by removing the table-text embedding similarity loss component. The third and fourth rows in Table 3 summarize the results. With the table-text embedding similarity loss, the BLEU and METEOR scores drop a little, but the PARENT and PARENT-T scores improve over the model without the loss. This is reasonable because the loss aims at improving faithfulness of generated texts, reflected by the PARENT-T score.
Effect of the OT constraint loss
We further compare the performance of the model (a) without using OT loss, (b) with using the whole table and text to compute OT, and (c) with using the extracted nouns from both table and text to compute OT. Results are presented in the third, fifth, and sixth rows of Table 3, respectively. The model with the OT loss improve performance on almost all scores, especially on the PARENT-T score. Furthermore, with only using the nouns to compute the OT loss, one can obtain even better results. These results demonstrate the effectiveness of the proposed OT loss on enforcing the model to be faithful to the original table.
3.7 Human Evaluation
Following Wang et al. (2018); Tian et al. (2019), we conduct extensive human evaluation on the generated descriptions and compare the results to the state-of-the-art methods. We design our evaluation criteria based on Wang et al. (2018); Tian et al. (2019), but our criteria differs from Tian et al. (2019) in several aspects. Specifically, for each group of generated texts, we ask the human raters to evaluate the grammar, fluency, and faithfulness. The human evaluation metrics of faithfulness is defined in terms of precision, recall and F1-score with respect to the reconstructed Knowledge-base table from a generated text sequence. To ensure accurate human evaluation, the raters are trained with word instructions and text examples of the grading standard beforehand. During evaluation, we randomly sample 100 examples from the predictions of each model on the Wikiperson test set, and provide these examples to the raters for blind testing. More details about the human evaluation are provided in the Appendix B. The human evaluation results in Table 4 clearly show the superiority of our proposed method.
4 Related Work
Table-to-text generation has been widely studied, and Seq2Seq models have achieved promising performance. Lebret et al. (2016b); Liu et al. (2018); Wiseman et al. (2018); Ma et al. (2019); Wang et al. (2018); Liu et al. (2019a).
For Transformer-based methods, the Seq2Seq Transformer is used by Ma et al. (2019) for table-to-text generation in low-resource scenario. Thus, instead of encoding an entire table as in our approach, only the predicted key facts are encoded in Ma et al. (2019). Extended transformer has been applied to game summary Gong et al. (2019) and E2E NLG tasks Gehrmann et al. (2018). However, their goals focus on matching the reference text instead of being faithful to the input.
Another line of work attempts to use external knowledge to improve the quality of generated text Chen et al. (2019b). These methods allow generation from an expanded external knowledge base that may contain information not relevant to the input table. Comparatively, our setting requires the generated text to be faithful to the input table. Nie et al. (2018) further study fidelity-data-to-text generation, where several executable symbolic operations are applied to guide text generation. Both models do not consider the matching between the input and generated output.
Regarding datasets, most previous methods are trained and evaluated on much simpler datasets like WikiBio Lebret et al. (2016b) that contains only one sentence as a reference description. Instead, we focus on the more complicated structured knowledge base dataset Wang et al. (2018) that aims to generate multi-sentence texts. Wang et al. (2018) propose a model based on the pointer network that can copy facts directly from the input knowledge base. Our model uses a similar strategy but obtains much better performance.
In terms of faithfulness, one related parallel work is Tian et al. (2019). However, our method is completely different from theirs. Specifically, Tian et al. (2019) develop a confidence oriented decoder that assigns a confidence score to each target position to reduce the unfaithful information in the generated text. Comparatively, our method enforces faithfulness by including the proposed table-text optimal-transport matching loss and table-text embedding similarity loss. Moreover, the faithfulness of Tian et al. (2019) only requires generated texts to be supported by either a table or the reference; whereas ours constrains generated texts to be faithful only to the table.
Other related works are Perez-Beltrachini and Lapata (2018); Liu et al. (2019b). For Perez-Beltrachini and Lapata (2018), the content selection mechanism training with multi-task learning and reinforcement learning is proposed. For Liu et al. (2019b), they propose force attention and reinforcement learning based method. Their learning methods are completely different from our method that simultaneously incorporates optimal-transport matching loss and embedding similarity loss. Moreover, the REINFORCE algorithm Williams (1992) and policy gradient method used in Perez-Beltrachini and Lapata (2018); Liu et al. (2019b) exhibits high variance when training the model.
5 Conclusion
In this paper, we propose a novel Transformer-based table-to-text generation framework to address the faithful text-generation problem. To enforce faithful generation, we propose a new table-text optimal-transport matching loss and a table-text embedding similarity loss. To evaluate the faithfulness of the generated texts, we further propose a new automatic evaluation metric specialized to the table-to-text generation problem. Extensive experiments are conducted to verify the proposed method. Both automatic and human evaluations show that our framework can significantly outperform the state-of-the-art methods.
Acknowledgements
We sincerely thank all the reviewers for providing valuable feedback. We thank Linfeng Song, Dian Yu, Wei-yun Ma, and Ruiyi Zhang for the helpful discussions.
References
- Bahdanau et al. (2015) Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. 2015. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations.
- Barzilay and Lapata (2005) Regina Barzilay and Mirella Lapata. 2005. Collective content selection for concept-to-text generation. In HLT/EMNLP 2005, Human Language Technology Conference and Conference on Empirical Methods in Natural Language Processing, Proceedings of the Conference, 6-8 October 2005, Vancouver, British Columbia, Canada.
- Beck et al. (2018) Daniel Beck, Gholamreza Haffari, and Trevor Cohn. 2018. Graph-to-sequence learning using gated graph neural networks. In Proceedings of the Annual Meeting of the Association for Computational Linguistics.
- Cawsey et al. (1997) Alison Cawsey, Bonnie L. Webber, and Ray B. Jones. 1997. Brief review: Natural language generation in health care. JAMIA, 4(6):473–482.
- Chen et al. (2019a) Liqun Chen, Yizhe Zhang, Ruiyi Zhang, Chenyang Tao, Zhe Gan, Haichao Zhang, Bai Li, Dinghan Shen, Changyou Chen, and Lawrence Carin. 2019a. Improving sequence-to-sequence learning via optimal transport. In Proceedings of the International Conference on Learning Representations.
- Chen et al. (2019b) Shuang Chen, Jinpeng Wang, Xiaocheng Feng, Feng Jiang, Bing Qin, and Chin-Yew Lin. 2019b. Enhancing neural data-to-text generation models with external background knowledge. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the International Joint Conference on Natural Language Processing.
- Denkowski and Lavie (2014) Michael Denkowski and Alon Lavie. 2014. Meteor universal: Language specific translation evaluation for any target language. In Proceedings of the Ninth Workshop on Statistical Machine Translation.
- Dhingra et al. (2019) Bhuwan Dhingra, Manaal Faruqui, Ankur Parikh, Ming-Wei Chang, Dipanjan Das, and William W. Cohen. 2019. Handling divergent reference texts when evaluating table-to-text generation. In Proceedings of 57th Annual Meeting of the Association for Computational Linguistics.
- Gehrmann et al. (2018) Sebastian Gehrmann, Falcon Z. Dai, Henry Elder, and Alexander M. Rush. 2018. End-to-end content and plan selection for data-to-text generation. In Proceedings of International Conference on Natural Language Generation.
- Genevay et al. (2018) Aude Genevay, Gabriel Peyré, and Marco Cuturi. 2018. Learning generative models with sinkhorn divergences. In Proceedings of the International Conference on Artificial Intelligence and Statistics.
- Gong et al. (2019) Li Gong, Josep Crego, and Jean Senellart. 2019. Enhanced transformer model for data-to-text generation. In Proceedings of the 3rd Workshop on Neural Generation and Translation (EMNLP).
- Kingma and Ba (2015) Diederik P. Kingma and Jimmy Ba. 2015. Adam: A method for stochastic optimization. In Proceedings of the International Conference for Learning Representations.
- Klein et al. (2017) Guillaume Klein, Yoon Kim, Yuntian Deng, Jean Senellart, and Alexander M. Rush. 2017. OpenNMT: Open-source toolkit for neural machine translation. In Proceedings of Annual Meeting of the Association for Computational Linguistics.
- Kuhn (1955) Harold W. Kuhn. 1955. The hungarian method for the assignment problem. In Naval research logistics quarterly.
- Lan et al. (2019) Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. 2019. Albert: A lite bert for self-supervised learning of language representations. In https://arxiv.org/abs/1909.11942.
- Lebret et al. (2016a) Rémi Lebret, David Grangier, and Michael Auli. 2016a. Neural text generation from structured data with application to the biography domain. In Proceedings of the Conference on Empirical Methods in Natural Language Processing.
- Lebret et al. (2016b) Rémi Lebret, David Grangier, and Michael Auli. 2016b. Neural text generation from structured data with application to the biography domain. In Proceedings of the Conference on Empirical Methods in Natural Language Processing.
- Liang et al. (2009) Percy Liang, Michael I. Jordan, and Dan Klein. 2009. Learning semantic correspondences with less supervision. In Proceedings of the Annual Meeting of the Association for Computational Linguistics and International Joint Conference on Natural Language Processing of the AFNLP.
- Lin (2004) Chin-Yew Lin. 2004. Rouge: A package for automatic evaluation of summaries. In Proceedings of Text Summarization Branches Out.
- Liu et al. (2019a) Tianyu Liu, Fuli Luo, Qiaolin Xia, Shuming Ma, Baobao Chang, and Zhifang Sui. 2019a. Hierarchical encoder with auxiliary supervision for neural table-to-text generation: Learning better representation for tables. In Proceedings of the AAAI Conference on Artificial Intelligence.
- Liu et al. (2019b) Tianyu Liu, Fuli Luo, Pengcheng Yang, Wei Wu, Baobao Chang, and Zhifang Sui. 2019b. Towards comprehensive description generation from factual attribute-value tables. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics.
- Liu et al. (2018) Tianyu Liu, Kexiang Wang, Lei Sha, Baobao Chang, and Zhifang Sui. 2018. Table-to-text generation by structure-aware seq2seq learning. In Proceedings of the AAAI Conference on Artificial Intelligence.
- Loper and Bird (2002) Edward Loper and Steven Bird. 2002. Nltk: The natural language toolkit. In https://arxiv.org/abs/cs/0205028.
- Ma et al. (2019) Shuming Ma, Pengcheng Yang, Tianyu Liu, Peng Li, Jie Zhou, and Xu Sun. 2019. Key fact as pivot: A two-stage model for low resource table-to-text generation. In https://arxiv.org/pdf/1908.03067.pdf.
- Nie et al. (2018) Feng Nie, Jinpeng Wang, Jin-Ge Yao, Rong Pan, and Chin-Yew Lin. 2018. Operation-guided neural networks for high fidelity data-to-text generation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing.
- Papineni et al. (2002) Kishore Papineni, Salim Roukos, Todd Ward, and WeiJing Zhu. 2002. Bleu: a method for automatic evaluation of machine translation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics.
- Perez-Beltrachini and Lapata (2018) Laura Perez-Beltrachini and Mirella Lapata. 2018. Bootstrapping generators from noisy data. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies.
- See et al. (2017) Abigail See, Peter J. Liu, and Christopher D. Manning. 2017. Get to the point: Summarization with pointer-generator networks. In https://arxiv.org/abs/1704.04368.
- Song et al. (2018) Linfeng Song, Yue Zhang, Zhiguo Wang, and Daniel Gildea. 2018. A graph-to-sequence model for amr-to-text generation. In Proceedings of the Annual Meeting of the Association for Computational Linguistics.
- Sutskever et al. (2014) Ilya Sutskever, Oriol Vinyals, and Quoc V. Le. 2014. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems.
- Tian et al. (2019) Ran Tian, Shashi Narayan, Thibault Sellam, and Ankur P. Parikh. 2019. Sticking to the facts: Confident decoding for faithful data-to-text generation. In https://arxiv.org/abs/1910.08684.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Advances in Neural Information Processing Systems.
- Wang et al. (2018) Qingyun Wang, Xiaoman Pan, Lifu Huang, Boliang Zhang, Zhiying Jiang, Heng Ji, and Kevin Knight. 2018. Describing a knowledge base. In International Conference on Natural Language Generation.
- Wang et al. (2017) Rui Wang, Andrew Finch, Masao Utiyama, and Eiichiro Sumita. 2017. Sentence embedding for neural machine translation domain adaptation. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics.
- Williams (1992) Ronald J. Williams. 1992. Simple statistical gradient-following algorithms for connectionist reinforcement learning. In Machine Learning.
- Wiseman et al. (2018) Sam Wiseman, Stuart M. Shieber, and Alexander M. Rush. 2018. Learning neural templates for text generation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing.
- Xie et al. (2018) Yujia Xie, Xiangfeng Wang, Ruijia Wang, and Hongyuan Zha. 2018. A fast proximal point method for computing exact wasserstein distance. In https://arxiv.org/pdf/1802.04307.pdf.
- Yang et al. (2019) Mingming Yang, Rui Wang, Kehai Chen, Masao Utiyama, Eiichiro Sumita, Min Zhang, and Tiejun Zhao. 2019. Sentence-level agreement for neural machine translation. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics.
Appendix A PARENT-T Metric
PARENT-T evaluates each instance separately, by computing the precision and recall of generated text against table . In other words, PARENT-T is a table-focused version of PARENT Dhingra et al. (2019).
When computing precision, we want to check what fraction of the n-grams in are correct. We consider an n-gram to be correct if it has a high probability of being entailed by the table. We use the word overlap model for entailment probability . The precision score for one instance is computed as follows:
| (6) | ||||
| (7) | ||||
| (8) |
where denotes all the lexical items present in the table , is the length of , and is the th token in . is the entailment probability, and is the entailed precision score for n-grams of order . denotes the count of n-gram in . The precision score is a combination of n-gram orders 1-4 using a geometric average.
For recall, we only compute it against table to ensure that texts that mention more information from the table get higher scores. is computed in the same way as in Dhingra et al. (2019):
| (9) |
where a table is a set of records , denotes the value string of record , and is the length of the longest common subsequence between and . Higher values of denote that more records are likely to be mentioned in .
Thus, the PARENT-T score (i.e. F score) for one instance is:
| (10) |
The system-level PARENT-T score for a model is the average of instance-level PARENT-T scores across the evaluation set.
Appendix B Details of Human Evaluation
The following are the details for instructing our human evaluation raters how to rate each generated sentence:
We only provide the input table and the generated text for the raters. There are 20 well-trained raters participating in the evaluation.
Fluency
:
4: The sentence meaning is clear and flow naturally and smoothly.
3: The sentence meaning is clear, but there are a few interruptions.
2: The sentence does not flow smoothly but people can understand its meaning.
1: The sentence is not fluent at all and people cannot understand its meaning.
Grammar
:
4 : There are no grammar errors.
3: There are a few grammar errors, but sentence meaning is clear.
2: There are some grammar errors, but not influencing its meaning.
1: There are many grammar errors. People cannot understand the sentence meaning.
Faithfulness
A sentence is faithful if it contains only information supported by the table. It should not contain additional information other than the information provided by the table or inferred from the table. Also, the generated sentence should cover as much information in the given table as possible. The raters first manually extract entities from the generated sentences and then calculate the precision as the percentage of entities in the generated text also appear in the table; calculate the recall as the percentage of entities in the table also appear in the generated text. For each table-text pair, its F-1 score is then calculated according to the precision and recall.
Appendix C IPOT algorithm
Given a pair of table and its corresponding text description, we can obtain table words embedding as , and the model output for sentence words embedding as . The cost matrix is then computed as in Section 2.4. Both and are used as inputs to the IPOT algorithm in Algorithm 1 to obtain the OT-matching distance.
Appendix D Details of Optimal Transport Loss
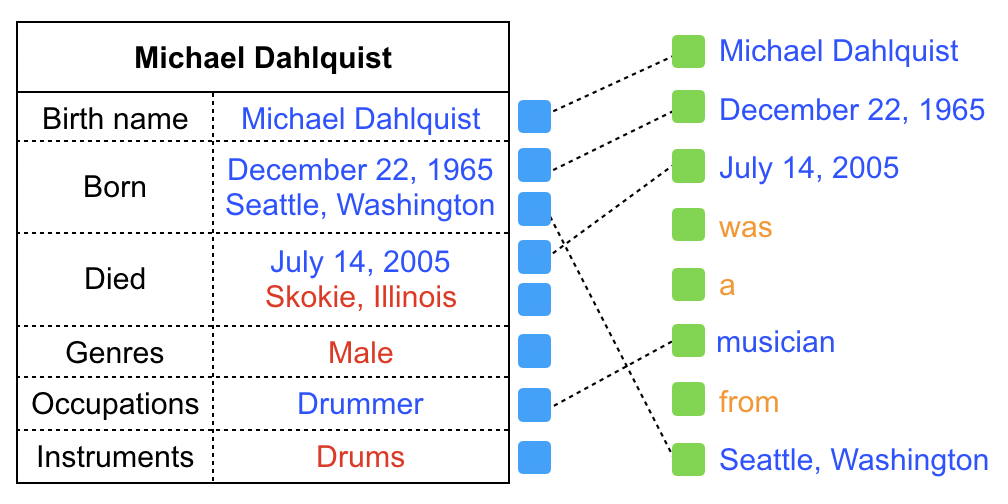
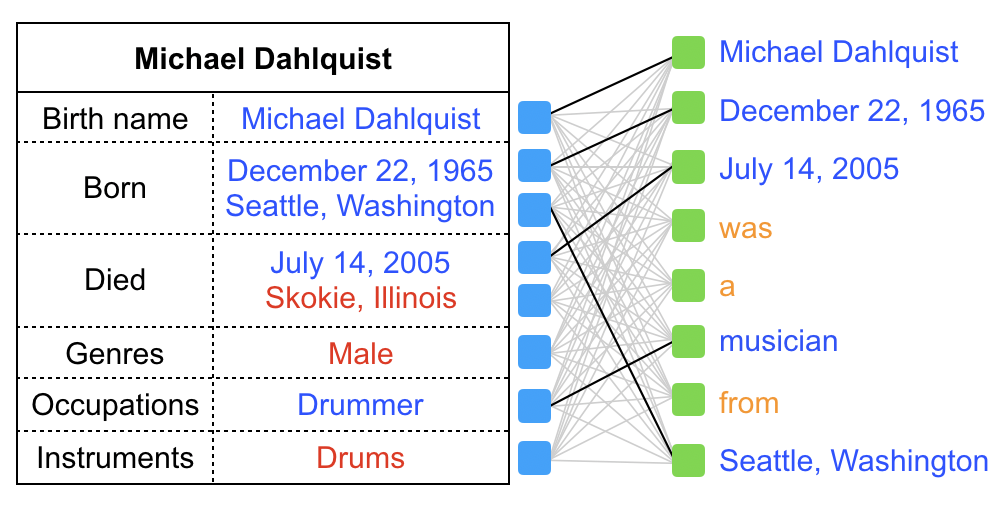
Figure 5 illustrates three matching cases from top to bottom, namely hard matching, soft bipartite matching, and optimal transport matching. The hard matching stands for exactly matching words between the table and the target sequences. This operation is non-differentiable. The soft bipartite matching, on the other hand, supposes the similarity between the word embedding and is , and finds the matching such that is minimized. This minimization can be solved exactly by the Hungarian algorithm Kuhn (1955). But, its objective is still non-differentiable. Our proposed optimal transport matching can be viewed as the relaxed problem of the soft bipartite matching by computing the distance between the distribution over the input table and the decoded text sentence. This distance in optimal transport matching is differentiable.
Appendix E More generation examples
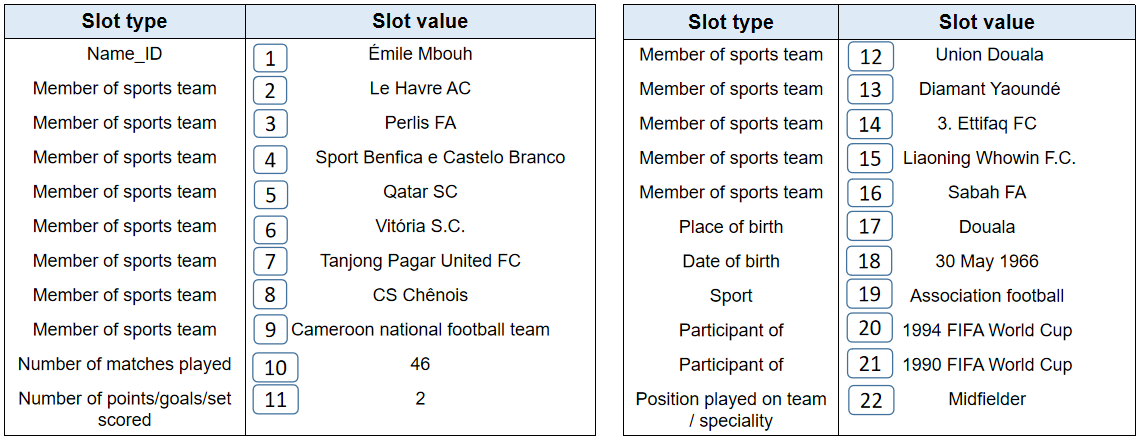
More generation examples from different models are shown in Figure 6, 7, and Table 6, 7. Specifically, Table 7 and Figure 7 show a more challenging example, as its table has 22 rows. In this example, we can observe that all the RNN-based models cannot capture such long term dependencies and miss most of the input records in the table. By contrast, our model miss much less input records.
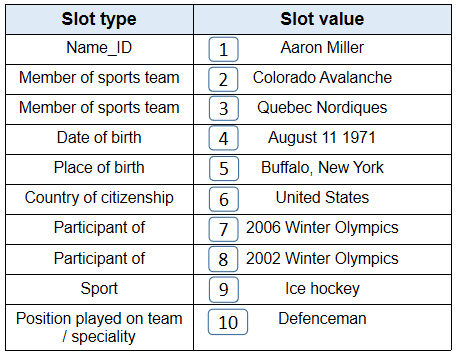
| Model | Miss | Generated texts |
|---|---|---|
| Wang et al. (2018) | 7, 8 | Aaron Miller ( born August 11 1971 ) is an United States former professional Ice hockey Defenceman who played in the National Hockey League ( NHL ) for the Quebec Nordiques and the Colorado Avalanche . he was born in Buffalo, New York and played for the Quebec Nordiques and the Ottawa Senators . |
| Pointer generator | 2, 7, 8 | Aaron Miller (born August 11 1971) is a retired United States professional Ice hockey Defenceman who played in the National Hockey League (NHL) for the Quebec Nordiques Quebec Nordiques Quebec Nordiques and the Quebec Nordiques . he was born in Buffalo, New York and grew up in New York City, |
| Seq2Seq | 3, 7, 8 | Aaron Miller (born August 11 1971) is an United States former professional Ice hockey Defenceman who played in the National Hockey League . miller was born in Buffalo, New York . he was drafted by the Colorado Avalanche in the second round of the 1994 NHL Entry Draft . he was drafted in the sixth round of the 1994 NHL Entry Draft by the Colorado Avalanche . he was drafted in the sixth round of the 1994 NHL Entry Draft by the Colorado Avalanche . |
| Structure-Aware | 7, 8 | Aaron Miller (born August 11 1971 in Buffalo, New York New York) is a retired United States professional Ice hockey Defenceman who played in the National Hockey League (NHL) for the Quebec Nordiques Colorado Avalanche Colorado Avalanche Colorado Avalanche Colorado Avalanche and Quebec Nordiques. he was drafted in the 2nd round of overall of the 2002 NHL Entry Draft. |
| Ours | None | Aaron Miller (born August 11 1971 in Buffalo, New York) is an United States former professional Ice hockey Defenceman who played in the National Hockey League (NHL) for the Quebec Nordiques and Colorado Avalanche . he was a member of the United States men’s national Ice hockey team at the 2002 Winter Olympics and 2006 Winter Olympics. |
| Model | Miss | Generated texts |
|---|---|---|
| Wang et al. (2018) | 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 14, 15, 16, 21, 22 | Émile Mbouh ( born 30 May 1966 ) is a former Cameroon national football team Association football . he was born in Douala and played for the Tanjong Pagar United FC in the 1994 FIFA World Cup . |
| Pointer generator | 2, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 16, 16, 20 | Émile Mbouh, (born 30 May 1966) is a Cameroon retired Association football who played as a Midfielder . he played for Cameroon national football team in the 1990 FIFA World Cup . he also played for Perlis FA and Liaoning Whowin F.C. . Émile was born in Douala, |
| Seq2Seq | 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 20 | Émile Mbouh, (born 30 May 1966) is a retired Cameroonian Association football who played as a Midfielder . he was born in Douala . he was a member of the Cameroon national football team at the 1990 FIFA World Cup . he was a member of the Cameroon national football team at the 1990 FIFA World Cup . he was a member of the Cameroon national football team at the 1990 FIFA World Cup . he was a member of the Cameroon national football team at the 1990 FIFA World Cup . |
| Structure-Aware | 2, 3, 4, 5, 6, 8, 10, 11, 12, 13, 14, 15, 16, 17, 21 | Émile Mbouh, (born 30 May 1966) is a Cameroonian retired Association football who played as a Midfielder . Le represented Cameroon national football team at the 1994 FIFA World Cup and 1994 FIFA World Cup . he played for Le FC Sport Yaoundé, United Yaoundé and Tanjong Pagar United FC |
| Ours | 2, 3, 5, 6, 8, 12, 13, 14 | Émile Mbouh (born 30 May 1966) is a Cameroonian retired Association football who played as a Midfielder . born in Douala Émile began his career with Sport Benfica e Castelo Branco and Tanjong Pagar United FC . he also represented Cameroon national football team at the 1994 FIFA World Cup and 1990 FIFA World Cup . he also played for Sabah FA and Liaoning Whowin F.C. in the Malaysia Super League . he also played for Tanjong Pagar United FC and Liaoning Whowin F.C. in the Chinese Super League. |