Transfer Function for Multi-copy Axion

Jiashuo Zhang¹¹1Email : joshua.z.0211@gmail.com, u3007845@connect.hku.hk Department of Physics, The University of Hong Kong, Pokfulam Road, Hong Kong

Abstract

Ultra-light axions are well-motivated fuzzy cold dark matter candidate that provide potential resolutions to various small scale problems faced by conventional heavy particle CDM. To date, great efforts have been made to understand the structure formation in fuzzy dark matter dominated Universe, but existing investigations focused primarily on scenarios involving a single axion copy. String axiverse, on the other hand, motivates the presence of multiple axion copies, each with a distinct mass. In this short article, we attempt to understand the anticipated structure formation in a multi-copy axion universe using linear perturbation theory, and propose a simplified parametrization for the transfer function of multi-copy axions. The latter could be helpful for future simulations to more easily implement the initial condition for each copy of axion.

I Introduction

Ultralight axions, of mass scale $\sim 10^{-22}$ eV, are well-motivated fuzzy cold dark matter candidates first proposed by Hu et al. (2000) to address the ”core-cusp problem”. Owing to their astronomical scale de Brogile wavelength ( $\sim$ kpc), ultralight axions naturally suppress small-scale structure formation with their wavy nature hence potentially mitigate also the ”missing satellite problem”. More recently, stellar velocity dispersions measured around dwarf galaxies supports the existence of fuzzy dark matter with mass $\sim 1.5-1.8\times 10^{-22}$ eV Pozo et al. (2024a, b). Furthermore, wave interference pattern distinct to fuzzy dark matter of this mass scale has been shown to be capable of explaining gravitational anomalies typically seen in smooth lens models (often associated with particle CDM), while avoiding the need to invoke fine-tuned population of substructures Amruth et al. (2023). Broadhurst et al. (2025) also demonstrated such interference pattern could explain the apparent skewness of micro-lensed stars to the negative parity side of lensing critical curve, while adding sub-halos to particle CDM lens model leads to wrong parity of skewness.

Despite being phenomenologically motivated, the favored mass scale $\sim 1-2\times 10^{-22}eV$ has been seen in disputes with various constraints on the mass scale of fuzzy dark matter. Most notably is the constraint from Lyman Alpha Forest, claiming that fuzzy dark matter of mass below $2\times 10^{-20}$ eV is excluded Rogers and Peiris (2021). The null detection of anticipated faint end turnover in the galactic luminosity functions (LF) has also been used to place an constraint on the fuzzy dark matter mass. For instance Winch et al. (2024), by combining the UV LFs measured by Bouwens et al. (2021) with CMB data, argued fuzzy dark matter of mass lighter than $2.51\times 10^{-22}$ eV is not favored at 95 $\%$ confidence.

However, it is worth mentioning that the aforementioned investigations focused primarily on the case where fuzzy dark matter is of a single copy. On the other hand, string axiverse motivates the presence of multiple copies of axions (depending on the structure of internal dimensions) each with a different mass. And in Luu et al. (2020), the presence of an second copy with mass $\sim 10^{-20}$ eV (even a third copy with $10^{-18}$ eV) is indicated.

While the impact of single copy axion on structure formation has been extensively considered/studied, there exist only a few works on investigating the structure formation with multi-copy axion dark matter. Nhan Luu et al. (2024) serves as one of the first works in this direction, by providing the first simulation with two copy of axions differed by a mass factor of 5. Such simulation is expected to be generalized to higher mass ratios and with more copies, but the relevant initial conditions for each species may be hard to generate.

In this short article, we attempt to understand the anticipated structure formation in multi-copy axion Universe using linear perturbation theory, and present a simplified parametrization for the transfer function of multi-copy axions. This could be helpful for future simulations to more easily implement the initial condition for each copy of axion. We further hypothesize that the structure formation in multi-copy axion Universe is expected to resemble the case of a single copy with an effective mass on large scale, whereas the effect from individual copies would be apparent in the non-linear regime (e.g. at the galactic level).

II Multi-copy axion Perturbation equations

We start from the Schrodinger Poisson equation for an arbitrary number of axion fields $\varphi_{I}$ in an expanding Universe

i(\partial_{t}+\frac{3}{2}\mathcal{H})\varphi_{I}=-\frac{\nabla^{2}\varphi_{I}}{2m_{I}a^{2}}+\Phi m_{I}\varphi_{I}

(1)

\nabla^{2}\Phi=4\pi Ga^{2}\sum_{I}\delta\rho_{I}

(2)

where $\rho_{I}=m_{I}^{2}|\varphi_{I}|^{2}$ and $\delta\rho_{I}$ describe the perturbation for each copy. To derive the perturbation equations, we perform Madelung decomposition with $\varphi_{I}=\sqrt{\rho_{I}}e^{iS_{I}}/m_{I}$ , in and Schrodinger Poisson equations could be arranged into

	$\displaystyle\dot{\rho_{I}}+3\mathcal{H}\rho_{I}+\frac{1}{a}\nabla\cdot(\rho_{I}v_{I})=0$		(3)
	$\displaystyle\dot{v_{I}}+\mathcal{H}v_{I}+\frac{1}{a^{3}}\nabla Q_{I}+\frac{1}{a}(v_{I}\cdot\nabla)v_{I}+\frac{1}{a}\nabla\Phi=0$		(4)

where the velocity field is defined as $v_{I}\equiv\nabla S_{I}/(m_{I}a)$ . $Q_{I}$ denotes the quantum pressure for each axion copy and is given by

Q_{I}\equiv-\frac{\nabla^{2}(\sqrt{\rho_{I}})}{2m_{I}^{2}\sqrt{\rho_{I}}}=-\frac{1}{2m_{I}^{2}}\bigg{(}\frac{\nabla^{2}\rho_{I}}{2\rho_{I}}+\frac{(\nabla\rho_{I})^{2}}{4\rho_{I}^{2}}\bigg{)}

(5)

By considering the density contrast $\delta_{I}\equiv\delta\rho_{I}/\overline{\rho_{I}}$ , we may derive a set of linear perturbation equations to first order in $\delta_{I},v_{I}$ , and the set of equations could be collectively arranged into a matrix form as

\partial_{t}^{2}\begin{pmatrix}\delta_{1}\\ \vdots\\ \delta_{I}\\ \vdots\\ \delta_{N}\end{pmatrix}+2\mathcal{H}\partial_{t}\begin{pmatrix}\delta_{1}\\ \vdots\\ \delta_{I}\\ \vdots\\ \delta_{N}\end{pmatrix}-\begin{pmatrix}4\pi G\overline{\rho_{1}}-\frac{k^{4}}{4m_{1}^{2}a^{4}}&\cdots&4\pi G\overline{\rho_{J}}&\cdots&4\pi G\overline{\rho_{N}}\\ 4\pi G\overline{\rho_{1}}&\cdots&4\pi G\overline{\rho_{J}}&\cdots&4\pi G\overline{\rho_{N}}\\ 4\pi G\overline{\rho_{1}}&\cdots&4\pi G\overline{\rho_{J}}-\frac{k^{4}}{4m_{J}^{2}a^{4}}&\cdots&4\pi G\overline{\rho_{N}}\\ 4\pi G\overline{\rho_{1}}&\cdots&4\pi G\overline{\rho_{J}}&\cdots&4\pi G\overline{\rho_{N}}\\ 4\pi G\overline{\rho_{1}}&\cdots&4\pi G\overline{\rho_{J}}&\cdots&4\pi G\overline{\rho_{N}}-\frac{k^{4}}{4m_{N}^{2}a^{4}}\end{pmatrix}\begin{pmatrix}\delta_{1}\\ \vdots\\ \delta_{J}\\ \vdots\\ \delta_{N}\end{pmatrix}=0

(6)

If we define a ’total’ perturbation contrast as $\overline{\rho_{tot}}\delta_{tot}=\sum_{I}\overline{\rho_{I}}\delta_{I}$ , then it could be verified that the time derivative of $\delta_{tot}$ satisfy

\dot{\delta_{tot}}=\frac{\sum_{I}\overline{\rho_{I}}\dot{\delta_{I}}}{\overline{\rho_{tot}}},\;\;\ddot{\delta_{tot}}=\frac{\sum_{I}\overline{\rho_{I}}\ddot{\delta_{I}}}{\overline{\rho_{tot}}}.

(7)

Then by summing density contrast equations for all axion copies, we could obtain

\ddot{\delta_{tot}}+2\mathcal{H}\dot{\delta_{tot}}-4\pi G\delta_{tot}\overline{\rho_{tot}}+\frac{k^{4}}{4m_{eff}^{2}a^{4}}\delta_{tot}=0

(8)

where the effective mass scale is defined by

\frac{1}{m_{eff}^{2}}\delta_{tot}\overline{\rho_{tot}}\equiv\sum_{I}\frac{\overline{\rho_{I}}\delta_{I}}{m_{I}^{2}}.

(9)

Equ.8 is essentially the same as the single copy axion case hence the corresponding transfer function for $\delta_{tot}$ could be well-approximated with the solution by Hu et al. (2000)

T_{tot}\approx\bigg{|}\frac{\cos x^{3}}{1+x^{8}}\bigg{|}T_{pCDM},\;\;x=\frac{1.61}{9}\frac{k}{m^{4/9}_{eff}}

(10)

in which the mass $m_{eff}$ is measured in units of $10^{-22}$ eV, wavenumber $k$ is measured in Mpc^-1 and $T_{pCDM}$ is the transfer function expected from particle CDM. In Passaglia and Hu (2022); Liu et al. (2024), an alternative fitting form was provided:

T_{tot}\approx\bigg{|}\frac{\sin x^{5/2}}{x^{5/2}(1+Bx^{7/2})}\bigg{|}T_{pCDM},\;\;x=\frac{A}{9}\frac{k}{m^{1/2}_{eff}}

(11)

where $A=2.22m_{eff}^{1/25-\ln(m_{eff})/1000}$ , $B=0.16m_{eff}^{-1/20}$ . Likewise, transfer function determined from Boltzman codes (e.g. AxionCAMB Hlozek et al. (2015)) for single copy axion case could also be used.

II.1 Limiting cases consideration

It could be seen that are two separate limiting cases for Equ.6.

Near the frequency $k$ where quantum pressure-led suppression from fuzzy dark matter just begins, the quartic term $k^{4}$ term remains relatively small than the gravity term and hence could be neglected. As a consequence, the last matrix term for Equ.6 is seen reduced to the same form for all copy of axions and also Equ.8. This grants each copy to be effectively equivalent and be parametrized by $\delta_{tot}$ . In Nhan Luu et al. (2024) this feature was observed for the double axion case: lighter and heavier copy were observed to both follow the same transfer near the onset of quantum pressure-led suppression.

The ’delayed’ onset of quantum pressure-led suppression could be understood as all copies are expected to follow the mutual gravitational potential, and here we have demonstrated this is a general consequence and holds for arbitrary number of axion copies. And the onset of suppression will not be dominated by the most heavy copy one might expect, instead is governed by the effective mass scale $m_{eff}$ .

Owing to the ’equivalence’ among $\delta_{I}$ and also with $\delta_{tot}$ near the onset of suppression, we could then cancel the density contrast dependence on both side in Equ.9 and write $\overline{\rho_{tot}}/m_{eff}^{2}=\sum_{I}\overline{\rho_{I}}/m_{I}^{2}$ . This suggests that the effective mass is solely determined by the relative contribution of each copy to the total matter density²²2To be more precise, this ratio will be fixed at the time for the lightest copy to start oscillate, as long as there are no mixing mechanism among different axion copies.

In Nhan Luu et al. (2024), it was also observed that at much larger $k$ where quartic term overwhelms the gravity term, the lighter and heavier copy tends to their respective single copy axion transfer functions. From Equ.6, this behavior could be inferred to hold true in general as the last term of Equ.6 effectively reduces to a diagonal form (i.e. different copies decouple).

II.2 Multi-copy transfer function

The two limiting cases discussed above could be re-casted into the following equations for each axion copy with mass $m_{I}$

	$\displaystyle\ddot{\hat{\delta}}_{I}+2\mathcal{H}\dot{\hat{\delta}}_{I}-4\pi G\overline{\rho_{tot}}\hat{\delta}_{I}+\frac{k^{4}\hat{\delta}_{I}}{4a^{4}m_{I}^{2}}=0$		(12)
	$\displaystyle\ddot{\hat{\delta}}_{tot}+2\mathcal{H}\dot{\hat{\delta}}_{tot}-4\pi G\overline{\rho_{tot}}\hat{\delta}_{tot}+\frac{k^{4}\hat{\delta}_{tot}}{4a^{4}m_{eff}^{2}}=0$		(13)

where $\hat{\delta}_{tot}$ and $\hat{\delta}_{I}$ denotes the two single-axion scheme solutions for $\delta_{I}$ under the two limiting cases. In the $\hat{\delta}_{I}$ equation, the gravity term should really be $4\pi G\overline{\rho_{I}}\hat{\delta}_{I}$ . However, as it corresponds to high $k$ limit where gravity term could be neglected, it is possible to replace $\overline{\rho_{I}}$ with $\overline{\rho_{tot}}$ .

II.3 Parameterizing Transfer Function

We assume the transition between two limiting case for each axion copy could be approximated with

\delta_{I}=A(k)\hat{\delta}_{I}+(1-A(k))\hat{\delta}_{tot}

(14)

where the frequency dependent coefficient $A(k)$ limits to 0 at low $k$ and $1$ at high $k$ , and $\delta_{I}$ is the solution to the original perturbation equation

\ddot{\delta}_{I}+2\mathcal{H}\dot{\delta}_{I}-4\pi G\overline{\rho_{tot}}\delta_{tot}+\frac{k^{4}\delta_{I}}{4a^{4}m_{I}^{2}}=0

(15)

seen from Equ.6. As $\hat{\delta}_{tot}=\delta_{tot}$ defined by Equ.7, performing the assumed decomposition and using the limiting case equations we can get

4\pi G\overline{\rho_{tot}}A(\hat{\delta}_{I}-\hat{\delta}_{tot})=(1-A)\frac{k^{4}}{4a^{4}}\bigg{(}\frac{1}{m_{eff}^{2}}-\frac{1}{m_{I}^{2}}\bigg{)}\hat{\delta}_{tot}

(16)

Hence the solution for $A(k)$ is given by

A=\frac{\frac{k^{4}}{4a^{4}}\bigg{(}\frac{1}{m_{eff}^{2}}-\frac{1}{m_{I}^{2}}\bigg{)}\hat{\delta}_{tot}}{4\pi G\overline{\rho_{tot}}(\hat{\delta}_{I}-\hat{\delta}_{tot})+\frac{k^{4}}{4a^{4}}\bigg{(}\frac{1}{m_{eff}^{2}}-\frac{1}{m_{I}^{2}}\bigg{)}\hat{\delta}_{tot}}

(17)

We could further simplify above expression using the fact $\hat{\delta}_{tot}/\hat{\delta}_{I}=T_{tot}/T_{I}$ and the definition of comoving quantum Jeans scale $k_{J}$ Kunkel et al. (2022) for $\delta_{tot}$ (given $\overline{\rho_{tot}}$ )

4\pi G\overline{\rho_{tot}}\cdot 4a^{4}\equiv\frac{a^{3}k_{J}^{4}}{m_{eff}^{2}}=6\mathcal{H}^{2}\Omega_{DM}

(18)

Hence the solution for $A$ reads

A=\frac{\frac{k^{4}}{\tilde{k}^{4}}\bigg{(}1-\frac{m_{eff}^{2}}{m_{I}^{2}}\bigg{)}}{\frac{T_{I}}{T_{tot}}-1+\frac{k^{4}}{\tilde{k}^{4}}\bigg{(}1-\frac{m_{eff}^{2}}{m_{I}^{2}}\bigg{)}}

(19)

where

\tilde{k}\equiv a^{3/4}k_{J}\approx\frac{44.7}{\text{Mpc}}\,\bigg{(}6E(a)\frac{\Omega_{DM}}{0.3}\bigg{)}^{1/4}\bigg{(}\frac{H_{0}}{70\,\frac{\text{km/s}}{\text{Mpc}}}\frac{m_{eff}}{10^{-22}\,\text{eV}}\bigg{)}^{1/2}

(20)

and $E(a)\equiv a^{4}(\Omega_{\Lambda}+\Omega_{m}/a^{3})$ .

Correspondingly, the transfer function for axion copy $\delta_{I}$ could be expressed as

T=AT_{I}+(1-A)T_{tot}.

(21)

using single copy axion transfer functions $T_{I},T_{tot}$ . An example is given in Fig.1 (at redshift 127) for a Universe with three copies of axion.

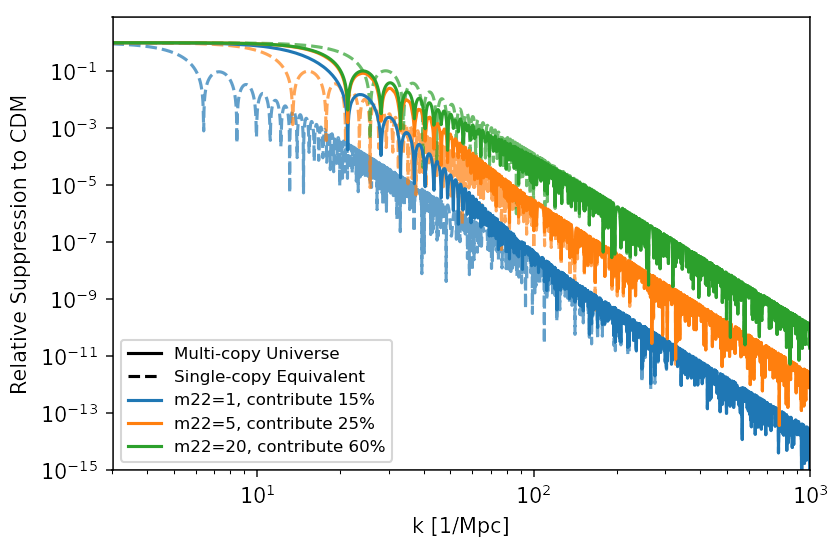
Refer to caption — Figure 1: Example transfer functions for each copy of axion for a Universe at redshift 127. The three copies have mass $1,5,20\times 10^{-22}$ eV respectively and contribute $15\%,25\%,60\%$ of the total dark matter density $\overline{\rho_{tot}}$ . Transfer functions $T_{I}$ s, $T_{tot}$ in single copy axion Universe are computed using Equ.11.

In the transfer function given by Equ.10, recall there is also the $\cos x^{3}$ (or $\sin x^{5/2}$ for Equ.11) term. In determination of $A(k)$ , such oscillatory term can be considered as higher order effect and not important. Hence in practice, one may approximate the the ratios between any two transfer functions as the ratio between envelop functions, i.e. $T_{a}/T_{b}=(1+x_{b}^{8})/(1+x_{a}^{8})$ and likewise for transfer function given by Equ.11. For transfer functions determined by Boltzmann codes, smoothing could be applied to find the corresponding envelop functions.

III Conclusion and Discussion

In this short article, we considered the transfer function for multi-copy axion Universe and provided a simplified, analytic expressions that may be useful for future simulations to determine the initial conditions for each axion copy. In particular we show that the transfer functions in a multi-copy axion could be parametrized as an interpolating sum of single copy axion transfer functions that are easier to compute (e.g. via axionCAMB).

We also identified an ’equivalence’ among all copies of axion and with total density contrast $\delta_{tot}$ in terms of the onset scale of structure suppression, this is due to their mutual coupling to the gravitational potential. This ’equivalence’ was also identified by Chen and Soda (2023), but here we removed their assumption of particle dark matter being the dominant contribution to CDM and considered full axion dark matter Universe. The identified ’equivalence’ could also suggest the large scale structure formed to resemble the single copy axion equivalent Universe with $m_{eff}$ . Correspondingly, the onset of faint end turnover in galactic luminosity functions would also be solely determined by this mass scale. Whereas on smaller (galactic) scale, effects from independent copy of axions will be apparent owing to the ’decoupling’ seen. This may then collectively explain the preference for ultralight fuzzy dark matter with mass $10^{-22}$ eV at low redshifts (in dwarfs) while also being able to accommodate the stringent constraints on fuzzy dark matter mass. The precise determination of Halo Mass Function and galactic luminosity function, however, remains best investigated with cosmological simulation.

References

Hu et al. (2000) W. Hu, R. Barkana, and A. Gruzinov, Phyics Review Letter 85, 1158 (2000), eprint astro-ph/0003365.
Pozo et al. (2024a) A. Pozo, T. Broadhurst, G. F. Smoot, T. Chiueh, H. N. Luu, M. Vogelsberger, and P. Mocz, Phyical Review D 109, 083532 (2024a), eprint 2302.00181.
Pozo et al. (2024b) A. Pozo, T. Broadhurst, I. de Martino, T. Chiueh, G. F. Smoot, S. Bonoli, and R. Angulo, Phyical Review D 110, 043534 (2024b), eprint 2010.10337.
Amruth et al. (2023) A. Amruth, T. Broadhurst, J. Lim, M. Oguri, G. F. Smoot, J. M. Diego, E. Leung, R. Emami, J. Li, T. Chiueh, et al., Nature Astronomy 7, 736 (2023), eprint 2304.09895.
Broadhurst et al. (2025) T. Broadhurst, S. K. Li, A. Alfred, J. M. Diego, P. Morilla, P. L. Kelly, F. Sun, M. Oguri, H. Williams, R. Windhorst, et al., Astrophysical Journal Letters 978, L5 (2025), eprint 2405.19422.
Rogers and Peiris (2021) K. K. Rogers and H. V. Peiris, Phyics Review Letter 126, 071302 (2021), eprint 2007.12705.
Winch et al. (2024) H. Winch, K. K. Rogers, R. Hložek, and D. J. E. Marsh, Astrophysical Journal 976, 40 (2024), eprint 2404.11071.
Bouwens et al. (2021) R. J. Bouwens, P. A. Oesch, M. Stefanon, G. Illingworth, I. Labbé, N. Reddy, H. Atek, M. Montes, R. Naidu, T. Nanayakkara, et al., Astronomical Journal 162, 47 (2021), eprint 2102.07775.
Luu et al. (2020) H. N. Luu, S. H. H. Tye, and T. Broadhurst, Physics of the Dark Universe 30, 100636 (2020), eprint 1811.03771.
Nhan Luu et al. (2024) H. Nhan Luu, P. Mocz, M. Vogelsberger, A. Pozo, T. Broadhurst, S. H. H. Tye, T. Liu, L. W. H. Fung, G. F. Smoot, R. Emami, et al., arXiv e-prints arXiv:2408.00827 (2024), eprint 2408.00827.
Passaglia and Hu (2022) S. Passaglia and W. Hu, Phyical Review D 105, 123529 (2022), eprint 2201.10238.
Liu et al. (2024) R. Liu, W. Hu, and D. Grin, arXiv e-prints arXiv:2412.15192 (2024), eprint 2412.15192.
Hlozek et al. (2015) R. Hlozek, D. Grin, D. J. E. Marsh, and P. G. Ferreira, Phyical Review D 91, 103512 (2015), eprint 1410.2896.
Kunkel et al. (2022) A. Kunkel, T. Chiueh, and B. M. Schäfer, arXiv e-prints arXiv:2211.01523 (2022), eprint 2211.01523.
Chen and Soda (2023) C.-B. Chen and J. Soda, Journal of Cosmology and Astroparticle Physics 2023, 049 (2023), eprint 2303.00999.