Transmit Optimization for Multi-functional MIMO Systems Integrating Sensing, Communication, and Powering

Future sixth-generation (6G) wireless networks need to incorporate billions of low-power Internet-of-things (IoT) devices and support their localization, sensing, communication, and control in a sustainable manner. Towards this end, simultaneous wireless information and power transfer (SWIPT) [1] and integrated sensing and communications (ISAC) [2] have emerged as two enabling techniques aiming to reuse radio signals to wirelessly charge massive IoT devices and provide sensing functionality, respectively. With their recent advancements, we envision that future 6G networks will integrate both SWIPT and ISAC to evolve towards new multi-functional wireless systems, which can provide sensing, communication, and powering capabilities at the same time. Such multi-functional wireless systems are expected to significantly enhance the utilization efficiency of scarce spectrum resources and densely deployed base station (BS) infrastructures, and facilitate the localization and powering of massive low-power devices to support emerging IoT applications.

In the literature, there have been extensive prior works investigating the transmit optimization for SWIPT (e.g., [3, 4]) and ISAC (e.g., [5, 6, 7, 8]) independently. For instance, the authors in [3] first studied a multiple-input multiple-output (MIMO) SWIPT system with one information decoding (ID) receiver and one energy harvesting (EH) receiver, in which the transmit covariance at the BS was designed to optimally balance the tradeoff between the communication rate versus the harvested energy level. This design was then extended to the broadcast channel with multiple ID receivers and multiple EH receivers (see, e.g., [4]). On the other hand, the works [5] and [6] considered the basic ISAC setup with one BS, one ID receiver, and one sensing target, in which the transmit strategies at the BS were optimized to balance the communication rate versus the estimation Cramér-Rao bound (CRB) as the sensing performance metric. Furthermore, the authors in [7] and [8] studied the ISAC system with multiple ID receivers and sensing targets, in which the transmit beamforming design at the BS was optimized to balance the communication and sensing performances.

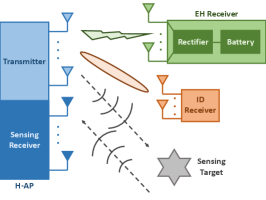
Different from these prior works, this paper studies a multi-functional MIMO system unifying ISAC and SWIPT as shown in Fig. 1, in which one single multi-antenna hybrid access point (H-AP) transmits wireless signals to simultaneously deliver information to one multi-antenna ID receiver, provide energy supply to one multi-antenna EH receiver, and estimate a sensing target based on the echo signals. For such a multi-functional wireless system, how to design the transmit strategies at the multi-antenna H-AP is essential to optimize the performance tradeoffs among sensing, communication, and powering. This problem, however, is particularly challenging, since the MIMO sensing (e.g., [9, 10]), communication (e.g., [11]), and powering (e.g., [3]) are designed based on distinct objectives and follow different principles. This thus motivates our study in this work.

In this paper, we consider the multi-functional MIMO system by focusing on the point target model for radar sensing, in which the H-AP aims to estimate the target angle. We aim to reveal the fundamental performance tradeoffs among sensing, communication, and powering, in terms of the angle estimation CRB, the achievable communication rate, and the harvested energy level. Towards this end, we characterize the complete CRB-rate-energy (C-R-E) region of this system, which is defined as the set of all C-R-E pairs that are simultaneously achievable. To find the points on the Pareto boundary surface of the C-R-E region, we propose to maximize the MIMO communication rate while ensuring the estimation CRB requirement for target sensing and the harvested energy requirement at the EH receiver, subject to the maximum transmit power constraint at the H-AP. We derive the well-structured optimal transmit covariance solution by using advanced convex optimization techniques. It is shown that the optimal transmit covariance follows the eigenmode transmission (EMT) structure based on a composite channel matrix, which can be generally divided into two parts, one for the triple roles of communication, sensing, and powering, and the other for sensing and powering only. Finally, numerical results validate the performance of our proposed design, in comparison to the benchmark scheme based on time switching.

Notations: Boldface letters are used for vectors (lower-case) and matrices (upper-case). For a square matrix $\boldsymbol{A}$, $\mathrm{tr}(\boldsymbol{A})$ and $\det(\boldsymbol{A})$ denote its trace and determinant, respectively, $\boldsymbol{A}\succeq\boldsymbol{0}$ means that $\boldsymbol{A}$ is positive semi-definite, and $\boldsymbol{A}\succ\boldsymbol{0}$ means that $\boldsymbol{A}$ is positive definite. For an arbitrary-size matrix $\boldsymbol{A}$, $\mathrm{rank}(\boldsymbol{A})$, $\boldsymbol{A}^{\dagger}$, $\boldsymbol{A}^{T}$, $\boldsymbol{A}^{H}$, and $\mathcal{R}(\boldsymbol{A})$ denote its rank, conjugate, transpose, conjugate transpose, and range space, respectively. For a vector $\boldsymbol{a}$, $\|\boldsymbol{a}\|$ denotes its Euclidean norm. For a complex number $a$, $|a|$ denotes its magnitude. For a real number $a$, $(a)^{+}\triangleq\max(a,0)$. $\mathrm{diag}(a_{1},\dots,a_{N})$ denotes a diagonal matrix whose diagonal entries are $a_{1},\dots,a_{N}$. $\boldsymbol{I}_{N}$ denotes the identity matrix with dimension $N\times N$. $\mathbb{C}^{M\times N}$ and $\mathbb{S}^{N}$denote the spaces of $M\times N$ complex matrices and $N\times N$ Hermitian matrices. $\mathbb{E}[\cdot]$ denotes the statistic expectation. $j=\sqrt{-1}$.

This paper considers a multi-functional MIMO system as shown in Fig. 1, which consists of one H-AP, one EH receiver, one ID receiver, and one sensing target to be estimated. The H-AP is equipped with a uniform linear array (ULA) of $M>1$ transmit antennas and $N_{\text{S}}>1$ receive antennas for sensing. The EH and ID receivers are equipped with $N_{\text{EH}}\geq 1$ and $N_{\text{ID}}\geq 1$ receive antennas, respectively.

We consider a quasi-static narrowband channel model, in which the wireless channels remain unchanged over the interested transmission block consisting of $L$ symbols, where $L$ is assumed to be sufficiently large. Let $\boldsymbol{H}_{\text{EH}}\in\mathbb{C}^{N_{\text{EH}}\times M}$ and $\boldsymbol{H}_{\text{ID}}\in\mathbb{C}^{N_{\text{ID}}\times M}$ denote the channel matrices from the H-AP to the EH receiver and the ID receiver, respectively. Let $\boldsymbol{H}_{\text{S}}\in\mathbb{C}^{N_{\text{S}}\times M}$ denote the target response matrix from the H-AP transmitter to the sensing target to the H-AP receiver, which will be specified later. It is assumed that the H-AP perfectly knows the information of $\boldsymbol{H}_{\text{EH}}$ and $\boldsymbol{H}_{\text{ID}}$, and the ID receiver perfectly knows $\boldsymbol{H_{\text{ID}}}$ to facilitate the transmit optimization, as commonly assumed in the literature [3, 4].

At each symbol $l\in\{1,\dots,L\}$, let $\boldsymbol{x}(l)\in\mathbb{C}^{M\times 1}$ denote the transmitted signal at the H-AP. The transmitted signal over the whole block is expressed as

$$\boldsymbol{X}=\big{[}\boldsymbol{x}(1),\dots,\boldsymbol{x}(L)\big{]}\in\mathbb{C}^{M\times L}.$$

(1)

Without loss of optimality, we consider the capacity-achieving Gaussian signaling, such that $\boldsymbol{x}(l)$’s are assumed to be circularly symmetric complex Gaussian (CSCG) random vectors with zero mean and covariance matrix $\boldsymbol{S}=\mathbb{E}\big{[}\boldsymbol{x}(l)\boldsymbol{x}(l)^{H}\big{]}\succeq\boldsymbol{0}$. As $L$ is sufficiently large, the sample covariance matrix $\frac{1}{L}\boldsymbol{X}\boldsymbol{X}^{H}$ is approximated as the statistical covariance matrix $\boldsymbol{S}$, i.e., $\frac{1}{L}\boldsymbol{X}\boldsymbol{X}^{H}\approx\boldsymbol{S}$, which is the optimization variable to be designed¹¹1This approximation has been widely adopted in MIMO radar and MIMO ISAC systems [12, 6].. Suppose that the H-AP is subject to a maximum transmit power budget $P$. We thus have $\mathbb{E}\big{[}\|\boldsymbol{x}(l)\|^{2}\big{]}=\mathrm{tr}(\boldsymbol{S})\leq P$.

First, we consider the radar sensing with a point target. Let $\alpha$ denote the complex reflection coefficient, and $\theta$ denote the angle of departure/arrival (AoD/AoA). The echo signal received by the H-AP receiver is

$$\boldsymbol{Y}_{\text{S}}=\boldsymbol{H}_{\text{S}}\boldsymbol{X}+\boldsymbol{Z}_{\text{S}}=\alpha\boldsymbol{A}(\theta)\boldsymbol{X}+\boldsymbol{Z}_{\text{S}},$$

(2)

where $\boldsymbol{A}(\theta)\triangleq\boldsymbol{a}_{r}(\theta)\boldsymbol{a}_{t}^{T}(\theta)$, with $\boldsymbol{a}_{r}(\theta)\in\mathbb{C}^{N_{\text{S}}\times 1}$ and $\boldsymbol{a}_{t}(\theta)\in\mathbb{C}^{M\times 1}$ denoting the receive and transmit array steering vectors, and $\boldsymbol{Z}_{\text{S}}\in\mathbb{C}^{N_{\text{S}}\times L}$ denotes the additive white Gaussian noise (AWGN) at the H-AP receiver that is a CSCG random matrix with independent and identically distributed (i.i.d.) entries each with zero mean and variance $\sigma_{\text{S}}^{2}$. By choosing the center of the ULA antennas as the reference point and assuming half-wavelength spacing between adjacent antennas, we have

	$\displaystyle\boldsymbol{a}_{t}(\theta)$	$\displaystyle=\big{[}e^{-j\frac{M-1}{2}\pi\sin\theta},e^{-j\frac{M-3}{2}\pi\sin\theta},\dots,e^{j\frac{M-1}{2}\pi\sin\theta}\big{]}^{T},$		(3)
	$\displaystyle\boldsymbol{a}_{r}(\theta)$	$\displaystyle=\big{[}e^{-j\frac{N_{\text{S}}-1}{2}\pi\sin\theta},e^{-j\frac{N_{\text{S}}-3}{2}\pi\sin\theta},\dots,e^{j\frac{N_{\text{S}}-1}{2}\pi\sin\theta}\big{]}^{T}.$

The objective of sensing is to estimate $\theta$ and $\alpha$ as the unknown parameters from the received echo signal $\boldsymbol{Y}_{\text{S}}$ in (2), in which the transmitted signal $\boldsymbol{X}$ is known by the H-AP. In this case, the CRB for estimating $\theta$ is adopted as the sensing performance metric²²2As the target information contained in $\alpha$ is hard to extract, in this paper we focus on the CRB for estimating $\theta$, similarly as in prior works [12, 13]., which is given by [10]

$$\mathrm{CRB}(\boldsymbol{S})=\frac{\sigma_{\text{S}}^{2}}{2|\alpha|^{2}L}\frac{\mathrm{tr}(\!\boldsymbol{A}^{H}\!\boldsymbol{A}\boldsymbol{S})}{\mathrm{tr}(\!\boldsymbol{\dot{A}}^{H}\!\boldsymbol{\dot{A}}\boldsymbol{S})\mathrm{tr}(\!\boldsymbol{A}^{H}\!\boldsymbol{A}\boldsymbol{S})-|\mathrm{tr}(\!\boldsymbol{\dot{A}}^{H}\!\boldsymbol{A}\boldsymbol{S})|^{2}},$$

(4)

where we define $\boldsymbol{A}\triangleq\boldsymbol{A}(\theta)$ and $\boldsymbol{\dot{A}}\triangleq\frac{\partial\boldsymbol{A}(\theta)}{\partial\theta}$.

Next, we consider the point-to-point MIMO communication from the H-AP to the ID receiver. The received signal by the ID receiver at symbol $l$ is given by

$$\boldsymbol{y}_{\text{ID}}(l)=\boldsymbol{H}_{\text{ID}}\boldsymbol{x}(l)+\boldsymbol{z}_{\text{ID}}(l),$$

(5)

where $\boldsymbol{z}_{\text{ID}}(l)\in\mathbb{C}^{N_{\text{ID}}\times 1}$ denotes the AWGN at the ID receiver that is a CSCG random vector with zero mean and covariance matrix $\sigma_{\text{ID}}^{2}\boldsymbol{I}_{N_{\text{ID}}}$. With the capacity-achieving Gaussian signaling, the achievable data rate (in bps/Hz) is [11]

$${R}(\boldsymbol{S})=\log_{2}\det\Big{(}\boldsymbol{I}_{N_{\text{ID}}}+\frac{1}{\sigma_{\text{ID}}^{2}}\boldsymbol{H}_{\text{ID}}\boldsymbol{S}\boldsymbol{H}_{\text{ID}}^{H}\Big{)}.$$

(6)

Then, we consider the WPT from the H-AP to the EH receiver, where the EH receiver uses the rectifiers to convert the received radio frequency (RF) signals into direct current (DC) signals for energy harvesting. In general, the harvested DC power is monotonically increasing with respect to the received RF power. As a result, we use the received RF power (energy over a unit time period, in Watt) at the EH receiver as the powering performance metric [1], i.e.,

$${E}(\boldsymbol{S})=\mathrm{tr}(\boldsymbol{H}_{\text{EH}}\boldsymbol{S}\boldsymbol{H}_{\text{EH}}^{H}).$$

(7)

Our objective is to reveal the fundamental performance tradeoff among the estimation CRB $\mathrm{CRB}(\boldsymbol{S})$ in (4), the achievable rate ${R}(\boldsymbol{S})$ in (6), and the received (unit-time) energy ${E}(\boldsymbol{S})$ in (7). Towards this end, we characterize the C-R-E region that is defined as all the C-R-E pairs simultaneously achievable in the multi-functional wireless MIMO system, i.e.,

	$\displaystyle\mathcal{C}\triangleq\big{\{}(\widehat{\mathrm{CRB}},\widehat{{R}},\widehat{{E}})|$	$\displaystyle\widehat{\mathrm{CRB}}\geq\mathrm{CRB}(\boldsymbol{S}),\widehat{{R}}\leq{R}(\boldsymbol{S}),$		(8)
		$\displaystyle\widehat{{E}}\leq{E}(\boldsymbol{S}),\mathrm{tr}(\boldsymbol{S})\leq P,\boldsymbol{S}\succeq\boldsymbol{0}\big{\}}.$

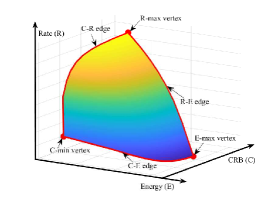
This section characterizes the C-R-E region of the multi-functional MIMO system $\mathcal{C}$ in (8), by finding its Pareto boundary, which corresponds to the set of points at which improving one performance metric will inevitably result in the deterioration of another. The complete Pareto boundary corresponds to a surface in a three-dimensional (3D) space as shown in Fig. 2, which is surrounded by three vertices corresponding to rate maximization (R-max), energy maximization (E-max), and CRB minimization (C-min), respectively, as well as three edges corresponding to the optimal C-R, R-E, and C-E tradeoffs, respectively.

In this section, we present the optimal solution to problem (P1). Notice that (P1) is not convex due to the estimation CRB constraint in (9c). Fortunately, based on the Schur complement, constraint (9c) is equivalent to

$$\begin{bmatrix}\mathrm{tr}(\boldsymbol{\dot{A}}^{H}\boldsymbol{\dot{A}}\boldsymbol{S})-\frac{1}{\Gamma_{\text{S},1}}&\mathrm{tr}(\boldsymbol{\dot{A}}^{H}\boldsymbol{A}\boldsymbol{S})^{\dagger}\\ \mathrm{tr}(\boldsymbol{\dot{A}}^{H}\boldsymbol{A}\boldsymbol{S})&\mathrm{tr}(\boldsymbol{A}^{H}\boldsymbol{A}\boldsymbol{S})\end{bmatrix}\succeq\boldsymbol{0},$$

(10)

where $\Gamma_{\text{S},1}\triangleq\frac{2|\alpha|^{2}L}{\sigma_{\text{S}}^{2}}\Gamma_{\text{S}}$. Thus, by replacing constraint (9c) as that in (10), (P1) is reformulated in a convex form, and can be optimally solved by using the Lagrangian duality method.

Let $\lambda\geq 0$, $\nu\geq 0$, and $\boldsymbol{Z}\triangleq\begin{bmatrix}z_{1}&z_{2}\\ z_{2}^{\dagger}&z_{3}\end{bmatrix}\succeq\boldsymbol{0}$ denote the dual variables associated with the constraints in (9b), (9d), and (10), respectively. The Lagrangian of problem (P1) is

	$\displaystyle\mathcal{L}(\boldsymbol{S},\lambda,\nu,\boldsymbol{Z})=$	$\displaystyle\log_{2}\det\Big{(}\boldsymbol{I}_{N_{\text{ID}}}+\frac{1}{\sigma_{\text{ID}}^{2}}\boldsymbol{H}_{\text{ID}}\boldsymbol{S}\boldsymbol{H}_{\text{ID}}^{H}\Big{)}$		(11)
	$\displaystyle-$	$\displaystyle\mathrm{tr}(\boldsymbol{D}\boldsymbol{S})-\lambda\Gamma_{\text{EH}}+\nu P-\frac{z_{1}}{\Gamma_{\text{S},1}},$

where $\boldsymbol{D}\triangleq\nu\boldsymbol{I}_{M}-\lambda\boldsymbol{H}_{\text{EH}}^{H}\boldsymbol{H}_{\text{EH}}-z_{1}\boldsymbol{\dot{A}}^{H}\boldsymbol{\dot{A}}-z_{2}\boldsymbol{\dot{A}}^{H}\boldsymbol{A}-z_{2}^{\dagger}\boldsymbol{A}^{H}\boldsymbol{\dot{A}}-z_{3}\boldsymbol{A}^{H}\boldsymbol{A}$.

Accordingly, the dual function of (P1) is defined as

$$g(\lambda,\nu,\boldsymbol{Z})=\max_{\boldsymbol{S}\succeq\boldsymbol{0}}\ \mathcal{L}(\boldsymbol{S},\lambda,\nu,\boldsymbol{Z}).$$

(12)

We have the following lemma, which can be verified similarly as in [6, Lemma 1].

Based on Lemma 1, the dual problem of (P1) is defined as

$$(\text{D}1):\min_{\lambda\geq 0,\nu\geq 0,\boldsymbol{Z}\succeq\boldsymbol{0}}\ g(\lambda,\nu,\boldsymbol{Z}),\ \mathrm{s.t.}\ \eqref{D1-constraint}.$$

(14)

Since problem (P1) is reformulated in a convex form and satisfies Slater’s condition, strong duality holds between (P1) and its dual problem (D1) [14]. Therefore, we can solve (P1) by equivalently solving (D1). In the following, we first obtain the dual function $g(\lambda,\nu,\boldsymbol{Z})$ with given dual variables, then search over $\lambda\geq 0$, $\nu\geq 0$, and $\boldsymbol{Z}\succeq\boldsymbol{0}$ to minimize $g(\lambda,\nu,\boldsymbol{Z})$.

This section evaluates the performance of our proposed optimal design. In the simulation, the H-AP is equipped with a ULA of $M=10$ and $N_{\text{S}}=16$ antennas with half-wavelength spacing between consecutive antennas. The target angle is $\theta=\frac{\pi}{3}$, and the reflection coefficient is set as $\alpha=10^{-8}$, accounting for a round-trip path loss of $160$ dB. The ID channel and the EH channel are set as $\boldsymbol{H}_{\text{ID}}=\alpha_{\text{ID}}\widehat{\boldsymbol{H}}_{\text{ID}}$ and $\boldsymbol{H}_{\text{EH}}=\alpha_{\text{EH}}\widehat{\boldsymbol{H}}_{\text{EH}}$, where $\alpha_{\text{ID}}^{2}$ and $\alpha_{\text{EH}}^{2}$ correspond to the path loss of $120$ dB and $60$ dB, respectively, and $\widehat{\boldsymbol{H}}_{\text{ID}}$ and $\widehat{\boldsymbol{H}}_{\text{EH}}$ correspond to the normalized channel accounting for the small-scale fading. The transmission frame length is set as $L=256$. The noise powers at the sensing receiver and the ID receiver, i.e., $\sigma_{\text{S}}^{2}$ and $\sigma_{\text{ID}}^{2}$, are set to be $-80$ dBm.

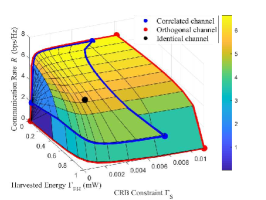
Fig. 3 shows the Pareto boundary of the C-R-E region with $N_{\text{ID}}=N_{\text{EH}}=1$ and $P=50$ dBm. In this figure, we consider the line-of-sight (LoS) channels for the ID and EH channels, i.e., $\widehat{\boldsymbol{H}}_{\text{ID}}=\boldsymbol{a}_{t}^{T}(\theta_{\text{ID}})$ and $\widehat{\boldsymbol{H}}_{\text{EH}}=\boldsymbol{a}_{t}^{T}(\theta_{\text{EH}})$. Furthermore, we set $\theta=0$, $\sin\theta_{\text{ID}}=\frac{2\gamma}{M}$, and $\sin\theta_{\text{EH}}=\frac{4\gamma}{M}$. We consider three cases with $\gamma=0$, $0.4$, and $1$, which correspond to the cases when the sensing, ID, and EH channels are identical, correlated, and orthogonal, respectively. It is observed that when $\gamma=0$, the Pareto boundary is a point, which means that the R-max, E-max, and C-min strategies are identical, and thus the three performance metrics are optimized at the same time. In is also observed that when $\gamma=1$, optimizing one metric (e.g., E-max) leads to poor performances for the other two metrics (e.g., zero rate and highest CRB), thus showing that the three objectives are competing. Furthermore, when $\gamma=0.4$, the C-R-E region boundary is observed to lie between those with $\gamma=1$ and $\gamma=0$, thus showing the C-R-E tradeoff when the channels are correlated.

Next, we evaluate the performance of our proposed design as compared to the benchmark scheme based on time switching. In this scheme, the transmission duration is divided into three portions, $t_{\text{ID}}\geq 0$, $t_{\text{EH}}\geq 0$, and $t_{\text{S}}\geq 0$, with $t_{\text{ID}}+t_{\text{EH}}+t_{\text{S}}=1$, during which the H-AP employs the transmit covariance matrices $\boldsymbol{S}_{\text{ID}}$, $\boldsymbol{S}_{\text{EH}}$, and $\boldsymbol{S}_{\text{S}}$, respectively. The corresponding communication rate, harvested energy, and estimation CRB in this scheme are expressed as ${R}_{\text{TS}}(t_{\text{ID}},t_{\text{EH}},t_{\text{S}})=t_{\text{ID}}{R}(\boldsymbol{S}_{\text{ID}})$, ${E}_{\text{TS}}(t_{\text{ID}},t_{\text{EH}},t_{\text{S}})=t_{\text{ID}}{E}(\boldsymbol{S}_{\text{ID}})+t_{\text{EH}}{E}(\boldsymbol{S}_{\text{EH}})+t_{\text{S}}{E}(\boldsymbol{S}_{\text{S}})$, and $\mathrm{CRB}_{\text{TS}}(t_{\text{ID}},t_{\text{EH}},t_{\text{S}})=\mathrm{CRB}(t_{\text{ID}}\boldsymbol{S}_{\text{ID}}+t_{\text{EH}}\boldsymbol{S}_{\text{EH}}+t_{\text{S}}\boldsymbol{S}_{\text{S}})$, respectively. Then, we optimize $t_{\text{ID}}$, $t_{\text{EH}}$, and $t_{\text{S}}$ to achieve different C-R-E tradeoffs.

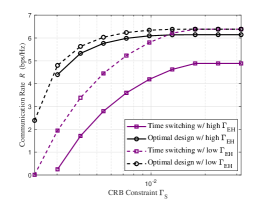
Fig. 4 shows the obtained communication rate ${R}$ by (P1) versus the estimation CRB constraint $\Gamma_{\text{S}}$, in which two EH constraints $\Gamma_{\text{EH}}=0.5{E}_{\mathrm{max}}$ (high $\Gamma_{\text{EH}}$ case) and $\Gamma_{\text{EH}}=0.05{E}_{\mathrm{max}}$ (low $\Gamma_{\text{EH}}$ case) are considered. Here, we set $N_{\text{ID}}=N_{\text{EH}}=4$ and $P=40$ dBm, and generate $\widehat{\boldsymbol{H}}_{\text{ID}}$ and $\widehat{\boldsymbol{H}}_{\text{EH}}$ as CSCG random matrices with each element being zero mean and unit variance. It is observed that under each EH constraint, our proposed optimal design outperforms the time switching scheme. For the case when $\Gamma_{\text{EH}}$ is high, the performance gap is observed to be significant over the whole regime of $\Gamma_{\text{S}}$. By contrast, for the case when $\Gamma_{\text{EH}}$ is low, the time switching scheme is observed to perform close to the optimal design when $\Gamma_{\text{S}}$ becomes large. This is due to the fact that both schemes can achieve the R-max vertex with the maximum communication rate in this case.

This paper studied the fundamental C-R-E tradeoff performance limits for a new multi-functional MIMO system integrating triple functions of sensing, communication, and powering. We characterized the Pareto boundary of the so-called C-R-E region, by optimally solving a new MIMO communication rate maximization problem subject to both energy harvesting and estimation CRB constraints. It was shown that the resultant C-R-E tradeoff highly depends on the correlations of the ID, EH, and sensing channels, and the proposed optimal design significantly outperforms the benchmark scheme based on time switching.