Transport properties of multilayer graphene

Ultra-clean materials such as graphene offer a new perspective on electronic transport. At low enough temperatures, momentum-relaxing scattering of the electrons such as the scattering off phonons or impurities is sub-dominant and the dominant source of collisions are the collisions of the electrons with themselves. This is the realm of electron hydrodynamics Lucas and Fong (2018). In the hydrodynamic regime the electron-electron scattering rate $\tau_{ee}^{-1}$ is larger than the electron-phonon scattering rate $\tau_{ep}^{-1}$. Both monolayer and bilayer graphene have garnered much attention in recent years for their supposed hydrodynamic transport Bandurin et al. (2016); Levitov and Falkovich (2016); Sulpizio et al. (2019); Svintsov et al. (2012); Pellegrino et al. (2017); Bistritzer and MacDonald (2009); Müller et al. (2009); Andreev et al. (2011); Narozhny et al. (2015). In the present paper, we focus on a related material: multilayer graphene.

The Boltzmann equation is an equation of motion for the distribution function of particles and has traditionally been applied to the classical kinetic theory of gases. Extending this approach to the study of electron gases in graphene and related materials leads to the celebrated quantum Boltzmann equation (QBE) Greenwood (1958); Fritz et al. (2008); Lux and Fritz (2013, 2012); Dumitrescu (2015); Müller and Sachdev (2008); Zarenia et al. (2019a, b).

In recent work, the present authors presented the QBE formalism for bilayer graphene Nguyen et al. (2020). It was then shown in Ref. Wagner et al. (2020) that the QBE results agree well with experimental measurements of the electrical conductivity of suspended bilayer graphene in Nam et al. (2017). Despite its success, the QBE is a heavy-handed approach and this led to the development of the two-fluid model. In bilayer graphene, the low-energy bandstructure consists of two gapless quadratic bands which can be populated with electrons and holes. The dynamics of the electron and hole fluids can be captured accurately from simple hydrodynamic equations, at least for the calculation of the electrical conductivity and thermopower Wagner et al. (2020).

In this work, we generalize the formalism we developed for BLG to multilayer graphene (MLG), in particular, we focus on Bernal (AB) stacked multilayers. We consider the special case of an even number of layers $N$, to avoid the additional complication of the linear band that arises for odd $N$. We study the regime near charge neutrality, i.e. $\beta\mu\lesssim 1$, where $\beta$ is inverse temperature and $\mu$ is the chemical potential. In fact, in this regime, we expect the behaviour for even $N$ and odd $N+1$ to be very similar, since the density of states is dominated by the quadratic bands. We use the QBE to compute the electrical conductivity, the thermal conductivity and thermopower for multilayers with $N=2$ to $N=8$ layers. We discuss how the transport properties evolve, as the number $N$ of layers is increased. In particular, in previous work Wagner et al. (2020); Nguyen et al. (2020), the present authors discussed two signatures of the hydrodynamic regime: The Wiedemann-Franz law violation and the fast increase of the electrical conductivity away from charge neutrality. We will show that both of the signatures remain, as we increase the number of layers in our graphene multilayer. We then develop a hydrodynamic approach in terms of a multicomponent fluid and show that it accurately matches the QBE predictions.

There has been previous theoretical work on transport in multilayer graphene using the Kubo formula Nakamura and Hirasawa (2008). Ref. Min et al. (2011) does study MLG using the Boltzmann formalism, however, they focus on the case where impurities are the main source of scattering. Ref. Lindsay et al. (2011) calculates the thermal conductivity due to phonons, however they do not explore the electronic contribution to the thermal conductivity.

The electrical conductivity of multilayer graphene has been measured experimentally for a range of temperatures and densities Nam et al. (2016, 2018). In Ref. Wang et al. (2008), measurements on the minimum of the electrical conductivity for different numbers of layers are reported. Further experiments by a different experimental group have been reported Ye et al. (2011), however, they consider the high-density regime which is the opposite limit to the one we will consider in this work.

The structure of our paper is as follows. We start by introducing the tight-binding model for MLG and we discuss the screening of the Coulomb interaction in MLG. We then introduce the QBE formalism and present the numerical results for different numbers of layers. Finally, we discuss how many of the salient features of our numerics can be captured by a simple hydrodynamic model.

For the Bernal (AB) stacking of $N$ graphene multilayers shown in Fig. 1, the tight-binding (Bloch) Hamiltonian expanded near the $K$ and $K^{\prime}$ valleys is the $2N\times 2N$ matrix Min and MacDonald (2008); Nakamura and Hirasawa (2008); Koshino and Ando (2007); Latil and Henrard (2006); Guinea et al. (2006); Ohta et al. (2007); Nilsson et al. (2008); Koshino and McCann (2010)

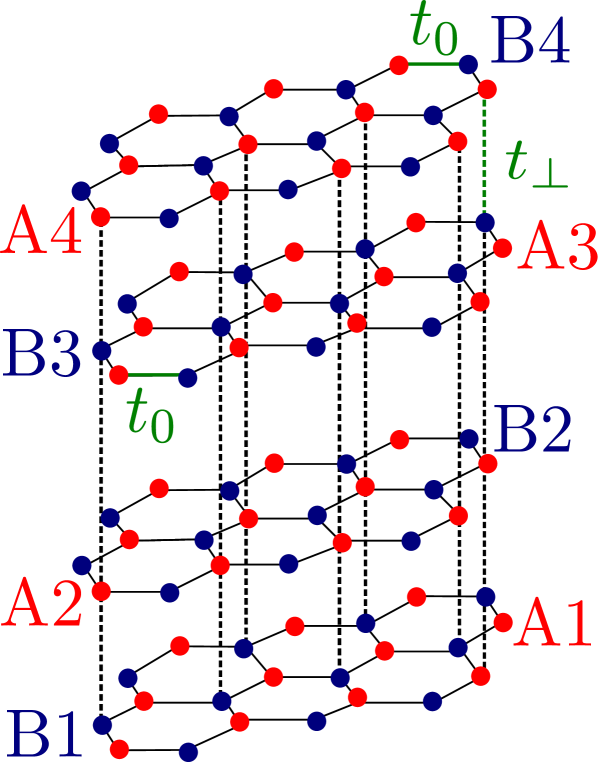
Here $\pi=\xi p_{x}+ip_{y}$, with valley index $\xi=\pm$. The Fermi velocity is $v=\frac{\sqrt{3}}{2}at_{0}$, where $t_{0}$ is the intralayer hopping parameter and $a$ is the lattice constant. $t_{\perp}$ is the interlayer hopping. The wavefunction is $\psi=(\varphi_{A_{1}},\varphi_{B_{1}},\varphi_{A_{2}},\varphi_{B_{2}},\cdots,\varphi_{A_{N}},\varphi_{B_{N}})$, where $\varphi_{A_{i}(B_{i})}$ is the wave function of an electron at site $A_{i}(B_{i})$.

At low energies, we can focus on the gapless bands. We write down a low energy $N\times N$ Hamiltonian for these $N$ quadratic bands, which we label with $r=(R,\sigma)$ where $R=1,\dots,N/2$ and $\sigma=\pm 1$. The energies are

where the mass is

with $m^{*}=t_{\perp}/2v^{2}$. Therefore the bands appear in pairs labelled by the same $R$ which have the same mass. For a fixed $R$, we have the same bandstructure as in BLG. We call the corresponding Bloch wavefunctions $|\psi_{R\sigma}(\mathbf{p})\rangle$. The matrix elements for the Bloch functions are

where $\cos\theta_{p}=\mathbf{p}\cdot\hat{\mathbf{x}}$. The derivations of the effective mass $m_{R}$ as well as the matrix elements (42) are left for Appendix A. There will be no vertex coupling electrons with different $R$ in the Coulomb interaction. For a pair of bands with the same value of $R$, the matrix elements are the same as for BLG. Using this result, one can perform the classic Lindhart calculation for the polarization $\Pi^{0}(\vec{q},\omega)$ in the limit $\beta\mu\lesssim 1$ and $\beta q^{2}/m\lesssim 1$. This is a calculation analogous to Refs. Lv and Wan (2010); Min et al. (2012) and the details are in Appendix B. We focus on the static polarization, which is valid at low enough temperatures. The result for the polarization is

where $N_{f}=2\times 2$ accounts for the spin and valley degrees of freedom. In the screening calculation we have assumed that the screening due to the phonons is negligible. The Thomas-Fermi screening wavevector is then given by

where $\alpha$ is the electromagnetic fine-structure constant. We will use the fully screened Coulomb interaction $V(q)=2\pi\alpha/q_{TF}(q)$, which is a good approximation at low temperatures, where the typical momentum of electrons is much smaller than $q_{TF}$. Now we approximately have the behaviour $q_{TF}\propto N$. Since each electron can now scatter off $N$ species of electrons, the electron-electron scattering rate will be $\tau_{ee}^{-1}\propto N/q_{TF}^{2}\propto 1/N$.

Away from charge neutrality, one needs to include momentum-relaxing scattering in order to obtain a well-defined conductivity. Based on the results in bilayer graphene, we expect electron-phonon collisions to be the dominant source of momentum-relaxing scattering and hence this is the only momentum-relaxing mechanism that we include in our calculations Wagner et al. (2020). Depending on the experimental conditions, we may envisage electron-impurity and electron-boundary scattering as well and this would be a simple extension of the present calculation. The phonon scattering is proportional to band mass and we extract the proportionality constant by comparing the BLG results to available experimental data Wagner et al. (2020). The QBE is an evolution equation for the distribution function $f_{r}(\mathbf{k},\mathbf{x},t)$ of the particles of species $r$ of the form

where $\mathbf{v}_{r}(\mathbf{k})=\partial_{\mathbf{k}}\epsilon_{r}(\mathbf{k})$, $e<0$ is the electron charge and the collision integral on the RHS includes electron-electron and electron-phonon collisions. The electron-electron collision integral can be derived from the Kadanoff-Baym equations Kadanoff and Baym (1962) using the Born approximation. The derivation is identical to the BLG case in Ref. Nguyen et al. (2020). The electron-phonon collision integral uses the simple relaxation-time approximation with scattering rate

where $D$ is the deformation potential, $\rho$ is the mass density of multilayer graphene and $c$ is the speed of sound. We also define the corresponding dimensionless parameter $\alpha_{ep}=\beta\tau_{ep}=\beta m^{*}/m_{r}\tau_{ep,r}^{-1}$. The full details of the QBE are shown in appendix C. We note that $\rho\propto N$ and $c=\textrm{const.}$, so assuming that $D$ only depends weakly on $N$, we have $\alpha_{ep}\propto 1/N$. We now see that both the electron-electron and the electron-phonon scattering rates behave like $1/N$, although the reasons behind this scaling are very different for the two scattering mechanisms. Based on this simple scaling, it stands to reason that the hydrodynamic window in multilayer graphene is similar to that of BLG: $\tau_{ee}^{-1}/\tau_{ep}^{-1}$ is only weakly $N$-dependent. Since we successfully applied a hydrodynamic model to BLG Wagner et al. (2020), we expect this to work for MLG as well.

In order to solve the QBE, we expand the distribution function in terms of $4N$ basis functions. Based on our previous work Wagner et al. (2020) this is a sufficient number of basis functions to obtain a convergent result. The QBE then turns into an equation for the expansion coefficients in front of the basis functions. Once we know the perturbation of the distribution function due to an applied thermal gradient $\nabla T$ or electric field $\mathbf{E}$, we can compute the electrical current

and heat current

We define the electrical conductivity $\sigma$, the thermal conductivity $K$ and the thermopower $\Theta$ by

Note that the open circuit thermal conductivity $\kappa$ measuring the heat current in the absence of electrical current is given by $\kappa=K-T\Theta\sigma^{-1}\Theta$. In the absence of a magnetic field, the transport coefficients are diagonal. In Fig. 2 we plot the dimensionless transport coefficients

for different values of $N$.

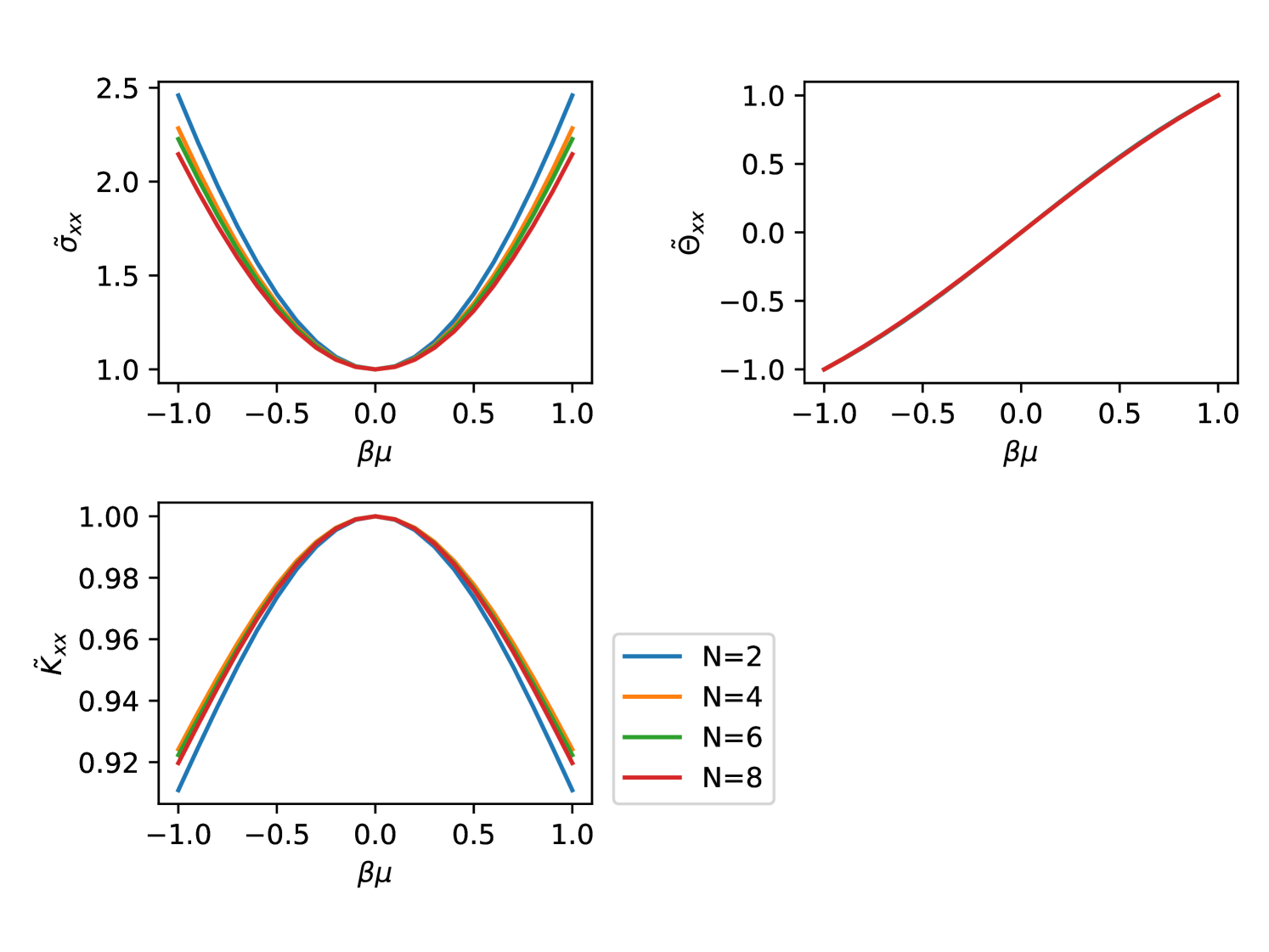
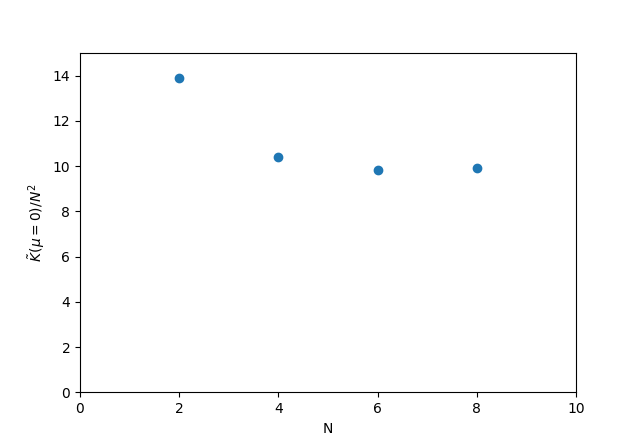
If we could treat the $N$-layer multilayer as $N/2$ independent bilayers, then we would expect the transport coefficients to increase proportionally to $N$. However, this is not what happens. Indeed we find approximately $K(\beta\mu=0)\propto N^{2}$ in Fig. 3. The reason for this behaviour is that $K$ at charge neutrality is limited by collisions with phonons – it would diverge in the absence of phonon scattering since Coulomb scattering does not relax the mode where all carriers move at the same velocity. Recall the formula from basic kinetic theory $K\sim\Lambda k_{B}^{2}n\tau_{ep}T/m$, where $\Lambda k_{B}$ is the heat capacity per particle and $n$ is the number density. Now $\tau\propto 1/N$ as explained in the previous section. We also have $n\propto N$. This explains the observed $K(\beta\mu=0)\propto N^{2}$ behaviour.

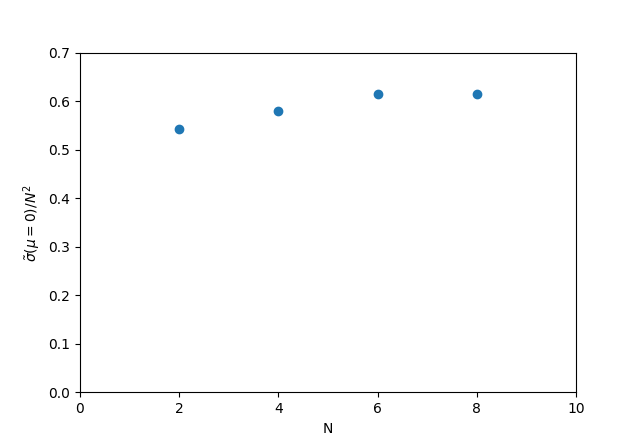
We plot the results for the electrical conductivity at charge neutrality as a function of $N$ in Fig. 4. We observe that the conductivity scales with $N$ approximately as $\sigma(\beta\mu=0)\propto N^{2}$. Recall the Drude formula $\sigma\sim e^{2}n\tau/m$, where $\tau$ is the collision time for current-relaxing collisions. For different species the individual conductivities will add up, ie $\sigma\sim\sum_{r}e^{2}n_{r}\tau_{r}/m_{r}$. $\sigma(\beta\mu=0)$ is well-defined even in the absence of phonons and indeed electron-electron collisions will dominate the current relaxation. As we increase $N$, we increase the density of states and hence the screening wavevector scales approximately as $q_{TF}\propto N$ and hence the potential scales as $V\sim 1/N$. Therefore Fermi’s Golden rule for scattering of particles of species $r$ off particles of species $r^{\prime}$ yields $\tau_{rr^{\prime}}^{-1}\propto|V|^{2}\propto 1/N^{2}$. The scattering time for species $r$ then roughly scales as $\tau_{r}^{-1}\equiv\sum_{r^{\prime}}\tau_{rr^{\prime}}^{-1}\propto 1/N$. So $\tau_{r}\propto N$ and with $n_{r}\propto m_{r}$, we find $\sigma\sim\sum_{r}e^{2}n_{r}\tau_{r}/m_{r}\propto\sum_{r}\tau_{r}\propto N^{2}$, as in the numerical results.

Let us discuss two signatures of the hydrodynamic regime: (i) the ratio $\sigma(\beta\mu=1)/\sigma(\beta\mu=0)$ and (ii) the Wiedemann-Franz law violation. The ratio $\sigma(1)/\sigma(0)$ stays relatively constant as $N$ is increased. Recall that for bilayer graphene, the reason for the large value of $\sigma(1)/\sigma(0)$ is that $\sigma(\beta\mu=0)$ is limited by electron-electron collisions, which operate on a time-scale $\tau_{ee}$. On the other hand, away from CN the momentum mode carries charge and this momentum mode is relaxed on a much longer time-scale $\tau_{ep}$. Since $\tau_{ep}\gg\tau_{ee}$ in the hydrodynamic regime, charge transport is greatly enhanced away from CN. Since both $\tau_{ee}$ and and $\tau_{ep}$ scale proportional to $N$, $\sigma(1)/\sigma(0)$ does not vary significantly with $N$. In the hydrodynamic regime, the Lorenz number is much larger than predicted by the Wiedemann-Franz law. Since $\sigma$ increases as fast as $K$ with $N$, the violation of the Wiedemann-Franz law at charge neutrality will also remain relatively constant as a function of $N$. We show plots of $\sigma(1)/\sigma(0)$ and the Lorenz number in Appendix E.

In Fig. 5 we show the results for the three transport properties considered for the representative case of $N=8$. Other even values of $N$ yield similar results. As $N\to\infty$ and we approach the graphite limit, our numerics become unmanageable and a full 3d theory becomes necessary, where the bands are dispersive along $k_{z}$, instead of having large number $N$ of 2d bands as in our 2d model. In fact, due to the approximations we have made, the low energy theory we have derived is valid in the limit $N\ll 100$ ¹¹1In (21), the gap $\Delta_{r}=\varepsilon_{r}^{+}(p=0)-\varepsilon_{r}^{-}(p=0)=2\gamma\cos(r\pi/(N+1))$. The smallest gap therefore occurs when $r=\frac{N/2}{N+1}$ and is $\Delta_{\textrm{min}}\approx 2\gamma\sin(\pi/N)\approx 2\gamma\pi/N$. We want the gap to be so large that we can neglect the gapped bands, i.e. $\Delta_{\textrm{min}}\gg\frac{1}{\beta}$. Using $\gamma\approx 0.3$eV McCann and Koshino (2013) and for $T=40K$ this leads to $N\ll 100$. .

Following the usual procedure for deriving hydrodynamic equations from kinetic theory, we can obtain the fluid equations from the full QBE. We have $r$ species of fermions in the low energy theory, and in the hydrodynamic description, we can associate each fluid species with a mean velocity $\mathbf{u}^{r}$. The equation of motion that follows from the QBE for $\mathbf{u}^{r}$ under an applied electric field $\mathbf{E}$ and thermal gradient $\mathbf{\nabla}T$ is

where $\tau_{rr^{\prime}}$ is the effective scattering time of particles of species $r$ off particles of species $r^{\prime}$ due to Coulomb interactions, $\tau_{ep,r}$ is the effective electron-phonon scattering time for species $r$ and $\Lambda^{r}$ is the entropy per particle:

Solving the fluid equations for a steady state flow yields an expression for $\mathbf{u}^{r}$. The electrical current is then given by

and the heat current by

The detailed derivation is in Appendix D.

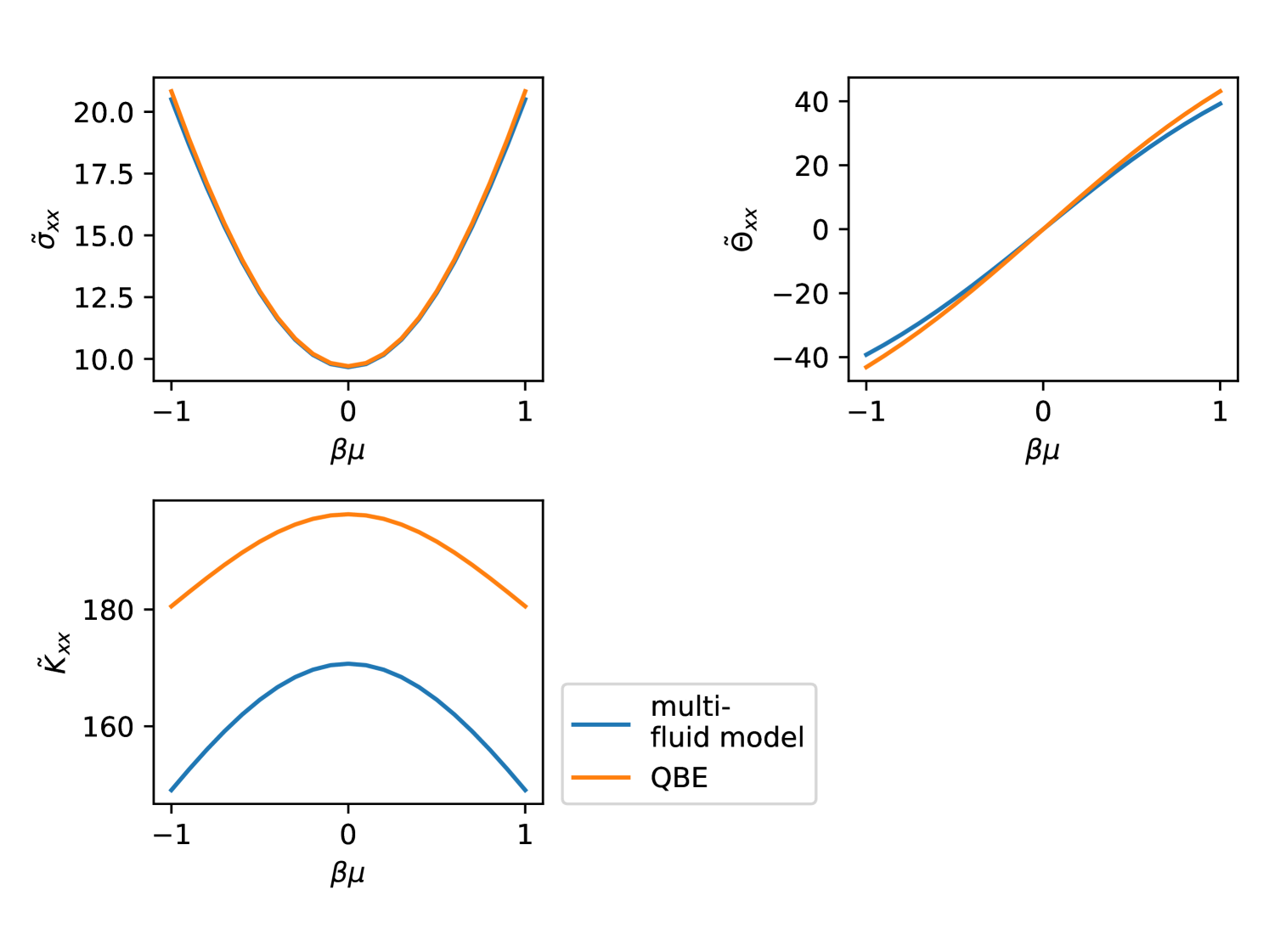
In Fig. 5 we compare the results from the multi-fluid model and the QBE and find that for the electrical conductivity the agreement is excellent, whereas for the thermal conductivity, the qualitative behaviour is correct but the quantitative agreement is off by around 20%. The reason for this is that the multi-fluid model is equivalent to solving the QBE by using only $N$ basis functions in the expansion of the distribution function. These basis functions correspond to uniform motion with velocity $\mathbf{u}^{r}$ of the fermions of species $r$. For an applied electric field, these modes capture the charge transport accurately, as exemplified by the good overlap in Fig. 5. On the other hand, for an applied thermal gradient, we do not accurately capture the heat transport with those modes. We found the same situation in Ref. Wagner et al. (2020) for BLG.

The success of the multi-fluid model as well as the two fluid model in our previous work on BLG Wagner et al. (2020) suggests that the hydrodynamic description of electrons in bilayer and multi-layer graphene is accurate. This once again confirms the idea that electrons in strongly interacting systems can be considered as (multi-component) fluids Lucas and Fong (2018).

We have applied the quantum Boltzmann formalism to study the transport properties of multilayer graphene. We find results very similar to bilayer graphene. We introduce a hydrodynamic model which agrees accurately with the QBE results for the electrical conductivity and thermopower. We hope that future experiments on transport in multilayer graphene will reveal whether the QBE formalism performs as well for multilayer graphene as it does for BLG, although we see no apparent reason why it should not.

We have only studied even $N$ in this paper. For odd $N$, the low energy theory consists of $N-1$ parabolic bands and one Dirac cone. However, in the regime $\beta\mu\lesssim 1$ the density of states will be dominated by the quadratic bands. Therefore the results for odd $N$ are expected to be similar to the results for even $N$, as long as one accounts for the different values of the band masses.

The behaviour of the transport properties as the number $N$ of layers is varied shows some interesting features. Firstly, the thermal conductivity at charge neutrality (CN) $K(\beta\mu=0)$ is approximately proportional to $N^{2}$. This is due to the fact that the thermal conductivity at CN is limited by phonons and the phonon scattering time is proportional to $N$, so $K(\beta\mu=0)\propto n\tau\propto N^{2}$. The electrical conductivity at CN $\sigma(\beta\mu=0)\propto N^{2}$ as well, but for a different reason. In contrast to $K(\beta\mu=0)$, $\sigma(\beta\mu=0)$ is limited by electron-electron collisions. As $N$ is increased, the screening increases and so the electron scattering time $\tau\propto N$, leading to $\sigma(\beta\mu=0)\propto n\tau\propto N^{2}$. Put together, this implies that the violation of the Wiedemann-Franz law stays constant as $N$ is increased. Finally, $\sigma(\beta\mu=1)/\sigma(\beta\mu=0)$, which is another measure of the relative size of the electron-electron and the electron-phonon scattering times. is relatively flat as a function of $N$.

In future work, we plan to compute the viscosity for MLG. Adding the viscosity to the multi-fluid model will give us the Navier-Stokes equations, which can then be used to simulate the electron fluid in MLG for realistic geometries. We expect those simulations to yield interesting results such as the vortices which have been predicted for single-layer graphene Levitov and Falkovich (2016) and negative resistivity, which has been seen in experiments in single-layer graphene Bandurin et al. (2016). One can go even further and consider spin-transport by applying a weak magnetic field. We then have a very interesting multi-component fluid which carries charge, heat and spin.

This work was supported by EPSRC grants EP/N01930X/1 and EP/S020527/1. DXN was supported partially by Brown Theoretical Physics Center.