Transverse circular photogalvanic effect associated with Lorentz-violating Weyl fermions
Nonlinear optical responses of quantum materials have recently undergone dramatic developments to unveil nontrivial geometry and topology. A remarkable example is the quantized longitudinal circular photogalvanic effect (CPGE) associated with the Chern number of Weyl fermions, while the physics of transverse CPGE in Weyl semimetals remains exclusive. Here, we show that the transverse CPGE of Lorentz invariant Weyl fermions is forced to be zero. We find that the transverse photocurrents of Weyl fermions are associated not only with the Chern numbers but also with the degree of Lorentz-symmetry breaking in condensed matter systems. Based on the generic two-band model analysis, we provide a new powerful equation to calculate the transverse CPGE based on the tilting and warping terms of Weyl fermions. Our results are more capable in designing large transverse CPGE of Weyl semimetals in experiments and are applied to more than tens of Weyl materials to estimate their photocurrents. Our method paves the way to study the CPGE of massless or massive quasiparticles to design next-generation quantum optoelectronics.
The past few years have witnessed rapid progress in our understanding of nonlinear optical responses of topological quantum materials Hasan2010TI ; Zhang2011 ; Bansil2016 ; Armitage2018 ; Nagaosa2020Transport ; Hasan2021Weyl ; Ma2021Topology ; Orenstein2021 ; Lv2021Exp ; Bao2022 ; acoustics2022 . Nonlinear electromagnetics creates new opportunities to uncover, probe, and control wavefunction geometry and topology which offers promise for future applications mciver2012control ; Wu2016 ; chan2017photocurrents ; Ma2017 ; Wu2017Giant ; xu2018Electrically ; BCYin2022 ; BCMa2022 . In non-magnetic materials, circular photogalvanic effects (CPGE) inducing a non-oscillating direct current can directly probe the band-resolved Berry curvature Ma2017 ; Nagaosa2020Transport ; Orenstein2021 . In this regard, Weyl semimetals hosting magnetic monopoles in momentum space provide an ideal platform to measure Berry curvature Armitage2018 ; xu2015 ; LVPRX2015 . It has been demonstrated theoretically that longitudinal CPGE of a chiral Weyl semimetal is quantized to the Chern number of Weyl fermions de2017quantized1 ; chang2017unconventional ; Chang2018 ; Flicker2018 . While recent experiments realized and verified the signature of quantized CPGE in topological chiral crystal RhSi family RhSiExp1 ; RhSiExp2 ; RhSiExp3 ; RhSiExp4 ; RhSiExp6 ; rees2020helicity ; ni2020linear ; ni2021giant ; RhSiExp5 . Surprisingly, the case of transverse CPGE is more important in practical application because the current flows perpendicular to the direction of the polarization of incident light which can be easily detected and utilized in next-generation light sensors, solar cells, and information processing. Despite intensive experimental studies and the giant transverse photocurrents detected in different Weyl materials Yan2017 ; Chang2018 ; Ma2019Nonlinear ; Osterhoudt2019 ; liu2020semimetals ; Ma2021Topology ; acoustics2022 ; mciver2012control ; Yuan2014TCPGE ; Ma2017 ; chang2020unconventional , a comprehensive and fundamental physical interpretation of the transverse CPGE in Weyl semimetal is still exclusive. This hinders the progress of the application of Weyl semimetals as the next-generation quantum photodetectors.
Therefore, it is crucial to explore the physics behind transverse CPGE and reveal the criteria to observe a large value of it. The second-order tensor of injection current is written as de2017quantized1 ; chang2017unconventional
| (1) |
where , is the energy difference between bands and , is the Fermi-Dirac distribution of the band , , , and is the off-diagonal Berry connection or interband transition matrix element. Numerically, one of the obstacles is too expensive to achieve transverse CPGE based on the product of a matrix element and joint density of state using Eq. 1 de2017quantized1 because it requires a very high density of -mesh near the Weyl nodes to obtain reliable results.
To study the CPGE response of a Weyl semimetal, we first start with a relativistic Weyl Hamiltonian:
| (2) |
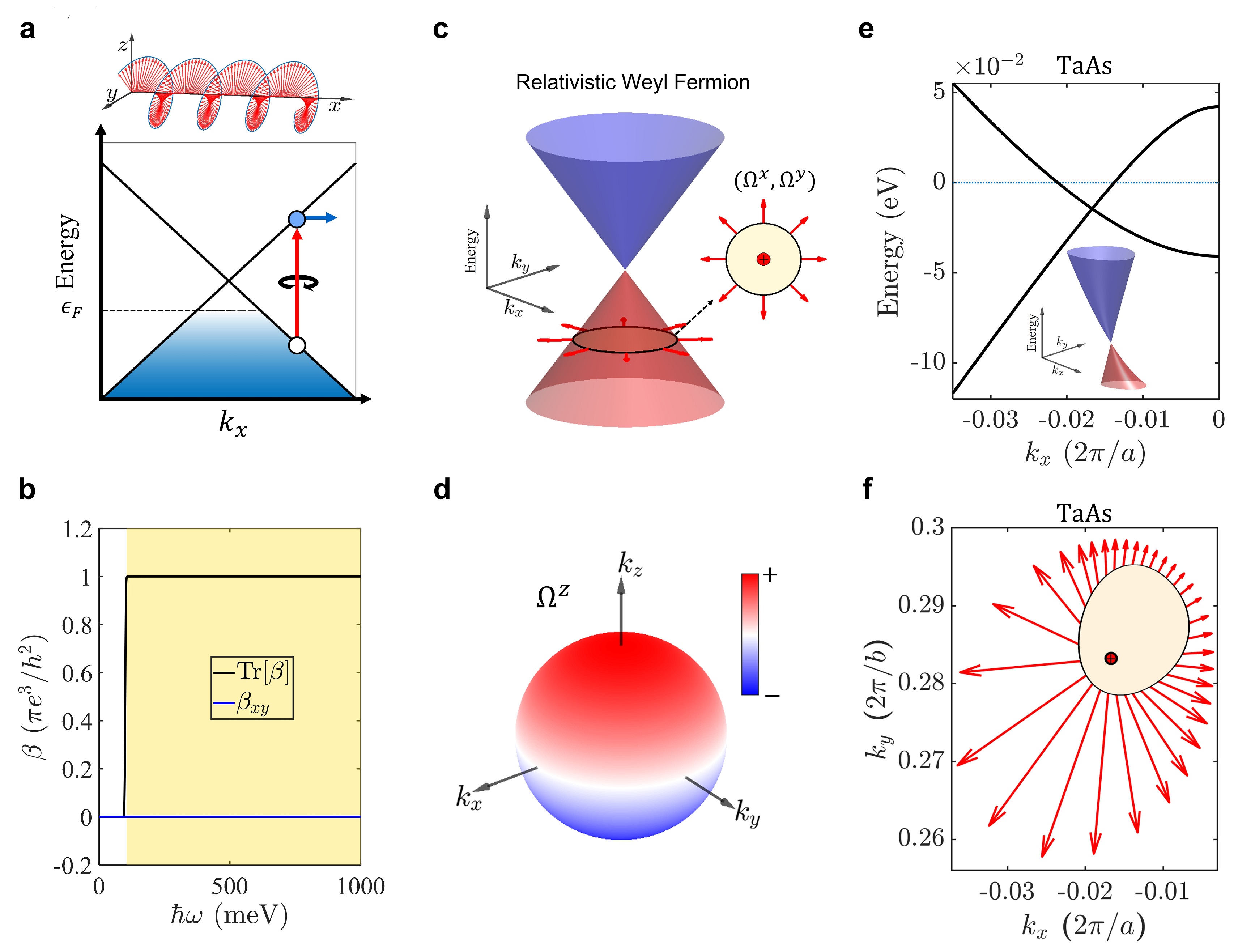
where is velocity, is Planck’s reduced constant, is momentum and are the Pauli matrices. We can see that, for isotropic relativistic Weyl fermions (Fig. 1a), the CPGE trace is quantized which are consistent with previous theory by Tr, where is the monopole charge of the Weyl fermion (Fig. 1b) de2017quantized1 . In contrast, all the off-diagonal components of the CPGE tensor for isotropic relativistic Weyl fermions are zero.
To better understand the result, we perform symmetry analysis concerning the Weyl point in the momentum space. In a relativistic Weyl Hamiltonian, an injection current of is proportional to the integral of at the k-points where optical transition happened, here is Berry curvature component along -direction. For a relativistic Weyl fermion which preserves the Lorentz symmetry, its dispersion and Berry curvatures are isotropic along all directions (Figs. 1c and 1d). In this case, concerning the Weyl point in the momentum space, is an odd function in -direction and even in other directions (details are in Supplementary Section I). Thus, in this condition, () is an even (odd) with respect to k. This explicitly demonstrates that the integral of over the Fermi surface is zero, indicating the off-diagonal elements of CPGE vanishes for the relativistic Weyl node.
Isotropic Weyl semimetal is equivalent to the Lorentz invariant Weyl fermion and respects the Lorentz symmetry soluyanov2015type ; LVPRX2015 (Fig. 1c). In fact, the actual band dispersion in the real materials will inevitably have warping and tilting, which break the Lorentz invariance of Weyl fermions from quantum field theory. In Fig. 1e, we show the band structure of TaAs around a Weyl node xu2015 ; huang2015weyl ; WangPRX2015 , showing the Weyl node is not strongly isotropic and does not respect the Lorentz symmetry. In this case, the Berry curvature penetrating through a closed Fermi surface is asymmetric, so anisotropic excitation can occur (Fig. 1f).
Our above analysis shows that the Lorentz violation terms guarantee the off-diagonal components of the CPGE tensor. Next, we aim to establish exact correspondence between the off-diagonal components of the CPGE tensor and the Lorentz violation term by inviting new formulae and comparing the results with that of Eq. 2. We next discuss under what conditions the off-diagonal components of the CPGE tensor remain non-zero.
The effects of warping corrections.
Firstly, we consider the warping correction terms in the Weyl Hamiltonian expressed as
| (3) |
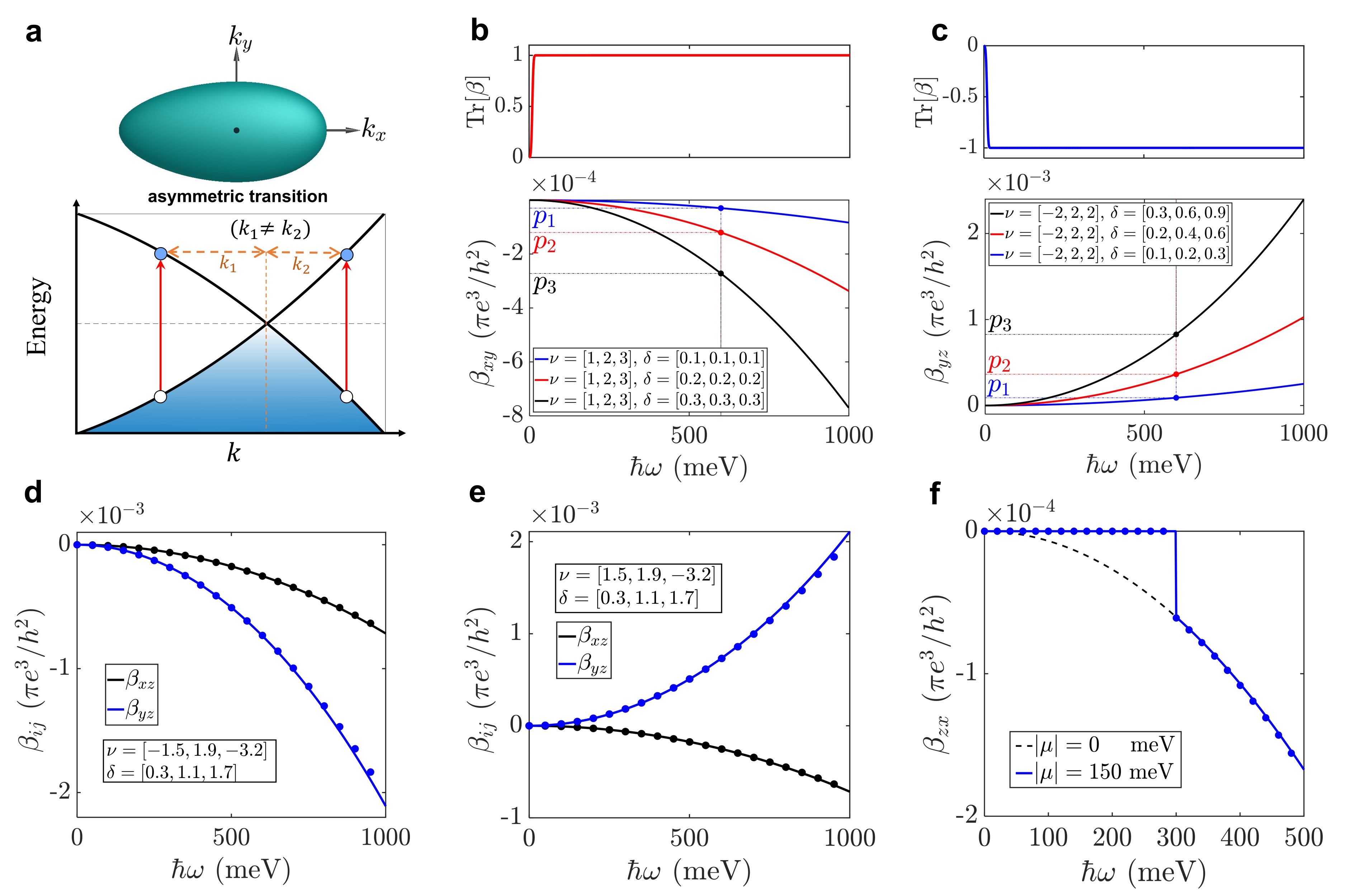
where is velocity, is warping corrections to Hamiltonian, and are the Pauli matrices. In the limit, , the model reduces to the Hamiltonian describing a standard Weyl point. After the inclusion of warping corrections, the Fermi surface is an asymmetric tapered oval centered away from the nodal point (Fig. 2a, top panel). As a result, for a fixed frequency of the laser, the optical transitions becomes anisotropic around the Weyl fermions (Fig. 2a, bottom panel).
To make a canonical formalism and precise that relates transverse CPGE with the warping correction terms of Hamiltonian, we first consider the case of the same value of in all three directions (Fig. 2b). Consistent with our previous analysis, nonzero transverse CPGE appears due to the breaking of Lorentz symmetry. Using as an example, one can see it scales linearly with the power of two of the warping term . Same for all the other transverse CPGE components (details are in Supplementary Section II). Then, we consider another parameter set, where the velocity terms are changed to reverse the Chern number and the warping terms are different (Fig. 2c). We can see the scaling between the transverse CPGE component and the warping terms is still valid. What is more, compared to Fig. 2b, the signs of transverse CPGE components are flipped in Fig. 2c. This indicates transverse CPGE component of a Weyl fermion is also related to its Chern number. We can also find that the amplitude of the transverse CPGE component decreases with the increase of velocity terms of Weyl fermions. Having determined the detailed transverse CPGE of different models (details are in Supplementary Section II), we can elucidate the correspondence between the warping correction and the transverse CPGE response. Our detailed analysis shows that the off-diagonal components of the CPGE tensor of the warping correction terms in the Weyl Hamiltonian have the form
| (4) |
The fitting performance of the above equation to the numerically direct calculation of the off-diagonal components of the CPGE tensor are compared in Fig. 2d,e for some arbitrary values of and . It can be seen that there is good agreement between both spectra.
In Eq. 4, we are setting the Fermi level exactly at the energy of Weyl nodes. In real materials, there will be an energy difference between the Weyl point energy and the Fermi energy (). To further examine the effect of on photocurrent, we compute the transverse CPGE as a function of photon energy for different values of (Fig. 2f). The abruptness of the jump in photocurrents at the characteristic photon energy, , depends on the Fermi energy and can be expressed as:
| (5) |
where is Heaviside step function. Comparing the fitting performance of the above equation with the numerically direct calculation shows that this formula corresponds to a clear physical picture of transverse CPGE of Weyl Hamiltonian with the warping correction terms. Our Eq. 5 shows that obtaining a large transverse CPGE response requires band structures to possess strong warping terms.
The effects of tilted velocity.
Another way to generate the off-diagonal components of the CPGE tensor is to consider the velocity tilting of the cone term in the Hamiltonian. The most general low-energy effective model describing a Weyl Hamiltonian has this form
| (6) |
where is velocity, is tilting velocity which breaks the degeneracy between the bands at k and -k, is chemical potential, are the Pauli matrices.
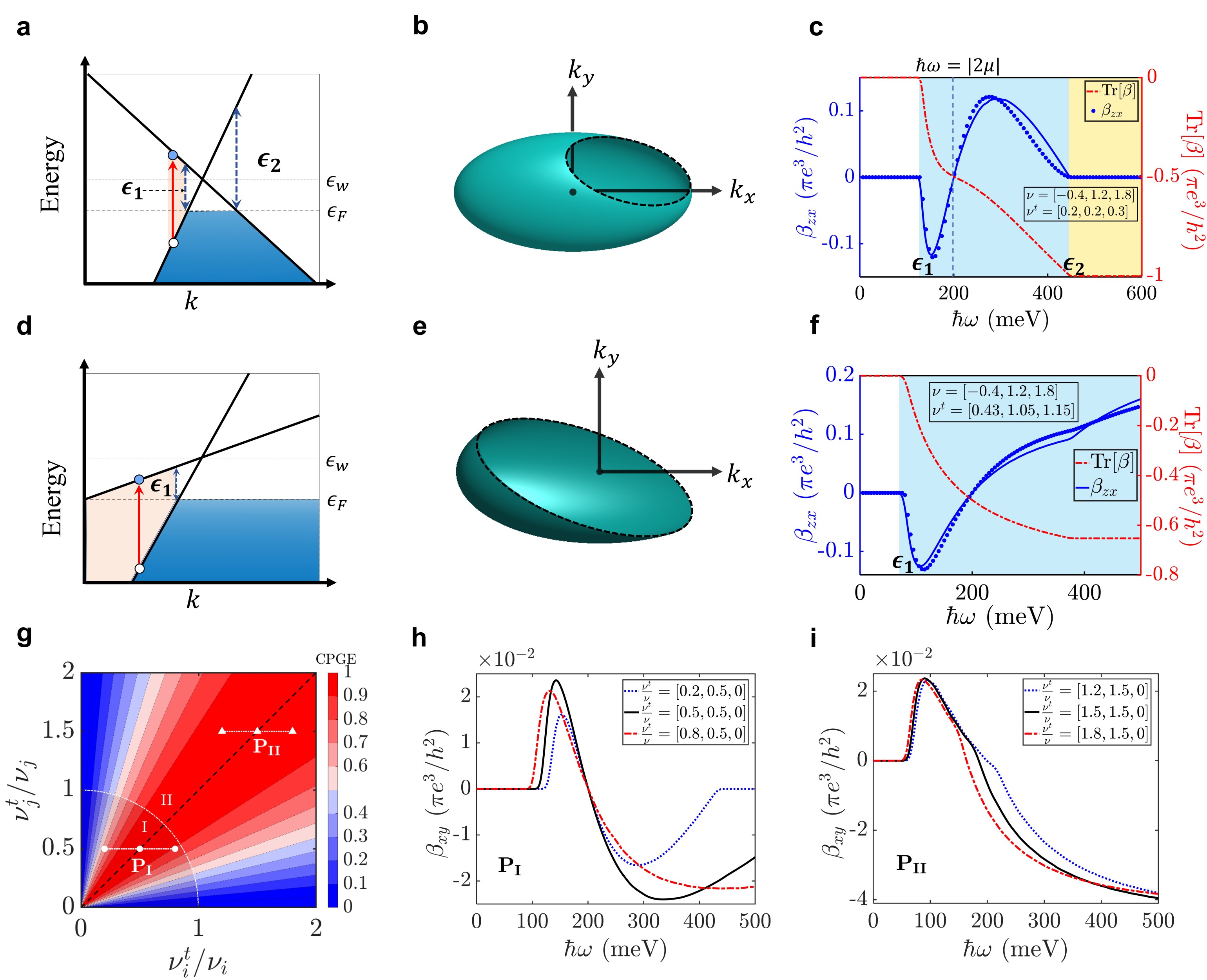
Different from warping terms which deform the shape of Fermi surfaces, titling terms will only shift relative position between a Weyl fermion and its exited Fermi surface under a laser, while the Fermi surface and its Berry curvature distribution remain isotropic (details are in Supplementary Section II). However, anisotropic optical excitation can still happen in Weyl fermions with tilting under a laser of low frequency. As shown in Fig. 3a, when the energy of the photon is larger than but smaller than , only electrons on the one side of the Weyl cone will be excited while the optical transition another side is forbidden. It corresponds to transitions for which only part of the spectrum is Pauli blocked. As a result, a hole will appear on the excited Fermi surface under a fix frequency of laser, inducing anisotropic optical excitation within the photon energy interval (Fig. 3b). The energy interval is determined by the direction of the largest titling: , where is the dimensionless tilt parameter which reveals the largest degree of tilting of the Weyl cone. (details are in Supplementary Section II).
In order to make a canonical formalism and the connection precise that relates transverse CPGE with the tilted terms of Hamiltonians, we followed the same steps above. Our analysis shows that the off-diagonal components of the CPGE tensor of the tilted term in the Weyl Hamiltonian have the form
| (7) |
with
| (8) |
To confirm the correctness of our formula, we investigated off-diagonal components of the CPGE tensor for arbitrary values of and in Fig. 3c (details are in Supplementary Section II). First, we can see, indeed, in the energy window () where anisotropic optical excitation happens, there is a nonzero transverse CPGE. This is both captured by calculation based on original Eq. 1 (Fig. 3c, solid blue curve) and our formula Eq. 7 (Fig. 3c, dotted curve). Second, inside the nonzero transverse CPGE allowed window, our results based on formula Eq. 7 match well with the direction calculations.
Along some specific directions in k-space, if the two dispersions forming the Weyl cone have the same sign of Fermi velocity, it is called the type-II Weyl nodes (Fig. 3d). In type-II Weyl semimetals, for any value of the when the energy of a photon is larger than , only electrons on the one side of the Weyl cone will be excited while the optical transition on other side is forbidden (Fig. 3d,e). Surprisingly, the equation 7 we get from type-I Weyl fermions () is still valid for type-II Weyl fermions soluyanov2015type (). To examine this, the fitting performance of the Eq. 7 to the results of an exact numerical calculation of the transverse CPGE using the Eq. 1 are compared in Fig. 3f for some arbitrary values of and . It can be seen that there is good agreement between both spectra.
Our formula can also help us find the condition where the titling terms can give rise to large transverse CPGE photocurrent analytically. Specifically, we focus on the peaks of the CPGE from Eq. 7(details are in Supplementary Section II). We find that is maximized at the condiction and . In an attempt to confirm this finding, we calculate the phase diagram as a function of the and the with . To obtain the maximum value of transverse CPGE, the peak value is checked within the photon energy in the case anisotropic excitation can occur. By calculating the normalized based on Eq. 7, we can see the maximum value of off-diagonal CPGE is significantly affected by tuning tilting velocity in and -direction (Fig. 3g). Now we verify our finding via the original formula Eq. 1. We can see, consistent with our analysis based on Eq. 7, is maxed when and for both type-I (Fig. 3h) and type-II (Fig. 3i) Weyl fermions. For the type-I Weyl fermions, the peak will decrease quickly when changing the parameters away from and (Fig. 3h). While for type-II Weyl fermions, the peak will change slowly when change the titling parameters.
Now we combine warping terms and tilting terms in Weyl equation,
| (9) |
Then, the generalized transverse CPGE of Weyl fermions has the following form,
| (10) |
The first part of our Eq. 10 from the titling terms has a dominant contribution to the transverse CPGE current tensor in the low frequency but the second part from the warping terms has a dominant contribution in the high frequency. We can also see that the transverse CPGE from the tilting term of a Weyl node must vanish exactly at (details are in Supplementary Section II). The transverse CPGE from the warping term when the In other words, if this photon energy is very close but smaller than , the measured transverse CPGE from Weyl will be approaching zero. Thus measuring the transverse CPGE of Weyl semimetals also provide a powerful tool to measure the energy of Weyl nodes relative to the Fermi level.
Transverse CPGE of the real materials.
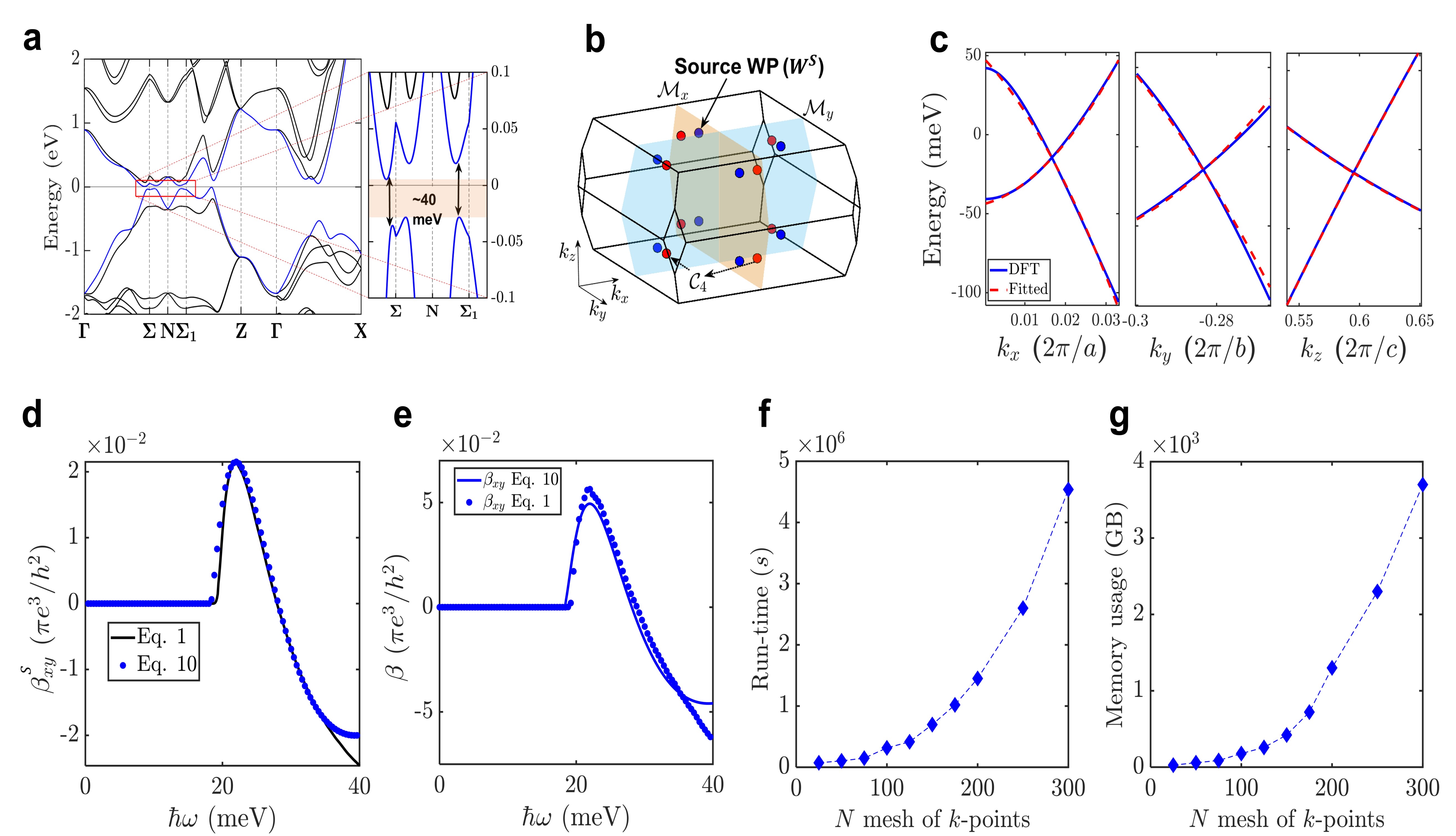
Now we apply our results to the first experimental discovered Weyl semimetal TaAs. TaAs is a nodal ring semimetal in the absence of spin-orbit coupling (SOC). After turning on SOC, a gap between conduction and valence bands of around 40 meV was open along the high symmetry lines xu2015 ; LVPRX2015 ; huang2015weyl ; WangPRX2015 (Fig. 4 a). To avoid the effect of massive nodal rings, here we focus on the low-frequency region. In Weyl semimetal TaAs, there are two classes of Weyl points: eight Weyl points on the plane and sixteen Weyl points away from the plane (Fig. 4 b). We only select the class of sixteen Weyl nodes since they are near the Fermi level and at low frequency (40 meV) only this class has contributed to the transverse CPGE (Fig. 4b).
We use our effective model in Eq. 9, whose parameters, , , and , are fitted to DFT band structures of TaAs around a source Weyl point (Fig. 4c). After that, the parameter of Hamiltonian in Eq. 9 sets obtained directly from the fitting, one can now calculate the off-diagonal components of the CPGE tensor using our formula in Eq. 10. We also routinely used Eq. 1 to calculate the CPGE around the source Weyl fermions and the result converges well under the mesh grind of . The results of the formula Eq. 10 first presented in this work are in good agreement with the direct calculation of Eq. 1 (Fig. 4d).
Once the transverse CPGE of the source Weyl points is known, we can use our Eq. 10 to get the CPGE of all the other Weyl points according to our symmetric analysis of transverse CPGE and thus the full CPGE can be reconstructed (see Table S1,S2 in Supplementary for details). In TaAs, the only nonzero CPGE are and . According to Eq. 10, all the six transverse components of the source Weyl point are nonzero (see Table S1,S2 in Supplementary for details). However, for the Weyl point which is related to the source Weyl point by mirror plane, the parameters , , and will gain a minus sign while all the other components are the same. As a result, and components of CPGE from the source Weyl fermion and its partner of mirror plane will cancel with each other. By considering all the symmetries, using Eq. 10 we can also see the off-diagonal CPGE will be nonzero along and in TaAs, which are consistent with experimental measurements. We now reconstruct the full off-diagonal components of the CPGE tensor of the TaAs from the source Weyl fermion based on . The reconstruction to the numerically direct calculation of the off-diagonal components of the CPGE tensor is compared in Fig. 4d. It can be seen that there is good agreement between both spectra. Our symmetry analysis shows that the above method can be extended to other space groups by calculating independent Weyl points using our invited formulae if the materials belong to one of these point groups , , , , , , , , , , and . See more details in Table S1,S2 in Supplementary information.
This result shows that the value of the non-zero transverse CPGE relied on the contributions from the transverse CPGE of individual Weyl nodes. We want to address that the formula developed in our work is much more powerful than the original Eq. 1 in studying the CPGE of Weyl fermions. It is expensive and time-consuming to study the CPGE of Weyl semimetals at the low-frequency region, especially for the infrared region where Weyl semimetals are good candidates as photodetectors. It has been found that based on the product of a matrix element and joint density of state de2017quantized1 , the transverse CPGE tends to converge slowly concerning the size number of -points used for the Brillouin zone integration. For example, in TaAs, it l took weeks (Fig. 4e) and it cost a memory of the order of terabytes (Fig. 4f) to get reliable results of the CPGE using the original formula. In contrast, using our formula the computing time and memory cost are negligible. With this advantage, thus we apply our method to more than other ten known Weyl materials: TaP, NbP, NbAs, LaAlGe, PrAlGe, CeAlGe, Ta3S2, WP2, MoP2, Co3Sn2S2, SrSi2, HgCr2Se4, CeSbTe, Ta2Se8I, and TaIrTe4 Hasan2021Weyl . The details of the transverse CPGE calculation of every Weyl semimetal, that we checked by our algorithm are given in Supplementary Sections IV,V.
Our work unveils that nonzero transverse CPGE of Weyl fermions can exist because of the Lorentz-symmetry breaking in condensed matter physics. Different from longitudinal CPGE in Weyl semimetal which only depends on the Chern number, we show that transverse CPGE has much richer correspondences with the degree of Lorentz-violation. We for the first time provide a new simple and powerful formula for the transverse CPGE of Weyl fermions, which can be widely applied to a vast of Weyl materials to find better candidates for photodetectors. Beyond Weyl fermions, it is also possible to apply the method developed to other quasiparticles with nontrivial wavefunction geometry, including but not limited to multi-fold chiral fermions, nodal rings, and massless or massive Dirac fermions in both three-dimensional and two-dimensional materials. Our results will greatly accelerate the process of searching for next-generation topological photodetectors.
Competing interests
The authors declare no competing interests.
Acknowledgments
This work at Nanyang Technological University was supported by the National Research Foundation, Singapore under its Fellowship Award (NRF-NRFF13-2021-0010) and the Nanyang Technological University startup grant (NTUSUG). Work at Princeton University was supported by the Gordon and Betty Moore Foundation (GBMF4547 and GBMF9461; M.Z.H.). The work at Northeastern University was supported by the Air Force Office of Scientific Research under award number FA9550-20-1-0322 and benefited from the computational resources of Northeastern University’s Advanced Scientific Computation Center (ASCC) and the Discovery Cluster. The work at National Cheng Kung University was supported by the 2030 Cross-Generation Young Scholars Program from the National Science and Technology Council (NSTC) in Taiwan (MOST111-2628-M-006-003-MY3), National Cheng Kung University (NCKU), Taiwan, and National Center for Theoretical Sciences, Taiwan. This research was supported, in part, by Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement at NCKU.
References
- (1) Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
- (2) Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057-1110 (2011).
- (3) Bansil, A., Lin, H. & Das, T. Topological band theory. Rev. Mod. Phys. 88, 021004 (2016).
- (4) Armitage, N. P., Mele, E. J., & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
- (5) Nagaosa, N., Morimoto, T. & Tokura, Y. Transport, magnetic and optical properties of Weyl materials. Nat. Rev. Mater. 5, 621 (2020).
- (6) Hasan, M. Z. et al. Weyl, Dirac and high-fold chiral fermions in topological quantum matter. Nat. Rev. Mater. 6, 784 (2021).
- (7) Ma, Q., Grushin, A. G. & Burch, K. S. Topology and geometry under the nonlinear electromagnetic spotlight. Nat. Mater. 20, 1601 (2021).
- (8) Orenstein, J. et al. Topology and symmetry of quantum materials via nonlinear optical responses. Annu. Rev. Condens. Matter. Phys. 12, 247 (2021).
- (9) Lv, B. Q., Qian, T. & Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 93, 025002 (2021).
- (10) Bao, C. et al. Light-induced emergent phenomena in 2D materials and topological materials. Nat. Rev. Phys. 4, 33-32 (2022).
- (11) Xue, H., Yang, Y. & Zhang, B. Topological acoustics Nat. Rev. Mater. 7, 974 (2022).
- (12) McIver, J., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96 (2012).
- (13) Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124 (2016).
- (14) Chan, C.-K., Lindner, N. H., Refael, G. & Lee, P. A. Photocurrents in Weyl semimetals. Phys. Rev. B 95, 041104 (2017).
- (15) Ma, Q. et al. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 13, 842 (2017).
- (16) Wu, L. et al. Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals. Nat. Phys. 13, 350 (2017).
- (17) Xu, S.-Y. et al. Electrically switchable Berry curvature dipole in the monolayer topological insulator WTe2. Nat. Phys. 14, 900 (2018).
- (18) Yin, J. et al. Tunable and giant valley-selective Hall effect in gapped bilayer graphene. Science 375, 1398-1402 (2022).
- (19) Ma, C. et al. Intelligent infrared sensing enabled by tunable moiré quantum geometry. Nature 604, 266-272 (2022).
- (20) Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613 (2015).
- (21) Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
- (22) de Juan, F., Grushin, A. G., Morimoto, T. & Moore, J. E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 8, 1 (2017).
- (23) Chang, G. et al. Unconventional chiral fermions and large topological fermi arcs in RhSi. Phys. Rev. Lett. 119, 206401 (2017).
- (24) Chang, G. et al. Topological quantum properties of chiral crystals. Nat. Mater. 17, 978 (2018).
- (25) Flicker, F. et al. Chiral optical response of multifold fermions. Phys. Rev. B 98, 155145 (2018).
- (26) Sanchez, D. S. et al. Topological chiral crystals with helicoid-arc quantum states. Nature 567, 500 (2019).
- (27) Zhao, R. et al. Observation of unconventional chiral fermions with long Fermi arcs in CoSi. Nature 567, 496 (2019).
- (28) Takane, D. et al. Observation of chiral fermions with a large topological charge and associated Fermi-arc surface states in CoSi. Phys. Rev. Lett. 122, 076402 (2019).
- (29) Schröter, N. B. M. et al. Chiral topological semimetal with multifold band crossings and long Fermi arcs. Nat. Phys. 15, 759 (2019).
- (30) Cochran, T. A. et al. A Fermi Arc Quantum Ladder. Preprint atarXiv 2004.11365 (2020).
- (31) Rees, D. et al. Helicity-dependent photocurrents in the chiral Weyl semimetal RhSi. Sci. Adv. 6, eaba0509 (2020).
- (32) Ni, Z. et al. Linear and nonlinear optical responses in the chiral multifold semimetal RhSi. npj Quantum Materials 5, 1 (2020).
- (33) Ni, Z. et al. Giant topological longitudinal circular photo-galvanic effect in the chiral multifold semimetal CoSi. Nat. Commun. 12, 1 (2021).
- (34) Sanchez, D. S. et al. Helicoid-arc van Hove singularities in topological chiral crystals. Preprint atarXiv 2108.13957 (2021).
- (35) Zhang, Y. et al. Photogalvanic effect in Weyl semimetals from first principles. Phys. Rev. B 97, 241118 (2018).
- (36) Ma, J. et al. Nonlinear photoresponse of type-II Weyl semimetals. Nat. Mater. 18, 476 (2019).
- (37) Osterhoudt, G. B. et al. Colossal mid-infrared bulk photovoltaic effect in a type-I Weyl semimetal. Nat. Mater. 18, 471 (2019).
- (38) Liu, J., Xia, F., Xiao, D., Garcia de Abajo, F. J. & Sun, D. Semimetals for high-performance photodetection. Nat. Mater. 19, 830 (2020).
- (39) Yuan, H. et al. Generation and electric control of spin-valley-coupled circular photo-galvanic current in WSe2. Nat. Nanotechnol. 9, 851 (2014).
- (40) Chang, G. et al. Unconventional photocurrents from surface fermi arcs in topological chiral semimetals. Phys. Rev. Lett. 124, 166404 (2020).
- (41) Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495 (2015).
- (42) Huang, S.-M. et al. A Weyl fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 1 (2015).
- (43) Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).