This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

PHENIX Collaboration

Transverse-energy distributions at midrapidity in pp++pp, dd++Au, and Au++Au collisions at sN​N=62.4\sqrt{s_{{}_{NN}}}=62.4–200 GeV and implications for particle-production models.

S.S. Adler Brookhaven National Laboratory, Upton, New York 11973-5000, USA    S. Afanasiev Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    C. Aidala Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA Department of Physics, University of Michigan, Ann Arbor, Michigan 48109-1040, USA    N.N. Ajitanand Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    Y. Akiba KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Al-Jamel New Mexico State University, Las Cruces, New Mexico 88003, USA    J. Alexander Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    K. Aoki Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    L. Aphecetche SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    R. Armendariz New Mexico State University, Las Cruces, New Mexico 88003, USA    S.H. Aronson Brookhaven National Laboratory, Upton, New York 11973-5000, USA    R. Averbeck Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    T.C. Awes Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    B. Azmoun Brookhaven National Laboratory, Upton, New York 11973-5000, USA    V. Babintsev IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    A. Baldisseri Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    K.N. Barish University of California - Riverside, Riverside, California 92521, USA    P.D. Barnes Deceased Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    B. Bassalleck University of New Mexico, Albuquerque, New Mexico 87131, USA    S. Bathe Baruch College, City University of New York, New York, New York, 10010 USA University of California - Riverside, Riverside, California 92521, USA Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    S. Batsouli Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    V. Baublis PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    F. Bauer University of California - Riverside, Riverside, California 92521, USA    A. Bazilevsky Brookhaven National Laboratory, Upton, New York 11973-5000, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    S. Belikov Deceased Brookhaven National Laboratory, Upton, New York 11973-5000, USA IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia Iowa State University, Ames, Iowa 50011, USA    R. Bennett Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    Y. Berdnikov Saint Petersburg State Polytechnic University, St. Petersburg, 195251 Russia    M.T. Bjorndal Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    J.G. Boissevain Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    H. Borel Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    K. Boyle Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    M.L. Brooks Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    D.S. Brown New Mexico State University, Las Cruces, New Mexico 88003, USA    N. Bruner University of New Mexico, Albuquerque, New Mexico 87131, USA    D. Bucher Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    H. Buesching Brookhaven National Laboratory, Upton, New York 11973-5000, USA Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    V. Bumazhnov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    G. Bunce Brookhaven National Laboratory, Upton, New York 11973-5000, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    J.M. Burward-Hoy Lawrence Livermore National Laboratory, Livermore, California 94550, USA Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    S. Butsyk Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    X. Camard SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    S. Campbell Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J.-S. Chai KAERI, Cyclotron Application Laboratory, Seoul, Korea    P. Chand Bhabha Atomic Research Centre, Bombay 400 085, India    W.C. Chang Institute of Physics, Academia Sinica, Taipei 11529, Taiwan    S. Chernichenko IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    C.Y. Chi Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    J. Chiba KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan    M. Chiu Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    I.J. Choi Yonsei University, IPAP, Seoul 120-749, Korea    R.K. Choudhury Bhabha Atomic Research Centre, Bombay 400 085, India    T. Chujo Brookhaven National Laboratory, Upton, New York 11973-5000, USA Vanderbilt University, Nashville, Tennessee 37235, USA    V. Cianciolo Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    C.R. Cleven Georgia State University, Atlanta, Georgia 30303, USA    Y. Cobigo Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    B.A. Cole Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    M.P. Comets IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    P. Constantin Iowa State University, Ames, Iowa 50011, USA    M. Csanád ELTE, Eötvös Loránd University, H - 1117 Budapest, Pázmány P. s. 1/A, Hungary    T. Csörgő Institute for Particle and Nuclear Physics, Wigner Research Centre for Physics, Hungarian Academy of Sciences (Wigner RCP, RMKI) H-1525 Budapest 114, POBox 49, Budapest, Hungary    J.P. Cussonneau SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    T. Dahms Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    K. Das Florida State University, Tallahassee, Florida 32306, USA    G. David Brookhaven National Laboratory, Upton, New York 11973-5000, USA    F. Deák ELTE, Eötvös Loránd University, H - 1117 Budapest, Pázmány P. s. 1/A, Hungary    H. Delagrange SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    A. Denisov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    D. d’Enterria Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    A. Deshpande RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    E.J. Desmond Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Devismes Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    O. Dietzsch Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil    A. Dion Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J.L. Drachenberg Abilene Christian University, Abilene, Texas 79699, USA    O. Drapier Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    A. Drees Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    A.K. Dubey Weizmann Institute, Rehovot 76100, Israel    A. Durum IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    D. Dutta Bhabha Atomic Research Centre, Bombay 400 085, India    V. Dzhordzhadze University of Tennessee, Knoxville, Tennessee 37996, USA    Y.V. Efremenko Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    J. Egdemir Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    A. Enokizono Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    H. En’yo RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    B. Espagnon IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    S. Esumi Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    D.E. Fields University of New Mexico, Albuquerque, New Mexico 87131, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    C. Finck SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    F. Fleuret Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    S.L. Fokin Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    B. Forestier LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France    B.D. Fox RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    Z. Fraenkel Deceased Weizmann Institute, Rehovot 76100, Israel    J.E. Frantz Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA Department of Physics and Astronomy, Ohio University, Athens, Ohio 45701, USA    A. Franz Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A.D. Frawley Florida State University, Tallahassee, Florida 32306, USA    Y. Fukao Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    S.-Y. Fung University of California - Riverside, Riverside, California 92521, USA    S. Gadrat LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France    F. Gastineau SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    M. Germain SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    A. Glenn University of Tennessee, Knoxville, Tennessee 37996, USA    M. Gonin Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    J. Gosset Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    Y. Goto RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    R. Granier de Cassagnac Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    N. Grau Department of Physics, Augustana College, Sioux Falls, South Dakota 57197, USA Iowa State University, Ames, Iowa 50011, USA    S.V. Greene Vanderbilt University, Nashville, Tennessee 37235, USA    M. Grosse Perdekamp University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    T. Gunji Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    H.-Å. Gustafsson Deceased Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    T. Hachiya Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    A. Hadj Henni SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    J.S. Haggerty Brookhaven National Laboratory, Upton, New York 11973-5000, USA    M.N. Hagiwara Abilene Christian University, Abilene, Texas 79699, USA    H. Hamagaki Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    A.G. Hansen Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    H. Harada Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    E.P. Hartouni Lawrence Livermore National Laboratory, Livermore, California 94550, USA    K. Haruna Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    M. Harvey Brookhaven National Laboratory, Upton, New York 11973-5000, USA    E. Haslum Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    K. Hasuko RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    R. Hayano Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    X. He Georgia State University, Atlanta, Georgia 30303, USA    M. Heffner Lawrence Livermore National Laboratory, Livermore, California 94550, USA    T.K. Hemmick Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J.M. Heuser RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    P. Hidas Institute for Particle and Nuclear Physics, Wigner Research Centre for Physics, Hungarian Academy of Sciences (Wigner RCP, RMKI) H-1525 Budapest 114, POBox 49, Budapest, Hungary    H. Hiejima University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA    J.C. Hill Iowa State University, Ames, Iowa 50011, USA    R. Hobbs University of New Mexico, Albuquerque, New Mexico 87131, USA    M. Holmes Vanderbilt University, Nashville, Tennessee 37235, USA    W. Holzmann Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    K. Homma Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    B. Hong Korea University, Seoul, 136-701, Korea    A. Hoover New Mexico State University, Las Cruces, New Mexico 88003, USA    T. Horaguchi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan    M.G. Hur KAERI, Cyclotron Application Laboratory, Seoul, Korea    T. Ichihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    H. Iinuma Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    V.V. Ikonnikov Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    K. Imai Advanced Science Research Center, Japan Atomic Energy Agency, 2-4 Shirakata Shirane, Tokai-mura, Naka-gun, Ibaraki-ken 319-1195, Japan Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    M. Inaba Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    M. Inuzuka Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    D. Isenhower Abilene Christian University, Abilene, Texas 79699, USA    L. Isenhower Abilene Christian University, Abilene, Texas 79699, USA    M. Ishihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    T. Isobe Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    M. Issah Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    A. Isupov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    B.V. Jacak Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J. Jia Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J. Jin Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    O. Jinnouchi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    B.M. Johnson Brookhaven National Laboratory, Upton, New York 11973-5000, USA    S.C. Johnson Lawrence Livermore National Laboratory, Livermore, California 94550, USA    K.S. Joo Myongji University, Yongin, Kyonggido 449-728, Korea    D. Jouan IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    F. Kajihara Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    S. Kametani Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan    N. Kamihara RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan    M. Kaneta RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    J.H. Kang Yonsei University, IPAP, Seoul 120-749, Korea    K. Katou Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan    T. Kawabata Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    T. Kawagishi Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    A.V. Kazantsev Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    S. Kelly University of Colorado, Boulder, Colorado 80309, USA Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    B. Khachaturov Weizmann Institute, Rehovot 76100, Israel    A. Khanzadeev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    J. Kikuchi Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan    D.J. Kim Yonsei University, IPAP, Seoul 120-749, Korea    E. Kim Seoul National University, Seoul, Korea    E.J. Kim Seoul National University, Seoul, Korea    G.-B. Kim Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    H.J. Kim Yonsei University, IPAP, Seoul 120-749, Korea    Y.-S. Kim KAERI, Cyclotron Application Laboratory, Seoul, Korea    E. Kinney University of Colorado, Boulder, Colorado 80309, USA    Á. Kiss ELTE, Eötvös Loránd University, H - 1117 Budapest, Pázmány P. s. 1/A, Hungary    E. Kistenev Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Kiyomichi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    C. Klein-Boesing Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    H. Kobayashi RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    L. Kochenda PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    V. Kochetkov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    R. Kohara Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    B. Komkov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    M. Konno Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    D. Kotchetkov University of California - Riverside, Riverside, California 92521, USA    A. Kozlov Weizmann Institute, Rehovot 76100, Israel    P.J. Kroon Brookhaven National Laboratory, Upton, New York 11973-5000, USA    C.H. Kuberg Deceased Abilene Christian University, Abilene, Texas 79699, USA    G.J. Kunde Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    N. Kurihara Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    K. Kurita RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan    M.J. Kweon Korea University, Seoul, 136-701, Korea    Y. Kwon Yonsei University, IPAP, Seoul 120-749, Korea    G.S. Kyle New Mexico State University, Las Cruces, New Mexico 88003, USA    R. Lacey Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    J.G. Lajoie Iowa State University, Ames, Iowa 50011, USA    A. Lebedev Iowa State University, Ames, Iowa 50011, USA Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    Y. Le Bornec IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    S. Leckey Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    D.M. Lee Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    M.K. Lee Yonsei University, IPAP, Seoul 120-749, Korea    M.J. Leitch Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    M.A.L. Leite Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil    X.H. Li University of California - Riverside, Riverside, California 92521, USA    H. Lim Seoul National University, Seoul, Korea    A. Litvinenko Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    M.X. Liu Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    C.F. Maguire Vanderbilt University, Nashville, Tennessee 37235, USA    Y.I. Makdisi Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Malakhov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    M.D. Malik University of New Mexico, Albuquerque, New Mexico 87131, USA    V.I. Manko Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    Y. Mao Peking University, Beijing 100871, P. R. China RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    G. Martinez SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    H. Masui Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    F. Matathias Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    T. Matsumoto Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan    M.C. McCain Abilene Christian University, Abilene, Texas 79699, USA University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA    P.L. McGaughey Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    Y. Miake Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    T.E. Miller Vanderbilt University, Nashville, Tennessee 37235, USA    A. Milov Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    S. Mioduszewski Brookhaven National Laboratory, Upton, New York 11973-5000, USA    G.C. Mishra Georgia State University, Atlanta, Georgia 30303, USA    J.T. Mitchell Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A.K. Mohanty Bhabha Atomic Research Centre, Bombay 400 085, India    D.P. Morrison morrison@bnl.gov Brookhaven National Laboratory, Upton, New York 11973-5000, USA    J.M. Moss Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    T.V. Moukhanova Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    D. Mukhopadhyay Vanderbilt University, Nashville, Tennessee 37235, USA Weizmann Institute, Rehovot 76100, Israel    M. Muniruzzaman University of California - Riverside, Riverside, California 92521, USA    J. Murata RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Physics Department, Rikkyo University, 3-34-1 Nishi-Ikebukuro, Toshima, Tokyo 171-8501, Japan    S. Nagamiya KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan    Y. Nagata Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    J.L. Nagle jamie.nagle@colorado.edu University of Colorado, Boulder, Colorado 80309, USA Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    M. Naglis Weizmann Institute, Rehovot 76100, Israel    T. Nakamura Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    J. Newby Lawrence Livermore National Laboratory, Livermore, California 94550, USA University of Tennessee, Knoxville, Tennessee 37996, USA    M. Nguyen Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    B.E. Norman Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    A.S. Nyanin Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    J. Nystrand Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    E. O’Brien Brookhaven National Laboratory, Upton, New York 11973-5000, USA    C.A. Ogilvie Iowa State University, Ames, Iowa 50011, USA    H. Ohnishi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    I.D. Ojha Department of Physics, Banaras Hindu University, Varanasi 221005, India Vanderbilt University, Nashville, Tennessee 37235, USA    K. Okada RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    O.O. Omiwade Abilene Christian University, Abilene, Texas 79699, USA    A. Oskarsson Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    I. Otterlund Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    K. Oyama Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    K. Ozawa Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan    D. Pal Vanderbilt University, Nashville, Tennessee 37235, USA Weizmann Institute, Rehovot 76100, Israel    A.P.T. Palounek Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    V. Pantuev Institute for Nuclear Research of the Russian Academy of Sciences, prospekt 60-letiya Oktyabrya 7a, Moscow 117312, Russia Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    V. Papavassiliou New Mexico State University, Las Cruces, New Mexico 88003, USA    J. Park Seoul National University, Seoul, Korea    W.J. Park Korea University, Seoul, 136-701, Korea    S.F. Pate New Mexico State University, Las Cruces, New Mexico 88003, USA    H. Pei Iowa State University, Ames, Iowa 50011, USA    V. Penev Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    J.-C. Peng University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA    H. Pereira Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    V. Peresedov Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    D.Yu. Peressounko Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    A. Pierson University of New Mexico, Albuquerque, New Mexico 87131, USA    C. Pinkenburg Brookhaven National Laboratory, Upton, New York 11973-5000, USA    R.P. Pisani Brookhaven National Laboratory, Upton, New York 11973-5000, USA    M.L. Purschke Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A.K. Purwar Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    H. Qu Georgia State University, Atlanta, Georgia 30303, USA    J.M. Qualls Abilene Christian University, Abilene, Texas 79699, USA    J. Rak Iowa State University, Ames, Iowa 50011, USA    I. Ravinovich Weizmann Institute, Rehovot 76100, Israel    K.F. Read Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA University of Tennessee, Knoxville, Tennessee 37996, USA    M. Reuter Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    K. Reygers Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    V. Riabov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    Y. Riabov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    G. Roche LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France    A. Romana Deceased Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    M. Rosati Iowa State University, Ames, Iowa 50011, USA    S.S.E. Rosendahl Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    P. Rosnet LPC, Université Blaise Pascal, CNRS-IN2P3, Clermont-Fd, 63177 Aubiere Cedex, France    P. Rukoyatkin Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    V.L. Rykov RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    S.S. Ryu Yonsei University, IPAP, Seoul 120-749, Korea    B. Sahlmueller Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    N. Saito Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    T. Sakaguchi Center for Nuclear Study, Graduate School of Science, University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo 113-0033, Japan Waseda University, Advanced Research Institute for Science and Engineering, 17 Kikui-cho, Shinjuku-ku, Tokyo 162-0044, Japan    S. Sakai Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    V. Samsonov PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    L. Sanfratello University of New Mexico, Albuquerque, New Mexico 87131, USA    R. Santo Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    H.D. Sato Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    S. Sato Brookhaven National Laboratory, Upton, New York 11973-5000, USA Advanced Science Research Center, Japan Atomic Energy Agency, 2-4 Shirakata Shirane, Tokai-mura, Naka-gun, Ibaraki-ken 319-1195, Japan KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    S. Sawada KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan    Y. Schutz SUBATECH (Ecole des Mines de Nantes, CNRS-IN2P3, Université de Nantes) BP 20722 - 44307, Nantes, France    V. Semenov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    R. Seto University of California - Riverside, Riverside, California 92521, USA    D. Sharma Weizmann Institute, Rehovot 76100, Israel    T.K. Shea Brookhaven National Laboratory, Upton, New York 11973-5000, USA    I. Shein IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    T.-A. Shibata RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan Department of Physics, Tokyo Institute of Technology, Oh-okayama, Meguro, Tokyo 152-8551, Japan    K. Shigaki Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    M. Shimomura Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    T. Shohjoh Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    K. Shoji Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    A. Sickles Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    C.L. Silva Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil    D. Silvermyr Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    K.S. Sim Korea University, Seoul, 136-701, Korea    C.P. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India    V. Singh Department of Physics, Banaras Hindu University, Varanasi 221005, India    S. Skutnik Iowa State University, Ames, Iowa 50011, USA    W.C. Smith Abilene Christian University, Abilene, Texas 79699, USA    A. Soldatov IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    R.A. Soltz Lawrence Livermore National Laboratory, Livermore, California 94550, USA    W.E. Sondheim Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    S.P. Sorensen University of Tennessee, Knoxville, Tennessee 37996, USA    I.V. Sourikova Brookhaven National Laboratory, Upton, New York 11973-5000, USA    F. Staley Dapnia, CEA Saclay, F-91191, Gif-sur-Yvette, France    P.W. Stankus Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    E. Stenlund Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    M. Stepanov New Mexico State University, Las Cruces, New Mexico 88003, USA    A. Ster Institute for Particle and Nuclear Physics, Wigner Research Centre for Physics, Hungarian Academy of Sciences (Wigner RCP, RMKI) H-1525 Budapest 114, POBox 49, Budapest, Hungary    S.P. Stoll Brookhaven National Laboratory, Upton, New York 11973-5000, USA    T. Sugitate Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan    C. Suire IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    J.P. Sullivan Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    J. Sziklai Institute for Particle and Nuclear Physics, Wigner Research Centre for Physics, Hungarian Academy of Sciences (Wigner RCP, RMKI) H-1525 Budapest 114, POBox 49, Budapest, Hungary    T. Tabaru RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    S. Takagi Institute of Physics, University of Tsukuba, Tsukuba, Ibaraki 305, Japan    E.M. Takagui Universidade de São Paulo, Instituto de Física, Caixa Postal 66318, São Paulo CEP05315-970, Brazil    A. Taketani RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    K.H. Tanaka KEK, High Energy Accelerator Research Organization, Tsukuba, Ibaraki 305-0801, Japan    Y. Tanaka Nagasaki Institute of Applied Science, Nagasaki-shi, Nagasaki 851-0193, Japan    K. Tanida RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA Seoul National University, Seoul, Korea    M.J. Tannenbaum Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Taranenko Chemistry Department, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    P. Tarján Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary    T.L. Thomas University of New Mexico, Albuquerque, New Mexico 87131, USA    M. Togawa Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    J. Tojo RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    H. Torii Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    R.S. Towell Abilene Christian University, Abilene, Texas 79699, USA    V-N. Tram Laboratoire Leprince-Ringuet, Ecole Polytechnique, CNRS-IN2P3, Route de Saclay, F-91128, Palaiseau, France    I. Tserruya Weizmann Institute, Rehovot 76100, Israel    Y. Tsuchimoto Hiroshima University, Kagamiyama, Higashi-Hiroshima 739-8526, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    S.K. Tuli Deceased Department of Physics, Banaras Hindu University, Varanasi 221005, India    H. Tydesjö Department of Physics, Lund University, Box 118, SE-221 00 Lund, Sweden    N. Tyurin IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    T.J. Uam Myongji University, Yongin, Kyonggido 449-728, Korea    C. Vale Iowa State University, Ames, Iowa 50011, USA    H. Valle Vanderbilt University, Nashville, Tennessee 37235, USA    H.W. van Hecke Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA    J. Velkovska Brookhaven National Laboratory, Upton, New York 11973-5000, USA Vanderbilt University, Nashville, Tennessee 37235, USA    M. Velkovsky Department of Physics and Astronomy, Stony Brook University, SUNY, Stony Brook, New York 11794-3400, USA    R. Vértesi Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary    V. Veszprémi Debrecen University, H-4010 Debrecen, Egyetem tér 1, Hungary    A.A. Vinogradov Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    M.A. Volkov Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    E. Vznuzdaev PNPI, Petersburg Nuclear Physics Institute, Gatchina, Leningrad region, 188300, Russia    M. Wagner Kyoto University, Kyoto 606-8502, Japan RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan    X.R. Wang Georgia State University, Atlanta, Georgia 30303, USA New Mexico State University, Las Cruces, New Mexico 88003, USA    Y. Watanabe RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    J. Wessels Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    S.N. White Brookhaven National Laboratory, Upton, New York 11973-5000, USA    N. Willis IPN-Orsay, Universite Paris Sud, CNRS-IN2P3, BP1, F-91406, Orsay, France    D. Winter Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    F.K. Wohn Iowa State University, Ames, Iowa 50011, USA    C.L. Woody Brookhaven National Laboratory, Upton, New York 11973-5000, USA    M. Wysocki University of Colorado, Boulder, Colorado 80309, USA    W. Xie University of California - Riverside, Riverside, California 92521, USA RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    A. Yanovich IHEP Protvino, State Research Center of Russian Federation, Institute for High Energy Physics, Protvino, 142281, Russia    S. Yokkaichi RIKEN Nishina Center for Accelerator-Based Science, Wako, Saitama 351-0198, Japan RIKEN BNL Research Center, Brookhaven National Laboratory, Upton, New York 11973-5000, USA    G.R. Young Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA    I. Younus Physics Department, Lahore University of Management Sciences, Lahore, Pakistan University of New Mexico, Albuquerque, New Mexico 87131, USA    I.E. Yushmanov Russian Research Center “Kurchatov Institute”, Moscow, 123098 Russia    W.A. Zajc Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    O. Zaudtke Institut für Kernphysik, University of Muenster, D-48149 Muenster, Germany    C. Zhang Columbia University, New York, New York 10027 and Nevis Laboratories, Irvington, New York 10533, USA    S. Zhou Science and Technology on Nuclear Data Laboratory, China Institute of Atomic Energy, Beijing 102413, P. R. China    J. Zimányi Deceased Institute for Particle and Nuclear Physics, Wigner Research Centre for Physics, Hungarian Academy of Sciences (Wigner RCP, RMKI) H-1525 Budapest 114, POBox 49, Budapest, Hungary    L. Zolin Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia    X. Zong Iowa State University, Ames, Iowa 50011, USA
(July 25, 2025)
Abstract

Measurements of the midrapidity transverse energy distribution, d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta, are presented for pp++pp, dd++Au, and Au++Au collisions at sN​N=200\sqrt{s_{{}_{NN}}}=200 GeV and additionally for Au++Au collisions at sN​N=62.4\sqrt{s_{{}_{NN}}}=62.4 and 130 GeV. The d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta distributions are first compared with the number of nucleon participants NpartN_{\rm part}, number of binary collisions NcollN_{\rm coll}, and number of constituent-quark participants Nq​pN_{qp} calculated from a Glauber model based on the nuclear geometry. For Au++Au, ⟨d​ET/d​η⟩/Npart\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle/N_{\rm part} increases with NpartN_{\rm part}, while ⟨d​ET/d​η⟩/Nq​p\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle/N_{qp} is approximately constant for all three energies. This indicates that the two component ansatz, d​ET/d​η∝(1−x)​Npart/2+x​NcolldE_{T}/d\eta\propto(1-x)N_{\rm part}/2+xN_{\rm coll}, which has been used to represent ETE_{T} distributions, is simply a proxy for Nq​pN_{qp}, and that the NcollN_{\rm coll} term does not represent a hard-scattering component in ETE_{T} distributions. The d​ET/d​ηdE_{T}/d\eta distributions of Au++Au and dd++Au are then calculated from the measured pp++pp ETE_{T} distribution using two models that both reproduce the Au++Au data. However, while the number-of-constituent-quark-participant model agrees well with the dd++Au data, the additive-quark model does not.

pacs:
25.75.Dw

I Introduction

Measurements of midrapidity transverse energy distributions d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta in pp++pp, dd++Au and Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200 GeV and Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =62.4 and 130 GeV are presented. The transverse energy ET{\rm E}_{T} is a multiparticle variable defined as the sum

ET=∑iEi​sin⁡θi\mbox{${\rm E}_{T}$}=\sum_{i}E_{i}\,\sin\theta_{i}\\ (1)
d​ET​(η)/d​η=sin⁡θ​(η)​d​E​(η)/d​η,d\mbox{${\rm E}_{T}$}(\eta)/d\eta=\sin\theta(\eta)\,dE(\eta)/d\eta, (2)

where θ\theta is the polar angle, η=−ln⁡tan⁡θ/2\eta=-\ln\tan\theta/2 is the pseudorapidity, EiE_{i} is by convention taken as the kinetic energy for baryons, the kinetic energy + 2 mNm_{N} for antibaryons, and the total energy for all other particles, and the sum is taken over all particles emitted into a fixed solid angle for each event. In the present measurement as in previous measurements Adcox et al. (2001a); Adler et al. (2005) the raw ET{\rm E}_{T}, denoted ET​EMC{\rm{E}}_{T\,{\rm EMC}}, is measured in five sectors of the PHENIX lead-scintillator (PbSc) electromagnetic calorimeter (EMCal) Adcox et al. (2001a) which cover the solid angle |η|≤0.38|\eta|\leq 0.38, Δ​ϕ=90∘+22.5∘\Delta\phi=90^{\circ}+22.5^{\circ}, and is corrected to total hadronic ET{\rm E}_{T}, more properly d​ET/d​η|η=0d\mbox{${\rm E}_{T}$}/d\eta|_{\eta=0}, within a reference acceptance of Δ​η=1.0,Δ​ϕ=2​π\Delta\eta=1.0,\Delta\phi=2\pi (details are given in section IV).

The significance of systematic measurements of midrapidity d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta and the closely related charged particle multiplicity distributions, d​Nch/d​ηd\mbox{$N_{\rm ch}$}/d\eta, as a function of AA and BB in AA+BB collisions is that they provide excellent characterization of the nuclear geometry of the reaction on an event-by-event basis, and are sensitive to the underlying reaction dynamics, which is the fundamental element of particle emission in pp++pp and AA+BB collisions at a given sN​N\sqrt{s_{{}_{NN}}}. For instance, measurements of d​Nch/d​ηd\mbox{$N_{\rm ch}$}/d\eta in Au++Au collisions at the Relativistic Heavy Ion Collider (RHIC), as a function of centrality expressed as the number of participating nucleons, NpartN_{\rm part}, do not depend linearly on NpartN_{\rm part} but have a nonlinear increase of ⟨d​Nch/d​η⟩\langle d\mbox{$N_{\rm ch}$}/d\eta\rangle with increasing NpartN_{\rm part}. The nonlinearity has been explained by a two component model Wang and Gyulassy (2001); Kharzeev and Nardi (2001) proportional to a linear combination of NcollN_{\rm coll} and NpartN_{\rm part}, with the implication that the NcollN_{\rm coll} term represents a contribution from hard scattering. Alternatively, it has been proposed that d​Nch/d​ηd\mbox{$N_{\rm ch}$}/d\eta is linearly proportional to the number of constituent-quark participants (NQP) model Eremin and Voloshin (2003), without need to introduce a hard-scattering component. For symmetric systems, the NQP model is identical to the Additive Quark Model (AQM) Bialas et al. (1982) used in the 1980’s, to explain the similar nonproportionality of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta with NpartN_{\rm part} in α−α\alpha-\alpha compared to pp++pp collisions at sN​N\sqrt{s_{{}_{NN}}} =31 GeV Ochiai (1987). In the AQM, constituent-quark participants in the two colliding nuclei are connected by color-strings; but with the restriction that only one color-string can be attached to a quark-participant. At midrapidity, the transverse energy production is proportional to the number of color-strings spanning between the projectile and the target nuclei. For asymmetric systems, such as dd++Au, the models differ because the number of color-strings is proportional only to the number of quark-participants in the projectile (the lighter nucleus). For symmetric A+A collisions, the number of quark-participants in the target is the same as number of quark-participants in the projectile, so the AQM is equivalent to the NQP model. These models will be described in detail and tested with the present data.

II Previous Measurements—A Historical Perspective

II.1 Charged Multiplicity Distributions

The charged particle multiplicity or multiplicity density in rapidity, d​Nch/d​yd\mbox{$N_{\rm ch}$}/dy, is one of the earliest descriptive variables in high energy particle and nuclear physics dating from cosmic-ray studies Camerini et al. (1952). An important regularity first observed in cosmic rays was that the produced pions have limited transverse momentum with respect to the collision axis, exponentially decreasing as e−6​pTe^{-6p_{T}}, commonly known as the “Cocconi Formula” Cocconi et al. (1961); Orear (1964).

By the early 1970’s the framework for the study of this “soft” multi-particle physics was well in place. One of the important conceptual breakthroughs was the realization that the distribution of multiplicity for multiple particle production would not be Poisson unless the particles were emitted independently, without any correlation, but that short-range rapidity correlations were expected as a consequence of “Regge-Pole-dominated” reactions Mueller (1971). In fact, in marked deviation from Poisson behavior, the total charged particle multiplicity distributions appeared to exhibit a universal form, “KNO scaling” Koba et al. (1972) (or “scaling in the mean”), when “scaled” at each s\sqrt{s} by the average multiplicity—i.e. d​Nch/d​zd\mbox{$N_{\rm ch}$}/dz was a universal function of the scaled multiplicity, z≡Nch/⟨Nch⟩z\equiv\mbox{$N_{\rm ch}$}/\langle\mbox{$N_{\rm ch}$}\rangle, where ⟨Nch⟩\langle\mbox{$N_{\rm ch}$}\rangle is the mean multiplicity at a given s\sqrt{s} Arnison et al. (1981). In the mid 1980’s, the UA5 group at the CERN Super Proton Synchrotron collider discovered that KNO scaling did not hold in general Alner et al. (1987), and found that their measured multiplicity distributions, both in limited rapidity intervals and over all phase space were described by negative binomial distributions (NBD), which since then have been shown to provide accurate descriptions for NchN_{\rm ch} distributions from high energy collisions of both particles and nuclei.

Also in this period, the central plateau of the rapidity distribution of identified charged particles, d​Nch​(y)/d​yd\mbox{$N_{\rm ch}$}(y)/dy, was discovered at the CERN-ISR egJ . Along with this discovery came the first interest to measure the multiplicity distribution in a restricted pseudorapidity range, |η|≤1.5|\eta|\leq 1.5, “wide enough to allow for good statistics, yet sufficiently remote from the edge of the rapidity plateau to permit specific analysis of the central region” Thomé et al. (1977). The first suggestion to use multiplicity distributions in restricted regions of rapidity for the study of reaction dynamics, specifically quantum optical coherence effects in pp++pp collisions, was made by Fowler and Weiner Fowler and Weiner (1977), who emphasized the importance of using small-regions, where energy-momentum-conservation constraints would not be significant.

II.2 ET{\rm E}_{T} Distributions

The phenomenology of ET{\rm E}_{T} measurements, which evolved over a similar time period as that of multiplicity distributions, was based initially on the search for the jets of hard-scattering in pp++pp collisions in “4​π4\pi-hadron calorimeters” as first proposed by Willis Willis (1972) and then by Bjorken Bjorken (1973), who specifically emphasized the need for the capability of measuring the total amount of energy emerging into small elements of solid angle to observe the event structure of what he called local cores (now jets) predicted for hard-scattering. Ochs and Stodolsky Ochs and Stodolsky (1977) later proposed the veto of energy by a calorimeter in the forward direction, which was elaborated by Landshoff and Polkinghorne Landshoff and Polkinghorne (1978) who coined the name “transverse energy”: “The energy not observed in the forward direction due to hard-scattering processes would be emitted as ‘transverse energy’ ”. The first experiment to measure an “ET{\rm E}_{T} distribution” corresponding to the terminology used at present was the NA5 experiment at CERN De Marzo et al. (1982), which utilized a full azimuth hadronic calorimeter covering the region −0.88<η<0.67-0.88<\eta<0.67. They demonstrated that instead of finding jets De Marzo et al. (1982), “The large ET{\rm E}_{T} observed is the result of a large number of particles with a rather small transverse momentum.” The close relationship between ET{\rm E}_{T} and multiplicity distributions was shown in a measurement by UA1 in p¯\bar{\rm p}+p collisions at s\sqrt{s} =540 GeV at the CERN Super Proton Synchrotron collider Arnison et al. , with a full azimuth “hermetic calorimeter” covering |Δ​η|≤3|\Delta\eta|\leq 3, which demonstrated that the “ET{\rm E}_{T} measured in the calorimeter was strongly correlated to the measured multiplicity” and that the KNO scaled ET{\rm E}_{T} and NchN_{\rm ch} distributions were “strikingly similar”. Ironically, this was to be presented at the same meeting (ICHEP82) at which UA2 presented the discovery of dijets Repellin et al. (1982) in the region of a break in the steep exponential slope of an ET{\rm E}_{T} distribution, to a flatter slope, 5–6 orders of magnitude down in cross section. Since then, it has been established that ET{\rm E}_{T} and NchN_{\rm ch} distributions are much less sensitive to hard-scattering than single inclusive measurements; and these distributions have been used to study the “soft” physics that dominates the pp++pp inelastic cross section  Appel et al. (1985). In fact, just a year after ICHEP82, Bjorken Bjorken (1983) stressed the importance of the region of the “central plateau” of rapidity for the study of the evolution of the Quark Gluon Plasma and proposed d​ET/d​y|y=0d\mbox{${\rm E}_{T}$}/dy|_{y=0} as an estimate of the co-moving energy density in a longitudinal expansion, proportional to the energy density in space, called the Bjorken Energy Density:

ϵB​j=d​ETd​y​1τ0​π​R2\epsilon_{Bj}=\frac{d\mbox{${\rm E}_{T}$}}{dy}\frac{1}{\tau_{0}\pi R^{2}} (3)

where τ0\tau_{0}, the formation time, is usually taken as 1 fm/cc and π​R2\pi R^{2} is the effective area of the collision. This formula is derived under the assumption that ⟨ET⟩\langle\mbox{${\rm E}_{T}$}\rangle per particle ∝T\propto T for a thermal medium, which has nothing to do with hard scattering.

II.3 Collisions of Relativistic Nuclei-Extreme Independent Models

The first experiments specifically designed to measure the dependence of the charged particle multiplicity in high energy p+Ap+A collisions as a function of the nuclear size were performed by Busza and collaborators Busza et al. (1975) at Fermilab using beams of ∼\sim50–200 GeV/cc hadrons colliding with various fixed nuclear targets. They found the extraordinary result Busza et al. (1975) that the charged particle multiplicity density, d​Nch/d​ηd\mbox{$N_{\rm ch}$}/d\eta, observed in proton+nucleus (pp+A) interactions was not simply proportional to the number of collisions, but increased much more slowly. The other striking observation Halliwell et al. (1977) was that a relativistic incident proton could pass through e.g. ν=4\nu=4 absorption-mean-free-paths of a target nucleus and emerge from the other side, and furthermore there was no intranuclear cascade of produced particles (a stark difference from what would happen to the same proton in a macroscopic 4 mean-free-path hadron calorimeter). In the forward fragmentation region of 200 GeV/cc pp+AA collisions, within one unit of rapidity from the beam ybeam=6.0y^{\rm beam}=6.0, there was essentially no change in d​Nch/d​ηd\mbox{$N_{\rm ch}$}/d\eta as a function of AA, while the peak of the distribution moved backwards from midrapidity (yN​Ncm∼3.0{y^{\rm cm}_{{}_{NN}}}\sim 3.0) with increasing AA and the total multiplicity increased, resulting in a huge relative increase of multiplicity in the target fragmentation region, η<1\eta<1 in the laboratory system.

These striking features of the ∼200\sim 200 GeV/cc fixed target hadron-nucleus data (sN​N∼19.4\mbox{$\sqrt{s_{{}_{NN}}}$}\sim 19.4 GeV) showed the importance of taking into account the time and distance scales of the soft multi-particle production process including quantum mechanical effects Fishbane and Trefil (1974a, b); Gottfried (1974); Goldhaber (1973); Białas and Czyż (1974); Andersson and Otterlund (1975). The observations had clearly shown that the target nucleus was rather transparent, so that a relativistic incident nucleon could make many successive collisions while passing through the nucleus and emerge intact. Immediately after a relativistic nucleon interacts inside a nucleus, the only thing that can happen consistent with relativity and quantum mechanics is for it to become an excited nucleon with roughly the same energy and reduced longitudinal momentum and rapidity. The relativistic nucleon remains in that state inside the nucleus, because the uncertainty principle and time dilation prevent it from fragmenting into particles until it is well outside the nucleus. This feature immediately eliminates the possibility of a cascade in the nucleus from the rescattering of the secondary products. Making the further assumptions (1) that an excited nucleon interacts with the same cross section as an unexcited nucleon and (2) that the successive collisions of the excited nucleon do not affect the excited state or its eventual fragmentation products Frankel (1993), leads to the conclusion that the elementary process for particle production in nuclear collisions is the excited nucleon. This also leads to the prediction that the multiplicity in nuclear interactions should be proportional to the total number of projectile and target participants, rather than to the total number of collisions, which is called the wounded-nucleon model (WNM) Białas et al. (1976). Common usage is to refer to the wounded nucleons (WN) as participants.

Interestingly, at midrapidity, the WNM works well only at roughly sN​N\sqrt{s_{{}_{NN}}} ∼20\sim 20 GeV where it was discovered. For sN​N\sqrt{s_{{}_{NN}}} <<∼\sim 5.4 GeV, particle production is smaller than the WNM due to the large stopping Ahle et al. (1998) with reduced transparency; and the ET{\rm E}_{T} distributions in AA+BB collisions can be represented by sums of convolutions of the pp+AA distribution according to the relative probability of the number of projectile participants, the wounded-projectile-nucleon model (WPNM) Ftacnik et al. (1987); Abbott et al. (1987, 2001). For sN​N\sqrt{s_{{}_{NN}}} ≥31\geq 31 GeV, particle production is larger than the WNM Angelis et al. (1984); Åkesson et al. (1989) and the AQM Bialas et al. (1982); Ochiai (1987), which is equivalent to a wounded-projectile-quark (color-string) model, has been used successfully. All three of the above models, as well as the models to be described below, are of the type referred to as extreme independent models (EIM). The effect of the nuclear geometry of the interaction can be calculated in EIMs, independently of the dynamics of particle production, which can be derived from experimental measurements, usually the pp++pp (or pp+AA) measurement in the same detector. In fact, the first published measurements at the CERN Bamberger et al. (1987) and BNL Remsberg et al. (1988) fixed target heavy ion programs in 1986-87 were ET{\rm E}_{T} distributions in which EIM, rather than cuts on centrality, were used to understand the data.

At RHIC (sN​N\sqrt{s_{{}_{NN}}} =19.6−200=19.6-200 GeV), PHOBOS Alver et al. (2011) has shown that the WNM works in Au++Au collisions for the total multiplicity, NchN_{\rm ch}, over the range |η|<5.4|\eta|<5.4, while at midrapidity, the WNM fails—the multiplicity density per participant pair, ⟨d​Nch/d​η⟩/(Npart/2)\langle d\mbox{$N_{\rm ch}$}/d\eta\rangle/(\mbox{$N_{\rm part}$}/2), increases with increasing number of participants, in agreement with previous PHENIX results Adcox et al. (2001b, a); Adler et al. (2005). Additionally, it has been shown using PHOBOS Au++Au data Eremin and Voloshin (2003); Nouicer (2007) and discussed for other data De and Bhattacharyya (2005) that the midrapidity ⟨d​Nch/d​η⟩\langle d\mbox{$N_{\rm ch}$}/d\eta\rangle as a function of centrality in Au++Au collisions is linearly proportional to the NQP model; however for symmetric systems this cannot be distinguished from the number of color-strings, the AQM Bialas (2008). The present work completes the cycle and demonstrates, using midrapidity ET{\rm E}_{T} distributions at sN​N\sqrt{s_{{}_{NN}}} =200 GeV in the asymmetric dd++Au system, as well as pp++pp and Au++Au collisions, that the asymmetric dd++Au measurement, which is crucial in distinguishing the color-string AQM from NQP models, clearly rejects the AQM and agrees very well with the NQP model.

While the concept of nucleon participants in collisions of nuclei is straightforward to understand, the concept of constituent-quark participants needs some elaboration. The nonrelativistic constituent-quark model Gell-Mann (1964); Feynman et al. (1964) is the basis of understanding the observed spectrum of the meson and baryon elementary particles as bound states, i.e. (q​q¯)(q\bar{q}) for mesons and (q​q​q)(qqq) for baryons. In addition to the masses and quantum numbers, other static properties such as the magnetic moments of baryons are also predicted in this model (see Refs. Morpurgo (1970); Kokkedee (1969), and references therein). However, these constituent-quarks are not the nearly massless uu and dd quarks (partons), called “current quarks” from their role in the currents of electroweak and QCD quantum field theories. The constituent-quarks are assumed to be complex objects or quasi-particles Shuryak (1982) made out of the point-like partons of QCD hard-scattering, the (current) quarks, anti-quarks and gluons. The constituent or valence quarks (valons) thus acquire masses on the order of 1/3 the nucleon mass (or 1/2 the ρ\rho-meson mass), called “chiral symmetry breaking” Diakonov (1996); Weinberg (2004), when bound in the nucleon (or meson). According to Shuryak Shuryak (1982) (see also Ref. Anisovich et al. (1978)), there are two scales for hadrons predicted in QCD, the confinement length given by the radii of hadrons, Rconf≈1R_{\rm conf}\approx 1 fm ≈Rhadron\approx R_{\rm hadron}, as well as objects at the scale 1/3 smaller, the constituent-quarks (valons Hwa (1980)). For instance, the consideration of constituent-quarks as ‘little bags’ with application to the σL/σT\sigma_{L}/\sigma_{T} puzzle in deep inelastic lepton-hadron scattering and other hard processes was made by T. Akiba Akiba (1982).

One other key feature of the constituent-quark model is additivity: the properties of a hadron are described as the independent sum of contributions of the individual quarks. In other words the three constituent-quarks in each nucleon in a nucleon-nucleon collision act like the three nucleons in each triton in a 3H+3H collision: i.e. apart from their spatial correlation, the three nucleons in each triton act independently in the collision. This additive quark assumption Levin and Frankfurt (1965); Lipkin (1966); Anisovich et al. (1978) gives the relation that the pion-nucleon total cross section is 2/3 the nucleon-nucleon total cross section, i.e. σ​(π​p)/σ​(p​p)=2/3\sigma(\pi p)/\sigma(pp)=2/3. The constituent-quark participant (NQP) model is simply an extension of this idea to multiplicity and ETE_{T} distributions (“soft” multi-particle physics) in pp++pp, pp+A and A+A collisions. Although proposed first Bialas et al. (1982), the AQM is a special case of the NQP model in which a color string connects two constituent-quarks which have scattered, and breaking of the color-string produces particles at midrapidity. However, in the AQM Bialas et al. (1982); Ochiai (1987), it is further assumed that multiple strings attached to the same projectile quark in a pp+A collision coalesce and collapse into one color string, so that the AQM is effectively a wounded projectile quark model.

In this paper, we compare extreme-independent models of soft multi-particle production based on the number of fundamental elements taken as nucleon participants, nuclear collisions, constituent quarks and color-strings (AQM) with our measurement of transverse energy production. It will be shown that the ansatz, d​ET/d​η∝(1−x)​Npart/2+x​Ncolld\mbox{${\rm E}_{T}$}/d\eta\propto(1-x)\mbox{$N_{\rm part}$}/2+x\mbox{$N_{\rm coll}$}, does not imply that there is a hard scattering component in multi-particle production, consistent with the direct observations noted above. Thus, possible models motivated by the fact that half of the momentum of a nucleon is carried by gluons when probed at high Q2Q^{2} in hard-scattering are not considered and we limit our comparison to the nucleon and constituent-quark participant models of soft-multiparticle production widely used since the 1970’s as discussed in the introduction.

III The PHENIX Detector

The PHENIX detector at Brookhaven National Laboratory’s RHIC comprises two central spectrometer arms and two muon spectrometer arms. A comprehensive description of the detector components and performance can be found elsewhere Adcox et al. (2003). The analysis described here utilizes five of the PbSc EMCal sectors Adcox et al. (2003) in the central arm spectrometers, as illustrated schematically in Figure 1. Each calorimeter sector covers a rapidity range of |η|<0.38|\eta|<0.38 and subtends 22.5o22.5^{o} in azimuth for a total azimuthal coverage of 112.5o112.5^{o}. Each sector, whose front face is 5.1 m from the beam axis, is comprised of 2,592 PbSc towers assembled in a 36 x 72 array. Each tower has a 5.535 cm x 5.535 cm surface area and an active depth of 37.5 cm corresponding to 0.85 nuclear interaction lengths or 18 radiation lengths. The PbSc EMCal energy resolution for test beam electrons is Δ​EE=8.1%E​(G​e​V)⊕\frac{\Delta E}{E}=\frac{8.1\%}{\sqrt{E}(GeV)}\oplus 2.1%, with a measured response proportional to the incident electron energy to within ±2%\pm 2\% over the range 0.3≤Ee≤400.3\leq E_{e}\leq 40 GeV.

A minimum-bias (MB) trigger for Au++Au, dd++Au, and pp++pp collisions is provided by two identical beam-beam counters (BBC), labeled North and South, each consisting of 64 individual Čerenkov counters. The BBCs cover the full azimuthal angle in the pseudorapidity range 3.0<|η|<3.93.0<|\eta|<3.9 Allen et al. (2003). For pp++pp and dd++Au collisions, events are required to have at least one counter fire in both the North and South BBCs. For Au++Au collisions, at least two counters must fire in both BBCs. Timing information from the BBCs are used to reconstruct the event vertex with a resolution of 6 mm for central Au++Au collisions. All events are required to have an event vertex within 20 cm of the origin. Centrality determination in 200 GeV and 130 GeV Au++Au collisions Adcox et al. (2003) is based upon the total charge deposited in the BBCs and the total energy deposited in the Zero Degree Calorimeters (ZDC) Allen et al. (2003), which are hadronic calorimeters covering the pseudorapidity range |η|>6|\eta|>6. For 62.4 GeV Au++Au collisions, only the BBCs are used to determine centrality due to the reduced acceptance of the ZDCs at lower energies Adare et al. (2012).

Table 1 gives a summary of the 2003 and 2004 data sets used in this analysis. Previously, PHENIX has studied transverse energy production in Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200 GeV, 130 GeV, and 19.6 GeV Adcox et al. (2001a); Adler et al. (2005) and shown that for ET{\rm E}_{T} measurements at midrapidity at a collider the EMCal acts as a thin but effective hadron calorimeter. Presented here is an extended analysis of 200 GeV Au++Au collision data taken during 2004 with the magnetic field turned on that increases the statistics of the previous analysis by a factor of 494 with 132.9 million MB events. These new results are consistent with the previously published results Adcox et al. (2001a); Adler et al. (2005).

The average luminosity delivered by RHIC has improved dramatically each year, by a factor of 5.75 for pp++pp collisions and 4.5 for dd++Au collisions from the 2003 to 2008 running periods. Due to the readout electronics implemented for the EMCal, with a pile-up window of 428 nsec, the increased luminosity results in an increasing rate-dependent background in the minimum-bias event sample due to multiple collisions, or pile-up, that artificially raises the transverse energy recorded in an event. To minimize this background, the 200 GeV pp++pp and 200 GeV dd++Au data samples presented hear are from the earlier 2003 running period.

Table 1: Summary of the data sets used in this analysis. NeventsN_{\rm events} represents the number of MB events analyzed and ℒave\mathcal{L}_{\rm ave} represents the average RHIC luminosity for the dataset.
sN​N\sqrt{s_{{}_{NN}}} (GeV) System Year NeventsN_{\rm events} ℒave​(c​m−2​s−1)\mathcal{L}_{\rm ave}(cm^{-2}s^{-1})
200 Au++Au 2004 132.9 M 5×10265\times 10^{26}
62.4 Au++Au 2004 20.0 M 0.6×10260.6\times 10^{26}
200 dd++Au 2003 50.1 M 3×10283\times 10^{28}
200 pp++pp 2003 14.6 M 4×10304\times 10^{30}
Refer to caption
Figure 1: Schematic diagram showing the locations of the PHENIX electromagnetic calorimeter sectors in the central arm spectrometer. The sectors labeled W1,W2,W3,E2 and E3 were used in this analysis

IV Data Analysis

The analysis procedure for d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta is described in detail in Adler et al. (2005) and summarized here. The absolute energy scale for the PbSc EMCal was calibrated using the π0\pi^{0} mass peak from pairs of reconstructed EMCal clusters. The uncertainty in the absolute energy scale is 2% in the 62.4 GeV Au++Au dataset and 1.5% in the 200 GeV Au++Au, pp++pp, and dd++Au datasets. The transverse energy for each event was computed using clusters with an energy greater than 30 MeV composed of adjacent towers each with a deposited energy of more than 10 MeV. Faulty towers and all towers in a 3​x​33x3 tower area around any faulty tower are excluded from the analysis.

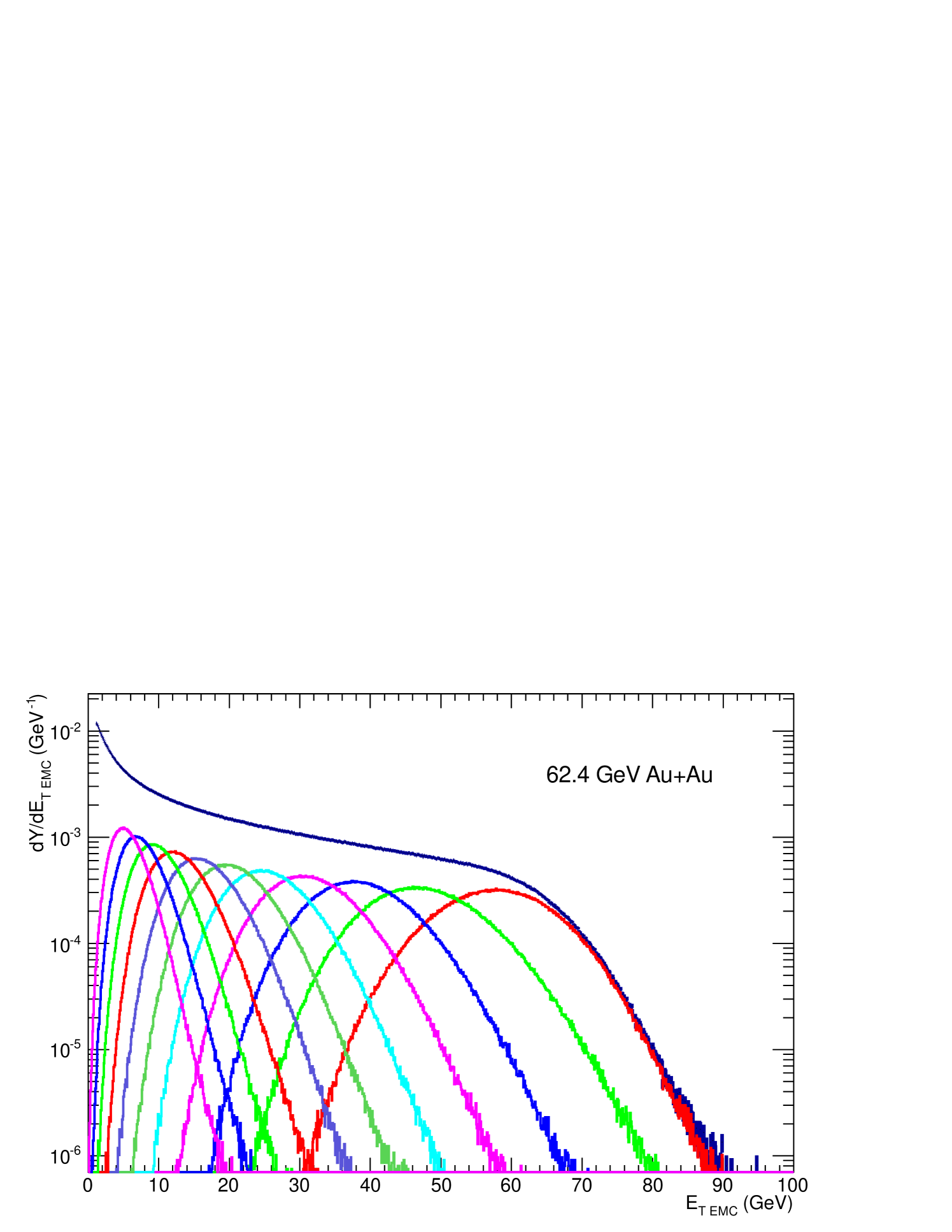
The raw spectra of the measured transverse energy ET​EMC{\rm{E}}_{T\,{\rm EMC}} in the fiducial aperture are given as histograms of the number of entries in a given raw ET​EMC{\rm{E}}_{T\,{\rm EMC}} bin such that the total number of entries sums up to the number of BBC counts. The distributions are then normalized to integrate to unity. As an example, the ET​EMC{\rm{E}}_{T\,{\rm EMC}} distributions as a function of centrality in 5% wide centrality bins are shown in Fig. 2 for 62.4 GeV Au++Au collisions.

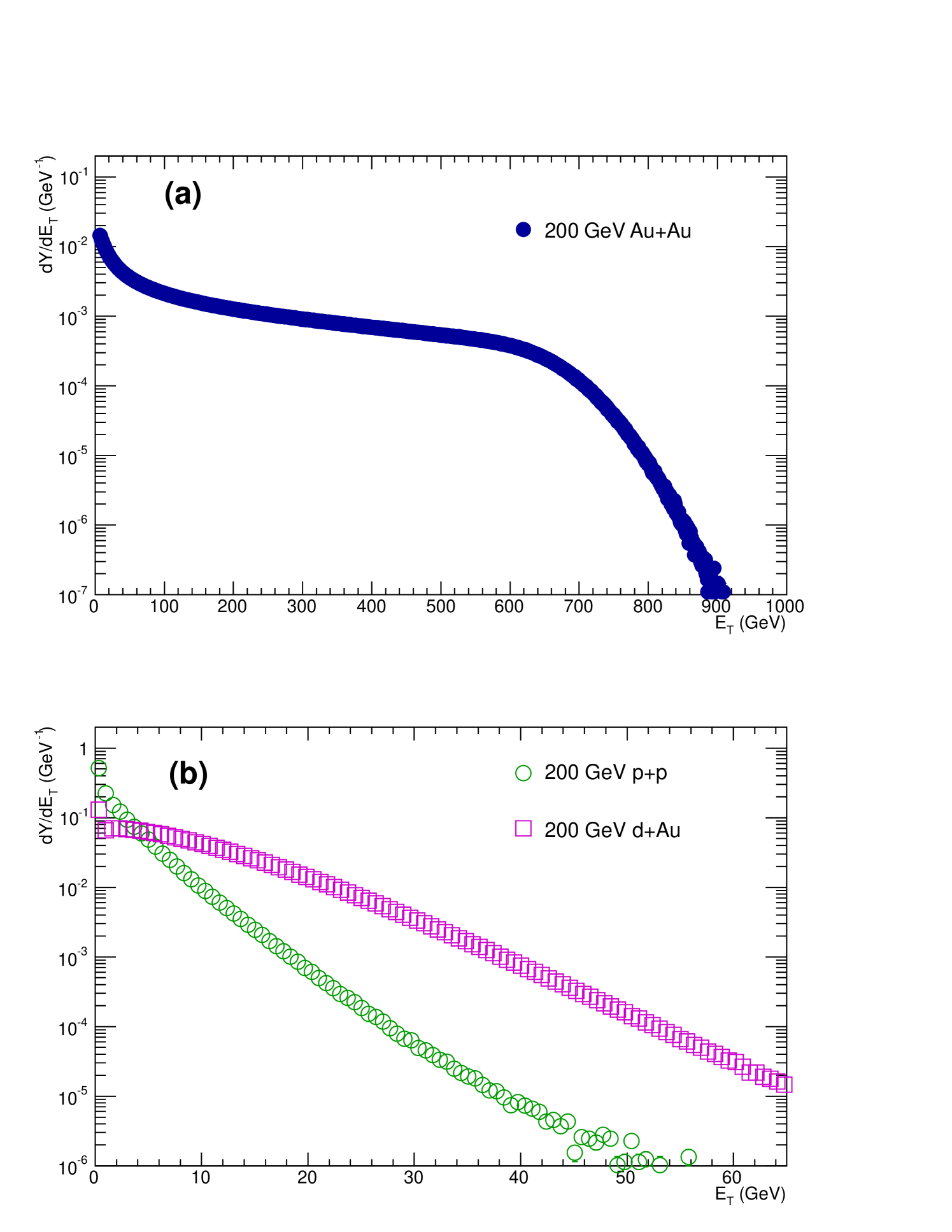
Refer to caption
Figure 2: (Color online) ET​EMC{\rm{E}}_{T\,{\rm EMC}} distributions for sNN=62.4\sqrt{s_{\rm NN}}=62.4 GeV Au++Au collisions. Shown are the MB distribution along with the distributions in 5% wide centrality bins selected using the BBCs. All the plots are normalized so that the integral of the MB distribution is unity.

To obtain the total hadronic ET{\rm E}_{T} within a reference acceptance of Δ​η=1.0,Δ​ϕ=2​π\Delta\eta=1.0,\Delta\phi=2\pi, more properly d​ET/d​η|η=0d\mbox{${\rm E}_{T}$}/d\eta|_{\eta=0}, from the measured raw transverse energy, ET​EMC{\rm{E}}_{T\,{\rm EMC}}, several corrections are applied. The total correction can be decomposed into three main components. First is a correction by a factor of 4.188 to account for the fiducial acceptance. Second is a correction by a factor of 1.262 for 200 GeV Au++Au, 1.236 for 62.4 GeV Au++Au, 1.196 for 200 GeV dd++Au, and 1.227 for 200 GeV pp++pp to account for disabled calorimeter towers not used in the analysis. Third is a factor, kk, which is the ratio of the total hadronic ET{\rm E}_{T} in the fiducial aperture to the measured ET​EMC{\rm{E}}_{T\,{\rm EMC}}. Details on the estimate of the values of the kk factor are given below. The total correction scale factors are obtained by multiplying these three components and are listed in Table 2. The corrected MB distributions for 200 GeV Au++Au, dd++Au, and pp++pp are shown in Fig 3.

Table 2: Summary of the total correction scale factors applied to the measured raw transverse energy, ET​EMC{\rm{E}}_{T\,{\rm EMC}}, to obtain d​ET/d​η|η=0d\mbox{${\rm E}_{T}$}/d\eta|_{\eta=0} for each dataset.
sN​N\sqrt{s_{{}_{NN}}} (GeV) System Correction Factor
200 Au++Au 6.87±0.406.87\pm 0.40
62.4 Au++Au 6.73±0.396.73\pm 0.39
200 dd++Au 6.51±0.546.51\pm 0.54
200 pp++pp 6.68±0.566.68\pm 0.56

The kk factor comprises three components. The first component, denoted kresponsek_{\rm response}, is due to the fact that the EMCal was designed for the detection of electromagnetic particles Adcox et al. (2001a). Hadronic particles passing through the EMCal only deposit a fraction of their total energy. The average EMCal response is estimated for the various particle species using the HIJING event generator Wang and Gyulassy (1991) processed through a geant-based Monte Carlo simulation of the PHENIX detector. The HIJING particle composition and pTp_{T} spectra are adjusted to reproduce the identified charged particle spectra and yields measured by PHENIX. For all of the data sets, 75% of the total energy incident on the EMCal is measured, thus kresponsek_{\rm response} = 1/0.75 = 1.33. The second component of the kk factor, denoted ki​n​f​l​o​wk_{inflow}, is a correction for energy inflow from outside the fiducial aperture of the EMCal. This energy inflow arises from two sources: from parent particles with an original trajectory outside of the fiducial aperture whose decay products are incident within the fiducial aperture, and from particles that reflect off of the PHENIX magnet poles into the EMCal fiducial aperture. The energy inflow contribution is 24% of the measured energy, thus kinflowk_{\rm inflow} = 1-0.24 = 0.76. The third component of the kk factor, denoted klossesk_{\rm losses}, is due to energy losses. There are three components to the energy loss: from particles with an original trajectory inside the fiducial aperture of the EMCal whose decay products are outside of the fiducial aperture (10%), from energy losses at the edges of the EMCal (6%), and from energy losses due to the energy thresholds (6%). The total contribution from energy losses is 22%, thus kl​o​s​s​e​sk_{losses} = 1/(1-0.22) = 1.282. The total kk factor correction is k=kresponse×kinflow×klossesk=k_{\rm response}\times k_{\rm inflow}\times k_{\rm losses} = 1.30.

Refer to caption
Figure 3: (Color online) Corrected ET=d​ET/d​η|η=0\mbox{${\rm E}_{T}$}=d\mbox{${\rm E}_{T}$}/d\eta|_{\eta=0} distributions at sNN=200\sqrt{s_{\rm NN}}=200 GeV for 5 sectors of PbSc (a) Au++Au; (b) pp++pp, dd++Au. The correction factors for each dataset are listed in Table 2. All the plots are normalized so that the integral of each distribution is unity.

When plotting transverse energy production as a function of centrality, systematic uncertainties are decomposed into three types. Type A uncertainties are point-to-point uncertainties that are uncorrelated between bins and are normally added in quadrature to the statistical uncertainties. However, because there are no Type A uncertainties in this analysis, the vertical error bars represent statistical uncertainties only. Type B uncertainties are bin-correlated such that all points move in the same direction, but not necessarily by the same factor. These are represented by a pair of lines bounding each point. Type C uncertainties are normalization uncertainties in which all points move by the same factor independent of each bin. These are represented as a single error band on the right hand side of each plot. In addition, there is an uncertainty on the estimate of the value of <Np0​.0​art><N_{\rm p0.0art}> at each centrality that is represented by horizontal error lines.

There are two contributions to Type B uncertainties, which are added in quadrature to obtain the total Type B uncertainty. The first contribution to Type B uncertainties arises from the uncertainty in the trigger efficiency. The method by which the trigger efficiency is determined is described in Adler et al. (2005). The BBC trigger efficiency is 92.2%−3.0%+2.5%{}^{+2.5\%}_{-3.0\%} for 200 GeV and 130 GeV Au++Au collisions, 83.7%±\pm3.2% for 62.4 GeV Au++Au collisions, 88%±\pm4% for 200 GeV dd++Au collisions, and 54.8%±\pm5.3% for 200 GeV pp++pp collisions Adler et al. (2007a). Because the centrality is defined for a given event as a percentage of the total geometrical cross section, an uncertainty in the trigger efficiency translates into an uncertainty in the centrality definition. This uncertainty is estimated by measuring the variation in d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta by redefining the centrality using trigger efficiencies that vary by ±1\pm 1 standard deviation. The second contribution to Type B uncertainties is the uncertainty due to random electronic noise in the EMCal towers. The noise, or background, contribution is estimated to be consistent with zero with uncertainties tabulated in Table 3 by measuring the average energy deposited per sector in events where all the particles are screened by the central magnet pole tips by requiring an interaction z-vertex of +50<z<+60+50<z<+60 cm and −50<z<−60-50<z<-60 cm. A summary of the magnitudes of the Type B uncertainty contributions is listed in Table 3.

There are several components to Type C uncertainties, which are also added in quadrature to obtain the total Type C uncertainty. The first contribution is the uncertainty of the energy response estimate. This uncertainty includes uncertainties in the absolute energy scale, uncertainties in the estimate of the hadronic response, and uncertainties from energy losses on the EMCal edges and from energy thresholds. The uncertainties in the hadronic response estimate include a 3% uncertainty estimated using a comparison of the simulated energy deposited by hadrons with different momenta with test beam data Aphecetche et al. (2003a) along with an additional 1% uncertainty in the particle composition and momentum distribution. Other Type C uncertainties include an uncertainty in the estimate of the EMCal acceptance, an uncertainty in the calculation of the fraction of the total energy incident on the EMCal fiducial area (losses and inflow), and an uncertainty in the centrality determination. A summary of the magnitudes of the Type C uncertainty contributions is listed in Table 3. For the MB distributions, the uncertainties on the scale factors previously quoted contain only Type C uncertainties from the energy response, acceptance, and from losses and inflow.

Table 3: Summary of the systematic uncertainties given in percent. Listed are uncertainties classified as Type B and Type C. A range is given for Type B uncertainties with the first number corresponds to the most central bin and the second number corresponds to the most peripheral bin.
Au++Au dd++Au pp++pp
Error type System 200 GeV 130 GeV 62.4 GeV 200 GeV 200 GeV
C Energy Resp. 3.9% 3.8% 3.9% 3.9% 3.9%
C Acceptance 3.0% 3.0% 3.0% 3.0% 3.0%
C Losses and Inflow 3.0% 3.0% 3.0% 3.0% 3.0%
C Centrality 0.5% 0.5% 0.5% n/a n/a
B Trigger 0.3%-16% 0.3%-16% 0.44%-16% n/a n/a
B Background 0.2%-6.0% 0.4%-10.0% 0.375%-13.3% 6.0% 6.0%
Table 4: The inelastic quark-quark cross sections used for each collision energy to reproduce the inelastic nucleon-nucleon cross section.
sN​N\sqrt{s_{{}_{NN}}} (GeV) σN​Ninel\sigma^{\rm inel}_{NN} (mb) σq​qinel\sigma^{\rm inel}_{qq} (mb)
200 42 9.36
130 40 8.60
62.4 35.6 7.08

V Estimating the Number of Nucleon and Quark Participants

A Monte-Carlo-Glauber (MC-Glauber) model calculation Miller et al. (2007) is used to obtain estimates for the number of nucleon participants at each centrality using the procedure described in Adler et al. (2005). A similar procedure can be used to estimate the number of quark participants, Nq​pN_{qp}, at each centrality. The quark-quark inelastic cross section for each collision energy is determined such that the inelastic nucleon-nucleon cross section is reproduced. The MC-Glauber calculation is then implemented so that the fundamental interactions are quark-quark rather than nucleon-nucleon collisions. Initially, the nuclei are assembled by distributing the centers of the nucleons according to a Woods-Saxon distribution. Once a nucleus is assembled, three quarks are then distributed around the center of each nucleon. The spatial distribution of the quarks is given by the Fourier transform of the form factor of the proton:

ρp​r​o​t​o​n​(r)=ρ0p​r​o​t​o​n×e−a​r,\rho^{proton}(r)=\rho^{proton}_{0}\times e^{-ar}, (4)

where a=12/rm=4.27a=\sqrt{12}/r_{m}=4.27 fm-1 and rm=0.81r_{m}=0.81 fm is the rms charge radius of the proton Hofstadter et al. (1958). The coordinates of the two colliding nuclei are shifted relative to each other by the impact parameter. A pair of quarks, one from each nucleus, interact with each other if their distance dd in the plane transverse to the beam axis satisfies the condition

d<σq​qinelπ,d<\sqrt{\frac{\sigma^{\rm inel}_{qq}}{\pi}}, (5)

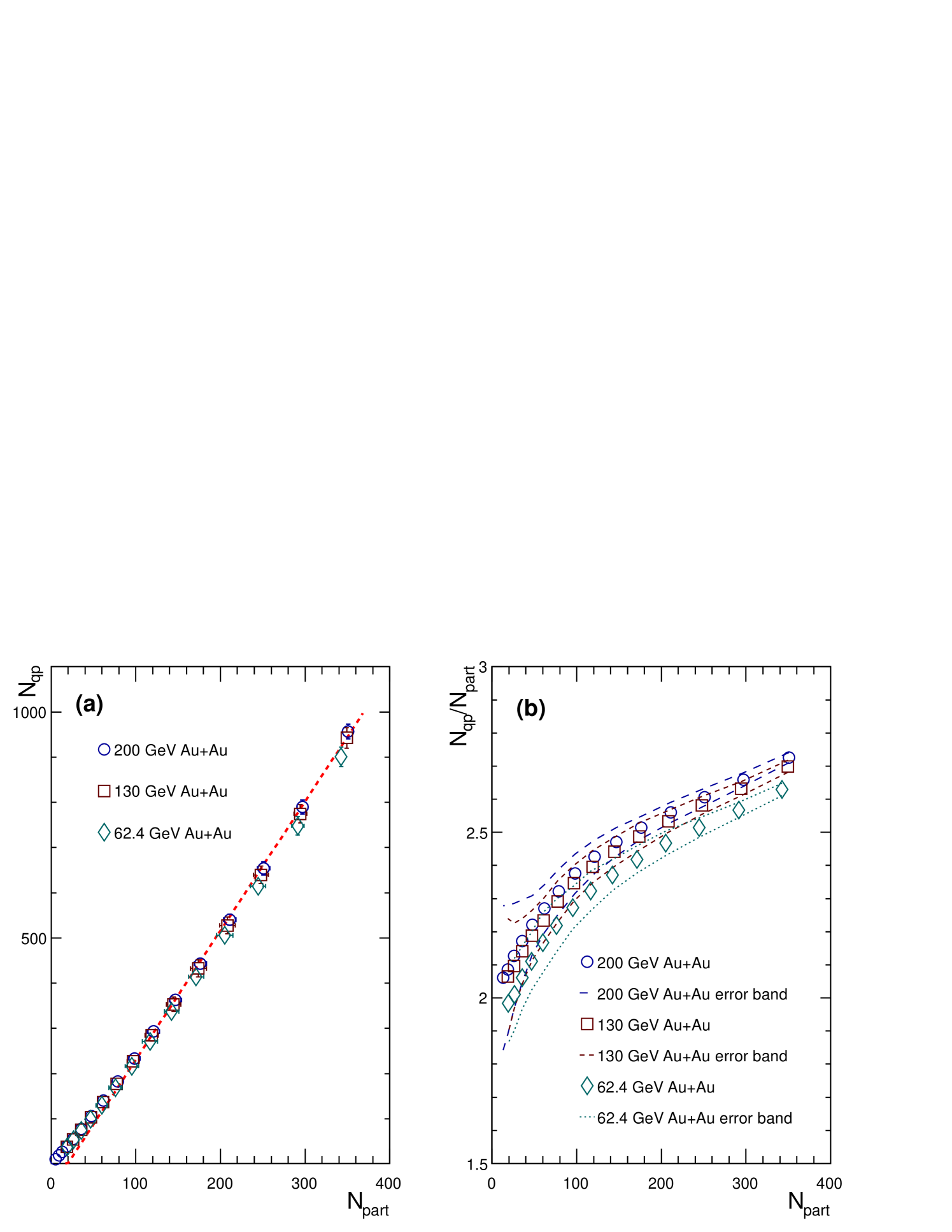
where σq​qinel\sigma^{\rm inel}_{qq} is the inelastic quark-quark cross section, which is varied for the case of nucleon-nucleon collisions until the known inelastic nucleon-nucleon cross section is reproduced and then used for the A+A calculations. The resulting inelastic quark-quark cross sections are tabulated in Table 4. Figure 4a shows the number of quark participants as a function of the number of nucleon participants. The relationship is nonlinear, especially for low values of NpartN_{\rm part}. Figure 4b shows the resulting ratio of the number of quark participants to the number of nucleon participants as a function of the number of nucleon participants.

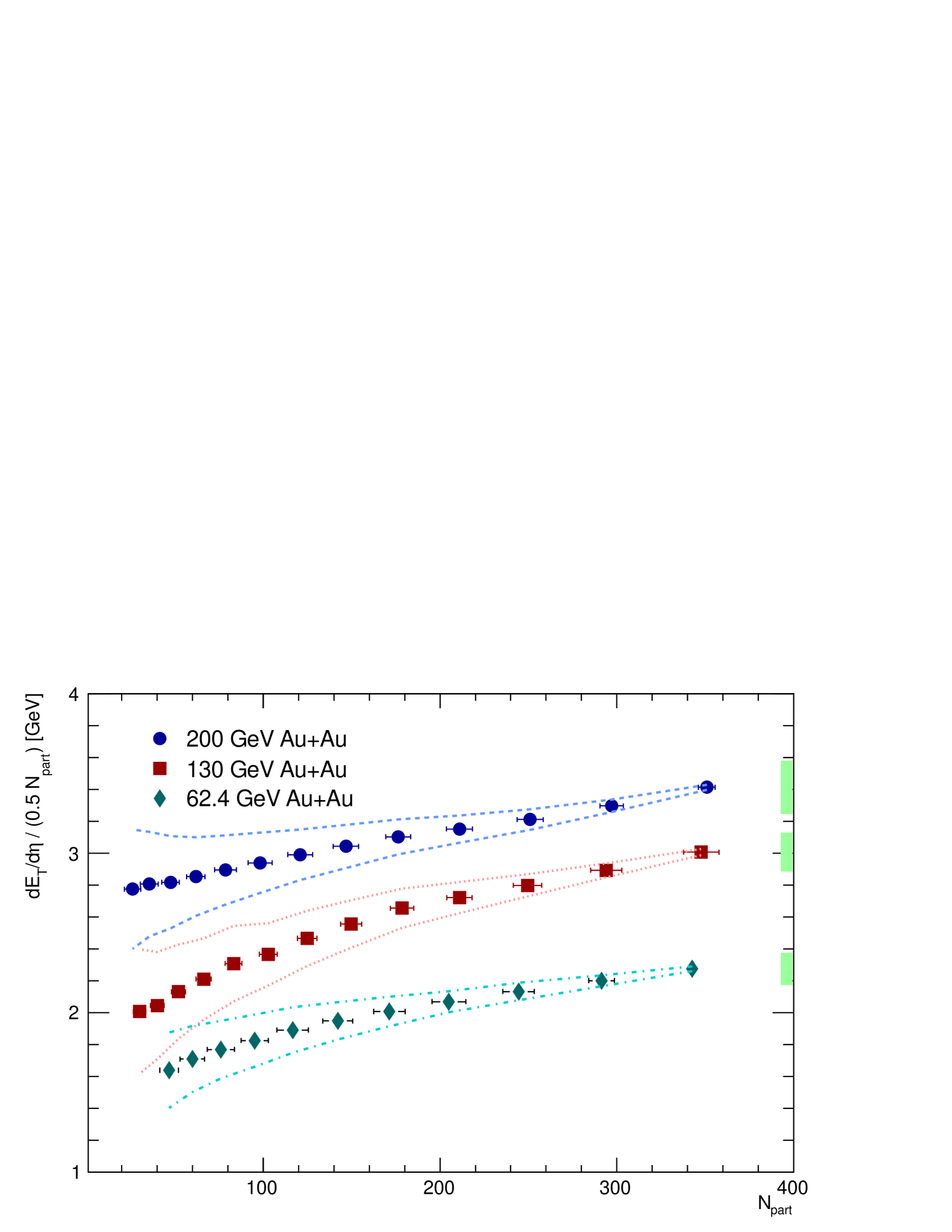
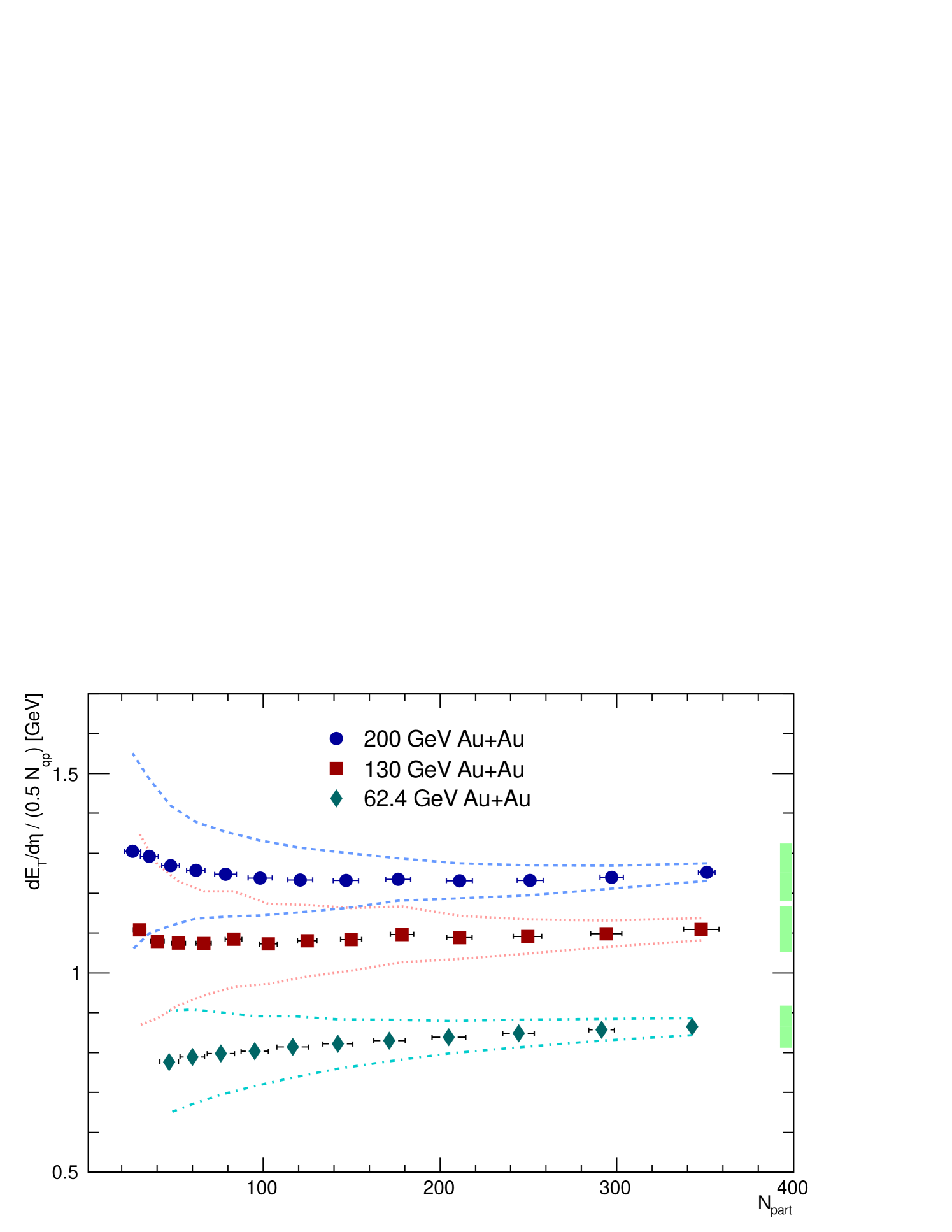
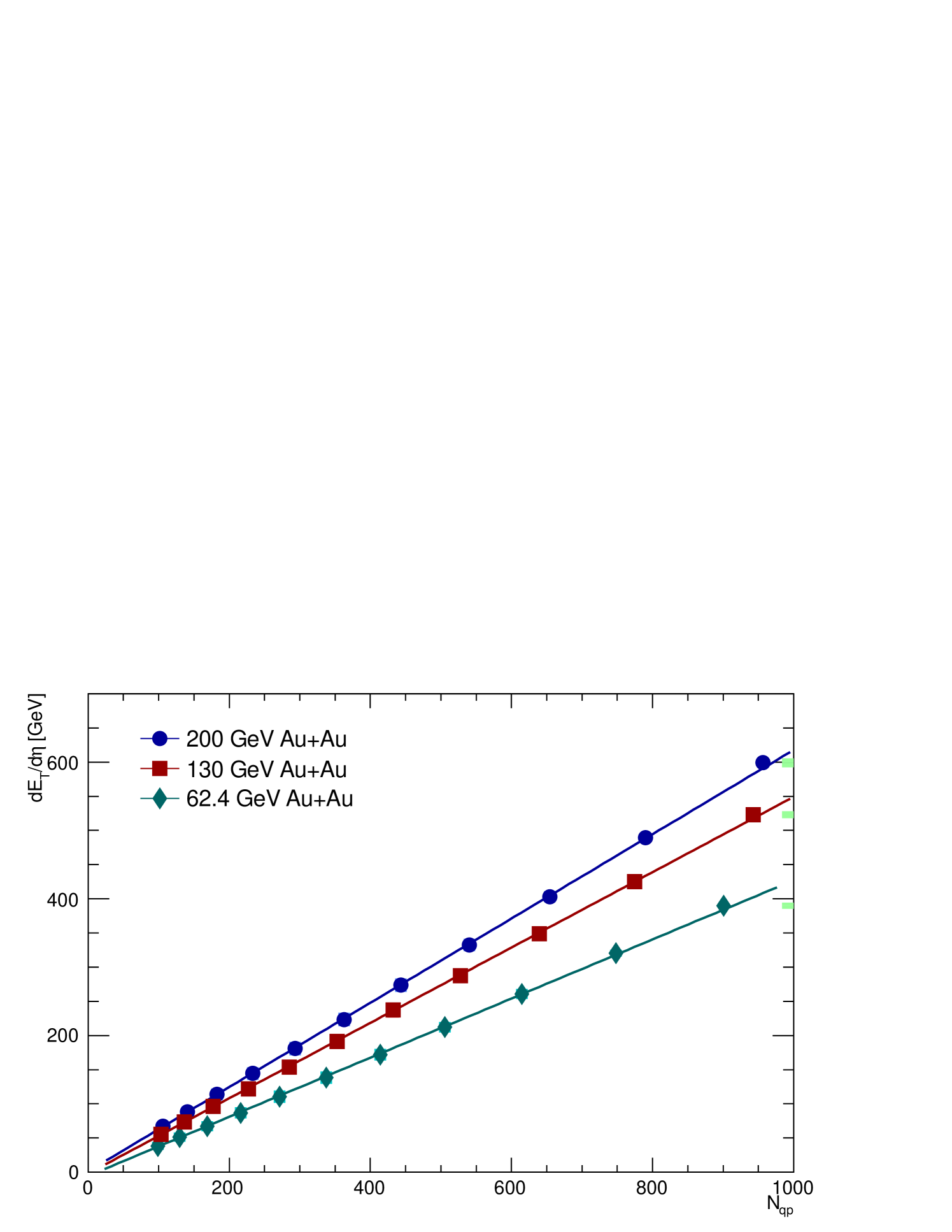
Refer to caption
Figure 4: (Color online) (a) The number of quark participants as a function of the number of nucleon participants. The error bars represent the systematic uncertainty estimate on the MC-Glauber calculation. The dashed line is a linear fit to the 200 GeV Au++Au points with Npart>100N_{\rm part}>100 to illustrate the nonlinearity of the correlation at low values of NpartN_{\rm part}. (b) The ratio of the number of quark participants to the number of nucleon participants as a function of the number of nucleon participants. The error bands represent the systematic uncertainty estimate on the MC-Glauber calculation.

VI d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta Results

Refer to caption
Figure 5: (Color online) d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta normalized by the number of participant pairs as a function of the number of participants for Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200, 130, and 62.4 GeV. The Type A uncertainties are represented by error bars about each point. The Type B uncertainties are represented by the lines bounding each point. The Type C uncertainties are represented by the error bands to the right of the most central data point.
Refer to caption
Figure 6: (Color online) d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta normalized by the number of participant quark pairs as a function of the number of participants for Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200, 130, and 62.4 GeV. The Type A uncertainties are represented by error bars about each point. The Type B uncertainties are represented by the lines bounding each point. The Type C uncertainties are represented by the error bands to the right of the most central data point.
Refer to caption
Figure 7: (Color online) d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta as a function of the number of quark participants for Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200, 130, and 62.4 GeV. The Type A uncertainties are represented by error bars about each point. The Type B uncertainties are represented by error bands about each point shown. The type A and type B uncertainties are typically less than the size of the data point. The Type C uncertainties are represented by the error bands to the right of the most central data point. The lines are straight line fits to the data.

The distribution of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta normalized by the number of participant pairs as a function of the number of participants is shown in Figure 5 for Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200, 130, and 62.4 GeV. The data are also tabulated in Table 5 for 200 GeV Au++Au, Table 6 for 130 GeV Au++Au, and Table 7 for 62.4 GeV Au++Au collisions. For all collision energies, the increase seen as a function of NpartN_{\rm part} is nonlinear, showing a saturation towards the more central collisions. However, when d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta is normalized by the number of quark participant pairs, as shown in Figure 6, the data are consistently flat within the systematic uncertainties. Transverse energy production can also be plotted as a function of the number of quark participants as shown in Figure 7. The data for each collision energy are well described by a straight line as shown. The slope parameters for each collision energy are summarized in Table 8. The consistency with zero of the values of the intercept bb establish a linear proportionality of ET{\rm E}_{T} with Nq​pN_{qp}. To summarize, transverse energy production scales linearly with the number of constituent-quark participants, in contrast to the nonlinear relationship between transverse energy and the number of participating nucleons.

This nonlinear relationship has been successfully parametrized as a function of centrality Adcox et al. (2001b); Wang and Gyulassy (2001); Kharzeev and Nardi (2001):

d​ETAA/d​η=(d​ETp​p/d​η)​[(1−x)​⟨Npart⟩/2+x​⟨Ncoll⟩],{d\mbox{${\rm E}_{T}$}^{\rm AA}/d\eta}=({d\mbox{${\rm E}_{T}$}^{pp}/d\eta})\ [(1-x)\,\langle\mbox{$N_{\rm part}$}\rangle/2+x\,\langle\mbox{$N_{\rm coll}$}\rangle], (6)

with the implication that the proportionality to NcollN_{\rm coll} is related to a contribution of hard-scattering to NchN_{\rm ch} and ET{\rm E}_{T} distributions Wang and Gyulassy (2001); Kharzeev and Nardi (2001). This seems to contradict the extensive measurements of NchN_{\rm ch} and ET{\rm E}_{T} distributions in pp++pp collisions described in Sec. II which show that these distributions represent measurements of the “soft” multiparticle physics that dominates the pp++pp inelastic cross section. Another argument against a hard-scattering component that the shape of the d​Nch/d​η/(0.5​Npart)d\mbox{$N_{\rm ch}$}/d\eta/(0.5\mbox{$N_{\rm part}$}) vs. NpartN_{\rm part} curves as in Fig. 5 is also the same at 2.76 TeV Pb++Pb collisions Aamodt et al. (2011) although the jet cross section increases by a very large factor. Furthermore, any supposed hard-component in the pp++pp distributions would be suppressed in A+A collisions Adcox et al. (2002). This apparent conflict can be resolved if Eq. 6 is just a proxy for the correct description of the underlying physics, because d​ETAA/d​ηd\mbox{${\rm E}_{T}$}^{\rm AA}/d\eta is strictly proportional to Nq​pN_{qp} (Fig. 7, Table 8). Using NpartN_{\rm part}, NcollN_{\rm coll} and Nq​pN_{qp} as a function of centrality, with the value x=0.08x=0.08 Adcox et al. (2001b); Back et al. (2004), the ansatz in brackets in Eq. 6 is compared to Nq​pN_{qp} as a function of centrality (Table 9). The striking result is that the ratio Nq​p/[(1−x)​⟨Npart⟩/2+x​⟨Ncoll⟩]=3.88\mbox{$N_{qp}$}/[(1-x)\,\langle\mbox{$N_{\rm part}$}\rangle/2+x\,\langle\mbox{$N_{\rm coll}$}\rangle]=3.88 on the average and varies by less than 1% over the entire range except for the most peripheral bin where it drops by 5%. This result demonstrates that rather than implying a hard-scattering component in NchN_{\rm ch} and ET{\rm E}_{T} distributions, Eq. 6 is instead a proxy for the number of constituent-quark-participants Nq​pN_{qp} as a function of centrality.

It is important to point out that the relationship breaks down more seriously for pp++pp collisions, with a ratio of 2.99 (Table 9). This is consistent with the PHOBOS Back et al. (2004) result that a fit of Eq. 6 to ⟨d​NchAA/d​η⟩\langle d\mbox{$N_{\rm ch}$}^{\rm AA}/d\eta\rangle leaving ⟨d​Nchp​p/d​η⟩\langle d\mbox{$N_{\rm ch}$}^{pp}/d\eta\rangle as a free parameter also projects above the pp++pp measurement. Because the key to the utility of Extreme Independent Models is that the pp++pp data, together with an independent calculation of the nuclear geometry can be used to predict the A+A distributions, we now turn to the analysis of the pp++pp, dd++Au and Au++Au ET{\rm E}_{T} distributions at sN​N\sqrt{s_{{}_{NN}}} =200 GeV in terms of these models to see whether the extrapolation from the pp++pp data using constituent-quark participants is more robust than from the ansatz.

Table 5: Transverse energy production results for 200 GeV Au++Au collisions. Listed are the total uncertainties (Type A, Type B, and Type C) for each centrality bin.
Centrality <Npart><N_{\rm part}> <Nq​p><N_{qp}> d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Npart>\frac{1}{0.5<N_{\rm part}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Nq​p>\frac{1}{0.5<N_{qp}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV]
0%–5% 350.9 ±\pm 4.7 956.6 ±\pm 16.2 599.0 ±\pm 34.7 3.41 ±\pm 0.20 1.25 ±\pm 0.08
5%–10% 297.0 ±\pm 6.6 789.8 ±\pm 15.3 489.7 ±\pm 28.9 3.29 ±\pm 0.19 1.24 ±\pm 0.08
10%–15% 251.0 ±\pm 7.3 654.2 ±\pm 14.5 403.0 ±\pm 25.0 3.21 ±\pm 0.19 1.23 ±\pm 0.08
15%–20% 211.0 ±\pm 7.3 540.2 ±\pm 12.3 332.5 ±\pm 21.2 3.15 ±\pm 0.20 1.23 ±\pm 0.08
20%–25% 176.3 ±\pm 7.0 443.3 ±\pm 10.4 273.6 ±\pm 18.6 3.10 ±\pm 0.21 1.23 ±\pm 0.09
25%–30% 146.8 ±\pm 7.1 362.8 ±\pm 12.2 223.4 ±\pm 16.4 3.04 ±\pm 0.22 1.23 ±\pm 0.09
30%–35% 120.9 ±\pm 7.0 293.3 ±\pm 11.0 180.8 ±\pm 14.3 2.99 ±\pm 0.23 1.23 ±\pm 0.10
35%–40% 98.3 ±\pm 6.8 233.5 ±\pm 9.2 144.5 ±\pm 12.6 2.94 ±\pm 0.25 1.24 ±\pm 0.11
40%–45% 78.7 ±\pm 6.1 182.7 ±\pm 6.8 113.9 ±\pm 10.9 2.90 ±\pm 0.27 1.25 ±\pm 0.12
45%–50% 61.9 ±\pm 5.2 140.5 ±\pm 5.3 88.3 ±\pm 9.3 2.85 ±\pm 0.29 1.26 ±\pm 0.14
50%–55% 47.6 ±\pm 4.9 105.7 ±\pm 5.5 67.1 ±\pm 8.1 2.82 ±\pm 0.33 1.27 ±\pm 0.15
55%–60% 35.6 ±\pm 5.1 77.3 ±\pm 6.8 50.0 ±\pm 6.7 2.81 ±\pm 0.36 1.29 ±\pm 0.17
60%–65% 26.1 ±\pm 4.7 55.5 ±\pm 7.1 36.2 ±\pm 5.4 2.77 ±\pm 0.40 1.30 ±\pm 0.20
Table 6: Transverse energy production results for 130 GeV Au++Au collisions. Listed are the total uncertainties (Type A, Type B, and Type C) for each centrality bin.
Centrality <Npart><N_{\rm part}> <Nq​p><N_{qp}> d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Npart>\frac{1}{0.5<N_{\rm part}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Nq​p>\frac{1}{0.5<N_{qp}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV]
0%–5% 347.7 ±\pm 10.0 942.6 ±\pm 22.6 522.8 ±\pm 27.7 3.01 ±\pm 0.16 1.11 ±\pm 0.06
5%–10% 294.0 ±\pm 8.9 774.7 ±\pm 20.3 425.2 ±\pm 23.3 2.89 ±\pm 0.16 1.10 ±\pm 0.07
10%–15% 249.5 ±\pm 8.0 639.6 ±\pm 19.4 349.0 ±\pm 20.3 2.80 ±\pm 0.16 1.09 ±\pm 0.07
15%–20% 211.0 ±\pm 7.2 527.7 ±\pm 18.3 287.2 ±\pm 18.3 2.72 ±\pm 0.17 1.09 ±\pm 0.08
20%–25% 178.6 ±\pm 6.6 432.5 ±\pm 19.0 237.1 ±\pm 16.6 2.66 ±\pm 0.19 1.10 ±\pm 0.09
25%–30% 149.7 ±\pm 6.0 353.0 ±\pm 15.9 191.3 ±\pm 14.9 2.56 ±\pm 0.20 1.08 ±\pm 0.10
30%–35% 124.8 ±\pm 5.5 284.9 ±\pm 13.2 153.9 ±\pm 13.3 2.47 ±\pm 0.22 1.08 ±\pm 0.11
35%–40% 102.9 ±\pm 5.1 227.1 ±\pm 11.0 121.8 ±\pm 11.7 2.37 ±\pm 0.23 1.07 ±\pm 0.12
40%–45% 83.2 ±\pm 4.7 177.1 ±\pm 8.8 96.0 ±\pm 10.8 2.31 ±\pm 0.27 1.08 ±\pm 0.13
45%–50% 66.3 ±\pm 4.3 136.5 ±\pm 7.1 73.3 ±\pm 8.9 2.21 ±\pm 0.28 1.07 ±\pm 0.14
50%–55% 52.1 ±\pm 4.0 103.3 ±\pm 6.5 55.5 ±\pm 7.8 2.13 ±\pm 0.32 1.07 ±\pm 0.16
55%–60% 40.1 ±\pm 3.8 76.0 ±\pm 7.3 41.0 ±\pm 6.6 2.04 ±\pm 0.35 1.08 ±\pm 0.20
60%–65% 30.1 ±\pm 3.6 54.5 ±\pm 7.1 30.2 ±\pm 5.5 2.01 ±\pm 0.40 1.11 ±\pm 0.25
Table 7: Transverse energy production results for 62.4 GeV Au++Au collisions. Listed are the total uncertainties (Type A, Type B, and Type C) for each centrality bin.
Centrality <Npart><N_{\rm part}> <Nq​p><N_{qp}> d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Npart>\frac{1}{0.5<N_{\rm part}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV] 10.5​<Nq​p>\frac{1}{0.5<N_{qp}>} d​ETd​η\frac{dE_{T}}{d\eta} [GeV]
0%–5% 342.6 ±\pm 4.9 900.9 ±\pm 21.7 389.7 ±\pm 25.9 2.27 ±\pm 0.13 0.87 ±\pm 0.06
5%–10% 291.3 ±\pm 7.3 748.0 ±\pm 20.4 320.5 ±\pm 21.9 2.20 ±\pm 0.13 0.86 ±\pm 0.06
10%–15% 244.5 ±\pm 8.9 614.7 ±\pm 17.9 260.6 ±\pm 18.8 2.13 ±\pm 0.13 0.85 ±\pm 0.07
15%–20% 205.0 ±\pm 9.6 505.8 ±\pm 16.9 212.1 ±\pm 15.9 2.07 ±\pm 0.13 0.84 ±\pm 0.07
20%–25% 171.3 ±\pm 8.9 414.3 ±\pm 15.2 171.9 ±\pm 14.4 2.01 ±\pm 0.15 0.83 ±\pm 0.08
25%–30% 142.2 ±\pm 8.5 337.2 ±\pm 12.5 138.6 ±\pm 12.9 1.95 ±\pm 0.16 0.82 ±\pm 0.08
30%–35% 116.7 ±\pm 8.9 271.1 ±\pm 12.8 110.4 ±\pm 11.7 1.89 ±\pm 0.18 0.81 ±\pm 0.09
35%–40% 95.2 ±\pm 7.7 216.3 ±\pm 11.0 86.9 ±\pm 10.2 1.83 ±\pm 0.19 0.80 ±\pm 0.10
40%–45% 76.1 ±\pm 7.7 168.8 ±\pm 11.3 67.3 ±\pm 8.7 1.77 ±\pm 0.21 0.80 ±\pm 0.12
45%–50% 59.9 ±\pm 6.9 129.8 ±\pm 9.7 51.2 ±\pm 7.5 1.71 ±\pm 0.23 0.79 ±\pm 0.13
50%–55% 46.8 ±\pm 5.2 98.8 ±\pm 6.1 38.4 ±\pm 6.4 1.64 ±\pm 0.25 0.78 ±\pm 0.14
Table 8: The slope parameters from a linear fit of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta as a function of Nq​pN_{qp}, d​ET/d​η=a×Nq​p+bd\mbox{${\rm E}_{T}$}/d\eta=a\times N_{qp}+b for each collision energy in Au++Au collisions. The value of χ2\chi^{2} has been calculated including Type A, Type B, and Type C uncertainties for each point.
sN​N\sqrt{s_{{}_{NN}}} (GeV) aa (GeV) bb (GeV) χ2\chi^{2} nd​o​fn_{dof}
200 0.617±0.0230.617\pm 0.023 1.2±7.01.2\pm 7.0 0.098 9
130 0.551±0.0200.551\pm 0.020 −2.1±6.5-2.1\pm 6.5 0.086 9
62.4 0.432±0.0190.432\pm 0.019 −5.4±5.4-5.4\pm 5.4 0.163 9
Table 9: Test of whether the ansatz, [(1−x)​⟨Npart⟩/2+x​⟨Ncoll⟩][(1-x)\,\langle\mbox{$N_{\rm part}$}\rangle/2+x\,\langle\mbox{$N_{\rm coll}$}\rangle], from Eq. 6, with x=0.08x=0.08, is a proxy for Nq​pN_{qp}. The errors quoted on ⟨Npart⟩\langle N_{\rm part}\rangle, ⟨Nq​p⟩\langle N_{qp}\rangle, ⟨Ncoll⟩\langle\mbox{$N_{\rm coll}$}\rangle are correlated Type C and largely cancel in the ⟨Nq​p⟩\langle\mbox{$N_{qp}$}\rangle/ansatz ratio.
Centrality ⟨Npart⟩\langle N_{\rm part}\rangle ⟨Nq​p⟩\langle N_{qp}\rangle ⟨Ncoll⟩\langle\mbox{$N_{\rm coll}$}\rangle ansatz ⟨Nq​p⟩\langle\mbox{$N_{qp}$}\rangle/ansatz
0%–5% 350.9±4.7350.9\pm 4.7 956.6±16.2956.6\pm 16.2 1064.1±110.01064.1\pm 110.0 246.5 3.88
5%–10% 297.0±6.6297.0\pm 6.6 789.8±15.3789.8\pm 15.3 838.0±87.2838.0\pm 87.2 203.7 3.88
10%–15% 251.0±7.3251.0\pm 7.3 654.2±14.5654.2\pm 14.5 661.1±68.5661.1\pm 68.5 168.3 3.89
15%–20% 211.0±7.3211.0\pm 7.3 540.2±12.3540.2\pm 12.3 519.1±53.7519.1\pm 53.7 138.6 3.90
20%–25% 176.3±7.0176.3\pm 7.0 443.3±10.4443.3\pm 10.4 402.6±39.5402.6\pm 39.5 113.3 3.91
25%–30% 146.8±7.1146.8\pm 7.1 362.8±12.2362.8\pm 12.2 311.9±31.8311.9\pm 31.8 92.5 3.92
30%–35% 120.9±7.0120.9\pm 7.0 293.3±11.0293.3\pm 11.0 237.8±24.2237.8\pm 24.2 74.6 3.93
35%–40% 98.3±6.898.3\pm 6.8 233.5±9.2233.5\pm 9.2 177.3±18.3177.3\pm 18.3 59.4 3.93
40%–45% 78.7±6.178.7\pm 6.1 182.7±6.8182.7\pm 6.8 129.6±12.6129.6\pm 12.6 46.6 3.92
45%–50% 61.9±5.261.9\pm 5.2 140.5±5.3140.5\pm 5.3 92.7±9.092.7\pm 9.0 35.9 3.91
50%–55% 47.6±4.947.6\pm 4.9 105.7±5.5105.7\pm 5.5 64.4±8.164.4\pm 8.1 27.0 3.91
55%–60% 35.6±5.135.6\pm 5.1 77.3±6.877.3\pm 6.8 43.7±7.643.7\pm 7.6 19.9 3.89
60%–65% 26.1±4.726.1\pm 4.7 55.5±7.155.5\pm 7.1 29.0±6.529.0\pm 6.5 14.3 3.87
65%–70% 18.7±4.018.7\pm 4.0 39.0±6.739.0\pm 6.7 18.8±5.318.8\pm 5.3 10.1 3.86
70%–75% 13.1±3.213.1\pm 3.2 27.0±4.927.0\pm 4.9 12.0±3.612.0\pm 3.6 7.0 3.86
75%–80% 9.4±2.19.4\pm 2.1 19.0±3.219.0\pm 3.2 7.9±2.27.9\pm 2.2 5.0 3.83
80%–92% 5.4±1.25.4\pm 1.2 10.3±1.510.3\pm 1.5 4.0±1.04.0\pm 1.0 2.8 3.67
pp++pp 2 2.99±0.052.99\pm 0.05 1 1 2.99

VII Extreme-Independent analyses in general

In Extreme Independent models for an AA+BB nucleus-nucleus reaction, the nuclear geometry, i.e. the relative probability of the assumed fundamental elements of particle production, such as number of binary nucleon-nucleon (N+N) collisions (NcollN_{\rm coll}), nucleon participants or wounded nucleons (NpartN_{\rm part},WN), constituent-quark participants (NQP), or color-strings (wounded projectile quarks - AQM), can be computed from the assumptions of the model in a standard Glauber Monte Carlo calculation Miller et al. (2007) without reference to either the detector Tannenbaum (2004) or the particle production by the fundamental elements. Once the nuclear geometry is specified in this manner, it can be applied to the measured pp++pp distribution (assumed equivalent to N+N) to derive the distribution (in the actual detector) of ET{\rm E}_{T} or multiplicity (or other additive quantity) for the fundamental elementary collision process, i.e. a collision, a wounded nucleon (nucleon participant), constituent-quark participant or a wounded projectile quark (color-string), which is then used as the basis of the analysis of an AA+BB reaction as the result of multiple independent elementary collision processes. The key experimental issue then becomes the linearity of the detector response to multiple collisions (better than 1% in the present case), and the stability of the response for the different AA+BB combinations and run periods used in the analysis. The acceptance of the detector is taken into account by making a correction for the probability, p0p_{0}, of measuring zero ET{\rm E}_{T} for an N+N inelastic collision, which can usually be determined from the data Tannenbaum (2004) (as shown below).

The method for the calculation of the ET{\rm E}_{T} distribution from an AA+BB reaction in a given detector is illustrated for the NcollN_{\rm coll} or number of binary N+N collision model. The ET{\rm E}_{T} distribution is equal to the sum:

(d​σd​ET)Ncoll=σB​A​∑n=1Nmaxwn​Pn​(ET)\bigg{(}{d\sigma\over d\mbox{${\rm E}_{T}$}}\bigg{)}_{\rm\mbox{$N_{\rm coll}$}}=\sigma_{BA}\sum^{\rm N_{\rm max}}_{n=1}w_{n}\,P_{n}(\mbox{${\rm E}_{T}$}) (7)

where σB​A\sigma_{BA} is the measured AA+BB cross section in the detector, wnw_{n} is the relative probability for nn N+N collisions in the AA+BB reaction with maximum value n=Nmaxn=\rm N_{\rm max}, and Pn​(ET)P_{n}(\mbox{${\rm E}_{T}$}) is the calculated ET{\rm E}_{T} distribution on the detector for nn independent N+N collisions. If f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}) is the measured ET{\rm E}_{T} spectrum on the detector for an N+N collision that gives a nonzero ET{\rm E}_{T}, and p0p_{0} is the probability for an N+N collision to produce no signal in the detector (zero ET{\rm E}_{T}) , then the correctly normalized ET{\rm E}_{T} distribution for one N+N collision is:

P1​(ET)=(1−p0)​f1​(ET)+p0​δ​(ET),P_{1}(\mbox{${\rm E}_{T}$})=(1-p_{0})f_{1}(\mbox{${\rm E}_{T}$})+p_{0}\delta(\mbox{${\rm E}_{T}$}), (8)

where δ​(ET)\delta(\mbox{${\rm E}_{T}$}) is the Dirac delta function and ∫f1​(ET)​𝑑ET=1\int f_{1}(\mbox{${\rm E}_{T}$})\,d\mbox{${\rm E}_{T}$}=1. Pn​(ET)P_{n}(\mbox{${\rm E}_{T}$}) (including the p0p_{0} effect) is obtained by convoluting P1​(ET)P_{1}(\mbox{${\rm E}_{T}$}) with itself n−1n-1 times

Pn​(ET)=∑i=0nn!(n−i)!​i!​p0n−i​(1−p0)i​fi​(ET)P_{n}(\mbox{${\rm E}_{T}$})=\sum^{n}_{i=0}{{n!}\over{(n-i)!\ i!}}\,p_{0}^{n-i}(1-p_{0})^{i}f_{i}(\mbox{${\rm E}_{T}$}) (9)

where f0​(ET)≡δ​(ET)f_{0}(\mbox{${\rm E}_{T}$})\equiv\delta(\mbox{${\rm E}_{T}$}) and fi​(ET)f_{i}(\mbox{${\rm E}_{T}$}) is the ii-th convolution of f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}):

fi​(x)=∫0x𝑑y​f1​(y)​fi−1​(x−y).f_{i}(x)=\int_{0}^{x}dy\,f_{1}(y)\,f_{i-1}(x-y)\;\;\;. (10)

Substituting Eq. 9 into Eq. 7 and reversing the indices gives a form that is less physically transparent, but considerably easier to compute:

(d​σd​ET)Ncoll=σB​A​∑i=1Nmaxw′i​(p0)​fi​(ET)\bigg{(}{d\sigma\over d\mbox{${\rm E}_{T}$}}\bigg{)}_{\rm\mbox{$N_{\rm coll}$}}=\sigma_{BA}\sum^{\rm N_{\rm max}}_{i=1}{w^{\prime}}_{i}(p_{0})\,f_{i}(\mbox{${\rm E}_{T}$}) (11)

where

w′i​(p0)=(1−p0)i​∑n=iNmaxn!(n−i)!​i!​p0n−i​wn,{w^{\prime}}_{i}(p_{0})=(1-p_{0})^{i}\,\sum^{\rm N_{\rm max}}_{n=i}{{n!}\over{(n-i)!\ i!}}\,p_{0}^{n-i}\,w_{n}, (12)

which represents the weight (or relative probability) for ii convolutions of the measured f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}) to contribute to the ET{\rm E}_{T} spectrum in an AA+BB collision, and where the term with w′i=0​(p0){w^{\prime}}_{i=0}(p_{0}) in Eq. 11 is left out because it represents the case when no signal is observed in the detector for an AA+BB collision, i.e. w′i=0​(p0)=p0B​A{w^{\prime}}_{i=0}(p_{0})=p_{0}^{BA}. Note that the above example works for any other basic element of particle production e.g. constituent-quark-participant, if the labels NQP are substituted above for “NcollN_{\rm coll}” and “N+N collision”. The method of determining p0NQPp_{0_{\rm NQP}} and f1NQP​(ET)f_{1}^{\rm NQP}(\mbox{${\rm E}_{T}$}) will be described below.

In general the convolutions of f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}) are performed analytically by fitting f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}) to a Gamma distribution

f1​(x)=bΓ​(p)​(b​x)p−1​e−b​x,f_{1}(x)=\frac{b}{\Gamma(p)}(bx)^{p-1}e^{-bx}, (13)

where

p>0,b>0,0≤x≤∞,p>0,\quad b>0,\quad 0\leq x\leq\infty\quad,

Γ​(p)\Gamma(p) is is the Gamma function, which equals (p−1)!(p-1)! if pp is an integer, and ∫0∞f1​(x)​𝑑x=1\int_{0}^{\infty}f_{1}(x)\,dx=1. The first few moments of the distribution are:

μ≡⟨x⟩=pbσ=pbσ2μ2=1p\mu\equiv\langle x\rangle=\frac{p}{b}\quad\sigma=\frac{\sqrt{p}}{b}\quad\quad\frac{\sigma^{2}}{\mu^{2}}=\frac{1}{p}

. There are two reasons for this. In general the shape of ET{\rm E}_{T} distributions in pp++pp collisions is well represented by the Gamma distribution and the nn-fold convolution (Eq. 10) is analytical

fn​(x)=bΓ​(n​p)​(b​x)n​p−1​e−b​x,f_{n}(x)=\frac{b}{\Gamma(np)}(bx)^{np-1}e^{-bx}, (14)

i.e. p→n​pp\rightarrow np while bb remains unchanged. Notice that the mean μn\mu_{n} and standard deviation σn\sigma_{n} of the nn-fold convolution obey the familiar rule:

μn=n​μ,σn=σ​n.\mu_{n}=n\mu,\quad\sigma_{n}=\sigma\sqrt{n}. (15)

VII.1 The importance of collisions which give zero measured ET{\rm E}_{T}

The importance of taking account of p0p_{0}, the probability to give zero signal on the detector for an inelastic N+N collision (or other basic element of the calculation) can not be overemphasized. The properly normalized ET{\rm E}_{T} distribution on the detector for one N+N collision is given by Eq. 8, and the detected signal for nn independent N+N collisions is given by the binomial distribution, Eq. 9. The true detected mean for nn independent N+N collisions is nn times the true mean for one N+N collision, or:

⟨ET⟩ntrue=∫ET​Pn​(ET)​𝑑ET=n​⟨ET⟩true,\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}_{n}=\int\mbox{${\rm E}_{T}$}\,P_{n}(\mbox{${\rm E}_{T}$})\,d\mbox{${\rm E}_{T}$}=n\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}, (16)

where

⟨ET⟩true\displaystyle\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true} =\displaystyle= ∫ET​P1​(ET)​𝑑ET\displaystyle\int\mbox{${\rm E}_{T}$}\,P_{1}(\mbox{${\rm E}_{T}$})\,d\mbox{${\rm E}_{T}$}
=\displaystyle= (1−p0)​∫ET​f1​(ET)​𝑑ET\displaystyle(1-p_{0})\int\mbox{${\rm E}_{T}$}\,f_{1}(\mbox{${\rm E}_{T}$})\,d\mbox{${\rm E}_{T}$}
=\displaystyle= (1−p0)​⟨ET⟩ref,\displaystyle(1-p_{0})\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref},

and ⟨ET⟩ref\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref} is the mean of the reference distribution, f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}), the measured ET{\rm E}_{T} spectrum for an N+N collision that gives nonzero ET{\rm E}_{T} on the detector (Eq. 8). It is important to contrast Eq. 16 with the mean of the nn-th convolution of the observed reference distribution, Eq. 10,

⟨ET⟩nref\displaystyle\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref}_{n} =\displaystyle= ∫ET​fn​(ET)​𝑑ET\displaystyle\int\mbox{${\rm E}_{T}$}\,f_{n}(\mbox{${\rm E}_{T}$})\,d\mbox{${\rm E}_{T}$}
=\displaystyle= n​⟨ET⟩ref,\displaystyle n\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref},

which is nn times the observed reference ⟨ET⟩ref\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref}, as it should be, and which differs from the mean of the true detected distribution, Pn​(ET)P_{n}(\mbox{${\rm E}_{T}$}), for nn independently interacting projectile nucleons (Eq. 16) by a factor of 1−p01-p_{0} for all nn, i.e.

⟨ET⟩ntrue\displaystyle\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}_{n} =\displaystyle= n​⟨ET⟩true\displaystyle n\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}
=\displaystyle= n​(1−p0)​⟨ET⟩ref=(1−p0)​⟨ET⟩nref.\displaystyle n(1-p_{0})\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref}=(1-p_{0})\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref}_{n}.

VIII Application to the present data

As discussed in section III above, the present measurements at sN​N\sqrt{s_{{}_{NN}}} =200 GeV include Au++Au ET{\rm E}_{T} distributions from the 2004 running period at RHIC and pp++pp and dd++Au distributions from the 2003 run. Although later runs with higher luminosity were tried, they suffer from tails due to pile-up of multiple interactions on the same event, which can be removed with fast electronics,111For continuous beams, in which fast triggered electronics are used with a short gate width, pile-up can be eliminated by a requirement that no additional interaction take place before or after the interaction of interest in a time interval corresponding to plus or minus the gate width Angelis et al. (1983). Of course this requirement reduces the useful luminosity. but which was not feasible with the present EMCal electronics Aphecetche et al. (2003b). This is most apparent for the pp++pp data which is used as the measured ET{\rm E}_{T} distribution, f1​(ET)f_{1}(\mbox{${\rm E}_{T}$}), for a single N+N collision. The measured ET{\rm E}_{T} distributions, with the requirement of a count (BBC≥1\geq 1) in both the North and South BBC counters, are given as histograms of the number of counts in a given raw ET​EMC{\rm{E}}_{T\,{\rm EMC}} bin such that the total number of counts sums up to the number of BBC counts (14,595,815 for pp++pp; 132,884,715 for Au++Au; 50,069,374 for dd++Au). The distributions are then normalized to integrate to unity (Fig. 3). Thus the normalized distributions are “per BBC trigger per GeV”, so that the cross section d​σ/d​ETd\sigma/d\mbox{${\rm E}_{T}$} would be obtained for all distributions by multiplying by the relevant BBC cross section. This is not important for the dd++Au or Au++Au data where the normalization is kept as the measured yield per BBC count per GeV in Au++Au or dd++Au collisions, but is crucial for the pp++pp measurement. As discussed previously and tabulated in Table 2, the correction scale factors are 6.68 for pp++pp, 6.51 for dd++Au and 6.87 for Au++Au, with Type C systematic uncertainties of ∼±6%\sim\pm 6\% which are not relevant for the purposes of this analysis, except as an overall ET{\rm E}_{T} scale uncertainty common to all 3 distributions to which the absolute scale uncertainty of ±1%\pm 1\% must be added. We emphasize that these uncertainties are also common to all the calculations of the dd++Au and Au++Au distributions to be presented, because they are based on the measured pp++pp distribution. Note also that the detailed shape of ET{\rm E}_{T} distributions has a slight dependence on the fiducial aperture due to statistical and dynamical fluctuations which are not taken into account by the simple scale correction. Thus an actual measurement in the reference acceptance will have slightly different upper tails in the region above the “knee” in the Au++Au distribution measured in the fiducial aperture Δ​η≈0.7,Δ​ϕ≈0.6​π\Delta\eta\approx 0.7,\Delta\phi\approx 0.6\pi (Fig. 3a) egs ; Tannenbaum (2006). Again this is not relevant to the present analysis in which the fiducial aperture is nearly identical for all three systems.

VIII.1 Determination of p0p_{0} in the EMCal for an N+N collision

The requirement of the BBC≥1\geq 1 trigger complicates the determination of the probability, p0p_{0}, of getting zero energy in the detector, in this case the EMCal, for an inelastic N+N collision, because it introduces a bias. For example, the high point clearly visible in the lowest bin of the pp++pp data (Fig. 3b) represents the events with zero ET{\rm E}_{T} in the EMCal for a BBC trigger (in addition to the events with nonzero ET{\rm E}_{T} in the lowest bin). This is a necessary quantity to measure but is not the same as p0p_{0}, the probability of getting zero ET{\rm E}_{T} in the EMCal for an inelastic N+N collision. However, the BBC bias can be measured and corrected so that the cross section for ET{\rm E}_{T} production in the EMCal in pp++pp collisions can be determined; where we assume that pp++pp and N+N are equivalent for ET{\rm E}_{T}. This is the standard method used for all PHENIX pp++pp cross section measurements in the EMCal, e.g. π0\pi^{0} Adler et al. (2003) and direct-γ\gamma Adler et al. (2007b), with details of the technique described in these references. The ratio of the measured ET{\rm E}_{T} cross section per pp++pp collision in the EMCal to the known pp++pp inelastic cross section, then gives 1−p01-p_{0} Abbott et al. (2001).

The pp++pp data are first fit to a Gamma distribution while expanding the error on the lowest data point by a factor of 10 so that it does not contribute to the fit. The Gamma distribution integrates to a fraction YΓp​pY_{\Gamma}^{pp} of the number of BBC triggers. Then the observed yield per BBC count is converted to the observed cross section by multiplying by the measured BBC cross section of σBBC=\sigma_{\rm BBC}= 23.0 mb ±9.7%\pm 9.7\%. This cross section must then be corrected for the BBC bias, 1−εbias1-\varepsilon_{\rm bias}, the probability of getting no BBC count when there is finite energy in the central spectrometer. This was measured using clock triggers for single charged particles in the central spectrometer as well as from the ratio of the yield of high pTp_{T} π0\pi^{0} with and without the BBC≥1\geq 1 trigger Adler et al. (2007b) and found to be a constant εbias=0.79±0.02\varepsilon_{\rm bias}=0.79\pm 0.02, independent of pTp_{T}. Thus, the measured ET{\rm E}_{T} cross section per pp++pp collision equals YΓp​p×σBBC/εbiasY_{\Gamma}^{pp}\times\sigma_{\rm BBC}/\varepsilon_{\rm bias}. The probability of detecting zero ET{\rm E}_{T} in the detector for an inelastic N+N collision is then computed from the ratio of the integrated cross section of the measured ET{\rm E}_{T} distribution to the 42 mb pp++pp inelastic cross section, σinel\sigma_{\rm inel}:

1−p0\displaystyle 1-p_{0} =\displaystyle= 1σinel​23.0​mb±9.7%0.79±0.02​YΓp​p\displaystyle{1\over\sigma_{\rm inel}}\,{23.0\,{\rm mb}\pm 9.7\%\over 0.79\pm 0.02}\,Y_{\Gamma}^{pp}
=\displaystyle= 0.693​(±10%)​YΓp​p.\displaystyle 0.693(\pm 10\%)\,Y_{\Gamma}^{pp}.

The procedure is a two-step process. First the fit is performed with the error in the lowest bin increased by a factor of 10, so that the counts with zero ET{\rm E}_{T} do not distort the fit. Then trial values of YΓp​pY_{\Gamma}^{pp} and 1−p01-p_{0} are derived from Eq. VIII.1 and the data are corrected to a data set for which the lowest bin in the distribution is replaced by the fitted value in this bin and the original error is restored, so that the distribution, d​Y/d​ETdY/d\mbox{${\rm E}_{T}$} which previously integrated to unity, now integrates to YΓp​pY_{\Gamma}^{pp}. This data set is then refit for the final results. The value of 1−p01-p_{0} is evaluated from the new YΓp​pY_{\Gamma}^{pp} which, with the procedure indicated, typically does not differ significantly from the trial value. The parameters for the fit of the pp++pp data to a Gamma distribution are given in Table 12. Only the data for ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV are used in the fit and the following analysis to avoid influence from the tail, which is presumed to be from residual pile-up. However, the fit was also extended to ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV as a systematic check (Fig. 8).

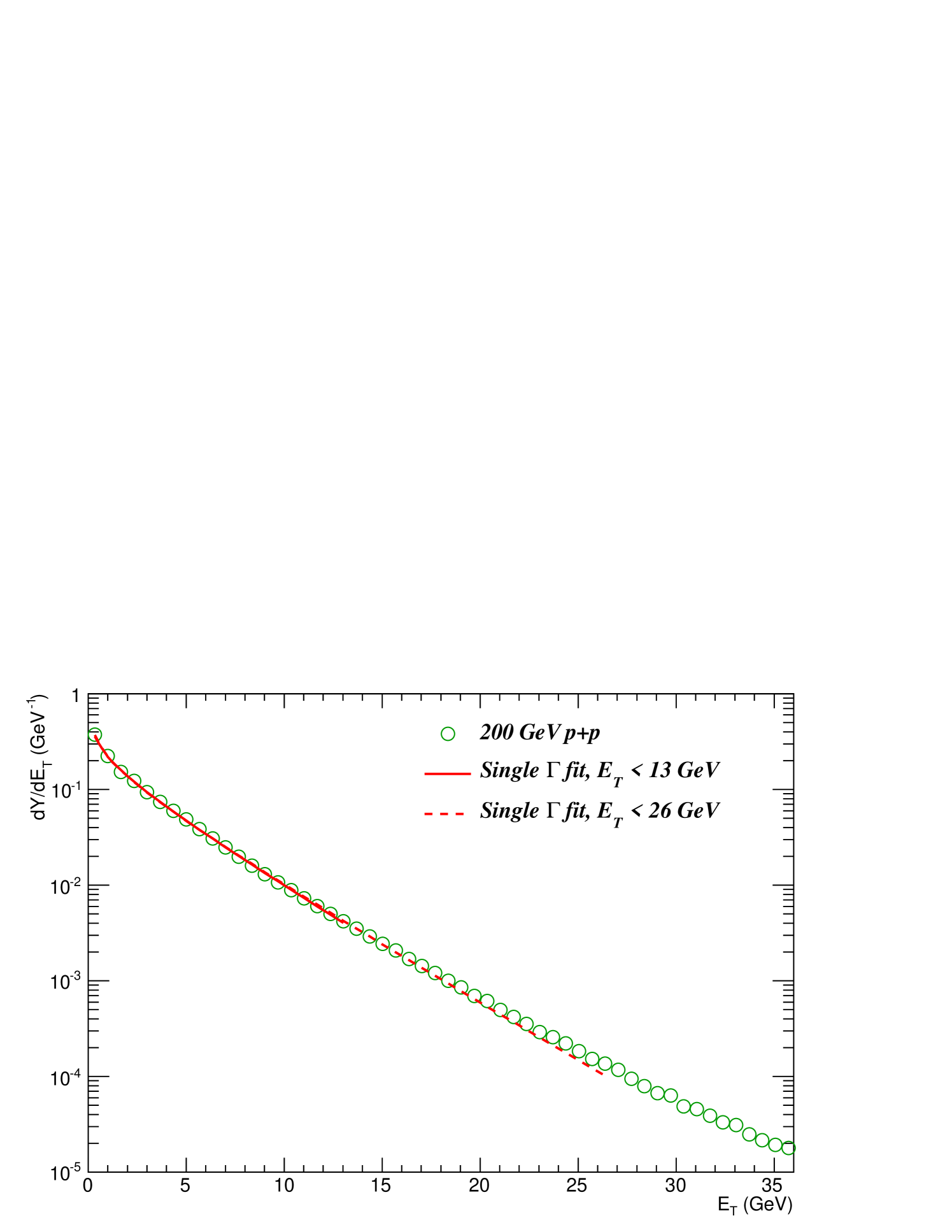
Refer to caption
Figure 8: (Color online) Fits of the pp++pp data to a single Γ\Gamma distribution for the ranges ET<13.3\mbox{${\rm E}_{T}$}<13.3 and ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV.

The poor χmin2\chi^{2}_{\rm min}/dof for both fits has at least two sources. For low ET{\rm E}_{T}, the statistical uncertainties with millions of events per bin are ∼1/1000\sim 1/1000 so any uncorrected few percent systematic effect for each data point (e.g. such as not bin-shifting for the falling spectrum) gives a large contribution to the χ2\chi^{2}. At larger ET>20\mbox{${\rm E}_{T}$}>20 GeV, the data clearly lie above the fit, which is emphasized by the fit with ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV. This difference is presumed to be due to residual pile-up. In any case, the fits for both ET{\rm E}_{T} ranges follow the pp++pp data for more than two orders of magnitude and have ⟨ETref⟩\langle\mbox{${\rm E}_{T}$}^{\rm ref}\rangle which differ by 0.6%, so are more than adequate for the multiple collision calculations, for which the dominant effect in convolutions is the mean value. An 0.6% variation in ⟨ETref⟩\langle\mbox{${\rm E}_{T}$}^{\rm ref}\rangle will result in an 0.6% change in the ET{\rm E}_{T} scale of the calculations which is negligible compared to the dominant systematic uncertainty to be discussed below. The tail only enters when the geometry is exhausted Abbott et al. (2001), which is not reached for the present dd++Au and Au++Au data. Following the standard practice, the uncertainties on the fitted parameters, YΓp​pY_{\Gamma}^{pp}, bb and pp, in Table 12 have been increased by a factor of 4866/17=16.9\sqrt{4866/17}=16.9 and 6715/37=13.4\sqrt{6715/37}=13.4, respectively. Thus, the fractional statistical uncertainty on 1−p01-p_{0} from the fitted YΓp​pY_{\Gamma}^{pp} is 0.006/0.933=0.6%0.006/0.933=0.6\%, which is still small compared to the uncertainties on the parameters in Eq. VIII.1 of which the 9.7% uncertainty in the BBC cross section is predominant. Adding the 0.6% fractional uncertainty in quadrature with the two fractional uncertainties on the parameters in Eq. VIII.1 gives a total systematic uncertainty on 1−p01-p_{0} of 10.1%. Thus, the values of 1−p01-p_{0} are taken as 0.647, 0.660, with a systematic uncertainty of 10% as indicated in Table 12.

VIII.2 Calculations of the various models

The starting point requires the relative probabilities, wnw_{n}, for the number of binary N+N collisions, nucleon participants, constituent-quark participants from q-q scattering (NQP), and wounded projectile quarks from q-N scattering (AQM) for sNN=200\sqrt{s_{\rm NN}}=200 GeV pp++pp, dd++Au, Au++Au collisions. These were calculated by the standard Glauber Monte Carlo method, as described in section V. For Au++Au they are plotted in Fig. 9.

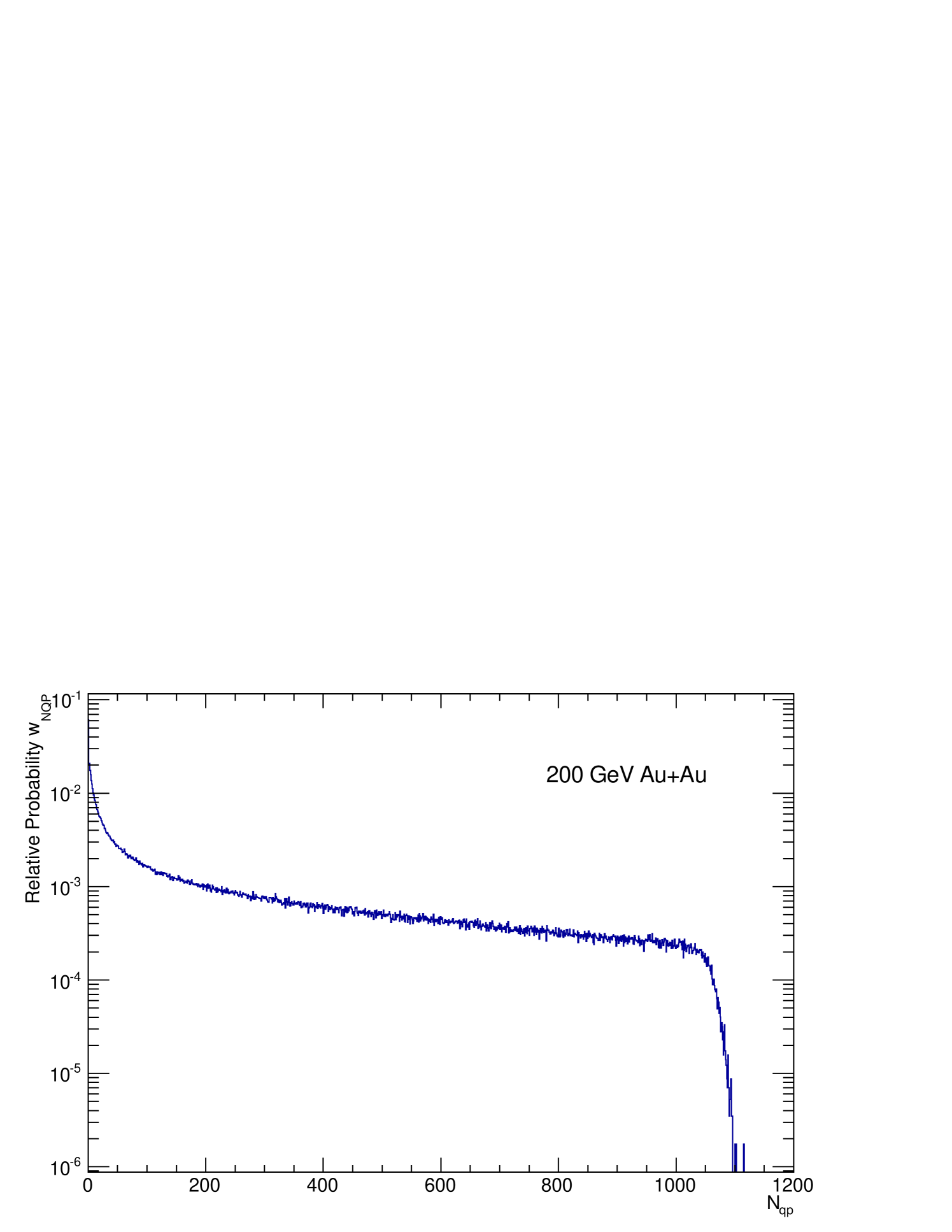
Refer to caption
Figure 9: (Color online) Distribution of the Number of Quark Participants in Au++Au at sNN=200\sqrt{s_{\rm NN}}=200 GeV

There was no explicit AQM calculation in Au++Au; the probability for nn wounded projectile quarks was taken to be the sum of the probabilities for 2​n2n and 2​n−12n-1 constituent-quark participants. The weights for pp++pp and dd++Au are tabulated in Tables. 12 and 12. The weights in these tables are defined as the ‘original’ weights, (p0=0p_{0}=0, ϵ≡1−p0=1.0\epsilon\equiv 1-p_{0}=1.0), before correction for p0p_{0}.

Table 10: Fitted parameters YΓp​pY_{\Gamma}^{pp} bb, pp of pp++pp data, and calculated 1−p01-p_{0}. Note that the standard errors on these parameters using χ2=χmin2+1\chi^{2}=\chi^{2}_{\rm min}+1 have been multiplied by χmin2/dof\sqrt{\chi^{2}_{\rm min}/{\rm dof}} in each case.
System YΓp​pY_{\Gamma}^{pp} bb (GeV)-1 pp ⟨ET⟩ref\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref} GeV χmin2\chi^{2}_{\rm min}/dof 1−p01-p_{0}
pp++pp ET<13.3\mbox{${\rm E}_{T}$}<13.3 0.933±0.0060.933\pm 0.006 0.273±0.0030.273\pm 0.003 0.724±0.0100.724\pm 0.010 2.64 4866/17 0.647±0.0650.647\pm 0.065
pp++pp ET<26.6\mbox{${\rm E}_{T}$}<26.6 0.952±0.0040.952\pm 0.004 0.263±0.0030.263\pm 0.003 0.692±0.0070.692\pm 0.007 2.63 6715/37 0.660±0.0660.660\pm 0.066
Table 11: Original weights wnw_{n} (p0=0p_{0}=0, ϵ≡1−p0=1.0\epsilon\equiv 1-p_{0}=1.0) for pp++pp and dd++Au at s=200\sqrt{s}=200 GeV. Note that σ=9.36\sigma=9.36 mb was used for q-q scattering to obtain a N+N σinel=42.0\sigma^{\rm inel}=42.0 mb. These AQM weights come from the q-q scattering calculation tabulated from the distribution of projectile participants, NQP (p), NQP(deuteron). The symbol “…...” in the table indicates additional weights for n≥7n\geq 7.
pp++pp dd++Au Au++Au
nn NQP AQM NQP AQM NpartN_{\rm part} NQP
1 0.00 0.609 0.00 0.131 0.00 0.00
2 0.465 0.285 0.0867 0.124 0.0660 0.0613
3 0.238 0.106 0.0516 0.202 0.0304 0.0204
4 0.169 0.0529 0.0925 0.0269 0.0209
5 0.0946 0.0473 0.118 0.0220 0.0176
6 0.0333 0.0451 0.332 0.0195 0.0157
7 … … …
Table 12: Original NcollN_{\rm coll} and AQM weights wnw_{n} (p0=0p_{0}=0, ϵ≡1−p0=1.0\epsilon\equiv 1-p_{0}=1.0) for Au++Au at s=200\sqrt{s}=200 GeV. Note that σ=9.36\sigma=9.36 mb was used for q-q scattering to obtain a N+N σinel=42.0\sigma^{\rm inel}=42.0 mb. The symbol “…...” in the table indicates additional weights for n≥7n\geq{7}.
nn Au++Au NcollN_{\rm coll} Au++Au AQM
1 0.0660 0.0613
2 0.0405 0.0414
3 0.0287 0.0333
4 0.0232 0.0263
5 0.0191 0.0214
6 0.0169 0.0184
7 … …

VIII.2.1 Correction of the weights wnw_{n} to w′i​(p0){w^{\prime}}_{i}(p_{0}) for NpartN_{\rm part}, NQP and AQM in pp++pp to account for p0p_{0}

Because the p0p_{0} is calculated for a pp++pp collision, one has to recompute the pp++pp weights in each model to find the p0AQMp_{0_{\rm AQM}}, p0NQPp_{0_{\rm NQP}}, and p0Npartp_{0_{\rm N_{\rm part}}} so that the new weights for the elementary processes sum up to 1−p01-p_{0} for the pp++pp collision. The value 1−p0=0.6471-p_{0}=0.647 for pp++pp collisions, from Table 12, gives the probability p0=0.353p_{0}=0.353 for an inelastic N+N collision to give zero energy into our acceptance, i.e. zero detected ET​EMC{\rm{E}}_{T\,{\rm EMC}}. For NcollN_{\rm coll}, which is based on N+N collisions, p0p_{0} is simply that of a pp++pp collision. For NpartN_{\rm part}, because a pp++pp collision is 2 participants, it is assumed that both participants had equal p0Npartp_{0_{\rm N_{\rm part}}}, and so the case when only 1 WN deposited energy is not counted. This is done because both BBCs are required to count on a N+N collision although there are certainly cases when both WN could give a BBC count but only 1 would give a nonzero ET{\rm E}_{T}. If the case when only 1 WN deposited energy were allowed, then the only way to get zero energy on a pp++pp collision is for both WN to give zero energy i.e. p0WN=p02=0.125p_{0_{\rm WN}}=p_{0}^{2}=0.125, ϵWN=0.875\epsilon_{\rm WN}=0.875, but then the weight for 1 WN would have to be included in this calculation. We chose instead to require both WN to deposit energy, hence a pp++pp collision equaled 2 WN, i.e. ϵp​p=1−p0=ϵWN2\epsilon_{pp}=1-p_{0}=\epsilon_{\rm WN}^{2}, so ϵWN=1−p0=0.804\epsilon_{\rm WN}=\sqrt{1-p_{0}}=0.804.

For NQP, Eq. 12 was used to calculate the value of w′i=0​(p0NQP){w^{\prime}}_{i=0}(p_{0_{\rm NQP}}) for any p0NQPp_{0_{\rm NQP}} with the case NQP=1 not allowed, so w′i=0​(p0NQP)+w′i=1​(p0NQP)=p0=0.353{w^{\prime}}_{i=0}(p_{0_{\rm NQP}})+{w^{\prime}}_{i=1}(p_{0_{\rm NQP}})=p_{0}=0.353 was solved, with result ϵQP=1−p0NQP=\epsilon_{\rm QP}=1-p_{0_{\rm NQP}}=0.659. For the AQM, the total efficiency of the projectile quarks (color-strings) should add up to the efficiency of a pp++pp collision at midrapidity. Thus the equation w′i=0​(p0AQM)=p0=1−0.647=0.353{w^{\prime}}_{i=0}(p_{0_{\rm AQM}})=p_{0}=1-0.647=0.353 was solved, with result ϵAQM=1−p0AQM=0.538\epsilon_{\rm AQM}=1-p_{0_{\rm AQM}}=0.538.

Note that there can be confusion in the AQM model because in a pp++pp collision, represented as 1 to 3 q+pp collisions, the struck proton may have the efficiency of a Wounded Nucleon rather than that of a Wounded Projectile Quark. Such an asymmetric AQM model can be calculated. However, if one thinks of the AQM model as the number of color strings rather than number of wounded projectile quarks, then the detection efficiency, ϵAQM=1−p0AQM=0.538\epsilon_{\rm AQM}=1-p_{0_{\rm AQM}}=0.538, can be thought of as the detection efficiency for a color string.

VIII.2.2 Correcting the pp++pp, dd++Au and Au++Au weights.

Applying p0AQMp_{0_{\rm AQM}}, p0NQPp_{0_{\rm NQP}}, and p0WNp_{0_{\rm WN}} to correct the pp++pp, dd++Au and Au++Au weights is straightforward and given by Eq. 12. The weights from Tables 12 and 12 corrected for these efficiencies are summarized in Tables 15 and 15.

Table 13: Corrected weights w′i{w^{\prime}}_{i} for pp++pp, dd++Au Au++Au,at s=200\sqrt{s}=200 GeV. Note that 1−p01-p_{0} is the sum of the weights in the column (including weights not tabulated) and is the not the BBC efficiency, but the probability to get a nonzero ET​EMC{\rm{E}}_{T\,{\rm EMC}} on an AA+BB collision.
pp++pp dd++Au Au++Au
NQP AQM NQP AQM NpartN_{\rm part} AQM
nn ϵNQP\epsilon_{\rm NQP}=0.659 ϵAQM\epsilon_{\rm AQM}=0.538 ϵNQP\epsilon_{\rm NQP}=0.659 ϵAQM\epsilon_{\rm AQM}=0.538 ϵWN\epsilon_{\rm WN}=0.804 ϵNQP\epsilon_{\rm NQP}=0.659
1 0.00 0.506 0.00 0.259 0.00 0.00
2 0.378 0.125 0.0918 0.251 0.0596 0.0474
3 0.173 0.0164 0.0726 0.199 0.0333 0.0270
4 0.0731 0.0664 0.120 0.0277 0.0231
5 0.0202 0.0601 0.0467 0.0230 0.0195
6 0.00272 0.0552 0.00802 0.0199 0.0168
7 … … …
1-p0p_{0} 0.647 0.647 0.926 0.883 0.973 0.956
Table 14: Corrected weights w′i{w^{\prime}}_{i} for Au++Au at s=200\sqrt{s}=200 GeV. Note that 1−p01-p_{0} is the sum of the weights in the column (including weights not tabulated) and is the not the BBC efficiency, but the probability to get a nonzero ET​EMC{\rm{E}}_{T\,{\rm EMC}} on the AA+BB collision.
NcollN_{\rm coll} AQM
nn ϵcoll\epsilon_{\rm coll}=0.647 ϵAQM\epsilon_{\rm AQM}=0.538
1 0.0723 0.0756
2 0.0433 0.0494
3 0.0312 0.0362
4 0.0247 0.0284
5 0.0205 0.0235
6 0.0175 0.0202
7 … …
1-p0p_{0} 0.970 0.958
Table 15: Parameters bb, pp of the element indicated from the fit to pp++pp data, cut for ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV (ET​EMC<2\mbox{${\rm{E}}_{T\,{\rm EMC}}$}<2 GeV). YΓf​i​tY_{\Gamma}^{fit} is the fitted integral of the pp++pp distribution. For NcollN_{\rm coll}, the fit is a single Γ\Gamma to the pp++pp distribution from which ϵp​p\epsilon_{pp} is calculated; for NpartN_{\rm part}, pW​N=pp​p/2p_{WN}=p_{pp}/2, ϵW​N=ϵp​p\epsilon_{WN}=\sqrt{\epsilon_{pp}}. For NQP and AQM the fits are the deconvolution of elements with weights w′i{w^{\prime}}_{i} which do not sum to unity but sum to ϵp​p=0.647\epsilon_{pp}=0.647 so that YΓp​p=YΓf​i​t×ϵp​pY_{\Gamma}^{pp}=Y_{\Gamma}^{fit}\times\epsilon^{pp}=0.948 (NQP), 0.944 (AQM), a good check (within 1.6% and 1.1% respectively).
Model ϵe​l​e​m​e​n​t\epsilon_{element} element YΓf​i​tY_{\Gamma}^{fit} bb (GeV)-1 pp ⟨ET⟩e​l​e​mref\langle\mbox{${\rm E}_{T}$}\rangle^{\rm ref}_{elem} (GeV) ⟨ET⟩e​l​e​mtrue\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}_{elem} (GeV)
NcollN_{\rm coll} 0.647 pp++pp 0.933 1.83/6.68 0.723 2.642.64 1.71
NpartN_{\rm part} 0.804 1 WN 0.933 1.83/6.68 0.363 1.321.32 1.06
NQP 0.659 1 QP 1.466 2.00/6.68 0.297 0.9940.994 0.655
AQM 0.538 1 string 1.460 2.10/6.68 0.656 2.092.09 1.12

VIII.2.3 Derivation of the ET{\rm E}_{T} distribution of the basic elements from the pp++pp ET{\rm E}_{T} distributions followed by calculation of the dd++Au and Au++Au distributions

At this point the raw ET​EMC{\rm{E}}_{T\,{\rm EMC}} distributions in the fiducial aperture had been corrected to the total hadronic ET=d​ET/d​η|η=0\mbox{${\rm E}_{T}$}=d\mbox{${\rm E}_{T}$}/d\eta|_{\eta=0} by making a change of scale from ET​EMC{\rm{E}}_{T\,{\rm EMC}} to ET{\rm E}_{T} by the correction factors of 6.68 for pp++pp, 6.51 for dd++Au and 6.87 for Au++Au (Fig. 3). The pp++pp and the elementary WN, NQP, AQM distributions fi​(ET)f_{i}(\mbox{${\rm E}_{T}$}) in Eqs. 8–11 are taken as Γ\Gamma distributions and then the pp++pp distribution (Fig. 3b) is deconvoluted using the efficiency corrected weights, w′i{w^{\prime}}_{i}, to find the parameters of the elementary NQP, or AQM distributions. For the WN the deconvolution from pp++pp is analytical.

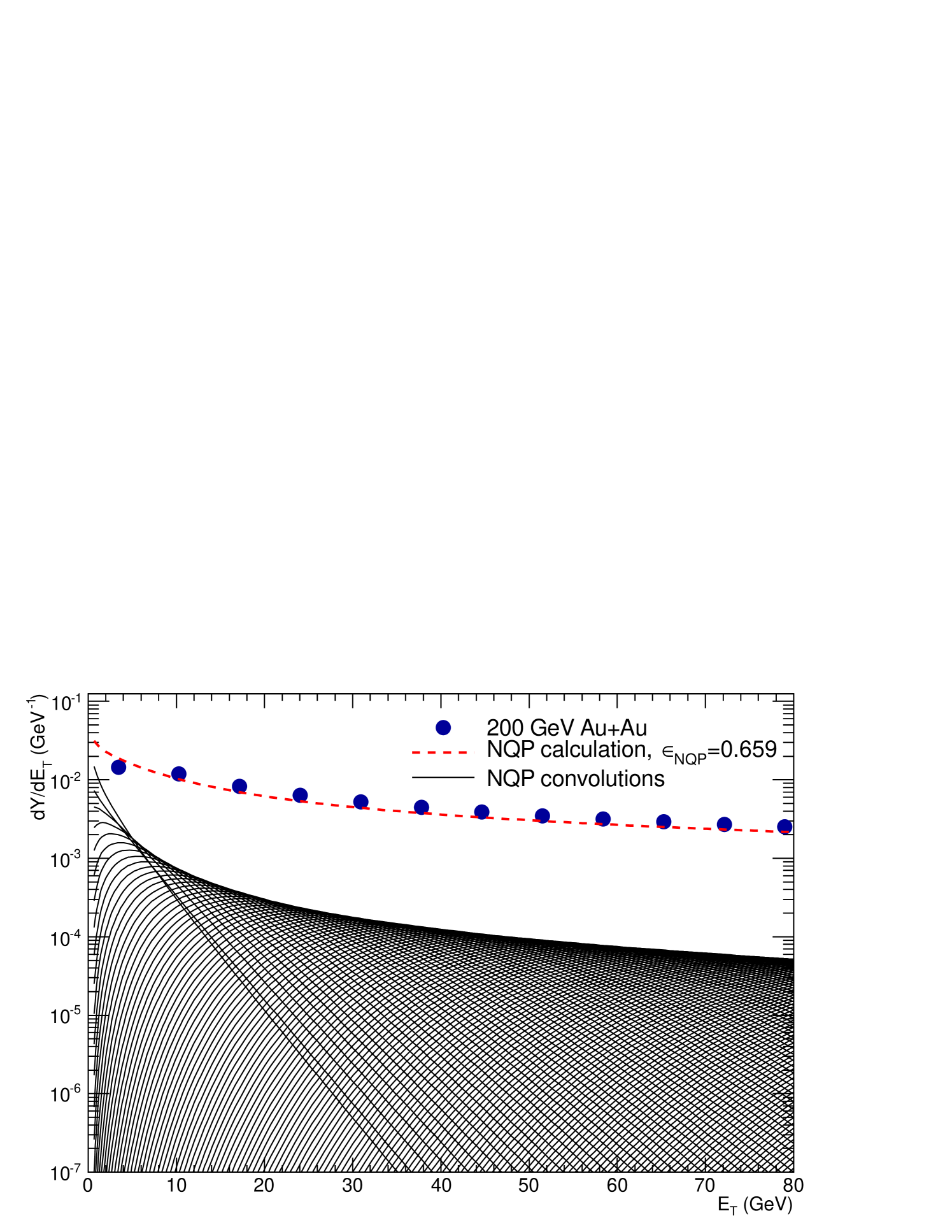
The results of the fit to a single Γ\Gamma distribution (pp++pp) were given in Table  12 and Fig. 8. The deconvolution of pp++pp to sums of elementary Γ\Gamma distributions with AQM and NQP weights w′i{w^{\prime}}_{i} are shown in Fig. 10 and given in Table 15.

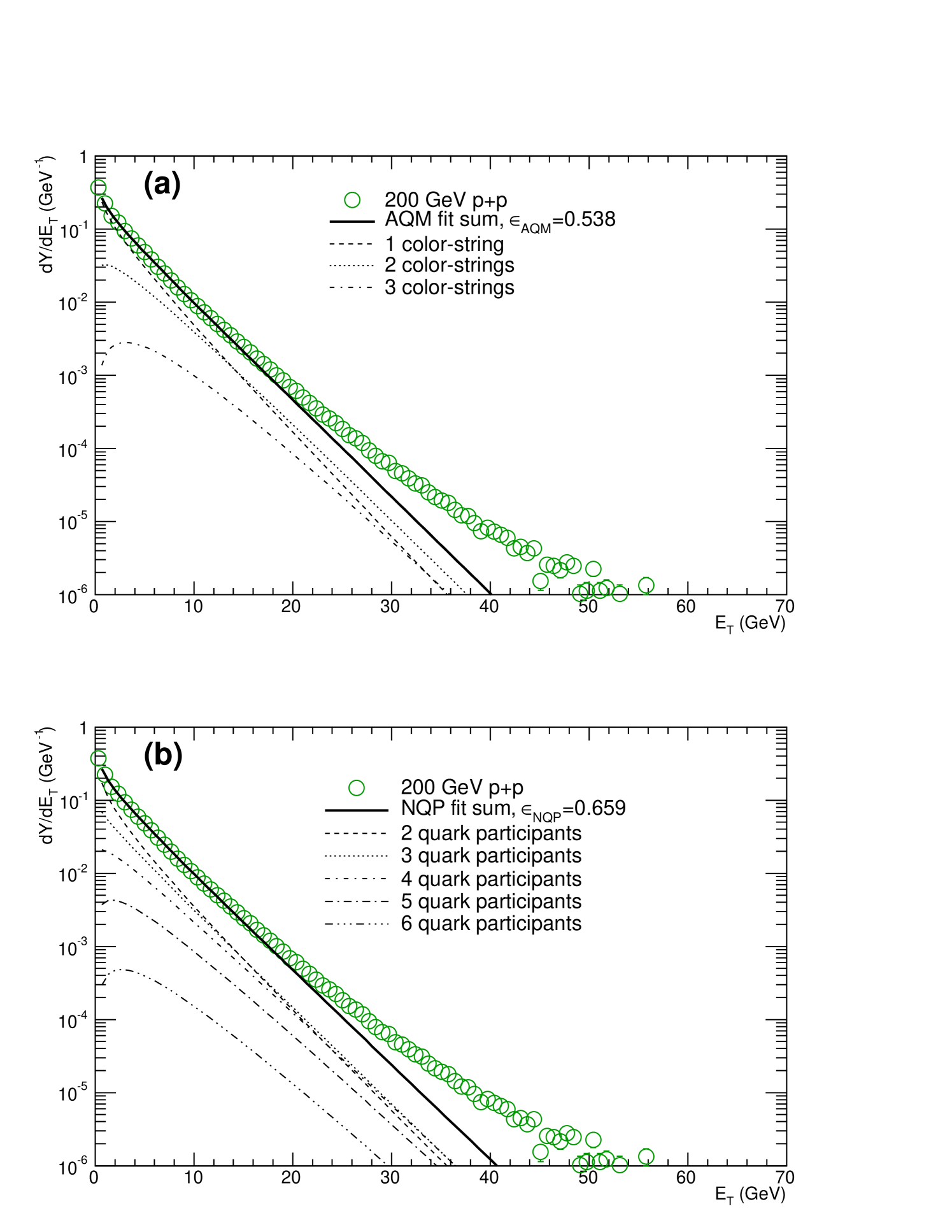
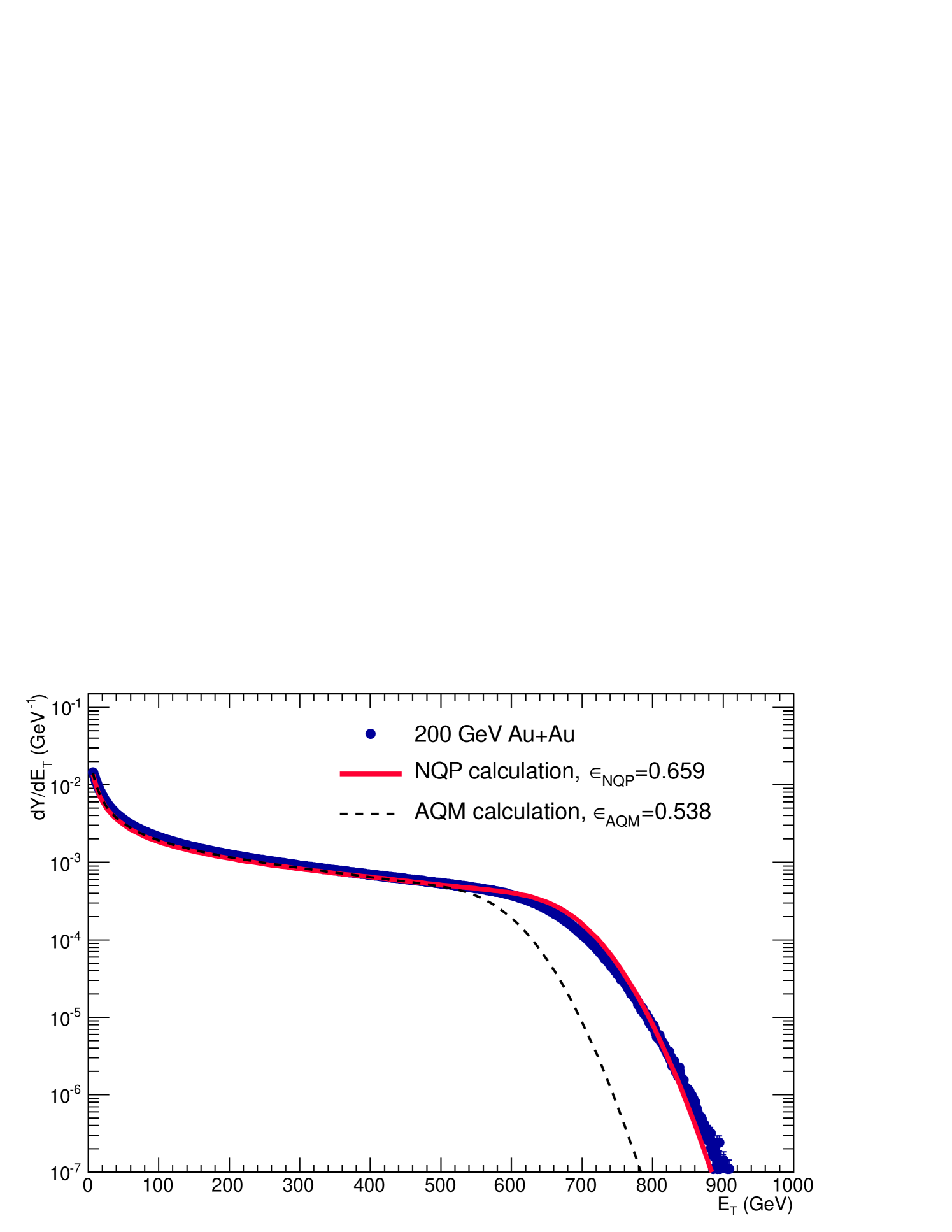
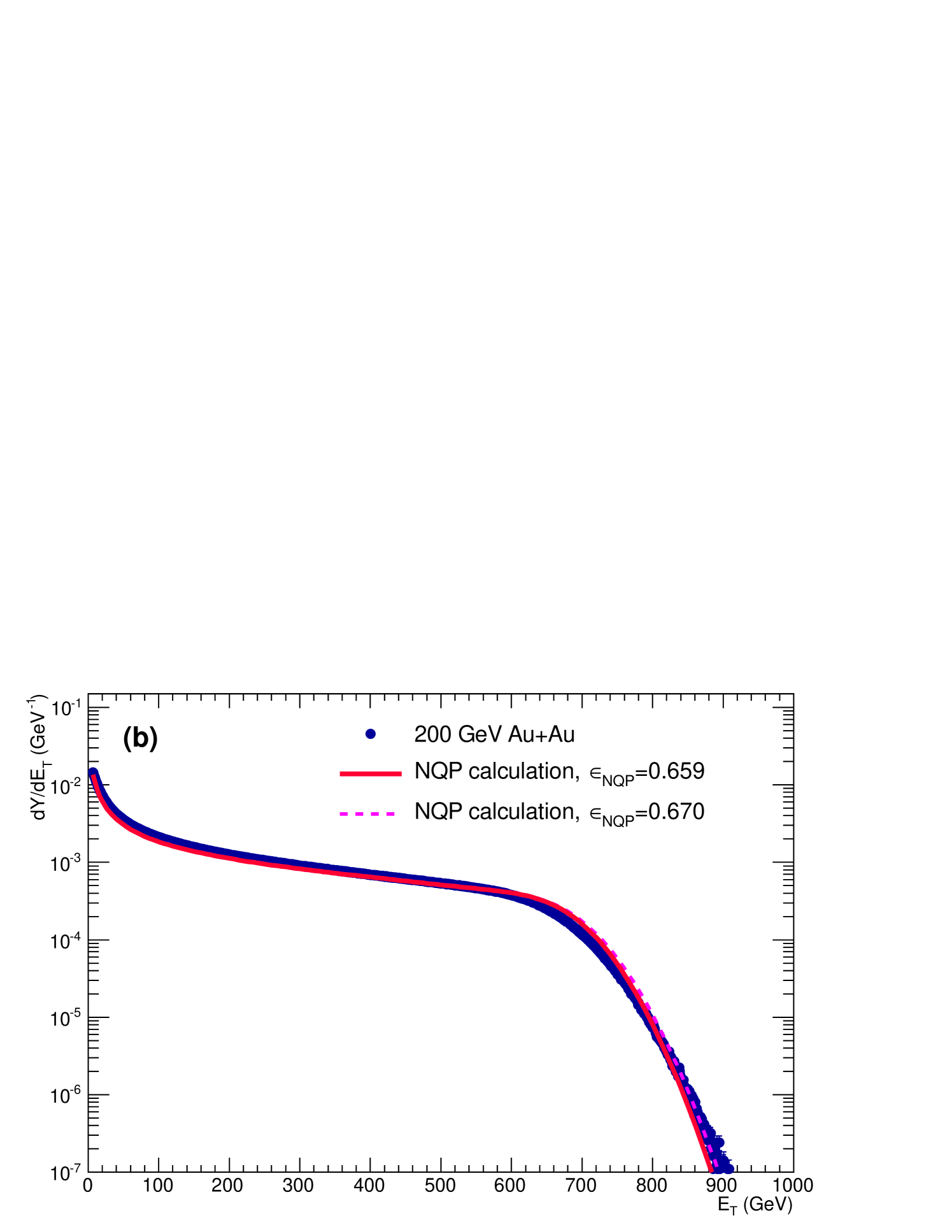
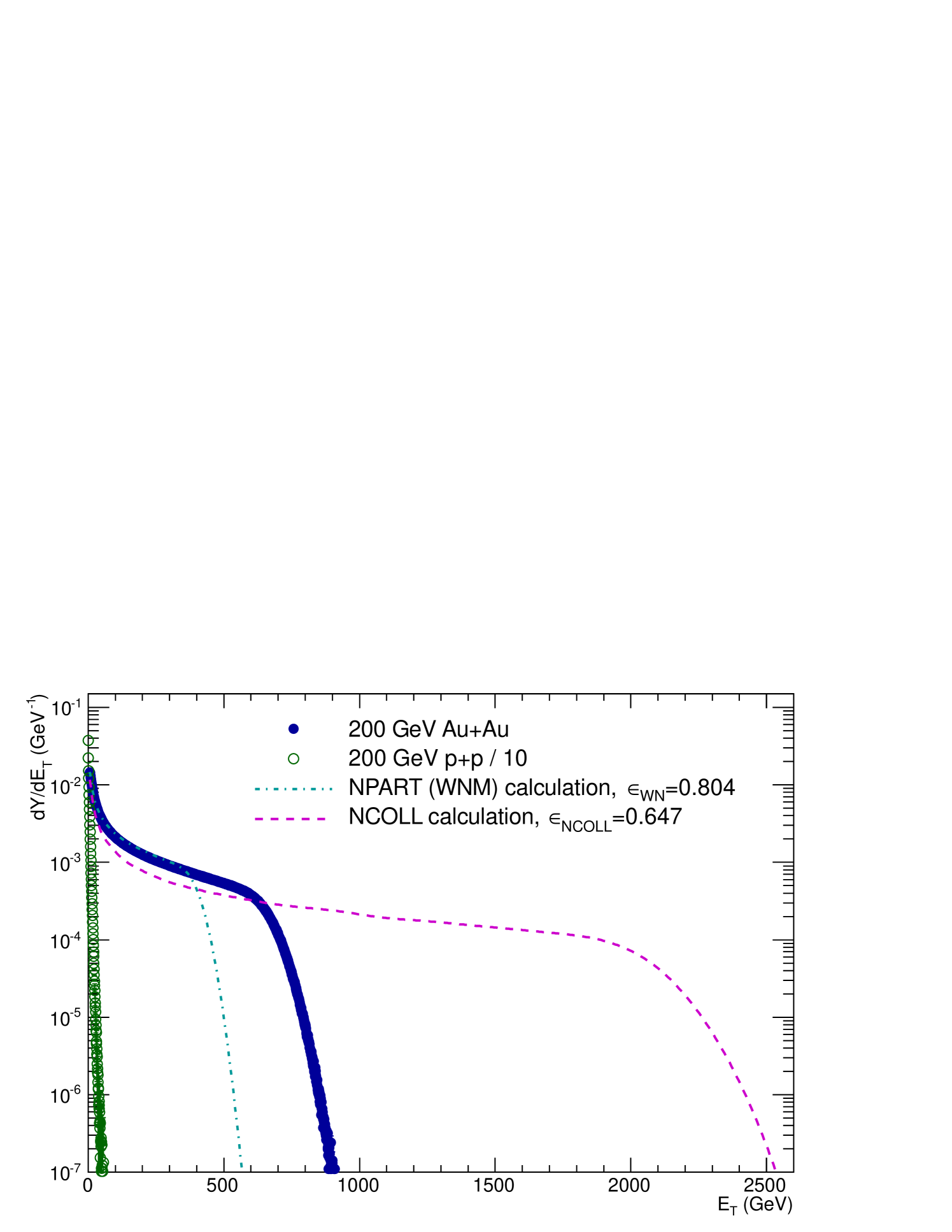
Refer to caption
Figure 10: (Color online) (a) Deconvolution fit to the pp++pp ET{\rm E}_{T} distribution for ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV at sNN=200\sqrt{s_{\rm NN}}=200 GeV with the corrected weights w′iAQM{w^{\prime}}^{\rm AQM}_{i} calculated in the Additive Quark model (AQM) using the symmetric color-string efficiency, ϵAQM=1−p0AQM=0.538\epsilon_{\rm AQM}=1-p_{0_{\rm AQM}}=0.538. Lines represent the properly weighted individual ET{\rm E}_{T} distributions for 1, 2, 3 color-strings plus the sum. On the y-axis intercept, the top line is the sum and the lower curves in descending order are the ET{\rm E}_{T} distributions of 1,2,3 color-strings. (b) Deconvolution fit to the same pp++pp ET{\rm E}_{T} distribution for ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV with the corrected weights w′iNQP{w^{\prime}}^{\rm NQP}_{i} with ϵN​Q​P=1−p0NQP=0.659\epsilon_{NQP}=1-p_{0_{\rm NQP}}=0.659 calculated in the NQP model. Lines represent the properly weighted individual ET{\rm E}_{T} distributions for the underlying 2, 3, 4, 5, 6 constituent-quark participants plus the sum.

These parameters are then used in Eq. 11 with the dd++Au and Au++Au corrected weights to compute the ET{\rm E}_{T} distributions for these systems. The results for the Additive Quark Model (AQM) using the above ϵAQM=1−p0AQM=0.538\epsilon_{\rm AQM}=1-p_{0_{\rm AQM}}=0.538 and the constituent-Quark Participant (NQP) model with ϵN​Q​P=1−p0NQP=0.659\epsilon_{NQP}=1-p_{0_{\rm NQP}}=0.659 are shown for Au++Au in Fig. 11. Both the shape and magnitude of the calculation with the NQP model are in excellent agreement with the entire Au++Au measurement including the upper edge of the calculation, which is essentially on top of the measured ET{\rm E}_{T} distribution, well within the principal ±10%\pm 10\% systematic uncertainty in 1−p01-p_{0} from the BBC cross section (Eq. VIII.1). This uncertainty is common to both AQM and NQP calculations so does not affect the difference in the AQM and NQP curves, both curves scale together in ET{\rm E}_{T} by the same ±10.1\pm 10.1% with respect to the data. Another advantage of the Extreme Independent Models is that all the calculations are based on the measured data. Thus the 6% Type C common systematic uncertainty on the absolute ET{\rm E}_{T} scale (Table 3) cancels in relative comparisons of the data to the calculations—all the curves and the data scale together by the same fraction in ET{\rm E}_{T}.

Interestingly, the AQM model is not identical to the NQP model for the symmetric Au++Au system, but 12% lower in the ET{\rm E}_{T} knee. This is due to the p0p_{0} effect in the pp++pp collision, which has different effects on the AQM and NQP calculations. This was checked by repeating the AQM (color-string) and NQP calculations with 1−p0=1.01-p_{0}=1.0 detection efficiency in a pp++pp collision to confirm that the AQM and NQP models really do give identical results in symmetric Au++Au collisions for 100% efficiency.

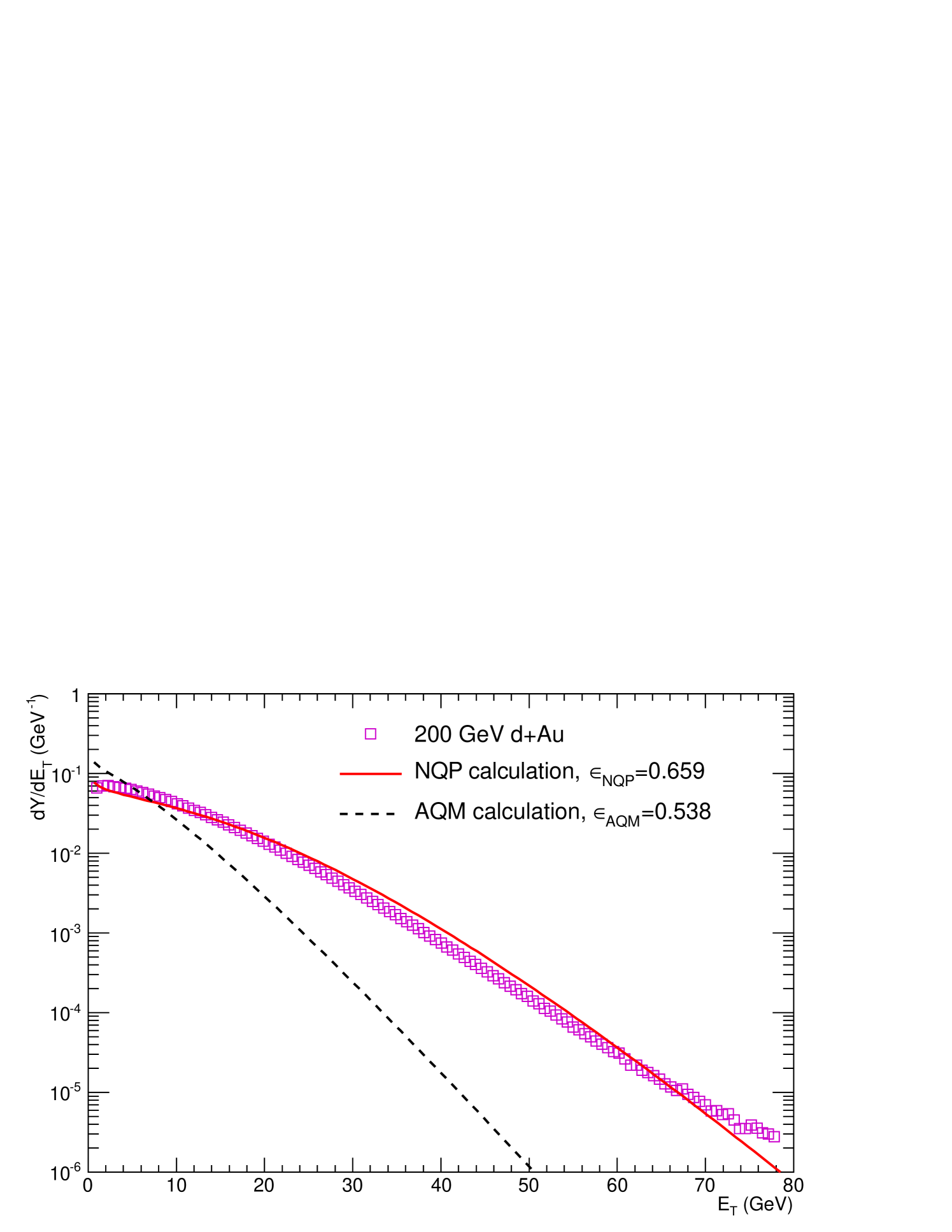
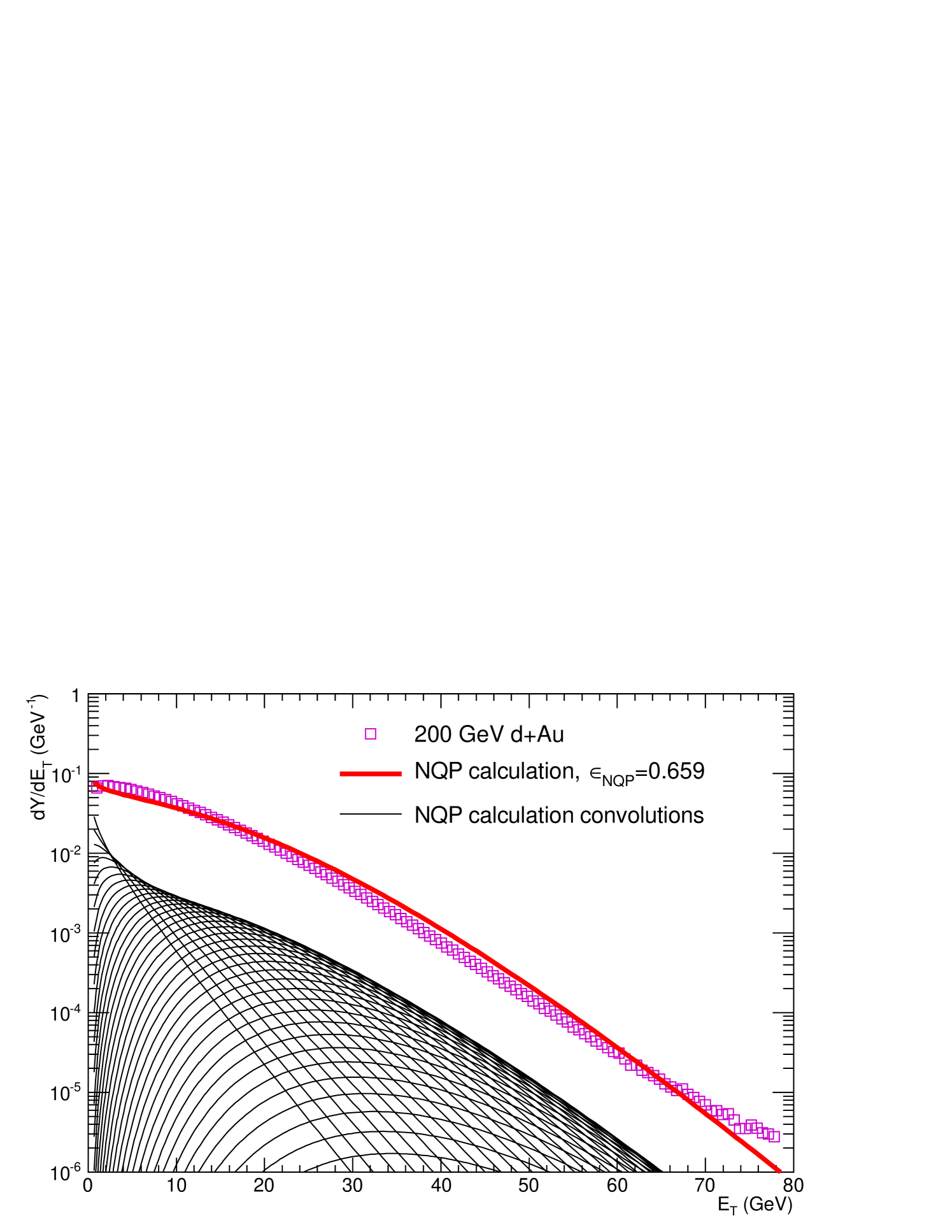
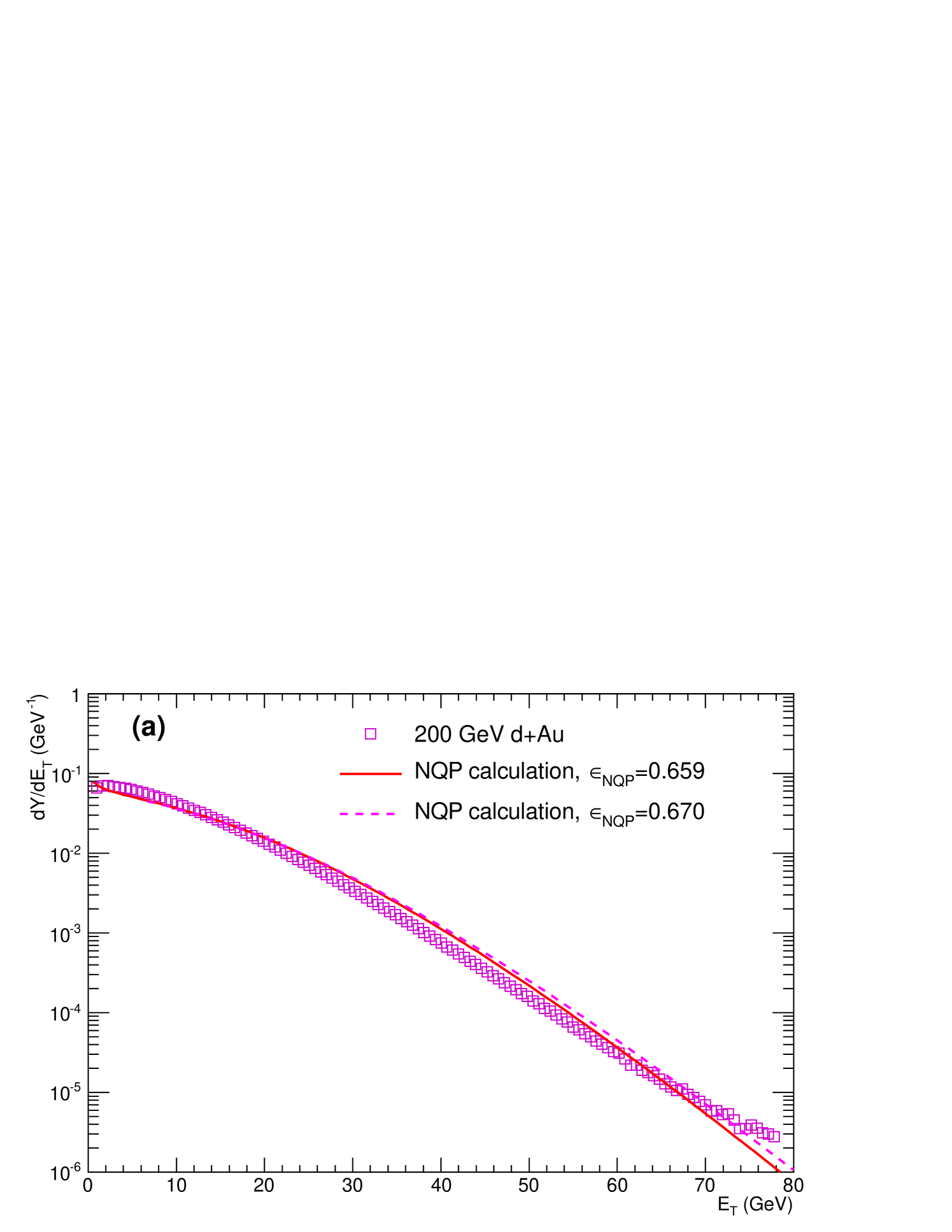
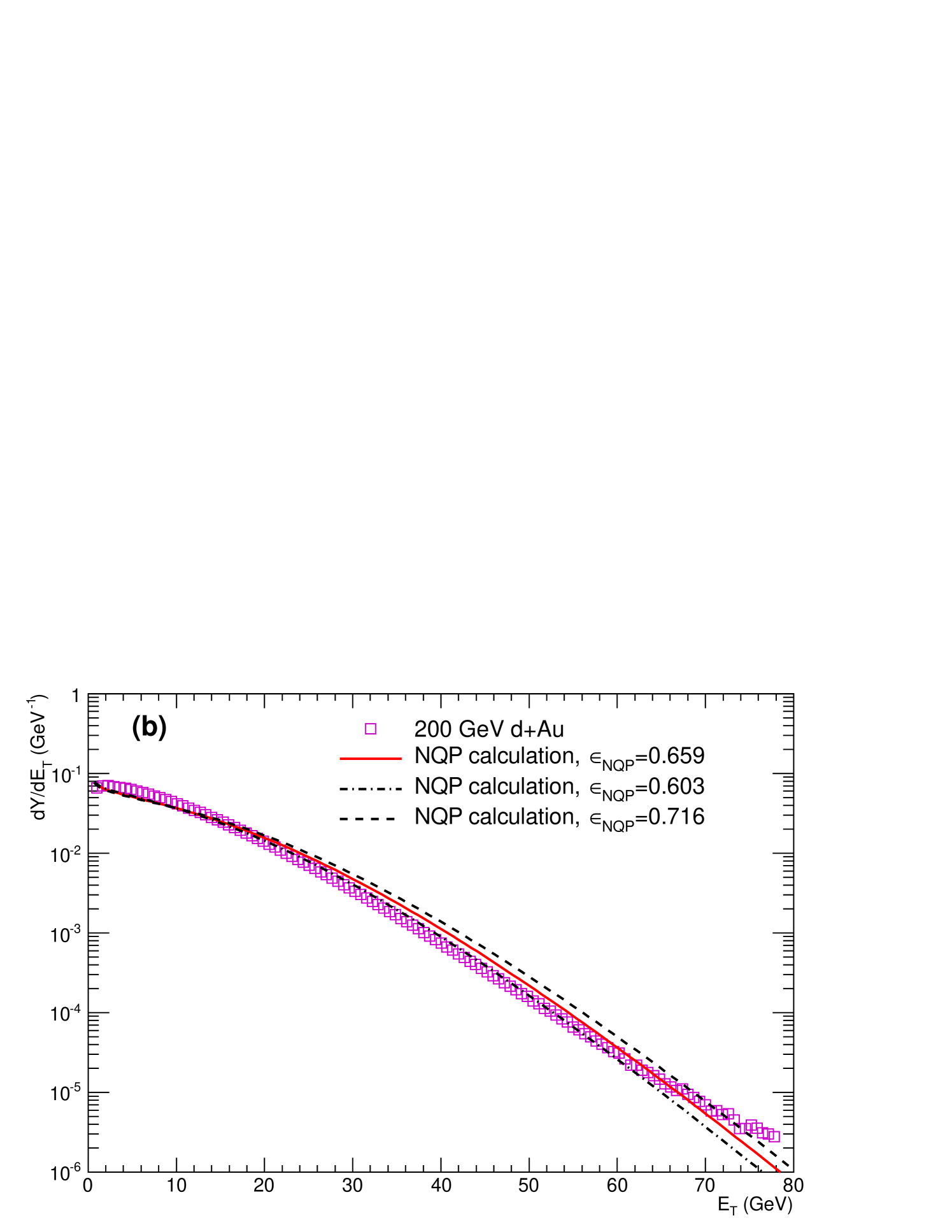
Refer to caption
Figure 11: (Color online) ET{\rm E}_{T} distributions at sNN=200\sqrt{s_{\rm NN}}=200 GeV calculated in the Number of constituent-Quark Participants or NQP model, with ϵN​Q​P=1−p0NQP=0.659\epsilon_{NQP}=1-p_{0_{\rm NQP}}=0.659 for Au++Au together with the AQM calculations with efficiencies indicated.
Refer to caption
Figure 12: (Color online) dd++Au measurements compared to the AQM and NQP model calculations.
Refer to caption
Figure 13: (Color online) ET{\rm E}_{T} distributions at sNN=200\sqrt{s_{\rm NN}}=200 GeV in dd++Au calculated in the Quark Participant (NQP) model with ϵNQP=1−p0NQP=0.659\epsilon_{\rm NQP}=1-p_{0_{\rm NQP}}=0.659 together with the individual visible convolutions for NQP, i.e. 2,3,…33, out of a maximum of 50 NQP considered.

The major difference in the NQP and AQM calculations with respect to the measurements shows up in the asymmetric dd++Au system, Fig. 12, where the NQP calculation closely follows the dd++Au ET{\rm E}_{T} distribution in shape and in magnitude over a range of a factor of 1000 in cross section. The AQM calculation disagrees both in shape and magnitude, with a factor of 1.7 less transverse energy emission than in the measurement. This clearly indicates the need for emission from additional quark participants in the Au target beyond those in the deuteron, as shown by the individual components of the NQP calculation for dd++Au (Fig. 13). It is also clear that having the comparison between the NQP and AQM models for asymmetric systems is crucial in distinguishing the models.

Previously, the hypothesis of quark-participant scaling in Au++Au collisions had been tested only for mean values by plotting ⟨d​ET/d​η⟩/(⟨Nq​p⟩/2)\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle/(\langle N_{qp}\rangle/2) vs NpartN_{\rm part} Eremin and Voloshin (2003); De and Bhattacharyya (2005); Nouicer (2007) as applied here in Fig. 6. The present work extends the NQP model to distributions, as described in section VIII and shown in Fig. 11. By doing so, we are able to make a crucial consistency check—the ⟨d​ET/d​η⟩/Nq​p=0.617±0.023\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle/{N_{qp}}=0.617\pm 0.023 GeV from the linear fit (Fig. 7) in Au++Au is equal (within <1<1 standard deviation) to the value ⟨ET⟩q​ptrue=0.655±0.066\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}_{qp}=0.655\pm 0.066 GeV derived for a quark-participant from the deconvolution of the pp++pp ET{\rm E}_{T} distribution (Table 15).

Refer to caption
Refer to caption
Figure 14: (Color online) Systematic checks of ET≡d​ET/d​η|y=0\mbox{${\rm E}_{T}$}\equiv d\mbox{${\rm E}_{T}$}/d\eta|_{y=0} calculations using pp++pp fits with ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV (a) dd++Au data compared to standard calculation in the NQP model with ϵNQP=1−p0NQP=0.659\epsilon_{\rm NQP}=1-p_{0_{\rm NQP}}=0.659, for 1−p0=0.6471-p_{0}=0.647 in a pp++pp collision from fit with ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV compared to ϵNQP=1−p0NQP=0.670\epsilon_{\rm NQP}=1-p_{0_{\rm NQP}}=0.670 for 1−p0=0.6601-p_{0}=0.660 when the fit to the pp++pp data is extended to ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV. (b) Au++Au calculation for the same conditions as dd++Au in (a).
Refer to caption
Figure 15: (Color online) Measured ET{\rm E}_{T} distribution in Au++Au at sNN=200\sqrt{s_{\rm NN}}=200 GeV on the same ET{\rm E}_{T} scale as Fig. 13 compared to the calculation in the Quark Participant (NQP) model with ϵNQP=1−p0NQP=0.659\epsilon_{\rm NQP}=1-p_{0_{\rm NQP}}=0.659 together with the individual visible convolutions for NQP in this ET{\rm E}_{T} range, i.e. 2,3, …114, out of 584 convolutions with visible contribution to the full distribution, out of a maximum of 1020 NQP considered.
Refer to caption
Refer to caption
Figure 16: (Color online) ET≡d​ET/d​η|y=0\mbox{${\rm E}_{T}$}\equiv d\mbox{${\rm E}_{T}$}/d\eta|_{y=0} distributions at sN​N=200\mbox{$\sqrt{s_{{}_{NN}}}$}=200 GeV: (a) Au++Au compared to the NQP calculations using the central 1−p0=0.6471-p_{0}=0.647 and ±1​σ\pm 1\sigma variations of 1−p0=0.582,0.7121-p_{0}=0.582,0.712 for the probability of getting zero ET{\rm E}_{T} on a pp++pp collision with resulting εNQP=0.659,0.603,0.716\varepsilon_{\rm NQP}=0.659,0.603,0.716, respectively. (b) dd++Au calculation for the same conditions as in (a).
Refer to caption
Figure 17: (Color online) Au++Au measurement of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta compared to the NpartN_{\rm part}-WNM (dot-dash) and NcollN_{\rm coll} (dashes) model calculations.
Refer to caption
Figure 18: (Color online) Au++Au measurement of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta, with 10%–15% centrality region indicated, compared to the calculation of the distribution given by Eq. 21 for NpartN_{\rm part}=254 and Ncoll=672N_{\rm coll}=672 corresponding to 10%–15% centrality.
Refer to caption
Figure 19: (Color online) Au++Au measurement of d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta, with 10%–15% centrality region indicated, compared to the calculation of the distribution given by Eq. 21 for NpartN_{\rm part}=254 and Ncoll=672N_{\rm coll}=672 corresponding to 10%–15% centrality, where the distributions have been scaled in ET{\rm E}_{T} by 0.92 and 0.08, respectively.

VIII.3 Additional Systematic Uncertainties

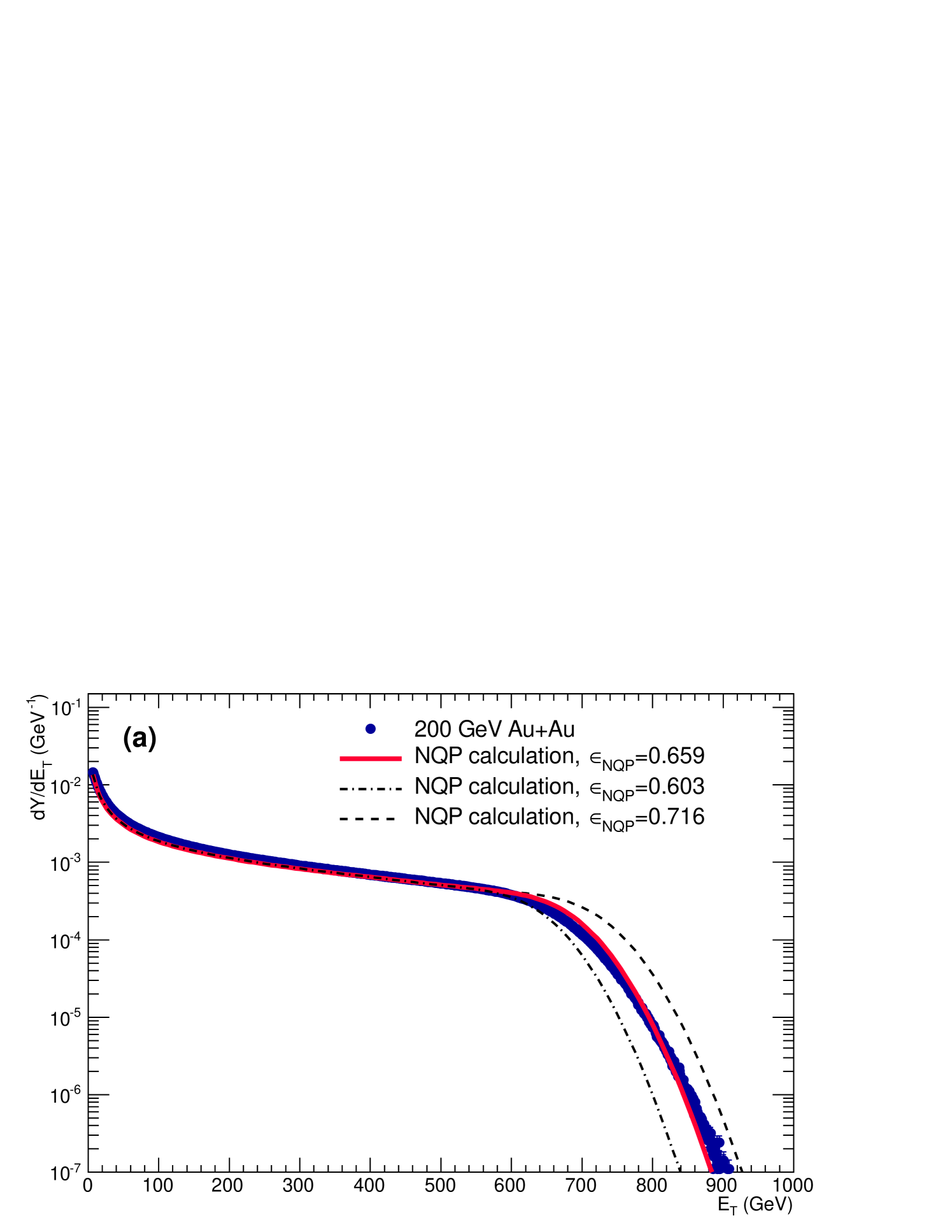
The probability p0p_{0} of detecting zero ET{\rm E}_{T} in the central detector for an N+N or other elementary collision plays a major role in this analysis. The predominant systematic uncertainty comes from the BBC cross section measurement (Eq. VIII.1) which leads to a total systematic uncertainty on 1−p01-p_{0} of 10.1% for a pp++pp collision as indicated in Table 12. The systematic uncertainty is propagated by varying 1−p01-p_{0} from 0.647 to 0.712 and 0.582, ±1\pm 1 standard deviation, from Eq. VIII.1 for standard ET​EMC<2\mbox{${\rm{E}}_{T\,{\rm EMC}}$}<2 GeV (ET<13.3\mbox{${\rm E}_{T}$}<13.3 GeV) pp++pp data and repeating all the calculations (to be shown in Sec. IX). Also all the fits were redone with the ET​EMC<4\mbox{${\rm{E}}_{T\,{\rm EMC}}$}<4 GeV (ET<26.6\mbox{${\rm E}_{T}$}<26.6 GeV) pp++pp data, and the calculations were again all repeated, with a small effect (Fig. 14).

Another important issue must be mentioned in the comparison of the calculations to the measurements. The calculations are per AA+BB collision (corrected for BBC efficiency) while the data are per BBC count and are not corrected for the BBC efficiency. This correction is complicated for both dd++Au and Au++Au, but larger for Au++Au due to the more severe BBC requirement. To get an idea of the size of the effect, Fig. 15 shows the Au++Au data and the NQP calculation of Fig. 11 on the same ET{\rm E}_{T} scale as in dd++Au collisions (see Fig. 13). The inefficiency in the data compared to the Au++Au calculation is negligible for ET≥7\mbox{${\rm E}_{T}$}\geq 7 GeV, as shown, which should be less severe for dd++Au and therefore does not affect the conclusion from Fig. 12 that rejects the AQM model in favor of the NQP model.

IX Final Results and discussion

The principal results were given in Figs. 11 and 12. The final results are now presented in Fig. 16 including the systematic uncertainties. In Fig. 16a, the Au++Au ET≡d​ET/d​η|y=0\mbox{${\rm E}_{T}$}\equiv d\mbox{${\rm E}_{T}$}/d\eta|_{y=0} distribution is shown compared to the NQP calculations using the central 1−p0=0.6471-p_{0}=0.647 and ±1​σ\pm 1\sigma variations of 1−p0=0.582,0.7121-p_{0}=0.582,0.712 for the probability of getting zero ET{\rm E}_{T} on a pp++pp collision, which correspond to ϵNQP=0.659,0.603,0.716\epsilon_{\rm NQP}=0.659,0.603,0.716 respectively. Both the shape and magnitude of the calculation with the NQP model are in excellent agreement with the Au++Au measurement. The upper edge of the calculation using the central 1−p01-p_{0} is essentially on top of the measured ET{\rm E}_{T} distribution, well within the principal ±10%\pm 10\% systematic uncertainty shown, while the AQM model (recall Fig. 11) was another 12% lower due to the nonzero p0p_{0} in pp++pp collisions in this measurement which leads to different efficiencies of a quark participant and a color string.

In Fig. 16b the dd++Au ET{\rm E}_{T} distribution is shown with the central 1−p0NQP1-p_{0_{\rm NQP}} and the ±1​σ\pm 1\sigma variations. The NQP calculation closely follows the dd++Au measurement in shape and in magnitude over a range of a factor of 1000 in cross section, while as previously seen in Fig. 12, the AQM calculation disagrees both in shape and magnitude, with nearly a factor of 2 less ET{\rm E}_{T} emission. A new independent check of the NQP model is the observation that the ⟨d​ET/d​η⟩/Nq​p=0.617±0.023\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle/N_{qp}=0.617\pm 0.023 GeV calculated from the linear fit (Fig. 7) of the Au++Au measurement as a function of centrality is equal (within <1<1 standard deviation) to the value ⟨ET⟩q​ptrue=0.655±0.066\langle\mbox{${\rm E}_{T}$}\rangle^{\rm true}_{qp}=0.655\pm 0.066 GeV derived for a quark-participant from the deconvolution of the pp++pp ET{\rm E}_{T} distribution (Table 15).

The availability of the pp++pp baseline ET{\rm E}_{T} distribution together with the Au++Au distribution allows a test of how the representation of d​Nch/d​η{d\mbox{$N_{\rm ch}$}/d\eta} or d​ET/d​η{d\mbox{${\rm E}_{T}$}/d\eta} as a function of centrality by this rewrite of Eq. 6 Adcox et al. (2001b); Wang and Gyulassy (2001); Kharzeev and Nardi (2001):

d​ETA​A/d​η\displaystyle{d\mbox{${\rm E}_{T}$}^{AA}/d\eta} =\displaystyle= [(1−x)⟨Npart⟩(dETp​p/dη)/2\displaystyle[(1-x)\,\langle\mbox{$N_{\rm part}$}\rangle(d\mbox{${\rm E}_{T}$}^{pp}/d\eta)/2
+\displaystyle+ x⟨Ncoll⟩(dETp​p/dη)],\displaystyle x\,\langle\mbox{$N_{\rm coll}$}\rangle(d\mbox{${\rm E}_{T}$}^{pp}/d\eta)],

which works for the average values, could be applied to the distributions.

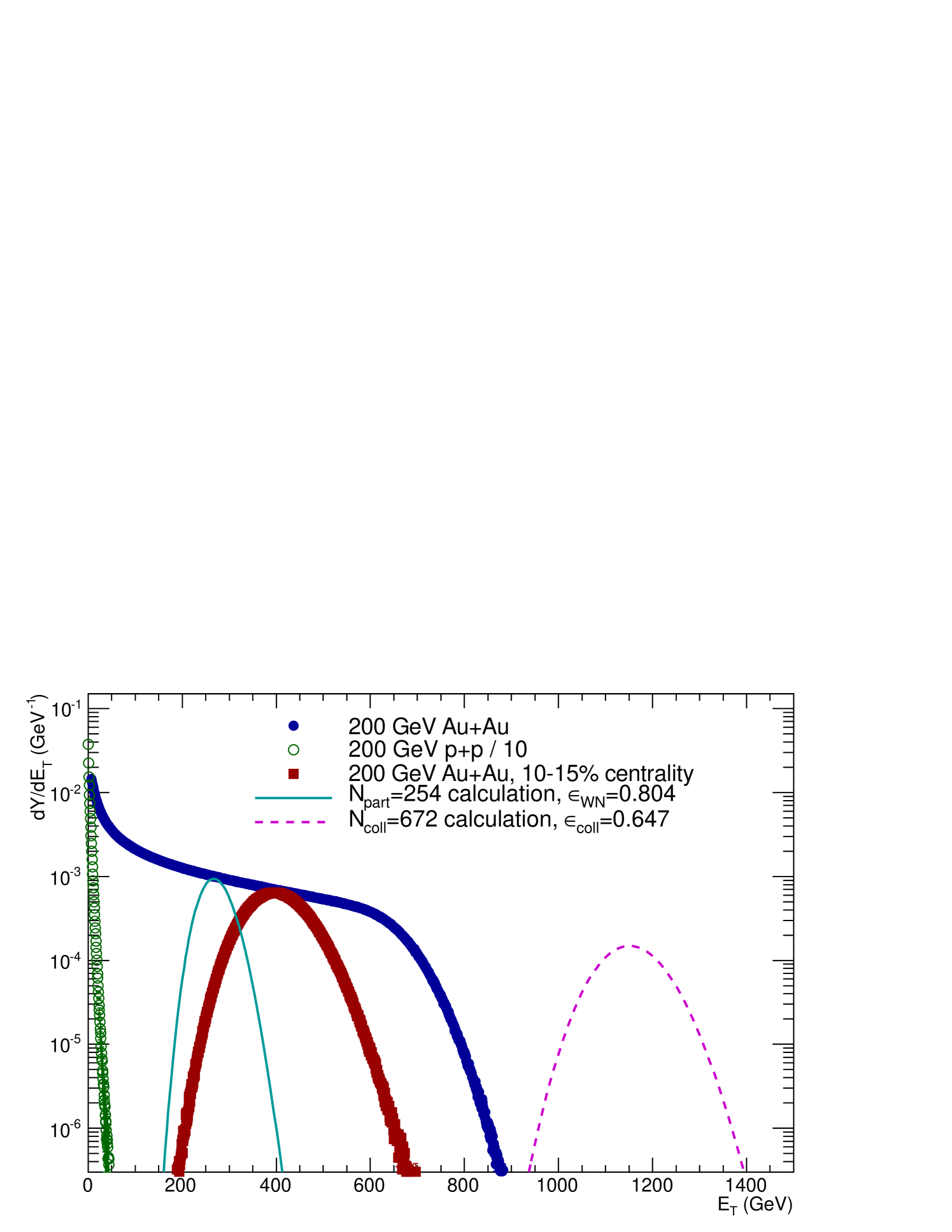
Figure 17 compares the Au++Au data to the NcollN_{\rm coll} and NpartN_{\rm part}-WNM calculations, including the efficiencies. One thing that is immediately evident from Fig. 17 is that if Eq. 6,21 were taken to represent the weighted sum of (1−x)×(1-x)\ \times the WNM-NpartN_{\rm part} curve + x×x\ \times the NcollN_{\rm coll} curve with x≈0.08x\approx 0.08 Adcox et al. (2001b); Back et al. (2004), then the representation of d​ET/d​η{d\mbox{${\rm E}_{T}$}/d\eta} by Eq. 6,21, which may seem reasonable for the average values, makes no sense for the distribution.

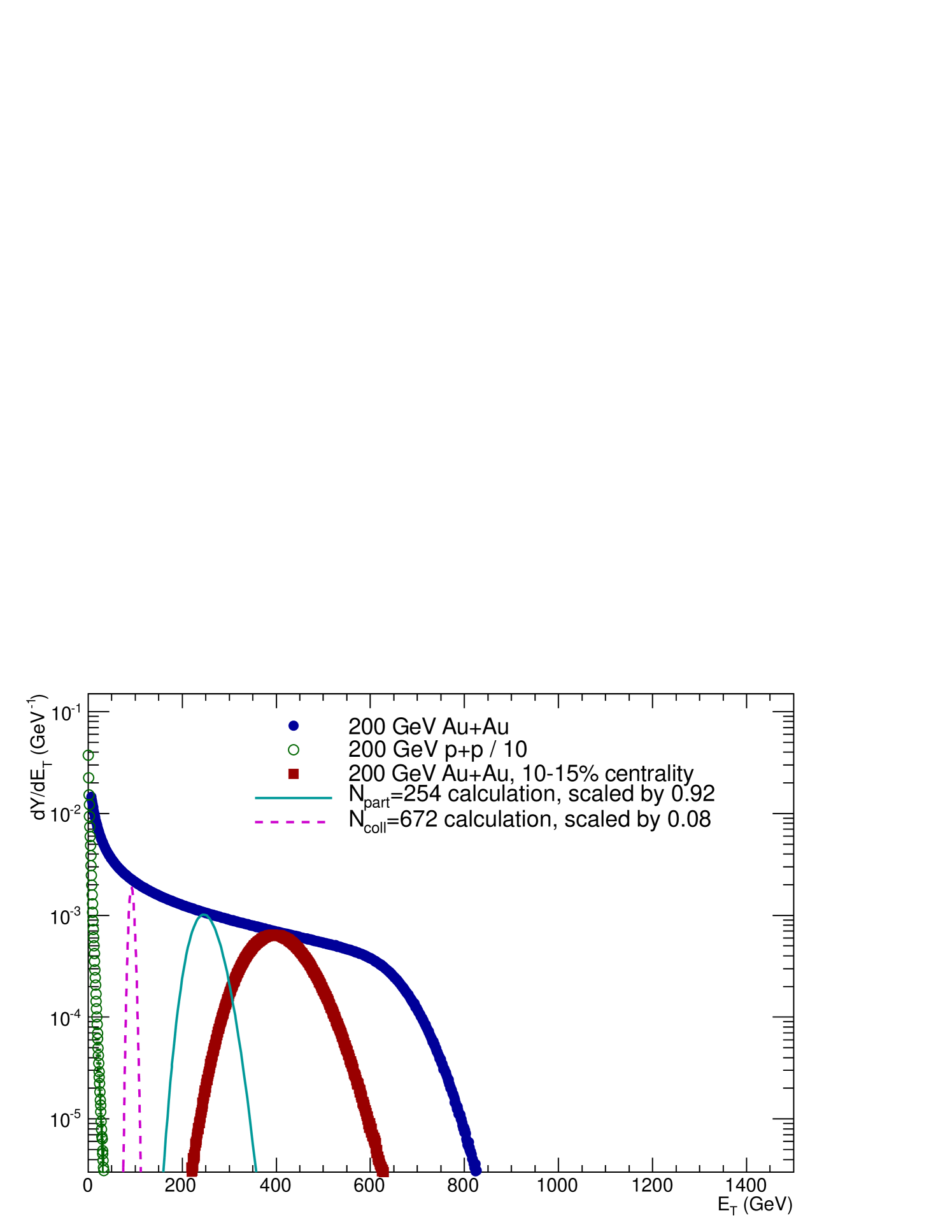
To further emphasize this point, shown in Fig. 18 is the calculation of the distribution given by Eq. 6,21 for 10%–15% centrality, namely the sum of the NpartN_{\rm part} distribution for ⟨Npart⟩=254\langle N_{\rm part}\rangle=254, weighted by (1-xx), and the NcollN_{\rm coll} distribution for ⟨Ncoll⟩=672\langle N_{\rm coll}\rangle=672 weighted by xx, compared to the measured Au++Au distribution for 10%–15% percentile centrality region. 222The curves in Fig. 18 are actually for 254×(ϵNpart=0.804)=204254\times(\epsilon_{N_{\rm part}}=0.804)=204 convolutions of f1Npartf_{1}^{N_{\rm part}} and 672×(ϵNcoll=0.647)=435672\times(\epsilon_{N_{\rm coll}}=0.647)=435 convolutions of the pp++pp measured reference distribution, f1Ncoll​(ET)f_{1}^{N_{\rm coll}}(\mbox{${\rm E}_{T}$}) following Eq. VII.1. Although it is reasonable that the weighted sum of the averages of the NcollN_{\rm coll} and NpartN_{\rm part} distributions could equal the average of the measured d​ET/d​η{d\mbox{${\rm E}_{T}$}/d\eta} distribution for 10%–15% centrality, the weighted sum of the actual NcollN_{\rm coll} and NpartN_{\rm part} distributions would look totally unreasonable and nothing like the measured d​ET/d​η{d\mbox{${\rm E}_{T}$}/d\eta} distribution cut on centrality. Thus Eq. 6 can not be interpreted as the weighted sum of the NcollN_{\rm coll} and NpartN_{\rm part} distributions. Furthermore, as shown in Fig. 19, neither can Eq. 6 be interpreted as the sum of the NcollN_{\rm coll} and NpartN_{\rm part} distributions scaled in ET{\rm E}_{T} by the factors xx and 1−x1-x respectively. Hence it does not seem that Eq. 6 can be computed in an extreme independent model.

Recent experiments at the Large Hadron Collider, the ATLAS experiment in particular Aad et al. (2012), have shown that computing Eq. 6 on an event-by-event basis as a nuclear geometry distribution in a standard Glauber calculation, agrees very well with their measured ET{\rm E}_{T} distribution in the pseudorapidity range 3.2<|η|<4.93.2<|\eta|<4.9 at sN​N\sqrt{s_{{}_{NN}}} =2.76 TeV Pb++Pb collisions. Similar results were obtained by ALICE Abelev et al. (2013). This confirms the observation noted previously (Sec. VI) that the success of the two component model is not because there are some contributions proportional to NpartN_{\rm part} and some proportional to NcollN_{\rm coll}, but rather because a particular linear combination of NpartN_{\rm part} and NcollN_{\rm coll} turns out to be an empirical proxy for the nuclear geometry of the number of constituent-quark participants, Nq​pN_{qp} in A+A collisions.

X Summary

To summarize, the midrapidity transverse energy distributions, d​ET/d​ηd\mbox{${\rm E}_{T}$}/d\eta, have been measured for sN​N\sqrt{s_{{}_{NN}}} =200 GeV pp++pp and dd++Au collisions, and for Au++Au collisions at sN​N\sqrt{s_{{}_{NN}}} =200, 130, and 62.4 GeV. As a function of centrality, the ⟨d​ET/d​η⟩\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle measured in Au++Au collisions at all three collision energies exhibit a nonlinear increase with increasing centrality when expressed as the number of nucleon participants, NpartN_{\rm part}. When expressed in terms of the number of constituent-quark participants, Nq​pN_{qp}, the ⟨d​ET/d​η⟩\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle increases linearly with Nq​pN_{qp}. Several Extreme Independent models of particle production have been compared to the data, including calculations based upon color-strings (the Additive Quark Model, AQM) and the constituent-Quark Participant model (NQP). When compared to data from symmetric systems (Au++Au and pp++pp), these two models cannot generally be distinguished from each other. In the present measurement, the different detection efficiency for a quark-participant and color string in the two cases allows a separation, with the NQP model favored. However, when compared to data from the asymmetric dd++Au system, the dd++Au measurement clearly rejects the AQM model and agrees very well with the NQP model. This implies that transverse energy production at midrapidity in relativistic heavy ion collisions is well described by particle production based upon the number of constituent-quark participants. Additional support for this conclusion is that the ansatz, [(1−x)​⟨Npart⟩/2+x​⟨Ncoll⟩][(1-x)\,\langle\mbox{$N_{\rm part}$}\rangle/2+x\,\langle\mbox{$N_{\rm coll}$}\rangle], which has been used successfully to represent the nonlinearity of ⟨d​ET/d​η⟩\langle d\mbox{${\rm E}_{T}$}/d\eta\rangle as a function of NpartN_{\rm part}, turns out to be simply a proxy for ⟨Nq​p⟩\langle\mbox{$N_{qp}$}\rangle in A+A collisions and does not represent a hard-scattering component in ET{\rm E}_{T} distributions.

ACKNOWLEDGMENTS

We thank the staff of the Collider-Accelerator and Physics Departments at Brookhaven National Laboratory and the staff of the other PHENIX participating institutions for their vital contributions. We acknowledge support from the Office of Nuclear Physics in the Office of Science of the Department of Energy, the National Science Foundation, Abilene Christian University Research Council, Research Foundation of SUNY, and Dean of the College of Arts and Sciences, Vanderbilt University (U.S.A), Ministry of Education, Culture, Sports, Science, and Technology and the Japan Society for the Promotion of Science (Japan), Conselho Nacional de Desenvolvimento Científico e Tecnológico and Fundação de Amparo à Pesquisa do Estado de São Paulo (Brazil), Natural Science Foundation of China (P. R. China), Centre National de la Recherche Scientifique, Commissariat à l’Énergie Atomique, and Institut National de Physique Nucléaire et de Physique des Particules (France), Bundesministerium für Bildung und Forschung, Deutscher Akademischer Austausch Dienst, and Alexander von Humboldt Stiftung (Germany), Hungarian National Science Fund, OTKA (Hungary), Department of Atomic Energy (India), Israel Science Foundation (Israel), National Research Foundation and WCU program of the Ministry Education Science and Technology (Korea), Physics Department, Lahore University of Management Sciences (Pakistan), Ministry of Education and Science, Russian Academy of Sciences, Federal Agency of Atomic Energy (Russia), VR and Wallenberg Foundation (Sweden), the U.S. Civilian Research and Development Foundation for the Independent States of the Former Soviet Union, the US-Hungarian NSF-OTKA-MTA, and the US-Israel Binational Science Foundation.

References

  • Adcox et al. (2001a) K. Adcox et al. (PHENIX Collaboration), Phys. Rev. Lett. 87, 052301 (2001a).
  • Adler et al. (2005) S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. C 71, 034908 (2005).
  • Wang and Gyulassy (2001) X.-N. Wang and M. Gyulassy, Phys. Rev. Lett. 86, 3496 (2001).
  • Kharzeev and Nardi (2001) D. Kharzeev and M. Nardi, Phys. Lett. B 507, 121 (2001).
  • Eremin and Voloshin (2003) S. Eremin and S. Voloshin, Phys. Rev. C 67, 064905 (2003).
  • Bialas et al. (1982) A. Bialas, W. Czyz, and L. Lesniak, Phys. Rev. D 25, 2328 (1982).
  • Ochiai (1987) T. Ochiai, Z. Phys. C 35, 209 (1987).
  • Camerini et al. (1952) U. Camerini, W. O. Lock, and D. Perkins, in Progress in Cosmic Ray Physics, edited by J. G. Wilson (North Holland, Amsterdam, 1952), vol. I, pp. 1–34.
  • Cocconi et al. (1961) G. Cocconi, L. J. Koester, and D. H. Perkins, Tech. Rep. UCRL-10022 (1961), Lawrence Radiation Laboratory (1961), p. 167, as cited by Ref. Orear (1964).
  • Orear (1964) J. Orear, Phys. Rev. Lett. 12, 112 (1964).
  • Mueller (1971) A. H. Mueller, Phys. Rev. D 4, 150 (1971).
  • Koba et al. (1972) Z. Koba, H. B. Nielsen, and P. Olesen, Nucl. Phys. B 40, 317 (1972).
  • Arnison et al. (1981) G. Arnison et al., Phys. Lett. B 107, 320 (1981).
  • Alner et al. (1987) G. J. Alner et al., Phys. Rpts. 154, 247 (1987).
  • (15) For instance, see Maurice Jacob’s Eulogy for the ISR in CERN report 84-13, (CERN, SIS, Geneva 1984).
  • Thomé et al. (1977) W. Thomé et al., Nucl. Phys. B129, 365 (1977).
  • Fowler and Weiner (1977) G. N. Fowler and R. M. Weiner, Phys. Lett. B 70, 201 (1977).
  • Willis (1972) W. J. Willis, in ISABELLE Physics Prospects (BNL-17522), edited by R. B. Palmer (Brookhaven National Laboratory, Upton, NY, 1972), pp. 207–234, (n.b. same report appears as CRISP-72-15, BNL-16841).
  • Bjorken (1973) J. D. Bjorken, Phys. Rev. D 8, 4098 (1973).
  • Ochs and Stodolsky (1977) W. Ochs and L. Stodolsky, Phys. Lett. B 69, 225 (1977).
  • Landshoff and Polkinghorne (1978) P. V. Landshoff and J. C. Polkinghorne, Phys. Rev. D 18, 3344 (1978).
  • De Marzo et al. (1982) C. De Marzo et al. (Bari-Cracow-Liverpool-Munich-Nijmegen), Phys. Lett. B 112, 173 (1982).
  • (23) G. Arnison et al. (UA1), Transverse energy distributions in the central calorimeters, presented to 21st Int. Conf. High Energy Physics, Paris, France, Jul 26-31, 1982, CERN-EP-82-122. (Unpublished). Also see reference Arnison et al. (1981).
  • Repellin et al. (1982) J.-P. Repellin et al., in Proc. 21st Int. Conf. High Energy Physics (Paris), edited by P. Petiau and M. Porneuf (Journal de Physique Colloques, Paris, 1982), vol. 43, pp. C3–571 – C3–578.
  • Appel et al. (1985) J. A. Appel et al., Phys. Lett. B 165, 441 (1985).
  • Bjorken (1983) J. D. Bjorken, Phys. Rev. D 27, 140 (1983).
  • Busza et al. (1975) W. Busza et al., Phys. Rev. Lett. 34, 836 (1975).
  • Halliwell et al. (1977) C. Halliwell et al., Phys. Rev. Lett. 39, 1499 (1977).
  • Fishbane and Trefil (1974a) P. M. Fishbane and J. S. Trefil, Phys. Rev. D 9, 168 (1974a).
  • Fishbane and Trefil (1974b) P. M. Fishbane and J. S. Trefil, Phys. Lett. B 51, 139 (1974b).
  • Gottfried (1974) K. Gottfried, Phys. Rev. Lett. 32, 957 (1974).
  • Goldhaber (1973) A. S. Goldhaber, Phys. Rev. D 7, 765 (1973).
  • Białas and Czyż (1974) A. Białas and W. Czyż, Phys. Lett. B 51, 179 (1974).
  • Andersson and Otterlund (1975) B. Andersson and I. Otterlund, Nucl. Phys. B 88, 349 (1975).
  • Frankel (1993) S. Frankel, Phys. Rev. C 48, R2170 (1993).
  • Białas et al. (1976) A. Białas, M. Bleszyński, and W. Czyż, Nucl. Phys. B 111, 461 (1976).
  • Ahle et al. (1998) L. Ahle et al., Phys. Rev. C 57, R466 (1998).
  • Ftacnik et al. (1987) J. Ftacnik, K. Kajantie, N. Pisutova, and J. Pisut, Phys. Lett. B 188, 279 (1987).
  • Abbott et al. (1987) T. Abbott et al., Phys. Lett. B 197, 285 (1987).
  • Abbott et al. (2001) T. Abbott et al., Phys. Rev. C 63, 064602 (2001).
  • Angelis et al. (1984) A. L. S. Angelis et al., Phys. Lett. B 141, 140 (1984).
  • Åkesson et al. (1989) T. Åkesson et al., Phys. Lett. B 231, 359 (1989).
  • Bamberger et al. (1987) A. Bamberger et al., Phys. Lett. B 184, 271 (1987).
  • Remsberg et al. (1988) L. P. Remsberg et al., Z. Phys. C 38, 35 (1988).
  • Alver et al. (2011) B. Alver et al., Phys. Rev. C 83, 024913 (2011).
  • Adcox et al. (2001b) K. Adcox et al. (PHENIX Collaboration), Phys. Rev. Lett. 86, 3500 (2001b).
  • Nouicer (2007) R. Nouicer, Eur. Phys. J. C 49, 281 (2007).
  • De and Bhattacharyya (2005) B. De and S. Bhattacharyya, Phys. Rev. C 71, 024903 (2005).
  • Bialas (2008) A. Bialas, J. Phys. G 35, 044053 (2008).
  • Gell-Mann (1964) M. Gell-Mann, Phys. Lett. 8, 214 (1964).
  • Feynman et al. (1964) R. P. Feynman, M. Gell-Mann, and G. Zweig, Phys. Rev. Lett. 13, 678 (1964).
  • Morpurgo (1970) G. Morpurgo, Annu. Rev. Nucl. Part. Sci. 20, 105 (1970).
  • Kokkedee (1969) J. J. J. Kokkedee, THE QUARK MODEL (W. A. Benmajin, Inc., New York, 1969).
  • Shuryak (1982) E. V. Shuryak, Nucl. Phys. B 203, 116 (1982).
  • Diakonov (1996) D. Diakonov, Prog. Part. Nucl. Phys. 36, 1 (1996).
  • Weinberg (2004) S. Weinberg, Eur. Phys. J. C 34, 5 (2004).
  • Anisovich et al. (1978) V. V. Anisovich, Y. M. Shabelsky, and V. M. Shekhter, Nucl. Phys. B 133, 477 (1978).
  • Hwa (1980) R. C. Hwa, Phys. Rev. D 22, 759 (1980).
  • Akiba (1982) T. Akiba, Phys. Lett. B 109, 477 (1982).
  • Levin and Frankfurt (1965) E. M. Levin and L. L. Frankfurt, JETP Lett. 2, 66 (1965).
  • Lipkin (1966) H. J. Lipkin, Phys. Rev. Lett. 16, 1015 (1966).
  • Adcox et al. (2003) K. Adcox et al. (PHENIX Collaboration), Nucl. Instrum. Methods A 499, 469 (2003).
  • Allen et al. (2003) M. Allen et al. (PHENIX Collaboration), Nucl. Instrum. Methods A 499, 549 (2003).
  • Adare et al. (2012) A. Adare et al. (PHENIX Collaboration), Phys. Rev. C86, 064901 (2012).
  • Wang and Gyulassy (1991) X.-N. Wang and M. Gyulassy, Phys. Rev. D 44, 3501 (1991).
  • Adler et al. (2007a) S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 98, 172302 (2007a).
  • Aphecetche et al. (2003a) L. Aphecetche et al. (PHENIX Collaboration), Nucl. Instrum. Methods A 499, 521 (2003a).
  • Miller et al. (2007) M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg, Ann. Rev. Nucl. Part. Sci. 57, 205 (2007).
  • Hofstadter et al. (1958) R. Hofstadter, F. Bumiller, and M. R. Yerian, Rev. Mod. Phys. 30, 482 (1958).
  • Aamodt et al. (2011) K. Aamodt et al., Phys. Rev. Lett. 106, 032301 (2011).
  • Adcox et al. (2002) K. Adcox et al. (PHENIX Collaboration), Phys. Rev. Lett. 88, 022301 (2002).
  • Back et al. (2004) B. Back et al., Phys. Rev. C 70, 021902(R) (2004).
  • Tannenbaum (2004) M. J. Tannenbaum, Phys. Rev. C 69, 064902 (2004).
  • Angelis et al. (1983) A. L. S. Angelis et al., Phys. Lett. B 126, 132 (1983).
  • Aphecetche et al. (2003b) L. Aphecetche et al., Nucl. Inst. Methods A 499, 521 (2003b).
  • (76) For example see Fig. 6 in reference Tannenbaum (2006).
  • Tannenbaum (2006) M. J. Tannenbaum, Rep. Prog. Phys. 69, 2005 (2006).
  • Adler et al. (2003) S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 91, 241803 (2003).
  • Adler et al. (2007b) S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 98, 012002 (2007b).
  • Aad et al. (2012) G. Aad et al., Phys. Lett. B 707, 330 (2012).
  • Abelev et al. (2013) B. Abelev et al., Phys. Rev. C 88, 044909 (2013).