Traveling-wave solutions for a higher-order Boussinesq system: existence and numerical analysis

Roberto de A. Capistrano–Filho Department of Mathematics, Universidade Federal de Pernambuco
Av. Prof. Moraes Rego, 1235 - Cidade Universitária, Recife - PE, 50670-901, Brasil roberto.capistranofilho@ufpe.br , Juan Carlos Muñoz Department of Mathematics, Universidad del Valle
Calle 13, 100-00
Cali - Colombia juan.munoz@correounivalle.edu.co and José R. Quintero Department of Mathematics, Universidad del Valle
Calle 13, 100-00
Cali - Colombia jose.quintero@correounivalle.edu.co

(Date: August 20, 2025)

Abstract.

We study the existence and numerical computation of traveling wave solutions for a family of nonlinear higher-order Boussinesq evolution systems with a Hamiltonian structure. This general Boussinesq evolution system includes a broad class of homogeneous and non-homogeneous nonlinearities. We establish the existence of traveling wave solutions using the variational structure of the system and the concentration-compactness principle by P.-L. Lions, even though the nonlinearity could be non-homogeneous. For the homogeneous case, the traveling wave equations of the Boussinesq system are approximated using a spectral approach based on a Fourier basis, along with an iterative method that includes appropriate stabilizing factors to ensure convergence. In the non-homogeneous case, we apply a collocation Fourier method supplemented by Newton’s iteration. Additionally, we present numerical experiments that explore cases in which the wave velocity falls outside the theoretical range of existence.

Résumé. Nous étudions l’existence et le calcul numérique de solutions en ondes progressives pour une famille de systèmes d’évolution de Boussinesq d’ordre supérieur non linéaires avec une structure hamiltonienne. Ce système général de Boussinesq inclut une large classe de non-linéarités homogènes et non homogènes. Nous établissons l’existence de solutions en ondes progressives en utilisant la structure variationnelle du système ainsi que le principe de concentration-compacité de P.-L. Lions, même si la non-linéarité peut être non homogène. Dans le cas homogène, les équations d’ondes progressives du système de Boussinesq sont approximées à l’aide d’une approche spectrale basée sur une base de Fourier, combinée à une méthode itérative incluant des facteurs de stabilisation appropriés pour garantir la convergence. Dans le cas non homogène, nous appliquons une méthode de collocation de Fourier complétée par l’itération de Newton. De plus, nous présentons des expériences numériques explorant des cas où la vitesse de l’onde se situe en dehors de la plage théorique d’existence.

Key words and phrases:

Boussinesq system, solitary waves, variational approach, spectral numerical methods

2020 Mathematics Subject Classification:

76B15, 35A15, 37K40, 65M70, 65M06

*Corresponding author: juan.munoz@correounivalle.edu.co

1. Introduction

Bona, Chen and Saut, in [2] and [3], derived some classical Boussinesq systems corresponding to the first- and second-order approximations to the full two-dimensional Euler equations, to describe the motion of short waves of small amplitude on the surface of an ideal fluid under gravity force. In particular, authors derived a four-parameter family of Boussinesq systems from the two-dimensional Euler equations, known as the $abcd$ Boussinesq system,

\begin{cases}\begin{array}[]{rl}\left(I-b\partial^{2}_{x}\right)\partial_{t}\eta+\partial_{x}w+a\partial_{x}^{3}w&=-\partial_{x}\left(\eta w\right),\\ \left(I-d\partial_{x}^{2}\right)\partial_{t}w+\partial_{x}\eta+c\partial_{x}^{3}\eta&=\frac{1}{2}\partial_{x}\left(w^{2}\right),\end{array}\end{cases}

with $a+b+c+d=\frac{1}{3}-\sigma$ ( $\sigma\geq 0$ is the surface tension), and an eight-parameter family of Boussinesq systems

(1.1)

\begin{cases}\begin{array}[]{rl}\left(I-d\partial^{2}_{x}+d_{2}\partial_{x}^{4}\right)\partial_{t}w+\partial_{x}\eta+c\partial_{x}^{3}\eta+c_{2}\partial_{x}^{5}\eta=\partial_{x}\left(H_{1}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,w,\partial_{x}w,\partial^{2}_{x}w)\right),\\ \\ \left(I-b\partial_{x}^{2}+b_{2}\partial_{x}^{4}\right)\partial_{t}\eta+\partial_{x}u+a\partial_{x}^{3}u+a_{2}\partial_{x}^{5}u=\partial_{x}\left(H_{2}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,w,\partial_{x}w,\partial^{2}_{x}w)\right),\end{array}\end{cases}

where $H_{i}$ for $i=1,2$ are given by

\displaystyle H_{1}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,w,\partial_{x}w,\partial^{2}_{x}w)

\displaystyle=\frac{1}{2}w^{2}-c\partial_{x}(w\partial_{x}w)-\eta\partial^{2}_{x}\eta-\frac{1}{2}\partial_{x}(w^{2})+(c+d)w\partial^{2}_{x}w,

and

\displaystyle H_{2}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,w,\partial_{x}w,\partial^{2}_{x}w)

\displaystyle=-\eta w+b\partial^{2}_{x}(\eta w)-\left(a+b-\frac{1}{3}\right)\eta\partial^{2}_{x}w,

with the constants $a$ , $a_{2}$ , $b$ , $b_{2}$ , $c_{2}$ , $d$ , and $d_{2}$ satisfying the following condition

a+b+c+d=\frac{1}{3}-\sigma,

and also that

a_{2}-b_{2}=-\frac{1}{2}(\theta^{2}-\frac{1}{3})b+\frac{5}{24}(\theta^{2}-\frac{1}{5})^{2},\ \ c_{2}-d_{2}=-\frac{1}{2}(1-\theta^{2})c+\frac{5}{24}(1-\theta^{2})(\theta^{2}-\frac{1}{5}),

for $\theta\in[0,1]$ .

In the present work, we study the existence of traveling waves of finite energy (solitons) for the one-dimensional higher-order Boussinesq evolution system derived from (LABEL:8-BS), namely

(1.2)

\left\{\begin{array}[]{rl}\left(I-d\partial^{2}_{x}+d_{2}\partial_{x}^{4}\right)\partial_{x}u+\partial_{x}\eta+c\partial_{x}^{3}\eta+c_{2}\partial_{x}^{5}\eta&=\partial_{x}\left(G_{1}(\eta,\partial_{x}\eta,\partial_{x}^{2}\eta,u,\partial_{x}u,\partial^{2}_{x}u)\right),\\ \\ \left(I-b\partial_{x}^{2}+b_{2}\partial_{x}^{4}\right)\partial_{t}\eta+\partial_{x}u+a\partial_{x}^{3}u+a_{2}\partial_{x}^{5}u&=\partial_{x}\left(G_{2}(\eta,\partial_{x}\eta,\partial_{x}^{2}\eta,u,\partial_{x}u,\partial^{2}_{x}u)\right),\end{array}\right.

where $\eta=\eta(x,t)$ and $u=u(x,t)$ are real-valued functions, and the nonlinearity $G=(G_{1},G_{2})^{t}$ has the variational structure

\begin{split}G_{1}(q,r,z,s,t,w)=&F_{q}(q,r,s,t)-rF_{qr}(q,r,s,t)-zF_{rr}(q,r,s,t)-tF_{sr}(q,r,s,t)\\ &-wF_{tr}(q,r,s,t),\end{split}

and

\begin{split}G_{2}(q,r,z,s,t,w)=&F_{s}(q,r,s,t)-rF_{qt}(q,r,s,t)-zF_{rt}(q,r,s,t)-tF_{st}(q,r,s,t)\\ &-wF_{tt}(q,r,s,t),\end{split}

where $F$ is a function with some properties, such as being $p+2$ -homogeneous. Let us briefly outline some aspects of the system considered in this work.

1.1. Background

It is important to highlight that, similar to the case of the $abcd$ -Boussinesq system and the KdV equation at the traveling wave level (see, for example, [6]), the higher-order Boussinesq system (LABEL:1bbl) at the traveling wave level is, depending on the nonlinearity, related to traveling wave solutions of the fifth-order KdV equation:

(1.3)

\partial_{t}u+\alpha\partial^{3}_{x}u+\beta\partial^{5}_{x}u=\partial_{x}(f(u,\partial_{x}u,\partial^{2}_{x}u)),

where the nonlinearity takes the variational form

f(q,r,s)=F_{q}(q,r)-rF{qr}(q,r)-sF_{rr}(q,r),

for some $C^{3}$ function $F$ , which is not necessarily homogeneous, as discussed by Esfahani and Levandosky in [12]. We mention that the model (1.3) has applications in various physical phenomena, as we see in different works. See, for instance, the references [8, 13, 14, 18, 20] and therein.

Numerical methods for approximating the solutions of initial-boundary value problems associated with Boussinesq-type systems have been extensively studied. For instance, in [5], the standard Galerkin finite element method was used for spatial discretization, combined with a fourth-order explicit Runge-Kutta scheme for time integration. In [10], soliton propagation and interactions were investigated using two finite difference schemes and two finite element methods with second- and third-order time discretizations. In [11], a collocation method based on exponential cubic B-spline functions was proposed to solve one-dimensional Boussinesq systems and simulate the motion of traveling waves. Furthermore, in [9], a Fourier collocation method was applied to study the dynamics of solitary-wave solutions under periodic boundary conditions.

Finally, for more details on higher-order Boussinesq systems, we refer the reader to the works of Benney [1], Craig and Groves [8], Hunter and Scheurle [13], Kichenassamy and Olver [15], Olver [18], Ponce [19], Bona, Chen, and Saut [2, 3], as well as Chen, Nguyen, and Sun [7], and Bona, Colin, and Lannes [4].

We mention this is only a brief overview of the state of the art. Therefore, we encourage readers to refer to the references cited in the mentioned works for further details.

1.2. Notations and main results

With this overview of the state of the art, we now present the primary objective of this work: proving the existence of traveling-wave solutions for the generalized Boussinesq system (LABEL:1bbl). To the best of our knowledge, this is the first result addressing this topic for higher-order Boussinesq systems. Specifically, we aim to demonstrate the existence of traveling-wave solutions for the system (LABEL:1bbl). In other words, we seek solutions $(\eta,u)$ of the form:

\eta(t,x)=\psi\left({x-\omega t}\right),\ \ u(x,t)=v\left({x-\omega t}\right).

In this case, we have that the traveling wave profile $(\psi,v)$ should satisfy the system

(1.4)

\left\{\begin{array}[]{rl}-\omega\left(v-dv^{\prime\prime}+d_{2}v^{(iv)}\right)+\psi+c\psi^{\prime\prime}+c_{2}\psi^{(iv)}-G_{1}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime})&=0,\\ \\ -\omega\left(\psi-b\psi^{\prime\prime}+b_{2}\psi^{(iv)}\right)+v+av^{\prime\prime}+a_{2}v^{(iv)}-G_{2}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime})&=0,\end{array}\right.

where we are assuming that $b=d>0$ , $b_{2}=d_{2}>0$ , $a,c<0$ and that $a_{2},c_{2}>0$ .

Note that the existence of solitons, traveling waves with finite energy, for the higher-order Boussinesq system (LABEL:1bbl) follows from a variational approach using a minimax-type result. Specifically, solutions $(\psi,v)$ of the system (LABEL:trav-eqs) are critical points of the functional $J_{\omega}$ given by:

(1.5)

J_{\omega}(\psi,v)=\frac{1}{2}I_{\omega}(\psi,v)-K(\psi,v),

where the functionals $I_{\omega}$ and $G$ are defined on the space $X=H^{2}(\mathbb{R})\times H^{2}(\mathbb{R})$ by

(1.6)

I_{\omega}(\psi,v)=I_{1}(\psi,v)+I_{2,{\omega}}(\psi,v),

and

(1.7)

K(\psi,v)=\int_{\mathbb{R}}F(\psi,\psi^{\prime},v,v^{\prime})\,dx,

with

\displaystyle I_{1}(\psi,v)

\displaystyle=

\displaystyle\int_{\mathbb{R}}\left[\psi^{2}-c(\psi^{\prime})^{2}+c_{2}(\psi^{\prime\prime})^{2}+v^{2}-a(v^{\prime})^{2}+a_{2}(v^{\prime\prime})^{2}\right]dx,

and

\displaystyle I_{2}(\psi,v)

\displaystyle=

\displaystyle\int_{\mathbb{R}}\left(\psi-b\psi^{\prime\prime}+b_{2}\psi^{(iv)}\right)v\,dx=\int_{\mathbb{R}}\left(\psi v+b\psi^{\prime}v^{\prime}+b_{2}v^{\prime\prime}\psi^{\prime\prime}\right)\,dx,

where $I_{2,\omega}=-2\omega I_{2}$ . Before we go further, from the assumptions we observe

K^{\prime}(\psi,v)=(G_{1}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime}),G_{2}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime}))^{t}.

Hereafter, we will say that weak solutions for (LABEL:trav-eqs) are critical points of the functional $J_{\omega}$ . Now, we set

(1.8)

P_{\omega}(\psi,v)=\left<J^{\prime}_{\omega}(\psi,v),(\psi,v)\right>=I_{\omega}(\psi,v)-N(\psi,v),

and

(1.9)

N(\psi,v)=\left<K^{\prime}(\psi,v),(\psi,v)\right>.

From this, we consider the manifold $\mathcal{M}_{\omega}\subset H^{2}(\mathbb{R})\times H^{2}(\mathbb{R})$ given by

(1.10)

\mathcal{M}_{\omega}=\{(\psi,v)\in H^{2}(\mathbb{R})\times H^{2}(\mathbb{R}):\ P_{\omega}(\psi,v)=0\},

and define the number

(1.11)

S(\omega)=\inf\{J_{\omega}(\psi,v):(\psi,v)\in{\mathcal{M}}_{\omega}\}.

Now, we state the assumptions on the nonlinear part $F$ in terms of the function

G(w)=w\cdot\nabla F(w),\quad\text{for}\quad w\in\mathbb{R}^{4}.

As done by Esfahani-Levandosky in [12], we will consider:

(a)

There exist $p>0$ such that for $w\cdot\nabla F(w)\geq(p+2)G(w)$ for $w\in\mathbb{R}^{4}$ .
(b)

There exist $0<q_{1}\leq q_{2}<\infty$ and $C>0$ such that for $w\in\mathbb{R}^{4}$ ,

$|D^{2}F(w)|\leq C(|w|^{q_{1}}+|w|^{q_{2}}).$
(c)

There exist $u,v\in H^{2}(\mathbb{R})$ such that

$\int_{\mathbb{R}}F(u,\partial_{x}u,v,\partial_{x}v)\,dx>0.$

With these previous notations in hand, traveling-wave solutions are established using the concentration-compactness principle by P.-L. Lions [16, 17]. So, the main result of our work can be read as follows.

Theorem 1.1.

(Existence of traveling waves). Let $0<|w|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}$ and the function $F$ satisfying items (a), (b) and (c). Given a minimizing sequence $(\psi_{n},v_{n})_{n}$ of $S(\omega)$ , there exist a subsequence $\left(\psi_{n_{k}},v_{n_{k}}\right)_{k}$ , a sequence of points $y_{k}\in\mathbb{R}$ and $(\psi_{0},v_{0})\in X\setminus\{0\}$ such that

(\psi_{n_{k}}(.+y_{k}),v_{n_{k}}(.+y_{k}))\rightarrow(\psi,v)\quad\text{in}\quad X

and $J_{\omega}(\psi_{0},v_{0})=S(\omega)$ . In other words, $(\psi_{0},v_{0})$ is a minimizer for $S(\omega)$ .

The second part of this work explores the numerical investigation of traveling-wave solutions for the generalized Boussinesq system (LABEL:1bbl), also a topic not previously addressed in the literature. Spectral numerical solvers are introduced to approximate these steady solutions for a given wave velocity and model parameters, considering both homogeneous and non-homogeneous nonlinearities $G_{1}$ and $G_{2}$ . In doing so, we validate the theoretical results and successfully compute some of these solutions within the parameter regimes and velocity ranges predicted by the theory developed in this paper. Furthermore, we present numerical experiments that go beyond the theoretical framework, investigating cases where the wave velocity falls outside the predicted range of existence. Our findings suggest that the existence of traveling-wave solutions to the system (LABEL:1bbl) is influenced by additional parameters, such as the power of the nonlinearities.

1.3. Outline

This paper is organized as follows. In Section 2, we present the preliminaries concerning the existence of solitons (traveling wave solutions of finite energy) for the higher-order Boussinesq system, employing the concentration-compactness principle, which fully characterizes the convergence of positive measures and provides a compact local embedding result. In Section 3, we introduce iterative numerical schemes called Fourier series-based method to approximate the solitons of the Boussinesq system (LABEL:1bbl) giving a numerical verification of our main result.

2. Existence of solitary waves for $b=d$ and $b_{2}=d_{2}$

In this section, we prove the existence of traveling waves for the generalized Boussinesq system (LABEL:1bbl). Based on the assumptions of Esfahani and Levandosky [12, Lemmas 2.5 and 2.6], we can directly extend these lemmas as follows:

Lemma 2.1.

Under the assumptions on $F$ , we have ,for $w,\tilde{w}\in\mathbb{R}^{2}$ , that

(i)

$G(w,\tilde{w})\geq(p+2)F(w,\tilde{w})$ .
(ii)

$F(\alpha(w,\tilde{w}))\geq\alpha^{p+2}F(w,\tilde{w})$ with $\alpha\geq 1$ and $F(\alpha(w,\tilde{w}))\leq\alpha^{p+2}F(w,\tilde{w})$ with $0<\alpha\leq 1$ .
(iii)

$|F(w,\tilde{w})|+|G(w,\tilde{w})|+|\left<(w,\tilde{w}),G(w,\tilde{w})\right>|\leq C(|(w,\tilde{w})|^{q_{1}+2}+|(w,\tilde{w})|^{q_{2}+2})$ .
(iv)

$N(\alpha w)\geq\alpha^{p+2}N(w)$ with $\alpha\geq 1$ and $N(\alpha w)\leq\alpha^{p+2}N(w)$ with $0<\alpha\leq 1$ .
(v)

$N(w)\geq(p+2)K(w)$ .
(vi)

$\left<N^{\prime}(w),w\right>\geq(p+2)N(w)$ .
(vii)

$|N(w)|+|K(w)|+|\left<N^{\prime}(w),w\right>|\leq C(|w|^{q_{1}+2}+|w|^{q_{2}+2})$ .

We note that under the assumption of $(p+2)$ -homogeneity on $F$ , we already have that

G(q,r,s,t)=qF_{q}(q,r,s,t)+rF_{q}(q,r,s,t)+sF_{s}(q,r,s,t)+tF_{t}(q,r,s,t)=(p+2)F(q,r,s,t).

Also, taking into account Esfahani-Levandosky’s work, we have the following examples of functional $F:\mathbb{R}^{4}\to\mathbb{R}$ that satisfy the previous assumptions, namely

a)

$F(u,v)=F_{1}(u)+F_{1}(v)$ , where

$F_{1}(u)=\frac{|u|^{q+2}}{q+2}+\frac{|u|^{p+2}}{p+2},$

with $0<p<q$ ;
b)

$F(u,v)=F_{1}(u)+F_{1}(v)$ , where $F_{1}$ is defined as

$F_{1}(u)=\sum_{j}^{m}a_{j}|u|^{q_{j}+2}-\sum_{k}^{n}b_{k}|u|^{p_{k}+2},$

with $a_{j},b_{k}>0$ and $0<p_{k}<q_{j}$ for all $j,k\in\mathbb{N}$ ;
c)

$F(u,\partial_{x}u,v,\partial_{x}v)=F_{1}(u,\partial_{x}u)+F_{1}(v,\partial_{x}v)$ , where $F_{1}=F_{2}+F_{3}$ with $F_{2}$ being a $(p+1)$ -homogeneous function and $F_{3}$ being a $(q+1)$ -homogeneous function for $0<p<q$ .

With this in hand, our first lemma ensures some boundedness for the quantity (1.6).

Lemma 2.2.

For $0<|w|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}$ , we have that

i)

the functional $I_{\omega}$ is nonnegative and there are positive constants $M_{1}(\omega,a,a_{2},b,b_{2},c,c_{2})$ and $M_{2}(\omega,a,a_{2},b,b_{2},c,c_{2})$ such that

(2.1) $M_{1}\|(\psi,v)\|_{X}^{2}\leq I_{\omega}(\psi,v)\leq M_{2}\|(\psi,v)\|_{X}^{2}.$
ii)

$S(\omega)$ exists, is positive and

(2.2) $S(\omega)=\inf\{J_{\omega}(\psi,v):P_{\omega}(\psi,v)\leq 0\},$

where $J_{\omega}$ is defined in (1.5) and $P_{\omega}$ is given by (1.8).

Proof.

i) Using the definition of $I_{\omega}$ given by (1.6), we see directly that

	$\displaystyle I_{\omega}(\psi,v)\leq$	$\displaystyle\int_{\mathbb{R}}\left[(1+\|\omega\|)\psi^{2}+\left(\|c\|+b\|\omega\|\right)(\psi^{\prime})^{2}+(1+\|\omega\|)v^{2}+\left(\|a\|+b\|\omega\|\right)(v^{\prime})^{2}\right.$
		$\displaystyle\left.+\left(a_{2}+b_{2}\|\omega\|\right)(\psi^{\prime\prime})^{2}+\left(c_{2}+b_{2}\|\omega\|\right)(v^{\prime\prime})^{2}\right]dx$
	$\displaystyle\leq$	$\displaystyle\max\left(1+\|\omega\|,\|c\|+b\|\omega\|,\|a\|+b\|\omega\|,a_{2}+b_{2}\|\omega\|,c_{2}+b_{2}\|\omega\|)\right)\\|(\psi,v)\\|^{2}_{X}.$

On the other hand, from Young inequality, we also have that

	$\displaystyle I_{\omega}(\psi,v)\geq$	$\displaystyle\int_{\mathbb{R}}\left[(1-\|\omega\|)\psi^{2}+\left(-c-b\|\omega\|\right)(\psi^{\prime})^{2}+(1-\|\omega\|)v^{2}+\left(-a-b\|\omega\|\right)(v^{\prime})^{2}\right.$
		$\displaystyle\left.+\left(a_{2}-b_{2}\|\omega\|\right)(\psi^{\prime\prime})^{2}+\left(c_{2}-b_{2}\|\omega\|\right)(v^{\prime\prime})^{2}\right]dx$
	$\displaystyle\geq$	$\displaystyle\min\left(1-\|\omega\|,-c-b\|\omega\|a,-a-b\|\omega\|,a_{2}-b_{2}\|\omega\|,c_{2}-b_{2}\|\omega\|)\right)\\|(\psi,v)\\|^{2}_{X},$

showing that the inequality (2.1) holds.

ii) Let $(\psi,v)\in{\mathcal{M}}_{\omega}$ , given by (1.10). Then we have that $I_{\omega}(\psi,v)=N(\psi,v)\geq 0$ . Using the properties of $N$ , see Lemma 2.1 item (vii) and the definition (1.9), the embedding $H^{2}(\mathbb{R})\hookrightarrow L^{q}(\mathbb{R})$ , for all $q\geq 1$ , and the Young’s inequality, we conclude that

(2.3)

\begin{split}|N(\psi,v)|&\leq M\left(\|\psi\|^{q_{1}+2}_{L^{q_{1}+2}(\mathbb{R})}+\|v\|^{q_{1}+2}_{L^{q_{1}+2}(\mathbb{R})}+\|\psi\|^{q_{2}+2}_{L^{q_{2}+2}(\mathbb{R})}+\|v\|^{q_{2}+2}_{L^{q_{2}+2}(\mathbb{R})}\right)\\ &\leq M\left(\|(\psi,v)\|_{X}^{q_{1}+2}+\|(\psi,v)\|_{X}^{q_{2}+2}\right)\\ &\leq 2M\|(\psi,v)\|_{X}^{q_{3}+2},\end{split}

where $q_{3}=q_{1}$ or $q_{3}=q_{2}$ . On the other hand, using (2.3) and (2.1), we get

0\leq I_{\omega}(\psi,v)=N(\psi,v)\leq 2M\|(\psi,v)\|_{X}^{q_{3}+2}\leq\frac{2M}{\sqrt{M_{1}}}\left(I_{\omega}(\psi,v)\right)^{\frac{q_{3}+2}{2}},

which implies that

(2.4)

I_{\omega}(\psi,v)\geq M_{2}>0,

where $M_{2}:=M_{2}(q_{3})$ depends of $q_{3},M$ and $M1$ . Now, from Lemma 2.1 item (iv) and (2.4), we have that

	$\displaystyle J_{\omega}(\psi,v)$	$\displaystyle=\frac{1}{2}I_{\omega}(\psi,v)-K(\psi,v)$
		$\displaystyle\geq\frac{1}{2}I_{\omega}(\psi,v)-\frac{1}{p+2}N(\psi,v)$
		$\displaystyle\geq\frac{1}{2}I_{\omega}(\psi,v)-\left(\frac{1}{p+2}\right)I_{\omega}(\psi,v)$
		$\displaystyle\geq\left(\frac{p}{2(p+2)}\right)I_{\omega}(\psi,v)\geq M_{3},$

with $M_{3}:=M_{3}(p,q_{3})>0$ depending of $q_{3},M,M_{1}$ and $p$ , where $K(\psi,v)$ is given by (1.7). Here, we are using that $P_{\omega}(\psi,v)=0$ . So, $S(\omega)$ given by (1.11) is positive.

Now, we set

\widetilde{S}(\omega)=\inf\{J_{\omega}(\psi,v):P_{\omega}(\psi,v)\leq 0\}.

Then, we have that $\widetilde{S}(\omega)\leq S(\omega)$ . Now, for $(\psi,v)\in X$ such that $P_{\omega}(\psi,v)\leq 0$ , we define the function $R(\alpha)=P_{\omega}(\alpha(\psi,v))$ . Thus, from Lemma 2.1 item (iv), we see that

R(\alpha)=P_{\omega}(\alpha(\psi,v))\geq\alpha^{2}\left(I_{\omega}(\psi,v)-\alpha^{r}N(\psi,v)\right),

for $0<\alpha<1$ . This implies that $R(\alpha)>0$ for $\alpha>0$ , but small enough. In other words, there is $(\widetilde{\psi},\widetilde{v})=\alpha_{0}(\psi,v)$ with $0<\alpha_{0}<1$ such that $R(\alpha_{0})=P_{\omega}(\widetilde{\psi},\widetilde{v})=0$ . Therefore, from this fact, we have that $S(\omega)\leq\widetilde{S}(\omega)$ , showing the (2.2) and the lemma is proved. ∎

In the next result, we establish that minimizers for $S(\omega)$ correspond to weak solutions for the higher order Boussinesq system.

Theorem 2.3.

Let $(\psi_{0},v_{0})\in X$ be such that $P_{\omega}(\psi_{0},v_{0})=0$ and $J_{\omega}(\psi_{0},v_{0})=S(\omega)$ . Then $(\psi_{0},v_{0})$ is a weak solution of (LABEL:trav-eqs).

Proof.

From the Lagrange multiplier theorem, there exists $\lambda\in\mathbb{R}$ such that

J^{\prime}_{\omega}(\psi_{0},v_{0})=\lambda P^{\prime}_{\omega}(\psi_{0},v_{0}).

On the other hand,

	$\displaystyle\left<P^{\prime}_{\omega}(\psi_{0},v_{0}),(\psi_{0},v_{0})\right>$	$\displaystyle=2\left<I^{\prime}_{\omega}(\psi_{0},v_{0}),(\psi_{0},v_{0})\right>-\left<N^{\prime}(\psi_{0},v_{0}),(\psi_{0},v_{0})\right>$
		$\displaystyle=2I_{\omega}(\psi_{0},v_{0})-\left<N^{\prime}(\psi_{0},v_{0}),(\psi_{0},v_{0})\right>,$
		$\displaystyle\leq 2I_{\omega}(\psi_{0},v_{0})-(p+2)N(\psi_{0},v_{0}),$
		$\displaystyle\leq-pI_{\omega}(\psi_{0},v_{0})<0,$

where in the first inequality we have used Lemma 2.1 item (iv) and in the third inequality that $I_{\omega}(\psi,v)=N(\psi,v)$ . So, we must have $\lambda=0$ , since $P_{\omega}(\psi_{0},v_{0})=\left<J^{\prime}_{\omega}(\psi_{0},v_{0}),(\psi_{0},v_{0})\right>=0$ , archiving the result. ∎

Remark 2.4.

For $0<|w|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}$ , we note that,

\begin{gathered}I_{\omega}(\psi,v)=\int_{\mathbb{R}}\left[(\psi-\omega v)^{2}+\left(\sqrt{|c|}\psi^{\prime}-(b\omega/\sqrt{|c|})v^{\prime}\right)^{2}+\left(1-|\omega|^{2}\right)\psi^{2}+\left(|a|-\left(b^{2}\omega^{2}/|c|\right)\right)\left(v^{\prime}\right)^{2}\right.\\ \left.+c_{2}\left(\psi^{\prime\prime}-\frac{\omega b_{2}}{c_{2}}v^{\prime\prime}\right)^{2}+\left(a_{2}-\frac{\omega^{2}b_{2}^{2}}{c_{2}}\right)(v^{\prime\prime})^{2}\right]dx\geq 0\end{gathered}

and

\begin{gathered}I_{\omega}(\psi,v)=\int_{\mathbb{R}}\left[(v-\omega\psi)^{2}+\left(\sqrt{|c|}v^{\prime}-(b\omega/\sqrt{|c|})\psi^{\prime}\right)^{2}+\left(1-|\omega|^{2}\right)v^{2}+\left(|a|-\left(b^{2}\omega^{2}/|c|\right)\right)\left(\psi^{\prime}\right)^{2}\right.\\ \left.+c_{2}\left(v^{\prime\prime}-\frac{\omega b_{2}}{c_{2}}\psi^{\prime\prime}\right)^{2}+\left(a_{2}-\frac{\omega^{2}b_{2}^{2}}{c_{2}}\right)(\psi^{\prime\prime})^{2}\right]dx\geq 0\end{gathered}

Before going further, let us give an important property of the minimizing sequences for $S(\omega)$ .

Lemma 2.5.

The minimizing sequences for $S(\omega)$ are bounded in $X$ .

Proof.

Let $(\psi_{n},v_{n})\in X$ be such that $I_{\omega}(\psi_{n},v_{n})=N(\psi_{n},v_{n})$ and that $J_{\omega}(\psi_{n},v_{n})=S(\omega)+o(1)$ , as $n\to\infty$ . Now, we note that

	$\displaystyle\frac{1}{2}I_{\omega}(\psi_{n},v_{n})$	$\displaystyle=J_{\omega}(\psi_{n},v_{n})+K(\psi_{n},v_{n})$
		$\displaystyle\leq J_{\omega}(\psi_{n},v_{n})+\frac{1}{p+2}N(\psi_{n},v_{n})$
		$\displaystyle\leq S(\omega)+\frac{1}{p+2}I_{\omega}(\psi_{n},v_{n})+o(1),$

which implies that $||(\psi_{n},v_{n})||_{X}$ is bounded, since

\left(\frac{p}{2(p+2)}\right)I_{\omega}(\psi_{n},v_{n})\leq S(\omega)+o(1).

So, consequently, we may assume that the sequence (or a subsequence of) $\{I_{\omega}(\psi_{n},v_{n})\}_{n}$ converges to some positive number $L$ , showing the lemma. ∎

Classically, to establish the existence of traveling-wave solutions, we will use the Lion’s concentration-compactness principle [16, 17]. We will apply this principle to the measure defined by the density $\rho$ given by

(2.5)

\rho(\psi,v)=\psi^{2}-c(\psi^{\prime})^{2}+c_{2}(\psi^{\prime\prime})^{2}+v^{2}-a(v^{\prime})^{2}+a_{2}(v^{\prime\prime})^{2}-2\omega\left(\psi v+b\psi^{\prime}v^{\prime}+b_{2}v^{\prime\prime}\psi^{\prime\prime}\right).

We note from the proof of inequality (2.1) that

(2.6)

M_{1}\sigma(\psi,v)\leq\rho(\psi,v)\leq M_{2}\sigma(\psi,v),

where $\sigma$ is giving by

\sigma(\psi,v)=\psi^{2}+v^{2}+(\psi^{\prime})^{2}+(v^{\prime})^{2}+(\psi^{\prime\prime})^{2}+(v^{\prime\prime})^{2}.

If we had a minimizing sequence $(\psi_{n},v_{n})_{n}\subset X$ for $S(\omega)$ , meaning that $P(\psi_{n},v_{n})=0$ and $J_{\omega}(\psi_{n},v_{n})\to S(\omega)$ , we consider the sequence of measures $\{\nu_{n}\}_{n}$ given by

\nu_{n}(A)=\int_{A}\rho(\psi_{n},v_{n})\,dx,

which is such that $\nu_{n}(\mathbb{R})\to L$ , according with the Lemma 2.5. Now, from Lion’s Concentration-compactness principle, there exists a subsequence of $\{\nu_{n}\}_{n}$ (which will be denoted with the same index) such that one of the following three conditions holds:

(1) Compactness: There exists a sequence $\{x_{n}\}_{n}\subset\mathbb{R}$ such that for any $\gamma>0$ there exists a radius $R>0$ such that

\int_{B_{R}(x_{n})}d\nu_{n}\geq L-\gamma,

for all $n$ .

(2)Vanishing: For all $R>0$ there holds:

\lim\limits_{n\rightarrow\infty}\left(\sup\limits_{y\in\mathbb{R}}\int_{\left|x-y\right|\leq R}d\nu_{n}\right)=0.

(3) Dichotomy: There exists $\theta\in\left(0,L\right)$ such that for any $\gamma>0$ , there exist a positive number $R$ and a sequence $\{x_{n}\}_{n}\subset\mathbb{R}$ with the following property: Given $R^{\prime}>R$ , there are nonnegative measures $\nu_{n,1}$ and $\nu_{n,2}$ such that:

(a)

$0\leq\nu_{n,1}+\nu_{n,2}\leq\nu_{n}$ ;
(b)

$supp(\nu_{n,1})\subset B_{R}(x_{n})$ and $supp(\nu_{n,2})\subset\mathbb{R}\setminus B_{R^{\prime}}(x_{n})$ ;
(c)

$\limsup\limits_{n\rightarrow\infty}\left(\left|\theta-\int_{\mathbb{R}}d\nu_{n,1}\right|+\left|(L-\theta)-\int_{\mathbb{R}}d\nu_{n,2}\right|\right)\leq\gamma$ .

The first step is to rule out vanishing.

Lemma 2.6.

Vanishing is impossible.

Proof.

We argue by contradiction. Assuming that vanishing is true, so for $R=1$ , we have that,

\lim\limits_{n\rightarrow\infty}\sup\limits_{y\in\mathbb{R}}\int_{B_{1}(y)}\rho(\psi_{n},v_{n})\,dx=0.

Thus, given $\epsilon>0$ , there is $n_{0}\in\mathbb{N}$ such that for $n\geq n_{0}$ we have that

\sup\limits_{y\in\mathbb{R}}\int_{B_{1}(y)}\rho(\psi_{n},v_{n})\,dx<\epsilon.

Now, we recall that $H^{1}(\mathbb{R})\hookrightarrow C_{b}(\mathbb{R})$ , so, we have that

\int_{B_{1}(y)}\left|\psi_{n}\right|^{p+2}\,dx\leq\left(\int_{B_{1}(y)}\left|\psi_{n}\right|^{2}\,dx\right)^{\frac{1}{2}}\left(\int_{B_{1}(y)}\left|\psi_{n}\right|^{2\left(p+1\right)}\right)^{\frac{1}{2}}\,dx.

We can cover $\mathbb{R}$ with intervals of the form $[k,k+1]$ , where $k$ is an integer, ensuring that any point in $\mathbb{R}$ is contained in at most two intervals. By summing over these intervals and applying the inequality above, we obtain the following inequality:

(2.7)

\begin{split}\int_{\mathbb{R}}(\left|\psi_{n}\right|^{p+2}+\left|v_{n}\right|^{p+2})\,dx&\leq 2\sup\limits_{y\in\mathbb{R}}\left(\int_{B_{1}(y)}\rho(\psi_{n},v_{n})\,dx\right)^{\frac{1}{2}}\left(\left\|\psi_{n}\right\|^{p+1}_{L^{2}\left(\mathbb{R}\right)}+\left\|v_{n}\right\|^{p+1}_{L^{2}\left(\mathbb{R}\right)}\right)\\ &\leq 2C\sup\limits_{y\in\mathbb{R}}\left(\int_{B_{1}(y)}\rho(\psi_{n},v_{n})\,dx\right)^{\frac{1}{2}}\left(\left\|\psi_{n}\right\|^{p+1}_{H^{1}(\mathbb{R})}+\left\|v_{n}\right\|^{p+1}_{H^{1}(\mathbb{R})}\right).\end{split}

A similar argument gives us that

(2.8)

\begin{split}\int_{\mathbb{R}}(\left|\partial_{x}\psi_{n}\right|^{p+2}+&\left|\partial_{x}v_{n}\right|^{p+2})\,dx\\ &\leq 2C\sup\limits_{y\in R}\left(\int_{B_{1}(y)}\rho(\psi_{n},v_{n})\,dx\right)^{\frac{1}{2}}\left(\left\|\partial_{x}\psi_{n}\right\|^{2\left(p+1\right)}_{H^{1}(\mathbb{R})}+\left\|\partial_{x}v_{n}\right\|^{2\left(p+1\right)}_{H^{1}(\mathbb{R})}\right).\end{split}

In other words, thanks (2.7) and (2.8), we have that $\psi_{n},v_{n},(\psi_{n})_{x},(v_{n})_{x},(\psi_{n})_{xx}$ and $(v_{n})_{xx}$ goes to $0$ in $L^{q}(\mathbb{R})$ , for $q>1$ . From this, we conclude that

\lim_{n\to\infty}K(\psi_{n},v_{n})=\lim_{n\to\infty}N(\psi_{n},v_{n})=0,

meaning that $\lim_{n\to\infty}I_{\omega}(\psi_{n},v_{n})=0$ due to the fact that $P(\psi_{n},v_{n})=0$ . Moreover, we also have that

S(\omega)=\lim_{n\to\infty}J_{\omega}(\psi_{n},v_{n})=0,

which is a contradiction. In other words, vanishing is ruled out, and the Lemma 2.6 is shown. ∎

Now, we are interested in ruling out dichotomy. The first step is to show that the sequence of measures $\{u_{n}\}_{n}$ associated with a minimizer sequence $\{(\psi_{n},v_{n})\}_{n}$ appropriately splits into two sequences of measures $\{\nu_{n,1}\}_{n}$ and $\{\nu_{n,2}\}_{n}$ that have disjoint supports. In this case, we can choose a sequence $\gamma_{n}\rightarrow 0$ and the corresponding sequence $R_{n}\rightarrow\infty$ , such that, passing to a subsequence with the same index, we can assume:

(2.9)

supp(\nu_{n,1})\subset B_{R_{n}}(x_{0}),\quad supp(\nu_{n,2})\subset\mathbb{R}\setminus B_{2R_{n}}(x_{0})

and

(2.10)

\limsup\limits_{n\rightarrow\infty}\left(\left|\theta-\int_{\mathbb{R}}d\nu_{n,1}\right|+\left|(L-\theta)-\int_{\mathbb{R}}d\nu_{n,2}\right|\right)=0.

Now, we see that conditions (2.9) and (2.10) imply that

(2.11)

\limsup\limits_{n\rightarrow\infty}\left(\int_{A(n)}\rho(\psi_{n},v_{n})\,dx\right)=0,

where $A(n)$ is the annulus $A(n)=B_{2R_{n}}(x_{0})\setminus B_{R_{n}}(x_{0})$ . In fact,

	$\displaystyle\int_{A(n)}\rho(\psi_{n},v_{n})\,dx=$	$\displaystyle\left\{\int_{\mathbb{R}}-\int_{B_{R_{n}}(x_{0})}-\int_{\mathbb{R}\setminus B_{2R_{n}}(x_{0})}\right\}\rho(\psi_{n},v_{n})\,dx$
	$\displaystyle=$	$\displaystyle\int_{\mathbb{R}}\rho(\psi_{n},v_{n})\,dx-L+\theta-\int_{B_{R_{n}}(x_{0})}\rho(\psi_{n},v_{n})\,dx+\left(L-\theta\right)$
		$\displaystyle-\int_{\mathbb{R}\setminus B_{2R_{n}}(x_{0})}\rho(\psi_{n},v_{n})\,dx$
	$\displaystyle\leq$	$\displaystyle\left(\int_{\mathbb{R}}\rho(\psi_{n},v_{n})\,dx-L\right)+\left\|\theta-\int_{\mathbb{R}}d\nu_{n,1}\right\|+\left\|(L-\theta)-\int_{\mathbb{R}}d\nu_{n,2}\right\|.$

Thanks to the Lemma 2.5 we have that

\int_{\mathbb{R}}\rho(\psi_{n},v_{n})\,dx\rightarrow L,

when $n\rightarrow\infty$ . This convergence, together with the conditions (2.9) and (2.10), gives that (2.11) holds.

Finally, to prove the next lemma, we aim to decompose the energy density into two nontrivial, well-separated parts, with one part remaining localized (up to a translation). More precisely, we seek a decomposition $\psi_{n}=\psi_{n,1}+\psi_{n,2}$ , where $\psi_{n,1}$ is supported in $B_{R_{n}}(x_{0})$ and $\psi_{n,2}$ is supported in $\mathbb{R}\setminus B_{2R_{n}}(x_{0})$ . To achieve this, we fix a function $\phi\in C^{\infty}_{0}(\mathbb{R},\mathbb{R}^{+})$ such that $supp(\phi)\subset(-2,2)$ and $\phi\equiv 1\text{ on }(-1,1)$ , and we define:

\begin{cases}\psi_{n,1}=\psi_{n}\phi_{n},\quad\text{and}\quad\psi_{n,2}=\psi_{n}(1-\phi_{n}),\\ v_{n,1}=v_{n}\phi_{n}\quad\text{and}\quad v_{n,2}=v_{n}(1-\phi_{n}),\end{cases}

where $\phi_{n}$ is given by

\phi_{n}(x)=\phi\left(\frac{x-x_{n}}{R_{n}}\right).

Using the following fact

\int_{A(n)}\left(|\partial^{i}_{x}\psi_{n})^{2}+|\partial^{i}_{x}v_{n})^{2}\right)\,dx=o(1),\ \ n\to\infty,

for $0\leq i\leq 2$ , the splitting of a minimizing sequence gives us the following:

	$\displaystyle I_{\omega}(\psi_{n},v_{n})$	$\displaystyle=I_{\omega}(\psi_{n,1},v_{n,1})+I_{\omega}(\psi_{n,2},v_{n,2})+o(1),$
	$\displaystyle K(\psi_{n},v_{n})$	$\displaystyle=K(\psi_{n,1},v_{n,1})+K(\psi_{n,2},v_{n,2})+o(1),$
	$\displaystyle J_{\omega}(\psi_{n},v_{n})$	$\displaystyle=J_{\omega}(\psi_{n,1},v_{n,1})+J_{\omega}(\psi_{n,2},v_{n,2})+o(1),$
	$\displaystyle P_{\omega}(\psi_{n},v_{n})$	$\displaystyle=P_{\omega}(\psi_{n,1},v_{n,1})+P_{\omega}(\psi_{n,2},v_{n,2})+o(1),$

and

\displaystyle N(\psi_{n},v_{n})

\displaystyle=N(\psi_{n,1},v_{n,1})+N(\psi_{n,2},v_{n,2})+o(1).

With this in hand, we will prove that dichotomy does not hold.

Lemma 2.7.

Dichotomy is not possible.

Proof.

First, we need to note that

\lim_{n\to\infty}I_{\omega}(\psi_{n,1},v_{n,1})=L_{1}\geq 0\quad\text{ and }\quad\ \ \lim_{n\to\infty}I_{\omega}(\psi_{n,2},v_{n,2})=L-L_{1}=L_{2}\geq 0.

Let $\lambda_{n,1}=P_{\omega}(\psi_{n,1},v_{n,1})$ and $\lambda_{n,2}=P_{\omega}(\psi_{n,2},v_{n,2})$ . Now, we set

\lambda_{1}=\lim\limits_{n\rightarrow\infty}\lambda_{n,1}\quad\text{and}\quad\lambda_{2}=\lim\limits_{n\rightarrow\infty}\lambda_{n,2}.

We first consider the case $\lambda_{1}=0$ and $\lambda_{2}=0$ . Using that $I_{\omega}$ is coercive, we have that $L_{1},L_{2}>0$ . In particular, we have that

\lim_{n\to\infty}N(\psi_{n,1},v_{n,1})=L_{1}>0,\quad\text{and}\quad\lim_{n\to\infty}N(\psi_{n,2},v_{n,2})=L_{2}>0,

Suppose that for some subsequence of $\{(\psi_{n,1},v_{n,1})\}$ , still denoted by the same index, we had that $P_{\omega}(\psi_{n,1},v_{n,1})>0$ , then from Lemma 2.1, we have that

	$\displaystyle P_{\omega}(\alpha(\psi_{n,1},v_{n,1}))$	$\displaystyle\leq\alpha^{2}N(\psi_{n,1},v_{n,1})\left(\frac{I_{\omega}(\psi_{n,1},v_{n,1})}{N(\psi_{n,1},v_{n,1})}-\alpha^{p}\right)$
		$\displaystyle\leq\alpha^{2}N(\psi_{n,1},v_{n,1})\left(1+o(1)-\alpha^{p}\right)<0,$

for $\alpha>1$ . Thus, there is $(\alpha_{n})_{n}$ with $\alpha_{n}\to 1^{+}$ such that $P_{\omega}(\alpha_{n}(\psi_{n,1},v_{n,1}))=0$ . Now, from the splitting result, we have that

	$\displaystyle J_{\omega}(\psi_{n},v_{n})=$	$\displaystyle\frac{1}{2}I_{\omega}(\psi_{n,1},v_{n,1})-K(\psi_{n,1},v_{n,1})+J_{\omega}(\psi_{n,2},v_{n,2})+o(1),$
	$\displaystyle=$	$\displaystyle\frac{1}{\alpha_{n}^{2}}\left(\frac{1}{2}I_{\omega}(\alpha_{n}(\psi_{n,1},v_{n,1}))-K(\alpha_{n}(\psi_{n,1},v_{n,1}))\right)$
		$\displaystyle+\left(\frac{1}{\alpha_{n}^{2}}K(\alpha_{n}(\psi_{n,1},v_{n,1}))-K(\psi_{n,1},v_{n,1})\right)+J_{\omega}(\psi_{n,2},v_{n,2})+o(1),$
	$\displaystyle\geq$	$\displaystyle\frac{1}{\alpha_{n}^{2}}S(\omega)+\frac{1}{\alpha_{n}^{2}}\left(K(\alpha_{n}(\psi_{n,1},v_{n,1}))-K(\psi_{n,1},v_{n,1})\right)+J_{\omega}(\psi_{n,2},v_{n,2})+o(1).$

Taking limit as $n\to\infty$ , we conclude that

0\geq\lim_{n\to\infty}J_{\omega}(\psi_{n,2},v_{n,2})\geq\lim_{n\to\infty}\left(\frac{1}{2}I_{\omega}(\psi_{n,2},v_{n,2})-\frac{1}{p+2}N(\psi_{n,2},v_{n,2})\right)=\left(\frac{p}{2(p+2)}\right)L_{2}.

which is a contradiction since $L_{2}>0$ . So, we already have that $P_{\omega}(\psi_{n,i},v_{n,i})\leq 0$ for $i=1,2$ . On the other hand, Lemma 2.2 item ii) gives that $J_{\omega}(\psi_{n,i},v_{n,i})\geq S(\omega)$ , for $i=1,2$ , which ensures us, again, a contradiction $S(\omega)\leq 0$ due to the splitting result.

Finally, we assume that $\lambda_{1}>0$ and $\lambda_{2}<0$ . So, for $n\in\mathbb{N}$ large enough, we have that $P_{\omega}(\psi_{n,1},v_{n,1})>0$ and $P_{\omega}(\psi_{n,2},v_{n,2})<0$ . Then, we see that

	$\displaystyle J_{\omega}(\psi_{n},v_{n})$	$\displaystyle=J_{\omega}(\psi_{n,1},v_{n,1})+J_{\omega}(\psi_{n,2},v_{n,2})+o(1),$
		$\displaystyle\geq J_{\omega}(\psi_{n,1},v_{n,1})+S(\omega)+o(1),$

which implies that

0\geq\lim_{n\to\infty}J_{\omega}(\psi_{n,1},v_{n,1})\geq\lim_{n\to\infty}\left(\frac{1}{2}I_{\omega}(\psi_{n,1},v_{n,1})-\frac{1}{p+2}N(\psi_{n,1},v_{n,1})\right)=\left(\frac{p}{2(p+2)}\right)L_{1}.

which is a contradiction with $L_{1}>0$ . In other words, we have ruled out Dichotomy, and Lemma 2.7 is proven. ∎

Now, we use the compactness property to determine the existence of non-trivial traveling waves for the generalized Boussinesq system in the cases $b=d$ and $b_{2}=d_{2}$ , that is, we are in a position to prove the main result of the work.

Proof of Theorem 1.1.

Let $(\psi_{0},v_{0})\in X$ be a weak limit of the bounded minimizing sequence $(\psi_{n},v_{n})_{n}$ of $\mathcal{I}_{\omega}$ ( $(\psi_{n},v_{n})\rightharpoonup(\psi_{0},v_{0})$ in $X$ ). From Lion’s concentration-compactness principle, after having ruled out dichotomy and vanishing, we have compactness property which gives the existence of a sequence $\left\{y_{k}\right\}_{k}\subset\mathbb{R}$ such that, for all $\epsilon>0$ there exists $R(\epsilon)>0$ satisfying

\int_{\left|x-y_{k}\right|<R(\epsilon)}\rho(\psi_{n},v_{n})\,dx\geq\int_{\mathbb{R}}\rho(\psi_{n},v_{n})\,dx-\epsilon.

The previous inequality is equivalent to the following one

\int_{\left|x\right|<R(\epsilon)}\rho(\tilde{\psi}_{n},\tilde{v}_{n})\,dx\geq\int_{\mathbb{R}}\rho(\tilde{\psi}_{n},\tilde{v}_{n})\,dx-\epsilon,

when translated to origin, where $\tilde{\eta}$ means $\tilde{\eta}(x)=\eta(x+y_{k})$ . In other words, we have that

\int_{\left|x\right|\geq R(\epsilon)}\rho(\tilde{\psi}_{n},\tilde{v}_{n})\,dx\leq\epsilon.

From the definition of $\rho$ in (2.5) and inequality (2.6), we get that

M_{1}\int_{\left|x\right|\geq R(\epsilon)}\left(\left(\partial^{j}_{x}\tilde{\psi}_{n}\right)^{2}+\left(\partial^{j}_{x}\tilde{v}_{n}\right)^{2}\right)\,dx\leq\int_{\left|x\right|\geq R(\epsilon)}\rho(\tilde{\psi}_{n},\tilde{v}_{n})\,dx\leq\epsilon.

From this fact, we conclude that

(2.12)

\displaystyle\int_{\mathbb{R}}\left(\partial^{i}_{x}\tilde{\psi}_{n}\right)^{2}\,dx

\displaystyle\leq\int_{\left|x\right|\leq R(\epsilon)}\left(\partial^{i}_{x}\tilde{\psi}_{n}\right)^{2}\,dx+\frac{\epsilon}{M_{1}},

and

(2.13)

\displaystyle\int_{\mathbb{R}}\left(\partial^{i}_{x}\tilde{v}_{n}\right)^{2}\,dx

\displaystyle\leq\int_{\left|x\right|\leq R(\epsilon)}\left(\partial^{i}_{x}\tilde{v}_{n}\right)^{2}\,dx+\frac{\epsilon}{M_{1}}.

Now, we will establish that

\partial^{i}_{x}\tilde{\psi}_{n}\rightarrow\partial^{i}_{x}\psi_{0},\ \ \partial^{i}_{x}\tilde{v}_{n}\rightarrow\partial^{i}_{x}v_{0}\ \ \mbox{in $L^{2}\left(\mathbb{R}\right)$, \quad\text{for $i=0,1,2$}. }

Observe that for any bounded open interval $I$ , and any $r>1$ , we have that the embedding $W^{1,r}(I)\hookrightarrow C^{\alpha}(\bar{I})$ is compact for $\alpha\in\left[0,1-\frac{n}{r}\right)$ , and so the embedding $W^{k,r}(I)\hookrightarrow L^{q}(I)$ , for $q\geq 1$ , is valid, since $C^{\alpha}(I)\hookrightarrow L^{q}(I)$ for $q\geq 1$ and for $k\geq 1$ the operators $W^{k,r}(I)\hookrightarrow W^{1,r}(I)$ are bounded. In particular, we have for $0\leq i\leq 2$ that

(2.14)

\displaystyle\partial_{x}^{i}\tilde{\psi}_{n}\rightharpoonup\partial_{x}^{i}\psi_{0}

\displaystyle,\ \ \mbox{in}\ \ H^{2-i}(\mathbb{R}),

and

(2.15)

\displaystyle\partial_{x}^{i}\tilde{v}_{n}\rightharpoonup\partial_{x}^{i}v_{0}

\displaystyle,\ \ \mbox{in}\ \ H_{loc}^{1-i}(\mathbb{R}).

From the convergence (2.14), using Fatou’s Theorem and thanks the inequality (2.12), we ensure that

	$\displaystyle\left\\|\partial^{i}_{x}\psi_{0}\right\\|^{2}_{L^{2}(\mathbb{R})}$	$\displaystyle\leq\liminf\limits_{n\to\infty}\left\\|\partial^{i}_{x}\tilde{\psi}_{n}\right\\|^{2}_{L^{2}(\mathbb{R})}$
		$\displaystyle\leq\liminf\limits_{n\to\infty}\left(\int_{\left\|x\right\|\leq R(\epsilon)}\left(\partial^{i}_{x}\tilde{\psi}_{n}\right)^{2}\,dx\right)+\frac{\epsilon}{M_{1}}$
		$\displaystyle\leq\int_{\left\|x\right\|\leq R(\epsilon)}\left(\partial^{i}_{x}\psi_{0}\right)^{2}\,dx+\frac{\epsilon}{M_{1}}$
		$\displaystyle\leq\left\\|\partial^{i}_{x}\psi_{0}\right\\|^{2}_{L^{2}(\mathbb{R})}+\frac{\epsilon}{M_{1}},$

for $0\leq i\leq 2$ . Thus,

\liminf\limits_{n\to\infty}\left\|\partial^{i}_{x}\tilde{\psi}_{n}\right\|^{2}_{L^{2}(\mathbb{R})}=\left\|\partial^{i}_{x}\psi_{0}\right\|^{2}_{L^{2}(\mathbb{R})}.

Analogously, using the convergence (2.15), once again, Fatou’s Theorem and now the inequality (2.13), we get

\displaystyle\left\|\partial^{i}_{x}v_{0}\right\|^{2}_{L^{2}(\mathbb{R})}\leq\liminf\limits_{n\to\infty}\left\|\partial^{i}_{x}\tilde{v}_{n}\right\|^{2}_{L^{2}(\mathbb{R})}\leq\left\|\partial^{i}_{x}v_{0}\right\|^{2}_{L^{2}(\mathbb{R})}+\frac{\epsilon}{M_{1}},

that is,

\liminf\limits_{n\to\infty}\left\|\partial^{i}_{x}\tilde{v}_{n}\right\|^{2}_{L^{2}(\mathbb{R})}=\left\|\partial^{i}_{x}v_{0}\right\|^{2}_{L^{2}(\mathbb{R})}.

Thanks to both inequalities, we have shown that

\left\|\partial^{i}_{x}\tilde{\psi}_{n}\right\|_{L^{2}(\mathbb{R})}\rightarrow\left\|\partial^{i}_{x}\psi_{0}\right\|_{L^{2}(\mathbb{R})},

and

\left\|\partial^{i}_{x}\tilde{v}_{n}\right\|_{L^{2}(\mathbb{R})}\rightarrow\left\|\partial^{i}_{x}v_{0}\right\|_{L^{2}(\mathbb{R})},

for $0\leq i\leq 2$ .

On the other hand, we also have that $\partial^{i}_{x}\psi_{n}\rightharpoonup\partial^{i}_{x}\psi_{0}$ and $\partial^{i}_{x}v_{n}\rightharpoonup\partial^{i}_{x}v_{0}$ weakly in $L^{2}(\mathbb{R})$ for $0\leq i\leq 2$ . Thus, using these facts, we conclude that

\partial^{i}_{x}\psi_{n}\rightarrow\partial^{i}_{x}\psi_{0}\quad\partial^{i}_{x}v_{n}\rightarrow\partial^{i}_{x}v_{0}\quad\text{in}\quad L^{2}(\mathbb{R}),

for $0\leq i\leq 2$ . Moreover, we also have that $P_{\omega}(\psi_{n},v_{n})\rightarrow P_{\omega}(\psi_{0},v_{0})=-1$ , since we know that $P_{\omega}$ is Lipschitz (continuous), and we have that $S(\omega)\leq J_{\omega}(\psi_{0},v_{0})$ . Thus, the weak convergence of $(\psi_{n},v_{n})$ to $(\psi_{0},v_{0})$ in $X$ and the weak lower semi-continuity of functional $J_{\omega}$ , yields that

J_{\omega}(\psi_{0},v_{0})\leq\liminf J_{\omega}(\tilde{\psi}_{n},\tilde{v}_{n})=S(\omega),

meaning that $J_{\omega}(\psi_{0},v_{0})=S(\omega)$ . In other words, $(\psi_{0},v_{0})$ is in fact a minimizer for $S(\omega)$ and $(\tilde{\psi}_{n},\tilde{v}_{n})\rightarrow(\psi_{0},v_{0})$ in $X$ , as claimed. ∎

Now, we define the set of ground states as

(2.16)

\mathcal{G}_{\omega}=\left\{(\psi,v)\in X\setminus\{0\}:J_{\omega}(\psi,v)=S(\omega),\ \mbox{and}\ P_{\omega}(\psi,v)\leq 0\right\}.

Lemma 2.8.

Let $0<|w|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}$ and $G_{\omega}$ defined by (2.16).

i)

If $0<\omega<1$ , then $S({\omega})$ is uniformly bounded.
ii)

If $0<{\omega}_{1}<\omega_{2}<1$ and $(\psi,v)\in\mathcal{G}_{\omega}$ , we find that $I_{2,{\omega}}(\psi,v)$ is uniformly bounded on $[{\omega}_{1},{\omega}_{2}]$ .
iii

For $0<\omega<1$ and $(u,v)\in\mathcal{G}_{\omega}$ , we have $S^{\prime}(\omega)=-I_{2}(u,v)$ .

Proof.

i) For any $0<\omega<1$ , we have that $I_{\omega}(\psi,v)=I^{1}(\psi)+I^{2}(v)-2\omega I_{2}(\psi,v)$ . So, we choose $\psi\in H^{2}(\mathbb{R})$ such that $2I^{1}(\psi)-N(\psi,0)=0$ . Thus, $P_{\omega}(\psi,0)=I^{1}(\psi)-N(\psi,0)=0$ . From this, we get that

S({\omega})\leq J_{\omega}(\psi,0)\leq I^{1}(\psi)+||\psi||_{H^{2}}^{p+2}\leq\left(||\psi||_{H^{2}}^{2}+||\psi||_{H^{2}}^{p+2}\right),

which implies that $S({\omega})\leq C$ , where $C>0$ is independent of $0<\omega<1$ .

ii) For $0<{\omega}_{1}<\omega<{\omega}_{2}<1$ and $(\psi,v)\in\mathcal{G}_{\omega}$ , we have that

C\geq S({\omega})=J_{\omega}(\psi,v)\geq\frac{1}{2}I_{\omega}(\psi,v)-\frac{1}{p+2}N(\psi,v)\geq\left(\frac{p}{2(p+2)}\right)I_{\omega}(\psi,v),

which implies that

I_{2,\omega}(\psi,v)\leq C|\omega|||(\psi,v)||_{X}^{2}\leq M_{2}(a,b,c,\omega_{1})|\omega_{2}|I_{\omega}(\psi,v),

where $M_{2}$ is defined in Lemma 2.2.

iii) Let ${\omega}_{1}<{\omega}_{2}$ and $(u^{{\omega}_{i}},v^{{\omega}_{i}})\in\mathcal{G}_{{\omega}_{i}}$ . In the case $I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})\leq I_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})$ , and we have that $P_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})\leq P_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})=0$ . This implies that

(2.17)

\begin{split}S(\omega_{1})&\leq J_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}}),\\ &\leq J_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})+(\omega_{2}-\omega_{1})I_{2}(u^{\omega_{2}},v^{\omega_{2}}),\\ &\leq S(\omega_{2})+(\omega_{2}-\omega_{1})I_{2}(u^{\omega_{2}},v^{\omega_{2}}).\end{split}

Now, we consider the case $I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})>I_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})$ . So, for $\alpha_{2}=\left(\frac{I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})}{I_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})}\right)^{\frac{1}{p}}>1$ , we have

	$\displaystyle P_{{\omega}_{1}}(\alpha(u^{\omega_{2}},v^{\omega_{2}}))$	$\displaystyle=\alpha^{2}I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})-N(\alpha(u^{\omega_{2}},v^{\omega_{2}})),$
		$\displaystyle\leq\alpha^{2}I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})-\alpha^{p+2}N(u^{\omega_{2}},v^{\omega_{2}}),$
		$\displaystyle\leq\alpha^{2}\left(I_{\omega_{1}}(u^{\omega_{2}},v^{\omega_{2}})-\alpha^{p}I_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})\right)$
		$\displaystyle\leq 0.$

From this fact, we conclude that

	$\displaystyle S(\omega_{1})$	$\displaystyle\leq J_{{\omega}_{1}}(\alpha_{2}(u^{\omega_{2}},v^{\omega_{2}}))$
		$\displaystyle\leq\alpha_{2}^{2}S(\omega_{2})+\alpha_{2}^{2}(\omega_{2}-\omega_{1})I_{2}(u^{\omega_{2}},v^{\omega_{2}})+\alpha_{2}^{2}K(u^{\omega_{2}},v^{\omega_{2}})-K(\alpha_{2}(u^{\omega_{2}},v^{\omega_{2}})).$

Now, pick $g(\alpha)=\alpha^{2}K(u^{\omega_{2}},v^{\omega_{2}})-K(\alpha(u^{\omega_{2}},v^{\omega_{2}}))$ . Then, we see that $g(1)=0$ and $g^{\prime}(1)=-2S(\omega_{2})$ . So, for $\omega_{1}-\omega_{2}\sim 0$ , we ensure that

g(\alpha_{2})=\alpha_{2}^{2}K(u^{\omega_{2}},v^{\omega_{2}})-K(\alpha_{2}(u^{\omega_{2}},v^{\omega_{2}}))=-2S(\omega_{2})(\alpha_{2}-1)+O((\alpha_{2}-1)^{2}),

where we are using that

\alpha_{2}-1=\frac{2(\omega_{2}-\omega_{1})}{p}\frac{I_{2}(u^{\omega_{2}},v^{\omega_{2}})}{I_{\omega_{2}}(u^{\omega_{2}},v^{\omega_{2}})}+O((\omega_{2}-\omega_{1})^{2}).

From these facts, we have that

(2.18)

\begin{split}S(\omega_{1})\leq&S(\omega_{2})+(\alpha_{2}^{2}-1)S(\omega_{2})+\alpha_{2}^{2}(\omega_{2}-\omega_{1})I_{2}(u^{\omega_{2}},v^{\omega_{2}})\\ &-2S(\omega_{2})(\alpha_{2}-1)+O((\alpha_{2}-1)^{2}),\\ \leq&S(\omega_{2})+(\alpha_{2}^{2}-1)S(\omega_{2})\left(\frac{\alpha_{2}-1}{\alpha_{2}+1}\right)\\ &+\alpha_{2}^{2}(\omega_{2}-\omega_{1})I_{2}(u^{\omega_{2}},v^{\omega_{2}})+O((\alpha_{2}-1)^{2}).\end{split}

Finally, from (2.17) and (2.18), we conclude that

(S^{\prime})^{-}(w_{2})=\lim_{\omega_{1}\to\omega_{2}^{-}}\frac{S(\omega_{1})-S(\omega_{2})}{\omega_{1}-\omega_{2}}\geq-I_{2}(u^{\omega_{2}},v^{\omega_{2}}).

In a similar way, interchanging the role $\omega_{1}$ and $\omega_{2}$ in an appropriated way, we see that

(S^{\prime})^{+}(w_{1})=\lim_{\omega_{2}\to\omega_{1}^{+}}\frac{S(\omega_{2})-S(\omega_{1})}{\omega_{2}-\omega_{1}}\leq-I_{2}(u^{\omega_{1}},v^{\omega_{1}}).

Putting previous inequalities together, we conclude for any $(\psi,v)\in\mathcal{G}_{\omega}$ that

S^{\prime}(\omega)=-I_{2}(\psi,v),

giving the result, and the Lemma 2.8 is achieved. ∎

3. Numerical experiments

In this section, we introduce numerical solvers to approximate the solutions of the solitary wave equations (LABEL:trav-eqs) and compute traveling wave solutions for a given wave velocity $\omega$ , based on the parameter regime outlined in the previous section. Additionally, some of our experiments investigate scenarios where the wave velocity lies outside the previously established theoretical range.

3.1. Homogeneous case

When the nonlinear functions $G_{1}$ and $G_{2}$ in the Boussinesq system (LABEL:1bbl) are homogeneous, we adapt the numerical solver from [12], originally developed for the fifth-order scalar KdV equation, to approximate the solutions of the traveling-wave equations (LABEL:trav-eqs). This method uses a Fourier basis and incorporates stabilizing factors for wave elevation $\eta$ and fluid velocity $u$ , ensuring the convergence of the iterative scheme employed in the numerical experiments presented here.

Taking Fourier transform of equations (LABEL:trav-eqs), we obtain

\displaystyle\begin{cases}-\omega(\hat{v}_{k}+dk^{2}\hat{v}_{k}+d_{2}k^{4}\hat{v}_{k})+\hat{\psi}_{k}-ck^{2}\hat{\psi}_{k}+c_{2}k^{4}\hat{\psi}_{k}&=\widehat{G_{1}},\\ -\omega(\hat{\psi}_{k}+bk^{2}\hat{\psi}_{k}+b_{2}k^{4}\hat{\psi}_{k})+\hat{v}_{k}-ak^{2}\hat{v}_{k}+a_{2}k^{4}\hat{v}_{k}&=\widehat{G_{2}}.\end{cases}

We recall that $b=d>0$ , $b_{2}=d_{2}>0$ , $a,c<0$ , $a_{2},c_{2}>0$ , and $\widehat{G_{1}},\widehat{G_{2}}$ are the Fourier transforms of the functions $G_{1}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime})$ and $G_{2}(\psi,\psi^{\prime},\psi^{\prime\prime},v,v^{\prime},v^{\prime\prime})$ , respectively.

Rewriting these equations, we get

\displaystyle\begin{cases}-\omega(1+dk^{2}+d_{2}k^{4})\hat{v}_{k}+(1-ck^{2}+c_{2}k^{4})\hat{\psi}_{k}&=\widehat{G_{1}},\\ (1-ak^{2}+a_{2}k^{4})\hat{v}_{k}-\omega(1+bk^{2}+b_{2}k^{4})\hat{\psi}_{k}&=\widehat{G_{2}},\end{cases}

and thus, we can write

(3.1)

\displaystyle\hat{v}_{k}=\frac{\widehat{G_{1}}D_{22}-\widehat{G_{2}}D_{12}}{D_{11}D_{22}-D_{21}D_{12}},

and

(3.2)

\displaystyle\hat{\psi}_{k}=\frac{\widehat{G_{2}}D_{11}-\widehat{G_{1}}D_{21}}{D_{11}D_{22}-D_{21}D_{12}},

where

D=\begin{pmatrix}D_{11}&D_{12}\\ D_{21}&D_{22}\end{pmatrix}=\begin{pmatrix}-\omega(1+dk^{2}+d_{2}k^{4})&1-ck^{2}+c_{2}k^{4}\\ 1-ak^{2}+a_{2}k^{4}&-\omega(1+bk^{2}+b_{2}k^{4})\end{pmatrix}.

On the other hand, by multiplying equation (3.1) by $\hat{v}_{k}$ and equation (3.2) by $\hat{\psi}_{k}$ , and then adding over $k$ , we obtain

\displaystyle P_{1}(v):=\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\hat{v}_{k}^{2}}{\sum_{k}(\widehat{G}_{1}D_{22}-\widehat{G_{2}}D_{12})\hat{v}_{k}}=1,

and

\displaystyle P_{2}(\psi):=\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\hat{\psi}_{k}^{2}}{\sum_{k}(\widehat{G_{2}}D_{11}-\widehat{G_{1}}D_{21})\hat{\psi}_{k}}=1.

To compute approximate solutions to the traveling wave equations, we select initial values $\psi^{0}$ and $v^{0}$ . Then, for $s\geq 0$ , we define the sequence

(3.3)

\displaystyle\hat{v}_{k}^{s+1}=\frac{\widehat{G_{1}}(\tilde{\psi^{s}},\tilde{\psi^{s}}^{\prime},\tilde{\psi^{s}}^{\prime\prime},\tilde{v^{s}},\tilde{v^{s}}^{\prime},\tilde{v^{s}}^{\prime\prime})D_{22}-\widehat{G_{2}}(\tilde{\psi^{s}},\tilde{\psi^{s}}^{\prime},\tilde{\psi^{s}}^{\prime\prime},\tilde{v^{s}},\tilde{v^{s}}^{\prime},\tilde{v^{s}}^{\prime\prime})D_{12}}{D_{11}D_{22}-D_{21}D_{12}},

and

(3.4)

\displaystyle\hat{\psi}_{k}^{s+1}=\frac{\widehat{G_{2}}(\tilde{\psi^{s}},\tilde{\psi^{s}}^{\prime},\tilde{\psi^{s}}^{\prime\prime},\tilde{v^{s}},\tilde{v^{s}}^{\prime},\tilde{v^{s}}^{\prime\prime})D_{11}-\widehat{G_{1}}(\tilde{\psi^{s}},\tilde{\psi^{s}}^{\prime},\tilde{\psi^{s}}^{\prime\prime},\tilde{v^{s}},\tilde{v^{s}}^{\prime},\tilde{v^{s}}^{\prime\prime})D_{21}}{D_{11}D_{22}-D_{21}D_{12}},

where $\tilde{v}^{s}:=\alpha_{s}v^{s}$ , $\tilde{\psi}^{s}:=\beta_{s}\psi^{s}$ , and $\alpha_{s}$ , $\beta_{s}\in\mathbb{R}$ are solutions of the following equations

(3.5)

\begin{cases}P_{1}(\alpha_{s}v^{s})=1,\\ P_{2}(\beta_{s}\psi^{s})=1.\end{cases}

We note that the quantities $\alpha_{s}$ and $\beta_{s}$ are stabilizing factors introduced to ensure the convergence of the iteration defined in (3.3) and (3.4).

Suppose that the functions $G_{1},G_{2}$ are both homogeneous of order $p+1$ . Then, given that the parameters $\alpha_{s}$ , $\beta_{s}$ are chosen at each iteration $s$ such that $P_{1}(\alpha_{s}v^{s})=1$ and $P_{2}(\beta_{s}\psi^{s})=1$ , we obtain that

(3.6)

\begin{cases}&\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\alpha_{s}^{2}\hat{v}_{k}^{2}}{\sum_{k}\alpha_{s}^{p+1}(\widehat{G}_{1}D_{22}-\widehat{G_{2}}D_{12})\alpha_{s}\hat{v}_{k}}=1,\\ \\ &\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\beta_{s}^{2}\hat{\psi}_{k}^{2}}{\sum_{k}\beta_{s}^{p+1}(\widehat{G_{2}}D_{11}-\widehat{G_{1}}D_{21})\beta_{s}\hat{\psi}_{k}}=1.\end{cases}

From equations (3.5) and (3.6), we obtain the explicit expressions for the parameters $\alpha_{s},\beta_{s}$ given by

\begin{cases}\alpha_{s}&=M_{s}^{1/p},\\ \beta_{s}&=N_{s}^{1/p},\end{cases}

where

\displaystyle M_{s}:=\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\hat{v}_{k}^{2}}{\sum_{k}(\widehat{G}_{1}D_{22}-\widehat{G_{2}}D_{12})\hat{v}_{k}},

and

\displaystyle N_{s}:=\frac{\sum_{k}(D_{11}D_{22}-D_{21}D_{12})\hat{\psi}_{k}^{2}}{\sum_{k}(\widehat{G_{2}}D_{11}-\widehat{G_{1}}D_{21})\hat{\psi}_{k}}.

As a consequence, the iteration defined by equations (3.3) and (3.4), can be rewritten as follows

(3.7)

\displaystyle\hat{v}_{k}^{s+1}=M_{s}^{\frac{p+1}{p}}\frac{\widehat{G_{1}}({\psi^{s}},{\psi^{s}}^{\prime},{\psi^{s}}^{\prime\prime},{v^{s}},{v^{s}}^{\prime},{v^{s}}^{\prime\prime})D_{22}-\widehat{G_{2}}(\psi^{s},{\psi^{s}}^{\prime},{\psi^{s}}^{\prime\prime},v^{s},{v^{s}}^{\prime},{v^{s}}^{\prime\prime})D_{12}}{D_{11}D_{22}-D_{21}D_{12}},

and

(3.8)

\displaystyle\hat{\psi}_{k}^{s+1}=N_{s}^{\frac{p+1}{p}}\frac{\widehat{G_{2}}({\psi^{s},\psi^{s}}^{\prime},{\psi^{s}}^{\prime\prime},{v^{s}},{v^{s}}^{\prime},{v^{s}}^{\prime\prime})D_{11}-\widehat{G_{1}}({\psi^{s}},{\psi^{s}}^{\prime},\tilde{\psi^{s}}^{\prime\prime},{v^{s}},{v^{s}}^{\prime},{v^{s}}^{\prime\prime})D_{21}}{D_{11}D_{22}-D_{21}D_{12}}.

Next, we compute some approximate solitary wave solutions to the Boussinesq system (LABEL:1bbl) for different model parameters using the numerical scheme introduced, with $G_{1}=u^{p+1}$ and $G_{2}=\eta^{p+1}$ .

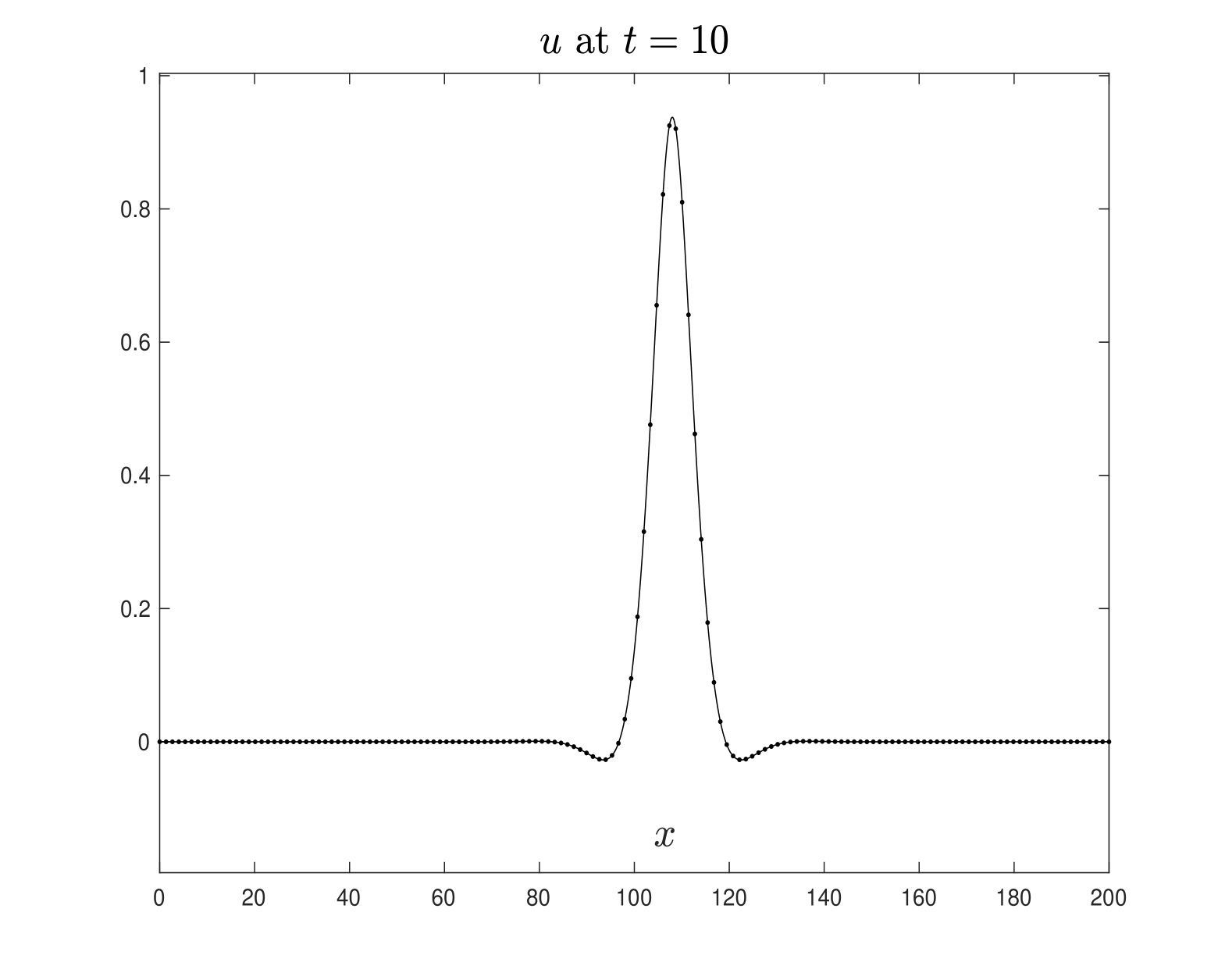
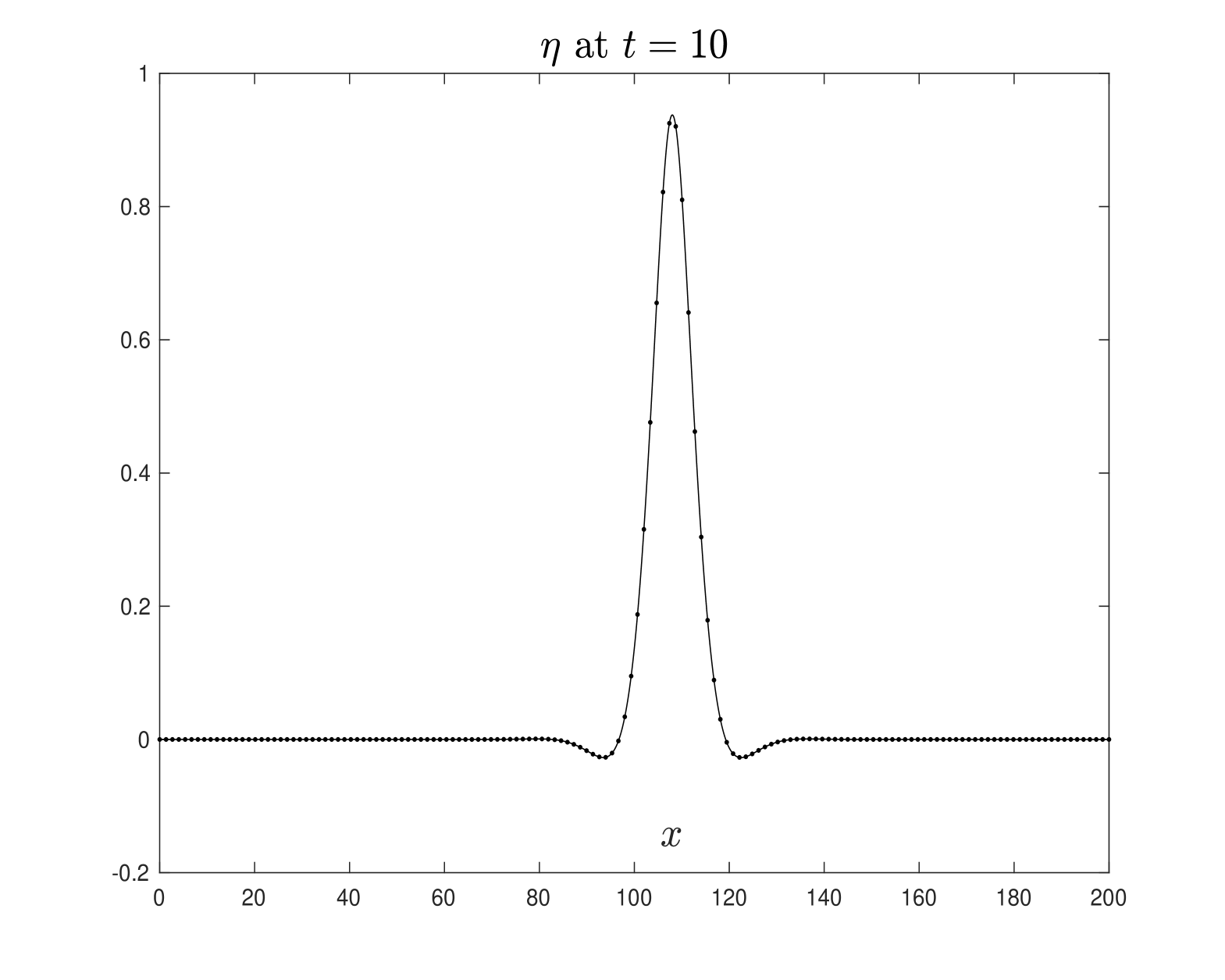
In Figure 1, we display the solitary wave solution $(u,\eta)$ computed using the iterative scheme (3.7)-(3.8), with initial values given by

(3.9)

v^{0}(x)=\psi^{0}(x)=e^{-0.5(x-a_{0})^{2}},

with $a_{0}=100$ . We have used $N=2^{12}$ spectral points in the spatial domain, with the computational domain defined as the interval $[0,L]=[0,200]$ .

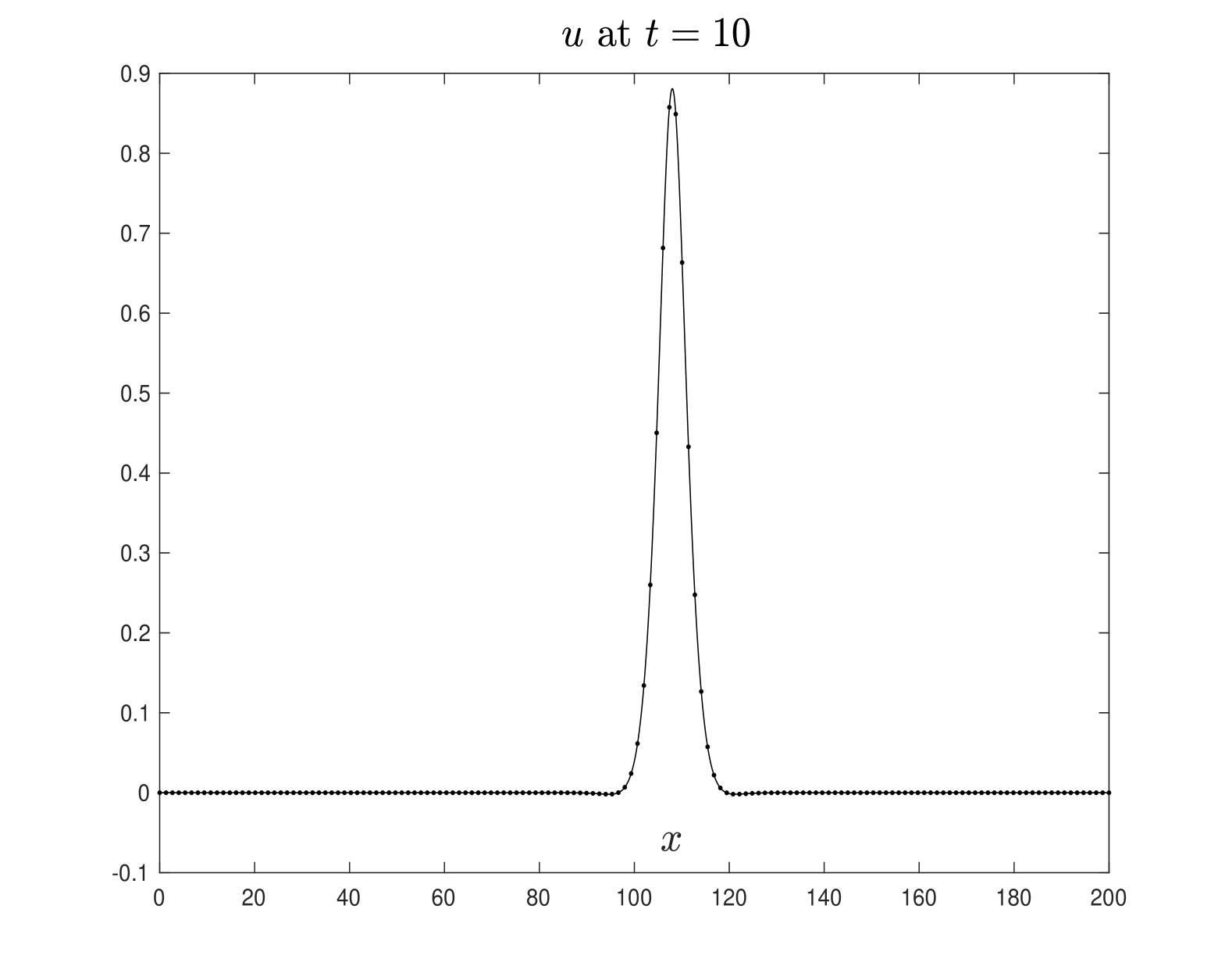
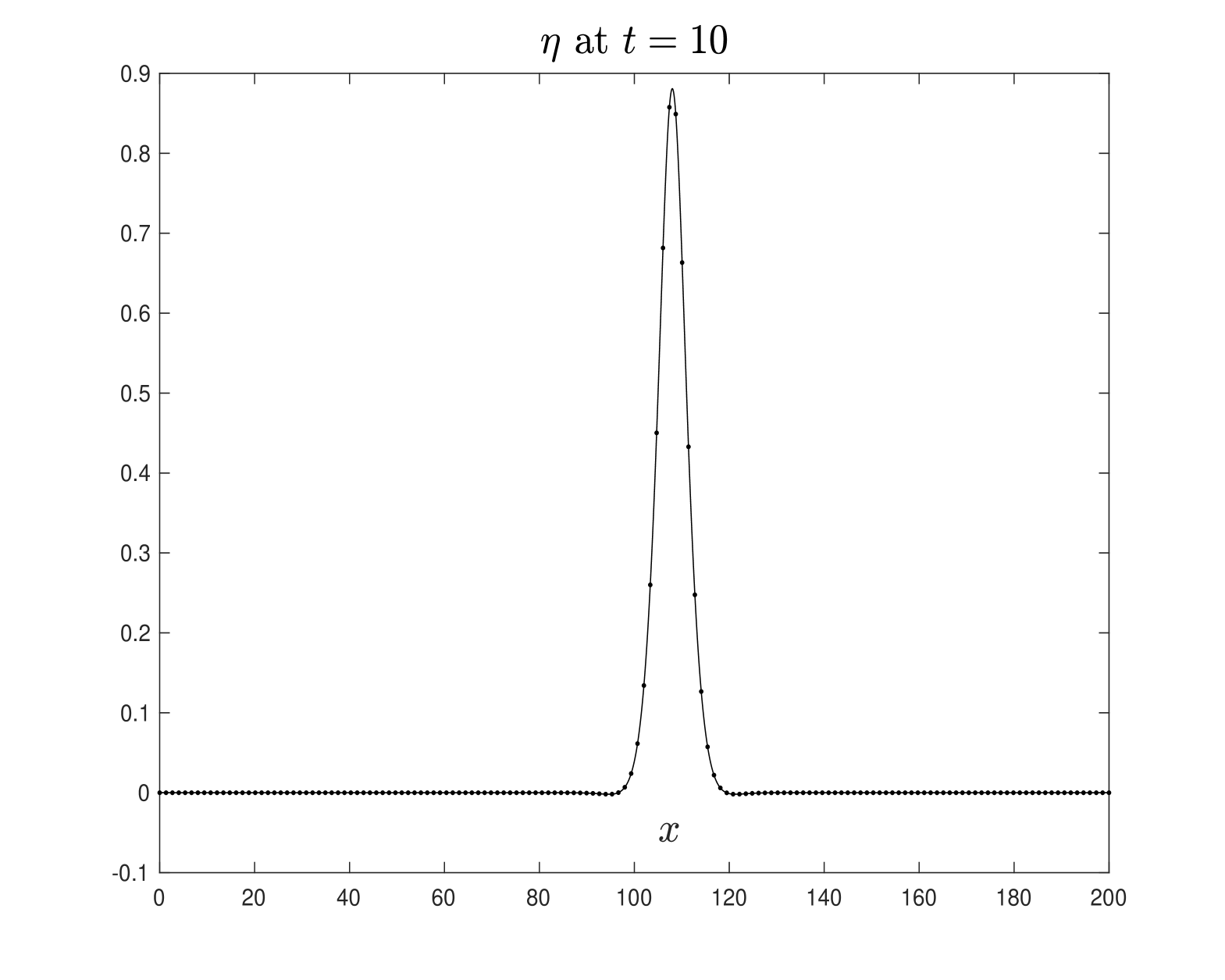
In Figure 2, we present the results obtained for different model parameters, using the same initial values as given in (3.9). Additionally, Figure 3 considers a case where the wave velocity is outside the theoretical interval of existence established in the previous section. We take the wave velocity as $\omega=0.4$ , which, for the parameters chosen for the adopted model, is outside the interval of existence $0<|\omega|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}=0.25$ . The computational domain is $[0,L]=150$ , and $a_{0}=75$ in (3.9). All other parameters are the same as those in the previous numerical experiments.

Refer to caption — Figure 1. Solitary wave of the Boussinesq system (LABEL:1bbl) computed with $b=d=2$ , $b_{2}=d_{2}=5$ , $a=-2$ , $c=-2$ , $a_{2}=20$ , $c_{2}=20$ , $p=8$ and wave velocity $\omega=0.8$ .

Figure 4 presents another experiment of this type with different model parameters, where we compute a solitary wave with velocity $\omega=0.4$ . In this case, the theoretical existence interval for solitary wave velocities is $0<|\omega|<\min\left\{1,\frac{\sqrt{ca}}{b},\frac{a_{2}}{b_{2}},\frac{c_{2}}{b_{2}}\right\}=0.33$ . All numerical parameters are identical to those used in Figure 3.

These numerical experiments indicate that solitary wave solutions of the Boussinesq system (LABEL:1bbl) may exist beyond the previously established theoretical interval. However, the exact velocity range for the existence of solitary waves seems to be influenced by additional factors, such as the nonlinear exponent $p$ .

3.1.1. Verifying the approximations of solitary wave solutions

We now aim to verify the approximations of the solitary wave solutions presented in Figures 1 and 2. To do this, we will compute the propagation of a solution in the one-dimensional fifth-order Boussinesq system (LABEL:1bbl). First, we apply the Fourier transform with respect to the spatial variable $x$ in this system, resulting in

\displaystyle\begin{cases}&(1+dk^{2}+d_{2}k^{4})\hat{u}_{t}+ik\hat{\eta}+c(ik)^{3}\hat{\eta}+c_{2}(ik)^{5}\hat{\eta}=ik\widehat{G}_{1},\\ &(1+bk^{2}+b_{2}k^{4})\hat{\eta}_{t}+ik\hat{u}+a(ik)^{3}\hat{u}+a_{2}(ik)^{5}\hat{u}=ik\widehat{G}_{2},\end{cases}

which can be rewritten as

(3.10)

\displaystyle\hat{u}_{t}=F_{1}\hat{\eta}+H_{1},

and

(3.11)

\displaystyle\hat{\eta}_{t}=F_{2}\hat{u}+H_{2},

where

	$\displaystyle F_{1}=\frac{-ik+cik^{3}-c_{2}ik^{5}}{1+dk^{2}+d_{2}k^{4}},\quad F_{2}=\frac{-ik+aik^{3}-a_{2}ik^{5}}{1+bk^{2}+b_{2}k^{4}},$
	$\displaystyle H_{1}=\frac{ik\widehat{G}_{1}}{1+dk^{2}+d_{2}k^{4}},\quad\text{and}\quad H_{2}=\frac{ik\widehat{G}_{2}}{1+bk^{2}+b_{2}k^{4}}.$

To approximate the time evolution of solutions to the full Boussinesq system (3.10)-(3.11) numerically, we utilize the following time-stepping scheme:

(3.12)

\displaystyle\frac{\hat{u}^{n+1}-\hat{u}^{n}}{\Delta t}=F_{1}(\theta\hat{\eta}^{n+1}+(1-\theta)\hat{\eta}^{n})+H_{1}^{n},

and

(3.13)

\displaystyle\frac{\hat{\eta}^{n+1}-\hat{\eta}^{n}}{\Delta t}=F_{2}(\theta\hat{u}^{n+1}+(1-\theta)\hat{u}^{n})+H_{2}^{n},

where $\theta\in[0,1]$ is a parameter. Now, by solving for $\hat{u}^{n+1}$ from equation (3.12), and substituting it into equation (3.13), we obtain the system

(3.14)

\displaystyle\hat{u}^{n+1}=\frac{(1+\Delta t^{2}F_{1}F_{2}\theta(1-\theta))\hat{u}^{n}+(\Delta tF_{1}(1-\theta)+\Delta t\theta F_{1})\hat{\eta}^{n}+\Delta t^{2}F_{1}\theta H_{2}^{n}+\Delta tH_{1}^{n}}{1-\Delta t^{2}F_{1}F_{2}\theta^{2}},

and

(3.15)

\displaystyle\hat{\eta}^{n+1}=\hat{\eta}^{n}+\Delta t\theta F_{2}\hat{u}^{n+1}+\Delta t(1-\theta)F_{2}\hat{u}^{n}+\Delta tH_{2}^{n}.

Here, the superscript $n$ indicates that the corresponding quantity is evaluated at time $t=n\Delta t$ .

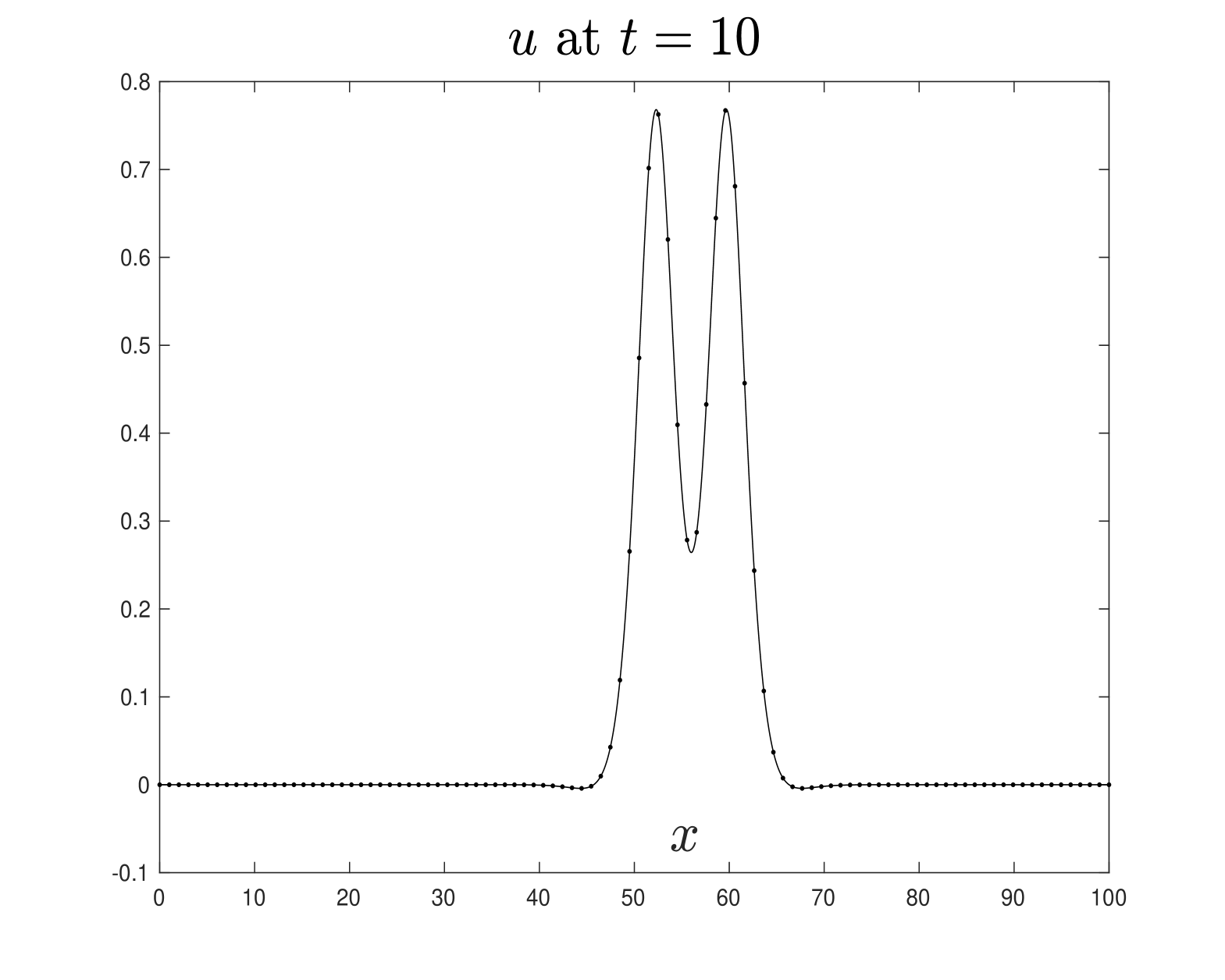
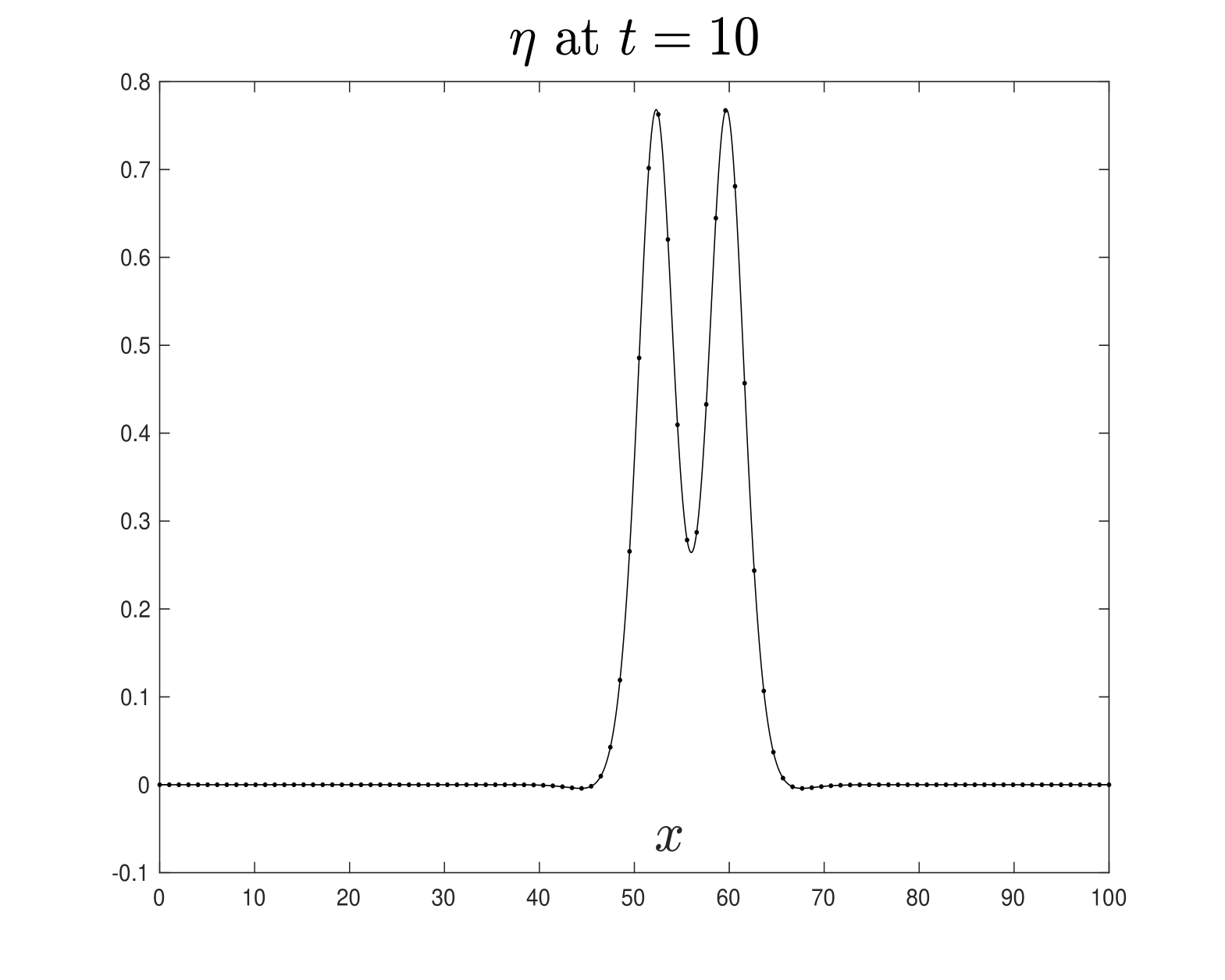
The quantities above allow us to assess the approximations of the solitary wave solutions depicted in Figures 1 and 2. Specifically, Figures 5 and 6, using the numerical scheme (3.14)-(3.15), confirm the approximations of the solitary wave solutions shown in Figures 1 and 2, respectively. The numerical parameters used are $N=2^{12}$ FFT points over the computational interval $[0,L]=200$ , $\Delta t=10/10000=0.001$ is the time step size. Note that in both experiments, the profiles of $u$ and $\eta$ propagate to the right with approximately constant shape and velocity $\omega=0.8$ , as expected. Neither dissipation nor dispersion is observed during wave propagation. These computer simulations provide evidence that the solutions computed using the scheme (3.7)-(3.8) behave as solitary wave solutions to the Boussinesq system (LABEL:1bbl), indicating that the numerical method performs quite well.

3.2. Non-homogeneous case

In this set of computer simulations, we aim to explore the case where the nonlinearities $G_{1},G_{2}$ are non-homogeneous. Specifically, we consider

F(\eta,\partial_{x}\eta,u,\partial_{x}u)=\frac{1}{4}u^{4}+\frac{1}{2}\partial_{x}(u^{2})+\frac{1}{4}\eta^{4}+\frac{1}{2}\partial_{x}(\eta^{2}).

By substituting into the expressions for the functions $G_{1},G_{2}$ , we obtain

\displaystyle G_{1}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,u,\partial_{x}u,\partial^{2}_{x}u)=\eta^{3}-(\partial_{x}\eta)^{2}-2(\partial_{x}^{2}\eta)\eta,

and

\displaystyle G_{2}(\eta,\partial_{x}\eta,\partial^{2}_{x}\eta,u,\partial_{x}u,\partial^{2}_{x}u)=u^{3}-(\partial_{x}u)^{2}-2(\partial^{2}_{x}u)u.

In this case, we use a different numerical scheme from the one applied in the homogeneous case, as the stabilizing factors cannot be directly computed.

To approximate the solitary wave equations (LABEL:trav-eqs), we expand the unknowns $\psi(x)$ and $v(x)$ functions with period $L=2l$ (for sufficiently large $l$ ), using the following cosine expansions:

\begin{cases}&\displaystyle\psi(x)=\psi_{0}+\sum_{k=1}^{N/2}\psi_{k}\cos\Big{(}\frac{k\pi x}{l}\Big{)},\\ \\ &\displaystyle v(x)=v_{0}+\sum_{k=1}^{N/2}v_{k}\cos\Big{(}\frac{k\pi x}{l}\Big{)}.\end{cases}

Substituting these expressions into the solitary wave equations (LABEL:trav-eqs), and evaluating at the $N/2+1$ collocation points

x_{j}=\frac{2l(j-1)}{N},~~j=1,...,N/2+1,

we obtain a system of $N+2$ nonlinear equations of the form

F(\psi_{0},\psi_{1},...,\psi_{N/2},v_{0},v_{1},...,v_{N/2})=0,

where the unknowns are the coefficients $\psi_{k},v_{k}$ . This nonlinear system is solved using Newton’s iteration. The iteration process is stopped when the relative difference between two successive approximations and the value of the field $F:\mathbb{R}^{N+2}\to\mathbb{R}^{N+2}$ is less than $10^{-12}$ . The initial guess for the Newton iteration is taken as

v^{0}(x)=\psi^{0}(x)=e^{-0.05(x-a0)^{2}},

with $a_{0}=50$ . The result of this numerical experiment is presented in Figure 7.

In Figure 8, we apply the numerical scheme defined by equations (3.14)-(3.15) to verify the approximation of the solitary wave solution shown in Figure 7. The numerical setup includes $N=2^{12}$ FFT points, with the computational spanning $[0,L]=[0,100]$ , and a time step size of $\Delta t=10/10000=0.001$ . As expected, the wave profiles propagate to the right, preserving their shape and moving at approximately the expected velocity.

Acknowledgment

R. de A. Capistrano–Filho was partially supported by CAPES/COFECUB grant number 88887.879175/2023-00, CNPq grant numbers 421573/2023-6 and 307808/2021-1, and Propesqi (UFPE). J. Quintero and J. C. Muñoz were supported by the Department of Mathematics of the Universidad del Valle (Colombia) under the C.I. 71360 project.

References

[1] D. J. Benney, A general theory for interactions between short and long waves, Stud. Appl. Math., 56, 81–94 (1977).
[2] J. L. Bona, M. Chen, and J. C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. I. Derivation and linear theory, J. Nonlinear Sci., 12, 283–318 (2002).
[3] J. L. Bona, M. Chen, and J. C. Saut, Boussinesq equations and other systems for small-amplitude long waves in nonlinear dispersive media. II: The nonlinear theory, Nonlinearity, 17, 925–952 (2004).
[4] J. L. Bona, T. Colin, and D. Lannes, Long wave approximations for water waves, Arch. Ration. Mech. Anal. 178:3, 373–410 (2005).
[5] J. L. Bona, V. A. Dougalis, and D. E. Mitsotakis, Numerical solution of Boussinesq systems of KdV-KdV type: II Evolution of radiating solitary waves, Nonlinearity 21, no. 12, 2825–2848 (2008).
[6] R. de A. Capistrano-Filho, J. Quintero, and S.-M. Sun, Orbital stability of the $abcd$ -Boussinesq system: The Hamiltonian case. arXiv:2306.17335 [math.AP].
[7] M. Chen, N. V. Nguyen, and S.-M. Sun, Existence of traveling-wave solutions to Boussinesq systems, Differ. Integral Equ. 24 (9–10), 895–908 (2011).
[8] W. Craig and M. D. Groves, Hamiltonian long-wave approximations to the water-wave problem, Wave Motion, 19, 367–389 (1994).
[9] V. A. Dougalis, A. Durán and L. Saridaki, On solitary-wave solutions of Boussinesq/Boussinesq systems for internal waves, Physica D: Nonlinear Phenomena 428, 133051 (2021).
[10] I. Dursun and D. Idris, Numerical simulations of the improved Boussinesq equation, Num. Met. Partial Diff. Eqs. 26, No. 6, 1316–1327 (2009).
[11] O. Ersoy, A. Korkmaz, and I. Dag, Exponential B-Splines for numerical solutions to some Boussinesq systems for water waves, Mediterranean J. Math. 13, 4975–4994 (2016).
[12] A. Esfahani and S. Levandosky, Existence and stability of traveling waves of the fifth-order KdV equation, Physica D, 421, 132872 (2021).
[13] J. Hunter and J. Scheurle, Existence of perturbed solitary wave solutions to a model equation for water waves, Physica D, 32, (1988) 253–268.
[14] T. Kawahara, Oscillatory solitary waves in dispersive media, Journal of the Physical Society of Japan, 33, 260–264 (1972).
[15] S. Kichenassamy and P. Olver, Existence and non-existence of solitary waves to higher-order evolution equations, IMA Preprint Series, 803 (1991).
[16] P.-L. Lions, The concentration-compactness principle in the calculus of variations. The locally compact case. Part I, Annales de l’Institut Henri Poincaré, Analyse Non Linéaire , 1, 109–145 (1984).
[17] P.-L. Lions, The concentration-compactness principle in the calculus of variations. The locally compact case. Part II, Annales de l’Institut Henri Poincaré, Analyse Non Linéaire, 1, 223–283 (1984).
[18] P. J. Olver, Hamiltonian and non-Hamiltonian models for water waves. In Lecture Notes in Physics, Springer-Verlag, 195, 273–290.
[19] G. Ponce, Lax pairs and higher-order models for water waves, Journal of Differential Equations, 102 (2), 360–381 (1993) .
[20] J. A. Zufiria, Symmetry breaking in periodic and solitary gravity-capillary waves on water of finite depth, Journal of Fluid Mechanics, 184, 183–206 (1987).

	$\displaystyle I_{\omega}(\psi,v)\leq$	$\displaystyle\int_{\mathbb{R}}\left[(1+\|\omega\|)\psi^{2}+\left(\|c\|+b\|\omega\|\right)(\psi^{\prime})^{2}+(1+\|\omega\|)v^{2}+\left(\|a\|+b\|\omega\|\right)(v^{\prime})^{2}\right.$
		$\displaystyle\left.+\left(a_{2}+b_{2}\|\omega\|\right)(\psi^{\prime\prime})^{2}+\left(c_{2}+b_{2}\|\omega\|\right)(v^{\prime\prime})^{2}\right]dx$
	$\displaystyle\leq$	$\displaystyle\max\left(1+\|\omega\|,\|c\|+b\|\omega\|,\|a\|+b\|\omega\|,a_{2}+b_{2}\|\omega\|,c_{2}+b_{2}\|\omega\|)\right)\\|(\psi,v)\\|^{2}_{X}.$

	$\displaystyle I_{\omega}(\psi,v)\geq$	$\displaystyle\int_{\mathbb{R}}\left[(1-\|\omega\|)\psi^{2}+\left(-c-b\|\omega\|\right)(\psi^{\prime})^{2}+(1-\|\omega\|)v^{2}+\left(-a-b\|\omega\|\right)(v^{\prime})^{2}\right.$
		$\displaystyle\left.+\left(a_{2}-b_{2}\|\omega\|\right)(\psi^{\prime\prime})^{2}+\left(c_{2}-b_{2}\|\omega\|\right)(v^{\prime\prime})^{2}\right]dx$
	$\displaystyle\geq$	$\displaystyle\min\left(1-\|\omega\|,-c-b\|\omega\|a,-a-b\|\omega\|,a_{2}-b_{2}\|\omega\|,c_{2}-b_{2}\|\omega\|)\right)\\|(\psi,v)\\|^{2}_{X},$

	$\displaystyle\left\\|\partial^{i}_{x}\psi_{0}\right\\|^{2}_{L^{2}(\mathbb{R})}$	$\displaystyle\leq\liminf\limits_{n\to\infty}\left\\|\partial^{i}_{x}\tilde{\psi}_{n}\right\\|^{2}_{L^{2}(\mathbb{R})}$
		$\displaystyle\leq\liminf\limits_{n\to\infty}\left(\int_{\left\|x\right\|\leq R(\epsilon)}\left(\partial^{i}_{x}\tilde{\psi}_{n}\right)^{2}\,dx\right)+\frac{\epsilon}{M_{1}}$
		$\displaystyle\leq\int_{\left\|x\right\|\leq R(\epsilon)}\left(\partial^{i}_{x}\psi_{0}\right)^{2}\,dx+\frac{\epsilon}{M_{1}}$
		$\displaystyle\leq\left\\|\partial^{i}_{x}\psi_{0}\right\\|^{2}_{L^{2}(\mathbb{R})}+\frac{\epsilon}{M_{1}},$

Traveling-wave solutions for a higher-order Boussinesq system: existence and numerical analysis

Abstract.

Key words and phrases:

2020 Mathematics Subject Classification:

1. Introduction

1.1. Background

1.2. Notations and main results

Theorem 1.1.

1.3. Outline

2. Existence of solitary waves for b=db=d and b2=d2b_{2}=d_{2}

Lemma 2.1.

Lemma 2.2.

Proof.

Theorem 2.3.

Proof.

Remark 2.4.

Lemma 2.5.

Proof.

Lemma 2.6.

Proof.

Lemma 2.7.

Proof.

Proof of Theorem 1.1.

Lemma 2.8.

Proof.

3. Numerical experiments

3.1. Homogeneous case

3.1.1. Verifying the approximations of solitary wave solutions

3.2. Non-homogeneous case

Acknowledgment

References

2. Existence of solitary waves for $b=d$ and $b_{2}=d_{2}$