Tree Representation, Growth Rate of Blockchain and Reward Allocation in Ethereum with Multiple Mining Pools
Abstract
It is interesting but difficult and challenging to study Ethereum with multiple mining pools. One of the main difficulties comes from not only how to represent such a general tree with multiple block branches (or sub-chains) related to the multiple mining pools, but also how to analyze a multi-dimensional stochastic system due to the mining competition among the multiple mining pools. In this paper, we first set up a mathematical representation for the tree with multiple block branches. Then we provide a block classification of Ethereum: Regular blocks (in the main chain), orphan blocks, uncle blocks, stale blocks, and nephew blocks, and give some key probabilities of generating the different types of blocks by applying the law of large numbers. Based on this, we further discuss the growth rate of blockchain, and the reward allocation among the multiple mining pools through applying the renewal reward theorem. Finally, we use some simulation experiments to verify our theoretical results, and show that the approximate computation approaches developed, such as the key probabilities, the long-term growth rate of blockchain, and the long-term reward allocation (rate) among the multiple mining pools, can have a faster convergence. Therefore, we provide a powerful tool for observing and understanding the influence of the selfish mining attacks on the performance of Ethereum with multiple mining pools. We believe that the methodology and results developed in this paper will shed light on the study of Ethereum with multiple mining pools, such that a series of promising research can be inspired potentially.
Keywords: Ethereum; selfish mining; multiple mining pools; tree representation; growth rate of blockchain; reward allocation; the law of large numbers; renewal reward theory.
1 Introduction
Bitcoin and blockchain have opened a new era of automatically processing and storing transactions since the pioneering work by Nakamoto [26]. The transactions can be automatically processed in the form of Bitcoin script through a language of Merkle tree in a P2P network. However, the Bitcoin language is not Turing-complete owing to robust concerns. On the other hand, Ethereum can break such a limitation by introducing Ethereum Virtual Machine featuring smart contract functionality, e.g., see [6, 7]. Note that Bitcoin and Ethereum are the two largest and most popular blockchain-based cryptocurrencies in the world. Ethereum has gained great attention in the development of blockchain technology. Interested readers are referred to Ethereum survey papers, for example, Wood [40], Vujičić et al. [35], Di Angelo et al. [10], Mohammed et al. [25]; Ethereum system security by Chen et al. [9] and Praitheeshan et al. [28]; and smart contracts by Wang et al. [36], Dika and Nowostawski [11], Wang et al. [37] and Atzei et al. [1]. At the same time, Ethereum has been developed into many practical applications from industry and academia, e.g., see sharing economy by Bogner et al. [5], healthcare by Sookhak et al. [34], IoT and logistics by Augusto et al. [2], emergency service by Aung and Tantidham [3], decentralized marketplace by Ranganthan et al. [29], and so forth.
Bitcoin and Ethereum applied the most widely used consensus mechanism: Proof-of-Work (PoW). In a PoW blockchain system, many miners (or mining pools) competitively mine each block which is generated by means of finding a nonce through solving a cryptographic puzzle of using all the foregoing information of that blockchain in front of this block, and then peg the block with the nonce to the blockchain. See Li et al. [20, 21] for more details. For the PoW blockchain system with two mining pools (honest and dishonest), Eyal and Sirer [12] found the selfish mining attacks and applied a simple Markov chain to study a few advantages of selfish mining. Li et al. [21] proposed the two-block leading competitive criterion, and set up a pyramid Markov (reward) process to analyze the operations efficiency and economic benefit of the blockchain selfish mining system. It is seen from [12] and [21] that the mining competition between the two mining pools can be described as a comparison of lengths of the two block branches, and the dishonest mining pool develops a selfish mining attack policy, see Figures 2 and 4 in Li et al. [21]. Clearly, the longest one of the two block branches is called the main chain, which is pegged on the blockchain; while another block branch is regarded as the chain of orphan blocks, which cannot be connected to blockchain and is returned to the transaction pool for reprocessing. Thus the orphan blocks generate a lot of waste of computing resources. Li et al. [21] applied the pyramid Markov (reward) process to give a detailed analysis for the orphan blocks and their waste of computing resources. Following the two block branches corresponding to the two mining pools, this paper analyzes the PoW blockchain system with multiple mining pools, and finds a general tree with multiple block branches where the dishonest block branches can fork at different positions of a honest block branch (see Section 3). Furthermore, under the two-block leading competitive criterion, this paper provides a mathematical representation of the general tree with multiple block branches, and shows that the main chain in the general tree can be determined easily by means of the longest chain principle. Note that here our general tree is different from that of the GHOST protocol given in Sompolinsky and Zohar [32, 33], since our general tree is directly built in the competing process of multiple mining pools, and the longest chain (main chain) can be easily determined by using the mathematical representation of the general tree with multiple block branches.
So far, only a few studies have been done on the PoW blockchain system with multiple mining pools. Important examples include the two different classes: (a) Simulation, and (b) extending the Markov chain method of Eyal and Sirer [12]. For (a) simulation, since the blockchain system with multiple mining pools is very complicated, the simulation method becomes effective and feasible. Leelavimolsilp et al. [17] used simulation to provide a preliminary investigation on the selfish mining strategy adopted by multiple miners, and analyzed the relative reward, the power threshold of selfish miners, and the safety level of the Bitcoin system. Under the assumptions of [17], Leelavimolsilp et al. [18] further studied the effectiveness of the selfish mining strategy. For (b) extending the Markov chain method of Eyal and Sirer [12], readers are referred to, for example, Liu et al. [22], Marmolejo-Cossío et al. [24], Bai et al. [4], Chang [15] and Xia et al. [41]. Note that Li et al. [21] indicated that the Markov chain given in Eyal and Sirer [12] has some deficiencies and defects compared to the theory of Markov processes.
The GHOST protocol was first introduced by Sompolinsky and Zohar [32, 33] in order to improve the security and throughput of the Bitcoin system by using the heaviest chain principle in a tree. On the other hand, Ethereum implements a simplified GHOST protocol which refers to orphan blocks when observing which chain is the longest. In this case, the referenced blocks are called the uncle blocks while the referencing blocks are called the nephew blocks. For the uncle and nephew blocks, the Ethereum system with multiple mining pools will be faced with two basic challenges. The first challenge is how to set up a tree structure with multiple block branches and forked positions, which expresses the competition process of multiple mining pools. The second challenge is how to design the rewards of uncle blocks and nephew blocks, which are used to increase the mining enthusiasm of the multiple mining pools, and especially when those mining pools cannot access the main chain. For the two challenging problems, so far there has not been a clear answer or a better research yet. This motivates us in this paper to explore both setting up the tree structure and designing the rewards of the uncle and nephew blocks. By finding the mathematical representation of a general Ethereum tree, this paper applies the law of large numbers and the reward renewal theorem to make some key and important progress in the study of Ethereum systems with multiple mining pools.
There have been a few works on the uncle and nephew blocks and their reward design in Ethereum up to now. Zhang et al. [43, 44] analyzed the benefits of selfish mining in Ethereum, and chose the maximum, 7/8 units as the uncle block reward, and 1/32 units as the nephew block reward. Lerner [19] found that the uncle block strategy may cause the deliberate increase in the supply of Ethereum, thus it indirectly reduces the value of Ethereum. Ritz and Zugenmaier [30] set up a Monte Carlo simulation platform to quantify how the uncle blocks affect the probability of selfish mining. Chang et al. [8] introduced the uncle block attacks to discuss the incentive compatibility among the different attacks. Werner et al. [39] formally reconstructed a Sybil attack to exploit the uncle block distribution policy in a queue-based mining pool. Chang et al. [8] and Werner et al. [39] provided the simulation analysis for the uncle blocks in Ethereum. Zhang [42] developed a Markov decision process model to analyze the profitability and threshold of the three-player attacks. In addition, the uncle block mechanism can improve the security of Ethereum systems with multiple mining pools. For the details of the two (honest and dishonest) mining pools, interested readers are referred to Feng and Niu [13], Grunspan and Pérez-Marco [14], Kang et al. [16], [23] and Wang et al. [38]. Comparing with the studies above, this paper proposes a new method with two consecutive rounds of mining competition for analyzing the uncle and nephew blocks, in which we set up a basic relation among the uncle and nephew blocks (see Figure 11) so that the rewards of the uncle and nephew blocks can be estimated easily (see Sections 4 and 8). Obviously, one key finding of this paper is to reveal that the uncle blocks and the nephew blocks must appear in two different rounds of mining competition. This is crucial and interesting in the research of Ethereum.
Based on the above analysis, we summarize the main contributions of this paper as follows:
-
1.
Under the two-block leading competitive criterion, we describe an Ethereum system with one honest mining pool and multiple dishonest mining pools, set up a general tree with multiple block branches where the multiple dishonest block branches can fork at different positions of the one honest block branch, and provide a mathematical representation of the general tree. By using the mathematical representation of tree, we provide an effective method to easily determine the main chain by means of the longest chain principle. (See Sections 2 and 3)
-
2.
By using the mathematical representation of tree, we propose a two-stage mechanism to find the uncle and nephew blocks and then design the uncle block and nephew block rewards in two consecutive rounds of mining competition. (See Sections 4 and 8)
-
3.
We apply the law of large numbers to study some key probabilities in the Ethereum system with multiple mining pools, and define and compute some key ratios: The main chain ratio, the orphan block ratio, the uncle block ratio, the stale block ratio, and the chain quality. Note that the key ratios are necessary and useful in the security analysis of Ethereum systems with multiple mining pools. (See Sections 5 and 6)
-
4.
On the one hand, we provide expression for the long-term growth rate of blockchain by using the renewal reward theory, which is one of the most important indicators for the Ethereum system, where the growth rate of blockchain is the block number in all the main chains increasing per unit time. (See Section 7). On the other hand, once the uncle and nephew block rewards are determined, we provide expressions both for the long-term reward allocation and for the long-term reward allocation rate to each mining pool by using the renewal reward theory. (See Sections 8 and 9)
-
5.
We use some simulation experiments to discuss the Ethereum system with one honest mining pool and two dishonest mining pools, verify how the key probabilities of Ethereum are obtained approximately by using the law of large numbers, and analyze the performance measures of the Ethereum system, for example, the long-term growth rate of blockchain, the long-term reward allocation and the long-term reward allocation rate to each mining pool. We show that the approximative computation of the performance measures of the Ethereum system can have a faster convergence. (See Section 10)
The remainder of this paper is organized as follows. Section 2 describes an Ethereum system with multiple mining pools and provides the mathematical representation of a general tree with multiple block branches. Section 3 gives some examples with one honest mining pool and two dishonest mining pools for analyzing the mathematical representation of the general tree. Section 4 introduces a classification of blocks, gives some conditions under which the orphan block can become an uncle block, and provides a two-stage mechanism to determine the uncle and nephew blocks. Section 5 studies some key probabilities of Ethereum by using the law of large numbers. Section 6 defines some key ratios for the general tree with multiple block branches. Section 7 applies the renewal reward theory to discuss the long-term growth rate of blockchain. Section 8 provides a long-term reward allocation to each mining pool by means of the renewal reward theory. Section 9 applies the renewal reward theory to study the reward allocation rates among the multiple mining pools. Section 10 conducts simulation experiments to analyze the performance measures of the Ethereum system. Section 11 provides some concluding remarks.
2 Model Description
In this section, we describe an Ethereum system with multiple mining pools. The mining competition among the multiple mining pools directly leads to a general tree forked at the different positions of the honest block branch by the multiple dishonest block branches. Based on this, one of our key findings is to provide a mathematical representation for such a tree with multiple block branches. In addition, we introduce some mathematical notations used in our later study.
In a PoW Ethereum with multiple mining pools, the mining competition among the multiple mining pools is a main way to build the blockchain by means of solving the PoW mathematical puzzles. In the process of mining competition, some transactions are first packaged as a block with finite sizes (see Li et al. [20]), and then the block needs a nonce which is found through solving the PoW mathematical puzzle among the multiple mining pools, in which the success of one mining pool is based on its mining power in proportion to the total mining power. Once the nonce is solved by one mining pool and is written into the block, then the block is successfully mined so that it can be pegged to the block branch of this mining pool.
In the multiple mining pools, when the last round of mining competition ends, it is easy to see the honest mining pool is major, so that it can begin to mine from the final block on the previous sub-chain. However, the first block mined by a dishonest mining pool can be connected to any position of the honest sub-chain, including the final block in the last round of mining competition, while it cannot be connected to one dishonest sub-chain mined by the other dishonest mining pools. Based on this, we describe the tree structure with multiple sub-chains. See Figure 1 for more details. Clearly, it is the key to provide a mathematical representation for the tree given in Figure 1.
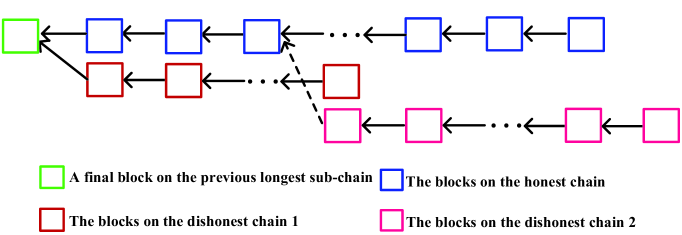
Note that the two-block leading competitive criterion was first proposed in Li et al. [21] in order to discuss the blockchain selfish mining with two mining pools. In this paper, such a two-block leading competitive criterion is further extended to the selfish mining with multiple mining pools. Based on this, we can set up the termination rule of mining competition among the multiple mining pools.
Now, we provide model description for the PoW Ethereum system with multiple mining pools as follows:
(1) Structure of PoW Ethereum system: There are mining pools in the PoW Ethereum system, where there are one honest mining pool and dishonest mining pools for . For simplicity, we regard the blocks or sub-chain mined by the honest mining pool as the honest blocks or sub-chain, and the blocks or sub-chains mined by dishonest mining pools as the dishonest blocks or sub-chains.
(2) Honest mining pool: The honest mining pool in Ethereum follows the PoW protocol with the two-block leading competitive criterion (also see 4-a below). Once a block is mined by the honest mining pool, the complete information of this block is immediately broadcasted to the entire P2P network so that each dishonest mining pool can monitor its block information. Thus, all the dishonest mining pools can learn about the length of the honest sub-chain in a timely manner.
(3) Dishonest mining pools: The dishonest mining pools in Ethereum follow the PoW protocol with the two-block leading competitive criterion (also see 4-b below), and they can carry out various selfish mining attacks. That is, when the dishonest mining pools launch selfish attack, the blocks mined by each dishonest mining pool may not be immediately broadcasted to the entire P2P network. In this case,only a part of the block branch mined by one dishonest mining pool may be pegged on the blockchain when this dishonest mining pool can set up the main chain; while another part of the block branch is left to keep the mining competitive advantage of this dishonest mining pool in the next round of mining competition. Thus, the honest mining pool and the other dishonest mining pools cannot know the accurate information of blocks mined by this dishonest mining pool.
(4) The two-block leading competitive criterion and its modification:
(4-a) If the honest mining pool takes the lead in mining and as long as the number of blocks mined by the honest mining pool is 2 blocks ahead of the second-longest sub-chain mined by one of the dishonest mining pools, then the round of mining competition terminates immediately, and the longest sub-chain mined by the honest mining pool becomes the main chain which is pegged onto the blockchain, while all the other sub-chains mined by the dishonest mining pools become the chains of orphan blocks, all of which are returned to the transaction pool without any new transaction fee.
(4-b) If one dishonest mining pool takes the lead in mining and as long as the number of blocks mined by this dishonest pool is at least 2 blocks ahead of the second-longest sub-chain among the other mining pools, then the sub-chain mined by this dishonest mining pool becomes the main chain, while this dishonest pool may release only a part of the main chain into the blockchain under a basic condition that the part of the main chain is still at least 2 blocks ahead of the second-longest sub-chain, and another part of the main chain is reserved for the next round of mining competition in order to keep the mining competitive advantage of this dishonest mining pool. Once the part of the main chain begins to peg onto the blockchain, the round of mining competition terminates immediately, and all the other sub-chains become the chains of orphan blocks, all of which are returned to the transaction pool without any new transaction fee.
(5) A key mathematical representation for the sub-chains of the tree:
Let denote the tree with sub-chains mined by one honest mining pool and dishonest mining pools, where is the sub-chain mined by the honest mining pool and is the sub-chain mined by the th dishonest mining pool for . We write
where denotes the th block mined by the honest mining pool for . That is, there are blocks in the sub-chain mined by the honest mining pool. Similarly, we write
where represents the number of honest blocks which have been mined by the honest mining pool before the th dishonest mining pool begins to fork after the block such that a new sub-chain with blocks is mined by the th dishonest mining pool, where denotes the th block mined by the th dishonest mining pool for ,. Figure 2 provides a more intuitive understanding for the sub-chains of the tree.
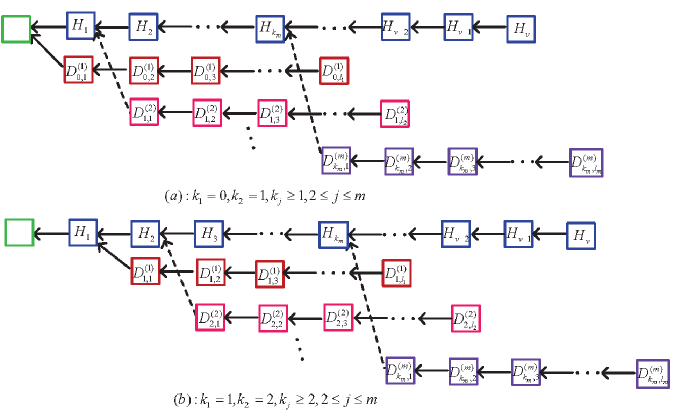
(6) A mathematical expression for the mining terminative rules:
From and for , we write
Further, we write
where, is the length of sub-chain mined by the honest mining pool, and is the generalized sub-chain mined by the th dishonest mining pool for . Based on this, the elements of the set are sorted from the largest to the smallest as follows:
(6-a) If comes from the honest mining pool and , then this round of mining competition terminates immediately; the sub-chain mined by the honest mining pool is the main chain and is pegged onto the blockchain, while all the sub-chains mined by the dishonest mining pools are returned to the transaction pool.
(6-b) If comes from the th dishonest mining pool and , then this round of mining competition may terminate, the sub-chain mined by the th dishonest mining pool is the main chain, and the part with blocks for of the main chain mined by the th dishonest mining pool begins to peg onto the blockchain, while another part with blocks of the main chain is reserved for the next round of mining competition in order to keep the mining competitive advantage of the th dishonest mining pool. In this case, all the sub-chains mined by the other (honest and dishonest) mining pools are returned to the transaction pool.
(6-c) If , then this round of mining competition cannot terminate and the mining pools continue to mine until the two-block leading competitive criterion is satisfied.
(7) The mining rewards: When a round of mining competition terminates, the main chain is pegged onto the blockchain, and all the other sub-chains become orphan blocks which are returned to the transaction pool, waiting for the next round of mining competition.
(7-a) If the main chain comes from the honest mining pool and , then the honest mining pool obtains the rewards of blocks.
(7-b) If the main chain comes from the th dishonest mining pool, and
then the honest mining pool obtains the rewards of blocks. Let , then the th dishonest mining pool obtains the rewards of blocks for . Note that the blocks of the main chain cannot be pegged onto the blockchain, thus they cannot lead to any reward for the th dishonest mining pool.
In addition, the uncle block rewards and associated reference rewards will be assumed and discussed in Section 4.
3 Examples for the Tree Representation
This section provides some examples to analyze the mathematical representation of the general tree with one honest mining pool and two dishonest mining pools. Note that the mathematical representation of tree plays a key role in the study of PoW Ethereum systems with multiple mining pools.
In the PoW Ethereum system with multiple mining pools, the tree with multiple sub-chains expresses the mining competition process among the honest mining pool and the dishonest mining pools. The following theorem provides an essential feature of the tree with multiple sub-chains.
Theorem 1
In a round of mining competition and from the two-block leading competitive criterion, we have
(a) if the sub-chain of the th dishonest mining pool is the first forked sub-chain among all the dishonest mining pools, then either or ; and
(b) if the sub-chain of the th dishonest mining pool is not the first forked sub-chain among all the dishonest mining pools, then .
Proof. (a) We provide the proof by contradiction. We assume that the sub-chain of the th dishonest mining pool is the first forked sub-chain among all the dishonest mining pools, and . In this case, by using the two-block leading competitive criterion, it is easy to see that the honest mining pool is at least 2 blocks ahead of the second-longest sub-chain among the other mining pools, the honest mining pool immediately terminates this round of mining competition. Obviously, it is impossible that the th dishonest mining pool can fork at . Therefore, this gives that either or .
(b) If the sub-chain of the th dishonest mining pool is not the first forked sub-chain among all the dishonest mining pools, then there must be a th dishonest mining pool who is the first one to fork at the tree for . By using (a), either or . In this case, our discussion has two different cases as follows:
(i) When , since the sub-chain of the th dishonest mining pool is not the first forked sub-chain among all the dishonest mining pools, it is easy to see that the th dishonest mining pool can fork at a later position than the dishonest pool , this gives , i.e., . In this case, .
(ii) When , since the sub-chain of the th dishonest mining pool is not the first forked sub-chain among all the dishonest mining pools, it is easy to see that the th dishonest mining pool can fork at a later position than the dishonest pool , this gives , i.e., . In this case, .
From the above two cases, we get that This completes the proof.
In the remainder of this section, we analyze some examples of the honest mining pool and one dishonest mining pool setting up the main chain, respectively.
3.1 The honest mining pool sets up the main chain
If the honest mining pool sets up the main chain in a round of mining competition, this subsection provides four different examples to express the tree with at most three sub-chains.
Tree one: The st and nd dishonest mining pools have not mined any block yet, while the honest mining pool has mined two blocks in a round of mining competition. Thus the round of mining competition is terminated immediately. See Figure 3.
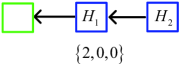
Tree two: The sub-chain lengths of the st and nd dishonest mining pools and the honest mining pool are , and , respectively. If , then the round of mining competition ends due to . If , then the round of mining competition ends due to . See Figure 4.
Tree three: The sub-chain lengths of the two dishonest mining pools are not , and the two sub-chains fork at the same position. If , the round of mining competition ends at the condition under which either or . If , the round of mining competition ends at the condition under which either or . See Figure 5.
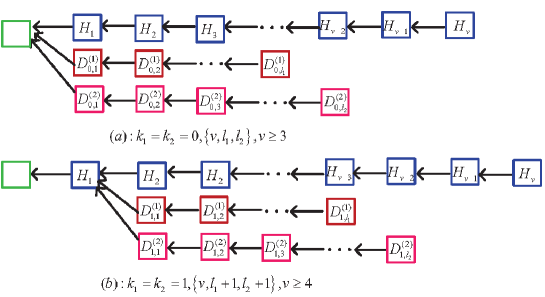
Tree four: The sub-chain lengths of the two dishonest mining pools are not 0, and the two sub-chains fork at two different positions. If , then the round of mining competition ends at the condition under which either or . If , then the round of mining competition ends at the condition under which either or . See Figure 6.
3.2 One dishonest mining pool sets up the main chain
If one dishonest mining pool sets up the main chain in a round of mining competition, this subsection provides four different examples to express the tree with at most three sub-chains.
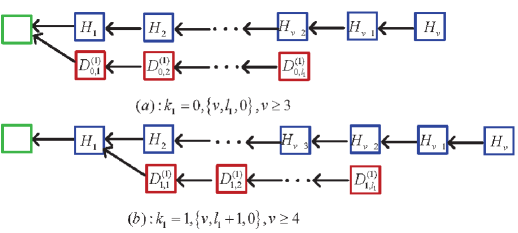
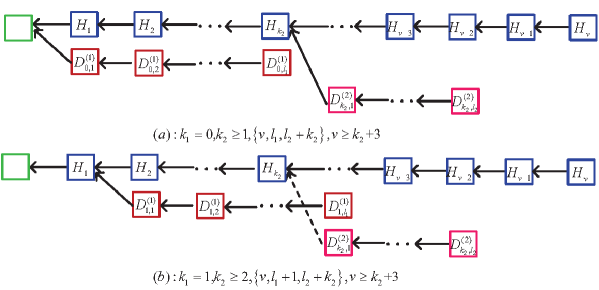
Tree one: The sub-chain length of the st dishonest mining pool is at least , but the sub-chain lengths of the nd dishonest mining pool and the honest mining pool after the st dishonest mining pool forks are . See Figure 7.
Tree two: The sub-chain lengths of the st dishonest mining pool and the honest mining pool after the st dishonest mining pool forks are positive, but the sub-chain length of the nd dishonest mining pool is . If , then the round of mining competition ends at the condition under which . If , then the round of mining competition ends at the condition under which . See Figure 8.
Tree three: The st and nd dishonest mining pools fork at the same position, and ; while the honest mining pool has a positive sub-chain length after the st and nd dishonest mining pools fork, thus, . If , then the round of mining competition ends with the condition under which either or . If , then the round of mining competition ends at the condition under or . See Figure 9.
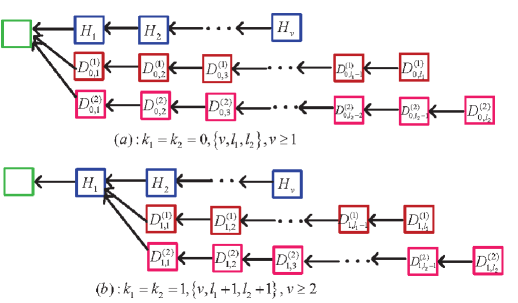
Tree four: The two dishonest mining pools do not fork at the same position, and ; while the honest mining pool has a positive sub-chain length after the st dishonest mining pool forks, i.e., . Now, we consider two cases: , and , . If the st dishonest mining pool sets up the main chain, then the round of mining competition ends at the condition under which either
or
If the nd dishonest mining pool sets up the main chain, then the round of mining competition ends at the condition under which either
or
See Figure 10.
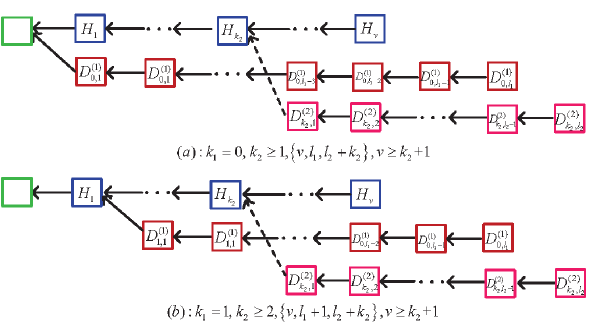
4 The Uncle Blocks and Reward Design
In this section, we introduce a classification of blocks, and give some conditions under which the orphan block can become an uncle block. Furthermore, we provide a two-stage mechanism to determine the uncle blocks and the nephew blocks.
In the multiple sub-chains of the tree corresponding to the PoW Ethereum systems with multiple mining pools, we divide the blocks into five different types: Regular blocks, orphan blocks, uncle blocks, stale blocks, and nephew blocks. Also, the orphan blocks are further divided into the uncle blocks and the stale blocks, if any. See Figure 11 for an intuitive understanding.
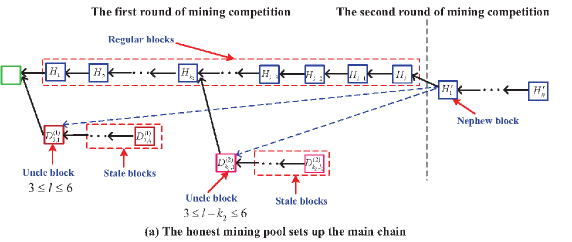
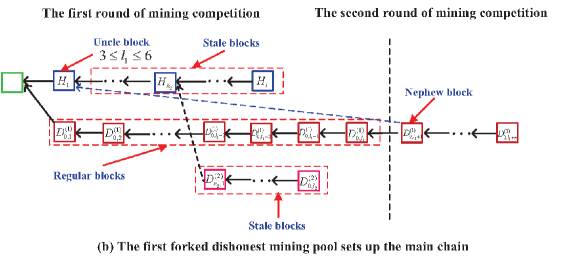
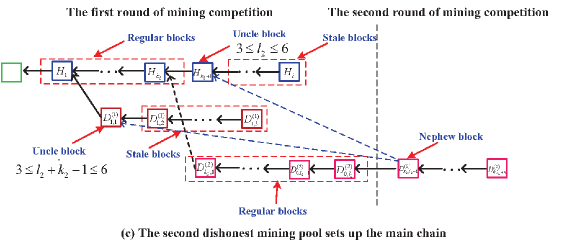
The regular block is a block of the main chain. The uncle block must satisfy a key condition under which the distance between the uncle block and the nephew block does not exceed blocks. The nephew block is the first block in the next round of mining competition, and it is used to determine the uncle blocks from the sub-chains of the tree, as seen in Figure 11. The stale blocks follow from an uncle block in a sub-chain of the tree, or the stale blocks are all the blocks in each sub-chain of orphan blocks.
For the mining pools in Ethereum, their reward include 4 parts: A regular block reward is given by Ethereum, transaction costs (i.e. gas fee), an uncle block reward, and a nephew reference reward. In this paper, we take the unit of economic measure as “block”, in other words, the regular reward given by the Ethereum systems is assumed to be 1.
In the PoW Ethereum system with multiple mining pools, the main purpose of introducing the uncle blocks is to inspire the mining enthusiasm of each mining pool, especially for those mining pools who cannot set up the main chain. In this case, they cannot obtain any reward but have to cover some costs associated with the mining processes, such as electricity, equipment investment, maintenance costs, staff salary, management fees and so on. Thus, providing the uncle block reward and the nephew reference reward can be a necessary and valuable support for the multiple mining pools that take an active part in each round of mining competition.
To show how to allocate the uncle block reward and the nephew reference reward, we provide a two-stage reward allocation mechanism through analyzing the position among the uncle blocks and the nephew blocks. For simplicity of analysis, the uncle blocks are determined at the moment that a round of mining competition has been over, and a nephew block (or the first block) is just generated in the next round of mining competition. That is, to determine the uncle blocks, we first need to have the nephew block in order that we can judge that the distance between the uncle block and the nephew block does not exceed blocks. Note that the nephew block comes from two different cases: (i) If all the blocks of the main chain are released at the ending moment of the last round of mining competition, then the nephew block is the first block mined by one of the mining pools in the next round of mining competition. (ii) If there are some blocks of the main chain reserved at the ending moment of the last round of mining competition, then these reserved blocks must come from one dishonest mining pool, and the nephew block is the first one of the reserved blocks.
It is worthwhile to note that such a reward allocation is well related to the distance between the uncle block and the nephew block. Table 1 shows the uncle block rewards at some different distances.
| Distance | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Uncle reward | 7/8 | 6/8 | 5/8 | 4/8 | 3/8 | 2/8 |
In what follows we discuss some conditions under which the orphan block can become an uncle block. Our description contains two different cases as follows:
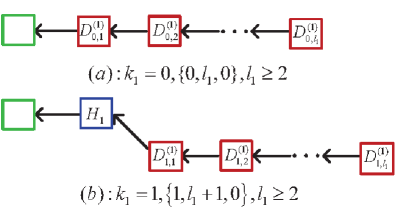
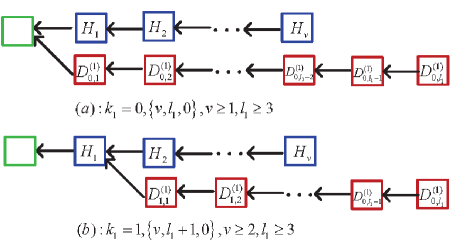
Case one: If the honest mining pool sets up the main chain, then one of the orphan blocks mined by the th dishonest mining pool becomes an uncle block and must satisfy the following two conditions (a-1) and (a-2), also see (a) of Figure 11.
(a-1) The distance between the orphan block and its corresponding nephew block does not exceed 7 blocks; and
(a-2) the orphan block is the first block mined by the th dishonest mining pool.
Case two: If the th dishonest mining pool sets up the main chain, then either one of the orphan blocks mined by the th dishonest mining pool for or one of the orphan blocks mined by the honest mining pool becomes an uncle block and must satisfy the following two conditions (b-1) and (b-2), also see (b) and (c) of Figure 11.
(b-1) The distance between the orphan block and its corresponding nephew block does not exceed 7 blocks; and
(b-2) either the orphan block is the first block mined by the th dishonest mining pool or the orphan block is the first block mined by the honest mining pool.
In addition to the uncle reward given in a round of mining competition, we still need to provide a reward to the nephew block, called the nephew reference reward, which is given in the next round of mining competition. A nephew block can obtain the nephew reference reward: , where is the number of uncle blocks in this round of mining competition. Note that, our above reward allocation is designed in two consecutive rounds of mining competition, and, thus, is called a two-stage reward allocation mechanism.
5 The Law of Large Numbers
In this section, we apply the law of large numbers to study some key probabilities, which are necessary and useful in our later study, such as the key ratios of Ethereum, the growth rate of blockchain, the reward allocation rates among the mining pools, and so forth.
In a round of mining competition, both the honest mining pool and one of the dishonest mining pools are possible to set up the main chain. Now, we provide an analysis for the number of main chains that can be set up by either the honest mining pool or the th dishonest mining pool. During the rounds of mining competition, we denote by and the numbers that the honest mining pool and the th dishonest mining pool can set up the main chain, respectively. It is clear that , , and . Thus we have
In the PoW Ethereum system with multiple mining pools, the competitively mining processes can be repeated round after round, as we repeat by the similar experiments round after round under the same conditions. Thus, we can apply the law of large numbers to study the frequencies: and , and to show that they can steadily approach some fixed values for . The following two theorems are obvious by the law of large numbers, and their proof are easy and omitted here for brevity.
Theorem 2
In the PoW Ethereum system with multiple mining pools, by using the law of large numbers, as , we have
and for
Also, it is clear that
When the honest mining pool sets up the main chain, during the rounds of mining competition, we denote by , and the numbers that the honest mining pool and the th dishonest mining pool can contain one nephew block, and the th dishonest mining pool can contain one uncle block, respectively.
When the th dishonest mining pool sets up the main chain for , during the rounds of mining competition, we denote by , , , and the numbers that the th dishonest mining pool, the honest mining pool, and the th dishonest mining pool can contain one nephew block, and the honest mining pool and the th dishonest mining pool can contain one uncle block, respectively.
Theorem 3
In the PoW Ethereum with multiple mining pools, by using the law of large numbers, as , for ,
and for and ,
It is clear that and for and and for and .
6 Some Key Ratios of Ethereum
This section defines some key ratios of the PoW Ethereum system with multiple mining pools, and provides a detailed analysis for the key ratios by means of the mathematical representation of tree with multiple sub-chains.
In a round of mining competition, the multiple mining pools use their mined blocks to set up a tree with multiple sub-chains. From the tree, we can classify five different types of blocks: Regular blocks, orphan blocks, uncle blocks, nephew blocks, and stale blocks. Based on this, we can set up some key ratios of the PoW Ethereum system with multiple mining pools. To this end, we define some key ratios of Ethereum from two perspectives of efficiency and benefit, such as chain quality, main chain length ratio, orphan block ratio, uncle block ratio, and stale block ratio.
Definition 1
In a round of mining competition, we define
(a) The chain quality : It is defined as the ratio that some blocks on the main chain mined by the honest mining pool occupy all the blocks of the main chain.
(b) The main chain length ratio : It is defined as the ratio that the number of blocks on the main chain over the number of blocks on the tree.
If the honest mining pool sets up the main chain, from and for , we have
and
If the th dishonest mining pool sets up the main chain for , due to the part with blocks for of the main chain are pegged on the blockchain, while the blocks of the main chain cannot be observed by all the other mining pools in the P2P network, then
and
Definition 2
In a round of mining competition, we define
(a) The orphan block ratio : It is defined as the ratio of the number of orphan blocks to the number of blocks on the tree.
(b) The uncle block ratio : It is defined as the ratio of the number of uncle blocks to the number of blocks on the tree.
It is easy to see from Definitions 1 and 2 that
and
In what follows, we first express the orphan block ratio . To this end, our computation needs to consider two different cases: The honest mining pool sets up the main chain, and one dishonest mining pool sets up the main chain.
If the honest mining pool sets up the main chain, then
| (1) |
If the th dishonest mining pool sets up the main chain for , due to the part with blocks for of the main chain are pegged onto the blockchain, while the blocks of the main chain cannot be observed by all the other mining pools in the P2P network, then
| (2) |
Now, we compute the uncle block ratio . Note that such a computation is a little bit complicated.
To compute the uncle block ratio , it is necessary to first determine how many orphan blocks can become uncle blocks. To this end, our computation also needs to consider two different cases: The honest mining pool sets up the main chain, and one dishonest mining pool sets up the main chain.
Case one: The honest mining pool sets up the main chain
In this case, from the tree with multiple sub-chains (e.g., see (a) of Figure 11), it is easy to determine the nephew block, and the uncle blocks and their number. Note that is the number of uncle blocks in the tree in this round of mining competition, thus the uncle block ratio is given by
| (3) |
Case two: One dishonest mining pool sets up the main chain
In this case, we assume that the th dishonest mining pool sets up the main chain, it is clear that . We further assume that the part with blocks for of the main chain are pegged onto the blockchain, while another part with blocks of the main chain is left in the next round of mining competition. It is easy to see that is the first block in the next round of mining competition. Now, our first task is to use the block to determine which blocks of and for can become uncle blocks. If is an uncle block, then for , is not an uncle block for
From the tree with multiple sub-chains (e.g., see (b) and (c) of Figure 11), it is easy to determine the nephew block, and the uncle blocks and their number. Note that is the number of uncle blocks in the tree, thus the uncle block ratio is given by
| (4) |
In the remainder of this section, we apply the law of large numbers to discuss the key ratios of the Ethereum system.
In the th round of mining competition, we denote by , , , and the chain quality, the main chain length ratio, the orphan block ratio, and the uncle block ratio, respectively. We assume that the part with blocks for of the main chain mined by the th dishonest mining pool are pegged onto the blockchain, where and are the first and second elements of the sorted set related to the th dishonest mining pool, respectively.
Theorem 4
In the PoW Ethereum system with multiple mining pools, by using the law of large numbers, as , we have
where
Proof. The proof is easy. We only take the first one as a example. To do this, we need to consider two different cases:
Case one: If the the honest mining pool sets up the main chain in the th round of mining competition for . In this case, we have , and
This gives that as ,
Case two: If the th dishonest mining pool sets up the main chain in the th round of mining competition for . In this case, it is worthwhile to note that is the number of honest blocks which have been mined by the honest mining pool before the th dishonest mining pool begins to fork to a new sub-chain with blocks, and note that the part with blocks of the main chain are pegged onto the blockchain, thus we have
Since the competitively mining processes of the multiple mining pools are repeated round after round, the random variable can be repeated by the similar experiments round after round under the same conditions. Based on this, the random variable sequence can be regarded as independent and identically distributed. When the number that the th dishonest mining pool can set up the main chain is , we obtain that as
which holds for each . This gives that as ,
From the above two cases, we get
This completes the proof.
7 The Growth Rate of Blockchain
In this section, we apply the renewal reward theory to study the long-term growth rate of blockchain in the PoW Ethereum system with multiple mining pools.
In the th round of mining competition, we denote by the number of blocks on the main chain when the honest mining pool sets up the main chain, denote by and the number of honest blocks first mined by the honest mining pool and the number of dishonest blocks mined by the th dishonest mining pool after forked when the th dishonest mining pool sets up the main chain, respectively. Note that the part with blocks of the main chain is pegged onto the blockchain.
Lemma 1
In the PoW Ethereum system with multiple mining pools, by using the law of large numbers, as , we have
for
and
where , , and are the means of four random variables , and , respectively.
It is worthwhile to note that in the PoW Ethereum system, the competitively mining processes of the multiple mining pools are repeated round after round, as we repeat the experiments under the same conditions. Thus, the moments that one round of mining competition is over and the next round of mining competition begins immediately are all renewal points. That is, let be the th moment that the th round of mining competition is over and the th round of mining competition begins immediately. In fact, represents a time interval that the th round of mining competition is underway. For simplicity of analysis, we assume that , i.e., the first round of mining competition begins at time . Let then { is a renewal process.
We assume that there are blocks of the main chain in the time interval , and is independent of the time interval . Let be the number of blocks of all the main chains generated in the time interval . Then, the following theorem provides the growth rate of blockchain in the PoW Ethereum system with multiple mining pools.
Theorem 5
In the PoW Ethereum system with multiple mining pools, if and , then as , we have
| (5) |
| (6) |
where
Proof. We give the proof for the equation 5 only. We write
Note that
is the time length of the renewal periods, and the random variables are independent and identically distributed, for . At the same time, the random variables are also independent and identically distributed,
Note that as By the strong law of large numbers, we obtain that as
By using the elementary renewal theorem (Chapter 7 of [31]), we obtain that
Therefore, we obtain that as
This completes the proof.
8 Average Reward Allocation among the Mining Pools
In this section, we propose a new method to compute the uncle block and nephew block rewards in two consecutive rounds of mining competition, and provide expressions for the long-term reward allocation and for the long-term reward allocation rate to each mining pool by using the renewal reward theory.
we provide a computational method of the reward allocation among the honest mining pool and the th dishonest mining pools.
To set up the reward allocation, it is easy to see that a regular block is paid the reward of block; an uncle block is paid the reward of blocks for , where is the distance between the uncle block and the nephew block; a nephew block is paid the reward of blocks, where is the number of uncle blocks; and a stale block is paid no reward.
In the PoW Ethereum system with multiple mining pools, it is worthwhile to note that in the tree with multiple sub-chains, the main chain can be obtained by either the honest mining pool or one of the dishonest mining pools, thus our reward allocation is considered as the following two different cases.
Case one: The honest mining pool sets up the main chain
In this case, by observing (a) of Figure 11, we consider two different cases as follows:
(i) The reward of the honest mining pool is given by
where is the number of blocks in the main chain, is the reward of a nephew block which is the first block of the main chain. Note that the nephew block refers to the uncle blocks in the previous round of mining competition. Thus we obtain
(ii) Note that each of the dishonest mining pools may mine only the orphan blocks, that is, either the uncle blocks or the stale blocks. In addition, it has a nephew block either if the main chain of the previous round of mining competition is completitively pegged onto the blockchain, and this dishonest mining pool is the first one to mine a block, that is, the firstly mined block is the nephew block; or if this dishonest mining pool sets up the main chain in the previous round of mining competition, and a non-empty part of this main chain is left to this round of mining competition, that is, the nephew block is the first block of the non-empty part. Based on this, the reward of the th dishonest mining pool is given by
where is the reward that if the th dishonest mining pool has an uncle block, and
for , where is the distance between the uncle block and the nephew block of the next round of mining competition; and
where is the number of uncle blocks in the previous round of mining competition if the nephew block belongs to the th dishonest mining pool. Based on this, we have
and
Case two: The th dishonest mining pool sets up the main chain
In this case, by observing (b) and (c) of Figure 11, we consider three different cases as follows:
(i) The reward of the th dishonest mining pool
Note that the th dishonest mining pool sets up the main chain, it is clear that . We assume that the part with blocks for of the main chain are pegged onto the blockchain, while another part with blocks of the main chain is left to the next round of mining competition.
The reward of the th dishonest mining pool is given by
where is the number of blocks in the part of the main chain, which is pegged onto the blockchain; and
where is the number of uncle blocks in the previous round of mining competition if the nephew block belongs to the th dishonest mining pool. Based on this, we have
(ii) The reward of the honest mining pool
If the th dishonest mining pool sets up the main chain, then the honest mining pool can mine only the orphan blocks after the th dishonest mining pool forks, that is, either the uncle blocks or the stale blocks. In addition, it may have a nephew block if the honest mining pool is the first one to mine a block in this round of mining competition. In this case, the reward of the honest mining pool contains the reward of regular blocks, the reward of one uncle block and the reward of a nephew block. Based on this, the reward of the honest mining pool is given by
where is the reward that if the honest mining pool has an uncle block, and
for , where is the distance between the uncle block and the nephew block of the next round of mining competition; and
where is the number of uncle blocks in the previous round of mining competition if the nephew block belongs to the honest mining pool. Based on this, we have
and
(iii) The reward of the th dishonest mining pool for
If the th dishonest mining pool sets up the main chain, then the th dishonest mining pool can mine only the orphan blocks, that is, either the uncle blocks or the stale blocks. In addition, it has a nephew block either if the main chain of the previous round of mining competition is completely pegged onto the blockchain, and the th dishonest mining pool is the first one to mine a block, that is, the firstly mined block is the nephew block that belongs to the th dishonest mining pool; or if the th dishonest mining pool sets up the main chain in the previous round of mining competition, and a non-empty part of this main chain is left to this round of mining competition, that is, the nephew block is the first block of the non-empty part. Based on this, the reward of the th dishonest mining pool is given by
where is the reward that if the th dishonest mining pool has an uncle block, and
for , where is the distance between the uncle block and the nephew block of the next round of mining competition; and
where is the number of uncle blocks in the previous round of mining competition if the nephew block belongs to the th dishonest mining pool. Based on this, we have
and
When the reward of each mining pool is regarded as random variables, we can apply the law of large numbers to further study the reward of each mining pool. In this situation, we obtain some interesting results, which can be applied to solving many practical problems owing to the fact that by using the law of large numbers, our experimental reward of each mining pool can steadily approach their corresponding fixed values. Such a statistical method is effective and useful in the study of the PoW Ethereum system with multiple mining pools, because analysis of the tree with multiple sub-chains always has a higher computational complexity.
In what follows, we apply the law of large numbers to study the reward obtained by each multiple mining pool in the PoW Ethereum system. Let and be the reward obtained by the honest mining pool or the th dishonest mining pool in the th round of competition for .
Theorem 6
In the PoW Ethereum system with multiple mining pools, by using the law of large numbers, as , we have
and for
Proof. The proof is easy. We only take the first one as a proof example. Here, we also need to consider two different cases:
Case one: The honest mining pool sets up the main chain in the th round of mining competition for . In this case,
where in the th round of mining competition, and are the number of blocks in the main chain, and the reward of a nephew block which is the first block of the main chain, respectively. Note that the main chain is mined by the honest mining pool.
Note that the competitively mining processes of the multiple mining pools are repeated round after round, the random variables and (thus ) can be repeated by the experiments round after round under the same conditions. Based on this, the random variable sequences and (thus ) can be regarded as independent and identically distributed. Therefore, we obtain
and
This gives
Case two: The th dishonest mining pool sets up the main chain in the th round of mining competition for .
In this case, the honest mining pool can mine only the orphan blocks, that is, either the uncle blocks or the stale blocks. In addition, it may have a nephew block if the honest mining pool is the first one to mine a block in a round of mining competition, that is, the firstly mined block is the nephew block. Thus, we have
where in the th round of mining competition, is the reward of uncle block if the honest mining pool has an uncle block.
Note that the competitively mining processes of the multiple mining pools are repeated round after round, the random variables and (thus ) can be repeated by the experiments round after round under the same conditions. Based on this, the random variable sequences and (thus ) can be regarded as independent and identically distributed. Therefore, we obtain
and
This gives
Therefore, we can get that as
This completes the proof.
9 Reward Rates Allocated among the Mining Pools
In this section, we apply the renewal reward processes to study the long-term reward allocation rates among the multiple mining pools.
Note that the competitively mining processes of the multiple mining pools are repeated round after round, as we repeat the experiments under the same conditions. Thus, the moments that one round of mining competition is over and the next round of mining competition begins immediately are all renewal points. Let be the th moment that the th round of mining competition is over and the th round of mining competition begins immediately. In fact, represents such a time interval that the th round of mining competition is underway. For simplicity, we assume that . Let then { is a renewal process.
Let and be the rewards allocated to the honest mining pool and the th dishonest mining pool in the time interval , respectively. Meanwhile, and are independent of the time interval . Let and be the rewards allocated to the honest mining pool and the th dishonest mining pool in the time interval . The following theorem respectively provides the reward allocation rates to the honest mining pool and the th dishonest mining pool in the PoW Ethereum system with multiple mining pools.
Theorem 7
In the PoW Ethereum system with multiple mining pools, if and , then as ,
| (7) |
| (8) |
| (9) |
| (10) |
where
Proof. We give the proof for equation 7 only. To do this, we write
Note that
is the time length of the renewal periods, and the random variables are independent and identically distributed, for . At the same time, the random variables are also independent and identically distributed,
Note that By the strong law of large numbers, we obtain that as
According to the elementary renewal theorem (Chapter 7 of [31]), we obtain that
Therefore, we obtain that as
This completes the proof.
10 Simulation Experiments
In this section, we use some simulation experiments to discuss the Ethereum system with one honest mining pool and two dishonest mining pools, verify how the key probabilities of Ethereum are obtained approximately by using the law of large numbers, and analyze the performance measures of the Ethereum system by means of the renewal reward theorem.
10.1 An Experiment Design
In order to analyze the competitive mining processes of multiple mining pools, our simulation experiment is designed as follows:
(1) In our simulation, we take a round of mining competition as a sampling, and then we repeat such a sampling round after round.
(2) Under the two-block leading competitive criterion, one dishonest mining pool may release a part of its sub-chain into the Ethereum system. Here, our simulation experiments consider the mining rule: . That is, the longest sub-chain length is 2 blocks longer than the second-longest sub-chain in the system.
Although is taken as a terminate rule to end a round of mining competition among the multiple mining pools, the dishonest mining pools can fork at any position of the sub-chain mined by the honest mining pool. Thus, the tree with multiple block sub-chains is still more complicated, and also represents the general practical mining structure of the PoW Ethereum system with multiple mining pools.
(3) For simplicity of simulation, our design is to consider the mining processes of the multiple mining pools. To do this, we take random variables as
where, is the block-generating and block-pegging time of the th mining pool, is the mining power of the th mining pool, and is the communication ability of the P2P network. Note that is used to show the independence between the mining power and the communication ability. At the same time, it is easy to see that decreases as or increases, this is consistent with our intuitive understanding on the mining times.
We assume that the random variable obeys an exponential distribution of the mean seconds, where the seconds are always chosen as the expected mining time of one block in the PoW Ethereum system. Let be a random number generated by the exponential distribution of , then we have
10.2 Simulation and results
In this subsection, we describe and analyze some interesting simulation results.
(1) The law of large numbers
Note that the probability that each mining pool wins the mining competition plays a key role in our research on the key ratios, the growth rate of blockchain, the reward allocation rates and so on. Here, it is necessary to verify how this probability is obtained approximately by using the law of large numbers. To this end, we take and
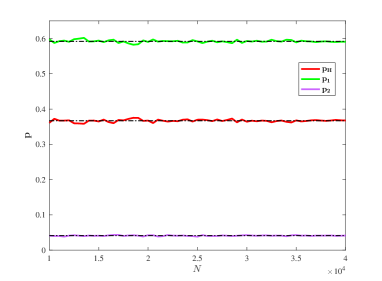
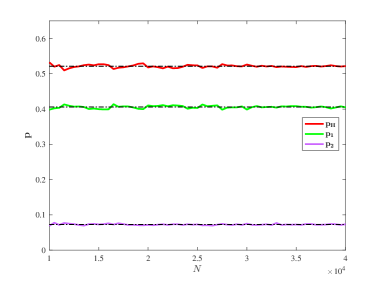
From Figure 12, it is easy to see that the three probabilities: and fluctuate around a certain value. This shows that the laws of large numbers is well applied to determine these probabilities.
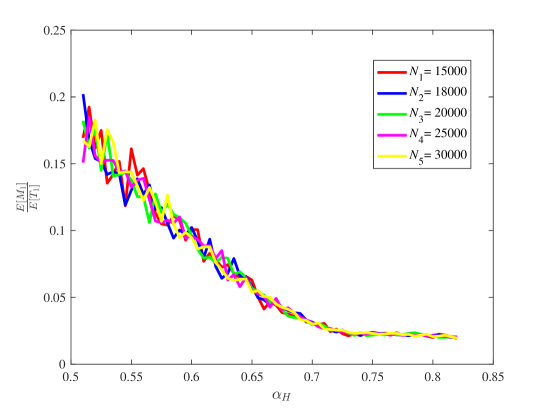
From the left part of Figure 12, it is seen that while in the right of the Figure 12. It shows that as increases, there exists a such that Furthermore, it is observed that as increases, the probability of the dishonest mining pools decreases. Thus, the influence of the dishonest pools decreases as increases.
In order to observe the interesting value we use a special experiment. Let Each of our simulations with rounds of mining competition is repeated times to calculate the average of the approximate probabilities and We denote the two average values by and . The results are shown in Figure 13.
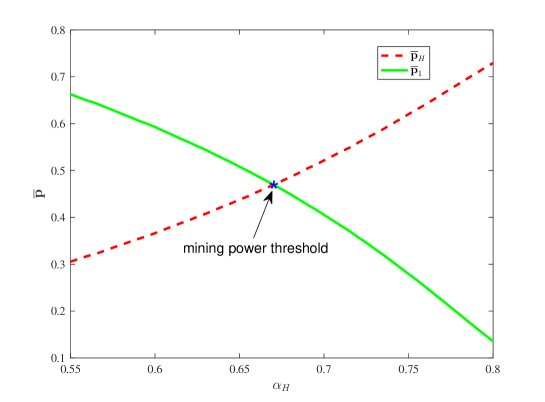
From Figure 13, it is seen that as increases, the average probability increases, and the average probability decreases. Also, it is observed that there exists a when , ; and when , . In our simulation experiments, we obtain that the confidence interval of the mining power is . This shows that when the mining power of the st dishonest mining pool exceeds the mining power threshold , the st dishonest pool has the biggest probability of setting up the main chain. Based on this, the dishonest mining pool with a smaller mining power can have the same probability of setting up the main chain as the honest mining pool. This is why the dishonest mining pool may fork at any position of the honest sub-chain.
In the remainder of this subsection, we explore how the performance measures of the Ethereum system depend on the mining powers of the three mining pools. To this end, we take the parameters as follows: The mining power of the honest mining pool the mining power of the nd dishonest mining pool and the mining power of the st dishonest mining pool the rate at which the block is pegged to the corresponding sub-chain , and the numbers of mining competition rounds are .
(2) Some key probabilities vs.
From Figure 14, it is seen that each of the probabilities is stably close to a certain value. This shows that the law of large numbers is successfully applied in our computation. See Theorem 3 for a comparison.
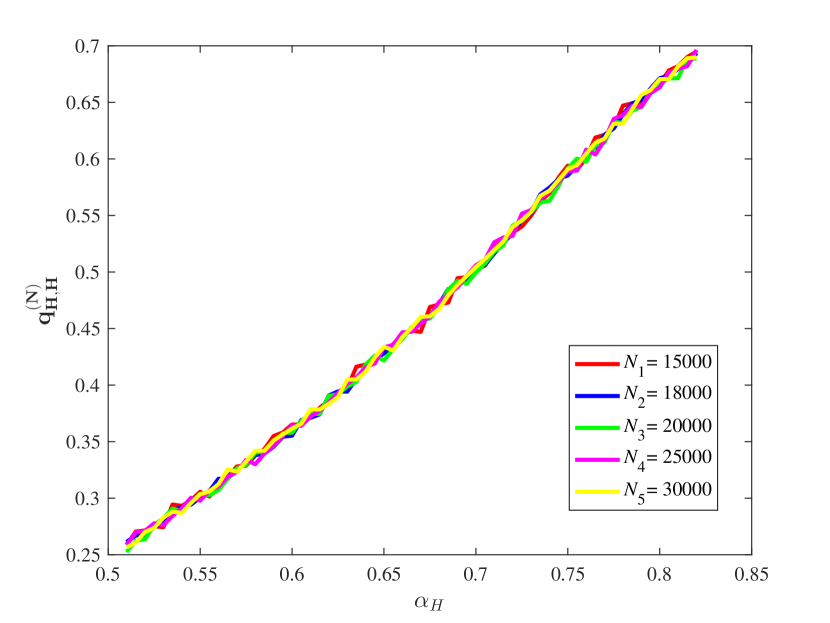
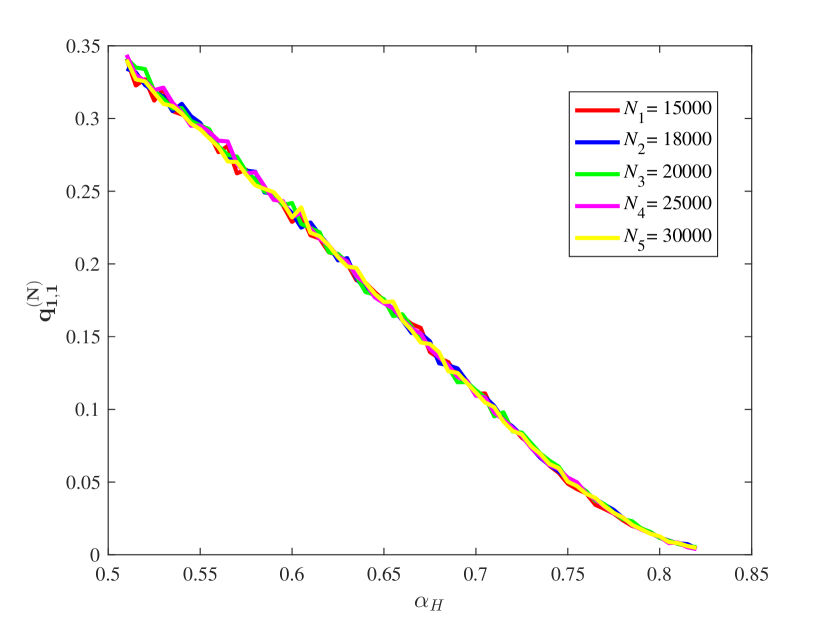
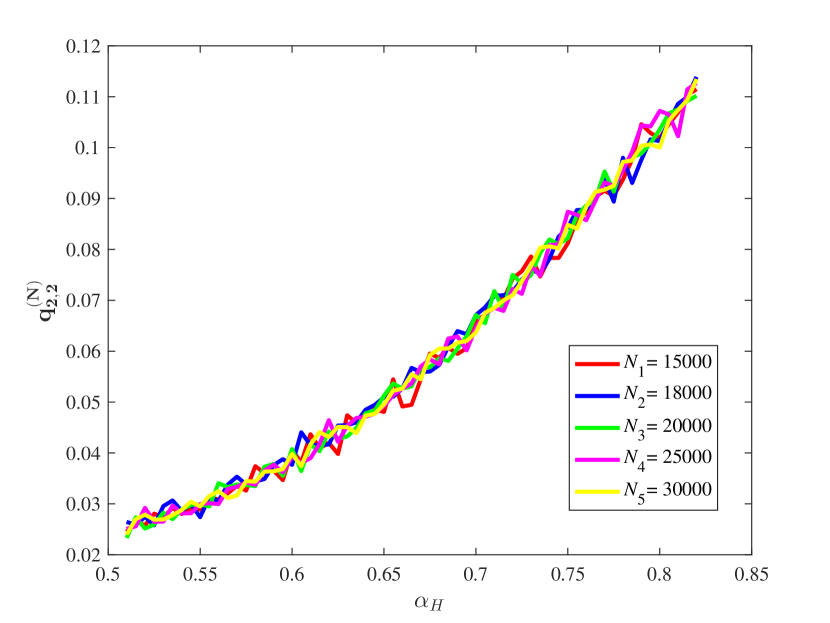
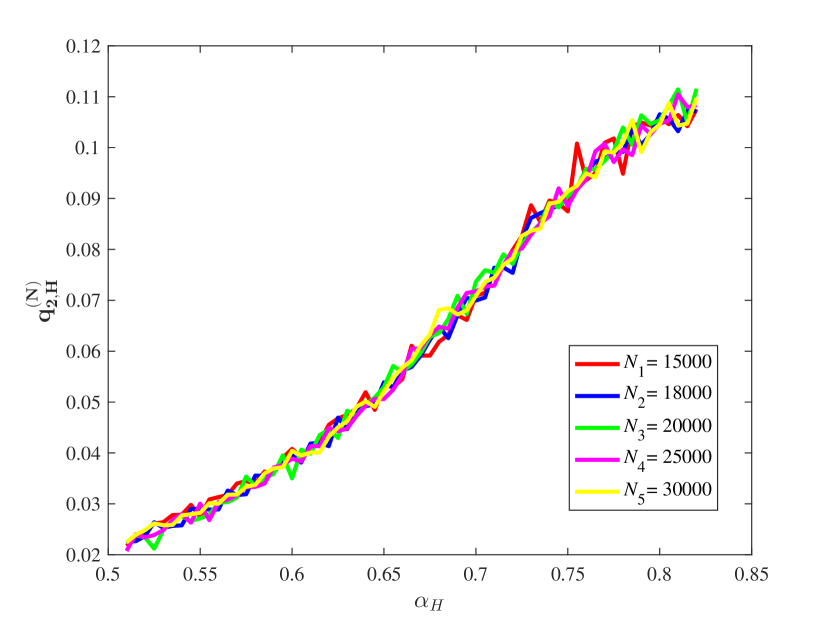
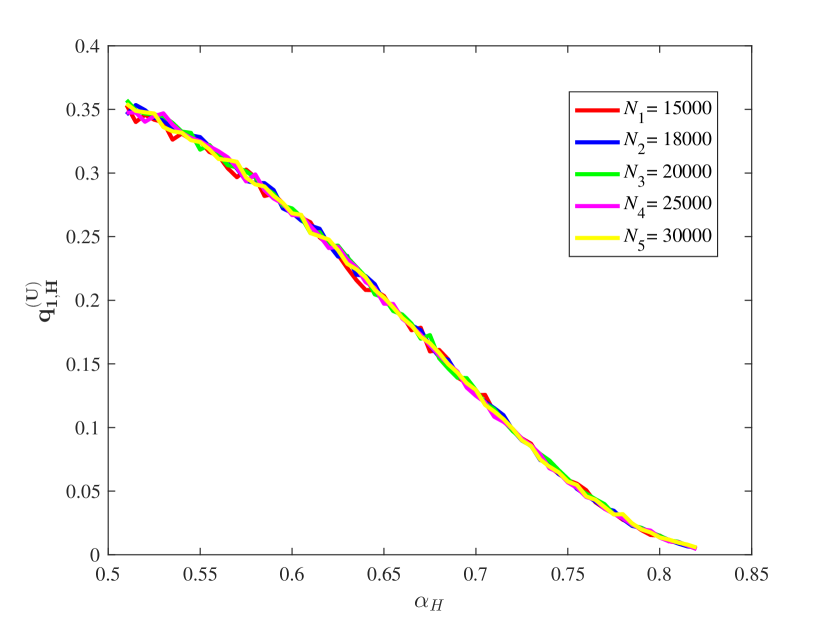
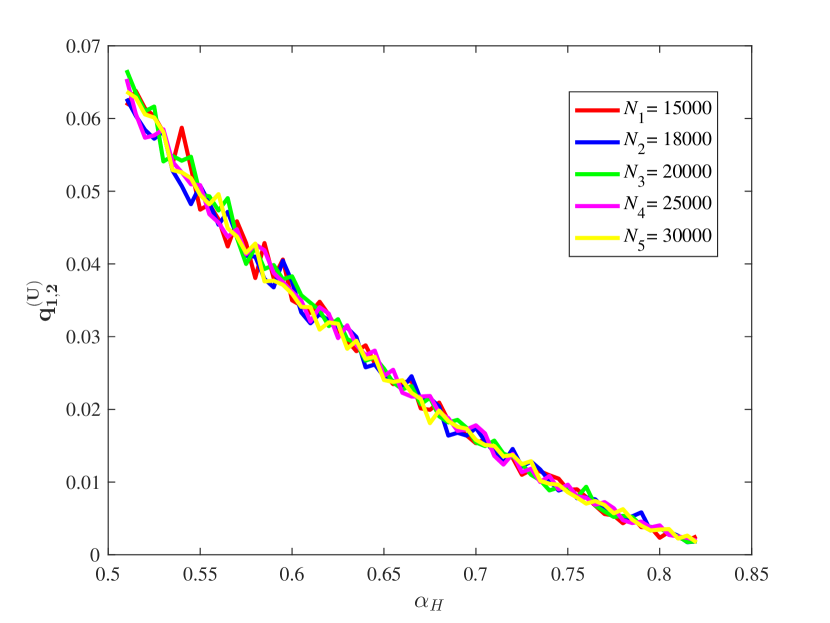
(3) Some key ratios vs.
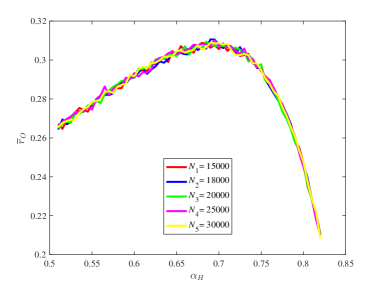
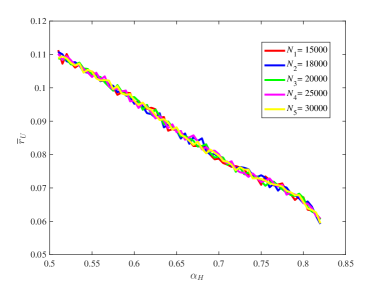
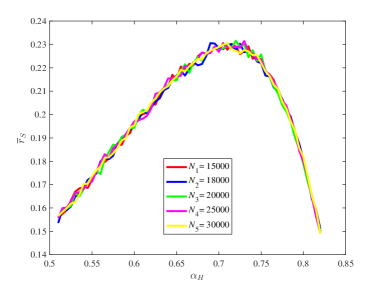
From Figure 15, it is observed that for some different values of the key ratios , , , and are all approximately stable in our computation by means of the law of large numbers. Also, the chain quality increases as increases, while the uncle block ratio decreases as the increases. For the main chain length ratio it first decreases and then increases as the increases. For the stale block ratio (resp. ), it first increases and then decreases as increases. It shows from and that when the mining power of the honest mining pool is close to , the mining competition among the three mining pools is the most intense, so that a lot of mining resources are wasted.
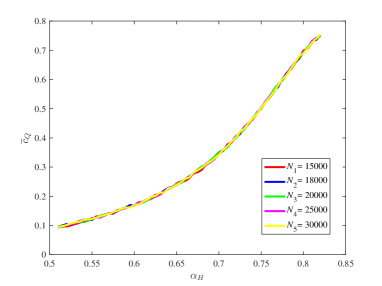
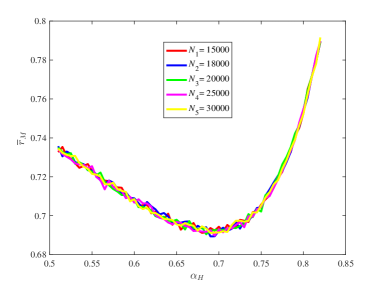
(4) The growth rate of blockchain vs.
From Figure 16, we can see that for some different values of , the growth rate of the blockchain can be effectively computed by means of the law of large numbers and the renewal theorem. In addition, there exists a value such that when , the growth rate of blockchain decreases as increases; while when , the growth rate of blockchain almost unchanged as increases. It indicates that the growth rate of blockchain reaches the lowest level once the honest mining pool masters the major mining power of the entire network. Also, it shows from the Figure 16 that the total mining power of the Ethereum system is dispersed into the multiple mining pools benefits the growth rate of blockchain.
(5) The reward of the honest mining pool vs.
Figure 17 shows the reward of the honest mining pool. For some different values of , the reward can be approximately computed by means of the law of large numbers. Also, the reward increases as increases, which is consistent with the fact that the reward of the honest mining pool is positively correlated with its mining power.
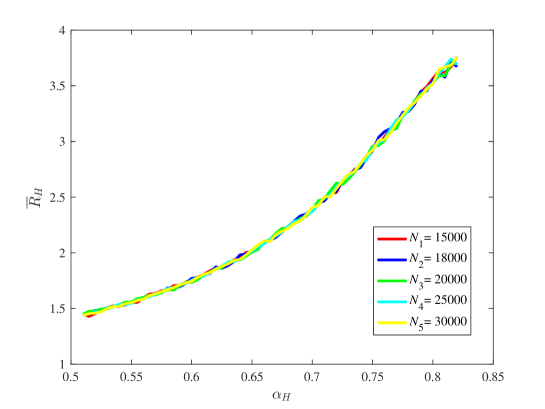
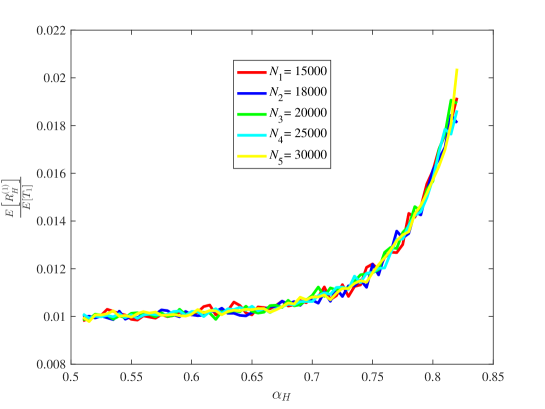
(6) The reward allocation rate of the honest mining pool vs.
Figure 18 shows the reward allocation rate of the honest mining pool. For different values of , the reward allocation rate of the honest mining pool can be effectively computed by using the law of large numbers and the renewal theorem. Also, the reward allocation rate increases as increases, which is also consistent with the fact that the reward allocation rate of the honest mining pool is positively correlated with its mining power.
11 Concluding Remarks
The growth of the PoW Ethereum system with multiple mining pools has created the need for not only development of blockchain technology but also setting up a general mathematical representation of tree and dealing with the multi-dimensional stochastic systems related to the multiple block branches of tree. In general, the research on such a tree and associated mathematical analysis is very difficult and challenging. It is worthwhile to note that our mathematical representation of tree is the first one in the study of blockchain with multiple mining pools, and it is different from that tree of the GHOST protocol given in Sompolinsky and Zohar [32, 33].
For a blockchain system with two mining pools, Eyal and Sirer [12] found the selfish mining and constructed a simple tree with two block branches. Following the tree with two block branches, Li et al. [21] established the two-dimensional Markov (reward) processes to analyze the efficiency and benefit of blockchain. However, so far a little research has worked on the blockchain systems with multiple mining pools although we need to answer questions such as how to mathematically represent a general tree with multiple block branches and how to analyze a complicated multi-dimensional stochastic system running on the general tree. It is obvious that the study of PoW Ethereum system with multiple mining pools will need to apply the multi-dimensional stochastic processes on a general tree, even simply, the fluid and diffusion approximations on a general tree.
In this paper, we described a PoW Ethereum system with multiple mining pools, which is controlled by the two-block leading competitive criterion proposed in Li et al. [21]. Here, a block branch will be generated by only one mining pool, Thus the mining competition among the multiple mining pools can generate a general tree with multiple block branches. When observing the general tree, one of our key findings is to learn that the block branches of the multiple dishonest mining pools can be forked at any (different) positions of the block branch of one honest mining pool. Based on this, we can provide a mathematical representation for the general tree with multiple block branches. Also, we can easily determine the main chain by means of the principle of longest chain, e.g., see Li et al. [21] for the blockchain with multiple mining pools.
By using the tree representation and observing multiple rounds of mining competitions, we can provide a block classification of Ethereum: Regular blocks (i.e., the main chain), orphan blocks, uncle blocks, stale blocks, and nephew blocks, and set up an approximate computation for the key probabilities of generating the different types of blocks by applying the law of large numbers. Based on the key probabilities, together with the tree representation, we develop an economic framework for computing the rewards allocated to the multiple mining pools. This is one of our key theoretical findings in the study of PoW Ethereum system with multiple mining pools.
By applying the renewal reward theorem, we further discuss the growth rate of blockchain, the reward allocation among the multiple mining pools, and the reward rates allocated among multiple mining pools, three of which become the key performance measures of PoW Ethereum system with multiple mining pools. Furthermore, we use simulation experiments to verify our theoretical results, and shows that our approximate computation is fast and effective for dealing with the three performance measures. Therefore, this paper provides a powerful tool for the performance evaluation of the PoW Ethereum system with multiple mining pools.
To the best of our knowledge, this paper is the first one to provide the mathematical representation of general tree, and to analyze the PoW Ethereum system with multiple mining pools through applying the law of large numbers and the renewal reward theorem. Therefore, we hope that our methodology and results given in this paper are applicable to the study of more general PoW Ethereum system with multiple mining pools. Along the research line, there are still a number of interesting directions for future research:
-
•
Setting up a new tree representation for the PoW Ethereum system with multiple honest mining pools and multiple dishonest mining pools. In the more complicated case, how to determine the main chain from such a tree? How to give the performance evaluation of the PoW Ethereum systems?
-
•
Developing some more effective simulation techniques in the study of PoW Ethereum system with multiple (honest and dishonest) mining pools through applying the law of large numbers and the renewal reward theorem.
-
•
Developing fliud approximation and/or diffusion approximation to analyze the PoW Ethereum system with multiple (honest and dishonest) mining pools.
-
•
Providing optimal methods and dynamic control (e.g., Markov decision processes and stochastic game) in the study of PoW Ethereum system with multiple (honest and dishonest) mining pools.
Acknowledgements
Quan-Lin Li was supported by the National Natural Science Foundation of China under grants No. 71671158 and 71932002.
References
- [1] Atzei, N., Bartoletti, M., & Cimoli, T. (2017). A survey of attacks on ethereum smart contracts (sok). In: International conference on principles of security and trust, Springer, pp. 164-186.
- [2] Augusto, L., Costa, R., Ferreira, J., et al. (2019). An application of ethereum smart contracts and IoT to logistics. In: 2019 International Young Engineers Forum, IEEE, pp. 1-7.
- [3] Aung, Y. N., & Tantidham, T. (2019). Ethereum-based emergency service for smart home system: smart contract implementation. In: The 21st International Conference on Advanced Communication Technology, IEEE, pp. 147-152.
- [4] Bai, Q., Zhou, X., Wang, X., Xu, Y., Wang, X., & Kong, Q. (2019). A deep dive into blockchain selfish mining. In: International Conference on Communications, pp. 1-6.
- [5] Bogner, A., Chanson, M., & Meeuw, A. (2016). A decentralised sharing app running a smart contract on the ethereum blockchain. In: Proceedings of the 6th International Conference on the Internet of Things, pp. 177-178.
- [6] Buterin, V. (2013). Ethereum whitepaper. https://github.com/ethereum/wiki/wiki/White-Paper.
- [7] Buterin, V. (2014). A next-generation smart contract and decentralized application platform. pp. 1-36. [Online]. Available: https://github.com/ethereum/wiki/wiki/White-Paper.
- [8] Chang, S. Y., Park, Y., Wuthier, S., & Chen C. W. (2019). Uncle-block attack: Blockchain mining threat beyond block withholding for rational and uncooperative miners. In: International Conference on Applied Cryptography and Network Security, pp. 241-258.
- [9] Chen, H., Pendleton, M., Njilla, L., et al. (2020). A survey on ethereum systems security: vulnerabilities, attacks, and defenses. ACM Computing Surveys, 53(3), 1-43.
- [10] Di Angelo, M., & Salzer, G. (2019). A survey of tools for analyzing Ethereum smart contracts. In: 2019 IEEE International Conference on Decentralized Applications and Infrastructures. IEEE, pp. 69-78.
- [11] Dika, A., & Nowostawski, M. (2018). Security vulnerabilities in ethereum smart contracts. In: 2018 IEEE International Conference on Internet of Things and IEEE Green Computing and Communications and IEEE Cyber, Physical and Social Computing and IEEE Smart Data. IEEE, pp. 955-962.
- [12] Eyal, I., & Sirer, E. G. (2018). Majority is not enough: Bitcoin mining is vulnerable. Communications of the ACM, 61(7), 95-102. ‘A early version of this paper was given in International Conference on Financial Cryptography and Data Security, 2014, Springer, pp. 436-454.’
- [13] Feng, C., & Niu, J. (2019) Selfish mining in ethereum. In: The 39th IEEE International Conference on Distributed Computing Systems. IEEE, pp. 1306-1316.
- [14] Grunspan, C., & Pérez-Marco, R. (2020). Selfish mining in ethereum. Mathematical Research for Blockchain Economy, Springer, 65-90.
- [15] Jain, P. (2019). Revenue generation strategy through selfish mining focusing multiple pools of honest miners. Bachelor of Technology, Computer Science & Applied Mathematics, Indraprastha Institute of Information Technology, New Delhi, India.
- [16] Kang, H., Chang, X., Yang, R., et al. (2021). Understanding Selfish Mining in Imperfect Bitcoin and Ethereum Networks with Extended Forks. IEEE Transactions on Network and Service Management, 18(3): 3079-3091. doi: 10.1109/TNSM.2021.3073414.
- [17] Leelavimolsilp, T., Tran-Thanh, L., & Stein, S. (2018). On the preliminary investigation of selfish mining strategy with multiple selfish miners. arXiv preprint, arXiv:1802.02218, pp. 1-20.
- [18] Leelavimolsilp, T., Nguyen, V. H., Stein, S., & Tranthanh, L. (2019). Selfish mining in Proof-of-Work blockchain with multiple miners: An empirical evaluation. In: International Conference on Principles and Practice of Multi-Agent Systems. Lecture Notes in Computer Science, volume 11873, Springer, pp. 219-234.
- [19] Lerner, S. D. (2016). Uncle mining, an Ethereum consensus protocol flaw. [Online]. Available: https://bitslog.wordpress.com/2016/04/28/uncle-mining-an-ethereum-consensus-protocol-aw.
- [20] Li, Q. L., Ma, J. Y., & Chang, Y. X. (2018). Blockchain queue theory. In: International Conference on Computational Social Networks. Springer, pp. 25-40.
- [21] Li, Q. L., Chang, Y. X., Wu, X., et al. (2021). A new theoretical framework of pyramid markov processes for blockchain selfish mining. Journal of Systems Science and Systems Engineering, 30(6), December 2021, pp. 667–711.
- [22] Liu, H., Ruan, N., Du, R., & Jia, W. (2018). On the strategy and behavior of Bitcoin mining with -attackers. In: Proceedings of Asia Conference on Computer and Communications Security, pp. 357-368.
- [23] Liu, Y., Hei, Y., Xu, T., & Liu, J. (2020). An evaluation of uncle block mechanism effect on Ethereum selfish and stubborn mining combined with an eclipse attack. IEEE Access, 8, 17489-17499.
- [24] Marmolejo-Cossío, F. J., Brigham, E., Sela, B., et al. (2019). Competing (semi-) selfish miners in bitcoin. In: Proceedings of the 1st ACM Conference on Advances in Financial Technologies. pp. 89-109.
- [25] Mohammed, A. H., Abdulateef, A. A., & Abdulateef, I. A. (2021). Hyperledger, Ethereum and blockchain technology: A short overview. In: The 3rd International Congress on Human-Computer Interaction, Optimization and Robotic Applications. IEEE, pp. 1-6.
- [26] Nakamoto, S. (2008). Bitcoin: a peer-to-peer electronic cash system. https://bitcoin.org/bitcoin.pdf.
- [27] Pinzón. C., Rocha, C., & Finke, J. (2020). Algorithmic analysis of blockchain efficiency with communication delay. In: Fundamental Approaches to Software Engineering. Springer, pp. 400-419.
- [28] Praitheeshan, P., Pan, L., Yu, J., et al. (2019). Security analysis methods on ethereum smart contract vulnerabilities: a survey. arXiv preprint, arXiv:1908.08605, pp. 1-21.
- [29] Ranganthan, V. P., Dantu R., Paul A., et al. (2018). A decentralized marketplace application on the Ethereum blockchain. In: 2018 IEEE 4th International Conference on Collaboration and Internet Computing. IEEE, pp. 90-97.
- [30] Ritz, F., & Zugenmaier, A. (2018). The impact of uncle rewards on selfish mining in ethereum. In: 2018 IEEE European Symposium on Security and Privacy Work-shops, EuroSP Workshops, London, United Kingdom, pp. 50–57.
- [31] Ross, S. . (2014). Introduction to Probability Models. Academic press.
- [32] Sompolinsky, Y., & Zohar, A. (2013). Accelerating bitcoin’s transaction processing. Fast money grows on trees, not chains. Cryptology ePrint Archive: Report 2013/881.
- [33] Sompolinsky, Y., & Zohar, A. (2015). Secure high-rate transaction processing in bitcoin. In: International Conference on Financial Cryptography and Data Security. Springer, pp. 507-527.
- [34] Sookhak, M., Jabbarpour, M. R., Safa, N. S., et al. (2021). Blockchain and smart contract for access control in healthcare: a survey, issues and challenges, and open issues. Journal of Network and Computer Applications, 178, 102950.
- [35] Vujičić, D., Jagodić, D., & Randić, S. (2018). Blockchain technology, bitcoin, and Ethereum: A brief overview. In: The 17th International Symposium Infoteh-Jahorina. IEEE, pp. 1-6.
- [36] Wang, S., Yuan, Y., Wang, X., et al. (2018). An overview of smart contract: architecture, applications, and future trends. In: 2018 IEEE Intelligent Vehicles Symposium. IEEE, pp. 108-113.
- [37] Wang, Z., Jin, H., Dai, W., Choo, K. K. R., & Zou, D. (2021). Ethereum smart contract security research: survey and future research opportunities. Frontiers of Computer Science, 15(2), 1-18.
- [38] Wang, Z., Liu, J., Wu, Q., Zhang, Y., Yu, H., & Zhou, Z. (2019). An analytic evaluation for the impact of uncle blocks by selfish and stubborn mining in an imperfect Ethereum network. Computers Security, 87, 101581.
- [39] Werner, S. M., Pritz, P. J., Zamyatin, A., & Knottenbelt, W. J. (2019). Uncle traps: Harvesting rewards in a queue-based ethereum mining pool. In: Proceedings of the 12th EAI International Conference on Performance Evaluation Methodologies and Tools, pp. 127-134.
- [40] Wood, G. (2017). Ethereum: A secure decentralized generalised transaction ledger EIP-150 revision. Ethereum project yellow paper, 1-34.
- [41] Xia, Q., Dou, W., Xi, T., et al. (2021). The impact analysis of multiple miners and propagation delay on selfish mining. In: 2021 IEEE 45th Annual Computers, Software, and Applications Conference (COMPSAC). IEEE, pp. 694-703.
- [42] Zhang, S. (2020). Analyzing the success of selfish mining with multiple players. Master of Science, School of Computer Science, McGill University, Canada.
- [43] Zhang, S., Zhang, K., & Kemme, B. (2020). A simulation-based analysis of multiplayer selfish mining. In: 2020 IEEE International Conference on Blockchain and Cryptocurrency. IEEE, pp. 1-5.
- [44] Zhang, S., Zhang, K., & Kemme, B. (2020). Analysing the benefit of selfish mining with multiple players. In: 2020 IEEE International Conference on Blockchain. IEEE, pp. 36-44.