Tuning the order of a deconfined quantum critical point
Abstract
We consider a Su-Schrieffer-Heeger model in the assisted hopping limit, where direct electron hopping is subdominant. At fixed electron-phonon coupling and in the absence of Coulomb interactions, the model shows a deconfined quantum critical point (DQCP) between a valence bond solid in the adiabatic limit and a quantum antiferromagnetic (AFM) phase at high phonon frequencies. Here, we show that by adding terms to the model that reinforce the AFM phase, thereby lowering the critical phonon frequency, the quantum phase transition becomes strongly first order. Our results do not depend on the symmetry of the model. In fact, adding a Hubbard- term to the model lowers the O(4) symmetry of the model to SU(2) such that the DQCP we observe has the same symmetries as other models that account for similar quantum phase transitions.
Introduction. Deconfined quantum criticality (DQC) [1, 2, 3] refers to a direct and continuous quantum phase transition between two different broken symmetry states. This lies at odds with order parameter based Ginzburg–Landau–Wilson (GLW) approaches that would generically predict a first-order transition. The missing element is topology. A very natural way to understand DQC is in terms of Dirac fermions and compatible or intertwined mass terms [4, 5, 6, 7] that describe various orders. For example, in 1+1 dimensions, compatible mass terms include the three antiferromagnetic (AFM) and single valence bond solid (VBS) masses. The algebraic requirement that compatible mass terms anticommute leads to the result that topological defects of one order carry the charge of the other order. For example, in the 1+1D setting, a domain wall of the VBS order hosts a spin-1/2 degree of freedom. In 2+1D, the three AFM and two VBS masses lead to the very same effect, namely that a VBS vortex carries a spin-1/2 degree of freedom [8]. In 1+1D, the critical point is know to be captured by the SO(4) non-linear sigma model with Wess-Zumino-Witten term. At the critical point, we observe an enhanced symmetry that allows to rotate between VBS and AFM orders. The theory has a marginal operator that breaks SO(4) symmetry down to : it is marginally relevant (irrelevant) on the VBS (AFM) side. We note that other instances of DQC have been observed in models where fermions are not gapped out [9, 10] and that do not fit in the aforementioned picture of compatible Dirac mass terms.
Here, we will concentrate on the 2+1-dimensional bosonic case. Interestingly, there are many models, spin models [11], loop models [12], fermion models [13] and electron-phonon models [14], which at finite energy scale all point to the same phenomenology as in 1+1 dimensions but with emergent SO(5) symmetry [15, 16]. However, the numerical value of the correlation length exponent lies at odds with conformal bootstrap bounds required to guarantee a single relevant operator [17]. In other words, the very existence of a critical point. This, as well as observed violations to scaling [12] at large distances, poses a lot of questions. Various scenarios including complex fixed points [3, 18, 19] as well as the possibility of a tricritical point have been put forward [20, 21]. Both scenarios imply that there must be a tuning parameter that does not break the underlying symmetries but that renders the deconfined quantum critical point (DQCP) strongly first order.
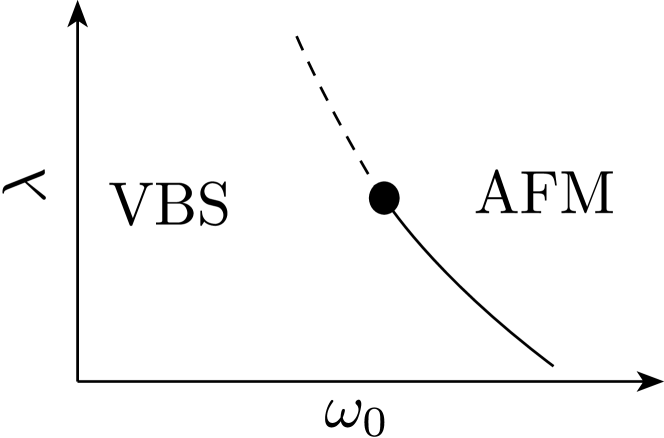
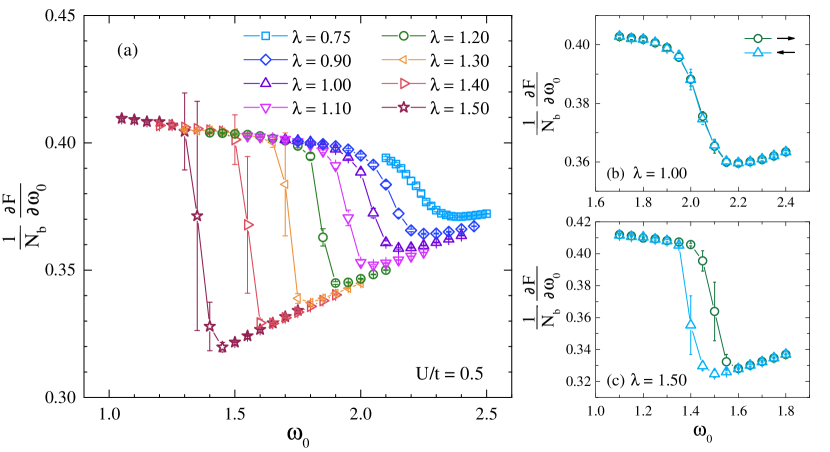
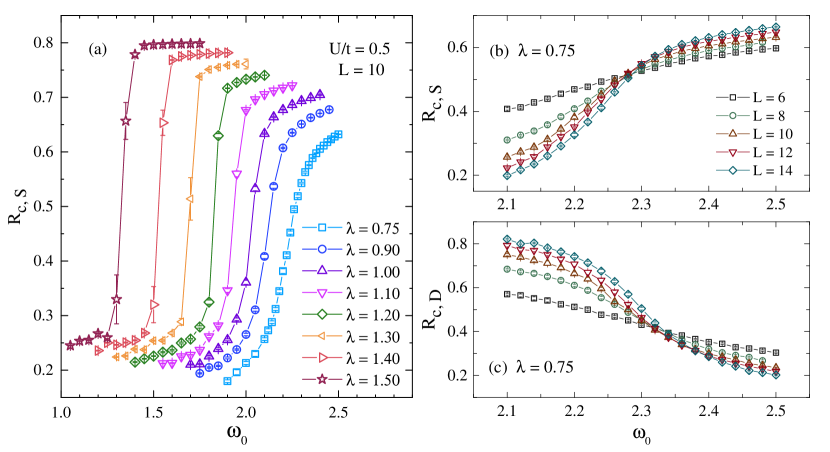
We consider a novel realization of DQC in a Su-Schrieffer-Heeger [22] model defined on a square lattice [14]. The key point is that the tuning parameter to observe DQC is the phonon frequency. By changing other parameters in the model, we can tune the critical phonon frequency. We observe that this allows to tune the DQCP from a continuous or weakly first order transition to a strong first order one (see Fig. 1). The interpretation of our result is not unique: the bullet point in Fig. 1 can be interpreted in terms of a Peierls transition of the U(1) gauge theory realized at the DQCP [23, 24], in terms of a complex SO(5) CFT stemming from fix-point annihilation [19, 18, 25], or in terms of an SO(5) multi-critical point [20, 21].
Model, symmetries and method. The model we consider has fermion degrees of freedom on the sites, , of a square lattice and bosonic degrees of freedom on the bonds, :
| (1) | |||||
The hopping operator is defined as with the fermion operators , , while and are the momentum and position operators of a harmonic oscillator. With a canonical transformation of the bosonic modes, we can set the spring constant to unity, thus justifying the term. In the notation of Eq. (1), the model is defined by the hopping , the phonon frequency, , by the electron-phonon coupling as well as the magnitude of the square hopping . In the runs presented below, we set the unit by fixing . We consider and vary , and the phonon frequency. At , this model has been studied in details in Ref. [14].
A key point of the model in the small limit is the emergence of a flux per plaquette that results in emergent Dirac fermions [14]. As discussed in the introduction, this sets the stage for exotic quantum criticality. The value of is such that the model harbors a flux per plaquette. At moderate values of considered in Ref. [14] and at , we observe a direct and continuous transition between a VBS and AFM phase as a function of increasing phonon frequency, . The aim of this article is twofold. First, we will augment the value of in the O(4) model. Since for
| (2) |
larger values of will favor antiferromagnetism and thereby lower the critical frequency at which the transition of VBS to AFM occurs. Here, and the Anderson pseudospin operator with the partial particle-hole symmetry:
| (3) |
with , in units where the lattice constant is set to unity. Second, we will add a Hubbard- term so as to reduce the O(4) symmetry to SO(4).
The O(4) symmetry of the model at becomes apparent when writing:
| (4) |
where are Majorana fermions. Here, labels the real and imaginary parts of the fermion operator. Combining and into a four-component index, , explicitly shows the O(4) symmetry:
| (5) |
with an O(4) matrix. Since partial particle-hole symmetry leaves the Hamiltonian invariant, the AFM state is degenerate with the -wave superconducting state and a charge density wave state.
In the Majorana representation, the Hubbard- term reads:
| (6) |
Under an O(4) rotation, the Hubbard interaction transforms as
| (7) |
As a consequence, the O(4) symmetry is reduced to SO(4).
From the technical point of view, the presence of the -term allows us to adapt a method proposed in Ref. [26] to integrate out the fermions. As shown in Ref. [14], this approach turns out to be efficient in terms of autocorrelation times. We have used the Algorithms for Lattice Fermions (ALF) [27, 28] implementation of the auxiliary-field quantum Monte Carlo algorithm [29, 30, 31] to carry out the numerical simulations. The reader is referred to [14] for a detailed account of our implementation. For our simulations, we have used a symmetric Trotter decomposition and set the imaginary time step to .
Results. The question we will ask is if the nature of the quantum phase transition changes as the critical phonon frequency diminishes. We will address the very same question for the O(4) () and SO(4) (finite ) models and we will see that the very same results hold.
O(4). Figure 2(a) plots the derivative of the free energy with respect to the phonon frequency
| (8) |
for various values of . As apparent, as increases, a step-like feature develops, thereby signaling a first-order transition. The data at correspond to the data taken in Ref. [14], where we argued in favor of a DQCP between the AFM and VBS state at a critical phonon frequency . The VBS breaks the symmetry and is a fourfold degenerate state. To capture this symmetry breaking, we compute the dimer-dimer correlation functions:
| (9) |
where
| (10) |
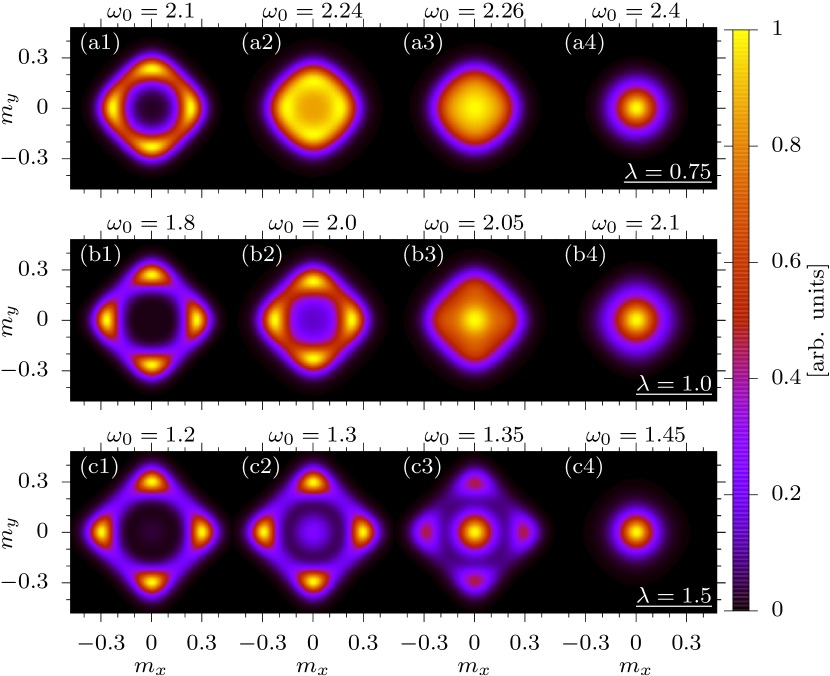
Figure 3 corresponds to histograms of the order parameters with , , and the number of lattice sites 111As in Ref. [14], we symmetrized the histograms by exploiting the symmetry of the model and the arbitrariness of the minus sign in the definition of the order parameter in Eq. (Tuning the order of a deconfined quantum critical point)..
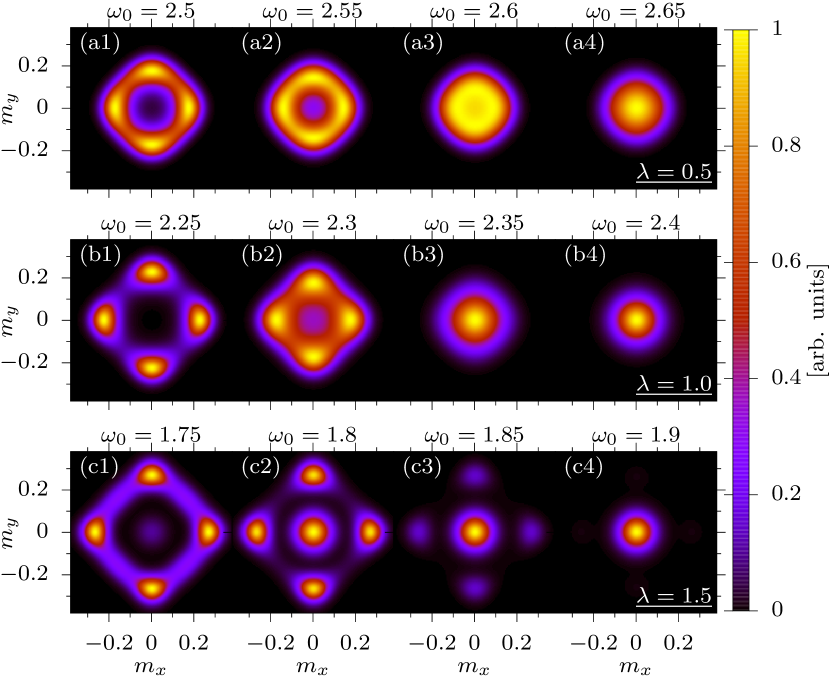
Deep in the VBS-ordered phases [Figs. 3(a1)(b1)(c1)], the histograms clearly show four peaks, thereby demonstrating the fourfold degeneracy. At , where we expect a DQCP, the symmetry gives way to an emergent U(1) symmetry that shows up in the form of a circular histogram in the vicinity of the critical point [Fig. 3(a3)]. In the AFM phase, the histogram shows a point-like feature at [Fig. 3(a4)]. In contrast, for a strongly first-order transition, one expects to observe a coexistence region of VBS and AFM. This is precisely seen in Figs. 3(c2)(c3) at , where both the four-peak structure and the central peak are simultaneously present. The results from the histograms are confirmed by the hysteresis curves of Figs. 2(b) and 2(c). Here, the final configuration of a simulation at is used as a starting configuration of a simulation at .
SO(4). Models of DQCP possess an [11, 12] or an symmetry [13]. The SO(4) symmetry accounts for SU(2) spin symmetry and SU(2) symmetry of the operators. For a repulsive Hubbard , even parity sites that define the Hilbert space on which the operators act correspond to excited states. Hence, in the low energy limit, our model with the Hubbard- term has the same symmetry as the aforementioned lattice models of DQCP. Throughout this section, we will consider , and retain the same value of . We will again vary and the phonon frequency.
The first point to confirm is that at small values of the numerical data supports the point of view of a DQCP, at least on our considered lattice sizes. Here, we will concentrate on the correlation ratio defined as
| (11) |
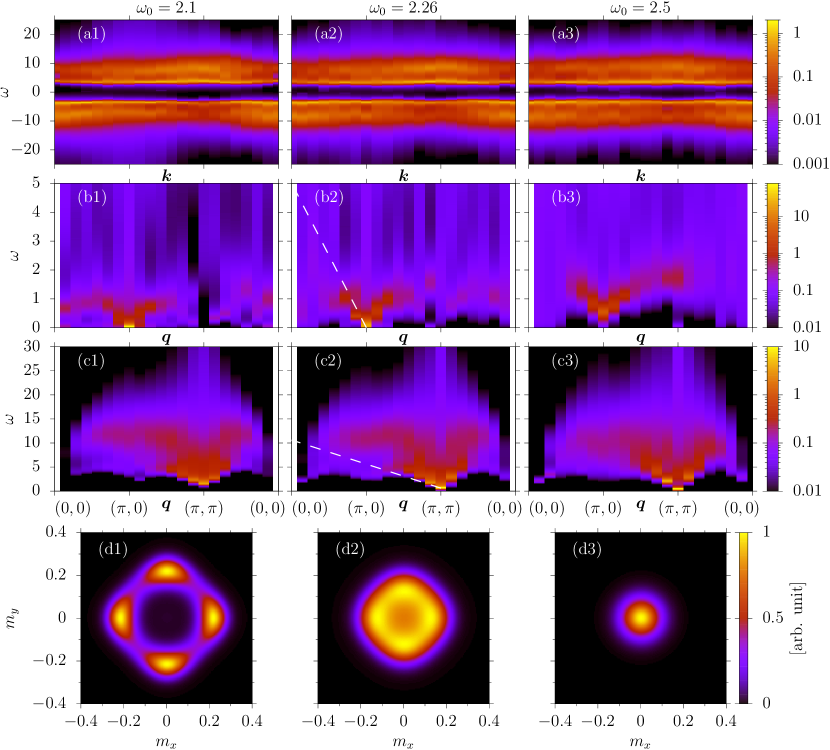
where is a correlation function of a local observable . We consider both the spin-spin correlations as well as the dimer-dimer correlations, see Eq. (Tuning the order of a deconfined quantum critical point). In the thermodynamic limit, converges to unity (zero) in the ordered (disordered) phase. is a renormalization group invariant quantity, such that in the vicinity of a critical point we expect . Here, is the correlation length exponent, the dynamical exponent and the leading correction to the scaling exponent. As we will confirm below, at criticality we observe Lorentz symmetry such that we can set and adopt a scaling. In the absence of corrections to scaling, the curves on various lattice sizes all cross at the critical point. Figures 4(b) and 4(c) show the correlation ratio as a function of system size for both the VBS and AFM correlations. The position of the crossing can only be approximately determined. However, within our accuracy, the data is consistent with a direct transition between the AFM and VBS phase at .
Figure 5 plots the single-particle, dimer, and spin spectral functions. These quantities are obtained by using the ALF-implementation [28] of the stochastic analytical continuation [33, 34, 35] method. At , our model reduces to an unconstrained gauge theory [14, 36]. In this limit, the electron carries a charge, such that the Green function becomes purely local [14, 37, 38, 39]. The spectral function at in Fig. 5(a) is close to this limit, shows very little dispersion, and a single-particle gap. The dimer and spin dynamical correlations are shown in Figs. 5(b) and 5(c). In the VBS (AFM) phase the spin (VBS) is gapped. In the vicinity of the critical point, we expect emergent Lorentz symmetry that requires the velocities of the AFM and VBS fluctuations to be identical. Within our precision, the data supports this point of view. Finally, Fig. 5(d) plots the histogram of the VBS order parameters. In Fig. 5(d2), we observe a clear sign of emergent U(1) symmetry.
In Fig. 4(a), we show the evolution of the spin correlation ratio as a function of for . It can be observed that a discontinuity emerges upon increasing . In the supplemental material, we show that as for the O(4) model, both and the histograms of the VBS order show the emergence of a first-order transition as is increased.
Discussion and conclusions. Our numerical results provide a tuning parameter, the value of the critical phonon frequency, that renders the DQCP strongly first order. Integrating out phonons leads to retarded interactions in imaginary time, with length scale set by the inverse phonon frequency. Since the DQCP enjoys Lorentz invariance, enhancing the range in imaginary times is identical to enhancing it in real space. From this perspective, our results are consistent with the ones observed in Ref. [21] that show that enhancing the real-space range of the interaction in - models results in a strong first-order transition. Importantly, this tuning parameter does not alter the symmetries of the model.
The DQCP is characterized by an emergent compact U(1) gauge theory [1, 2, 40, 3]. On the square lattice, the U(1) symmetry is reduced to symmetry thereby allowing for quadruple monopole instances, which are understood to be dangerously irrelevant. In Refs. [23, 24], it is argued that the very same theory has a Peierls instability owing to the coupling of phonons to monopoles of the emergent U(1) gauge field. In this framework, our results can be understood in terms of a Peierls instability of the compact U(1) gauge theory. The critical frequency at which this transition occurs corresponds to the bullet in Fig. 1. It is interesting to note that one can formulate monopole free realizations of DQC [13]. Such a model should not exhibit a Peierls instability and hence this scenario can be tested. Furthermore, models where lattice fluctuations are absent show the same phenomena. Hence, the Peierls instability scenario cannot be the only interpretation of our results.
There is an emerging consensus that the DQCP is a weakly first-order transition. The assumption that the DQCP is a critical point places strong constraints on the correlation length exponent [17] that seem at odds with Monte Carlo results [41, 12]. Furthermore, there has been considerable numerical evidence for emergent SO(5) symmetry [15, 16]. One possible way of understanding this is in terms of fixed point annihilation [3] resulting in a non-unitary SO(5)-CFT [25]. Assuming that the complex fixed point is close to the real plane, then the flow in the proximity of this fixed point will be very slow. In this scenario, models with short range interactions would exhibit an RG flow that approaches the complex critical point. As such, very large system sizes are required to detect the first order nature of the transition. Models with longer ranged interactions would exhibit flows that flow away from the fixed point. Thereby, much smaller system sizes are required to resolve the first order nature of the transition. Following this point of view, the bullet point in Fig. 1 corresponds to a complex fixed point in the proximity of which the RG flow is very slow, but always flows in one direction.
The aforementioned bound on the correlation length exponent holds only for a critical point that, by definition, has a single relevant operator. It does not prohibit an understanding of the DQCP in terms of an SO(5) multi-critical point, where the leading SO(5) singlet operator is relevant [20]. This is the point of view put forward in [21]. In this context, enhancing tunes away from the multi-critical point resulting in a strong first-order transition. In this reading of our data, the bullet point in Fig. 1 corresponds to an SO(5) multi-critical point.
For a generic critical point with no dangerously irrelevant operators, a small symmetry preserving change in the range of the interaction—that merely corresponds to a different lattice regularization of the relevant operator—should not change the criticality. The fact that we see a big change in criticality even under a small change of the critical frequency points to the very special nature of DQC. Our results hold for both the O(4) as well as the generic realizations of DQC. The interaction range provides the missing tuning parameter that must exist in the complex CFT or in the multi-critical interpretations of DQCP.
Acknowledgments. We would like to thank discussions with J. Willsher and J. Carvalho Inácio. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer SuperMUC-NG at the Leibniz Supercomputing Centre (www.lrz.de). The authors gratefully acknowledge the scientific support and HPC resources provided by the Erlangen National High Performance Computing Center (NHR@FAU) of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) under NHR Project No. 80069. NHR funding is provided by federal and Bavarian state authorities. NHR@FAU hardware is partially funded by the German Research Foundation (DFG) through Grant No. 440719683. F.F.A. thanks the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter ct.qmat (EXC 2147, project-id 390858490), and A.G. acknowledges the DFG funded SFB 1170 on Topological and Correlated Electronics at Surfaces and Interfaces (Project No. 258499086). N.C.C is grateful to the Brazilian Agencies Conselho Nacional de Desenvolvimento Cientifíco e Tecnológico (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior (CAPES), and Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro, FAPERJ. N.C.C. acknowledges support from FAPERJ Grant No. E-26/200.258/2023 - SEI-260003/000623/2023, and CNPq Grant No. 313065/2021-7.
References
- Senthil et al. [2004a] T. Senthil, L. Balents, S. Sachdev, A. Vishwanath, and M. P. A. Fisher, Quantum criticality beyond the landau-ginzburg-wilson paradigm, Phys. Rev. B 70, 144407 (2004a).
- Senthil et al. [2004b] T. Senthil, A. Vishwanath, L. Balents, S. Sachdev, and M. P. A. Fisher, Deconfined quantum critical points, Science 303, 1490 (2004b).
- Wang et al. [2017] C. Wang, A. Nahum, M. A. Metlitski, C. Xu, and T. Senthil, Deconfined quantum critical points: Symmetries and dualities, Phys. Rev. X 7, 031051 (2017).
- Tanaka and Hu [2005] A. Tanaka and X. Hu, Many-body spin berry phases emerging from the -flux state: Competition between antiferromagnetism and the valence-bond-solid state, Phys. Rev. Lett. 95, 036402 (2005).
- Abanov and Wiegmann [2000] A. Abanov and P. Wiegmann, Theta-terms in nonlinear sigma-models, Nuclear Physics B 570, 685 (2000).
- Senthil and Fisher [2006] T. Senthil and M. P. A. Fisher, Competing orders, nonlinear sigma models, and topological terms in quantum magnets, Phys. Rev. B 74, 064405 (2006).
- Ryu et al. [2009] S. Ryu, C. Mudry, C.-Y. Hou, and C. Chamon, Masses in graphenelike two-dimensional electronic systems: Topological defects in order parameters and their fractional exchange statistics, Phys. Rev. B 80, 205319 (2009).
- Levin and Senthil [2004] M. Levin and T. Senthil, Deconfined quantum criticality and néel order via dimer disorder, Phys. Rev. B 70, 220403 (2004).
- Liu et al. [2022] Z. H. Liu, M. Vojta, F. F. Assaad, and L. Janssen, Metallic and deconfined quantum criticality in dirac systems, Phys. Rev. Lett. 128, 087201 (2022).
- Liu et al. [2024] Z. H. Liu, M. Vojta, F. F. Assaad, and L. Janssen, Critical properties of metallic and deconfined quantum phase transitions in dirac systems, Phys. Rev. B 110, 125123 (2024).
- Sandvik [2007] A. W. Sandvik, Evidence for deconfined quantum criticality in a two-dimensional heisenberg model with four-spin interactions, Phys. Rev. Lett. 98, 227202 (2007).
- Nahum et al. [2015a] A. Nahum, J. T. Chalker, P. Serna, M. Ortuño, and A. M. Somoza, Deconfined quantum criticality, scaling violations, and classical loop models, Phys. Rev. X 5, 041048 (2015a).
- Liu et al. [2019] Y. Liu, Z. Wang, T. Sato, M. Hohenadler, C. Wang, W. Guo, and F. F. Assaad, Superconductivity from the condensation of topological defects in a quantum spin-Hall insulator, Nature Communications 10, 2658 (2019).
- Götz et al. [2024] A. Götz, M. Hohenadler, and F. F. Assaad, Phases and exotic phase transitions of a two-dimensional su-schrieffer-heeger model, Phys. Rev. B 109, 195154 (2024).
- Nahum et al. [2015b] A. Nahum, P. Serna, J. T. Chalker, M. Ortuño, and A. M. Somoza, Emergent so(5) symmetry at the néel to valence-bond-solid transition, Phys. Rev. Lett. 115, 267203 (2015b).
- Sato et al. [2023] T. Sato, Z. Wang, Y. Liu, D. Hou, M. Hohenadler, W. Guo, and F. F. Assaad, Simulation of fermionic and bosonic critical points with emergent so(5) symmetry, Phys. Rev. B 108, L121111 (2023).
- Nakayama and Ohtsuki [2016] Y. Nakayama and T. Ohtsuki, Necessary condition for emergent symmetry from the conformal bootstrap, Phys. Rev. Lett. 117, 131601 (2016).
- Ma and Wang [2020] R. Ma and C. Wang, Theory of deconfined pseudocriticality, Phys. Rev. B 102, 020407 (2020).
- Nahum [2020] A. Nahum, Note on wess-zumino-witten models and quasiuniversality in dimensions, Phys. Rev. B 102, 201116 (2020).
- Chester and Su [2024] S. M. Chester and N. Su, Bootstrapping deconfined quantum tricriticality, Phys. Rev. Lett. 132, 111601 (2024).
- Takahashi et al. [2024] J. Takahashi, H. Shao, B. Zhao, W. Guo, and A. W. Sandvik, So(5) multicriticality in two-dimensional quantum magnets, arXiv:2405.06607 (2024), arXiv:2405.06607 [cond-mat.str-el] .
- Su et al. [1980] W. P. Su, J. R. Schrieffer, and A. J. Heeger, Soliton excitations in polyacetylene, Phys. Rev. B 22, 2099 (1980).
- Seifert et al. [2024] U. F. P. Seifert, J. Willsher, M. Drescher, F. Pollmann, and J. Knolle, Spin-peierls instability of the u(1) dirac spin liquid, Nature Communications 15, 7110 (2024).
- Hofmeier et al. [2024] D. Hofmeier, J. Willsher, U. F. P. Seifert, and J. Knolle, Spin-peierls instability of deconfined quantum critical points, Phys. Rev. B 110, 125130 (2024).
- Wang et al. [2021] Z. Wang, M. P. Zaletel, R. S. K. Mong, and F. F. Assaad, Phases of the () Dimensional SO(5) Nonlinear Sigma Model with Topological Term, Phys. Rev. Lett. 126, 045701 (2021).
- Karakuzu et al. [2018] S. Karakuzu, K. Seki, and S. Sorella, Solution of the sign problem for the half-filled hubbard-holstein model, Phys. Rev. B 98, 201108 (2018).
- Bercx et al. [2017] M. Bercx, F. Goth, J. S. Hofmann, and F. F. Assaad, The ALF (Algorithms for Lattice Fermions) project release 1.0. Documentation for the auxiliary field quantum Monte Carlo code, SciPost Phys. 3, 013 (2017).
- Assaad et al. [2022] F. F. Assaad, M. Bercx, F. Goth, A. Götz, J. S. Hofmann, E. Huffman, Z. Liu, F. P. Toldin, J. S. E. Portela, and J. Schwab, The ALF (Algorithms for Lattice Fermions) project release 2.0. Documentation for the auxiliary-field quantum Monte Carlo code, SciPost Phys. Codebases , 1 (2022).
- Blankenbecler et al. [1981] R. Blankenbecler, D. J. Scalapino, and R. L. Sugar, Monte carlo calculations of coupled boson-fermion systems., Phys. Rev. D 24, 2278 (1981).
- White et al. [1989] S. White, D. Scalapino, R. Sugar, E. Loh, J. Gubernatis, and R. Scalettar, Numerical study of the two-dimensional hubbard model, Phys. Rev. B 40, 506 (1989).
- Assaad and Evertz [2008] F. Assaad and H. Evertz, World-line and determinantal quantum monte carlo methods for spins, phonons and electrons, in Computational Many-Particle Physics, Lecture Notes in Physics, Vol. 739, edited by H. Fehske, R. Schneider, and A. Weiße (Springer, Berlin Heidelberg, 2008) pp. 277–356.
- Note [1] As in Ref. [14], we symmetrized the histograms by exploiting the symmetry of the model and the arbitrariness of the minus sign in the definition of the order parameter in Eq. (Tuning the order of a deconfined quantum critical point).
- Beach [2004] K. S. D. Beach, Identifying the maximum entropy method as a special limit of stochastic analytic continuation, arXiv e-prints , cond-mat/0403055 (2004), arXiv:cond-mat/0403055 [cond-mat.str-el] .
- Sandvik [1998] A. Sandvik, Stochastic method for analytic continuation of quantum monte carlo data, Phys. Rev. B 57, 10287 (1998).
- Shao and Sandvik [2023] H. Shao and A. W. Sandvik, Progress on stochastic analytic continuation of quantum monte carlo data, Physics Reports 1003, 1 (2023), progress on stochastic analytic continuation of quantum Monte Carlo data.
- Assaad and Grover [2016] F. F. Assaad and T. Grover, Simple fermionic model of deconfined phases and phase transitions, Phys. Rev. X 6, 041049 (2016).
- Nandkishore et al. [2012] R. Nandkishore, M. A. Metlitski, and T. Senthil, Orthogonal metals: The simplest non-fermi liquids, Phys. Rev. B 86, 045128 (2012).
- Hohenadler and Assaad [2018] M. Hohenadler and F. F. Assaad, Fractionalized Metal in a Falicov-Kimball Model, Phys. Rev. Lett. 121, 086601 (2018).
- Hohenadler and Assaad [2019] M. Hohenadler and F. F. Assaad, Orthogonal metal in the Hubbard model with liberated slave spins, Phys. Rev. B 100, 125133 (2019).
- Xu et al. [2019] X. Y. Xu, Y. Qi, L. Zhang, F. F. Assaad, C. Xu, and Z. Y. Meng, Monte Carlo Study of Lattice Compact Quantum Electrodynamics with Fermionic Matter: The Parent State of Quantum Phases, Phys. Rev. X 9, 021022 (2019).
- Shao et al. [2016] H. Shao, W. Guo, and A. W. Sandvik, Quantum criticality with two length scales, Science 352, 213 (2016).
Supplemental Material for: Tuning the order of a deconfined quantum critical point
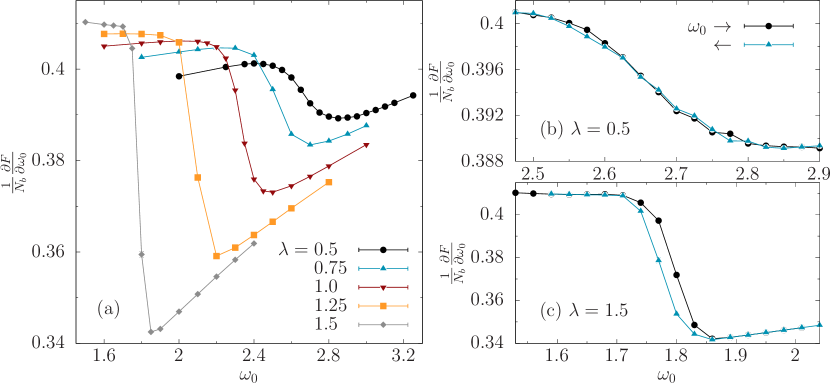
Relevance of interaction range for the SO(4) model
Figures S1 and S2 depict the very same quantities as in Figs. 2 and 3 but at . Similar phenomena can be observed: upon increasing and thereby decreasing the critical phonon frequency, a strong first-order transition emerges.