Turbulent transport and heating of trace heavy ions in hot, magnetized plasmas
Abstract
Scaling laws for the transport and heating of trace heavy ions in low-frequency, magnetized plasma turbulence are derived and compared with direct numerical simulations. The predicted dependences of turbulent fluxes and heating on ion charge and mass number are found to agree with numerical results for both stationary and differentially rotating plasmas. Heavy ion momentum transport is found to increase with mass, and heavy ions are found to be preferentially heated, implying a mass-dependent ion temperature for very weakly collisional plasmas and for partially-ionized heavy ions in strongly rotating plasmas.
pacs:
52.20.Hv,52.30.Gz,52.65.-yIntroduction.
Heavy ions are present in hot, magnetized plasmas both in laboratory experiments and in nature. These heavy ions are often trace, i.e., their densities are small enough that they have only a small direct effect on the bulk plasma dynamics. Nonetheless, trace heavy ions are important in numerous contexts: main ion properties are often inferred from heavy ion measurements because heavy ions radiate more readily islerPPCF94 ; accumulation of heavy ions leads to dilution and increased radiative energy losses in magnetic confinement fusion meserveyNF76 ; tokarNF97 ; and temperature measurements of minority ions in space and astrophysical plasmas indicate the existence of a novel heating mechanism schmidtGRL80 ; collierGRL96 ; kohlSP97 .
Considerable effort has gone into understanding the particle transport of trace heavy ions, or impurities, in the context of magnetized toroidal plasmas for fusion. In particular, the scaling with charge number and mass number of the impurity particle flux were predicted with a quasilinear fluid model and found to be in relatively good agreement with numerical and experimental results angioniPRL06 ; angioniPPCF09 . However, little to no work has been done on impurity momentum and energy fluxes or for turbulent heating of impurities. The latter may play a role not only in fusion plasmas, but also in the context of astrophysical plasmas, where the temperature of minority ions has been observed to increase with increasing ion mass schmidtGRL80 ; collierGRL96 ; kohlSP97 . Cyclotron heating cranmerApJ99 and stochastic heating via large-amplitude fluctuations chandranApJ10a have been proposed as possible explanations for this mass dependence. The turbulent heating mechanism described here provides an alternative explanation for the mass dependence of the minority ion temperature that is present even for low frequency, low amplitude fluctuations.
In this Letter we use local, nonlinear, -gyrokinetic theory cattoPP78 ; friemanPoF82 ; howesApJ06 to provide scaling predictions for trace heavy ion particle, momentum, and energy fluxes, as well as turbulent heating in hot, magnetized plasmas. This approach has already proven successful in determining scalings of temperature-gradient driven turbulence in tokamaks barnesPRL11b . We consider an inhomogeneous, axisymmetric plasma rotating toroidally at angular frequency , immersed in a curved, inhomogeneous magnetic field. To simplify our analysis, we restrict our attention to a region of plasma with rotation speed well below the ion sound speed but with a strong rotation gradient. We also consider only moderate values of , where is the mean plasma pressure and is the mean magnetic field magnitude. This is directly applicable to toroidal confinement experiments in magnetic confinement fusion, but the scaling laws we obtain are general: they do not change for a stationary, homogeneous plasma slab and therefore also pertain to various space and astrophysical plasmas.
Gyrokinetic turbulence.
The -gyrokinetic theory is obtained by performing an asymptotic expansion in the small ratio of the Larmor radius, , to system size, , and averaging over the fast Larmor motion of particles. It is valid for low-amplitude turbulence with time scales long compared to the Larmor frequency, , and spatial scales comparable to and in the directions across and along the mean magnetic field, respectively. While initially developed for magnetic confinement fusion plasmas, -gyrokinetics can also be applied to small-scale turbulence in the solar wind, solar corona, accretion disks, and galaxy clusters howesJGR08 ; schekApJ09 .
We use () as our coordinate system, where is the position of the center of a particle’s Larmor orbit, its kinetic energy, and its magnetic moment, with its mass and its speed. The subscripts and are used to denote the components perpendicular and parallel to the mean magnetic field, respectively, with the magnetic field magnitude given by . With this choice of coordinates, the electromagnetic gyrokinetic equation governing the evolution of the fluctuating piece of the distribution function, , is
| (1) |
where , denotes an average over Larmor angle at fixed , 111The fields , , and are independent of Larmor angle at fixed particle position, , but not at fixed . Thus care must be taken to specify which spatial coordinate is held fixed for velocity integration. The -integral contained in is performed at fixed , but all other velocity integrals in this Letter are performed at fixed ., is the fluctuating electrostatic potential, and are the parallel components of the fluctuating magnetic vector potential and magnetic field, respectively, is the charge number, the proton charge, the speed of light, the mean temperature, is a stationary Maxwellian distribution of velocities in the frame rotating with velocity , is the toroidal angle, the plasma major radius, , , with the drift velocity due to a curved, inhomogeneous mean magnetic field and the drift due to the fluctuating electromagnetic fields, the unit vector along the mean magnetic field, the Larmor frequency, and describes two-particle Coulomb interactions. Plasma species is indicated by the subscript , which we henceforth drop unless it is needed to avoid ambiguity.
By definition, the trace ions considered here do not contribute to the fields. They are instead determined solely by the electron and main ion dynamics through the low-frequency Maxwell’s equations, supplemented by the quasineutrality constraint:
| (2) | ||||
| (3) | ||||
| (4) |
where enters Eqs. (2-4) through the definition for given below Eq. (1).
With and specified by Eqs. (1-4), one can evaluate the turbulent heating,
| (5) |
and the turbulent fluxes,
| (6) | ||||
| (7) | ||||
| (8) | ||||
where labels surfaces of constant mean pressure, is an integral over all velocity space and over a volume of width () encompassing the mean magnetic field line of interest, and , , and are the particle, toroidal angular momentum, and energy fluxes, respectively. Note that the momentum flux defined in Eq. (8) does not include each species’ contribution to the Maxwell stress.
| or | |||
| 1 or | 1 or | 1 | |
| 1 or | or | 1 | |
| 1 or | or | 1 | |
| or | |||
| , , or | or |
Expansion in .
To obtain scaling laws for the turbulent fluxes and heating of trace heavy ions, we take , , and expand in powers of . Here is the main ion thermal speed. We restrict our attention to , and assume the collisional mean free path is sufficiently long that collisions may be neglected in our analysis. In what follows, we keep and dependences separate so that we can consider the subsidiary expansion .
Because the heavy ions are trace, their space and time scales are those of the bulk plasma turbulence. Thus, and only enter Eq. (1) through explicit factors of , , and , as well as through itself. In what follows, we assume the ratio of the heavy ion to proton temperature is much smaller than , giving . The two lowest order equations in our expansion are thus
| (9) | ||||
| (10) | ||||
where and .
There are two possible scalings for both and due to a competition between terms with different and dependences in Eqs. (9) and (10). In particular, , and . By considering the limits and , the number of such scalings is reduced. The - and -scalings for and in these limits, as well as for the general case, are summarized in Table 1.
Flux and heating scalings.
If is a solution to Eq. (9), then is also a solution. Thus, , where the overline denotes a statistical average. As a result, does not contribute to the lowest order (i.e., electrostatic) heating or particle and heat fluxes, Eqs. (5)-(7), whose integrands are otherwise even functions of . Conversely, the lowest order momentum flux integrand has a component proportional to , so . Using our scalings for , we see that has competing terms scaling as and , respectively.
Note that Eq. (10) has a symmetry that is opposite that of Eq. (9): if is a solution, then is also a solution. Furthermore, for all higher order equations, one can show that the symmetry in alternates between that of Eqs. (9) and (10). As a result, the only components of that contribute to the particle and heat fluxes and heating are , , etc. Using Eqs. (6) and (7), we have , which in the general case has competing terms scaling as and (no or dependence), respectively.
The first term in the heating expression, (5), is the Joule heating and is scaled up by an explicit factor of (arising from the current), while the second term is viscous heating. At lowest order, the Joule heating term gives , giving . The viscous heating is proportional to . thus has competing terms scaling as , , and , respectively. The scalings of the various fluxes and heating are summarized in Table 1.
Minority ion temperature.
Integrating Eq. (5) by parts in time and using Eq. (1), the heating can be expressed as krommesPoP94 ; howesApJ06 ; abelRPP12
| (11) |
Our scalings indicate that increases in magnitude with or , but and do not. The first term in Eq. (11) must thus dominate for or large. This term, which we identify as the collisional entropy generation, is positive definite when summed over species. We argue that it is also positive species by species for the low collisionalities considered here.
The collision operator, , consists of a test-particle piece, which is a diffusion operator in velocity space, and a field-particle piece, which is an integral operator helander . Both contributions are inversely proportional to the collisional mean free path and thus small, except at small scales in the velocity space where large derivatives in the test-particle operator compensate abelPoP08 ; barnesPoP09 ; schekApJ09 . The test-particle operator should thus dominate in weakly collisional plasmas, and its diffusive nature ensures that its contribution to entropy generation is positive-definite.
Consequently, trace heavy ions must be heated by turbulence instead of cooled. For this heating process to subside, the trace ion temperature must become large enough to interfere with our large expansion. This happens when the heavy ion temperature exceeds the main ion temperature by a factor of . In this limit, the turbulent heating becomes comparable to the heat flux so that is no longer required to be positive definite. Our theory thus predicts that heavy ions will be hotter than light ions by a factor of – but only if turbulent heating is larger than collisional temperature equilibration.
The collisional temperature equilibration of the main ions, , and a trace heavy ion species, , is , where , and is the mean free path for collisions between the main ions. From Eq. (5), we estimate , where is the scaling of with and given in Table 1, and we have assumed . The ratio of turbulent heating to collisional temperature equilibration is thus , with the characteristic time scale over which the equilibrium density and temperature vary.
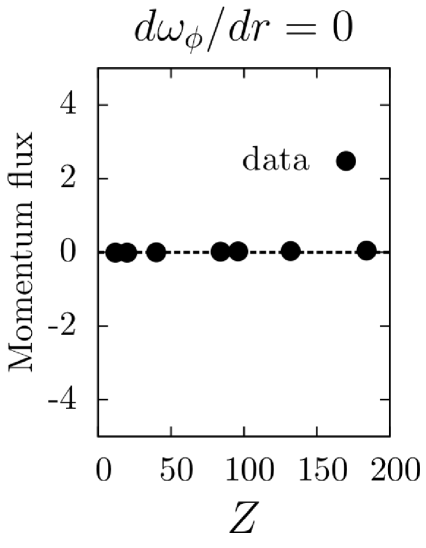
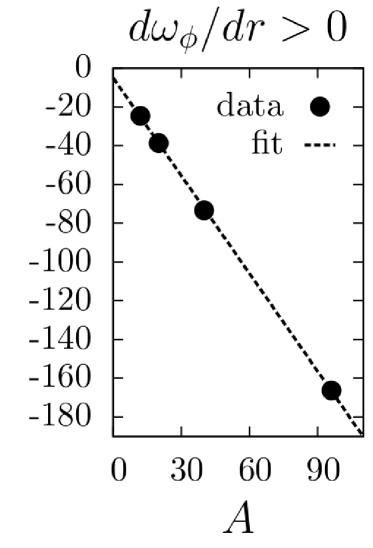
Numerical results.
To test our predictions for the scalings of turbulent transport and heating, we employ the local, -gyrokinetic code GS2 dorlandPRL00 . We consider an axisymmetric system with sheared magnetic field lines mapping out nested toroidal surfaces with circular cross sections (known as the Cyclone Base Case dimitsPoP00 and parametrized using the Miller local equilibrium model millerPoP98 ). Each simulation is electrostatic and includes kinetic electrons, as well as kinetic main and trace heavy ions with a wide range of and values. The turbulence is driven by gradients in the mean ion and electron densities and temperatures, with for the electrons and main ions, and for all species, with the major radius at the center of the constant pressure surface. The collision frequency is chosen small, , so that heavy ion collisions do not affect our scalings.
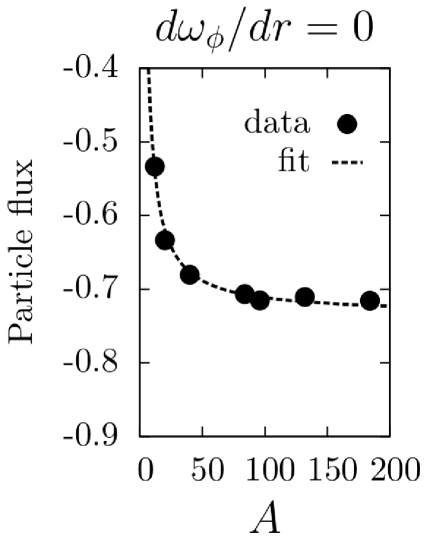
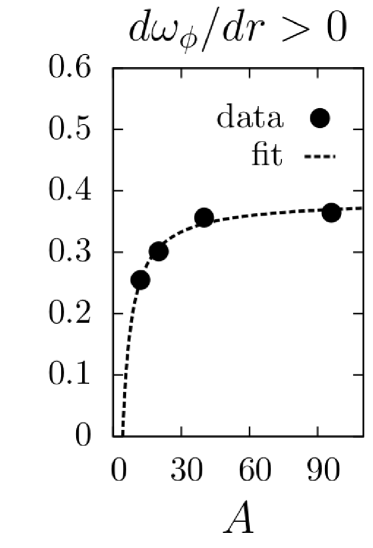
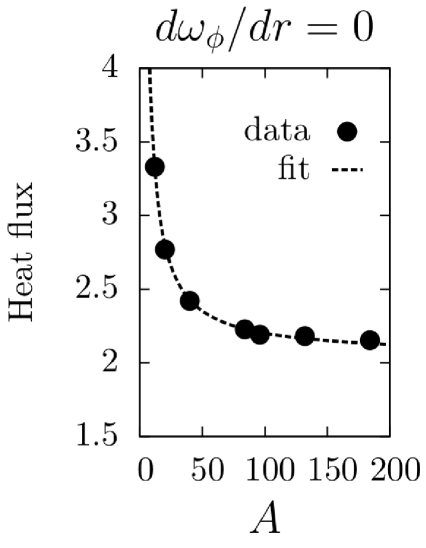
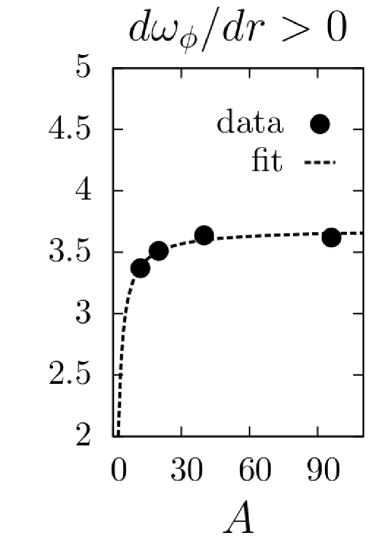
Two sets of simulations were carried out: one with a stationary plasma () and one with a differentially rotating plasma (). The simulation results are shown in Figs. (1)-(4). Data points for fluxes and heating at various and values are plotted as solid circles and fit using a least-squares analysis with the predicted lowest order and dependences, as well as the first order correction. In each case, the predicted scalings fit the data well. It should be noted that the momentum flux for is zero for all species due to a fundamental symmetry of the -gyrokinetic equation parraPoP11 .
Discussion.
We now discuss the implications of the trace heavy ion scalings derived in this Letter. First, the preferential heating of heavy ions should lead to large temperature disparities between different ion species in nearly collisionless plasmas. Many space and astrophysical plasmas are weakly collisional enough (i.e., ) that turbulent heating should dominate over collisional equilibration, and preferential heating of heavy ions is indeed observed schmidtGRL80 ; collierGRL96 . However, for such low collisionalities the equilibrium can deviate strongly from the isotropic Maxwellian assumed in our analysis, which cannot consequently address the large values observed in coronal holes and the fast solar wind kohlSP97 .
Magnetic confinement fusion plasmas typically have so that collisional temperature equilibration dominates over turbulent heating and all ions have the same temperature. However, for rotating plasmas our results indicate that the turbulent heating is enhanced by an additional factor of relative to the equilibration. It may therefore be possible for heavy, partially ionized impurities to be heated by turbulence to temperatures significantly larger than the main ions.
Because the momentum transport of heavy ions is enhanced by , it can generate flows of order the ion thermal speed for densities as small as . In this limit, heavy ions could thus significantly alter bulk plasma momentum transport.
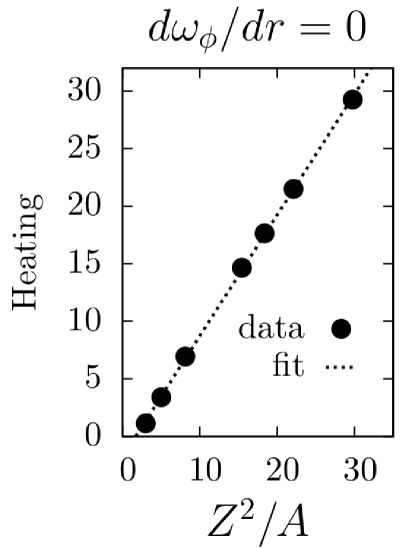
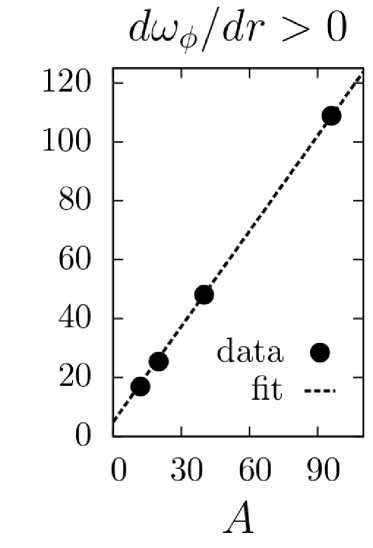
We thank S. C. Cowley, E. Quataert, and A. A. Schekochihin for useful discussions. M.B. was supported by a US DoE FES Postdoctoral Fellowship, F.I.P. was supported by US DoE Grant No DE-FG02-91ER-54109, and computing time was provided by HPC-FF (Jülich).
References
- (1) R. C. Isler, Plasma Phys. Control. Fusion 36, 171 (1994).
- (2) E. B. Meservey, N. Bretz, D. L. Dimock, and E. Hinnov, Nucl. Fusion 16, 593 (1976).
- (3) M. Z. Tokar et al., Nucl. Fusion 37, 1691 (1997).
- (4) W. K. H. Schmidt, H. Rosenbauer, E. G. Shelly, and J. Geiss, Geophys. Res. Lett. 7, 697 (1980).
- (5) M. R. Collier et al., Geophys. Res. Lett. 23, 1191 (1996).
- (6) J. L. Kohl et al., Solar Physics 175, 613 (1997).
- (7) C. Angioni and A. G. Peeters, Phys. Rev. Lett. 96, 095003 (2006).
- (8) C. Angioni et al., Plasma Phys. Control. Fusion 51, 124017 (2009).
- (9) S. R. Cranmer, G. B. Field, and J. L. Kohl, Astrophys. J. 518, 937 (1999).
- (10) B. D. G. Chandran et al., Astrophys. J. 720, 503 (2010).
- (11) P. J. Catto, Plasma Phys. 20, 719 (1978).
- (12) E. A. Frieman and L. Chen, Phys. Fluids 25, 502 (1982).
- (13) G. G. Howes et al., Astrophys. J. 651, 590 (2006).
- (14) M. Barnes, F. I. Parra, and A. A. Schekochihin, Phys. Rev. Lett. 107, 115003 (2011), arxiv:1104.4514.
- (15) G. G. Howes et al., J. Geophys. Res. 113, A05103 (2008).
- (16) A. A. Schekochihin et al., Astrophys. J. Suppl 182, 310 (2009), arXiv: 0704.0044.
- (17) J. A. Krommes and G. Hu, Phys. Plasmas 1, 3211 (1994).
- (18) I. G. Abel et al., Reviews on Progress in Physics, submitted (2012).
- (19) P. Helander and D. J. Sigmar, Collisional transport in magnetized plasmas (Cambridge University Press, 2002).
- (20) I. G. Abel et al., Phys. Plasmas 15, 122509 (2008), arXiv:0806.1069.
- (21) M. Barnes et al., Phys. Plasmas 16, 072107 (2009).
- (22) W. Dorland, F. Jenko, M. Kotschenreuther, and B. N. Rogers, Phys. Rev. Lett 85, 5579 (2000).
- (23) A. M. Dimits et al., Phys. Plasmas 7, 969 (2000).
- (24) R. L. Miller et al., Phys. Plasmas 5, 973 (1998).
- (25) F. I. Parra, M. Barnes, and A. G. Peeters, Phys. Plasmas 18, 062501 (2011).