Two-carrier Magnetoresistance: Applications to Ca3Ru2O7
Abstract
Ambipolar transport is a commonly occurring theme in semimetals and semiconductors. Here we present an analytical formulation of the conductivity for a two-band system. Electron and hole carrier densities and their respective conductivities are mapped into a two-dimensional unit-less phase space. Provided that one of the carrier densities is known, the dimensionless phase space can be probed through magnetoresistance measurements. This formulation of the two-band model for conductivity is applied to magnetoresistance experiments on Ca3Ru2O7. While previous such measurements focused on the low-temperature limit, we cover a broad temperature range and find negative magnetoresistance in an intermediate interval below the electronic transition at 48 K. The low-temperature magnetoresistance in Ca3Ru2O7 is consistent with a two-band structure. However, the model fails to describe the full temperature and magnetic field dependence. Negative magnetoresistance found in an intermediate temperature range is, for example, not captured by this model. We thus conclude that the electronic and magnetic structure in this intermediate temperature range render the system beyond the most simple two-band model.
1 Introduction
The combination of electron and hole charge carriers is a common theme of condensed matter physics [(1)]. It is also essential for many applications such as semiconductor junctions, excitonic solar cells and light emitting diodes. Transport properties of semimetals are defined by electron and hole charge carriers. In its simplest form, a semimetal consists of just one electron- and one hole-like band crossing the Fermi level. Exposed to a magnetic field, the electrons and holes experience a Lorentz force which results in a negative or positive Hall effect depending on whether conductivity is dominated by electrons or holes. Compensated ambipolar transport properties stem from the detailed balance between electron and hole mobilities [(2)]. Most semimetals/metals have more than two bands crossing the Fermi level. Nevertheless, a two-band model can still be of some relevance and is widely used to discuss transport experiments [(3), (4), (5), (6), (7), (8), (9), (10), (11)]. In some multiband systems, only two Fermi surface sheets host high-mobility carriers – making the two-band model approximately viable. Orbital selectivity found in systems with strong Hunds coupling [(12)] may also trigger selective Fermi surface gapping while other sheets are untouched – thus providing another route to two-band physics. Finally, electronic reconstruction of single band systems is a common motif that can generate two-band structures [(13), (14), (15)]. The wide applicability justifies a detailed analysis of the two-band model.
Here we show that the electron and hole transport properties can be described by two dimensionless parameters and . This (,) phase space connects smoothly the ambipolar transport with the mono-carrier dominated regime. For constant filling, the system must move along (,) specific contour lines. If the carrier density of – say the electrons – is known from angle resolved photoemission spectroscopy (ARPES) [(16)] or quantum oscillation [(17)] experiments, the temperature dependent parameters and can be determined from a magnetotransport experiment. We apply this new formulation of the two-band model to magnetoresistance experiments of the semimetallic phase of Ca3Ru2O7. While previous studies focused entirely on the low-temperature limit [(18)], we cover a broad temperature range and find negative magnetoresistance for 30 K K. For selected temperatures ( K), the observed low-field magnetoresistance is captured well by the two-carrier model. However, as a function of temperature (warming) the (,) parametrisation is inconsistent with a constant filling. For the case of Ca3Ru2O7, the two-band model fails to explain the full temperature and magnetic field dependence of the magnetoresistance. The most pronounced limitation of the two-band model is its inability to explain the negative magnetoresistance found for 30 K K. We discuss these discrepancies in terms of a two-stage Fermi surface reconstruction. Below 48 K, the system is a semimetal but with a Fermi surface including more than two sheets. A second reconstruction across 30 K simplifies the Fermi surface such that it hosts only a single electron- and hole-like pocket. Within this structure reasonable consistency with the two band model is reached at low temperatures.
2 Methods
High quality single crystals of Ca3Ru2O7 were grown by the floating zone techniques [(19), (20)]. The orthorhombic (Bb21m) crystals were detwinned, by pressing along an orthorhombic axis, using a thermo-mechanical detwinning device [(21)] in combination with a polarized light microscope. The longitudinal resistivity (along the -axis), Hall, magnetization and thermoelectric measurements were carried out in a Quantum Design Magnetic Property Measurement system and a Physical Property Measurement System with magnetic field applied along the crystallographic -axis. For the thermoelectric experiments, temperature gradients along the orthorhombic -axis (the longer lattice parameter) were recorded using Cernox chips [(22)].
3 Results
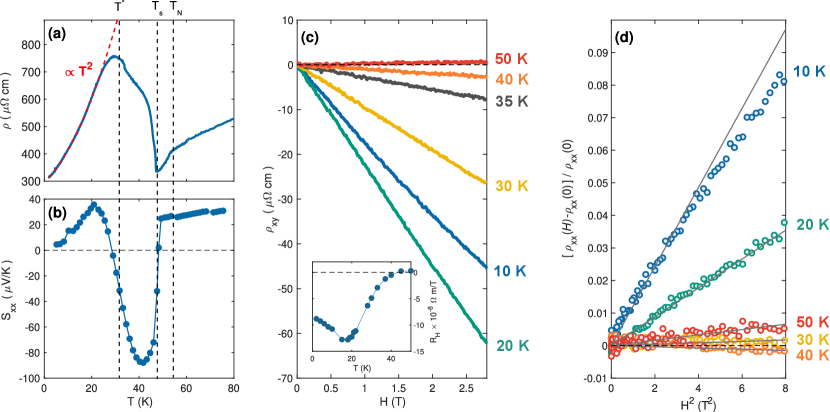
In Figs. 1 a,b, we are plotting the zero magnetic field resistivity (along b - axis) and thermopower versus temperature. The temperature dependence of both curves are in agreement with all previous experiments [(23), (24), (25)]. Resistivity displays a weak drop across the AFM-a Néel ordering temperature K and a sharp upturn below the spin-flip transition K into the AFM-b phase. The latter transition is associated with a Fermi surface reconstruction, signaled by a sharp sign change of the Seebeck coefficient [(24)] (Fig. 1b). Below 30 K, the resistivity recovers a metallic Fermi-liquid-like () temperature dependence (Fig. 1a). Hall resistivity isotherms ( versus magnetic field ) – shown in Fig. 1c for temperatures as indicated – are also consistent with previous reports. Negative Hall resistivity is found for [(26)].
Magnetoresistance plotted as versus is displayed in Fig. 1d for temperatures as indicated. The low-temperature positive magnetoresistance is consistent with previous studies [(27), (24)], all of which showed, with mobility T-1. Here we focus on the temperature dependent magnetoresistance in Ca3Ru2O7. For , a small positive magnetoresistance is found whereas for 30 K it is negative before turning to large positive values in the limit. The derivative is shown in Fig. 2a as a function of temperature and magnetic field. The onset of negative magnetoresistance and history dependent magnetic susceptibility (Fig. 2b) clearly correlate. Both effects appear below .
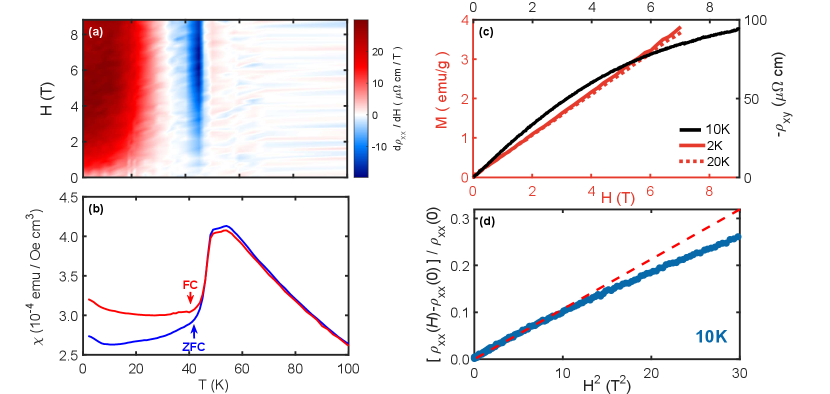
The low-temperature magnetization and Hall resistivity isotherms display different field dependence (Fig. 2c). The magnetization is linear in magnetic field whereas is displaying non-linear field dependence suggesting that these two quantities are not directly coupled. The linear trend of the low temperature magnetization data (Fig. LABEL:fig:70028Fig2c) excludes the possibility of an anomalous Hall effect. We also point out that although in the low-field () regime, significant deviations are observed in larger magnetic field (see Fig. 2d and Reference.[(27)]). In what follows, we discuss the low-temperature large positive and intermediate-temperature negative magnetoresistance behaviour within the two-band model.
4 Modelling
For metals with two Fermi surface sheets of different band curvature, the magnetoresistance is given by [(28), (3), (4), (5), (6)]:
| (1) |
| (2) |
The model consists of four parameters , and . The hole and electron conductivities are denoted by () and the hole and electron Hall coefficients are indicated by (). Given that and where , the model can also be expressed in terms of electron and hole carrier density (, ) and mobility (, ). This model generally assumes that the mobilities are independent of the applied magnetic field. Analysis of and isotherms in terms of the four parameters (,,) is typically associated with ambiguity [(6)]. Although and are coupled parameters, since in zero-field, , the problem has three free parameters.
To make progress, we assume that the electron carrier density is known, for example, from ARPES [(16)] or quantum oscillation [(17)] experiments. The problem then reduces to two equations with two unknowns ( and ), lifting the ambiguity. In the low-field limit, the problem can be expressed in terms of two dimensionless parameters and :
| (3) |
and
| (4) |
with defined by where is the residual resistivity. Solving with respect to and yields , = and where the analytical function is expressed in the appendix. These three ratios (, and ) are plotted in Fig. 3 within the ”phase space” of the two dimensionless parameters and .
These parameters are measurable (modulus ) and typically temperature dependent. Perhaps is the most intuitive parameter. Within an electron-hole two-band model, it varies in the interval . Ambipolar transport, defined by comparable electron and hole contributions to the conductivity, typically leads to . By contrast, for conductivity is dominated by electrons. The second dimensionless parameter is given by the ratio between the magnetoresistance coefficient and the conductivity modulus .
We notice that the two-carrier model was recently expressed in a similar scheme with two dimensionless parameters [(6)]. In the work of Eguchi and Paschen (Ref. 6), magnetoresistance is expressed in terms of dimensionless carrier and mobility ratios. Here, we use the inverse approach where the carrier and mobility ratios are expressed in terms of dimensionless parameters and obtained from magnetoresistance. This formulation has some advantages. With our notation, solutions have the following properties. First, for to take real values, and hence must be satisfied. As , and are all measurable quantities, this provides a test as to whether a two-band model is applicable. We notice that this is independent of our initial input for . Second, constant filling implies that is invariant. Therefore, if remains constant, the system must stay on a -contour. These contour lines ”flow” from the electron to the hole dominated limit via the ambipolar BelPRL2003 regime (see Fig. 3a).
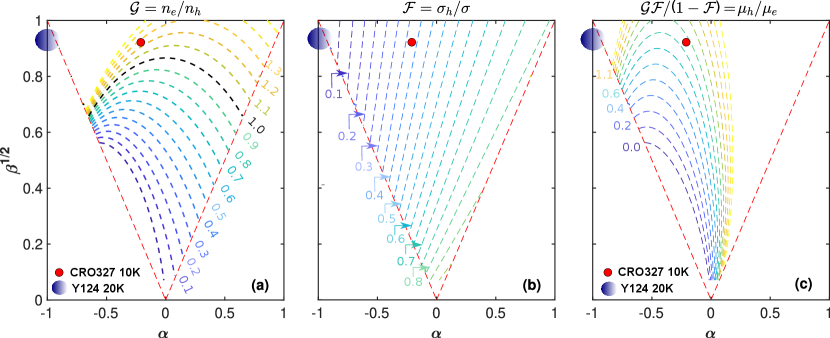
For example, increasingly negative Hall coefficient implies and hence should decrease for the system to stay on a constant contour. Since both and scale with , the shape of the contour lines are independent of . A third solution property stems from the contour line EomPRB2012 ; PisoniPRB2016 ; RULLIERALBENQUE2016164 given by . If a system is known to be hole-doped, i.e. (), it must satisfy and . Deviation from any of the three properties implies: (a) non-constant filling, (b) the system is not having a two-band structure or (c) the two-band model assumptions are too simplistic.
5 Discussion
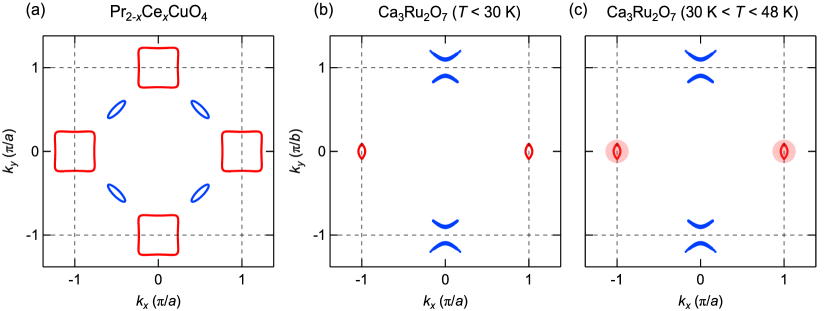
Before analysing the magnetoresistance of Ca3Ru2O7, we start by illustrating the use of the aforementioned solution properties. In doing so, we consider results obtained on hole and electron doped cuprates. For hole doped YBa2Cu3O7-x and YBa2Cu4O8, quantum oscillation experiments yields an electron-like Fermi surface sheet with an area corresponding to mm3C-1 YellandPRL2007 ; Doiron-Leyraud-Nat2007 . Since the system is hole-doped, we expect . Hall effect experiments suggest that LebeoufNature2007 . Already here a contradiction emerges as is impossible for a two-carrier hole-doped system. Evaluation of positions the system in the region where RourkePRB2010 . In fact is not strictly satisfied. A plausible explanation for these contradictory results is that the Fermi surface structure contains more than two sheets. Since the Fermi surface is likely reconstructed by an incommensurate charge-density-wave order Wu11 ; GhiringhelliSCI12 ; chang12 , a more complex multi-band structure is expected MillisPRB2007 . On the electron doped side (), by contrast, the Fermi surface is expected to fold around the antiferromagnetic zone boundary leading to a two-band structure HePNAS2019 (see Fig. 4a).
Quantum oscillation Hall experiments on Pr1.86Ce0.14CuO4 (PCCO) Breznay and Nd1.85Ce0.15CuO4 (NCCO) HelmPRL2009 ; HelmPRB2015 reveal a small hole pocket with giving . To compare to our model results, we use momentarily and . We therefore have and evaluation of the magnetoresistance for both NCCO and PCCO Breznay ; GollnikPRB1998 yields less than as expected. These systems are thus not incompatible with a two-band model.
Next, we discuss our magnetoresistance experiments on Ca3Ru2O7. Recent ARPES data suggest that Ca3Ru2O7, at base temperature, is a semimetal with a single electron and two identical hole pockets Horio2019 ; markovi2020 ; PuggioniPRR2020 (see Figure. 4b). The electron pocket - corresponds to a carrier density , consistent with the dominant quantum oscillation frequency KikugawaJPSJ2010 . The electron Hall coefficient is therefore known within the confidence provided by ARPES and quantum oscillation experiments. Our low magnetic-field magnetoresistance data permit extraction of , and as a function of temperature. At K, we find and and with that, all model parameters are now known: , and (see Fig. 3). The electron-hole carrier ratio is consistent with the low-temperature ARPES derived Fermi surface Horio2019 . Our results also imply that the electron carriers are more mobile than the holes. This is consistent with the fact that the largest quantum oscillation amplitude KikugawaJPSJ2010 is found for the frequency corresponding to the electron pocket in the ARPES experiment Horio2019 ; markovi2020 . So far, the two-band model seems to sensibly describe the magnetoresistance experiment. However, there are at least three problematic issues with the two-band model. (i) Even in the temperature range 2 K – 30 K, and vary in a fashion that is inconsistent with a constant . (ii) For intermediate temperatures negative magnetoresistance is observed. (iii) We used the low-field limit for our analysis. On top of this, higher order magnetic field terms can be derived. However, these higher-order terms are not large enough to account for the deviation from under higher fields (Fig. 2d).
In what follows, we discuss possible reasons for these discrepancies. We start by stressing that the underlying assumption that carrier mobility is magnetic-field independent is not the sole culprit. Field dependent mobilities could explain (iii) but not (i) and (ii). We also point out that carrier density ratio may, in fact, be temperature dependent. Recent density-functional-theory (DFT) calculations suggest a strong coupling between detailed lattice structure and a temperature dependent Coulomb interaction PuggioniPRR2020 . Early neutron diffraction experiments indeed demonstrated the temperature dependence of ruthenium-oxygen bond angles yoshida_crystal_2005 . It is therefore not inconceivable that the chemical potential and even the low-energy electronic structure is temperature dependent. In fact, recent ARPES studies reported a two stage reconstruction with characteristic temperatures of K and K Horio2019 ; markovi2020 . Since the negative magnetoresistance is found for , it is very likely linked to the intermediately reconstructed electronic structure (see Figure. 4c). ARPES experiments suggest that these Fermi surface consists for more than two sheets Horio2019 . Furthermore, out-of-plane resistivity indicate that a finite inter-layer interaction is still present yoshida_quasi-two-dimensional_2004 . As such the electronic structure contains complexity beyond the most simple two-band model. In addition, our magnetization data (see Figure. 2b) suggests the existence of weak ferromagnetism (on top of the antiferromagnetic coupling) below . It is not uncommon that magnetic correlations generate a negative magnetoresistance PhysRevB.66.024433 ; yamada1972negative that is comparable or larger than the orbital component. It is also not unusual that the ferromagnetic contribution is largest just below the ordering temperature Destraznpj2020 . The negative magnetoresistance in Ca3Ru2O7 therefore is likely linked both to the electronic structure and ferromagnetic properties.
6 Conclusions
In summary, we have carried out a magnetoresistance study of Ca3Ru2O7. As a function of temperature, three different regimes are identified: weak positive magnetoresistance for K, negative magnetoresistance for 30 K K and large positive magnetoresistance below K. These characteristic temperatures are directly linked to reconstructions of the low-energy electronic structure. We analysed the low-temperature magnetoresistance within a two-band model. An analytical solution to the two-band model for conductivity is developed and expressed in terms of two dimensionless (but measurable) parameters. Whereas reasonable values of electron/hole carrier density and mobility is found for selected temperatures ( K), the two band model is not capturing the full magnetic field and temperature dependence. The most pronounced limitation of the model is its inability to explain negative magnetoresistance. On top of a two-stage electronic reconstruction, we argue that the Fermi surface structure – and with that the electron/hole carrier density – is temperature dependent. This in combination with ferromagnetism generates the complicated magnetoresistance in Ca3Ru2O7.
Acknowledgements.
We thank Benoit Fauque for fruitful discussions. L.D., Y. X, M.H., K.v.A, T.S., and J.C. acknowledge support by the Swiss National Science Foundation. L. D. was partially funded through Excellence Scholarship by the Swiss Government.Appendix A
In the main text, the dimensionless parameters and are expressed in terms of and – Equations (3) and (4). Solving with respect to and yields:
| (5) |
and
| (6) |
with
| (7) | ||||
It is now possible to express the longitudinal and transverse resistance in terms of and :
| (8) |
| (9) |
For a semimetal with (), Equations 8 and 9 simplify to and . Therefore, no saturation of magnetoresistance or Hall effect is expected. For , however, the magnetoresistance should eventually saturate and non-linear isotherms should occur in the high-field limit. As shown in Fig. 2d, we indeed observe saturation of the and as magnetic field strength is increased. In the same field range, the magnetization scales perfectly with . Hence ferromagnetism as a source for the saturating magnetoresistance can thus be excluded. As we find close to unity, this saturation effect is stronger than what can be explained by the two-carrier model. It is possible to fit the entire field range, however the resulting parameters (,,,) are difficult to reconcile with the quantum oscillation and ARPES experiments. We are therefore concluding that the electron mobility is magnetic field dependent for T.
References
- (1) B. Fauqué B, X. Yang, W. Tabis, M. Shen, Z. Zhu, C. Proust, Y. Fuseya and K. Behnia, Phys. Rev. Materials 2, 114201 (2018).
- (2) R. Bel, K. Behnia and H. Berger, Phys. Rev. Lett. 91 066602 (2003).
- (3) Li P, Balakirev F F and Greene R L 2007 Phys. Rev. Lett. 99(4) 047003
- (4) Rourke P M C, Bangura A F, Proust C, Levallois J, Doiron-Leyraud N, LeBoeuf D, Taillefer L, Adachi S, Sutherland M L and Hussey N E 2010 Phys. Rev. B 82(2) 020514
- (5) Rana K G, Dejene F K, Kumar N, Rajamathi C R, Sklarek K, Felser C and Parkin S S P 2018 Nano Lett. 18 6591–6596 pMID: 30241438
- (6) Eguchi G and Paschen S 2019 Phys. Rev. B 99(16) 165128
- (7) Watts S M, Wirth S, Von Molnar S, Barry A and Coey J 2000 Phys. Rev. B 61 9621
- (8) Tokumoto T, Jobiliong E, Choi E, Oshima Y and Brooks J 2004 Solid State Commun. 129 599–604
- (9) Peramaiyan G, Sankar R, Muthuselvam I P and Lee W L 2018 Sci. Rep. 8 1–8
- (10) Wang A, Graf D, Liu Y, Du Q, Zheng J, Lei H and Petrovic C 2017 Phys. Rev. B 96(12) 121107
- (11) Fournier P, Jiang X, Jiang W, Mao S N, Venkatesan T, Lobb C J and Greene R L 1997 Phys. Rev. B 56(21) 14149–14156
- (12) Georges A, de’ Medici L and Mravlje J 2013 Annu. Rev. Condens. Matter Phys 4 137–178
- (13) He J, Rotundu C R, Scheurer M S, He Y, Hashimoto M, Xu K J, Wang Y, Huang E W, Jia T, Chen S, Moritz B, Lu D, Lee Y S, Devereaux T P and Shen Z X 2019 Proc. Natl. Acad. Sci. U.S.A. 116 3449–3453 ISSN 0027-8424 (Preprint
- (14) Sachdev S, Metlitski M A and Punk M 2012 J. Phys.: Condens. Matter 24 294205
- (15) Chang J, Sassa Y, Guerrero S, Månsson M, Shi M, Pailhés S, Bendounan A, Mottl R, Claesson T, Tjernberg O, Patthey L, Ido M, Oda M, Momono N, Mudry C and Mesot J 2008 New J. Phys. 10 103016
- (16) Damascelli A, Hussain Z and Shen Z X 2003 Rev. Mod. Phys. 75(2) 473–541
- (17) Sebastian S E and Proust C 2015 Annu. Rev. Condens. Matter Phys. 6 411–430 (Preprint
- (18) Kikugawa N, Winfried Rost A, William Hicks C, John Schofield A and Peter Mackenzie A 2010 J. Phys. Soc. Jpn. 79 024704
- (19) Fukazawa H, Nakatsuji S and Maeno Y 2000 Physica B 281 613–614
- (20) Nakatsuji S and Maeno Y 2001 J. Solid State Chem. 156 26 – 31
- (21) E Burkhardt Z G Y and Schmid H 1995 Rev. Sci. Instrum. 66(7) 3888
- (22) Destraz D, Das L, Tsirkin S S, Xu Y, Neupert T, Chang J, Schilling A, Grushin A G, Kohlbrecher J, Keller L, Puphal P, Pomjakushina E and White J S 2020 npj Quantum Mater. 5 5
- (23) Yoshida Y, Nagai I, Ikeda S I, Shirakawa N, Kosaka M and Môri N 2004 Phys. Rev. B 69 220411 ISSN 1098-0121, 1550-235X
- (24) Xing H, Wen L, Shen C, He J, Cai X, Peng J, Wang S, Tian M, Xu Z A, Ku W, Mao Z and Liu Y 2018 Phys. Rev. B 97(4) 041113
- (25) Iwata K, Kosaka M, Katano S, Môri N, Yoshida Y and Shirakawa N 2007 J. Magn. Magn. Mater. 310 1125 – 1127 ISSN 0304-8853 proceedings of the 17th International Conference on Magnetism
- (26) Yoshida Y, Ikeda S I and Shirakawa N 2007 J. Phys. Soc. Jpn. 76 085002
- (27) Kikugawa N, Winfried Rost A, William Hicks C, John Schofield A and Peter Mackenzie A 2010 J. Phys. Soc. Jpn. 79 024704
- (28) Ashcroft N and Mermin N 1976 Solid State Physics (Fort Worth: Saunders College Publishing)
- (29) Eom M J, Na S W, Hoch C, Kremer R K and Kim J S 2012 Phys. Rev. B 85(2) 024536
- (30) Pisoni A, Szirmai P, Katrych S, Náfrádi B, Gaál R, Karpinski J and Forró L 2016 Phys. Rev. B 93(9) 094519
- (31) Rullier-Albenque F 2016 C R Phys. 17 164 – 187 ISSN 1631-0705 iron-based superconductors / Supraconducteurs à base de fer
- (32) Yelland E A, Singleton J, Mielke C H, Harrison N, Balakirev F F, Dabrowski B and Cooper J R 2008 Phys. Rev. Lett. 100(4) 047003
- (33) Doiron-Leyraud N, Proust C, LeBoeuf D, Levallois J, Bonnemaison J B, Liang R, Bonn D A, Hardy W N and Taillefer L 2007 Nature 447 565–568
- (34) LeBoeuf D, Doiron-Leyraud N, Levallois J, Daou R, Bonnemaison J B, Hussey N E, Balicas L, Ramshaw B J, Liang R, Bonn D A, Hardy W N, Adachi S, Proust C and Taillefer L 2007 Nature 450 533–536
- (35) Wu T, Mayaffre H, Krämer S, Horvatic M, Berthier C, Hardy W N, Liang R, Bonn D A and Julien M H 2011 Nature 477 191
- (36) Ghiringhelli G, Tacon M L, Minola M, Blanco-Canosa S, Mazzoli C, Brookes N B, Luca G M D, Frano A, Hawthorn D G, He F, Loew T, Sala M M, Peets D C, Salluzzo M, Schierle E, Sutarto R, Sawatzky G A, Weschke E, Keimer B and Braicovich L 2012 Science 337 821–825
- (37) Chang J, Blackburn E, Holmes A T, Christensen N B, Larsen J, Mesot J, Liang R, Bonn D A, Hardy W N, Watenphul A, v Zimmermann M, Forgan E M and Hayden S M 2012 Nat. Phys. 8 871–876
- (38) Millis A J and Norman M R 2007 Phys. Rev. B 76(22) 220503
- (39) Breznay N P, Hayes I M, Ramshaw B J, McDonald R D, Krockenberger Y, Ikeda A, Irie H, Yamamoto H and Analytis J G 2016 Phys. Rev. B 94(10) 104514
- (40) Helm T, Kartsovnik M V, Bartkowiak M, Bittner N, Lambacher M, Erb A, Wosnitza J and Gross R 2009 Phys. Rev. Lett. 103(15) 157002
- (41) Helm T, Kartsovnik M V, Proust C, Vignolle B, Putzke C, Kampert E, Sheikin I, Choi E S, Brooks J S, Bittner N, Biberacher W, Erb A, Wosnitza J and Gross R 2015 Phys. Rev. B 92(9) 094501
- (42) Gollnik F and Naito M 1998 Phys. Rev. B 58(17) 11734–11752
- (43) Horio M, Wang Q, Granata V, Kramer K P, Sassa Y, Jöhr S, Sutter D, Bold A, Das L, Xu Y, Frison R, Fittipaldi R, Kim T K, Cacho C, Rault J E, Fèvre P L, Bertran F, Plumb N C, Shi M, Vecchione A, Fischer M H and Chang J 2019 Electron-driven -symmetric Dirac semimetal uncovered in Ca3Ru2O7
- (44) Marković I, Watson M D, Clark O J, Mazzola F, Morales E A, Hooley C A, Rosner H, Polley C M, Balasubramanian T, Mukherjee S, Kikugawa N, Sokolov D A, Mackenzie A P and King P D C 2020 Proc. Natl. Acad. Sci. U.S.A. 117 15524–15529
- (45) Puggioni D, Horio M, Chang J and Rondinelli J.M 2020 Phys. Rev. Research 2(2) 023141
- (46) Yoshida Y, Ikeda S.I, Matsuhata H, Shirakawa N, Lee C. H and Katano S 2005 Phys. Rev. B 72 054412 ISSN 1098-0121, 1550-235X
- (47) Raquet B, Viret M, Sondergard E, Cespedes O and Mamy R 2002 Phys. Rev. B 66(2) 024433
- (48) Yamada H and Takada S 1972 Prog. Theor. Phys. 48 1828–1848
- (49) Sokolov D, Kikugawa N, Helm T, Borrmann H, Burkhardt U, Cubitt R, White J, Ressouche E, Bleuel M, Kummer K, Mackenzie A. P , and Rößler U. K. 2019 Nat. Phys. 15 671–677