Two-connected signed graphs with maximum nullity at most two
Abstract
A signed graph is a pair , where is a graph (in which parallel edges are permitted, but loops are not) with and . The edges in are called odd and the other edges of even. By we denote the set of all symmetric matrices with if and are adjacent and connected by only even edges, if and are adjacent and connected by only odd edges, if and are connected by both even and odd edges, if and and are non-adjacent, and for all vertices . The parameters and of a signed graph are the largest nullity of any matrix and the largest nullity of any matrix that has the Strong Arnold Property, respectively. In a previous paper, we gave a characterization of signed graphs with and of signed graphs with . In this paper, we characterize the -connected signed graphs with and the -connected signed graphs with .
keywords:
signed graph, nullity, symmetricMSC:
05C22, 05C50, 15A031 Introduction
A signed graph is a pair , where is a graph (in which parallel edges are permitted, but loops are not) and . (We refer to [3] for the notions and concepts in graph theory.) The edges in are called odd and the other edges even. If , we denote by the set of all real symmetric matrices with
-
1.
if and are adjacent and all edges between and are even,
-
2.
if and are adjacent and all edges between and are odd,
-
3.
if and are connected by odd and even edges,
-
4.
if and and are non-adjacent, and
-
5.
for all vertices .
In [1] we introduced for any signed graph , among other parameters, the signed graph parameters and . For a signed graph , is the maximum of the nullities of the matrices in . In order to describe the parameter we need the notion of Strong Arnold Property (SAP for short). A matrix has the SAP if is the only symmetric matrix such that if and are adjacent vertices or , and . Then is defined as the largest nullity of any matrix satisfying the SAP. It is clear that for any signed graph . This signed graph parameter is analogous to the parameter for simple graphs introduced by Barioli, Fallat, and Hogben [2].
If is a graph and , then denotes the set of edges of with one end in and the other end in . The symmetric difference of two sets and is the set . If is a signed graph and , we say that and are sign-equivalent and call the operation re-signing on . Re-signing on amounts to performing a diagonal similarity on the matrices in , and hence it does not affect and .
Let be a signed graph. If is a subgraph of , then we say that is odd if has an odd number of elements, otherwise we call even. Zaslavsky showed in [7] that two signed graphs are sign-equivalent if and only if they have the same set of odd cycles. Thus, two signed graphs and that have the same set of odd cycles have .
In [1], we showed that a signed graph has if and only if is sign-equivalent to a signed graph , where is a graph whose underlying simple graph is a path. Furthermore, we showed that a signed graph has if and only if is sign-equivalent to a signed graph , where is a graph whose underlying simple graph is a disjoint union of paths. Observe that in case the signed graph is connected, if and only if . In this paper, we characterize the class of -connected signed graphs with . We will see that this class coincides with the class of signed graphs with .
The above characterizations are extensions of results known for simple graphs to signed graphs. For a simple graph , denote by the set of all real symmetric matrices with if and are connected by an edge, if and and are non-adjacent, and for all vertices . The maximum nullity of a simple graph is the maximum of the nullities of the matrices in . Fiedler [4] proves that a simple graph has if and only if is a path. In [6], Johnson, Loewy, and Smith characterize the class of simple graphs with . Barioli, Fallat, and Hogben introduced in [2] the parameter . For a simple graph , is defined as the largest nullity of any matrix satisfying the SAP. In [2], they prove that a graph has if and only if is a subgraph of a path. In [5], Hogben and van der Holst give a characterization of the class of simple graphs with .
2 The maximum nullity of some signed graphs
Contracting an edge with ends and in a graph means deleting and identifying the vertices and . A signed graph is a weak minor of a signed graph if can be obtained from by deleting edges and vertices, contracting edges, and re-signing around vertices. We use weak minor to distinguish it from minor in which only even edges are allowed to be contracted (possibly after re-signing around vertices). The parameter has the nice property that if is a weak minor of the signed graph , then .
Let us now introduce some signed graphs. By and we denote the signed graphs and , respectively. By we denote the signed graph , where is the graph obtained from by adding to each edge an edge in parallel, and where is the set of edges of . By we denote the signed graph , where is an edge of . By and , we denote the signed graphs and , where is an edge of , respectively.
The following lemma follows from Proposition 4 in [1].
Lemma 1.
.
From Proposition 8 in [1], the following lemma follows.
Lemma 2.
and .
The following lemma follows from Proposition 34 in [1].
Lemma 3.
.
The following lemma follows from Proposition 35 in [1].
Lemma 4.
and .
From Lemmas 2 and 4, it follows that signed graphs with cannot have a weak -, -, or -minor. If a signed graph has no weak -, -, or -minor, the graph can still have a - or -minor. However, these minors force the signed graph to have additional structure. We will study this in the next section.
By we denote the graph obtained from by adding a new vertex , called the hub, and connecting it to each vertex of . The subgraph in is called the rim of . Any edge between and a vertex of the rim of is called a spoke. Let be two nonadjacent edges of the in . By , we denote the signed graph . See Figure 1 for a picture of ; here a bold edge is an odd edge and a thin edge an even edge. This signed graph appears as a special case in the characterization of -connected signed graphs with .
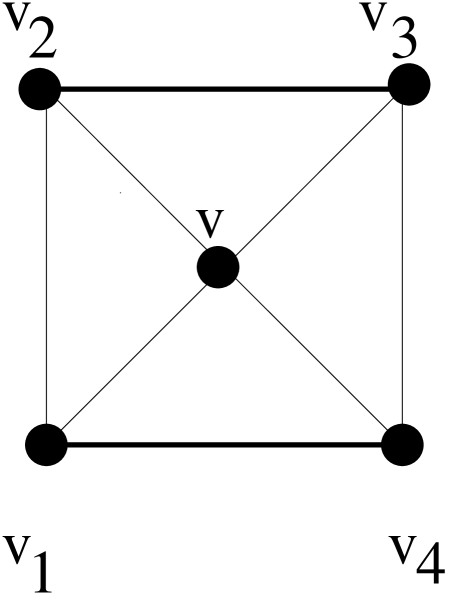
Lemma 5.
Proof.
Let be the vertices on the rim of in this cyclic order, and let be the hub of . We assume that the edges between and and between and are even. Suppose for a contradiction that . Then there exists a matrix with nullity . Since , there exist nonzero vectors with and . If , then from it would follow that . This contradiction shows that . We may assume that . Then, since the edge between and is even, the edge between and is odd, and , it follows that . Similarly, . Let denote the row of corresponding to . Then , and, since , , , it follows that .
We will now do the same with the vector . If , then it would follow that . This contradiction shows that . We may assume that . Then, since the edge between and is even, the edge between and is even, and , it follows that . Similarly, . Since and , , , it follows that . We have arrived at a contradiction, and we can conclude that . Since contains an odd cycle, , and hence . ∎
3 Wide separations
Let be a signed graph. A pair of subgraphs of is a wide separation of if there exists an odd -cycle such that , , , , and , where and are nonadjacent vertices of and and are nonadjacent vertices of . We call the vertices of attachment of and the vertices of attachment of in the wide separation. See Figure 2 for an illustration. Here a bold edge is an odd edge and a thin edge an even edge.
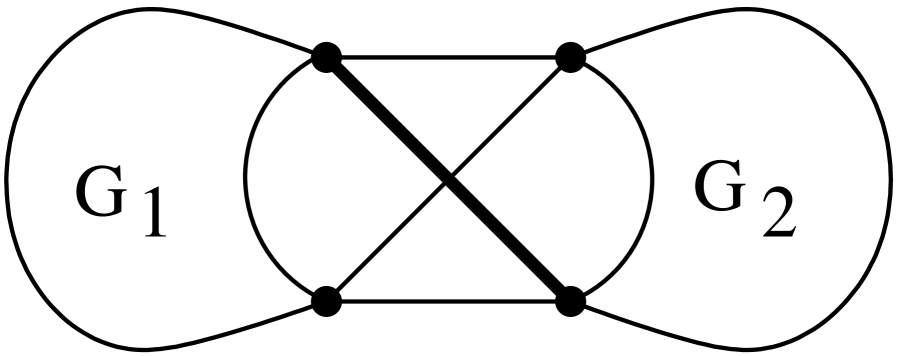
Lemma 6.
Let be a signed graph with no weak minor isomorphic to , , or . If has a -minor, but no -minor, then has a wide separation.
Proof.
Since has a -minor and all vertices of have degree three, has a subgraph isomorphic to a subdivision of . Hence there are distinct vertices and openly disjoint paths of length in , where has ends and , has ends and , has ends and , has ends and , has ends and , and has ends and . Let be the subgraph spanned by and . Since has no weak - or -minor, has no weak - or -minor.
By re-signing if needed, we may assume that, in , is an odd path and that are even paths. We can see that the paths , , , and consist of single edges as follows. is a single edge, for otherwise, possibly after re-signing, we contract an odd edge in and obtain a signed graph that contains as a weak minor. is a single edge, for otherwise, we contract an odd edge in and obtain a signed graph that contains as a weak minor. If both and have length , then, possibly after re-signing, we contract an odd edge in and in , and obtain a signed graph that has as a weak minor. Hence at least one of and consists of a single edge. In the same way, at least one of and consists of a single edge. If both and have length , then possibly after re-signing, we contract an odd edge in and in , and obtain a signed graph that has as a weak minor. Hence at least one of and consists of a single edge. In the same way, at least one of and consists of a single edge. If one of and has length , then and consist each of a single edge. Hence, we can conclude that both and consist of single edges, or that both and consist of single edges. By symmetry we may assume that and consist of single edges.
Since has no -minor, each path connecting a vertex of to a vertex of must contain at least one vertex of and at least one vertex of . Thus has a wide separation. ∎
The graph with two vertices and no edges is denoted by .
Lemma 7.
Let be a graph with no weak -minor. If has a -minor but no -minor, then has a wide separation , where is isomorphic to .
Proof.
Since has a -minor, has a subgraph isomorphic to a subdivision of . Hence there are vertices and openly disjoint paths of length in , where has ends and , has ends and , has ends and , has ends and , has ends and , and has ends and . We now view the paths as paths in the signed graph . As has no weak -minor, has a weak -minor. Hence we may re-sign such that is odd and are even.
is a single edge, for otherwise, possibly after re-signing, we contract an odd edge in and obtain a signed graph that contains as a weak minor. Similarly, is a single edge. If both and have length , then, possibly after re-signing, we contract an odd edge in and in , and obtain a signed graph that has as a weak minor. Hence, at least one of and consists of a single edge. Similarly, at least one of and consists of a single edge, at least one of and consists of a single edge, and at least one of and consists of a single edge. Hence at most one path of has length . By symmetry, we may assume that each path of consists of a single edge. Let be the concatenation of and . Since has no -minor, there are no paths in connecting and , there are no paths in connecting and an internal vertex of , and there are no paths in connecting and an internal vertex of . Hence, has a wide separation , where is isomorphic to . ∎
4 The signed four-wheel
In this section we show that if is a signed graph with no weak -, -, or -minor, but has a -minor, then the edges in each parallel class of have the same parity and, after removing all but one edge from each parallel class, we obtain .
Lemma 8.
Let be a signed graph with no weak -, -, or -minor. Then is sign-equivalent to .
Proof.
If at most one triangle of is even, then has a weak -minor. If at most one triangle of is odd, then has a weak -minor. So we may assume that has exactly two odd triangles. If they share an edge, then has a weak -minor. If they do not share an edge, then is sign-equivalent to . ∎
Lemma 9.
Let be obtained from by adding an odd or even edge between nonadjacent vertices. Then has a weak - or -minor.
Proof.
Let be the vertices on the rim of in this order. Up to symmetry there is only one possibility to add an edge between two nonadjacent vertices in . We may assume that we add the edge between and . If is an even edge, then the resulting signed graph has a weak -minor. If is an odd edge, then the resulting graph has a weak -minor. ∎
Lemma 10.
Let be a signed graph which has an edge whose contraction yields . Then has a weak - or -minor.
Proof.
If has a vertex of degree two, then arises from by inserting a new vertex on an edge of , which results in a path of length two in . If is an even edge on the rim of , then, possibly after re-signing, we contract all but one odd edge of . The resulting signed graph contains a weak -minor. If is an odd edge on the rim of , then, possibly after re-signing, we contract all but one even edge of . The resulting signed graph contains a weak -minor. If is a spoke of , then, possibly after re-signing, we contract all but one odd edge of . The resulting signed graph contains a weak -minor.
So we may assume that has no vertex of degree two. Then is isomorphic either to the prism, (see Figure 3), or to . Let be the edge in such that contracting yields .
If is isomorphic to , then contains a weak -minor. Suppose next that is isomorphic to the prism. Then has either two odd triangles or two even triangles. If has two odd triangles, then, possibly after re-signing, we contract and another edge not on the two odd triangles, and obtain a signed graph that contains a as a signed subgraph. If has two even triangles, then, possibly after re-signing, we contract and another edge not on the two even triangles, and obtain a signed graph that contains a as a signed subgraph. ∎
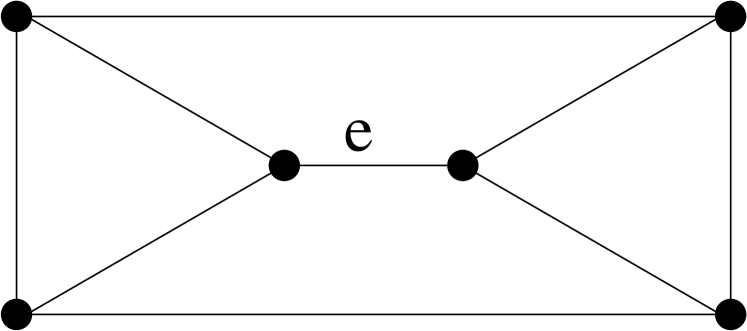
Lemma 11.
Let be a signed graph. If has a -minor, then at least one of the following holds:
-
1.
has a weak -, -, or -minor, or
-
2.
the edges in each parallel class of have the same parity and, after removing from each parallel class all but one edge, we obtain .
Proof.
Suppose for a contradiction that there exists a signed graph such that has a -minor, but has no weak -, -, or -minor and it is not the case that the edges in each parallel class of have the same parity and, after removing from each parallel class all but one edge, we obtain . We take with as small as possible.
If the underlying simple graph of is isomorphic to , then there must be parallel edges of different parity in . In this case has a weak -, -, or -minor by Lemma 8. So we may assume that the underlying simple graph of is not isomorphic to . Since has a -minor and is connected, there exists a signed graph such that is a minor of , the underlying simple graph of is not isomorphic to , and can be obtained from by deleting or contracting one edge. If can be obtained from by deleting an edge , then connects nonadjacent vertices of . In this case, has a weak - or -minor by Lemma 9, and hence has a - or -minor. If can be obtained from by contracting an edge , then has a weak - or -minor by Lemma 10, and hence has a weak - or -minor. ∎
5 Partial wide -path
In this section, we first make some new definitions. A sided -path is defined recursively as follows:
-
1.
Let be a triangle and let be a set of two distinct edges in this triangle. Then is a sided -path.
-
2.
If is a sided -path and is obtained from by adding edges parallel to the edges in , then is a sided -path.
-
3.
Let be a sided -path and let and be distinct edges in a disjoint triangle . If is obtained from by identifying the edge of with an edge in , then is a sided -path.
The edges in are called the sides of the sided -path. A -path is a graph for which there exists a set of two distinct edges of such that is a sided -path. A partial -path is a subgraph of a -path. A -connected partial -path with no parallel edges is the same as a linear singly edge articulated cycle graph (LSEAC), a type of graph introduced by Johnson et al. [6], and it is the same as a linear 2-tree, a type of graph introduced by Hogben and van der Holst [5].
Lemma 12.
Let be a -connected graph with no -, -, or -minor. Then is a partial -path.
Proof.
Since has no - and no -minor, is outerplanar. Hence can be embedded in the plane such that all its vertices are incident to the infinite face. Add edges such that all finite faces are either triangles or cycles with exactly two edges, and let the resulting graph be . Construct the following tree . The vertices of are all finite faces of the plane embedding. Connect two vertices of the tree if the corresponding faces have an edge in common. Then is a path. For if not, there would be a face that has edges in common with at least three other faces. Such a graph has a -minor. By induction it can now be shown that is a -path. Hence is a partial -path. ∎
A pair of nonadjacent edges in is called split if both and belong to an even and an odd triangle.
A sided wide -path is defined recursively as follows:
-
1.
Let be an even or odd triangle or a . If is a triangle, let be two distinct edges in this triangle. If , let be a split pair of edges in . Then is a sided wide -path.
-
2.
If is a sided wide -path and is obtained from by adding odd and even edges parallel to edges in , then is a sided wide -path.
-
3.
Let be a sided wide -path and let and be distinct edges in an even or odd triangle . If is obtained from by identifying the edge of with an edge in , then is a sided wide -path.
-
4.
Let be a sided wide -path and let be a split pair of edges in . If is obtained from by identifying the edge of with an edge in , then is a sided wide -path.
The edges in are called the sides of the sided wide -path. A wide -path is a signed graph for which there exists a set of two distinct edges of such that is a sided wide -path. A signed graph is a partial wide -path if it is a spanning subgraph of a wide -path. Observe that if is a partial -path, then is a partial wide -path.
Lemma 13.
Let be a -connected signed graph. If has no minor isomorphic to -, -, , or , then, after removing in each parallel class all but one edge of the same parity, is either isomorphic to or is a partial wide -path.
Proof.
If has a -minor, then is isomorphic to , by Lemma 11. We may therefore assume that has no -minor.
Suppose has a -minor. Then, by Lemma 6, has a wide separation . For , let be obtained from by adding between the vertices of attachment of in the wide separation an odd and even edge in parallel. Then , , contains no weak minor isomorphic to , , , , or , for otherwise would contain a weak minor isomorphic to , , , , or .
Let and be the vertices of attachment of in the wide separation . Suppose contains more than one component; let be the components. Then, as is -connected, each contains a path of length connecting and . If there are components and such that both and contain an even path connecting and , then has a -minor, a contradiction. Similarly, there are no two components and such that both and contain an odd path connecting and . Hence has exactly two components and . If contains a path of length connecting and and contains an even path connecting and , then, possibly after re-signing, we contract an edge of to obtain an even path. Then has a -minor. The cases where has an odd path connecting and , and where has a path of length connecting and are similar.
If has parallel edges whose ends are not and , then and contain paths connecting and of equal parity. Then has a . A similar statement holds for . Hence and are paths of length and have different parity. Thus is a subgraph of a sided wide -path where one of the parallel edges between and is a side.
Suppose contains exactly one component. By induction is a partial wide -path. Since, in the construction of a wide -path, parallel edges appear only parallel to the edges in of a sided wide -path and has exactly one component, there exists a set of two distinct edges, one of which is between and , of such that is a sided wide -path.
Similarly there exists a set of two distinct edge, one of which is between the vertices of attachments of such that is a sided wide -path. Then is a partial wide -path. We may therefore assume that has no -minor.
Suppose has a -minor. Then, by Lemma 7, has a wide separation , where is isomorphic to . Let be obtained from by adding between the vertices attachment of in the wide separation an odd and even edge in parallel. Then contains no minor isomorphic to , , , , or . By induction is a partial wide -path. Similar as above, there is a sided wide -path such that is a subgraph of and one of the edges of is an edge between the attachments of in the wide separation . Then is a partial wide -path. We may therefore assume that has no -minor.
Since has no -, -, or -minor, is a partial -path, and so is a partial wide -path. ∎
Lemma 14.
If is a -connected partial wide -path, then .
Proof.
Suppose for a contradiction that . Then there exists a matrix with . Since is a partial wide -path, is a spanning subgraph of a wide -path .
If a wide separation in does not yield a wide separation in , then we replace the in by two adjacent triangles. We may therefore assume that for each wide separation in , is a wide separation in . For a vertex of , we denote by the th row of .
Let be the two ends of an edge in the set of the wide -path . As , there exists a nonzero vector with . If belongs to a triangle, let be the edge distinct from in the construction of the wide -path . Exactly one end of belongs to , let’s say , while the other end, , is adjacent in to . From it follows that .
If belongs to a , then belongs to an odd and even triangle of . Let and be the vertices of this distinct from and . By symmetry, we may assume that the edges , , and are even and that the edge is odd. Suppose . From , it follows that . From , it follows that . This contradiction shows that . In the same way, it is not possible that . Hence . From , it then follows that .
Repeating the above shows that , which contradicts that is a nonzero vector in . Thus . ∎
We now arrive at our main result.
Theorem 15.
Let be a -connected signed graph. Then the following are equivalent:
-
(i)
,
-
(ii)
,
-
(iii)
has no minor isomorphic to , , , or .
-
(iv)
is a partial wide -path or is isomorphic to .
6 References
References
- [1] M. Arav, F. Hall, Z. Li, and H. van der Holst. The inertia set of a signed graph. Linear Algebra Appl., 439(5):1506–1529, 2013.
- [2] F. Barioli, S. Fallat, and L. Hogben. A variant on the graph parameters of Colin de Verdière: implications to the minimum rank of graphs. Electron. J. Linear Algebra, 13:387–404, 2005.
- [3] R. Diestel. Graph Theory. Springer-Verlag, New York, second edition, 2000.
- [4] M. Fiedler. A characterization of tridiagonal matrices. Linear Algebra and Appl., 2:191–197, 1969.
- [5] L. Hogben and H. van der Holst. Forbidden minors for the class of graphs with . Linear Algebra Appl., 423(1):42–52, 2007.
- [6] C. R. Johnson, R. Loewy, and P. A. Smith. The graphs for which the maximum multiplicity of an eigenvalue is two. Linear Multilinear Algebra, 57(7):713–736, 2009.
- [7] T. Zaslavsky. Signed graphs. Discrete Appl. Math., 4(1):47–74, 1982.