1]\orgdivSchool of Mathematics, \orgnameShandong University, \orgaddress\cityJinan, \postcode250100, \countryChina

Two methods addressing variable-exponent fractional initial and boundary value problems and Abel integral equation

\fnmXiangcheng \surZheng xzheng@sdu.edu.cn [

Abstract

Variable-exponent fractional models attract increasing attentions in various applications, while the rigorous analysis is far from well developed. This work provides general tools to address these models. Specifically, we first develop a convolution method to study the well-posedness, regularity, an inverse problem and numerical approximation for the sundiffusion of variable exponent. For models such as the variable-exponent two-sided space-fractional boundary value problem (including the variable-exponent fractional Laplacian equation as a special case) and the distributed variable-exponent model, for which the convolution method does not apply, we develop a perturbation method to prove their well-posedness. The relation between the convolution method and the perturbation method is discussed, and we further apply the latter to prove the well-posedness of the variable-exponent Abel integral equation and discuss the constraint on the data under different initial values of variable exponent.

keywords:

Variable exponent, Fractional differential equation, Integral equation, Mathematical analysis

pacs:

[

MSC Classification]35R11, 45D05, 65M12

1 Introduction

Variable-exponent fractional models attract increasing attentions in various fields. For instance, the variable-exponent subdiffusion equation has been widely used in the anomalous transient dispersion [47, 48], while the variable-exponent two-sided space-fractional diffusion equation has been applied in, e.g., the turbulent channel flow [44] and the transport through a highly heterogeneous medium [41, 56]. More applications of variable-exponent fractional models can be found in a comprehensive review [49].

Nevertheless, the theoretical study of variable-exponent fractional initial and boundary value problems as well as the corresponding integral equations is far from well developed. For the subdiffusion model, a typical fractional initial value problem, there exist extensive investigations and significant progresses for the constant-exponent case [4, 17, 18, 27, 28, 29, 32, 34, 35, 38, 54, 55], while much fewer investigations for the variable exponent case can be found in the literature. There exist some mathematical and numerical results for the case of space-variable-dependent variable exponent [26, 31, 58]. For the time-variable-dependent case, there are some recent works changing the exponent in the Laplace domain [7, 16] such that the Laplace transform of the variable-exponent fractional operator is available. For the case that the exponent changes in the time domain, the only available results focus on the piecewise-constant variable exponent case such that the solution representation is available on each temporal piece [25, 51]. It is also commented in [25] that the case of smooth exponent remains an open problem. Recently, a local modification of subdiffusion by variable exponent $\alpha(t)$ is proposed in [60], where the techniques work only for the case $\alpha(0)=0$ such that this is mathematically a special case of the variable-exponent subdiffusion model. The general case $0<\alpha(0)<1$ remains untreated.

For fractional and nonlocal boundary value problems, there also exist sophisticated investigations for the constant-exponent case, see e.g. [2, 8, 11, 12, 13, 14, 24]. For the variable-exponent case, there are some corresponding theoretical results such as heat kernel estimates for variable-exponent nonlocal operators [6] and well-posedness study for a nonlocal model involving the doubly-variable fractional exponent and possibly truncated interaction [9]. Numerically, some efficient algorithms have been developed for the variable-exponent nonlocal and fractional Laplacian operators [9, 52]. Furthermore, a solution landscape approach has been applied for nonlinear problems involving variable-exponent spectral fractional Laplacian [53]. Nevertheless, rigorous analysis of variable-exponent fractional boundary value problems defined via fractional derivatives, e.g., the variable-exponent two-sided space-fractional diffusion equation in the form as [14], is not available in the literature.

For weakly singular integral equations such as the Abel integral equation, extensive results for the constant-exponent models can be found in the literature, see e.g. the books [5, 19]. For the case of variable exponent, there are rare studies. Recently, some works consider the mathematical and numerical analysis for the second-kind weakly singular Volterra intrgral equation of the variable exponent [33, 61]. For the first-kind integral equations, [59] develops an approximate inverse technique to convert the non-convolutional Abel intrgral equation of variable exponent to a second-kind weakly singular Volterra intrgral equation to facilitate the analysis. For the variable-exponent Abel intrgral equation of convolutional form, which is a more natural way to introduce the variable exponent, the corresponding study is not available.

The main difficulty for investigating variable-exponent fractional initial or boundary value problems as well as the first-kind variable-exponent Volterra integral equations is that the variable-exponent Abel kernel in these models could not be analytically treated by, e.g. the integral transform, and may not be positive definite or monotonic such that existing methods for partial differential equations do not apply directly. It is worth mentioning that in some variable-exponent fractional models considered in, e.g. [61, 62], both integer-order and variable-exponent fractional terms exist at the same time in space or time such that the latter serve as low-order terms. For this case, the complexity of the variable-exponent operators is weakened such that the analysis could be performed. For models considered in the current work, where the variable-exponent fractional terms serve as leading terms, the methods in [61, 62] do not apply.

In this work, we develop two methods, i.e. the convolution method and the perturbation method, to address the aforementioned issues, which provide general tools for analyzing different kinds of variable-exponent nonlocal models, including variable-exponent initial and boundary value problems and the variable-exponent Abel integral equation. Specifically, the main contributions are enumerated as follows:

$\blacktriangleright$

Convolution method for initial value problems
We develop a convolution method to treat the variable-exponent fractional initial value problems, the idea of which is to calculate the convolution of the original model and a suitable kernel to get a more feasible formulation such that the analysis could be considered. The key of this method lies in introducing a “nice” kernel such that its convolution with the variable-exponent kernel leads to a so-called generalized identity function, which has favorable properties. Thus, the variable-exponent term could be transformed to a more feasible form without deteriorating the properties of the other terms in the model (as the introduced kernel is nice) such that the transformed model becomes tractable.
We apply the convolution method to give a mathematical and numerical analysis for subdiffusion of variable exponent, a typical fractional initial value problem, including the following contents:
- $\bullet$
  
  We prove its well-posedness and regularity by means of resolvent estimates, and characterize the singularity of the solutions in terms of the initial value $\alpha(0)$ of the exponent, which indicates an intrinsic factor of variable-exponent models.
- $\bullet$
  
  The semi-discrete and fully-discrete numerical methods are developed and their error estimates are proved, without any regularity assumption on solutions or requiring specific properties of the variable-exponent Abel kernel such as positive definiteness or monotonicity. We again characterize the convergence order by $\alpha(0)$ .
- $\bullet$
  
  Since the $\alpha(0)$ plays a critical role in characterizing properties of the model and the numerical method, we present a preliminary result for the inverse problem of determining $\alpha(0)$ .
$\blacktriangleright$

Perturbation method for boundary value problems and integral equations
For problems such as variable-exponent two-sided space-fractional boundary value problems or distributed variable-exponent problems, the convolution method do not apply, cf. Section 5.1 for detailed reasons. Thus, we develop an alternative method called the perturbation method to treat these models, the idea of which is to replace the variable-exponent kernel by a suitable “nice” kernel such that their difference is a low-order perturbation term. Note that different from the convolution method, the perturbation method treats the variable-exponent term locally such that all other terms in the model keep unchanged.
Then we investigate and apply the perturbation method from the following aspects:
- $\bullet$
  
  We first show that for some models such as the variable-exponent subdiffusion, the convolution method and the perturbation method are indeed the same method in the sense that both methods could lead to the same transformed model.
- $\bullet$
  
  We apply the perturbation method to prove the well-posedness of variable-exponent two-sided space-fractional diffusion-advection-reaction equation (including the variable-exponent fractional Laplacian equation as a special case) by showing the coercivity and continuity of the corresponding bilinear form, which are difficult to prove from the original form of the model since the variable-exponent fractional operators are not positive definite or monotonic.
- $\bullet$
  
  We apply the perturbation method to prove the well-posedness of the weak solution of a distributed variable-exponent model.
- $\bullet$
  
  We further apply the perturbation method to analyze the well-posedness of the variable-exponent Abel integral equation for three cases: $0<\alpha(0)<1$ , $\alpha(0)=0$ and $\alpha(0)=1$ . In particular, we observe that for the last two cases, an additional constraint is required to ensure the well-posedness, and a further extension implies that the well-posedness of the variable-exponent subdiffusion with $\alpha(0)=1$ also requires an additional constraint on initial values of the data.

The rest of the work is organized as follows: In Section 2 we introduce notations and preliminary results. In Section 3 we introduce the convolution method and then apply it to prove the well-posedness and regularity of the subdiffusion of variable exponent, as well as an inverse problem of determining the $\alpha(0)$ . In Section 4, semi-discrete and fully-discrete schemes for subdiffusion of variable exponent are proposed and analyzed. In Section 5, we introduce the perturbation method and then apply it to analyze the variable-exponent two-sided space-fractional boundary value problem and the distributed variable-exponent model. In Section 6 we further apply the perturbation method to analyze the variable-exponent Abel integral equation.

2 Preliminaries

2.1 Notations

Let $L^{p}(\Omega)$ with $1\leq p\leq\infty$ be the Banach space of $p$ th power Lebesgue integrable functions on $\Omega$ . Denote the inner product of $L^{2}(\Omega)$ as $(\cdot,\cdot)$ . For a positive integer $m$ , let $W^{m,p}(\Omega)$ be the Sobolev space of $L^{p}$ functions with $m$ th weakly derivatives in $L^{p}(\Omega)$ (similarly defined with $\Omega$ replaced by an interval $\mathcal{I}$ ). Let $H^{m}(\Omega):=W^{m,2}(\Omega)$ and $H^{m}_{0}(\Omega)$ be its subspace with the zero boundary condition up to order $m-1$ . For $\frac{1}{2}<s\leq 1$ , $H^{s}_{0}(\Omega)$ is defined via interpolation of $L^{2}(\Omega)$ and $H^{1}_{0}(\Omega)$ [1].

Let $\{\lambda_{i},\phi_{i}\}_{i=1}^{\infty}$ be eigen-pairs of the problem $-\Delta\phi_{i}=\lambda_{i}\phi_{i}$ with the zero boundary condition. We introduce the Sobolev space $\check{H}^{s}(\Omega)$ for $s\geq 0$ by $\check{H}^{s}(\Omega):=\big{\{}q\in L^{2}(\Omega):\|q\|_{\check{H}^{s}}^{2}:=\sum_{i=1}^{\infty}\lambda_{i}^{s}(q,\phi_{i})^{2}<\infty\big{\}},$ which is a subspace of $H^{s}(\Omega)$ satisfying $\check{H}^{0}(\Omega)=L^{2}(\Omega)$ and $\check{H}^{2}(\Omega)=H^{2}(\Omega)\cap H^{1}_{0}(\Omega)$ [50]. For a Banach space $\mathcal{X}$ , let $W^{m,p}(0,T;\mathcal{X})$ be the space of functions in $W^{m,p}(0,T)$ with respect to $\|\cdot\|_{\mathcal{X}}$ . All spaces are equipped with standard norms [1, 15].

Before introducing fractional derivative spaces, we present fractional operators. For $0<\mu<1$ , define

\beta_{\mu}(t):=\frac{t^{\mu-1}}{\Gamma(\mu)},

the left-sided fractional integral operator

I_{t}^{\mu}q:=\beta_{\mu}*q=\int_{0}^{t}\beta_{\mu}(t-s)q(s)ds,

the left-sided Riemann-Liouville fractional derivative operator $\partial_{t}^{\mu}q:=\partial_{t}(\beta_{1-\mu}*q)$ and the left-sided Caputo fractional derivative operator ${}^{c}\partial_{t}^{\mu}q:=\beta_{1-\mu}*(\partial_{t}q)$ [22]. The right-sided operators are denoted as $\hat{I}_{t}^{\mu}$ , $\hat{\partial}_{t}^{\mu}$ and ${}^{c}\hat{\partial}_{t}^{\mu}$ , respectively, with standard definitions [22]. On a finite interval $\Omega$ , the following semigroup property and the adjoint property hold

\displaystyle I_{x}^{\mu_{1}}I_{x}^{\mu_{2}}q=I_{x}^{\mu_{1}+\mu_{2}}q,~{}~{}\mu_{1},\mu_{2}\geq 0;~{}~{}(I_{x}^{\mu}q,\bar{q})=(q,\hat{I}_{x}^{\mu}\bar{q}),

(1)

and it is proved in [14] that the following equivalent formulas hold for $u,v\in H^{\mu}_{0}(\Omega)$ with $0<\mu<\frac{1}{2}$ or $\frac{1}{2}<\mu<1$ and for some positive constants $c_{1}$ – $c_{4}$

	$\displaystyle c_{1}\\|u\\|^{2}_{H^{\mu}(\Omega)}\leq(-1)^{\sigma}(\partial_{x}^{\mu}u,\hat{\partial}_{x}^{\mu}u)\leq c_{2}\\|u\\|^{2}_{H^{\mu}(\Omega)},$
	$\displaystyle~{}~{}c_{3}\\|\partial_{x}^{\mu}u\\|_{L^{2}(\Omega)}\leq\\|u\\|_{H^{\mu}(\Omega)}\leq c_{4}\\|\partial_{x}^{\mu}u\\|_{L^{2}(\Omega)},$		(2)
	$\displaystyle~{}~{}c_{3}\\|\hat{\partial}_{x}^{\mu}u\\|_{L^{2}(\Omega)}\leq\\|u\\|_{H^{\mu}(\Omega)}\leq c_{4}\\|\hat{\partial}_{x}^{\mu}u\\|_{L^{2}(\Omega)},$

where $\sigma=0$ for $0<\mu<\frac{1}{2}$ and $\sigma=1$ for $\frac{1}{2}<\mu<1$ .

We use $Q$ to denote a generic positive constant that may assume different values at different occurrences. We use $\|\cdot\|$ to denote the $L^{2}$ norm of functions or operators in $L^{2}(\Omega)$ , set $L^{p}(\mathcal{X})$ for $L^{p}(0,T;\mathcal{X})$ for brevity, and drop the notation $\Omega$ in the spaces and norms if no confusion occurs. For instance, $L^{2}(L^{2})$ implies $L^{2}(0,T;L^{2}(\Omega))$ . Furthermore, we will drop the space variable $\bm{x}$ in functions, e.g. we denote $q(\bm{x},t)$ as $q(t)$ , when no confusion occurs.

For $\theta\in(\pi/2,\pi)$ and $\delta>0$ , let $\Gamma_{\theta}$ be the contour in the complex plane defined by $\Gamma_{\theta}:=\big{\{}z\in\mathbb{C}:|{\rm arg}(z)|=\theta,|z|\geq\delta\big{\}}\cup\big{\{}z\in\mathbb{C}:|{\rm arg}(z)|\leq\theta,|z|=\delta\big{\}}.$ For any $q\in L^{1}_{loc}(\mathcal{I})$ , the Laplace transform $\mathcal{L}$ of its extension $\tilde{q}(t)$ to zero outside $\mathcal{I}$ and the corresponding inverse transform $\mathcal{L}^{-1}$ are denoted by

\displaystyle\mathcal{L}q(z):=\int_{0}^{\infty}\tilde{q}(t)e^{-tz}dt,\quad\mathcal{L}^{-1}(\mathcal{L}q(z)):=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta}}e^{tz}\mathcal{L}q(z)dz=q(t).

The following inequalities hold for $0<\mu<1$ and $Q=Q(\theta,\mu)$ [3, 37, 42]

\int_{\Gamma_{\theta}}|z|^{\mu-1}|e^{tz}|\,|dz|\leq Qt^{-\mu},~{}~{}t\in(0,T];~{}~{}\|(z^{\mu}-\Delta)^{-1}\|\leq Q|z|^{-\mu},~{}~{}\forall z\in\Gamma_{\theta},

(3)

and we have $\mathcal{L}(\partial_{t}^{\mu}q)=z^{\mu}\mathcal{L}q-(I_{t}^{1-\mu}q)(0)$ [22].

In Sections 2–5, we consider smooth variable exponent $0<\alpha(t)<1$ on $t\in[0,T]$ or $t\in[0,1]$ such that $\alpha(t)$ is three times differentiable with $|\alpha^{\prime}(t)|+|\alpha^{\prime\prime}(t)|+|\alpha^{\prime\prime\prime}(t)|\leq L$ for some $L>0$ . In the last section, the special cases $\alpha(0)=0$ or $\alpha(0)=1$ (with $0<\alpha(t)<1$ on $t\in(0,T]$ ) will be considered. Furthermore, we denote $\alpha_{0}=\alpha(0)$ and $\alpha_{1}=\alpha(1)$ for simplicity.

2.2 A generalized identity function

We propose the concept of the generalized identity function. For the variable-exponent Abel kernel

k(t):=\frac{t^{-\alpha(t)}}{\Gamma(1-\alpha(t))},

direct calculations show that

$\displaystyle(\beta_{\alpha_{0}}*k)(t)=$	$\displaystyle\int_{0}^{t}\frac{(t-s)^{\alpha_{0}-1}}{\Gamma(\alpha_{0})}\frac{s^{-\alpha(s)}}{\Gamma(1-\alpha(s))}ds$
	$\displaystyle\overset{z=s/t}{=}\int_{0}^{1}\frac{(t-tz)^{\alpha_{0}-1}}{\Gamma(\alpha_{0})}\frac{(tz)^{-\alpha(tz)}}{\Gamma(1-\alpha(tz))}tdz$	(4)
	$\displaystyle=\int_{0}^{1}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz=:g(t).$

It is clear that if $\alpha(t)\equiv\alpha$ for some constant $0<\alpha<1$ , then

g(t)=\int_{0}^{1}\frac{1}{\Gamma(\alpha)\Gamma(1-\alpha)}(1-z)^{\alpha-1}z^{-\alpha}dz=1.

For the variable exponent $\alpha(t)$ , $g(t)\not\equiv 1$ in general. However, as

\lim_{t\rightarrow 0^{+}}|(\alpha_{0}-\alpha(tz))\ln tz|\leq\lim_{t\rightarrow 0^{+}}Ltz|\ln tz|=0,

we have $\lim_{t\rightarrow 0^{+}}(tz)^{\alpha_{0}-\alpha(tz)}=\lim_{t\rightarrow 0^{+}}e^{(\alpha_{0}-\alpha(tz))\ln tz}=1,$ which implies

\displaystyle g(0)=\int_{0}^{1}\frac{1}{\Gamma(\alpha_{0})\Gamma(1-\alpha_{0})}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz=1.

(5)

Based on this property, we call $g(t)$ a generalized identity function, which will play a key role in reformulating the model (9) to more feasible forms for mathematical and numerical analysis.

It is clear that $g$ is bounded over $[0,T]$ . To bound derivatives of $g$ , we use $(tz)^{\alpha_{0}-\alpha(tz)}\leq Q$ to obtain

	$\displaystyle\Big{\|}\partial_{t}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle=\Big{\|}(tz)^{\alpha_{0}-\alpha(tz)}z\Big{(}-\alpha^{\prime}(tz)\ln(tz)+\frac{\alpha_{0}-\alpha(tz)}{tz}\Big{)}\Big{\|}$
		$\displaystyle\leq Qz\big{(}\|\ln(tz)\|+1\big{)},$
	$\displaystyle\Big{\|}\partial_{t}^{2}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle=\Big{\|}\big{[}\partial_{t}(tz)^{\alpha_{0}-\alpha(tz)}\big{]}z\Big{(}-\alpha^{\prime}(tz)\ln(tz)+\frac{\alpha_{0}-\alpha(tz)}{tz}\Big{)}$
		$\displaystyle\quad+(tz)^{\alpha_{0}-\alpha(tz)}z^{2}\Big{(}-\alpha^{\prime\prime}(tz)\ln(tz)-2\frac{\alpha^{\prime}(tz)}{tz}-\frac{\alpha_{0}-\alpha(tz)}{(tz)^{2}}\Big{)}\Big{\|}$
		$\displaystyle\leq Qz^{2}\big{(}\|\ln(tz)\|+1\big{)}^{2}+z^{2}(\|\ln(tz)\|+\frac{1}{tz})\leq Q\frac{z^{2}}{tz}=Q\frac{z}{t},$
	$\displaystyle\Big{\|}\partial_{t}^{3}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle\leq\frac{Q}{t^{2}}~{}(\text{We omit the calculations here}).$

We apply them to bound $g^{\prime}(t)$ , $g^{\prime\prime}(t)$ and $g^{\prime\prime\prime}(t)$ as

$\displaystyle\|g^{\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}$
	$\displaystyle\leq Q\int_{0}^{1}z\big{(}\|\ln(tz)\|+1\big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz$
	$\displaystyle\leq Q\big{(}\|\ln t\|+1\big{)}\int_{0}^{1}z\frac{\|\ln t\|+\|\ln z\|+1}{\|\ln t\|+1}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\leq Q\big{(}\|\ln t\|+1\big{)},$	(6)
$\displaystyle\|g^{\prime\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}^{2}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}\leq\frac{Q}{t},$	(7)
$\displaystyle\|g^{\prime\prime\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}^{3}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}\leq\frac{Q}{t^{2}}.$	(8)

3 Convolution method

We develop the convolution method to analyze the fractional initial value problems of variable exponent, the main idea of which is to calculate the convolution of the original model and a suitable kernel to get a more feasible formulation. We illustrate this idea by the following subdiffusion model with variable exponent, which is a typical fractional parabolic equation

\begin{array}[]{c}{}^{c}\partial_{t}^{\alpha(t)}u(\bm{x},t)-\Delta u(\bm{x},t)=f(\bm{x},t),~{}~{}(\bm{x},t)\in\Omega\times(0,T],\end{array}

(9)

equipped with initial and boundary conditions

u(\bm{x},0)=u_{0}(\bm{x}),~{}\bm{x}\in\Omega;\quad u(\bm{x},t)=0,~{}(\bm{x},t)\in\partial\Omega\times[0,T].

(10)

Here $\Omega\subset\mathbb{R}^{d}$ is a simply-connected bounded domain with the piecewise smooth boundary $\partial\Omega$ with convex corners, $\bm{x}:=(x_{1},\cdots,x_{d})$ with $1\leq d\leq 3$ denotes the spatial variables, $f$ and $u_{0}$ refer to the source term and the initial value, respectively, and the fractional derivative of order $0<\alpha(t)<1$ is defined via the variable-exponent Abel kernel $k$ [36]

{}^{c}\partial_{t}^{\alpha(t)}u:=k*\partial_{t}u.

It is worth mentioning that although we focus the attention on the fractional parabolic equation (i.e. $0<\alpha(t)<1$ ), the proposed method also works for the fractional hyperbolic equation (i.e. $1<\alpha(t)<2$ ) based on resolvent estimates proposed in, e.g. [57]. The latter is also known as the fractional diffusion-wave equation, for which the $\partial_{t}^{\alpha(t)}u$ is defined as

{}^{c}\partial_{t}^{\alpha(t)}u:=\tilde{k}*\partial_{t}^{2}u,~{}~{}\tilde{k}(t):=\frac{t^{1-\alpha(t)}}{\Gamma(2-\alpha(t))}.

3.1 A transformed model

To demonstrate the idea of the convolution method, we calculate the convolution of (9) and $\beta_{\alpha_{0}}$ as

\beta_{\alpha_{0}}*[(k*\partial_{t}u)-\Delta u-f]=0.

We invoke (4) to obtain

\displaystyle g*\partial_{t}u-\beta_{\alpha_{0}}*\Delta u-\beta_{\alpha_{0}}*f=0.

(11)

We finally use (5) to formally differentiate it to get the transformed model

\partial_{t}u+g^{\prime}*\partial_{t}u-\partial_{t}^{1-\alpha_{0}}\Delta u=\partial_{t}^{1-\alpha_{0}}f,

(12)

equipped with the initial and boundary conditions (10).

We then take the Laplace transform of (12) to obtain

z\mathcal{L}u-u_{0}-z^{1-\alpha_{0}}\Delta\mathcal{L}u=\mathcal{L}p_{u},~{}~{}p_{u}(t):=\partial_{t}^{1-\alpha_{0}}f-g^{\prime}*\partial_{t}u,

that is, $\mathcal{L}u=z^{\alpha_{0}-1}(z^{\alpha_{0}}-\Delta)^{-1}(u_{0}+\mathcal{L}p_{u}).$ Take the inverse Laplace transform to get

\displaystyle u=F(t)u_{0}+\int_{0}^{t}F(t-s)p_{u}(s)ds

(13)

where the operator $F(\cdot):L^{2}(\Omega)\rightarrow L^{2}(\Omega)$ is defined as

F(t)q:=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta}}e^{tz}z^{\alpha_{0}-1}(z^{\alpha_{0}}-\Delta)^{-1}qdz,~{}~{}\forall q\in L^{2}(\Omega),

with the following properties [22]

\displaystyle\|F(t)q\|_{\check{H}^{\mu}}\leq Qt^{\frac{\gamma-\mu}{2}\alpha_{0}}\|q\|_{\check{H}^{\gamma}}\text{ for }\mu,\gamma\in\mathbb{R}\text{ and }\gamma\leq\mu\leq\gamma+2.

(14)

3.2 Well-posedness of transformed model

We show the well-posedness of model (12) with the initial and boundary conditions (10) in the following theorem.

Theorem 1.

Suppose $f\in W^{1,1}(L^{2})$ and $u_{0}\in\check{H}^{2}$ , then model (12)–(10) admits a unique solution in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ for $1<p<\frac{1}{1-\alpha_{0}}$ and

\displaystyle\|u\|_{W^{1,p}(L^{2})}+\|u\|_{L^{p}(\check{H}^{2})}\leq Q\big{(}\|f\|_{W^{1,1}(L^{2})}+\|u_{0}\|_{\check{H}^{2}}\big{)}.

Proof.

By $C([0,T];L^{2})\subset W^{1,1}(L^{2})$ [1], we have the following relations for $0<\varepsilon\ll\frac{1}{p}-(1-\alpha_{0})$

\displaystyle I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f=I_{t}^{\alpha_{0}-\varepsilon}f,~{}~{}\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f=\beta_{\alpha_{0}-\varepsilon}f(0)+\beta_{\alpha_{0}-\varepsilon}*\partial_{t}f,

(15)

which means that

\displaystyle(I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f)|_{t=0}=0,~{}~{}\|\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f\|_{L^{p}(L^{2})}\leq Q\|f\|_{W^{1,1}(L^{2})}.

(16)

Thus we take $0<\varepsilon\ll\frac{1}{p}-(1-\alpha_{0})$ throughout this proof.

We first consider the case of zero initial condition, i.e. $u_{0}\equiv 0$ , and define the space $\tilde{W}^{1,p}(L^{2}):=\{q\in W^{1,p}(L^{2}):q(0)=0\}$ equipped with the norm $\|q\|_{\tilde{W}^{1,p}(L^{2})}:=\|e^{-\sigma t}\partial_{t}q\|_{L^{p}(L^{2})}$ for some $\sigma\geq 1$ , which is equivalent to the standard norm $\|q\|_{W^{1,p}(L^{2})}$ for $q\in\tilde{W}^{1,p}(L^{2})$ . Define a mapping $\mathcal{M}:\tilde{W}^{1,p}(L^{2})\rightarrow\tilde{W}^{1,p}(L^{2})$ by $w=\mathcal{M}v$ where $w$ satisfies

\partial_{t}w-\partial_{t}^{1-\alpha_{0}}\Delta w=p_{v},~{}~{}(\bm{x},t)\in\Omega\times(0,T],

(17)

equipped with zero initial and boundary conditions. By (13), $w$ could be expressed as

w=\int_{0}^{t}F(t-s)p_{v}(s)ds.

(18)

To show the well-posedness of $\mathcal{M}$ , we differentiate (18) to obtain

\partial_{t}w=p_{v}(t)+\int_{0}^{t}F^{\prime}(t-s)p_{v}(s)ds.

(19)

We use the Laplace transform to evaluate the second right-hand side term to get

\displaystyle\mathcal{L}\bigg{[}\int_{0}^{t}F^{\prime}(t-s)p_{v}(s)ds\bigg{]}=z^{\alpha_{0}}(z^{\alpha_{0}}-\Delta)^{-1}\mathcal{L}p_{v}=\big{(}z^{\alpha_{0}-\varepsilon}(z^{\alpha_{0}}-\Delta)^{-1}\big{)}\big{(}z^{\varepsilon}\mathcal{L}p_{v}\big{)}.

(20)

We apply $(I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f)(0)=0$ to take the inverse Laplace transform of (20) to get

\displaystyle\int_{0}^{t}F^{\prime}(t-s)p_{v}(s)ds=\int_{0}^{t}\mathcal{R}(t-s)\partial_{s}^{\varepsilon}p_{v}(s)ds,

(21)

where $\mathcal{R}(t):=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta}}z^{\alpha_{0}-\varepsilon}(z^{\alpha_{0}}-\Delta)^{-1}e^{zt}\mathrm{d}z.$ We use (3) to bound $\mathcal{R}$ by

	$\displaystyle\\|\mathcal{R}(t-s)\\|$	$\displaystyle\leq Q\int_{\Gamma_{\theta}}\|z\|^{\alpha_{0}-\varepsilon}\\|(z^{\alpha_{0}}-\Delta)^{-1}\\|\|e^{z(t-s)}\|\|dz\|$
		$\displaystyle\leq Q\int_{\Gamma_{\theta}}\|z\|^{\alpha_{0}-\varepsilon}\|z\|^{-\alpha_{0}}\|e^{z(t-s)}\|\|dz\|\leq\frac{Q}{(t-s)^{1-\varepsilon}}.$		(22)

To estimate $\partial_{t}^{\varepsilon}p_{v}$ , recall that $p_{v}(t)=\partial_{t}^{1-\alpha_{0}}f-g^{\prime}*\partial_{t}v$ , which implies

\partial_{t}^{\varepsilon}p_{v}(t)=\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f-\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v).

(23)

We reformulate $\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v)$ as

\displaystyle\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v)=\partial_{t}\big{(}\beta_{1-\varepsilon}*(g^{\prime}*\partial_{t}v)\big{)}=\partial_{t}\big{(}(\beta_{1-\varepsilon}*g^{\prime})*\partial_{t}v\big{)},

(24)

where

\displaystyle\beta_{1-\varepsilon}*g^{\prime}=\int_{0}^{t}\frac{(t-s)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime}(s)ds=t^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime}(tz)dz.

(25)

By (6), we have

	$\displaystyle\|\beta_{1-\varepsilon}*g^{\prime}\|$	$\displaystyle\leq Qt^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}(1+\|\ln(tz)\|)dz$
		$\displaystyle\leq Qt^{1-\varepsilon}\int_{0}^{1}(1-z)^{-\varepsilon}\frac{(tz)^{\varepsilon}(1+\|\ln(tz)\|)}{(tz)^{\varepsilon}}dz\leq Qt^{1-2\varepsilon},$		(26)

which means that $(\beta_{1-\varepsilon}*g^{\prime})(0)=0$ . We apply this to further rewrite (24) as

\displaystyle\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v)=\big{(}\partial_{t}(\beta_{1-\varepsilon}*g^{\prime})\big{)}*\partial_{t}v.

(27)

Based on (25) we apply (7) and a similar estimate as (26) to obtain

	$\displaystyle\|\partial_{t}(\beta_{1-\varepsilon}*g^{\prime})\|$	$\displaystyle=\Big{\|}(1-\varepsilon)t^{-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime}(tz)dz$
		$\displaystyle\qquad+t^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime\prime}(tz)zdz\Big{\|}\leq Qt^{-2\varepsilon}.$		(28)

Thus, we finally bound $\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v)$ as

\displaystyle|\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}v)|\leq Qt^{-2\varepsilon}*|\partial_{t}v|.

(29)

We invoke (16) and (29) to conclude that

$\displaystyle\\|e^{-\sigma t}\partial_{t}^{\varepsilon}p_{v}(t)\\|_{L^{p}(L^{2})}$	$\displaystyle\leq\\|\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}+Q\\|e^{-\sigma t}(t^{-2\varepsilon}*\|\partial_{t}v\|)\\|_{L^{p}(L^{2})}$
	$\displaystyle\leq\\|f\\|_{W^{1,1}(L^{2})}+Q\\|(e^{-\sigma t}t^{-2\varepsilon})*(e^{-\sigma t}\\|\partial_{t}v\\|)\\|_{L^{p}(0,T)}$
	$\displaystyle\leq\\|f\\|_{W^{1,1}(L^{2})}+Q\\|e^{-\sigma t}t^{-2\varepsilon}\\|_{L^{1}(0,T)}\\|e^{-\sigma t}\\|\partial_{t}v\\|\\|_{L^{p}(0,T)}$
	$\displaystyle\leq\\|f\\|_{W^{1,1}(L^{2})}+Q\sigma^{2\varepsilon-1}\\|v\\|_{\tilde{W}^{1,p}(0,T;L^{2})},$	(30)

where we used the fact that

\displaystyle\|e^{-\sigma t}t^{-2\varepsilon}\|_{L^{1}(0,T)}=\int_{0}^{T}e^{-\sigma t}t^{-2\varepsilon}dt\leq\sigma^{2\varepsilon-1}\int_{0}^{\infty}e^{-t}t^{-2\varepsilon}dt\leq Q\sigma^{2\varepsilon-1}.

(31)

Consequently, we apply (22), (30) and the Young’s convolution inequality in (21) to bound the second right-hand side term of (19)

	$\displaystyle\Big{\\|}e^{-\sigma t}\int_{0}^{t}F^{\prime}(t-s)p_{v}(s)ds\Big{\\|}_{L^{p}(L^{2})}\leq Q\\|t^{\varepsilon-1}*\\|e^{-\sigma t}\partial_{t}^{\varepsilon}p_{v}\\|\\|_{L^{p}(0,T)}$
	$\displaystyle~{}~{}~{}~{}\leq Q\\|e^{-\sigma t}\partial_{t}^{\varepsilon}p_{v}(t)\\|_{L^{p}(L^{2})}\leq Q\\|f\\|_{W^{1,1}(L^{2})}+Q\sigma^{2\varepsilon-1}\\|v\\|_{\tilde{W}^{1,p}(L^{2})}.$

The first right-hand side term of (19) could be bounded by similar and much simper estimates as above

	$\displaystyle\\|e^{-\sigma t}p_{v}\\|_{L^{p}(L^{2})}$	$\displaystyle\leq\\|\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}+\\|(e^{-\sigma t}g^{\prime})*(e^{-\sigma t}\partial_{t}v)\\|_{L^{p}(L^{2})}$
		$\displaystyle\leq\\|\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}+Q\sigma^{\varepsilon-1}\\|v\\|_{\tilde{W}^{1,p}(L^{2})}.$

In particular, we could apply $(I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f)(0)=0$ and the Young’s convolution inequality to further bound $\partial_{t}^{1-\alpha_{0}}f$ as

	$\displaystyle\\|\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}$	$\displaystyle=\\|\partial_{t}I_{t}^{\varepsilon}I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}=\\|I_{t}^{\varepsilon}\partial_{t}I_{t}^{1-\varepsilon}\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}$
		$\displaystyle\leq Q\\|I_{t}^{\varepsilon}\\|\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f\\|\\|_{L^{p}(0,T)}\leq Q\\|\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}f\\|_{L^{p}(L^{2})}\leq Q\\|f\\|_{W^{1,1}(L^{2})}.$		(32)

We summarize the above two estimates to conclude that

\|w\|_{\tilde{W}^{1,p}(L^{2})}\leq Q\big{(}\|f\|_{W^{1,1}(L^{2})}+\sigma^{2\varepsilon-1}\|v\|_{\tilde{W}^{1,p}(L^{2})}\big{)},

(33)

which implies that $w\in\tilde{W}^{1,p}(L^{2})$ such that $\mathcal{M}$ is well-posed.

To show the contractivity of $\mathcal{M}$ , let $w_{1}=\mathcal{M}v_{1}$ and $w_{2}=\mathcal{M}v_{2}$ such that $w_{1}-w_{2}$ satisfies (17) with $v=v_{1}-v_{2}$ and $f\equiv 0$ . Thus (33) implies $\|w_{1}-w_{2}\|_{\tilde{W}^{1,p}(L^{2})}\leq Q\sigma^{2\varepsilon-1}\|v_{1}-v_{2}\|_{\tilde{W}^{1,p}(L^{2})}$ . Choose $\sigma$ large enough such that $Q\sigma^{2\varepsilon-1}<1$ , that is, $\mathcal{M}$ is a contraction mapping such that there exists a unique solution $u\in\tilde{W}^{1,p}(L^{2})$ for model (12) with zero initial and boundary conditions, and the stability estimate could be derived directly from (33) with $v=w=u$ and large $\sigma$ and the equivalence between two norms $\|\cdot\|_{\tilde{W}^{1,p}(L^{2})}$ and $\|\cdot\|_{W^{1,p}(L^{2})}$ for $u\in\tilde{W}^{1,p}(L^{2})$

\|u\|_{W^{1,p}(L^{2})}\leq Q\|f\|_{W^{1,1}(L^{2})}.

(34)

For the case of non-zero initial condition, a variable substitution $v=u-u_{0}$ could be used to reach the equation (12) with $u$ and $f$ replaced by $v$ and $f+\Delta u_{0}$ , respectively, equipped with zero initial and boundary conditions. As $u_{0}\in H^{2}$ , we apply the well-posedness of (12) with zero initial and boundary conditions to find that there exists a unique solution $v\in\tilde{W}^{1,p}(L^{2})$ with the stability estimate $\|v\|_{W^{1,p}(L^{2})}\leq Q\|f+\Delta u_{0}\|_{W^{1,1}(L^{2})}$ derived from (34). By $v=u-u_{0}$ , we finally conclude that $u=v+u_{0}$ is a solution to (12)–(10) in $W^{1,p}(L^{2})$ with the estimate

\|u\|_{W^{1,p}(L^{2})}\leq Q\|f\|_{W^{1,1}(L^{2})}+Q\|u_{0}\|_{H^{2}}.

(35)

The uniqueness of the solutions to (12)–(10) follows from that to this model with $u_{0}\equiv 0$ . To estimate the $L^{p}(H^{2})$ norm of $u$ , we apply $\Delta$ on both sides of (13) and employ (14) to obtain

	$\displaystyle\\|\Delta u\\|$	$\displaystyle\leq\\|\Delta F(t)u_{0}\\|+\\|\int_{0}^{t}\Delta F(t-s)p_{u}(s)ds\\|$
		$\displaystyle\leq Q\\|F(t)u_{0}\\|_{\check{H}^{2}}+Qt^{-\alpha_{0}}\\|p_{u}\\|\leq Q\\|u_{0}\\|_{\check{H}^{2}}+Qt^{-\alpha_{0}}\\|p_{u}\\|.$		(36)

We combine this with the Young’s convolution inequality, (32), (35) and the estimate of $p_{u}$

	$\displaystyle\\|p_{u}\\|_{L^{p}(L^{2})}$	$\displaystyle=\\|\partial_{t}^{1-\alpha_{0}}f-g^{\prime}*\partial_{t}u\\|_{L^{p}(L^{2})}$		(37)
		$\displaystyle\leq Q\\|f\\|_{W^{1,1}(L^{2})}+Q\\|g^{\prime}\\|_{L^{1}(0,T)}\\|\partial_{t}u\\|_{L^{p}(L^{2})}\leq Q\\|u_{0}\\|_{\check{H}^{2}}+Q\\|f\\|_{W^{1,1}(L^{2})}$

to get

	$\displaystyle\\|\Delta u\\|_{L^{p}(L^{2})}$	$\displaystyle\leq Q\\|u_{0}\\|_{\check{H}^{2}}+Q\\|t^{-\alpha_{0}}*\\|p_{u}\\|\\|_{L^{p}(0,T)}$
		$\displaystyle\leq Q\\|u_{0}\\|_{\check{H}^{2}}+Q\\|p_{u}\\|_{L^{p}(L^{2})}\leq Q\\|u_{0}\\|_{\check{H}^{2}}+Q\\|f\\|_{W^{1,1}(L^{2})},$

which completes the proof. ∎

3.3 Well-posedness of original model

The well-posedness of the original model (9)–(10) is proved in the following theorem.

Theorem 2.

Suppose $f\in W^{1,1}(L^{2})$ and $u_{0}\in\check{H}^{2}$ , then model (9)–(10) admits a unique solution in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ for $1<p<\frac{1}{1-\alpha_{0}}$ and

\displaystyle\|u\|_{W^{1,p}(L^{2})}+\|u\|_{L^{p}(\check{H}^{2})}\leq Q\big{(}\|f\|_{W^{1,1}(L^{2})}+\|u_{0}\|_{\check{H}^{2}}\big{)}.

Proof.

We first show that a solution to (12)–(10), which uniquely exists in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ by Theorem 1, is also a solution to (9)–(10). If $u\in W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ for $1<p<\frac{1}{1-\alpha_{0}}$ solves (12)–(10), then (12) could be rewritten as

\partial_{t}(\beta_{\alpha_{0}}*k*\partial_{t}u-\beta_{\alpha_{0}}*\Delta u-\beta_{\alpha_{0}}*f)=0,

which means that

\displaystyle g*\partial_{t}u-\beta_{\alpha_{0}}*\Delta u-\beta_{\alpha_{0}}*f=c_{0}

(38)

for some constant $c_{0}$ . We apply the $\|\cdot\|_{L^{\infty}(0,t;L^{2})}$ on both sides and use the boundedness of $g$ to obtain

$\displaystyle\|c_{0}\|\|\Omega\|^{1/2}$	$\displaystyle\leq Q\\|\|g\|\\|\partial_{t}u\\|\\|_{L^{\infty}(0,t)}+\\|\beta_{\alpha_{0}}\Delta u\\|_{L^{\infty}(0,t;L^{2})}+Q\\|\beta_{\alpha_{0}}*\\|f\\|\\|_{L^{\infty}(0,t)}$
	$\displaystyle\leq Q\\|g\\|_{L^{\gamma}(0,t)}\\|\partial_{t}u\\|_{L^{p}(L^{2})}+\\|\beta_{\alpha_{0}}*\Delta u\\|_{L^{\infty}(0,t;L^{2})}+Q\\|\beta_{\alpha_{0}}\\|_{L^{1}(0,t)}\\|f\\|_{L^{\infty}(L^{2})}$
	$\displaystyle\leq Qt^{\frac{1}{\gamma}}+Qt^{\alpha_{0}}+Q\\|\beta_{\alpha_{0}}*\\|\Delta u\\|\\|_{L^{\infty}(0,t)}$	(39)

for some $\gamma<\infty$ satisfying $\frac{1}{\gamma}+\frac{1}{p}=1$ . To estimate $\|\beta_{\alpha_{0}}*\|\Delta u\|\|_{L^{\infty}(0,t)}$ , we employ (36) to obtain

\displaystyle\beta_{\alpha_{0}}*\|\Delta u\|

\displaystyle\leq Q\beta_{\alpha_{0}}*\|u_{0}\|_{\check{H}^{2}}+Q\beta_{\alpha_{0}}*t^{-\alpha_{0}}*\|p_{u}\|\leq Qt^{\alpha_{0}}\|u_{0}\|_{\check{H}^{2}}+Q(1*\|p_{u}\|).

We then take the $\|\cdot\|_{L^{\infty}(0,t)}$ on both sides and apply (37) to find

	$\displaystyle\\|\beta_{\alpha_{0}}*\\|\Delta u\\|\\|_{L^{\infty}(0,t)}$	$\displaystyle\leq Qt^{\alpha_{0}}\\|u_{0}\\|_{\check{H}^{2}}+Q\\|1*\\|p_{u}\\|\\|_{L^{\infty}(0,t)}$
		$\displaystyle\leq Qt^{\alpha_{0}}\\|u_{0}\\|_{\check{H}^{2}}+Qt^{\frac{1}{\gamma}}\\|p_{u}\\|_{L^{p}(L^{2})}\leq Qt^{\alpha_{0}}\\|u_{0}\\|_{\check{H}^{2}}+Qt^{\frac{1}{\gamma}}(\\|u_{0}\\|_{\check{H}^{2}}+Q\\|f\\|_{W^{1,1}(L^{2})})$

for some $\gamma<\infty$ satisfying $\frac{1}{\gamma}+\frac{1}{p}=1$ . We invoke this in (39) to finally obtain $|c_{0}||\Omega|^{1/2}\leq Qt^{\frac{1}{\gamma}}+Qt^{\alpha_{0}}.$ Passing $t\rightarrow 0+$ implies $c_{0}=0$ , which, together with (38), gives $g*\partial_{t}u-\beta_{\alpha_{0}}*\Delta u-\beta_{\alpha_{0}}*f=0.$ We then calculate its convolution with $\beta_{1-\alpha_{0}}$ and apply $\beta_{1-\alpha_{0}}*g=\beta_{1-\alpha_{0}}*\beta_{\alpha_{0}}*k=1*k$ to obtain $1*k*\partial_{t}u-1*\Delta u-1*f=0.$ Differentiating this equation leads to (9), which implies $u$ solves (9)–(10).

To prove the uniqueness of the solutions to (9)–(10) in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ , suppose (9)–(10) with $f\equiv 0$ and $u_{0}\equiv 0$ has a solution $u\in W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ . Then $u$ satisfies (11) with $f\equiv 0$ . As $g*\partial_{t}u\in W^{1,p}(L^{2})$ , so does $\beta_{\alpha_{0}}*\Delta u$ such that we differentiate (11) to get (12) with $f\equiv 0$ . Then we apply Theorem 1 to get $u\equiv 0$ , which completes the proof. ∎

3.4 Solution regularity

We give pointwise-in-time estimates of the temporal derivatives of the solutions to model (9)–(10), which are feasible for numerical analysis.

Theorem 3.

Suppose $u_{0}\in\check{H}^{2(m+1)}$ and $f\in W^{1,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2m})$ for $0<\sigma\ll\alpha_{0}$ for $m=0,1$ . Then

\displaystyle\|\partial_{t}u\|_{\check{H}^{2m}}

\displaystyle\leq Qt^{\alpha_{0}-1}(\|u_{0}\|_{\check{H}^{2(m+1)}}+\|f\|_{W^{1,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2m})}),~{}~{}a.e.~{}t\in(0,T].

Remark 1.

For $\alpha(t)\equiv\alpha$ for some $0<\alpha<1$ , this theorem implies $\partial_{t}u\sim t^{\alpha-1}$ , which is consistent with the classical results shown in, e.g. [38, 43, 45], and indicates that the singularity of the solutions to variable-exponent subdiffusion could be essentially characterized by the initial behavior of the variable exponent.

Proof.

We mainly prove the case $m=1$ since the case $m=0$ could be proved by the same procedure. As shown in the proof of Theorem 2, the unique solution to (12)–(10) in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ is also the unique solution to (9)–(10). Thus we could perform analysis based on (13). We differentiate both sides of (13) with respect to $t$ and apply $\frac{d}{dt}F(t)=\Delta E(t)$ [22, Lemma 6.2] with $E(t):=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta}}e^{tz}(z^{\alpha_{0}}-\Delta)^{-1}dz$ to obtain $\partial_{t}u=\Delta E(t)u_{0}+p_{u}+\int_{0}^{t}F^{\prime}(t-s)p_{u}(s)ds.$ Then we further apply $\Delta$ on both sides of this equation to obtain

\displaystyle\partial_{t}\Delta u=E(t)\Delta^{2}u_{0}+\tilde{p}_{u}+\int_{0}^{t}F^{\prime}(t-s)\tilde{p}_{u}(s)ds,

(40)

where $\tilde{p}_{u}:=\partial_{t}^{1-\alpha_{0}}\Delta f-g^{\prime}*\partial_{t}\Delta u$ . We apply $\|\cdot\|$ on both sides and invoke $\|E(t)\|\leq Qt^{\alpha_{0}-1}$ [22, Theorem 6.4] to get

\displaystyle\|\partial_{t}\Delta u\|\leq Qt^{\alpha_{0}-1}\|u_{0}\|_{\check{H}^{4}}+\|\tilde{p}_{u}\|+\Big{\|}\int_{0}^{t}F^{\prime}(t-s)\tilde{p}_{u}(s)ds\Big{\|}.

(41)

By (6) and

\displaystyle\partial_{t}^{1-\alpha_{0}}\Delta f=\beta_{\alpha_{0}}\Delta f(0)+\beta_{\alpha_{0}}*\partial_{t}\Delta f,

(42)

we have

	$\displaystyle\\|\tilde{p}_{u}\\|$	$\displaystyle\leq\beta_{\alpha_{0}}\\|\Delta f(0)\\|+Q\beta_{\alpha_{0}}\\|\partial_{t}\Delta f\\|+Qt^{-\varepsilon}\\|\partial_{t}\Delta u\\|$
		$\displaystyle\leq\beta_{\alpha_{0}}\\|\Delta f(0)\\|+Qt^{\alpha_{0}-1}\\|\Delta f\\|_{W^{1,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}+Qt^{-\varepsilon}*\\|\partial_{t}\Delta u\\|$		(43)

for a.e. $t\in(0,T]$ where we applied the Young’s convolution inequality with $\frac{1}{\gamma}+\frac{1}{\frac{1}{\alpha_{0}-\sigma}}=1$ for some $0<\sigma\ll\alpha_{0}$ (such that $\gamma<\frac{1}{1-\alpha_{0}}$ ) to get

	$\displaystyle\\|\beta_{\alpha_{0}}*\\|\partial_{t}\Delta f\\|\\|_{L^{\infty}(0,t)}$	$\displaystyle\leq\\|\beta_{\alpha_{0}}\\|_{L^{\gamma}(0,t)}\\|\\|\partial_{t}\Delta f\\|\\|_{L^{\frac{1}{\alpha_{0}-\sigma}}(0,t)}$
		$\displaystyle\leq Qt^{\alpha_{0}-1+\frac{1}{\gamma}}\\|\Delta f\\|_{W^{1,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}\leq Q\\|\Delta f\\|_{W^{1,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}.$		(44)

We invoke (43) in (41) and apply the same treatment as (20)–(22) to bound the last right-hand side term of (41) to obtain for $0<\varepsilon\ll\alpha_{0}$

\displaystyle\|\partial_{t}\Delta u\|

\displaystyle\leq QMt^{\alpha_{0}-1}+Qt^{-\varepsilon}*\|\partial_{t}\Delta u\|+Qt^{\varepsilon-1}*\|\partial_{t}^{\varepsilon}\tilde{p}_{u}\|.

(45)

where $M:=\|u_{0}\|_{\check{H}^{4}}+\|\Delta f\|_{W^{1,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}$ . According to (15), we have $\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}\Delta f=\beta_{\alpha_{0}-\varepsilon}\Delta f(0)+\beta_{\alpha_{0}-\varepsilon}*\partial_{t}\Delta f,$ while by the same treatment as (24)–(29), we have $|\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}\Delta u)|\leq Qt^{-2\varepsilon}*|\partial_{t}\Delta u|.$ We invoke these two equations in (45) to obtain

	$\displaystyle\\|\partial_{t}\Delta u\\|$	$\displaystyle\leq QMt^{\alpha_{0}-1}+Qt^{-\varepsilon}*\\|\partial_{t}\Delta u\\|$
		$\displaystyle\qquad+Q\beta_{\varepsilon}[\beta_{\alpha_{0}-\varepsilon}\\|\Delta f(0)\\|+\beta_{\alpha_{0}-\varepsilon}\\|\partial_{t}\Delta f\\|+\beta_{1-2\epsilon}*\\|\partial_{t}\Delta u\\|]$
		$\displaystyle\leq QMt^{\alpha_{0}-1}+Q[\beta_{\alpha_{0}}\\|\Delta f(0)\\|+\beta_{\alpha_{0}}\\|\partial_{t}\Delta f\\|+\beta_{1-\varepsilon}\\|\partial_{t}\Delta u\\|],$

which, together with (44), yields

\displaystyle\|\partial_{t}\Delta u\|

\displaystyle\leq QMt^{\alpha_{0}-1}+Q\beta_{1-\varepsilon}*\|\partial_{t}\Delta u\|

(46)

for a.e. $t\in(0,T]$ , that is,

\displaystyle\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|

\displaystyle\leq QM+Q\int_{0}^{t}e^{-\theta(t-s)}\frac{t^{1-\alpha_{0}}}{s^{1-\alpha_{0}}}\frac{\|e^{-\theta s}s^{1-\alpha_{0}}\partial_{s}\Delta u\|}{(t-s)^{\varepsilon}}ds

for $a.e.~{}t\in(0,T]$ and $\theta>0$ . For a fixed $\bar{t}\in(0,T]$ , we have for a.e. $t\in(0,\bar{t}]$

\displaystyle\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|

\displaystyle\leq QM+Q\int_{0}^{t}\frac{t^{1-\alpha_{0}}}{s^{1-\alpha_{0}}}\frac{e^{-\theta(t-s)}}{(t-s)^{\varepsilon}}ds\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|_{L^{\infty}(0,\bar{t};L^{2})}

Note that

	$\displaystyle\int_{0}^{t}\frac{t^{1-\alpha_{0}}}{s^{1-\alpha_{0}}}\frac{e^{-\theta(t-s)}}{(t-s)^{\varepsilon}}ds=t^{1-\varepsilon}\int_{0}^{1}e^{-\theta ty}(1-y)^{\alpha_{0}-1}y^{-\varepsilon}dy$
	$\displaystyle\qquad=\frac{t^{\frac{1-\varepsilon}{2}}}{\theta^{\frac{1-\varepsilon}{2}}}\int_{0}^{1}(t\theta y)^{\frac{1-\varepsilon}{2}}e^{-\theta ty}(1-y)^{\alpha_{0}-1}y^{-\varepsilon-\frac{1-\varepsilon}{2}}dy$
	$\displaystyle\qquad\leq\frac{t^{\frac{1-\varepsilon}{2}}}{\theta^{\frac{1-\varepsilon}{2}}}\int_{0}^{1}(1-y)^{\alpha_{0}-1}y^{-\frac{\alpha_{0}}{2}-\frac{1}{2}}dy\leq\frac{Q}{\theta^{\frac{1-\varepsilon}{2}}}.$

We combine the above two equations to get for a.e. $t\in(0,\bar{t}]$

\displaystyle\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|

\displaystyle\leq QM+\frac{Q}{\theta^{\frac{1-\varepsilon}{2}}}\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|_{L^{\infty}(0,\bar{t};L^{2})},

which implies

\displaystyle\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|_{L^{\infty}(0,\bar{t};L^{2})}

\displaystyle\leq QM+\frac{Q}{\theta^{\frac{1-\varepsilon}{2}}}\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|_{L^{\infty}(0,\bar{t};L^{2})}.

Selecting $\theta$ large enough we find $\|e^{-\theta t}t^{1-\alpha_{0}}\partial_{t}\Delta u\|_{L^{\infty}(0,\bar{t};L^{2})}\leq QM,$ which means

\displaystyle\|\partial_{t}\Delta u\|

\displaystyle\leq QMt^{\alpha_{0}-1},~{}~{}a.e.~{}t\in(0,\bar{t}].

(47)

We take $\bar{t}=T$ to complete the proof. ∎

Theorem 4.

Suppose $u_{0}\in\check{H}^{2(m+1)}$ and $f\in W^{2,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2m})$ for $0<\sigma\ll\alpha_{0}$ and $m=0,1$ . Then

\displaystyle\|\partial_{t}^{2}u\|_{\check{H}^{2m}}

\displaystyle\leq Qt^{\alpha_{0}-2}(\|u_{0}\|_{\check{H}^{2(m+1)}}+\|f\|_{W^{2,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2m})}),~{}~{}a.e.~{}t\in(0,T].

Proof.

We mainly prove the case $m=1$ since the case $m=0$ could be proved by the same procedure. We apply (21) to (40) and multiply the resulting equation by $t$ to obtain

\displaystyle t\partial_{t}\Delta u=tE(t)\Delta^{2}u_{0}+t\tilde{p}_{u}+\int_{0}^{t}(t-s)\mathcal{R}(t-s)\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)ds+\int_{0}^{t}\mathcal{R}(t-s)s\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)ds.

Differentiating this equation with respect to $t$ yields

	$\displaystyle t\partial^{2}_{t}\Delta u$
	$\displaystyle\quad=-\partial_{t}\Delta u+E(t)\Delta^{2}u_{0}+tE^{\prime}(t)\Delta^{2}u_{0}+\partial_{t}(t\tilde{p}_{u})+\lim_{s\rightarrow t^{-}}[(t-s)\mathcal{R}(t-s)\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)]$
	$\displaystyle\qquad+\int_{0}^{t}\mathcal{R}(t-s)\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)ds+\int_{0}^{t}(t-s)\mathcal{R}^{\prime}(t-s)\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)ds$
	$\displaystyle\qquad+\lim_{s\rightarrow t^{-}}\mathcal{R}(s)[\theta\partial_{\theta}^{\varepsilon}\tilde{p}_{u}]\|_{\theta=t-s}+\int_{0}^{t}\mathcal{R}(t-s)\partial_{s}(s\partial_{s}^{\varepsilon}\tilde{p}_{u}(s))ds=:\sum_{i=1}^{9}J_{i}.$		(48)

Then we bound the $\|\cdot\|$ norms of $J_{1}$ – $J_{9}$ . By Theorem 3, we have $\|J_{1}\|\leq QMt^{\alpha_{0}-1}$ for a.e. $t\in(0,T]$ . We then apply $\|E(t)\|+t\|E^{\prime}(t)\|\leq Qt^{\alpha_{0}-1}$ [22, Theorem 6.4] to bet $\|J_{2}+J_{3}\|\leq Qt^{\alpha_{0}-1}\|u_{0}\|_{H^{4}}.$ To bound $J_{4}$ , we apply (42) to obtain

\displaystyle t\tilde{p}_{u}=t\beta_{\alpha_{0}}\Delta f(0)+t(\beta_{\alpha_{0}}*\partial_{t}\Delta f)-(tg^{\prime})*\partial_{t}\Delta u-g^{\prime}*(t\partial_{t}\Delta u).

Differentiate this equation to get

	$\displaystyle\partial_{t}(t\tilde{p}_{u})$	$\displaystyle=\alpha_{0}\beta_{\alpha_{0}}\Delta f(0)+\beta_{\alpha_{0}}\partial_{t}\Delta f+t(\beta_{\alpha_{0}}\partial_{t}\Delta f(0)+\beta_{\alpha_{0}}\partial_{t}^{2}\Delta f)$
		$\displaystyle\qquad-(tg^{\prime})^{\prime}\partial_{t}\Delta u-g^{\prime}[\partial_{t}(t\partial_{t}\Delta u)].$

We apply Theorem 3, (6), (7) and a similar argument as (44) to obtain

	$\displaystyle\\|J_{4}\\|$	$\displaystyle\leq Qt^{\alpha_{0}-1}\\|\Delta f\\|_{W^{2,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}+QMt^{-\varepsilon}t^{\alpha_{0}-1}+Qt^{-\varepsilon}\\|t\partial_{t}^{2}\Delta u\\|$
		$\displaystyle\leq Q\tilde{M}t^{\alpha_{0}-1}+Qt^{-\varepsilon}*\\|t\partial_{t}^{2}\Delta u\\|,$

where $\tilde{M}:=\|u_{0}\|_{\check{H}^{4}}+\|\Delta f\|_{W^{2,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}$ .

To treat the other terms, we apply the same derivations as (23)–(29), (15) and Theorem 3 to obtain for $0<\varepsilon\ll\alpha_{0}$

$\displaystyle\\|\partial_{t}^{\varepsilon}\tilde{p}_{u}(t)\\|$	$\displaystyle=\\|\partial_{t}^{\varepsilon}\partial_{t}^{1-\alpha_{0}}\Delta f-\partial_{t}^{\varepsilon}(g^{\prime}*\partial_{t}\Delta u)\\|$
	$\displaystyle=\\|\beta_{\alpha_{0}-\varepsilon}\Delta f(0)+\beta_{\alpha_{0}-\varepsilon}\partial_{t}\Delta f-\partial_{t}^{\varepsilon}(g^{\prime}\partial_{t}\Delta u)\\|$
	$\displaystyle\leq\beta_{\alpha_{0}-\varepsilon}\\|\Delta f(0)\\|+Q\beta_{\alpha_{0}-\varepsilon}\\|\partial_{t}\Delta f\\|+Qt^{-2\varepsilon}\\|\partial_{t}\Delta u\\|$
	$\displaystyle\leq\beta_{\alpha_{0}-\varepsilon}\\|\Delta f(0)\\|+Q\beta_{\alpha_{0}-\varepsilon}*\\|\partial_{t}\Delta f\\|+QMt^{\alpha_{0}-2\varepsilon},$	(49)
$\displaystyle t\partial_{t}^{\varepsilon}\tilde{p}_{u}(t)$	$\displaystyle=t\beta_{\alpha_{0}-\varepsilon}\Delta f(0)+t(\beta_{\alpha_{0}-\varepsilon}*\partial_{t}\Delta f)$
	$\displaystyle\quad-\big{(}t\partial_{t}(\beta_{1-\varepsilon}g^{\prime})\big{)}\partial_{t}\Delta u-\big{(}\partial_{t}(\beta_{1-\varepsilon}g^{\prime})\big{)}(t\partial_{t}\Delta u).$	(50)

We then apply (22) and (49) to bound

\|J_{5}\|\leq\lim_{s\rightarrow t^{-}}(t-s)^{\varepsilon}\|\partial_{s}^{\varepsilon}\tilde{p}_{u}(s)\|=0

and

	$\displaystyle\\|J_{6}\\|$	$\displaystyle\leq Qt^{\varepsilon-1}\\|\partial_{t}^{\varepsilon}\tilde{p}_{u}(t)\\|\leq Q\big{[}\beta_{\alpha_{0}}\\|\Delta f(0)\\|+\beta_{\alpha_{0}}\\|\partial_{t}\Delta f\\|+Mt^{\alpha_{0}-\varepsilon}\big{]}$
		$\displaystyle\leq QM+Q\\|\Delta f\\|_{W^{2,1+\sigma}(L^{2})}.$

To bound $J_{7}$ , we follow the idea proposed in, e.g. [22, Page 190], to set $\delta=t^{-1}$ in $\Gamma_{\theta}$ and apply the variable substitution $z=s\cos\phi+\rm is\sin\phi$ to bound $\mathcal{R}^{\prime}(t)$ as

\displaystyle\|\mathcal{R}^{\prime}(t)\|=\Big{\|}\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta}}z^{1+\alpha_{0}-\varepsilon}(z^{\alpha_{0}}-\Delta)^{-1}e^{zt}\mathrm{d}z\Big{\|}\leq\int_{\Gamma_{\theta}}e^{\mathfrak{R}(z)t}|z|^{1-\varepsilon}|dz|\leq Qt^{\varepsilon-2}.

We apply this and a similar estimate as $J_{6}$ to bound $J_{7}$ as

\|J_{7}\|\leq Qt^{\varepsilon-1}*\|\partial_{t}^{\varepsilon}\tilde{p}_{u}(t)\|\leq QM+Q\|\Delta f\|_{W^{2,1+\sigma}(L^{2})}.

To bound $J_{8}$ , we apply (27) to bound (50) as

	$\displaystyle\\|t\partial_{t}^{\varepsilon}\tilde{p}_{u}(t)\\|$	$\displaystyle\leq t\beta_{\alpha_{0}-\varepsilon}\\|\Delta f(0)\\|+Qt(\beta_{\alpha_{0}-\varepsilon}*\\|\partial_{t}\Delta f\\|)$
		$\displaystyle\quad+Qt^{1-2\varepsilon}\\|\partial_{t}\Delta u\\|+Qt^{-2\varepsilon}\\|t\partial_{t}\Delta u\\|\leq Q(M+\\|\Delta f\\|_{W^{2,1+\sigma}(L^{2})})t^{\alpha_{0}-\varepsilon},$

which, together with (22), implies

\|J_{8}\|\leq\lim_{s\rightarrow t^{-}}Qs^{\varepsilon-1}(t-s)^{\alpha_{0}-\varepsilon}=0.

To bound $J_{9}$ , we differentiate (50) with respect to $t$ to obtain

	$\displaystyle\partial_{t}(t\partial_{t}^{\varepsilon}\tilde{p}_{u})$	$\displaystyle=\partial_{t}(t\beta_{\alpha_{0}-\varepsilon})\Delta f(0)+\beta_{\alpha_{0}-\varepsilon}\partial_{t}\Delta f+t\partial_{t}(\beta_{\alpha_{0}-\varepsilon}\partial_{t}\Delta f)$
		$\displaystyle\quad-\big{[}\partial_{t}\big{(}t\partial_{t}(\beta_{1-\varepsilon}g^{\prime})\big{)}\big{]}\partial_{t}\Delta u-\big{(}\partial_{t}(\beta_{1-\varepsilon}g^{\prime})\big{)}[\partial_{t}(t\partial_{t}\Delta u)].$		(51)

By (28), we have

\displaystyle t\partial_{t}(\beta_{1-\varepsilon}*g^{\prime})

\displaystyle=(1-\varepsilon)t^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime}(tz)dz+t^{2-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime\prime}(tz)zdz,

which, together with (7) and (8), implies

	$\displaystyle\|\partial_{t}(t\partial_{t}(\beta_{1-\varepsilon}*g^{\prime}))\|$
	$\displaystyle\quad=\Big{\|}(1-\varepsilon)^{2}t^{-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime}(tz)dz+(1-\varepsilon)t^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime\prime}(tz)zdz$
	$\displaystyle\qquad+(2-\varepsilon)t^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime\prime}(tz)zdz+t^{2-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}g^{\prime\prime\prime}(tz)z^{2}dz\Big{\|}\leq Qt^{-2\varepsilon}.$

Furthermore, $|t\partial_{t}(\beta_{\alpha_{0}-\varepsilon}*\partial_{t}\Delta f)|\leq Qt^{\alpha_{0}-\varepsilon}|(\partial_{t}\Delta f)(0)|+Qt(\beta_{\alpha_{0}-\varepsilon}*|\partial_{t}^{2}\Delta f|).$ We incorporate these estimates and (28) with (51) to obtain

	$\displaystyle\\|\partial_{t}(t\partial_{t}^{\varepsilon}\tilde{p}_{u})\\|$	$\displaystyle\leq Qt^{\alpha_{0}-\varepsilon-1}\\|\Delta f(0)\\|+Q\beta_{\alpha_{0}-\varepsilon}*\\|\partial_{t}\Delta f\\|$
		$\displaystyle+Qt^{\alpha_{0}-\varepsilon}\\|(\partial_{t}\Delta f)(0)\\|+Qt(\beta_{\alpha_{0}-\varepsilon}\\|\partial_{t}^{2}\Delta f\\|)+Qt^{-2\varepsilon}\\|\partial_{t}\Delta u\\|+Qt^{-2\varepsilon}*\\|t\partial_{t}^{2}\Delta u\\|$
		$\displaystyle\leq Q(1+t^{\alpha_{0}-\varepsilon-1})\\|\Delta f\\|_{W^{2,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}+QM+Qt^{-2\varepsilon}*\\|t\partial_{t}^{2}\Delta u\\|$

for a.e. $t\in(0,T]$ where we used the Young’s convolution inequality to bound $\beta_{\alpha_{0}-\varepsilon}*\|\partial_{t}^{2}\Delta f\|$ as (44). We invoke this and (22) to bound $J_{9}$ as

\displaystyle\|J_{9}\|

\displaystyle\leq Qt^{\alpha_{0}-1}\|\Delta f\|_{W^{2,\frac{1}{\alpha_{0}-\sigma}}(L^{2})}+QM+Qt^{-\varepsilon}*\|t\partial_{t}^{2}\Delta u\|.

We invoke the estimates of $J_{1}$ – $J_{9}$ in (48) to conclude that

\displaystyle\|t\partial^{2}_{t}\Delta u\|\leq Q\tilde{M}t^{\alpha_{0}-1}+Qt^{-\varepsilon}*\|t\partial_{t}^{2}\Delta u\|,~{}a.e.~{}t\in(0,T].

Then we follow exactly the same procedure as (46)–(47) to complete the proof of this theorem. ∎

3.5 An inverse problem

From previous results, we notice that the initial value $\alpha_{0}$ plays a critical role in determining the properties of the model. Thus, it is meaningful to determine $\alpha_{0}$ from observations of $u$ , which formulates an inverse problem. Here we follow the proof of [22, Theorem 6.31] to present a preliminary result for demonstrating the usage of equivalent formulations derived by the generalized identity function.

Theorem 5.

For (9)–(10) with $f\equiv 0$ , $u_{0}\in C^{\infty}_{0}$ and $\Delta u_{0}(x_{0})\neq 0$ for some $x_{0}\in\Omega$ , we have

\alpha_{0}=\lim_{t\rightarrow 0^{+}}\frac{t\partial_{t}u(x_{0},t)}{u(x_{0},t)-u_{0}(x_{0})}.

Proof.

By Theorem 2 the model (9)–(10) is well-posed and could be reformulated as (12). We then further calculate the convolution of (12) with $f\equiv 0$ and $\beta_{1-\alpha_{0}}$ to get

\beta_{1-\alpha_{0}}*(\partial_{t}u)+\beta_{1-\alpha_{0}}*(g^{\prime}*\partial_{t}u)-\Delta u=0,

(52)

the solution of which could be expressed as $u=F(t)u_{0}+\mathcal{H}$ where $\mathcal{H}$ could be expressed via the Mittag-Leffler function $E_{a,b}(\cdot)$ [20]

\displaystyle\mathcal{H}:=\sum_{j=1}^{\infty}\rho*(-\beta_{1-\alpha_{0}}*(g^{\prime}*\partial_{t}u),\phi_{j})\phi_{j},~{}~{}\rho:=t^{\alpha_{0}-1}E_{\alpha_{0},\alpha_{0}}(-\lambda_{j}t^{\alpha_{0}}).

Also, (52) implies $\Delta u|_{\partial\Omega}=0$ . Then one could follow the proof of Theorem 3 to further show that $\|\partial_{t}\Delta^{2}u\|\leq Qt^{\alpha_{0}-1}$ , which will be used later.

By the derivations of [22, Theorem 6.31] we find that if we can show

\lim_{t\rightarrow 0^{+}}t^{1-\alpha_{0}}\partial_{t}\mathcal{H}(x_{0},t)=0\text{ and }\lim_{t\rightarrow 0^{+}}t^{-\alpha_{0}}\mathcal{H}(x_{0},t)=0,

(53)

then the proof of [22, Theorem 6.31] is not affected at all by the term $\mathcal{H}$ such that we immediately reach the conclusion by [22, Theorem 6.31].

To show the first statement, we first apply integration by parts to obtain

\displaystyle\mathcal{H}=\sum_{j=1}^{\infty}\frac{1}{\lambda_{j}^{2}}\rho*(-\beta_{1-\alpha_{0}}*(g^{\prime}*\partial_{t}\Delta^{2}u),\phi_{j})\phi_{j},

and we follow similar derivations as (25)–(28) to obtain $|\partial_{t}(\beta_{1-\alpha_{0}}*g^{\prime})|\leq t^{-\alpha_{0}-\varepsilon}$ for $0<\epsilon\ll 1-\alpha_{0}$ . We invoke this and apply $\|\phi_{j}\|_{L^{\infty}}\leq Q\lambda_{j}^{\frac{\kappa}{2}}$ for $\kappa>\frac{d}{2}$ [22, Page 257] to bound $\partial_{t}\mathcal{H}$ as

	$\displaystyle\|\partial_{t}\mathcal{H}\|$	$\displaystyle\leq Q\sum_{j=1}^{\infty}\frac{1}{\lambda_{j}^{2-\frac{\kappa}{2}}}\rho\big{(}\|\partial_{t}(\beta_{1-\alpha_{0}}g^{\prime})\|*\\|\partial_{t}\Delta^{2}u\\|\big{)}$
		$\displaystyle\leq Q\sum_{j=1}^{\infty}\frac{1}{\lambda_{j}^{2-\frac{\kappa}{2}}}\rho\big{(}t^{-\alpha_{0}-\varepsilon}t^{\alpha_{0}-1}\big{)}\leq Q\sum_{j=1}^{\infty}\frac{1}{\lambda_{j}^{2-\frac{\kappa}{2}}}\rho*t^{-\varepsilon}.$

We combine this with the following estimates [20]

\rho*t^{-\varepsilon}=\Gamma(\alpha_{0})t^{\alpha_{0}-\varepsilon}E_{\alpha_{0},1+\alpha_{0}-\varepsilon}(-\lambda_{j}t^{\alpha_{0}})\leq Q\frac{t^{\alpha_{0}-\varepsilon}}{1+\lambda_{j}t^{\alpha_{0}}}=Q\frac{t^{-\varepsilon}}{\lambda_{j}}\frac{\lambda_{j}t^{\alpha_{0}}}{1+\lambda_{j}t^{\alpha_{0}}}\leq Q\frac{t^{-\varepsilon}}{\lambda_{j}}

to obtain

\displaystyle t^{1-\alpha_{0}}|\partial_{t}\mathcal{H}|

\displaystyle\leq Qt^{1-\alpha_{0}-\varepsilon}\sum_{j=1}^{\infty}\frac{1}{\lambda_{j}^{3-\frac{\kappa}{2}}}\leq Qt^{1-\alpha_{0}-\varepsilon}\sum_{j=1}^{\infty}\frac{1}{j^{\frac{2}{d}(3-\frac{\kappa}{2})}}

where we used the Weyl’s law $\lambda_{j}\sim j^{\frac{2}{d}}$ for $j\rightarrow\infty$ . We set $\kappa=\frac{d}{2}+1$ to obtain $\frac{2}{d}(3-\frac{\kappa}{2})=\frac{5}{d}-\frac{1}{2}>1$ for $1\leq d\leq 3$ . Thus we have $t^{1-\alpha_{0}}|\partial_{t}\mathcal{H}|\leq Qt^{1-\alpha_{0}-\varepsilon}$ , which implies the first statement in (53). The second statement could be proved similarly and we thus omit the details. ∎

4 Numerical approximation

4.1 A numerically-feasible formulation

We turn the attention to numerical approximation. As the kernel $k(t)$ in (9) may not be positive definite or monotonic, it is not convenient to perform numerical analysis for numerical methods of model (9). Here a convolution kernel $\beta(t)$ is said to be positive definite if for each $0<\bar{t}\leq T$

\int_{0}^{\bar{t}}q(t)(\beta*q)(t)dt\geq 0,~{}~{}\forall q\in C[0,\bar{t}],

and $\beta_{\mu,\lambda}(t):=e^{-\lambda t}\beta_{\mu}(t)$ with $0<\mu<1$ and $\lambda\geq 0$ is a typical positive definite convolution kernel, see e.g. [40].

To find a feasible model for numerical discretization, we recall that the convolution of (9) and $\beta_{\alpha_{0}}$ generates (11), and we apply the integration by parts $g*\partial_{t}u=u(t)-g(t)u_{0}+g^{\prime}*u$ to rewrite (11) as

\displaystyle u+g^{\prime}*u-\beta_{\alpha_{0}}*\Delta u=gu_{0}+\beta_{\alpha_{0}}*f.

(54)

It is clear that the solution $u\in W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ to model (9)–(10) solves (54)–(10). Then we intend to show that (54)–(10) has a unique solution in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ such that both (9)–(10) and (54)–(10) have the same unique solution in $W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ .

Suppose $u_{1},u_{2}\in W^{1,p}(L^{2})\cap L^{p}(\check{H}^{2})$ solves (54)–(10), then $\varepsilon_{u}=u_{1}-u_{2}$ solves

\varepsilon_{u}+g^{\prime}*\varepsilon_{u}-\beta_{\alpha_{0}}*\Delta\varepsilon_{u}=0

with homogeneous initial and boundary conditions. As the first two terms belong to $W^{1,p}(L^{2})$ , so does the third term such that we differentiate this equation to get

\partial_{t}\varepsilon_{u}+g^{\prime}*\partial_{t}\varepsilon_{u}-\partial_{t}^{1-\alpha_{0}}*\Delta\varepsilon_{u}=0,

that is, $\varepsilon_{u}$ satisfies the transformed model (12) with $f\equiv 0$ and homogeneous initial and boundary conditions. Then Theorem 1 leads to $\|\varepsilon_{u}\|_{W^{1,p}(L^{2})}=\|\varepsilon_{u}\|_{L^{p}(\check{H}^{2})}=0$ , which implies that it suffices to numerically solve (54)–(10) in order to get the solutions to the original model (9)–(10). Furthermore, one could apply the substitution $\tilde{u}=u-u_{0}$ to transfer the initial condition of (54)–(10) to $0$ in order to apply the positive-definite quadrature rules

		$\displaystyle\tilde{u}+g^{\prime}\tilde{u}-\beta_{\alpha_{0}}\Delta\tilde{u}=\mathcal{F}:=\beta_{\alpha_{0}}*(\Delta u_{0}+f),~{}~{}(\bm{x},t)\in\Omega\times(0,T];$		(55)
		$\displaystyle\qquad\qquad\tilde{u}(0)=0,~{}\bm{x}\in\Omega;\quad\tilde{u}=0,~{}(\bm{x},t)\in\partial\Omega\times[0,T].$		(56)

For the sake of numerical analysis, we further multiply $e^{-\lambda t}$ on both sides of (55) to get an equivalent model with respect to $v=e^{-\lambda t}\tilde{u}$

		$\displaystyle v+(e^{-\lambda t}g^{\prime})v-\beta_{\alpha_{0},\lambda}\Delta v=e^{-\lambda t}\mathcal{F},~{}~{}(\bm{x},t)\in\Omega\times(0,T];$		(57)
		$\displaystyle\qquad~{}v(0)=0,~{}\bm{x}\in\Omega;\quad v=0,~{}(\bm{x},t)\in\partial\Omega\times[0,T].$		(58)

Note that $v=e^{-\lambda t}(u-u_{0})$ has the same regularity as $u$ and if we find the numerical solution to (57)–(58), we could immediately define the numerical solution to (55)–(56) by the relation $u=e^{\lambda t}v+u_{0}$ as shown later.

4.2 Semi-discrete scheme and error estimate

Define a quasi-uniform partition of $\Omega$ with mesh diameter $h$ and let $S_{h}$ be the space of continuous and piecewise linear functions on $\Omega$ with respect to the partition. Let $I$ be the identity operator. The Ritz projection $\Pi_{h}:H^{1}_{0}\rightarrow S_{h}$ defined by $\big{(}\nabla(q-\Pi_{h}q),\nabla\chi\big{)}=0$ for any $\chi\in S_{h}$ has the approximation property $\big{\|}(I-\Pi_{h})q\big{\|}\leq Qh^{2}\|q\|_{H^{2}}$ for $q\in H^{2}\cap H_{0}^{1}$ [50].

The weak formulation of (57)–(58) reads for any $\chi\in H^{1}_{0}$

\displaystyle(v,\chi)+\big{(}(e^{-\lambda t}g^{\prime})*v,\chi)+(\beta_{\alpha_{0},\lambda}*\nabla v,\nabla\chi)=(e^{-\lambda t}\mathcal{F},\chi),

(59)

and the corresponding semi-discrete finite element scheme is: find $v_{h}\in S_{h}$ such that

\displaystyle(v_{h},\chi)+\big{(}(e^{-\lambda t}g^{\prime})*v_{h},\chi)+(\beta_{\alpha_{0},\lambda}*\nabla v_{h},\nabla\chi)=(e^{-\lambda t}\mathcal{F},\chi),~{}~{}\forall\chi\in S_{h}.

(60)

After obtaining $v_{h}$ , define the approximation $u_{h}$ to the solution of (55)–(56) as

u_{h}=e^{\lambda t}v_{h}+\Pi_{h}u_{0}.

Theorem 6.

Suppose $u_{0}\in\check{H}^{4}$ and $f\in W^{1,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2})$ for $0<\sigma\ll\alpha_{0}$ . Then the following error estimate holds

\displaystyle\|u-u_{h}\|_{L^{2}(L^{2})}\leq Qh^{2}.

Proof.

Set $v-v_{h}=\xi+\eta$ with $\eta=v-\Pi_{h}v$ and $\xi=\Pi_{h}v-v_{h}$ . Then we subtract (59) from (60) and select $\chi=\xi$ to obtain

\displaystyle(\xi,\xi)+\big{(}(e^{-\lambda t}g^{\prime})*\xi,\xi)+(\beta_{\alpha_{0},\lambda}*\nabla\xi,\nabla\xi)=-(\eta,\xi)-\big{(}(e^{-\lambda t}g^{\prime})*\eta,\xi),

which, together with $|ab|\leq a^{2}+\frac{b^{2}}{4}$ , implies

\displaystyle\|\xi\|^{2}+4(\beta_{\alpha_{0},\lambda}*\nabla\xi,\nabla\xi)\leq 4\|(e^{-\lambda t}g^{\prime})*\xi\|^{2}+4\|\eta\|^{2}+4\|(e^{-\lambda t}g^{\prime})*\eta\|^{2}.

Integrate this equation on $(0,T)$ and apply the positive definiteness of $\beta_{\alpha_{0},\lambda}$ to obtain

\displaystyle\|\xi\|^{2}_{L^{2}(L^{2})}\leq 4\|(e^{-\lambda t}g^{\prime})*\xi\|^{2}_{L^{2}(L^{2})}+4\|\eta\|^{2}_{L^{2}(L^{2})}+4\|(e^{-\lambda t}g^{\prime})*\eta\|^{2}_{L^{2}(L^{2})}.

(61)

By Theorem 3 we have

\|u\|_{\check{H}^{2}}=\|\Delta u\|\leq\|\Delta u_{0}\|+Q\int_{0}^{t}\|\partial_{s}\Delta u(s)\|ds\leq\|\Delta u_{0}\|+Q\int_{0}^{t}s^{\alpha_{0}-1}ds\leq Q.

Thus, $\|v\|_{\check{H}^{2}}\leq Q$ such that

\displaystyle\|\eta\|\leq Qh^{2},

(62)

which, together with (61), leads to

\displaystyle\|\xi\|^{2}_{L^{2}(L^{2})}\leq 4\|(e^{-\lambda t}g^{\prime})*\xi\|^{2}_{L^{2}(L^{2})}+Qh^{4}.

We bound the first right-hand side term as

\displaystyle\|(e^{-\lambda t}g^{\prime})*\xi\|^{2}_{L^{2}(L^{2})}

\displaystyle\leq Q\big{(}\||e^{-\lambda t}g^{\prime}|*\|\xi\|\|_{L^{2}(0,T)}\big{)}^{2}\leq Q\|e^{-\lambda t}g^{\prime}\|^{2}_{L^{1}(0,T)}\|\xi\|^{2}_{L^{2}(L^{2})}.

By (6) and a similar argument as (31), we have

\|e^{-\lambda t}g^{\prime}\|_{L^{1}(0,T)}\leq Q\|e^{-\lambda t}t^{-\varepsilon}\|_{L^{1}(0,T)}\leq Q\lambda^{\varepsilon-1}

for $0<\varepsilon\ll 1$ . We combine the above three estimates and set $\lambda$ large enough to get $\|\xi\|_{L^{2}(L^{2})}\leq Qh^{2}$ and thus $\|v-v_{h}\|_{L^{2}(L^{2})}\leq Qh^{2}$ . We finally apply $u=e^{\lambda t}v+u_{0}$ and $u_{h}=e^{\lambda t}v_{h}+\Pi_{h}u_{0}$ to complete the proof. ∎

4.3 Fully-discrete scheme and error estimate

Partition $[0,T]$ by $t_{n}:=n\tau$ for $\tau:=T/N$ and $0\leq n\leq N$ . Let $I_{\tau}$ be the piecewise linear interpolation operator with respect to this partition. We approximate the convolution terms in (57) by the quadrature rule proposed in, e.g. [39, Equation (4.16)]

	$\displaystyle((e^{-\lambda t}g^{\prime})*v)(t_{n})$	$\displaystyle=((e^{-\lambda t}g^{\prime})*I_{\tau}v)(t_{n})+R_{n}=C_{n}(v)+R_{n};$
	$\displaystyle(-\beta_{\alpha_{0},\lambda}*\Delta v)(t_{n})$	$\displaystyle=(\beta_{\alpha_{0},\lambda}*I_{\tau}(-\Delta v))(t_{n})+\tilde{R}_{n}=\tilde{C}_{n}(-\Delta v)+\tilde{R}_{n},$

where

	$\displaystyle C_{n}(v)$	$\displaystyle:=\sum_{i=1}^{n}\kappa_{n,i}v(t_{i}),~{}~{}\kappa_{n,i}:=\frac{1}{\tau}\int_{t_{n-1}}^{t_{n}}\int_{t_{i-1}}^{\min\{t_{i},t\}}e^{-\lambda(t-s)}g^{\prime}(t-s)dsdt;$
	$\displaystyle\tilde{C}_{n}(-\Delta v)$	$\displaystyle:=\sum_{i=1}^{n}\tilde{\kappa}_{n,i}(-\Delta v(t_{i})),~{}~{}\tilde{\kappa}_{n,i}:=\frac{1}{\tau}\int_{t_{n-1}}^{t_{n}}\int_{t_{i-1}}^{\min\{t_{i},t\}}\beta_{\alpha_{0},\lambda}(t-s)dsdt$

with truncation errors $R_{n}$ and $\tilde{R}_{n}$ , respectively. Note that $\kappa_{n,i}$ is indeed a function of $n-i$ . To see this, direct calculations yield

\displaystyle\kappa_{n,i}

\displaystyle=\frac{1}{\tau}\int_{t_{n-1}}^{t_{n}}\int^{t-t_{i-1}}_{t-\min\{t_{i},t\}}e^{-\lambda y}g^{\prime}(y)dydt=\frac{1}{\tau}\int_{-\tau}^{0}\int^{t_{n}+z-t_{i-1}}_{t_{n}+z-\min\{t_{i},t_{n}+z\}}e^{-\lambda y}g^{\prime}(y)dydz.

It is clear that $t_{n}-t_{i-1}=(n-i+1)\tau$ , and $t_{n}+z-\min\{t_{i},t_{n}+z\}=(n-i)\tau+z$ for $i\leq n-1$ and $t_{n}+z-\min\{t_{i},t_{n}+z\}=0$ for $i=n$ . Thus we have $\kappa_{n,i}=\bar{\kappa}_{n-i}$ where $\bar{\kappa}_{m}$ for $0\leq m\leq N-1$ is defined as

\displaystyle\bar{\kappa}_{m}=\frac{1}{\tau}\int_{-\tau}^{0}\int^{(m+1)\tau+z}_{m\tau+z}e^{-\lambda y}g^{\prime}(y)dydz,~{}~{}1\leq m\leq N-1

(63)

and

\displaystyle\bar{\kappa}_{0}=\frac{1}{\tau}\int_{-\tau}^{0}\int^{\tau+z}_{0}e^{-\lambda y}g^{\prime}(y)dydz.

(64)

It is shown in [39, Lemma 4.8] that the quadrature rule $\tilde{C}_{n}$ is weakly positive such that, since $v(0)=0$ , the following relation holds

\displaystyle\sum_{n=1}^{n^{*}}\tilde{C}_{n}(\Phi)\Phi_{n}\geq 0,~{}~{}\text{ for }1\leq n^{*}\leq N

(65)

where $\Phi=\{\Phi_{1},\cdots,\Phi_{N}\}$ . Furthermore, [39, Lemma 4.8] gives the estimates of the truncation errors as follows

$\displaystyle\|R_{n}\|$	$\displaystyle\leq 2\mu_{n-1}\int_{0}^{\tau}\|\partial_{t}v\|dt+\tau\sum_{j=2}^{n}\mu_{n-j}\int_{t_{j-1}}^{t_{j}}\|\partial_{t}^{2}v\|dt;$
$\displaystyle\|\tilde{R}_{n}\|$	$\displaystyle\leq 2\tilde{\mu}_{n-1}\int_{0}^{\tau}\|\partial_{t}\Delta v\|dt+\tau\sum_{j=2}^{n}\tilde{\mu}_{n-j}\int_{t_{j-1}}^{t_{j}}\|\partial_{t}^{2}\Delta v\|dt;$	(66)
$\displaystyle\mu_{j}$	$\displaystyle:=\int_{t_{j}}^{t_{j+1}}\|e^{-\lambda s}g^{\prime}(s)\|ds,~{}~{}\tilde{\mu}_{j}:=\int_{t_{j}}^{t_{j+1}}\|\beta_{\alpha_{0},\lambda}(s)\|ds.$

Thus the weak formulation of (57)–(58) reads for any $\chi\in H^{1}_{0}$

\displaystyle(v_{n},\chi)+(C_{n}(v),\chi)+(\tilde{C}_{n}(\nabla v),\nabla\chi)=(e^{-\lambda t_{n}}\mathcal{F}_{n},\chi)-(R_{n}+\tilde{R}_{n},\chi),

(67)

and the corresponding fully-discrete finite element method reads: find $V_{n}\in S_{h}$ for $1\leq n\leq N$ such that

\displaystyle(V_{n},\chi)+(C_{n}(V),\chi)+(\tilde{C}_{n}(\nabla V),\nabla\chi)=(e^{-\lambda t_{n}}\mathcal{F}_{n},\chi),~{}~{}\forall\chi\in S_{h}.

(68)

After solving this scheme for $V$ , we define the numerical approximation for the solution $u$ of (55)–(56) as

\displaystyle U_{n}:=e^{\lambda t_{n}}V_{n}+\Pi_{h}u_{0},~{}~{}1\leq n\leq N.

(69)

Define the discrete-in-time $l^{2}$ norm as $\|\Phi\|^{2}_{l^{2}(0,t_{n};L^{2})}:=\tau\sum_{i=1}^{n}\|\Phi_{i}\|^{2}$ . We prove error estimate of $u-U$ under the norm $\|\cdot\|_{l^{2}(0,T;L^{2})}$ in the following theorem.

Theorem 7.

Suppose $u_{0}\in\check{H}^{4}$ and $f\in W^{2,\frac{1}{\alpha_{0}-\sigma}}(\check{H}^{2})$ for $0<\sigma\ll\alpha_{0}$ . Then the following error estimate holds

\displaystyle\|u-U\|_{l^{2}(0,T;L^{2})}\leq Qh^{2}+Q\tau^{\frac{1}{2}+\frac{3}{2}\alpha_{0}}.

Proof.

Denote $v_{n}-V_{n}=\xi_{n}+\eta_{n}$ with $\eta_{n}:=v_{n}-\Pi_{h}v_{n}$ and $\xi_{n}:=\Pi_{h}v_{n}-V_{n}$ . We subtract (67) from (68) with $\chi=\xi_{n}$ to obtain

	$\displaystyle(\xi_{n},\xi_{n})+(\tilde{C}_{n}(\nabla\xi),\nabla\xi_{n})$
	$\displaystyle\qquad=-(\eta_{n},\xi_{n})-(C_{n}(\xi),\xi_{n})-(C_{n}(\eta),\xi_{n})-(R_{n}+\tilde{R}_{n},\xi_{n}).$

We sum this equation multiplied by $\tau$ from $n=1$ to $n^{*}$ for some $n^{*}\leq N$ and apply (65) and $|ab|\leq\frac{1}{8}a^{2}+2b^{2}$ to obtain

	$\displaystyle\\|\xi\\|^{2}_{l^{2}(0,t_{n^{}};L^{2})}\leq 2\\|\eta_{n}\\|^{2}_{l^{2}(0,t_{n^{}};L^{2})}+2\\|C_{n}(\xi)\\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}$
	$\displaystyle\qquad+2\\|C_{n}(\eta)\\|^{2}_{l^{2}(0,t_{n^{}};L^{2})}+\frac{1}{2}\\|\xi\\|^{2}_{l^{2}(0,t_{n^{}};L^{2})}+2\\|R_{n}+\tilde{R}_{n}\\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}.$		(70)

Then we intend to bound the right-hand side terms. By (62) we have

\displaystyle\|C_{n}(\eta)\|\leq\sum_{i=1}^{n}|\kappa_{n,i}|\|\eta_{i}\|\leq Qh^{2}\frac{1}{\tau}\int_{t_{n-1}}^{t_{n}}\int_{0}^{t}e^{-\lambda(t-s)}|g^{\prime}(t-s)|dsdt\leq Qh^{2},

(71)

which leads to $\|\eta_{n}\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}+\|C_{n}(\eta)\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}\leq Qh^{4}.$

By Theorems 3 and 4 and $v=e^{-\lambda t}u$ , we have $\|\Delta^{m}\partial_{t}v\|\leq Qt^{\alpha_{0}-1}$ and $\|\Delta^{m}\partial^{2}_{t}v\|\leq Qt^{\alpha_{0}-2}$ for $m=0,1$ . Also, the fact that $|t^{\alpha_{0}}-\bar{t}^{\alpha_{0}}|\leq|t-\bar{t}|^{\alpha_{0}}$ for $t,\bar{t}\in[0,T]$ implies $\tilde{\mu}_{n}\leq Q\tau^{\alpha_{0}}$ . We apply them to bound $\|\tilde{R}_{n}\|$ by (66)

	$\displaystyle\\|\tilde{R}_{n}\\|$	$\displaystyle\leq Q\tilde{\mu}_{n-1}\int_{0}^{\tau}t^{\alpha_{0}-1}dt+Q\tau\sum_{j=2}^{n}\tilde{\mu}_{n-j}\int_{t_{j-1}}^{t_{j}}t^{\alpha_{0}-2}dt$		(72)
		$\displaystyle\leq Q\tau^{2\alpha_{0}}+Q\tau^{1+\alpha_{0}}\int_{t_{1}}^{t_{n}}t^{\alpha_{0}-2}dt\leq Q\tau^{2\alpha_{0}}+Q\tau^{1+\alpha_{0}}t_{1}^{\alpha_{0}-1}\leq Q\tau^{2\alpha_{0}}.$		(73)

Then we invoke both (72) and (73) to bound $\|\tilde{R}_{n}\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}$ as

	$\displaystyle\\|\tilde{R}_{n}\\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}$	$\displaystyle\leq\tau\sum_{n=1}^{n_{}}\\|\tilde{R}_{n}\\|^{2}\leq Q\tau^{1+2\alpha_{0}}\sum_{n=1}^{n_{}}\\|\tilde{R}_{n}\\|$
		$\displaystyle\leq Q\tau^{1+2\alpha_{0}}\Big{[}\sum_{n=1}^{n_{}}\tilde{\mu}_{n-1}\int_{0}^{\tau}t^{\alpha_{0}-1}dt+\tau\sum_{n=2}^{n_{}}\sum_{j=2}^{n}\tilde{\mu}_{n-j}\int_{t_{j-1}}^{t_{j}}t^{\alpha_{0}-2}dt\Big{]}$
		$\displaystyle\leq Q\tau^{1+2\alpha_{0}}\Big{[}\tau^{\alpha_{0}}+\tau\int_{t_{1}}^{t_{n_{*}}}t^{\alpha_{0}-2}dt\Big{]}\leq Q\tau^{1+3\alpha_{0}}.$

The $\|R_{n}\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}$ could be estimated following exactly the same procedure with the bound dominated by $Q\tau^{1+3\alpha_{0}}$ . We invoke the above estimates in (70) to get

\displaystyle\|\xi\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}\leq Qh^{4}+Q\tau^{1+3\alpha_{0}}+4\|C_{n}(\xi)\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}.

By $\kappa_{n,i}=\bar{\kappa}_{n-i}$ with the definition of $\bar{\kappa}_{m}$ in (63)–(64), the discrete Young’s convolution inequality and a similar estimate as (71), we have

	$\displaystyle\\|C_{n}(\xi)\\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}$	$\displaystyle\leq Q\tau\sum_{n=1}^{n^{*}}\Big{(}\sum_{i=1}^{n}\|\bar{\kappa}_{n-i}\|\\|\xi_{i}\\|\Big{)}^{2}$
		$\displaystyle\leq Q\tau\sum_{n=1}^{n^{}}\sum_{i=1}^{n}\|\bar{\kappa}_{n-i}\|\sum_{i=1}^{n}\|\bar{\kappa}_{n-i}\|\\|\xi_{i}\\|^{2}\leq Q\tau\sum_{n=1}^{n^{}}\sum_{i=1}^{n}\|\bar{\kappa}_{n-i}\|\\|\xi_{i}\\|^{2}$
		$\displaystyle\leq Q\tau\sum_{i=0}^{N-1}\|\bar{\kappa}_{i}\|\sum_{i=1}^{n^{}}\\|\xi_{i}\\|^{2}\leq Q\\|\xi\\|^{2}_{l^{2}(0,t_{n^{}};L^{2})}\sum_{i=0}^{N-1}\|\bar{\kappa}_{i}\|.$

By (63)–(64) and (6), we have

\displaystyle\sum_{i=0}^{N-1}|\bar{\kappa}_{i}|\leq\frac{1}{\tau}\int_{-\tau}^{0}\int^{N\tau+z}_{0}e^{-\lambda y}|g^{\prime}(y)|dydz\leq Q\int_{0}^{T}e^{-\lambda y}y^{-\frac{1}{2}}dy\leq Q\lambda^{-\frac{1}{2}}.

Combining the above three equations lead to

\displaystyle\|\xi\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}\leq Qh^{4}+Q\tau^{1+3\alpha_{0}}+Q\lambda^{-\frac{1}{2}}\|\xi\|^{2}_{l^{2}(0,t_{n^{*}};L^{2})}.

Setting $\lambda$ large enough and choosing $n^{*}=N$ yield

\displaystyle\|\xi\|_{l^{2}(0,T;L^{2})}\leq Qh^{2}+Q\tau^{\frac{1}{2}+\frac{3}{2}\alpha_{0}}.

We combine this with $\|\eta_{n}\|\leq Qh^{2}$ to get

\displaystyle\|v-V\|_{l^{2}(0,T;L^{2})}\leq Qh^{2}+Q\tau^{\frac{1}{2}+\frac{3}{2}\alpha_{0}},

and we apply this and $u=e^{\lambda t}v+u_{0}$ and (69) to complete the proof. ∎

4.4 Numerical experiments

4.4.1 Initial singularity of solutions

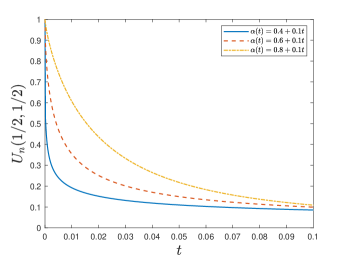
Let $\Omega=(0,1)^{2}$ , $\alpha(t)=\alpha_{0}+0.1t$ , $u_{0}=\sin(\pi x)\sin(\pi y)$ and $f=x(1-x)y(1-y)$ . As we focus on the initial behavior of the solutions, we take a small terminal time $T=0.1$ . We use the uniform spatial partition with the mesh size $h=1/64$ and a very fine temporal mesh size $\tau=1/3000$ to capture the singular behavior of the solutions near $t=0$ . Numerical solutions $U_{n}(\frac{1}{2},\frac{1}{2})$ defined by (69) is presented in Figure 1 (left) for three cases:

(\text{i})~{}\alpha_{0}=0.4;~{}(\text{ii})~{}\alpha_{0}=0.6;~{}(\text{iii})~{}\alpha_{0}=0.8.

(74)

We find that as $\alpha_{0}$ decreases, the solutions change more rapidly, indicating a stronger singularity that is consistent with the analysis result $\partial_{t}u\sim t^{\alpha_{0}-1}$ in Theorem 3.

4.4.2 Numerical accuracy

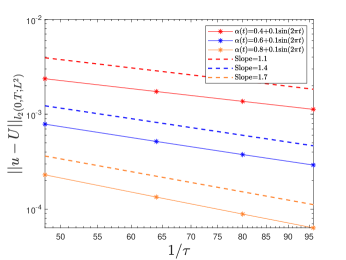
Let $\Omega=(0,1)^{2}$ , $T=1$ and the exact solution $u(x)=(1+t^{\alpha_{0}})\sin(\pi x)\sin(\pi y).$ The source term $f$ is evaluated accordingly and we select $\alpha(t)=\alpha_{0}+0.1\sin(2\pi t).$ As the spatial discretization is standard, we only investigate the temporal accuracy of the numerical solution defined by (69). We use the uniform spatial partition with the mesh size $h=1/256$ and present log-log plots of errors under the $\|\cdot\|_{l^{2}(0,T;L^{2})}$ norm in Figure 1 (right) for different $\alpha_{0}$ in (74), which indicates the convergence order of $\frac{1}{2}+\frac{3}{2}\alpha_{0}$ as proved in Theorem 7.

Refer to caption — Figure 1: (left) Plots of $U_{n}$ at $(\frac{1}{2},\frac{1}{2})$ under different $\alpha_{0}$ ; (right) Errors under different $\alpha_{0}$ and $\tau$ .

5 Perturbation method

5.1 Motivation

Despite the applicability of the convolution method to fractional initial value problems with variable exponent, it has some restrictions. Below we give two examples that the convolution method does not apply, which motivates an alternative method to analyze these problems.

Example 1. Consider a two-sided space-fractional diffusion-advection-reaction equation with variable exponent $\alpha(x)\in(1,2)$ [41, 44], which is a variable-exponent extension of the standard space-fractional boundary value problem proposed in [14]

		$\displaystyle-\partial_{x}\big{(}rI_{x}^{2-\alpha(x)}+(1-r)\hat{I}_{x}^{2-\alpha(x)}\big{)}\partial_{x}u$		(75)
		$\displaystyle\qquad\qquad\qquad+b(x)\partial_{x}u+c(x)u=f(x),~{}~{}x\in\Omega:=(0,1);$
		$\displaystyle\qquad\qquad u(0)=u(1)=0,$		(76)

where the left and right fractional integrals of variable exponent are defined as

I_{x}^{2-\alpha(x)}q:=\int_{0}^{x}\frac{(x-s)^{1-\alpha(x-s)}}{\Gamma(2-\alpha(x-s))}q(s)ds,~{}~{}\hat{I}_{x}^{2-\alpha(x)}q:=\int_{x}^{1}\frac{(s-x)^{1-\alpha(1-(s-x))}}{\Gamma(2-\alpha(1-(s-x))}q(s)ds.

We focus on the two-sided case, i.e. $0<r<1$ , since the one-sided case $r=0$ or $r=1$ is simpler.

It is worth mentioning that for $b(x)=c(x)\equiv 0$ , $r=1/2$ and $\alpha(x)\equiv\alpha$ for some $1<\alpha<2$ , it is shown in [2, Lemma 2.3] that the operator on the left-hand side of (75) is indeed the fractional Laplacian operator of order $\alpha$ . Thus, (75) could also be viewed as a variable-exponent extension of the fractional Laplacian equation under $b(x)=c(x)\equiv 0$ and $r=1/2$ .

Due to the impacts of $\alpha(x)$ , it is difficult to apply analytical methods to study (75), and the convolution method does not apply due to the existence of both left and right fractional integrals of variable exponent. To be specific, although one could employ the convolution method to convert the term $-\partial_{x}I_{x}^{2-\alpha(x)}\partial_{x}u$ to a more feasible form, the operator $-\partial_{x}\hat{I}_{x}^{2-\alpha(x)}\partial_{x}$ is accordingly transformed to a much more complicated Fredholm type operator, which hinders further analysis.

Example 2. Consider a variable-exponent version of the distributed-order diffusion equation, which is firstly proposed in [36] and $\beta(t)$ could serve as a pointwise-in-time shift of the domain of the exponent

		$\displaystyle~{}~{}~{}\partial_{t}^{[\mu,\beta]}u(\bm{x},t)-\Delta u(\bm{x},t)=f(\bm{x},t),~{}~{}(\bm{x},t)\in\Omega\times(0,T],$		(77)
		$\displaystyle u(\bm{x},0)=u_{0}(\bm{x}),~{}\bm{x}\in\Omega;\quad u(\bm{x},t)=0,~{}(\bm{x},t)\in\partial\Omega\times[0,T],$		(78)

where the distributed variable-exponent time-fractional derivative is defined as

\displaystyle\partial_{t}^{[\mu,\beta]}u:=\partial_{t}(k_{\mu,\beta}*(u-u_{0})),~{}~{}k_{\mu,\beta}(t):=\int_{0}^{1}\frac{t^{-\alpha+\beta(t)}}{\Gamma(1-\alpha+\beta(t))}\mu(\alpha)d\alpha

for some non-negative continuous function $\mu(\alpha)$ satisfying $\text{supp}\,\mu=[b_{1},b_{2}]$ with $0\leq b_{1}<b_{2}<1$ and $\beta(t)$ satisfying $b_{2}-1+\varepsilon_{0}\leq\beta\leq b_{1}$ over $[0,T]$ for some $0<\varepsilon_{0}\ll 1$ . Without loss of generality, we assume $\beta(0)=0$ . Otherwise, one could apply the variable substitution to transfer the initial value of $\beta(t)$ to $0$ . Note that when $\beta(t)\equiv 0$ , (77)–(78) is a standard distributed-order diffusion equation. Furthermore, the conditions on $\beta$ ensure that

\displaystyle 0\leq\alpha-\beta(t)\leq 1-\varepsilon_{0},~{}~{}\text{ for }\alpha\in[b_{1},b_{2}]\text{ and }t\in[0,T].

(79)

Due to the impacts of $\beta(t)$ , it is difficult to apply analytical methods to study (77), while the convolution method does not apply since the existence of the distributed-order integral makes it difficult to find a suitable kernel such that the its convolution with $k_{\mu}$ generates a generalized identity function.

5.2 Idea of the method

Motivated by the aforementioned questions, we propose an alternative method called the perturbation method to resolve them. The main idea of the perturbation method is to replace the variable-exponent kernel by a suitable kernel such that their difference serves as a low-order perturbation term, without affecting other terms in the model.

To illustrate this idea based on the subdiffusion model (9)–(10), we split the kernel $k(t)$ into two parts as follows

\displaystyle k(t)

\displaystyle=\frac{t^{-\alpha(t)}}{\Gamma(1-\alpha(t))}=\frac{t^{-\alpha_{0}}}{\Gamma(1-\alpha_{0})}+\int_{0}^{t}\partial_{z}\frac{t^{-\alpha(z)}}{\Gamma(1-\alpha(z))}dz=:\beta_{1-\alpha_{0}}+\tilde{g}(t),

(80)

where, by direct calculations and the notation $\gamma(z):=\frac{\Gamma^{\prime}(z)}{\Gamma(z)}$ ,

\displaystyle\tilde{g}(t)=\int_{0}^{t}\frac{t^{-\alpha(z)}}{\Gamma(1-\alpha(z))}\big{(}-\alpha^{\prime}(z)\ln t+\gamma(1-\alpha(z))\alpha^{\prime}(z)\big{)}dz.

t^{-\alpha(z)}=t^{-\alpha_{0}}t^{\alpha_{0}-\alpha(z)}=t^{-\alpha_{0}}e^{(\alpha_{0}-\alpha(z))\ln t}\leq t^{-\alpha_{0}}e^{Qz|\ln t|}\leq t^{-\alpha_{0}}e^{Qt|\ln t|}\leq Qt^{-\alpha_{0}},

$\tilde{g}$ could be bounded as

\displaystyle|\tilde{g}|\leq Q\int_{0}^{t}t^{-\alpha_{0}}(1+|\ln t|)dz\leq Qt^{1-\alpha_{0}}(1+|\ln t|)\rightarrow 0\text{ as }t\rightarrow 0^{+}.

(81)

By similar estimates we bound $\tilde{g}^{\prime}$ as

\displaystyle|\tilde{g}^{\prime}|\leq Qt^{-\alpha_{0}}(1+|\ln t|)\in L^{1}(0,T).

(82)

We then invoke (80) in (9) to get

\displaystyle^{c}\partial_{t}^{\alpha_{0}}u+\tilde{g}*\partial_{t}u-\Delta u=f.

(83)

We apply the integration by parts to get

\tilde{g}*\partial_{t}u=-\tilde{g}u_{0}+\tilde{g}^{\prime}*u,

which, together with (83), leads to

{}^{c}\partial_{t}^{\alpha_{0}}u+\tilde{g}^{\prime}*u-\Delta u=f+\tilde{g}u_{0}.

As the term $\tilde{g}^{\prime}*u$ is a low-order term compared with ${}^{c}\partial_{t}^{\alpha_{0}}u$ , one could analyze this model by means of Laplace transform as we did in Section 3.

Relation between two methods

Note that the transformed model (83) looks different from (12). However, if we further apply $\partial_{t}^{1-\alpha_{0}}$ on both sides of (83), we have

\displaystyle\partial_{t}u+\partial_{t}^{1-\alpha_{0}}(\tilde{g}*\partial_{t}u)-\partial_{t}^{1-\alpha_{0}}\Delta u=\partial_{t}^{1-\alpha_{0}}f.

(84)

Now the two transformed models (84) and (12) are exactly the same equation if we can show that

\partial_{t}^{1-\alpha_{0}}(\tilde{g}*\partial_{t}u)=g^{\prime}*\partial_{t}u.

To prove this relation, recall that $g=\beta_{\alpha_{0}}*k$ with $g(0)-1=0$ and $\tilde{g}=k-\beta_{1-\alpha_{0}}$ . Then direct calculations show that

\partial_{t}^{1-\alpha_{0}}(\tilde{g}*\partial_{t}u)=\partial_{t}\big{[}\beta_{\alpha_{0}}*(k-\beta_{1-\alpha_{0}})*\partial_{t}u\big{]}=\partial_{t}\big{[}(g-1)*\partial_{t}u\big{]}=g^{\prime}*\partial_{t}u.

Thus, for models such as the variable-exponent subdiffusion equation (9), both the convolution method and the perturbation method could transform the original problem to the same model such that the analysis such as those in Section 3 could be performed. Nevertheless, the perturbation method applies to more complicated models such as those in Examples 1-2 , as we will see later.

5.3 Space-fractional problem with variable exponent

We consider the two-sided space-fractional diffusion-advection-reaction equation (75)–(76) proposed in Example 1. It is worth mentioning that if we denote the equation (75) as $\mathcal{L}_{x,r}^{\alpha(t)}u=f$ , the upcoming analysis also applies to the multi-dimensional case, e,g, the two-dimensional case $\mathcal{L}_{x,r}^{\alpha(x)}u+\mathcal{L}_{y,\bar{r}}^{\bar{\alpha}(x)}u=f$ for some $0<\bar{r}<1$ and $1<\bar{\alpha}(x)<2$ on $(x,y)\in(0,1)^{2}$ .

Recall that $\alpha_{0}=\alpha(0)$ and $\alpha_{1}=\alpha(1)$ . Following the idea of the perturbation method, we split the kernels in $I_{x}^{2-\alpha(x)}$ and $\hat{I}_{x}^{2-\alpha(x)}$ as

\frac{x^{1-\alpha(x)}}{\Gamma(2-\alpha(x))}=\beta_{2-\alpha_{0}}+g_{l}(x),~{}~{}g_{l}(x):=\int_{0}^{x}\partial_{z}\frac{x^{1-\alpha(z)}}{\Gamma(2-\alpha(z))}dz,

and

\frac{x^{1-\alpha(1-x)}}{\Gamma(2-\alpha(1-x))}=\beta_{2-\alpha_{1}}+g_{r}(x),~{}~{}g_{r}(x):=\int_{0}^{x}\partial_{z}\frac{x^{1-\alpha(1-z)}}{\Gamma(2-\alpha(1-z))}dz.

By similar estimates as (81)–(82), we have the following estimates for $0<\varepsilon\ll 1$

	$\displaystyle g_{l}(0)=g_{r}(0)=0,~{}~{}\|g_{l}^{\prime}\|\leq Q_{1}x^{1-\alpha_{0}-\varepsilon},~{}~{}\|g_{r}^{\prime}\|\leq Q_{1}x^{1-\alpha_{1}-\varepsilon},$
	$\displaystyle\hskip 85.27806pt\|g_{l}^{\prime\prime}\|\leq Q_{2}x^{-\alpha_{0}-\varepsilon},~{}~{}\|g_{r}^{\prime\prime}\|\leq Q_{2}x^{-\alpha_{1}-\varepsilon}.$		(85)

Then equation (75) is equivalently rewritten as

	$\displaystyle-\partial_{x}\big{(}rI_{x}^{2-\alpha_{0}}+(1-r)\hat{I}_{x}^{2-\alpha_{1}}\big{)}\partial_{x}u$
	$\displaystyle\quad-r\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)ds+(1-r)\int_{x}^{1}g_{r}^{\prime}(s-x)\partial_{s}u(s)ds$
	$\displaystyle\quad+b(x)\partial_{x}u+c(x)u=f(x).$

By integration by parts, we define the corresponding bilinear form by

	$\displaystyle a(u,v):=$	$\displaystyle r\big{(}I_{x}^{1-\frac{\alpha_{0}}{2}}\partial_{x}u,\hat{I}_{x}^{1-\frac{\alpha_{0}}{2}}\partial_{x}v\big{)}+(1-r)\big{(}I_{x}^{1-\frac{\alpha_{1}}{2}}\partial_{x}u,\hat{I}_{x}^{1-\frac{\alpha_{1}}{2}}\partial_{x}v\big{)}$
		$\displaystyle\quad-r(\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)ds,v)+(1-r)(\int_{x}^{1}g_{r}^{\prime}(s-x)\partial_{s}u(s)ds,v)$
		$\displaystyle\quad+(b(x)\partial_{x}u,v)+(c(x)u,v).$

Then the variational formulation of (75)–(76) reads: find $u\in H^{\alpha^{*}}_{0}$ where $\alpha^{*}=\frac{\max\{\alpha_{0},\alpha_{1}\}}{2}$ such that

\displaystyle a(u,v)=(f,v),~{}~{}\forall v\in H^{\alpha^{*}}_{0}.

(86)

The following estimates are critical in both mathematical and numerical analysis.

Lemma 1.

Suppose $b\in C^{1}[0,1]$ and $c$ is bounded. Then there exist a positive constant $\bar{c}$ such that when

\displaystyle c-\frac{1}{2}b^{\prime}\geq\bar{c},\text{ for }x\in[0,1],

the following properties hold for any $u,v\in H^{\alpha^{*}}_{0}$

\displaystyle a(u,u)\geq c_{*}\|u\|_{H^{\alpha^{*}}}^{2},~{}~{}|a(u,v)|\leq c^{*}\|u\|_{H^{\alpha^{*}}}\|v\|_{H^{\alpha^{*}}},

for some positive constants $c_{*}$ and $c^{*}$ .

Proof.

By the Sobolev embedding theorem, we have $u,v\in C[0,1]$ . To show the coercivity, we apply (2) to get

	$\displaystyle r\big{(}I_{x}^{1-\frac{\alpha_{0}}{2}}\partial_{x}u,\hat{I}_{x}^{1-\frac{\alpha_{0}}{2}}\partial_{x}u\big{)}+(1-r)\big{(}I_{x}^{1-\frac{\alpha_{1}}{2}}\partial_{x}u,\hat{I}_{x}^{1-\frac{\alpha_{1}}{2}}\partial_{x}u\big{)}$
	$\displaystyle\quad\geq rc_{1}\\|u\\|_{H^{\frac{\alpha_{0}}{2}}}^{2}+(1-r)c_{1}\\|u\\|_{H^{\frac{\alpha_{1}}{2}}}^{2}.$		(87)

Then an integration by parts yields

\displaystyle(b(x)\partial_{x}u,u)+(c(x)u,u)=\big{(}(c-\frac{1}{2}b^{\prime})u,u\big{)}.

(88)

The estimate of the term containing $g_{l}$ requires technical derivations. By (1),direct calculations yield

	$\displaystyle(\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)ds,u)$
	$\displaystyle\quad=\int_{0}^{1}\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)dsu(x)dx$
	$\displaystyle\quad=\int_{0}^{1}\partial_{s}u(s)\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dxds$
	$\displaystyle\quad=\int_{0}^{1}\partial_{s}(I^{1}_{s}\partial_{s}u(s))\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dxds$
	$\displaystyle\quad=-\int_{0}^{1}\big{(}I^{1}_{s}\partial_{s}u(s)\big{)}\partial_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dxds$
	$\displaystyle\quad=-\int_{0}^{1}\big{(}I^{1-\frac{\alpha_{0}}{2}}_{s}\partial_{s}u(s)\big{)}\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\big{(}\partial_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dx\big{)}ds.$

By the relation $\partial_{s}\hat{I}^{\frac{\alpha_{0}}{2}}_{s}q=\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\partial_{s}q$ when $q(1)=0$ [22], we have

	$\displaystyle(\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)ds,u)$
	$\displaystyle\quad=-\int_{0}^{1}\big{(}I^{1-\frac{\alpha_{0}}{2}}_{s}\partial_{s}u(s)\big{)}\partial_{s}\big{(}\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dx\big{)}ds.$		(89)

By variable substitution $z=\frac{y-s}{x-s}$ we have

	$\displaystyle\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dx=\int_{s}^{1}\frac{(y-s)^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}\int_{y}^{1}g_{l}^{\prime}(x-y)u(x)dxdy$
	$\displaystyle\quad=\int_{s}^{1}u(x)\int_{s}^{x}\frac{(y-s)^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime}(x-y)dydx$		(90)
	$\displaystyle\quad=\int_{s}^{1}u(x)(x-s)^{\frac{\alpha_{0}}{2}}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime}((x-s)(1-z))dzdx.$

By (85) we have

	$\displaystyle\Big{\|}u(x)(x-s)^{\frac{\alpha_{0}}{2}}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime}((x-s)(1-z))dz\Big{\|}$
	$\displaystyle\quad\leq Q(x-s)^{1-\frac{\alpha_{0}}{2}-\varepsilon}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}(1-z)^{1-\alpha_{0}-\varepsilon}dz\rightarrow 0\text{ as }x\rightarrow s^{+},$

then we invoke (90) to get

	$\displaystyle\Big{\|}\partial_{s}\big{(}\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dx\big{)}\Big{\|}$
	$\displaystyle\quad=\Big{\|}\partial_{s}\int_{s}^{1}u(x)(x-s)^{\frac{\alpha_{0}}{2}}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime}((x-s)(1-z))dzdx\Big{\|}$
	$\displaystyle\quad=\Big{\|}-\frac{\alpha_{0}}{2}\int_{s}^{1}u(x)(x-s)^{\frac{\alpha_{0}}{2}-1}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime}((x-s)(1-z))dzdx$
	$\displaystyle\qquad-\int_{s}^{1}u(x)(x-s)^{\frac{\alpha_{0}}{2}}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}g_{l}^{\prime\prime}((x-s)(1-z))(1-z)dzdx\Big{\|}$
	$\displaystyle\quad\leq Q_{1}\frac{\alpha_{0}}{2}\int_{s}^{1}\|u(x)\|(x-s)^{-\frac{\alpha_{0}}{2}-\varepsilon}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}(1-z)^{1-\alpha_{0}-\varepsilon}dzdx$
	$\displaystyle\qquad+Q_{2}\int_{s}^{1}\|u(x)\|(x-s)^{\frac{-\alpha_{0}}{2}-\varepsilon}\int_{0}^{1}\frac{z^{\frac{\alpha_{0}}{2}-1}}{\Gamma(\frac{\alpha_{0}}{2})}(1-z)^{1-\alpha_{0}-\varepsilon}dzdx\Big{\|}$
	$\displaystyle\quad\leq\frac{Q_{3}}{\Gamma(1-\frac{\alpha_{0}}{2}-\varepsilon)}\int_{s}^{1}\|u(x)\|(x-s)^{-\frac{\alpha_{0}}{2}-\varepsilon}dx=Q_{3}\hat{I}_{s}^{1-\frac{\alpha_{0}}{2}-\varepsilon}\|u\|,$

which, together with the fact that $\hat{I}_{s}^{1-\frac{\alpha_{0}}{2}-\varepsilon}$ is a bounded linear operator in $L^{2}$ , leads to

\displaystyle\Big{\|}\partial_{s}\big{(}\hat{I}^{\frac{\alpha_{0}}{2}}_{s}\int_{s}^{1}g_{l}^{\prime}(x-s)u(x)dx\big{)}\Big{\|}\leq Q_{3}\|\hat{I}_{s}^{1-\frac{\alpha_{0}}{2}-\varepsilon}|u|\|\leq Q_{4}\|u\|.

We invoke this in (89) to finally obtain for $\varepsilon_{1}>0$

	$\displaystyle\Big{\|}(\int_{0}^{x}g_{l}^{\prime}(x-s)\partial_{s}u(s)ds,u)\Big{\|}$
	$\displaystyle\qquad\leq Q_{4}\\|\partial_{x}^{\frac{\alpha_{0}}{2}}u\\|\\|u\\|\leq\frac{Q_{4}}{c_{3}}\\|u\\|_{H^{\frac{\alpha_{0}}{2}}}\\|u\\|\leq\varepsilon_{1}\\|u\\|_{H^{\frac{\alpha_{0}}{2}}}^{2}+\frac{Q_{4}^{2}}{4c_{3}^{2}\varepsilon_{1}}\\|u\\|^{2}.$		(91)

By similar estimates, we have the analogous result

	$\displaystyle\Big{\|}(\int_{x}^{1}g_{r}^{\prime}(s-x)\partial_{s}u(s)ds,u)\Big{\|}$
	$\displaystyle\qquad\leq Q_{5}\\|\hat{\partial}_{x}^{\frac{\alpha_{1}}{2}}u\\|\\|u\\|\leq\frac{Q_{5}}{c_{3}}\\|u\\|_{H^{\frac{\alpha_{1}}{2}}}\\|u\\|\leq\varepsilon_{1}\\|u\\|_{H^{\frac{\alpha_{1}}{2}}}^{2}+\frac{Q_{5}^{2}}{4c_{3}^{2}\varepsilon_{1}}\\|u\\|^{2}.$		(92)

Combining (87), (88), (91) and (92) leads to

	$\displaystyle a(u,u)\geq r(c_{1}-\varepsilon_{1})\\|u\\|_{H^{\frac{\alpha_{0}}{2}}}^{2}+(1-r)(c_{1}-\varepsilon_{1})\\|u\\|_{H^{\frac{\alpha_{1}}{2}}}^{2}$
	$\displaystyle\quad+\big{(}(c-\frac{1}{2}b^{\prime}-r\frac{Q_{4}^{2}}{4c_{3}^{2}\varepsilon_{1}}-(1-r)\frac{Q_{5}^{2}}{4c_{3}^{2}\varepsilon_{1}})u,u\big{)}.$

Thus, for $\varepsilon_{1}<c_{1}$ and

c-\frac{1}{2}b^{\prime}\geq r\frac{Q_{4}^{2}}{4c_{3}^{2}\varepsilon_{1}}+(1-r)\frac{Q_{5}^{2}}{4c_{3}^{2}\varepsilon_{1}},

we reach the coercivity.

The proof of the second statement follows from (2) and the above estimates and is thus omitted. The only issue that needs to be pointed out is that the condition $b\in C^{1}[0,1]$ is used to ensure $\|bv\|_{H^{\alpha^{*}}}\leq Q\|v\|_{H^{\alpha^{*}}}$ by [14, Lemma 3.2] such that the term $(b\partial_{x}u,v)$ could be bounded by $Q\|u\|_{H^{\alpha^{*}}}\|v\|_{H^{\alpha^{*}}}$ , see e.g. [14, Equation 28]. ∎

Based on Lemma 1 and the estimate for $f\in H^{-\alpha^{*}}$

|(f,v)|\leq\|f\|_{H^{-\alpha^{*}}}\|v\|_{H^{\alpha^{*}}},

which means that $F(v):=(f,v)$ is a continuous linear functional over $H^{\alpha^{*}}$ , we apply the Lax-Milgram theorem to reach the following conclusion.

Theorem 8.

Under the conditions of Lemma 1 and $f\in H^{-\alpha^{*}}$ , there exists a unique solution to (86) in $H^{\alpha^{*}}_{0}$ such that

\|u\|_{H^{\alpha^{*}}}\leq Q\|f\|_{H^{-\alpha^{*}}}.

5.4 Distributed variable-exponent model

We employ the idea of the perturbation method to analyze the distributed variable-exponent model (77)–(78) in Example 2. We apply $\beta(0)=0$ to split $k_{\mu}(t)$ into two parts as follows

	$\displaystyle k_{\mu,\beta}(t)$	$\displaystyle=\int_{0}^{1}\frac{t^{-\alpha}}{\Gamma(1-\alpha)}\mu(\alpha)d\alpha+\int_{0}^{1}\int_{0}^{t}\partial_{z}\frac{t^{-\alpha+\beta(z)}}{\Gamma(1-\alpha+\beta(z))}dz\mu(\alpha)d\alpha$
		$\displaystyle=:k_{\mu}(t)+\int_{0}^{1}g(t;\alpha)\mu(\alpha)d\alpha,~{}~{}g(t;\alpha):=\int_{0}^{t}\partial_{z}\frac{t^{-\alpha+\beta(z)}}{\Gamma(1-\alpha+\beta(z))}dz.$		(93)

Based on (79), direct calculations show that

$\displaystyle\|g(t;\alpha)\|$	$\displaystyle=\Big{\|}\int_{0}^{t}\frac{t^{-\alpha+\beta(z)}}{\Gamma(1-\alpha+\beta(z))}\Big{(}\beta^{\prime}(z)\ln t-\frac{\beta^{\prime}(z)}{\Gamma(1-\alpha+\beta(z))}\Big{)}dz\Big{\|}$
	$\displaystyle\leq Qt^{1-\alpha+\beta(z)}(\|\ln t\|+1)\leq Qt^{\varepsilon_{0}}(\|\ln t\|+1);~{}~{}\lim_{t\rightarrow 0^{+}}g(t;\alpha)=0;$	(94)
$\displaystyle\|\partial_{t}g(t;\alpha)\|$	$\displaystyle=\Big{\|}\frac{t^{-\alpha+\beta(t)}}{\Gamma(1-\alpha+\beta(t))}\Big{(}\beta^{\prime}(t)\ln t-\frac{\beta^{\prime}(t)}{\Gamma(1-\alpha+\beta(t))}\Big{)}$
	$\displaystyle\qquad+\int_{0}^{t}\partial_{t}\Big{[}\frac{t^{-\alpha+\beta(z)}}{\Gamma(1-\alpha+\beta(z))}\Big{(}\beta^{\prime}(z)\ln t-\frac{\beta^{\prime}(z)}{\Gamma(1-\alpha+\beta(z))}\Big{)}\Big{]}dz\Big{\|}$
	$\displaystyle\leq Qt^{-(1-\varepsilon_{0})}(\|\ln t\|+1)\leq Qt^{-(1-\frac{\varepsilon_{0}}{2})}.$	(95)

We then invoke (93) in (77) and apply (94) to get

\displaystyle~{}~{}~{}\partial_{t}^{[\mu]}u+\int_{0}^{1}\partial_{t}g(t;\alpha)\mu(\alpha)d\alpha*(u-u_{0})-\Delta u=f,

(96)

where $\partial_{t}^{[\mu]}$ is the standard distributed-order operator defined as [30, 36]

\partial_{t}^{[\mu]}u:=\partial_{t}(k_{\mu}*(u-u_{0})).

Then we follow [23, Section 3] to take the Laplace transform of (96) to represent $u$ as

\displaystyle u=S_{1}(t)u_{0}+\int_{0}^{t}S_{2}(t-s)\Big{(}-\int_{0}^{1}\partial_{s}g(s;\alpha)\mu(\alpha)d\alpha*(u-u_{0})+f(s)\Big{)}ds.

(97)

Here $S_{1}$ and $S_{2}$ are given as

	$\displaystyle S_{1}(t)q$	$\displaystyle:=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta_{1}}}e^{tz}(\mathcal{V}(z)-\Delta)^{-1}z^{-1}\mathcal{V}(z)qdz,$
	$\displaystyle S_{2}(t)q$	$\displaystyle:=\frac{1}{2\pi\rm i}\int_{\Gamma_{\theta_{1}}}e^{tz}(\mathcal{V}(z)-\Delta)^{-1}qdz,$

where $\mathcal{V}(z):=\int_{0}^{1}z^{\alpha}\mu(\alpha)d\alpha$ and $\theta_{1}\in(0,\frac{2\theta-\pi}{8})$ with $\theta\in(\frac{\pi}{2},\min\{\frac{\pi}{2b_{2}},\pi\})$ , with the following estimates [23, Lemma 3.1]

\displaystyle\|S_{1}(t)\|\leq Qt^{\frac{b_{1}+b_{2}}{2}-1},~{}~{}\|S_{2}(t)\|\leq Qt^{\frac{b_{1}-b_{2}}{2}}.

(98)

Then we follow [23] to define a weak solution to (77)–(78): a function $u\in L^{1}(L^{2})$ is a weak solution to (77)–(78) if it satisfies (97). The following theorem gives the existence and uniqueness of the weak solution to (77)–(78).

Theorem 9.

Suppose $u_{0}\in L^{2}$ and $f\in L^{1}(L^{2})$ , then model (77)–(78) admits a unique weak solution $u\in L^{1}(L^{2})$ with the following estimate

\|u\|_{L^{1}(L^{2})}\leq Q(\|u_{0}\|+\|f\|_{L^{1}(L^{2})}).

Proof.

Define a mapping $\mathcal{M}:\,L^{1}(L^{2})\rightarrow L^{1}(L^{2})$ by $v=\mathcal{M}w$ where $v$ satisfies

\displaystyle v=S_{1}(t)u_{0}+\int_{0}^{t}S_{2}(t-s)\Big{(}-\int_{0}^{1}\partial_{s}g(s;\alpha)\mu(\alpha)d\alpha*(w-u_{0})+f(s)\Big{)}ds.

(99)

For $\lambda\geq 0$ , the equivalent norm $\|\cdot\|_{L^{1}_{\lambda}(L^{2})}$ of $L^{1}(L^{2})$ is given as $\|q\|_{L^{1}_{\lambda}(L^{2})}:=\|e^{-\lambda t}q\|_{{}_{L^{1}(L^{2})}}$ . Then we first show that $\mathcal{M}$ is well defined. For $w\in L^{1}(L^{2})$ , we apply the $\|\cdot\|_{L^{1}_{\lambda}(L^{2})}$ norm on both sides of (99) and use (98) and (95) to get

	$\displaystyle\\|v\\|_{L^{1}_{\lambda}(L^{2})}\leq\\|S_{1}(t)u_{0}\\|_{L^{1}_{\lambda}(L^{2})}$
	$\displaystyle\qquad+\Big{\\|}\int_{0}^{t}S_{2}(t-s)\Big{(}-\int_{0}^{1}\partial_{s}g(s;\alpha)\mu(\alpha)d\alpha*(w-u_{0})+f(s)\Big{)}ds\Big{\\|}_{L^{1}_{\lambda}(L^{2})}$
	$\displaystyle~{}~{}\leq Q\\|t^{\frac{b_{1}+b_{2}}{2}-1}\\|_{L^{1}(0,T)}\\|u_{0}\\|+Q\big{\\|}t^{\frac{b_{1}-b_{2}}{2}}\big{(}t^{-(1-\frac{\varepsilon_{0}}{2})}\\|w-u_{0}\\|+\\|f\\|\big{)}\big{\\|}_{L^{1}_{\lambda}(0,T)}$
	$\displaystyle~{}~{}\leq Q(\\|u_{0}\\|+\\|f\\|_{L^{1}(L^{2})})+Q\\|e^{-\lambda t}t^{\frac{b_{1}-b_{2}}{2}}\\|_{L^{1}(0,T)}\\|w\\|_{L^{1}_{\lambda}(L^{2})}$
	$\displaystyle~{}~{}\leq Q(\\|u_{0}\\|+\\|f\\|_{L^{1}(L^{2})})+Q\sigma^{\frac{b_{2}-b_{1}}{2}-1}\\|w\\|_{L^{1}_{\lambda}(L^{2})},$		(100)

where we applied a similar estimate as (31)

\displaystyle\|e^{-\sigma t}t^{\frac{b_{1}-b_{2}}{2}}\|_{L^{1}(0,T)}=\int_{0}^{T}e^{-\sigma t}t^{\frac{b_{1}-b_{2}}{2}}dt\leq\sigma^{\frac{b_{2}-b_{1}}{2}-1}\int_{0}^{\infty}e^{-t}t^{\frac{b_{1}-b_{2}}{2}}dt\leq Q\sigma^{\frac{b_{2}-b_{1}}{2}-1}.

Thus, $v\in L^{1}(L^{2})$ such that $\mathcal{M}$ is well defined. To show the contractivity, it suffices to consider (99) with $w=v$ and $u_{0}=f=0$ . Then (100) gives

\displaystyle\|v\|_{L^{1}_{\lambda}(L^{2})}\leq Q\sigma^{\frac{b_{2}-b_{1}}{2}-1}\|v\|_{L^{1}_{\lambda}(L^{2})}.

Choosing $\sigma$ large enough ensures $Q\sigma^{\frac{b_{2}-b_{1}}{2}-1}<1$ , which implies that $\mathcal{M}$ is a contraction mapping such that there exists a unique solution $u$ in $L^{1}(L^{2})$ to (97). The stability estimate follows from (100) with $v=w=u$ and $\sigma$ large enough. The proof is thus completed. ∎

6 Application to Abel integral equation

We further demonstrate the usage of the perturbation method by analyzing the following Abel integral equation of variable exponent, a typical first-kind Volterra integral equation with weak singularity that would broaden the usefulness of its constant-exponent version as commented in [33]

\displaystyle(k*u)(t)=f(t),~{}~{}t\in[0,T].

(101)

6.1 The case $0<\alpha_{0}<1$

We prove the well-posedness of (101) in the following theorem.

Theorem 10.

Suppose $f\in W^{1,1}(0,T)$ . Then the integral equation (101) admits a unique solution in $L^{1}(0,T)$ such that

\|u\|_{L^{1}(0,T)}\leq Q\|f\|_{W^{1,1}(0,T)}.

If further $f\in W^{1,\frac{1}{\alpha_{0}-\sigma}}(0,T)$ for $0<\sigma\ll\alpha_{0}$ , then

|u|\leq Q|f(0)|t^{\alpha_{0}-1}+Q\|f^{\prime}\|_{L^{\frac{1}{\alpha_{0}-\sigma}}(0,T)},~{}~{}t\in(0,T].

Proof.

By the idea of the perturbation method, we split $k$ as (80) such that the integral equation (101) could be equivalently rewritten as

\displaystyle\beta_{1-\alpha_{0}}*u=-\tilde{g}*u+f.

(102)

As $\partial_{t}^{1-\alpha_{0}}$ is the inverse operator of $I_{t}^{1-\alpha_{0}}$ , we apply $\partial_{t}^{1-\alpha_{0}}$ on both sides of this equation to get

\displaystyle u=-\partial_{t}^{1-\alpha_{0}}(\tilde{g}*u)+\partial_{t}^{1-\alpha_{0}}f=-\big{[}(\beta_{\alpha_{0}}*\tilde{g})*u\big{]}^{\prime}+\partial_{t}^{1-\alpha_{0}}f.

(103)

As $\tilde{g}$ is bounded (see (81)), we have $|\beta_{\alpha_{0}}*\tilde{g}|\rightarrow 0$ as $t\rightarrow 0^{+}$ such that (104) could be further rewritten as a second-kind Volterra integral equation

\displaystyle u=-(\beta_{\alpha_{0}}*\tilde{g})^{\prime}*u+\partial_{t}^{1-\alpha_{0}}f.

(104)

By $\tilde{g}(0)=0$ and (82), we have

\displaystyle|(\beta_{\alpha_{0}}*\tilde{g})^{\prime}|=|\beta_{\alpha_{0}}*\tilde{g}^{\prime}|\leq Q\beta_{\alpha_{0}}*t^{-\alpha_{0}-\varepsilon}\leq Qt^{-\varepsilon},

(105)

which means that $(\beta_{\alpha_{0}}*\tilde{g})^{\prime}\in L^{1}(0,T)$ . Furthermore, for $f\in W^{1,1}(0,T)$ , we have

\displaystyle\partial_{t}^{1-\alpha_{0}}f=(\beta_{\alpha_{0}}*f)^{\prime}=\beta_{\alpha_{0}}f(0)+\beta_{\alpha_{0}}*f^{\prime}\in L^{1}(0,T).

(106)

Thus, by classical results on the second-kind Volterra integral equation, see e.g. [21, Theorem 2.3.5], model (104) admits a unique solution in $L^{1}(0,T)$ . As the convolution of $\beta_{1-\alpha_{0}}$ and (104) leads to (103) and thus (101), the original model (101) has an $L^{1}$ solution. The uniqueness of the $L^{1}$ solution of (101) follows from that of (104).

To derive the first stability estimate, we multiply (104) by $e^{-\lambda t}$ for some $\lambda>0$ to get

\displaystyle e^{-\lambda t}u=-[e^{-\lambda t}(\beta_{\alpha_{0}}*\tilde{g})^{\prime}]*[e^{-\lambda t}u]+e^{-\lambda t}\partial_{t}^{1-\alpha_{0}}f.

Apply the $L^{1}$ norm on both sides of this equation and employ (105)–(106) and the Young’s convolution inequality to get

	$\displaystyle\\|e^{-\lambda t}u\\|_{L^{1}(0,T)}$	$\displaystyle\leq Q\\|e^{-\lambda t}t^{-\varepsilon}\\|_{L^{1}(0,T)}\\|e^{-\lambda t}u\\|_{L^{1}(0,T)}+Q\\|f\\|_{W^{1,1}(0,T)}$
		$\displaystyle\leq Q\lambda^{\varepsilon-1}\\|e^{-\lambda t}u\\|_{L^{1}(0,T)}+Q\\|f\\|_{W^{1,1}(0,T)}$		(107)

where we use a similar estimate as (31) to bound $\|e^{-\lambda t}t^{-\varepsilon}\|_{L^{1}(0,T)}$ . Then we choose $\lambda$ large enough to get the first stability result.

To obtain the second estimate of this theorem, (104), (105) and (106) imply

|u|\leq QI_{t}^{1-\varepsilon}|u|+\beta_{\alpha_{0}}|f(0)|+\beta_{\alpha_{0}}*|f^{\prime}|.

We apply the Young’s convolution inequality with $\frac{1}{\frac{1}{1-\alpha_{0}+\sigma}}+\frac{1}{\frac{1}{\alpha_{0}-\sigma}}=1$ for $0<\sigma\ll\alpha_{0}$ to get

\|\beta_{\alpha_{0}}*|f^{\prime}|\|_{L^{\infty}(0,t)}\leq Qt^{\sigma}\|f^{\prime}\|_{L^{\frac{1}{\alpha_{0}-\sigma}}(0,T)}.

Combine the above two equations leads to

|u|\leq QI_{t}^{1-\varepsilon}|u|+\beta_{\alpha_{0}}|f(0)|+Q\|f^{\prime}\|_{L^{\frac{1}{\alpha_{0}-\sigma}}(0,T)}.

Then an application of the weakly singular Gronwall inequality, see e.g. [22, Theorem 4.2], leads to the second estimate of this theorem and thus completes the proof. ∎

6.2 The case $\alpha_{0}=0$

We consider the special case $\alpha_{0}=0$ . If $\alpha_{0}=0$ , then $\beta_{1-\alpha_{0}}=1$ such that (102) becomes

\displaystyle\int_{0}^{t}u(s)ds=-\tilde{g}*u+f.

Differentiate this equation and use the estimate (81) lead to

\displaystyle u=-\tilde{g}^{\prime}*u+f^{\prime}.

(108)

Theorem 11.

Suppose $f\in W^{1,1}(0,T)$ , $\alpha_{0}=0$ . Then if $f(0)=0$ , the integral equation (101) admits a unique solution in $L^{1}(0,T)$ such that

\|u\|_{L^{1}(0,T)}\leq Q\|f\|_{W^{1,1}(0,T)}.

If further $|f^{\prime}|\leq L_{f}$ for $t\in[0,T]$ for some constant $L_{f}>0$ , then

|u|\leq QL_{f},~{}~{}t\in[0,T].

Proof.

By (82), $\tilde{g}^{\prime}\in L^{1}(0,T)$ such that we apply similar and simpler estimates as (101)–(107) to reach that (108) admits a unique $L^{1}$ solution with the estimate

\|u\|_{L^{1}(0,T)}\leq Q\|f^{\prime}\|_{L^{1}(0,T)}.

Then we integrate (108) to obtain

	$\displaystyle\int_{0}^{t}u(s)ds$	$\displaystyle=-\int_{0}^{t}\tilde{g}^{\prime}*uds+\int_{0}^{t}f^{\prime}(s)ds$
		$\displaystyle=-\int_{0}^{t}(\tilde{g}u)^{\prime}(s)ds+\int_{0}^{t}f^{\prime}(s)ds=\tilde{g}u+f-f(0).$

Thus, the condition $f(0)=0$ implies that the original problem (101) has an $L^{1}$ solution. The uniqueness follows from that of (108). The second estimate follows immediately from the weakly singular Gronwall inequality. ∎

6.3 The case $\alpha_{0}=1$

For this case, we further assume $\alpha^{\prime}(0)\neq 0$ to simplify the derivations and highlight the main ideas. We apply the idea of the perturbation method to give a different splitting of $k(t)$ from (80) as follows

k(t)=\lim_{t\rightarrow 0^{+}}k(t)+\bar{g}.

Direct calculations show that

\displaystyle\lim_{t\rightarrow 0^{+}}k(t)=\lim_{t\rightarrow 0^{+}}\frac{t^{-\alpha(t)}}{\Gamma(1-\alpha(t))}=\lim_{t\rightarrow 0^{+}}\frac{1}{\Gamma(2-\alpha(t))}\frac{1-\alpha(t)}{t^{\alpha(t)}}.

(109)

As $\lim_{t\rightarrow 0^{+}}|(1-\alpha(t))\ln t|\leq\lim_{t\rightarrow 0^{+}}|Qt\ln t|=0$ , we have

\lim_{t\rightarrow 0^{+}}t^{\alpha(t)-1}=\lim_{t\rightarrow 0^{+}}e^{(\alpha(t)-1)\ln t}=1

such that

\displaystyle\lim_{t\rightarrow 0^{+}}\frac{1-\alpha(t)}{t^{\alpha(t)}}=\lim_{t\rightarrow 0^{+}}\frac{-\alpha^{\prime}(t)}{t^{\alpha(t)}(\alpha^{\prime}(t)\ln t+\frac{\alpha(t)}{t})}=-\alpha^{\prime}(0).

(110)

Combine the above three estimates to get

k(t)=-\alpha^{\prime}(0)+\bar{g},~{}~{}\bar{g}:=k(t)+\alpha^{\prime}(0)\text{ such that }\bar{g}(0)=0.

We thus rewrite (101) as

\displaystyle-\alpha^{\prime}(0)\int_{0}^{t}u(s)ds=-\bar{g}*u+f.

By (110), $\bar{g}$ is bounded. Then we apply the expression of $k$ in (109) to evaluate $\bar{g}^{\prime}=k^{\prime}$ as

\displaystyle\bar{g}^{\prime}=\Big{(}\frac{1}{\Gamma(2-\alpha(t))}\Big{)}^{\prime}\frac{1-\alpha(t)}{t^{\alpha(t)}}+\frac{1}{\Gamma(2-\alpha(t))}\frac{-\alpha^{\prime}(t)-(1-\alpha(t))(\alpha^{\prime}(t)\ln t+\frac{\alpha(t)}{t})}{t^{\alpha(t)}}.

By (110), the first right-hand side term is bounded. For the second right-hand side term, we rewrite the numerator as

-\alpha^{\prime}(t)(1-\alpha(t))(1+\ln t)+\alpha(t)(-\alpha^{\prime}(t)-\frac{1-\alpha(t)}{t}).

By (110), we have

\Big{|}\frac{-\alpha^{\prime}(t)(1-\alpha(t))(1+\ln t)}{t^{\alpha(t)}}\Big{|}\leq Q(1+|\ln t|),

and direct calculations yield

\displaystyle\Big{|}\frac{-\alpha^{\prime}(t)-\frac{1-\alpha(t)}{t}}{t^{\alpha(t)}}\Big{|}=\Big{|}\frac{-t\alpha^{\prime}(t)-(1-\alpha(t))}{t^{1+\alpha(t)}}\Big{|}=\Big{|}\frac{\int_{0}^{t}\int_{s}^{t}-\alpha^{\prime\prime}(y)dyds}{t^{1+\alpha(t)}}\Big{|}\leq Q\frac{t^{2}}{t^{1+\alpha(t)}}\leq Q.

Combine the above four estimates to get

|\bar{g}^{\prime}|\leq Q(1+|\ln t|).

Thus, we follow exactly the same analysis procedure as that in Section 6.2 to reach the same conclusions as Theorem 11 for the case $\alpha_{0}=1$ .

6.4 Comments on the restriction

From the above analysis, we find that for either $\alpha_{0}$ or $\alpha_{1}$ , the restriction $f(0)=0$ is required to ensure the well-posedness, which is not needed for the case that $0<\alpha_{0}<1$ . The inherent reason is that for either $\alpha_{0}=0$ or $\alpha_{0}=1$ , the kernel $k$ in the integral equation (101) is indeed a non-singular kernel. Specifically, for $\alpha_{0}=0$ we could apply

\lim_{t\rightarrow 0^{+}}|-\alpha(t)\ln t|\leq\lim_{t\rightarrow 0^{+}}|Qt\ln t|=0

to get $\lim_{t\rightarrow 0^{+}}k(t)=1$ , and for $\alpha_{0}=1$ with $\alpha^{\prime}(0)\neq 0$ , (110) implies $\lim_{t\rightarrow 0^{+}}k(t)=-\alpha^{\prime}(0)$ . As for the case of non-singular kernels, the solutions are usually bounded under smooth data (cf. Theorem 11), one could pass the limit $t\rightarrow 0^{+}$ in the integral equation (101) to find that $f(0)$ needs to be $0$ to ensure the consistency.

Restriction for subdiffusion (9) with $\alpha_{0}=1$

The above observation could also be extended for the variable-exponent subdiffusion model (9) with $\alpha_{0}=1$ . By the estimate (110) we have $\lim_{t\rightarrow 0^{+}}k(t)=-\alpha^{\prime}(0)$ . If $\alpha^{\prime}(0)\neq 0$ , the kernel $k$ is a non-singular kernel. Thus when we pass the limit $t\rightarrow 0^{+}$ on both sides of (9), its well-posedness may require the condition

-\Delta u(0)=f(0),

if $u(\bm{x},t)$ is an absolutely continuous function for each $x\in\Omega$ . In fact, such condition has been pointed out in, e.g. [10, 46] for nonlocal-in-time diffusion models with non-singular kernels, and what we did above is showing that the kernel $k(t)$ is such a non-singular kernel when $\alpha_{0}=1$ and $\alpha^{\prime}(0)\neq 0$ .

Conflict of interest statement
On behalf of all authors, the corresponding author states that there is no conflict of interest.

Data availability statement
No datasets were generated or analyzed during the current study.

Acknowledgments
This work was partially supported by the National Natural Science Foundation of China (No. 12301555), the National Key R&D Program of China (No. 2023YFA1008903), and the Taishan Scholars Program of Shandong Province (No. tsqn202306083).

References

[1] R. Adams and J. Fournier, Sobolev Spaces, Elsevier, San Diego, 2003.
[2] G. Acosta, J. Borthagaray, O. Bruno and M. Maas, Regularity theory and high order numerical methods for the (1D)-fractional Laplacian. Math. Comp., 87 (2018),1821–1857.
[3] G. Akrivis, B. Li and C. Lubich, Combining maximal regularity and energy estimates for time discretizations of quasilinear parabolic equations. Math. Comp., 86 (2017), 1527–1552.
[4] L. Banjai and C. Makridakis, A posteriori error analysis for approximations of time-fractional subdiffusion problems. Math. Comp., 91 (2022), 1711–1737.
[5] H. Brunner, Volterra Integral Equations. Cambridge Monographs on Applied and Computational Mathematics, vol. 30. Cambridge: Cambridge University Press, 2017.
[6] X. Chen, Z. Chen and J. Wang, Heat kernel for nonlocal operators with variable-order. Stoch. Proc. Appl., 130 (2020), 3574–3647.
[7] E. Cuesta, M. Kirane, A. Alsaedi and B. Ahmad, On the sub-diffusion fractional initial value problem with time variable order. Adv. Nonlinear Anal., 10 (2021), 1301–1315.
[8] M. D’Elia, Q. Du, C. Glusa, M. Gunzburger, X. Tian and Z. Zhou, Numerical methods for nonlocal and fractional models. Acta Numer., 29 (2020), 1–124.
[9] M. D’Elia and C. Glusa, A fractional model for anomalous diffusion with increased variability: Analysis, algorithms and applications to interface problems. Numer. Methods Partial Differ. Eq., 38 (2022), 2084–2103.
[10] K. Diethelm, R. Garrappa, A. Giusti and M. Stynes, Why fractional derivatives with nonsingular kernels should not be used. Fract. Calc. Appl. Anal., 23 (2020), 610–634.
[11] Q. Du, Nonlocal Modeling, Analysis, and Computation, SIAM, Philadelphia, 2019.
[12] Q. Du, M. Gunzburger, R. Lehoucq and K. Zhou, Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev., 54 (2012), 667–696.
[13] V. Ervin, Regularity of the solution to fractional diffusion, advection, reaction equations in weighted Sobolev spaces. J. Differ. Equ. 278 (2021), 294–325.
[14] V. Ervin and J. Roop, Variational formulation for the stationary fractional advection dispersion equation. Numer. Meth. PDEs, 22 (2006), 558–576.
[15] L. Evans, Partial Differential Equations, Graduate Studies in Mathematics, V 19, American Mathematical Society, Rhode Island, 1998.
[16] R. Garrappa and A. Giusti, A computational approach to exponential-type variable-order fractional differential equations. J. Sci. Comput., 96 (2023), 63.
[17] Y. Giga, Q. Liu and H. Mitake, On a discrete scheme for time fractional fully nonlinear evolution equations. Asymptot. Anal., 120 (2020), 151–162.
[18] Y. Giga, H. Mitake and S. Sato, On the equivalence of viscosity solutions and distributional solutions for the time-fractional diffusion equation. J. Differ. Equ., 316 (2022), 364–386.
[19] R. Gorenflo and S. Vessella, Abel Integral Equations. Analysis and Applications. Springer-Verlag, Berlin, 1991.
[20] R. Gorenflo, A. Kilbas, F. Mainardi and S. Rogosin, Mittag-Leffler Functions, Related Topics and Applications. Springer, New York, 2014.
[21] G. Gripenberg, S. Londen and O. Staffans, Volterra Integral and Functional Equations, in: Encyclopedia Math. Appl., vol. 34, Cambridge University, Cambridge, 1990.
[22] B. Jin, Fractional differential equations–an approach via fractional derivatives, Appl. Math. Sci. 206, Springer, Cham, 2021.
[23] B. Jin and Y. Kian, Recovery of a distributed order fractional derivative in an unknown medium. Commun. Math. Sci., 21 (2023), 1791–1813.
[24] B. Jin, R. Lazarov, J. Pasciak and Z. Zhou, Error analysis of a finite element method for the space-fractional parabolic equation. SIAM J. Numer. Anal., 52 (2014), 2272–2294.
[25] Y. Kian, M. Slodička, É. Soccorsi and K. Bockstal, On time-fractional partial differential equations of time-dependent piecewise constant order. arXiv:2402.03482.
[26] Y. Kian, E. Soccorsi and M. Yamamoto, On time-fractional diffusion equations with space-dependent variable order, Ann. Henri Poincaré, 19 (2018), 3855–3881.
[27] Y. Kian, Z. Li, Y. Liu and M. Yamamoto, The uniqueness of inverse problems for a fractional equation with a single measurement. Math. Ann., 380 (2021), 1465–1495.
[28] N. Kopteva, Error analysis of an L2-type method on graded meshes for a fractional-order parabolic problem. Math. Comp., 90 (2021), 19–40.
[29] A. Kubica, K. Ryszewska, M. Yamamoto, Time-fractional differential equations, Springer Briefs in Mathematics. Springer Nature, Singapore, 2020.
[30] A. Kubica, K. Ryszewska and R. Zacher, Hölder continuity of weak solutions to evolution equations with distributed order fractional time derivative. Math. Ann., (2024) https://doi.org/10.1007/s00208-024-02806-y
[31] K. Le and M. Stynes, An $\alpha$ -robust semidiscrete finite element method for a Fokker-Planck initial-boundary value problem with variable-order fractional time derivative. J. Sci. Comput., 86 (2021), 22.
[32] D. Li, J. Zhang and Z. Zhang, Unconditionally optimal error estimates of a linearized Galerkin method for nonlinear time fractional reaction-subdiffusion equations, J. Sci. Comput., 76 (2018), 848–866.
[33] H. Liang and M. Stynes, A general collocation analysis for weakly singular Volterra integral equations with variable exponent. IMA J. Numer. Anal., 2023. (online).
[34] H. Liao, T. Tang and T. Zhou, A second-order and nonuniform time-stepping maximum-principle preserving scheme for time-fractional Allen-Cahn equations. J. Comput. Phys., 414 (2020), 109473.
[35] C. Lin and G. Nakamura, Classical unique continuation property for multi-term time-fractional evolution equations. Math. Ann., 385 (2023), 551–574.
[36] C. Lorenzo and T. Hartley, Variable order and distributed order fractional operators, Nonlinear Dyn., 29 (2002), 57–98.
[37] C. Lubich, Convolution quadrature and discretized operational calculus. I and II, Numer. Math., 52 (1988) 129–145 and 413–425.
[38] Y. Luchko, Initial-boundary-value problems for the one-dimensional time-fractional diffusion equation. Fract. Calc. Appl. Anal., 15 (2012), 141–160.
[39] W. McLean and V. Thomée, Numerical solution of an evolution equation with a positive-type memory term. J. Austral. Math. Soc. Ser. B, 35 (1993), 23–70.
[40] K. Mustapha and W. McLean, Discontinuous Galerkin method for an evolution equation with a memory term of positive type. Math. Comp., 78 (2009), 1975–1995.
[41] G. Pang, P. Perdikaris, W. Cai and G. Karniadakis, Discovering variable fractional orders of advection-dispersion equations from field data using multi-fidelity Bayesian optimization. J. Comput. Phys., 348 (2017), 694–714.
[42] J. Shi and M. Chen, High-order BDF convolution quadrature for subdiffusion models with a singular source term. SIAM J. Numer. Anal., 61 (2023), 2559–2579.
[43] K. Sakamoto and M. Yamamoto, Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems, J. Math. Anal. Appl., 382 (2011), 426–447.
[44] F. Song and G. Karniadakis, Variable-order fractional models for wall-bounded turbulent flows. Entropy, 23 (2021), 782.
[45] M. Stynes, E. O’Riordan, and J. Gracia, Error analysis of a finite difference method on graded mesh for a time-fractional diffusion equation, SIAM J. Numer. Anal., 55 (2017), 1057–1079.
[46] M. Stynes, Fractional-order derivatives defined by continuous kernels are too restrictive. Appl. Math. Lett., 85 (2018), 22–26.
[47] H. Sun, Y. Zhang, W. Chen and D. Reeves, Use of a variable-index fractional-derivative model to capture transient dispersion in heterogeneous media, J. Contam. Hydrol., 157 (2014) 47–58.
[48] H. Sun, W. Chen and Y. Chen, Variable-order fractional differential operators in anomalous diffusion modeling. Physica A, 388 (2009), 4586–4592.
[49] H. Sun, A. Chang, Y. Zhang and W. Chen, A review on variable-order fractional differential equations: mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal., 22 (2019), 27–59.
[50] V. Thomée, Galerkin Finite Element Methods for Parabolic Problems, Lecture Notes in Mathematics 1054, Springer-Verlag, New York, 1984.
[51] S. Umarov and S. Steinberg, Variable order differential equations with piecewise constant order-function and diffusion with changing modes. Z. Anal. Anwend., 28 (2009), 131–150.
[52] Y. Wu and Y. Zhang, Variable-order fractional Laplacian and its accurate and efficient computations with meshfree methods. arXiv:2402.02284.
[53] B. Yu, X. Zheng, P. Zhang and L. Zhang, Computing solution landscape of nonlinear space-fractional problems via fast approximation algorithm. J. Comput. Phys., 468 (2022), 111513.
[54] R. Zacher, A De Giorgi-Nash type theorem for time fractional diffusion equations. Math. Ann., 356 (2013), 99–146.
[55] R. Zacher, Time fractional diffusion equations: solution concepts, regularity, and long-time behavior. Handbook of fractional calculus with applications, Vol. 2, 159–179, De Gruyter, Berlin, 2019.
[56] F. Zeng, Z. Zhang and G. Karniadakis, A generalized spectral collocation method with tunable accuracy for variable-order fractional differential equations, SIAM J. Sci. Comput., 37 (2015), A2710–A2732.
[57] Z. Zhang and Z. Zhou, Backward diffusion-wave problem: Stability, regularization, and approximation. SIAM J. Sci. Comput., 44 (2022), A3183–A3216.
[58] T. Zhao, Z. Mao and G. Karniadakis, Multi-domain spectral collocation method for variable-order nonlinear fractional differential equations. Comput. Meth. Appl. Mech. Engrg., 348 (2019), 377–395.
[59] X. Zheng, Approximate inversion for Abel integral operators of variable exponent and applications to fractional Cauchy problems. Fract. Calc. Appl. Anal., 25 (2022), 1585–1603.
[60] X. Zheng, Y. Li and W. Qiu, Local modification of subdiffusion by initial Fickian diffusion: Multiscale modeling, analysis and computation. arXiv:2401.16885.
[61] X. Zheng and H. Wang, An optimal-order numerical approximation to variable-order space-fractional diffusion equations on uniform or graded meshes. SIAM J. Numer. Anal., 58 (2020), 330–352.
[62] X. Zheng and H. Wang, An error estimate of a numerical approximation to a hidden-memory variable-order space-time fractional diffusion equation, SIAM J. Numer. Anal., 58 (2020), 2492–2514.

	$\displaystyle c_{1}\\|u\\|^{2}_{H^{\mu}(\Omega)}\leq(-1)^{\sigma}(\partial_{x}^{\mu}u,\hat{\partial}_{x}^{\mu}u)\leq c_{2}\\|u\\|^{2}_{H^{\mu}(\Omega)},$
	$\displaystyle~{}~{}c_{3}\\|\partial_{x}^{\mu}u\\|_{L^{2}(\Omega)}\leq\\|u\\|_{H^{\mu}(\Omega)}\leq c_{4}\\|\partial_{x}^{\mu}u\\|_{L^{2}(\Omega)},$		(2)
	$\displaystyle~{}~{}c_{3}\\|\hat{\partial}_{x}^{\mu}u\\|_{L^{2}(\Omega)}\leq\\|u\\|_{H^{\mu}(\Omega)}\leq c_{4}\\|\hat{\partial}_{x}^{\mu}u\\|_{L^{2}(\Omega)},$

	$\displaystyle\Big{\|}\partial_{t}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle=\Big{\|}(tz)^{\alpha_{0}-\alpha(tz)}z\Big{(}-\alpha^{\prime}(tz)\ln(tz)+\frac{\alpha_{0}-\alpha(tz)}{tz}\Big{)}\Big{\|}$
		$\displaystyle\leq Qz\big{(}\|\ln(tz)\|+1\big{)},$
	$\displaystyle\Big{\|}\partial_{t}^{2}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle=\Big{\|}\big{[}\partial_{t}(tz)^{\alpha_{0}-\alpha(tz)}\big{]}z\Big{(}-\alpha^{\prime}(tz)\ln(tz)+\frac{\alpha_{0}-\alpha(tz)}{tz}\Big{)}$
		$\displaystyle\quad+(tz)^{\alpha_{0}-\alpha(tz)}z^{2}\Big{(}-\alpha^{\prime\prime}(tz)\ln(tz)-2\frac{\alpha^{\prime}(tz)}{tz}-\frac{\alpha_{0}-\alpha(tz)}{(tz)^{2}}\Big{)}\Big{\|}$
		$\displaystyle\leq Qz^{2}\big{(}\|\ln(tz)\|+1\big{)}^{2}+z^{2}(\|\ln(tz)\|+\frac{1}{tz})\leq Q\frac{z^{2}}{tz}=Q\frac{z}{t},$
	$\displaystyle\Big{\|}\partial_{t}^{3}(tz)^{\alpha_{0}-\alpha(tz)}\Big{\|}$	$\displaystyle\leq\frac{Q}{t^{2}}~{}(\text{We omit the calculations here}).$

$\displaystyle\|g^{\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}$
	$\displaystyle\leq Q\int_{0}^{1}z\big{(}\|\ln(tz)\|+1\big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz$
	$\displaystyle\leq Q\big{(}\|\ln t\|+1\big{)}\int_{0}^{1}z\frac{\|\ln t\|+\|\ln z\|+1}{\|\ln t\|+1}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\leq Q\big{(}\|\ln t\|+1\big{)},$	(6)
$\displaystyle\|g^{\prime\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}^{2}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}\leq\frac{Q}{t},$	(7)
$\displaystyle\|g^{\prime\prime\prime}\|$	$\displaystyle=\Big{\|}\int_{0}^{1}\partial_{t}^{3}\Big{(}\frac{(tz)^{\alpha_{0}-\alpha(tz)}}{\Gamma(\alpha_{0})\Gamma(1-\alpha(tz))}\Big{)}(1-z)^{\alpha_{0}-1}z^{-\alpha_{0}}dz\Big{\|}\leq\frac{Q}{t^{2}}.$	(8)

	$\displaystyle\\|\mathcal{R}(t-s)\\|$	$\displaystyle\leq Q\int_{\Gamma_{\theta}}\|z\|^{\alpha_{0}-\varepsilon}\\|(z^{\alpha_{0}}-\Delta)^{-1}\\|\|e^{z(t-s)}\|\|dz\|$
		$\displaystyle\leq Q\int_{\Gamma_{\theta}}\|z\|^{\alpha_{0}-\varepsilon}\|z\|^{-\alpha_{0}}\|e^{z(t-s)}\|\|dz\|\leq\frac{Q}{(t-s)^{1-\varepsilon}}.$		(22)

	$\displaystyle\|\beta_{1-\varepsilon}*g^{\prime}\|$	$\displaystyle\leq Qt^{1-\varepsilon}\int_{0}^{1}\frac{(1-z)^{-\varepsilon}}{\Gamma(1-\varepsilon)}(1+\|\ln(tz)\|)dz$
		$\displaystyle\leq Qt^{1-\varepsilon}\int_{0}^{1}(1-z)^{-\varepsilon}\frac{(tz)^{\varepsilon}(1+\|\ln(tz)\|)}{(tz)^{\varepsilon}}dz\leq Qt^{1-2\varepsilon},$		(26)

Two methods addressing variable-exponent fractional initial and boundary value problems and Abel integral equation

Abstract

keywords:

pacs:

1 Introduction

2 Preliminaries

2.1 Notations

2.2 A generalized identity function

3 Convolution method

3.1 A transformed model

3.2 Well-posedness of transformed model

Theorem 1.

Proof.

3.3 Well-posedness of original model

Theorem 2.

Proof.

3.4 Solution regularity

Theorem 3.

Remark 1.

Proof.

Theorem 4.

Proof.

3.5 An inverse problem

Theorem 5.

Proof.

4 Numerical approximation

4.1 A numerically-feasible formulation

4.2 Semi-discrete scheme and error estimate

Theorem 6.

Proof.

4.3 Fully-discrete scheme and error estimate

Theorem 7.

Proof.

4.4 Numerical experiments

4.4.1 Initial singularity of solutions

4.4.2 Numerical accuracy

5 Perturbation method

5.1 Motivation

5.2 Idea of the method

5.3 Space-fractional problem with variable exponent

Lemma 1.

Proof.

Theorem 8.

5.4 Distributed variable-exponent model

Theorem 9.

Proof.

6 Application to Abel integral equation

6.1 The case 0<α0<10<\alpha_{0}<1

Theorem 10.

Proof.

6.2 The case α0=0\alpha_{0}=0

Theorem 11.

Proof.

6.3 The case α0=1\alpha_{0}=1

6.4 Comments on the restriction

References

6.1 The case $0<\alpha_{0}<1$

6.2 The case $\alpha_{0}=0$

6.3 The case $\alpha_{0}=1$