Two-neutrino double electron capture of ¹²⁴Xe
in the first LUX-ZEPLIN exposure

The LUX-ZEPLIN (LZ) Collaboration
J. Aalbers^1,2, D.S. Akerib^1,2, A.K. Al Musalhi^3,¹¹1aiham.almusalhi@ucl.ac.uk, F. Alder³, C.S. Amarasinghe^4,5, A. Ames^1,2, T.J. Anderson^1,2, N. Angelides⁶, H.M. Araújo⁶, J.E. Armstrong⁷, M. Arthurs^1,2, A. Baker⁶, S. Balashov⁸, J. Bang⁹, J.W. Bargemann⁴, E.E. Barillier^10,5, K. Beattie¹¹, A. Bhatti⁷, A. Biekert^11,12, T.P. Biesiadzinski^1,2, H.J. Birch^10,5, E. Bishop¹³, G.M. Blockinger¹⁴, B. Boxer¹⁵, C.A.J. Brew⁸, P. Brás¹⁶, S. Burdin¹⁷, M. Buuck^1,2, M.C. Carmona-Benitez¹⁸, M. Carter¹⁷, A. Chawla¹⁹, H. Chen¹¹, Y.T. Chin¹⁸, N.I. Chott²⁰, M.V. Converse²¹, R. Coronel^1,2, A. Cottle³, G. Cox²², D. Curran²², C.E. Dahl^24,23, A. David³, J. Delgaudio²², S. Dey²⁵, L. de Viveiros¹⁸, L. Di Felice⁶, C. Ding⁹, J.E.Y. Dobson³, E. Druszkiewicz²¹, S. Dubey⁹, S.R. Eriksen²⁶, A. Fan^1,2, N.M. Fearon²⁵, N. Fieldhouse²⁵, S. Fiorucci¹¹, H. Flaecher²⁶, E.D. Fraser¹⁷, T.M.A. Fruth²⁷, R.J. Gaitskell⁹, A. Geffre²², J. Genovesi²⁰, C. Ghag³, R. Gibbons^11,12, S. Gokhale²⁸, J. Green²⁵, M.G.D.van der Grinten⁸, J.J. Haiston²⁰, C.R. Hall⁷, S. Han^1,2, E. Hartigan-O’Connor⁹, S.J. Haselschwardt¹¹, M.A. Hernandez^10,5, S.A. Hertel²⁹, G. Heuermann⁵, G.J. Homenides³⁰, M. Horn²², D.Q. Huang³¹, D. Hunt²⁵, E. Jacquet⁶, R.S. James^3,³³3Also at The University of Melbourne, School of Physics, Melbourne, VIC 3010, Australia, J. Johnson¹⁵, A.C. Kaboth¹⁹, A.C. Kamaha³¹, M. Kannichankandy¹⁴, D. Khaitan²¹, A. Khazov⁸, I. Khurana³, J. Kim⁴, Y.D. Kim³², J. Kingston¹⁵, R. Kirk⁹, D. Kodroff^18,11, L. Korley⁵, E.V. Korolkova³³, H. Kraus²⁵, S. Kravitz³⁴, L. Kreczko²⁶, V.A. Kudryavtsev³³, D.S. Leonard³², K.T. Lesko¹¹, C. Levy¹⁴, J. Lin^11,12, A. Lindote^16,²²2alex@coimbra.lip.pt, W.H. Lippincott⁴, M.I. Lopes¹⁶, W. Lorenzon⁵, C. Lu⁹, S. Luitz^1,2, P.A. Majewski⁸, A. Manalaysay¹¹, R.L. Mannino³⁵, C. Maupin²², M.E. McCarthy²¹, G. McDowell⁵, D.N. McKinsey^11,12, J. McLaughlin²³, J.B. McLaughlin³, R. McMonigle¹⁴, E. Mizrachi^35,7, A. Monte⁴, M.E. Monzani^1,2,36, E. Morrison²⁰, B.J. Mount³⁷, M. Murdy²⁹, A.St.J. Murphy¹³, A. Naylor³³, H.N. Nelson⁴, F. Neves¹⁶, A. Nguyen¹³, C.L. O’Brien³⁴, I. Olcina^11,12, K.C. Oliver-Mallory⁶, J. Orpwood³³, K.Y Oyulmaz¹³, K.J. Palladino²⁵, J. Palmer¹⁹, N.J. Pannifer²⁶, N. Parveen¹⁴, S.J. Patton¹¹, B. Penning^10,5, G. Pereira¹⁶, E. Perry³, T. Pershing³⁵, A. Piepke³⁰, Y. Qie²¹, J. Reichenbacher²⁰, C.A. Rhyne⁹, Q. Riffard¹¹, G.R.C. Rischbieter^10,5, E. Ritchey⁷, H.S. Riyat¹³, R. Rosero²⁸, T. Rushton³³, D. Rynders²², D. Santone¹⁹, A.B.M.R. Sazzad³⁰, R.W. Schnee²⁰, G. Sehr³⁴, B. Shafer⁷, S. Shaw¹³, T. Shutt^1,2, J.J. Silk⁷, C. Silva¹⁶, G. Sinev²⁰, J. Siniscalco³, R. Smith^11,12, V.N. Solovov¹⁶, P. Sorensen¹¹, J. Soria^11,12, A. Stevens^3,6, K. Stifter²⁴, B. Suerfu^11,12, T.J. Sumner⁶, M. Szydagis¹⁴, D.R. Tiedt²², M. Timalsina¹¹, Z. Tong⁶, D.R. Tovey³³, J. Tranter³³, M. Trask⁴, M. Tripathi¹⁵, A. Vacheret⁶, A.C. Vaitkus⁹, O. Valentino⁶, V. Velan¹¹, A. Wang^1,2, J.J. Wang³⁰, Y. Wang^11,12, J.R. Watson^11,12, L. Weeldreyer³⁰, T.J. Whitis⁴, K. Wild¹⁸, M. Williams⁵, W.J. Wisniewski¹, L. Wolf¹⁹, F.L.H. Wolfs²¹, S. Woodford¹⁷, D. Woodward^18,11, C.J. Wright²⁶, Q. Xia¹¹, J. Xu³⁵, Y. Xu³¹, M. Yeh²⁸, D. Yeum⁷, W. Zha¹⁸, E.A. Zweig³¹ ¹ SLAC National Accelerator Laboratory, Menlo Park, CA 94025-7015, USA ² Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, Stanford, CA 94305-4085 USA ³ University College London (UCL), Department of Physics and Astronomy, London WC1E 6BT, UK ⁴ University of California, Santa Barbara, Department of Physics, Santa Barbara, CA 93106-9530, USA ⁵ University of Michigan, Randall Laboratory of Physics, Ann Arbor, MI 48109-1040, USA ⁶ Imperial College London, Physics Department, Blackett Laboratory, London SW7 2AZ, UK ⁷ University of Maryland, Department of Physics, College Park, MD 20742-4111, USA ⁸ STFC Rutherford Appleton Laboratory (RAL), Didcot, OX11 0QX, UK ⁹ Brown University, Department of Physics, Providence, RI 02912-9037, USA ¹⁰ University of Zurich, Department of Physics, 8057 Zurich, Switzerland ¹¹ Lawrence Berkeley National Laboratory (LBNL), Berkeley, CA 94720-8099, USA ¹² University of California, Berkeley, Department of Physics, Berkeley, CA 94720-7300, USA ¹³ University of Edinburgh, SUPA, School of Physics and Astronomy, Edinburgh EH9 3FD, UK ¹⁴ University at Albany (SUNY), Department of Physics, Albany, NY 12222-0100, USA ¹⁵ University of California, Davis, Department of Physics, Davis, CA 95616-5270, USA ¹⁶ Laboratório de Instrumentação e Física Experimental de Partículas (LIP), University of Coimbra, P-3004 516 Coimbra, Portugal ¹⁷ University of Liverpool, Department of Physics, Liverpool L69 7ZE, UK ¹⁸ Pennsylvania State University, Department of Physics, University Park, PA 16802-6300, USA ¹⁹ Royal Holloway, University of London, Department of Physics, Egham, TW20 0EX, UK ²⁰ South Dakota School of Mines and Technology, Rapid City, SD 57701-3901, USA ²¹ University of Rochester, Department of Physics and Astronomy, Rochester, NY 14627-0171, USA ²² South Dakota Science and Technology Authority (SDSTA), Sanford Underground Research Facility, Lead, SD 57754-1700, USA ²³ Northwestern University, Department of Physics & Astronomy, Evanston, IL 60208-3112, USA ²⁴ Fermi National Accelerator Laboratory (FNAL), Batavia, IL 60510-5011, USA ²⁵ University of Oxford, Department of Physics, Oxford OX1 3RH, UK ²⁶ University of Bristol, H.H. Wills Physics Laboratory, Bristol, BS8 1TL, UK ²⁷ The University of Sydney, School of Physics, Physics Road, Camperdown, Sydney, NSW 2006, Australia ²⁸ Brookhaven National Laboratory (BNL), Upton, NY 11973-5000, USA ²⁹ University of Massachusetts, Department of Physics, Amherst, MA 01003-9337, USA ³⁰ University of Alabama, Department of Physics & Astronomy, Tuscaloosa, AL 34587-0324, USA ³¹ University of California, Los Angeles, Department of Physics & Astronomy, Los Angeles, CA 90095-1547, USA ³² IBS Center for Underground Physics (CUP), Yuseong-gu, Daejeon, Korea ³³ University of Sheffield, Department of Physics and Astronomy, Sheffield S3 7RH, UK ³⁴ University of Texas at Austin, Department of Physics, Austin, TX 78712-1192, USA ³⁵ Lawrence Livermore National Laboratory (LLNL), Livermore, CA 94550-9698, USA ³⁶ Vatican Observatory, Castel Gandolfo, V-00120, Vatican City State ³⁷ Black Hills State University, School of Natural Sciences, Spearfish, SD 57799-0002, USA

Abstract

The broad physics reach of the LUX-ZEPLIN (LZ) experiment covers rare phenomena beyond the direct detection of dark matter. We report precise measurements of the extremely rare decay of ¹²⁴Xe through the process of two-neutrino double electron capture (2 $\nu$ 2EC), utilizing a $\qty{1.39}{kg\times yr}$ isotopic exposure from the first LZ science run. A half-life of $T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=(1.09\pm 0.14_{\text{stat}}\pm 0.05_{\text{sys}})\times\qty{e22}{yr}$ is observed with a statistical significance of \qty8.3σ, in agreement with literature. First empirical measurements of the KK capture fraction relative to other K-shell modes were conducted, and demonstrate consistency with respect to recent signal models at the \qty1.4σ level.

1 Introduction

Alongside a world-leading sensitivity to keV-scale scatters from weakly interacting massive particles (WIMPs), dual-phase xenon time projection chambers (TPCs) are also capable of searching for rare phenomena beyond dark matter interactions [1, 2]. Most notably, this encompasses experimental probes for the fundamental nature of the neutrino mass such as neutrinoless double beta decay ( $0\nu\beta\beta$ ), the observation of which may indicate that neutrinos are Majorana particles [3, 4, 5, 6]. Neutrinoless double electron capture ( $0\nu$ 2EC) is an analogous process that would be associated with the proton-rich side of the binding energy parabola for even-even isobars [7, 8, 9]; $0\nu$ 2EC decays have yet to be observed, with extremely long expected half-lives in excess of \qtye29yr [10]. Models and predictions for this process may be developed through measurements of the adjacent process of two-neutrino double electron capture (2 $\nu$ 2EC) [11], which involves the absorption of two atomic electrons and the subsequent conversion of a pair of protons into neutrons, along with the simultaneous emission of two neutrinos. Measured half-lives for this decay inform the underlying nuclear matrix element $M^{(2\nu)}$ through the relation

\left(T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}\right)^{-1}=G_{2\nu}^{2\mathrm{EC}}g^{4}_{A}\left|m_{e}c^{2}M^{(2\nu)}\right|^{2},

(1)

where $g_{A}$ denotes the weak axial-vector coupling strength, $m_{e}$ is the electron mass, and the phase space factor $G_{2\nu}^{2\mathrm{EC}}$ is proportional to the reaction Q-value taken to the fifth power [12]. Thus far, 2 $\nu$ 2EC has only been observed for ¹³⁰Ba [13, 14], ⁷⁸Kr [15, 16], and ¹²⁴Xe [17, 18].

In this work, the extensive physics program of the LUX-ZEPLIN (LZ) experiment is highlighted with a precise measurement of the ¹²⁴Xe decay half-life through 2 $\nu$ 2EC. This result is extended with the first measurement of the relative capture fractions between atomic shell combinations. A brief description of the LZ experiment and its first exposure is provided in section 2. This is followed by a detailed overview of the analysis given in section 3, which covers the employed signal model, construction of the background model with an emphasis on the dominant ¹²⁵I background, and an outline of the fit procedure. Finally, results of the analysis, including the measured relative capture fractions, are discussed in section 4.

2 The LUX-ZEPLIN experiment

The LZ experiment [19, 20] is situated \qty1480m underground within the Davis Cavern at the Sanford Underground Research Facility in Lead, South Dakota. With a \qty1100m ( $\qty{4300}{\mathrm{m.w.e}}$ ) rock overburden, the flux of cosmic muons in the cavern is attenuated by a factor of \qty3e6 with respect to that at the surface [21, 22]. The detector is housed within a tank holding \qty238t of ultra-pure water for additional shielding from ambient radiation. Combined with an extensive radioassay campaign and strict cleanliness protocols in assembly, this establishes an ultra-low background environment [23].

At the core of the LZ detector is a dual-phase xenon TPC with an active volume containing \qty7t of liquid xenon (LXe). Energy depositions in the LXe generate vacuum ultraviolet scintillation photons (S1), as well as ionization electrons. The electrons drift to the liquid surface under a vertical electric field and are subsequently extracted into the gas phase by a stronger field, where they produce a secondary scintillation signal (S2). Light is detected by two arrays of 3-inch photomultiplier tubes (PMTs), with 253 at the top and 241 at the bottom. To enhance background rejection, the detector features two anti-coincidence veto systems: an optically isolated LXe skin surrounding the TPC, which is instrumented with 93 1-inch and 38 2-inch PMTs; and a near-hermetic outer detector (OD) comprised of acrylic tanks filled with gadolinium-loaded liquid scintillator, viewed by 120 8-inch PMTs in the water tank. These detectors enable the rejection of events with coincident gamma rays or neutrons.

The detector response is calibrated with a variety of dedicated sources [24]. In particular, dispersed mono-energetic sources such as ^83mKr and ^131mXe are used to correct the S1 and S2 observables for position-dependent effects; the corrected versions are denoted as S1c and S2c, and are measured in units of photons detected (phd) [25]. These quantities are combined to reconstruct the energy of an event according to

E=W\left(\frac{\mathrm{S1c}}{g_{1}}+\frac{\mathrm{S2c}}{g_{2}}\right),

(2)

where $g_{1}=\qty{0.114(2)}{phd/photon}$ and $g_{2}=\qty{47.1(11)}{phd/electron}$ respectively describe the photon detection efficiency and the effective charge gain, and $W=\qty{13.5}{eV}$ is the assumed work function [26].

Of the calibration sources deployed during the first exposure of LZ, a \qty4.5d calibration campaign partway through the run is of particular relevance to this work. This utilized neutrons generated by deuterium-deuterium (DD) fusion to characterize the nuclear recoil response of the detector [27, 28]. The deployment of neutron calibrations introduces additional transient backgrounds from activation of xenon isotopes. Treatment of these sources for the background model is detailed in section 3.2.

3 Analysis overview

The data analyzed here are from Science Run 1 (SR1), acquired between December 23rd, 2021, and May 11th, 2022. For the first LZ WIMP search (WS) result [25], a suite of data quality cuts were developed to target accidental coincidence backgrounds, which originate from false pairings of uncorrelated S1s and S2s, as well as other unique detector pathologies such as photon pileup and delayed electron emission. A number of these cuts involved the exclusion of periods with elevated detector activity, and hence posed a substantial impact on the accrued live time. For the purpose of this analysis, the contribution of such effects is not significant as the focus is at a higher energy regime, and hence only a minimal set of cuts need be applied: a fiducial volume (FV) cut to reject external backgrounds near the TPC boundaries; pulse area thresholds of $\left(\mathrm{S1c}>\qty{100}{phd}\right)$ and $\left(\mathrm{S2}>\qty{600}{phd}\right)$ to mitigate for tails of accidental backgrounds; and vetoes from the skin and OD to tackle events with multiple interaction vertices. This results in an overall exposure of \qty96.4(10) live days. The same \qty5.5(2)t FV definition was maintained as the SR1 WS analysis. Constraints on various background rates in the FV were informed by dedicated measurements from several studies [29].

3.1 Signal model

For ¹²⁴Xe, 2 $\nu$ 2EC proceeds as

{}^{124}\mathrm{Xe}+2e^{-}\longrightarrow{}^{124}\mathrm{Te}+2\nu_{e}+(\text{X-rays \& Auger electrons}),

(3)

with a reaction Q-value of $\qty{2856.73(12)}{keV}$ [30]. Most of this energy is carried away by the neutrinos, whilst the nuclear recoil energy is only $\mathcal{O}(10)\>\text{eV}$ [31], and hence the only detectable signal consists entirely of deposits from the X-rays and Auger cascade in the subsequent atomic de-excitation of the ¹²⁴Te daughter. The energy of the experimental signature is determined by the combination of atomic shells from which electrons were captured. Here we assume the same relative shell capture fractions and energies as the XENON collaboration [18]; these are summarized in table 1. All capture combinations are expected to manifest as single-scatter (SS) interactions due to the sub-millimeter reach in LXe at the energy scale of the emitted X-rays and Auger electrons.

The half-life $T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}$ is related to the activity $A_{2\nu 2\mathrm{EC}}$ by

T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=\frac{\eta N_{A}}{A_{2\nu 2\mathrm{EC}}M_{A}}\ln{2},

(4)

where $N_{A}$ is Avogadro’s constant, $M_{A}=\qty{131.293(6)}{g\per mol}$ is the molar mass of xenon [32], and $\eta$ is the isotopic abundance of ¹²⁴Xe. It is assumed that the isotopic composition of xenon in LZ is consistent with that of atmospheric xenon. At the natural ¹²⁴Xe abundance $\eta=\qty{0.0952(3)}{\%}$ [33], the isotopic exposure is $\qty{1.39}{kg\times yr}$ . Out of ${\sim}400$ decays over the course of this exposure (for $T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=\qty{1.1e22}{yr}$ [18]), $<10$ events are expected to occur from double L-shell (LL) and higher-shell electron captures. Therefore, a 20–100 keV interval was set as the region of interest (ROI) for this search; the lower bound reflects the lack of sensitivity to these modes, whereas the upper bound encapsulates the energies of flat backgrounds extending beyond the signal peaks.

Table 1: Energies and relative capture fractions for different shell combinations in the ¹²⁴Xe 2

\nu

2EC signal model, as adopted in [18]. Decay modes are labeled by the combination of shells from which electrons were captured.

Decay mode Capture fraction [%] Energy [keV]

KK 72.4 64.3

KL 20.0 36.7–37.3

KM 4.3 32.9–33.3

KN 1.0 32.3–32.4

LL 1.4 8.8–10.0

Other 0.9 $<10$

Decay mode	Capture fraction [%]	Energy [keV]
KK	72.4	64.3
KL	20.0	36.7–37.3
KM	4.3	32.9–33.3
KN	1.0	32.3–32.4
LL	1.4	8.8–10.0
Other	0.9	$<10$

3.2 Background model

The majority of backgrounds within the 20–\qty100keV 2 $\nu$ 2EC ROI, listed in table 2, exhibit flat and continuous energy spectra, enabling straightforward modeling. Furthermore, their rates in SR1 have been well-constrained by a variety of sideband studies, as reported in reference [29]. A subset of these backgrounds is comprised of unstable xenon isotopes, which were produced via cosmogenic activation during transport, as well as through neutron activation as a result of deploying neutron sources to calibrate the detector response to nuclear recoils. Aside from ¹³³Xe, which features as a beta spectrum with a shoulder starting at the \qty81.0keV gamma-ray line [34], these can deposit energies within close proximity to the secondary (KL + KM + KN) ¹²⁴Xe signal peak, denoted here as KX. Isotopes with decays involving a single electron capture, namely ¹²⁵Xe and ¹²⁷Xe, involve cascades with a total deposited energy of \qty33.2keV for K-shell captures [35]. However, these decays are accompanied by a gamma ray, which often gives rise to a multiple-scatter (MS) topology or is tagged by the veto detectors, with an efficiency of \qty78.0(50)%, and hence they are suppressed by the SS and veto cuts. Similarly, ^129mXe emits a pair of coincident \qty196.6keV and \qty39.6keV internal conversion electrons in its transitions to the ground state [36], with a very low probability of detecting the lower energy gamma ray in isolation.

Table 2: Summary of backgrounds to the ¹²⁴Xe

2\nu 2

EC measurement. Reported rate estimates are for SS events within the ROI, after the application of area thresholds, vetoes, and the FV cut. Solar neutrino and detector material backgrounds consist of a sum over all relevant sources. K-shell EC and single gamma-ray rates are for cases where the skin veto fails to tag an outgoing associated gamma ray; ¹²⁵Xe is excluded as its average rate is effectively zero in this context. Half-lives are quoted from nuclear data sheets [37, 35, 36, 34], and otherwise omitted in cases where they exceed the lifetime of the experiment, or for sources that are continually produced.

Source	ROI signature	Half-life	Average rate [mHz]

¹²⁵I	Multiple EC peaks	\qty59.4d	\qty1.75(38)e-1
¹²⁷Xe	K-shell EC (\qty33.2keV)	\qty36.3d	\qty3.98(25)e-3
^129mXe	$\gamma$ (\qty39.6keV)	\qty8.9d	\qty7.31(52)e-4
¹³³Xe	$\beta+\gamma$ (\qty81.0keV)	\qty5.2d	\qty7.36(75)e-1
¹³⁶Xe $2\nu\beta\beta$	continuous	-	\qty1.34(32)e-1
²¹²Pb	continuous	-	\qty5.70(3)e-3
²¹⁴Pb	continuous	-	\qty2.16(5)e-1
⁸⁵Kr	continuous	-	\qty3.83(92)e-2
Solar neutrinos	continuous	-	\qty2.71(7)e-2
Materials	continuous	-	\qty8.25(3)e-4

An especially problematic background is ¹²⁵I, which is produced by the neutron activation of ¹²⁴Xe according to the following steps

	$\displaystyle{}^{124}\text{Xe}+n$	$\displaystyle\longrightarrow{}^{125}\text{Xe}+\gamma,$		(5)
	$\displaystyle{}^{125}\text{Xe}+e^{-}$	$\displaystyle\mathrel{\overset{\text{\scriptsize{EC}}}{\underset{\text{\scriptsize{\qty{16.9}{h}}}}{\longrightarrow}}}{}^{125}\text{I}+\nu_{e}+\gamma+(\text{X-rays \& Auger electrons}),$		(6)

and decays to an excited state of ¹²⁵Te via electron capture as

{}^{125}\text{I}+e^{-}\mathrel{\overset{\text{\scriptsize{EC}}}{\underset{\text{\scriptsize{\qty{59.4}{d}}}}{\longrightarrow}}}{}^{125}\text{Te}+\nu_{e}+\gamma+(\text{X-rays \& Auger electrons}).

(7)

The combination of the subsequent de-excitation cascades and the \qty35.5keV nuclear transition of the ¹²⁵Te daughter generates peaks that significantly overlap with the ¹²⁴Xe signals. For instance, the K-shell capture mode of ¹²⁵I has an associated total energy of \qty67.3keV; with a measured energy resolution of \qty4.5(4)%, this peak is \qty1σ from the \qty64.3keV KK peak ¹²⁴Xe. This is similarly the case for the other ¹²⁵I decay modes, as shown in table 3.

Table 3: Energies and capture fractions for ¹²⁵I background peaks. The capture fractions are quoted from [38], and the binding energies are taken from [39, 40] with uncertainties excluded as they are of

\mathcal{O}(1)\>\text{eV}

Decay mode	Capture fraction [%]	Energy [keV]
$\gamma$ + K	$80.11\pm 0.17$	67.3 (35.5 + 31.8)
$\gamma$ + L	$15.61\pm 0.13$	40.4 (35.5 + 4.9)
$\gamma$ + M	$3.49\pm 0.07$	36.5 (35.5 + 1.0)

In SR1, ¹²⁵I was predominantly produced during the DD calibration campaign. Whilst it has a natural half-life of \qty59.4d [37], it is efficiently removed by the LZ online purification system, which employs a hot zirconium getter [19]. To quantify the removal rate during SR1, the \qty67.3keV peak associated with K-shell ECs in ¹²⁵I was selected in data immediately following the DD calibration using the \qty2σ contour of a two-dimensional Gaussian fit of the corresponding population in $(\mathrm{S1c},\mathrm{S2c})$ space. Events passing this selection along with the specified minimal set of cuts were divided into one-day bins according to their registered trigger timestamps, with the rate calculated in each bin adjusted for the experimental dead time.

The observed time profile of ¹²⁵I rates over the course of SR1 is visualized in figure 1, with a pronounced growth due to neutron activation following the DD calibrations. To model the behavior of its rate in the post-DD period, the number of ¹²⁵I nuclei at a given time, $N_{{}^{125}\mathrm{I}}(t)$ , was described by a differential equation

\frac{dN_{{}^{125}\mathrm{I}}(t)}{dt}=\lambda_{{}^{125}\mathrm{Xe}}N_{{}^{125}\mathrm{Xe}}(t)-\left(\lambda_{{}^{125}\mathrm{I}}+\lambda_{g}\right)N_{{}^{125}\mathrm{I}}(t),

(8)

in which the positive term represents the production of ¹²⁵I from the decay of ¹²⁵Xe, and the effective decay constant $\lambda_{\mathrm{eff}}=\left(\lambda_{{}^{125}\mathrm{I}}+\lambda_{g}\right)$ consists of a getter removal component $\lambda_{g}$ and a natural decay component $\lambda_{{}^{125}\mathrm{I}}$ . A fit to the post-DD exponential decay in figure 1 yields a getter removal half-life of $t_{1/2}^{g}=\qty{3.8(2)}{d}$ , which translates into an effective ¹²⁵I half-life of $t_{1/2}^{\mathrm{eff}}=\qty{3.6(2)}{d}$ with the natural decay component included. For reference, the values reported for $t_{1/2}^{g}$ by LUX and XENON1T are \qty3.7(3)d and \qty4.6(1.6)d, respectively [31, 18]. In each case, the corresponding getter removal time constant was consistent with the interval for xenon to flow through one cycle of the circulation system.

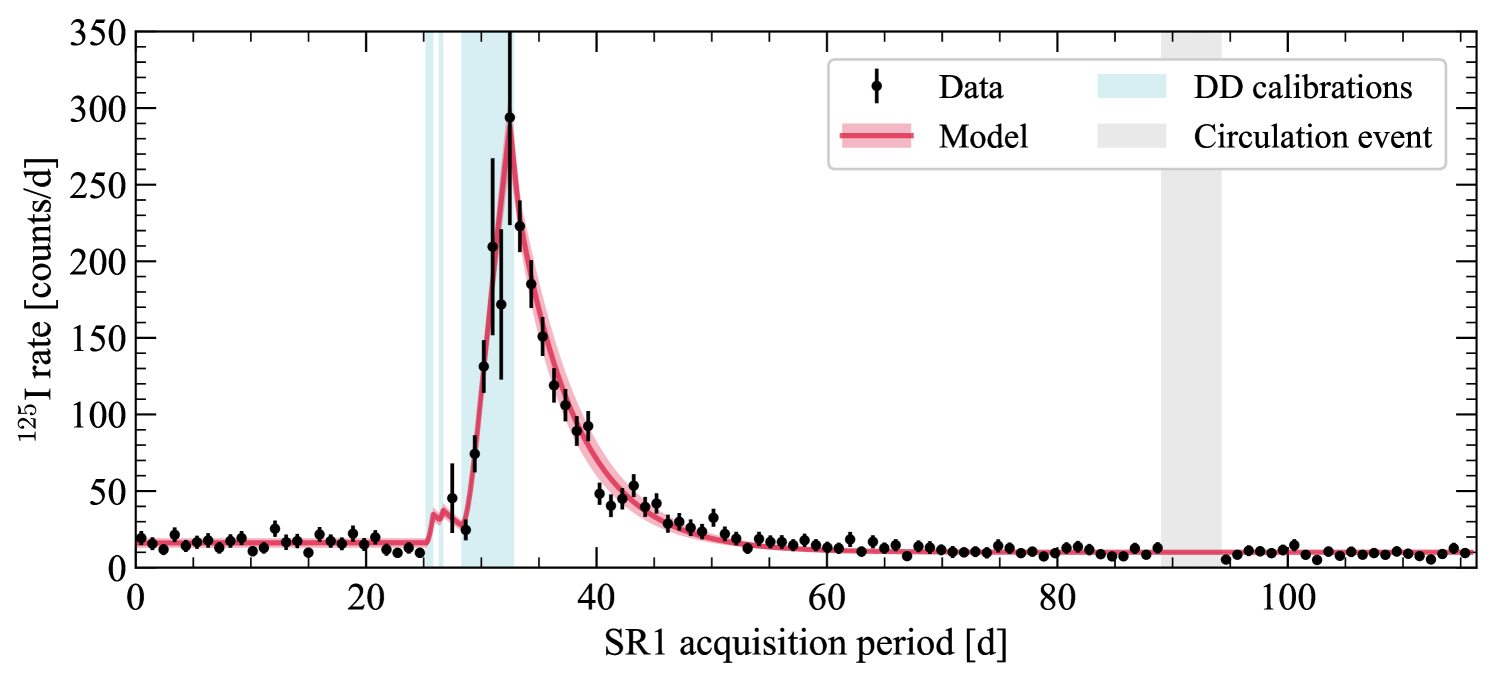
Refer to caption — Figure 1: Rate of events in the FV over SR1 for a selection dominated by ¹²⁵I. Along with skin and OD vetoes, a \qty2σ elliptical contour was applied from a two-dimensional Gaussian fit to the ¹²⁵I K-shell EC population in (S1c, S2c) space. The overlaid profile represents a combination of the neutron activation model and a fit to the post-DD decay trend. The additional intermission window beyond the DD calibration period was caused by a circulation event, over which the detector purity temporarily decreased.

In addition, the expected amount of ¹²⁵I was also constrained by an activation model. The activation rate was characterized using DD calibration data by profiling the rates of both ¹²⁵I and ¹²⁵Xe within the vicinity of the neutron conduit at the top of the TPC. This subsequently informed the predicted ¹²⁵I rate through the DD period given the measured getter removal time constant. The projected rate within the post-DD period is in very close agreement with the direct fit of the decay trend, and hence the latter is adopted for the combined model curve overlaid in figure 1.

In general, the baseline rate was expected to consist of continuous backgrounds, some contamination from the $2\nu$ KK mode of ¹²⁴Xe, and a flat rate of ¹²⁵I from thermal neutron activation. However, a shift was observed between the pre-DD and post-DD baseline rates, from \qty16.1(32)counts\perd down to \qty10.0(0.5)counts\perd. This was attributed to a residual ¹²⁵I population in the pre-DD window from activation during longer neutron calibrations performed a month prior to the start of SR1. With different circulation settings used in the physics commissioning period leading up to SR1, such as a higher flow rate through the getter, the ¹²⁵I removal efficiency was slightly lower and hence extended the pre-DD decay curve. Nevertheless, the low pre-DD ¹²⁵I rate is sufficiently well-approximated as flat over time.

3.3 Fit procedure

Since the signals and backgrounds both produce electron recoils (ERs), reconstructed energy was adopted as the main observable. Furthermore, rather than excluding a post-DD window with elevated background rates, the full exposure can be preserved by leveraging the temporal variation of the primary ¹²⁵I background, which motivates the use of calendar time as an additional observable. Given the substantial overlap in energy between ¹²⁵I and the signal, incorporating this temporal information leads to a boost in sensitivity.

Two-dimensional fits in energy and time were performed according to a binned extended maximum likelihood approach, using a likelihood function of the form

\ln{\mathcal{L}(\boldsymbol{d}|\boldsymbol{\theta},\boldsymbol{\mu},\boldsymbol{\sigma})}=\sum_{i}^{N_{E}}\sum_{j}^{N_{t}}d_{ij}\ln f_{ij}(\boldsymbol{\theta})-\nu(\boldsymbol{\theta})-\sum_{k}^{N_{c}}\frac{1}{2}\left(\frac{\theta_{k}-\mu_{k}}{\sigma_{k}}\right)^{2},

(9)

where observed counts $d_{ij}$ and expected counts $f_{ij}(\boldsymbol{\theta})$ are divided into $N_{E}$ \qty1keV energy bins and $N_{t}$ \qty1d time bins. For each of the $N_{c}$ signal plus background components, there is an associated energy PDF $p_{k}$ and time PDF $t_{k}$ , both of which are scaled by the corresponding rate parameter $\theta_{k}$ such that $f_{ij}(\boldsymbol{\theta})=\sum^{N_{c}}_{k}\theta_{k}p_{ik}t_{jk}$ . Energy spectra produced by the LZ parametric simulations chain were normalized to produce $p_{k}$ [41], whereas $t_{k}$ represents the live time distribution over calendar time scaled by rate profile of the $k$ th component, which is either constant or an exponential decay. The extended Poisson term $\nu(\boldsymbol{\theta})=\sum_{i}^{N_{E}}\sum_{j}^{N_{t}}f_{ij}(\boldsymbol{\theta})$ serves to include information from the total sample size.

To simplify the fit procedure, the SR1 dataset was split into pre-DD and post-DD subsets consisting of 23.1 and 73.3 live days each, and evaluated with a simultaneous likelihood fit. The model contains a total of 10 parameters: 6 are shared between the two likelihoods, and a pair of unique pre-DD and post-DD rates is associated with each of ¹²⁵I and ¹³³Xe as they are impacted by the DD calibrations. Rates for ²¹²Pb and detector materials were fixed as they were comparatively subdominant.

The model parameters $\boldsymbol{\theta}$ are regularized by a Gaussian constraint term, which penalizes significant deviations from the expected rates $\boldsymbol{\mu}$ as a fraction of their uncertainties $\boldsymbol{\sigma}$ . Whereas the signal term was left unconstrained, initial estimates for background rates and their constraints were derived from the results of sideband analyses [29]. In particular, tight constraints on ¹²⁵I were enabled by the activation model outlined in section 3.2. Goodness of fit is quantified in terms of the metric $\chi^{2}_{\lambda}=2\sum_{i}^{N_{E}}\sum_{j}^{N_{t}}f_{ij}(\boldsymbol{\theta})\hskip 0.85pt-\hskip 0.85ptd_{ij}\hskip 0.85pt+\hskip 0.85ptd_{ij}\ln(d_{ij}/f_{ij}(\boldsymbol{\theta}))$ , which is constructed by means of a Poisson likelihood ratio test [42].

4 Results and discussion

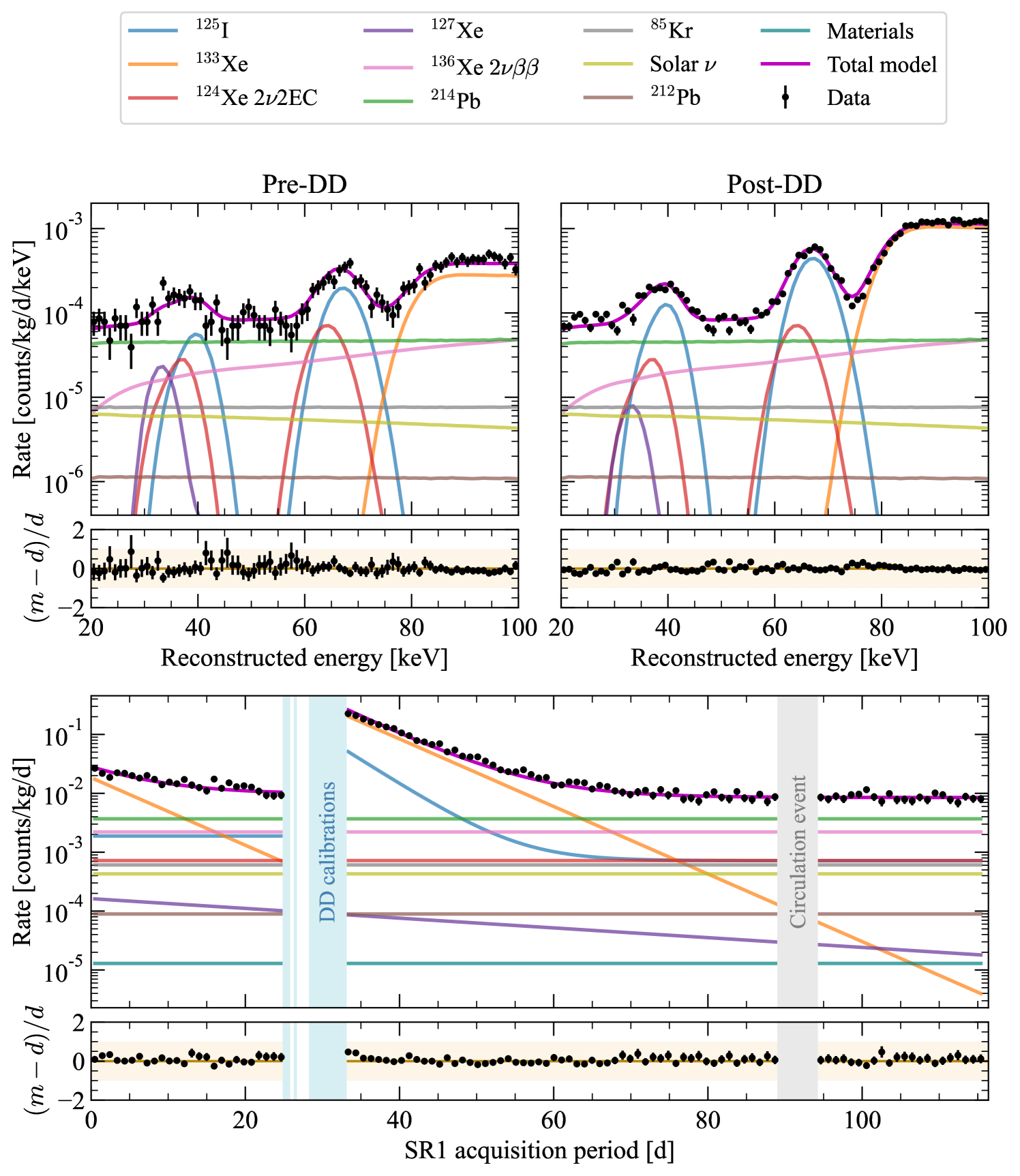
The outcome of the fit is presented in figure 2 as separate projections in energy and time, with a best-fit activity of $A_{2\nu 2\text{EC}}=\qty{0.28(4)}{counts\per\per yr}$ . Evaluation of a likelihood ratio test statistic with respect to the the background-only case yields a significance of \qty8.3σ for the presence of a 2 $\nu$ 2EC signal. The half-life inferred using equation 4 is

T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=(1.09\pm 0.14_{\text{stat}}\pm 0.05_{\text{sys}})\times\qty{e22}{yr},

(10)

which is in excellent agreement with the previously reported measurement by XENON1T at $T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=(1.1\pm 0.2_{\text{stat}}\pm 0.1_{\text{sys}})\times\qty{e22}{yr}$ [18]. A breakdown of the systematic uncertainties is given in table 4. The dominant contribution is formed by the uncertainty on the FV mass. Secondary sources of uncertainty stem from the energy reconstruction parameters $g_{1}$ and $g_{2}$ as calibrated for the WS, as well as the live time estimate.

Table 4: Summary of systematic uncertainties on the ¹²⁴Xe

2\nu 2

EC half-life, with the total calculated by summing the individual contributions in quadrature.

Contribution Uncertainty [\qtye22yr] Relative uncertainty [%]

Fiducial mass 0.04 3.7

Energy reconstruction 0.02 1.8

Live time 0.01 0.9

Total 0.05 4.6

Contribution	Uncertainty [\qtye22yr]	Relative uncertainty [%]
Fiducial mass	0.04	3.7
Energy reconstruction	0.02	1.8
Live time	0.01	0.9

Total	0.05	4.6

A first measurement of the relative capture fractions is performed by introducing an additional parameter for the KK fraction, allowing the two signal peaks to float separately. Relative ratios of modes comprising the KX peak were kept fixed. Bounds at $[0,0.977]$ were imposed on this value, such that the 2.3% proportion of ¹²⁴Xe signal below the ROI is preserved, and the KX fraction can be inferred directly; the KK fraction was otherwise left unconstrained. The fitted KK and KX fractions are \qty64.8(53)% and \qty32.9(53)%, with an associated overall $\chi^{2}_{\lambda}/N_{\text{dof}}=4843.42/4461=1.09$ . At \qty1.4σ away from the values in table 1, these fit results are reasonably consistent with the assumed model. Future LZ runs will enable more precise measurements of these fractions, and may provide sensitivity towards the substructure of the KX peak.

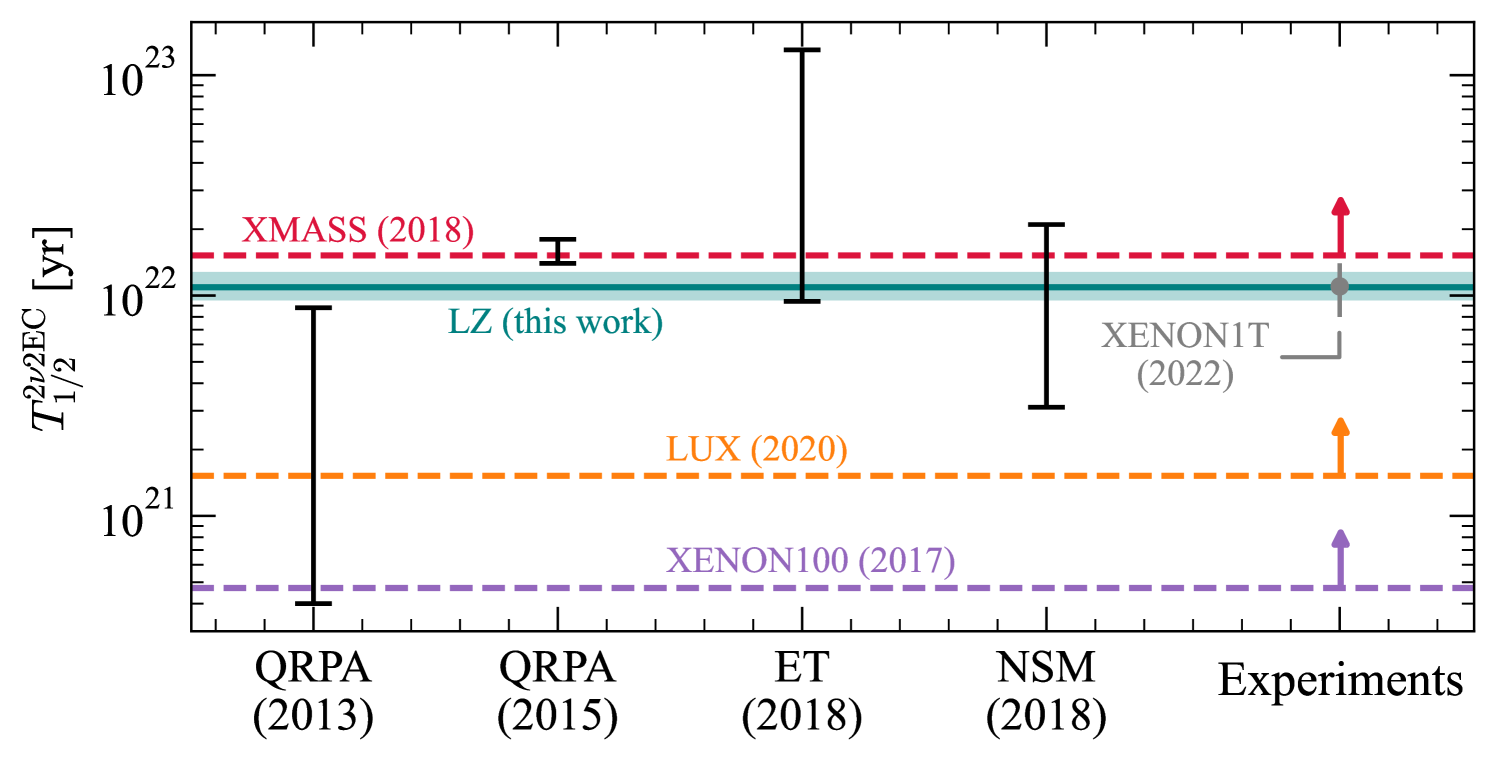
The measured half-life is compared with recent predictions from various theoretical frameworks, as well as measurements and lower limits set by other experiments, in figure 3. The result obtained here is compatible with effective theory (ET) and large-scale nuclear shell model (NSM) calculations [43], and is in agreement with those from the quasiparticle random-phase approximation (QRPA) [44, 45] approach at the \qty2σ level. Moreover, this measurement is also consistent with the 90% confidence level lower limits set by XENON100 [46] and LUX [31], though a discrepancy is observed with respect to the limit produced by XMASS [47].

5 Conclusion and outlook

In this paper, we reported on the search for 2 $\nu$ 2EC of ¹²⁴Xe in the first science run of the LZ experiment. With an isotopic exposure of $\qty{1.39}{kg\times yr}$ , we observed a half-life of $T_{1/2}^{\hskip 0.85358pt2\nu 2\mathrm{EC}}=(1.09\pm 0.14_{\text{stat}}\pm 0.05_{\text{sys}})\times\qty{e22}{yr}$ at a significance of \qty8.3σ, demonstrating the versatility of LZ in exploring physics beyond its primary goal of searching for dark matter. We also report on the first measurement of the relative capture fractions for this decay, at \qty64.8(53)% and \qty32.9(53)% for the KK and summed (KL + KM + KN) modes respectively, which are relatively consistent with the adopted signal model [18]. Additional data from upcoming LZ exposures will allow for these capture fractions to be measured with higher precision, and will ultimately enable searches for rarer variants of ¹²⁴Xe decay, namely $2\nu\mathrm{EC}\beta^{+}$ and $2\nu 2\beta^{+}$ , along with their neutrinoless counterparts [10]. Moreover, it may be of interest to also probe for enhancements to recombination in ¹²⁴Xe decays in future work, as has been observed for single electron captures [48].

Acknowledgments

The research supporting this work took place in part at the Sanford Underground Research Facility (SURF) in Lead, South Dakota. Funding for this work is supported by the U.S. Department of Energy, Office of Science, Office of High Energy Physics under Contract Numbers DE-AC02-05CH11231, DE-SC0020216, DE-SC0012704, DE-SC0010010, DE-AC02-07CH11359, DE-SC0015910, DE-SC0014223, DE-SC0010813, DE-SC0009999, DE-NA0003180, DE-SC0011702, DE-SC0010072, DE-SC0006605, DE-SC0008475, DE-SC0019193, DE-FG02-10ER46709, UW PRJ82AJ, DE-SC0013542, DE-AC02-76SF00515, DE-SC0018982, DE-SC0019066, DE-SC0015535, DE-SC0019319, DE-SC0024225, DE-SC0024114, DE-AC52-07NA27344, & DE-SC0012447. This research was also supported by U.S. National Science Foundation (NSF); the UKRI’s Science & Technology Facilities Council under award numbers ST/W000490/1, ST/W000482/1, ST/W000636/1, ST/W000466/1, ST/W000628/1, ST/W000555/1, ST/W000547/1, ST/W00058X/1, ST/X508263/1, ST/V506862/1, ST/X508561/1, ST/V507040/1 , ST/W507787/1, ST/R003181/1, ST/R003181/2, ST/W507957/1, ST/X005984/1, ST/X006050/1; Portuguese Foundation for Science and Technology (FCT) under award numbers PTDC/FIS-PAR/2831/2020; the Institute for Basic Science, Korea (budget number IBS-R016-D1); the Swiss National Science Foundation (SNSF) under award number 10001549. This research was supported by the Australian Government through the Australian Research Council Centre of Excellence for Dark Matter Particle Physics under award number CE200100008. We acknowledge additional support from the UK Science & Technology Facilities Council (STFC) for PhD studentships and the STFC Boulby Underground Laboratory in the U.K., the GridPP [49, 50] and IRIS Collaborations, in particular at Imperial College London and additional support by the University College London (UCL) Cosmoparticle Initiative, and the University of Zurich. We acknowledge additional support from the Center for the Fundamental Physics of the Universe, Brown University. K.T. Lesko acknowledges the support of Brasenose College and Oxford University. The LZ Collaboration acknowledges the key contributions of Dr. Sidney Cahn, Yale University, in the production of calibration sources. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We gratefully acknowledge support from GitLab through its GitLab for Education Program. The University of Edinburgh is a charitable body, registered in Scotland, with the registration number SC005336. The assistance of SURF and its personnel in providing physical access and general logistical and technical support is acknowledged. We acknowledge the South Dakota Governor’s office, the South Dakota Community Foundation, the South Dakota State University Foundation, and the University of South Dakota Foundation for use of xenon. We also acknowledge the University of Alabama for providing xenon. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission. Finally, we respectfully acknowledge that we are on the traditional land of Indigenous American peoples and honor their rich cultural heritage and enduring contributions. Their deep connection to this land and their resilience and wisdom continue to inspire and enrich our community. We commit to learning from and supporting their effort as original stewards of this land and to preserve their cultures and rights for a more inclusive and sustainable future.

References

[1] Benetti P et al. 1993 Nucl. Instrum. Methods Phys. Res. A 332 395–412
[2] Cline D et al. 2000 Astropart. Phys. 12 373–377
[3] Majorana E 1937 Nuovo Cim. 14 171–184
[4] Dell’Oro S et al. 2016 Adv. High Energy Phys. 2016 2162659
[5] Dolinski M J, Poon A W and Rodejohann W 2019 Annu. Rev. Nucl. Part. Sci. 69 219–251
[6] Agostini M et al. 2023 Rev. Mod. Phys 95 025002
[7] Bernabeu J, De Rujula A and Jarlskog C 1983 Nucl. Phys. B 223 15–28
[8] Sujkowski Z and Wycech S 2004 Phys. Rev. C 70 052501
[9] Šimkovic F, Krivoruchenko M and Faessler A 2011 Prog. Part. Nucl. Phys. 66 446–451
[10] Wittweg C et al. 2020 Eur. Phys. J. C 80 1161
[11] Suhonen J and Civitarese O 1998 Phys. Rep. 300 123–214
[12] Kotila J and Iachello F 2013 Phys. Rev. C 87 024313
[13] Meshik A P et al. 2001 Phys. Rev. C 64 035205
[14] Pujol M et al. 2009 Geochim. Cosmochim. Acta 73 6834–6846
[15] Gavrilyuk Y M et al. 2013 Phys. Rev. C 87 035501
[16] Ratkevich S S et al. 2017 Phys. Rev. C 96 065502
[17] Aprile E et al. (XENON Collaboration) 2019 Nature 568 532–535
[18] Aprile E et al. (XENON Collaboration) 2022 Phys. Rev. C 106 024328
[19] Akerib D et al. (LZ Collaboration) 2020 Nucl. Instrum. 953 163047 ISSN 0168-9002
[20] Mount B J et al. (LZ Collaboration) 2017 LUX-ZEPLIN (LZ) Technical Design Report
[21] Mei D M et al. 2010 Astropart. Phys 34 33–39
[22] Kudryavtsev V A 2009 Comput. Phys. Commun. 180 339–346
[23] Akerib D S et al. (LZ Collaboration) 2020 Eur. Phys. J. C 80
[24] Aalbers J et al. (LZ Collaboration) 2024 J. Instrum. 19 P08027
[25] Aalbers J et al. (LZ Collaboration) 2023 Phys. Rev. Lett. 131 041002
[26] Szydagis M et al. 2021 Instrum. 5 13
[27] Verbus J R et al. 2017 Nucl. Instrum. Methods Phys. Res. A 851 68–81
[28] Akerib D S et al. (LUX Collaboration) 2016 arXiv:1608.05381
[29] Aalbers J et al. (LZ Collaboration) 2022 Phys. Rev. D 108 012010
[30] Nesterenko D A et al. 2012 Phys. Rev. C 86 044313
[31] Akerib D S et al. (LUX Collaboration) 2020 J. Phys. G 47 105105
[32] De Laeter J R et al. 2003 Pure Appl. Chem. 75 683–800
[33] Valkiers S et al. 1998 Int. J. Mass Spectron. 173 55–63
[34] Khazov Y, Rodionov A and Kondev F 2011 Nuclear Data Sheets for A = 133
[35] Bé M M et al. 2016 Table of radionuclides (Vol. 8 – A = 41 to 198)
[36] Timar J, Elekes Z and Singh B 2014 Nuclear Data Sheets for A = 129
[37] Katakura J 2011 Nuclear Data Sheets for A = 125
[38] Bé M M et al. 2011 Table of radionuclides (Vol. 6 – A = 22 to 242)
[39] Deslattes R D et al. 2003 Rev. Mod. Phys. 75 35–99
[40] Thompson A et al. 2009 X-ray data booklet
[41] Akerib D S et al. (LZ Collaboration) 2021 Astropart. Phys. 125 102480
[42] Baker S and Cousins R D 1984 Nucl. Instrum. 221 437–442 ISSN 0167-5087
[43] Coello Pérez E A, Menéndez J and Schwenk A 2019 Phys. Lett. B 797 134885
[44] Suhonen J 2013 J. Phys. G 40 075102
[45] Pirinen P and Suhonen J 2015 Phys. Rev. C 91 054309
[46] Aprile E et al. (XENON Collaboration) 2017 Phys. Rev. C 95 024605
[47] Abe K et al. (XMASS Collaboration) 2018 Prog. Theor. Exp. Phys. 053D03
[48] Temples D J et al. 2021 Phys. Rev. D 104 112001
[49] Faulkner P J W et al. 2005 J. Phys. G 32 N1
[50] Britton D et al. 2009 Philos. Trans. R. Soc. A 367 2447–2457

Two-neutrino double electron capture of 124Xe in the first LUX-ZEPLIN exposure

Abstract

1 Introduction

2 The LUX-ZEPLIN experiment

3 Analysis overview

3.1 Signal model

3.2 Background model

3.3 Fit procedure

4 Results and discussion

5 Conclusion and outlook

Acknowledgments

References

References

Two-neutrino double electron capture of ¹²⁴Xe
in the first LUX-ZEPLIN exposure