Two-particle quantum interference in a nonlinear optical medium:
a witness of timelike indistinguishability

Chao Chen These authors contributed equally to this work. National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China School of Physical Science and Technology, Ningbo University, Ningbo 315211, China Shu-Tian Xue These authors contributed equally to this work. National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Yu-Peng Shi National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Jing Wang National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Zi-Mo Cheng National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Pei Wan National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Zhi-Cheng Ren National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Michael G. Jabbour mjabbour@telecom-sudparis.eu SAMOVAR, Télécom SudParis, Institut Polytechnique de Paris, 91120 Palaiseau, France Centre for Quantum Information and Communication, Ecole polytechnique de Bruxelles, Université libre de Bruxelles, 1050 Bruxelles, Belgium Department of Physics, Technical University of Denmark, 2800 Kongens Lyngby, Denmark Nicolas J. Cerf nicolas.cerf@ulb.be Centre for Quantum Information and Communication, Ecole polytechnique de Bruxelles, Université libre de Bruxelles, 1050 Bruxelles, Belgium Xi-Lin Wang xilinwang@nju.edu.cn National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Hefei National Laboratory, Hefei 230088, China Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China, Hefei 230026, China Hui-Tian Wang htwang@nju.edu.cn National Laboratory of Solid State Microstructures and School of Physics, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

(July 30, 2025)

Abstract

The Hong-Ou-Mandel effect is a paradigmatic quantum phenomenon demonstrating the interference of two indistinguishable photons that are linearly coupled at a 50:50 beam splitter. Here, we transpose such a two-particle quantum interference effect to the nonlinear regime, when two single photons are impinging on a parametric down-conversion crystal. Formally, this transposition amounts to exchanging space and time variables, giving rise to an unknown form of timelike quantum interference. The two-photon component of the output state is a superposition of the incident photons being either transmitted or reborn, that is, replaced by indistinguishable substitutes due to their interaction with the nonlinear crystal. We experimentally demonstrate the suppression of the probability of detecting precisely one photon pair when the amplification gain is tuned to 2, which arises from the destructive interference between the transmitted and reborn photon pairs. This heretofore unobserved quantum manifestation of indistinguishability in time pushes nonlinear quantum interference towards a new regime with multiple photons. Hence, composing this effect with larger linear optical circuits should provide a tool to generate multimode quantum non-Gaussian states, which are essential resources for photonic quantum computers.

Quantum interference lies at the heart of fundamental quantum mechanics [1]. One typical optical interference configuration is the Mach-Zehnder (MZ) interferometer (Fig. 1a), which shows oscillatory interference fringes due to the relative phase between the upper and lower optical paths. The linear MZ interferometer can be extended to SU(1,1) nonlinear quantum interferometry [2] by replacing the beam splitters (BSs) with parametric down-conversion (PDC) crystals. PDC-based MZ interferometers shape the fields of induced coherence by path identity [3, 4, 5, 6, 7, 8] or stimulated emission [9, 10, 11], and have shown attractive potential application in quantum imaging [12, 13] and quantum metrology [14] by exploiting the phase-sensitive output. In comparison, the celebrated Hong-Ou-Mandel (HOM) effect [15] relies on phase-independent quantum interference when two indistinguishable photons interfere at a 50:50 BS (Fig. 1b). The coincidence of detecting one photon at each output port vanishes because two photons being both transmitted or both reflected interfere destructively. Being of major fundamental interest, the HOM effect has been demonstrated not only with photons [16, 17, 18] but also with surface plasmons [19], atoms [20] and phonons [21]. Furthermore, the HOM effect has aroused the interference of multiple quantum light sources [22, 23], which have applications in quantum computation [24, 25, 26, 27, 28, 29].

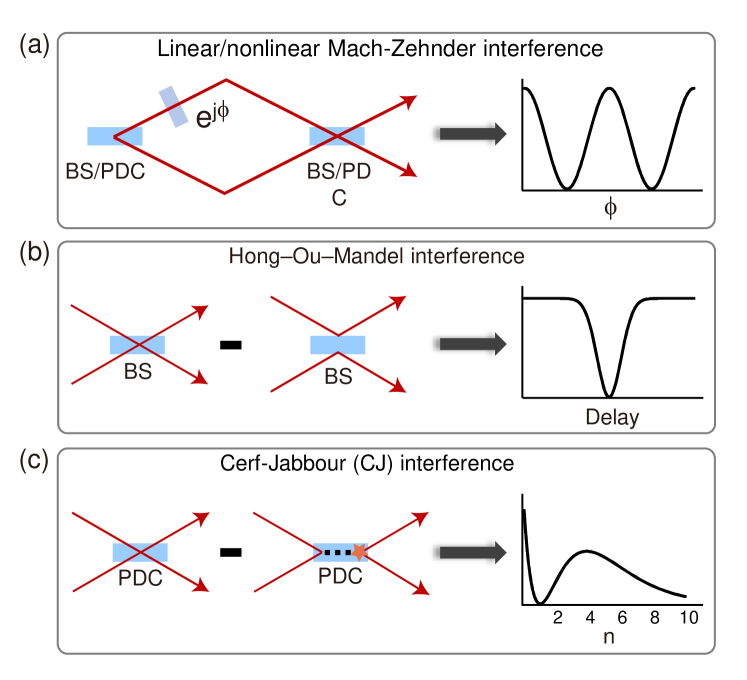
Refer to caption — Figure 1: Quantum interferometer configurations. (a), Mach-Zehnder (MZ) interferometer: following the first beam splitter (BS), photons travel through two possible optical paths and interfere at another BS. The light intensity at any output oscillates with the relative phase between the paths. If the BS are replaced with parametric down-conversion (PDC) crystals, we obtain a SU(1,1) nonlinear interferometer and phase-sensitive stimulated emission is observed. (b), Hong-Ou-Mandel (HOM) interference: two single photons impinge on a BS from different input modes. The photons being both transmitted interfere destructively with those being both reflected, leading to vanishing coincidence at the output for a splitting ratio 1/2. (c), Cerf-Jabbour (CJ) interference: two incident single photons interfere at a PDC crystal. The photons evolve into a superposition of being either directly transmitted or being reborn in the PDC (replaced by indistinguishable substitutes via up- and down-conversion). The interference between these two components cancels the probability of outputting precisely one pair of photons for a gain 2.

Intriguingly, when transposing the HOM effect to the nonlinear regime, an overlooked quantum interference mechanism emerges [30], which can in principle be observed when two single photons impinge on a PDC crystal (Fig. 1c). Owing to the creation and annihilation terms in the PDC Hamiltonian (1), the output photons can be the two originally incident ones or, instead, two newly generated photons (meanwhile the incident ones are annihilated), which we call reborn photons. Remember that the HOM effect stems from the Bose statistics of indistinguishable photons. Likewise here, the transmitted photon pair destructively interferes with the reborn photon pair, leading to a depletion of the probability of outputting one photon pair. This two-photon nonlinear interference in a PDC, which we dub Cerf-Jabbour (CJ) interference [30], is a striking manifestation of indistinguishability in time (roughly speaking, one cannot recognize whether the output photons are “the same as” the input photons or not).

Although multi-photon nonlinear interferences have been reported in the literature (see, e.g., [31, 6, 8]), such experiments belong to the class depicted in Fig. 1(a), which exploits path-identity induced coherence [7]. Here, we demonstrate the two-photon CJ interference, which fundamentally differs from previous experiments as it is the nonlinear counterpart to the HOM experiment. To match a 50:50 BS, the gain $g$ of the PDC should be tuned to $2$ , such that up- and downconversion are simultaneously at play on a fifty-fifty basis. We achieve this strong interaction of photons (very high $g$ ) via a PDC process pumped by an ultra-tightly focused high-power femtosecond laser that has a meticulous mode matching with heralded single photons in all degrees of freedom. Moreover, we successfully retrieve photon-number distribution through six-channel coincidence measurement and post-processing via a direct inverse technique and a fitted experimental model, which enables us to observe a depletion of the probability of outputting precisely one pair of photons and demonstrate nonlinear destructive interference.

Our experiment thus hints that timelike indistinguishability has very unsuspected consequences and pushes nonlinear quantum interference [2, 33, 34] to a multi-photon regime, necessitating nonlinear interaction of single photons. Aside from the fundamental physics implications, we also show that a strongly non-Gaussian Wigner-negative regime could be accessed by integrating this CJ nonlinear interference within a large-scale linear optical interferometer based on a cascade network, which would be valuable for the development of photonic quantum computers [35, 36, 37].

Experiment.

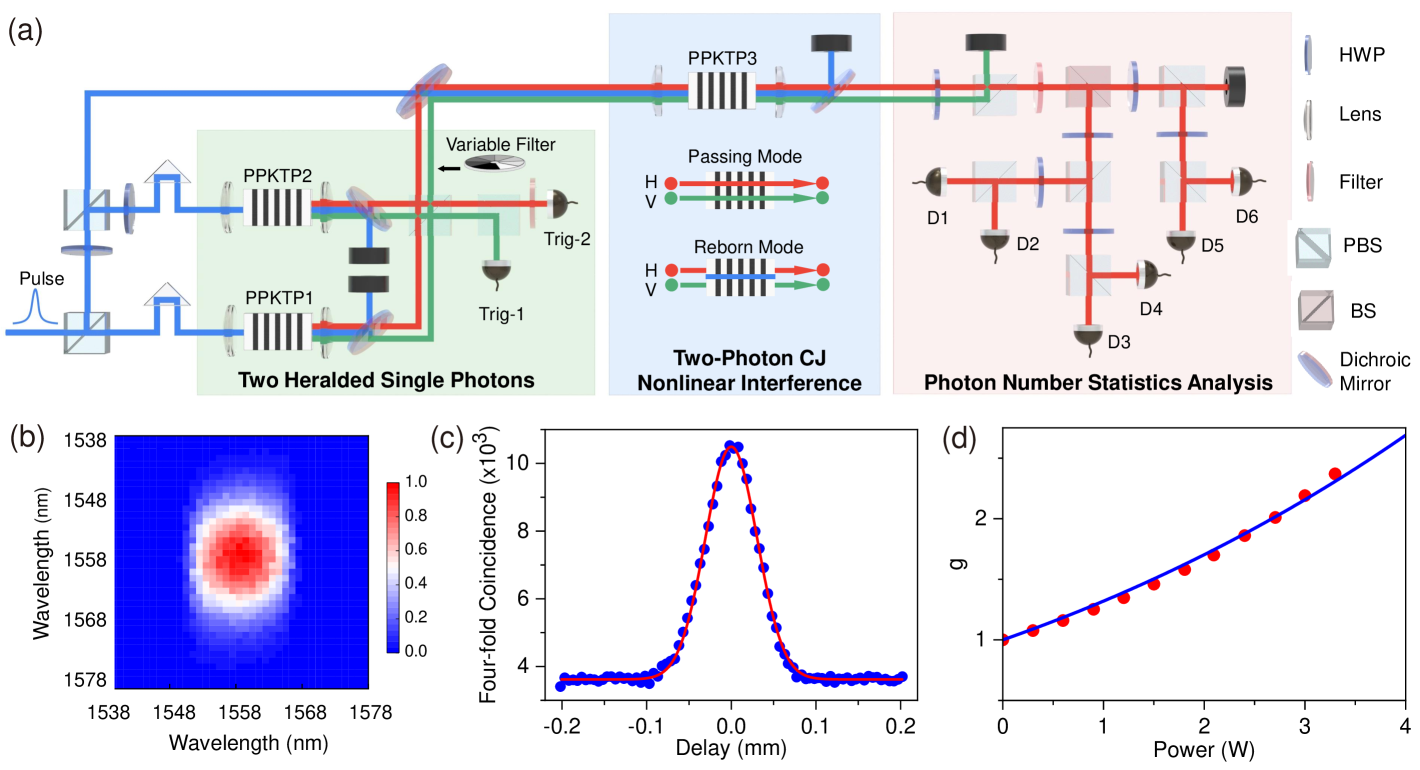
In our experiment, shown in Fig. 2, the core unit – the parametric amplifier – is a type-II periodically poled potassium titanyl phosphate (PPKTP) crystal, which allows a horizontally polarized pump photon at 779 nm to be down-converted into a pair of photons at 1558 nm being horizontally and vertically polarized respectively. The unitary operation of the PPKTP reads

U_{g}^{\text{PDC}}=\text{exp}[r(\hat{a}_{\text{H}}\hat{a}_{\text{V}}-\hat{a}_{\text{H}}^{\dagger}\hat{a}_{\text{V}}^{\dagger})],

(1)

where $\hat{a}_{\text{H(V)}}$ is the signal (idler) mode operator with horizontal (vertical) polarization and $r$ is the squeezing parameter, related to the parametric gain $g$ via $g=\cosh^{2}{r}$ . Photons are created (annihilated) by pairs as a result of down-conversion (up-conversion) of pump photons due to the structure of $U_{g}^{\text{PDC}}$ , and we denote as $P_{n}$ the probability of observing $n$ pairs at the output (i.e., the output state $\ket{n,n}$ ). The gain $g$ governs the depth of the two-photon CJ nonlinear interference, just like the splitting ratio of a BS determines the visibility of HOM interference. When $g=2$ , two-photon events vanish due to fully destructive interference, that is, we should observe $P_{1}=0$ in ideal conditions (see Supplementary Information).

In the experimental setup shown in Fig. 2(a), a femtosecond pulsed laser beam (blue) is divided by beam splitters to pump three identical PPKTP crystals coherently. The heralded two single photons are generated through spontaneous PDC processes in PPKTP1 and PPKTP2 at low pump power of \qty100mW. To match the polarization states of the PDC photons in PPKTP3, heralded H- (in red) and V-polarized (in green) single photons are generated in PPKTP1 and PPKTP2, respectively, by triggering their counterpart photons. We combine the two heralded H- and V-polarized single photons at a polarization beam splitter (PBS). Then, the two single photons are aligned to interact with PPKTP3, whose output is analyzed by multi-channel single-photon coincidence measurement. To achieve high gain for PPKTP3, the laser with tunable power up to $\qty{3}{W}$ is tightly focused on the crystal. The beam waist of the pump laser is $\qty{30}{\mu m}$ , which is smaller than that was employed in Jiuzhang 2.0 quantum computer[38].

We optimize our experimental setup to realize mode match between the two heralded single photons and the PDC photon pair in PPKTP3 in spectral, spatial and temporal degrees of freedom. The spectral indistinguishability is enforced in two ways: (1) all three PPKTP crystals are temperature controlled to generate down-converted photon pairs with degenerate central wavelength at 1558 nm; (2) the side lobes in joint spectrum are removed by a 15-nm filter, so that the two modes are frequency uncorrelated, as shown in Fig. 2(b). The average pairwise purity estimated by unheralded second order correlation is 0.92 ([39, 29] and see Supplementary Information). The spatial modes of the heralded photons are carefully aligned with those of the down-converted photons from PPKTP3. As for temporal match, the arriving time of the heralded single photons at PPKTP3 is adjusted by two delay lines (two prisms on motorized stages). For example, when the H-polarized single photon is temporally overlapped with the H-polarized PDC mode in PPKTP3, we verify that the emission of down-converted photons is stimulated, as shown in Fig. 2(c). To clearly confirm temporal mode matching, both PPKTP1/2 and PPKTP3 are pumped by laser beams of high power for obtaining a remarkable stimulated emission peak. With all the above optimizations, the overall mode match of the heralded single photon and the PDC modes in PPKTP3 is about 0.65 (see Supplementary Information), which outperforms the result in [40] and is sufficient to clearly show the two-photon suppression due to the CJ nonlinear interference.

To observe the suppression of the probability $P_{1}$ of outputting one pair, which is a direct evidence of the two-photon CJ nonlinear quantum interference, analysis of photon number distribution is of the essence. Provided the heralded photons impinge PPKTP3 in pairs, the output photon number distributions of the H- and V-polarized modes are in principle symmetric, rendering measurement of only one of these two modes sufficient to analyze the photon-pair probability distribution. For resource saving, we uniformly distribute the H-polarized output photons into six superconducting nanowire single-photon detectors with average detection efficiency of $80\%$ , and leave the V-polarized photons undetected. By analyzing the measured multi-channel coincidence, we use direct inverse method (see Supplementary Information) to obtain the probability of outputting one H-polarized photon, which we associate with $P_{1}$ . When the pump laser of PPKTP1 and PPKTP2 is blocked, the output state of PPKTP3 is a two-mode squeezed vacuum state. In Fig. 2(d), we show the parametric gain $g$ as deduced from our multi-channel coincidence measurement, plotted against the pump power of PPKTP3.

Results.

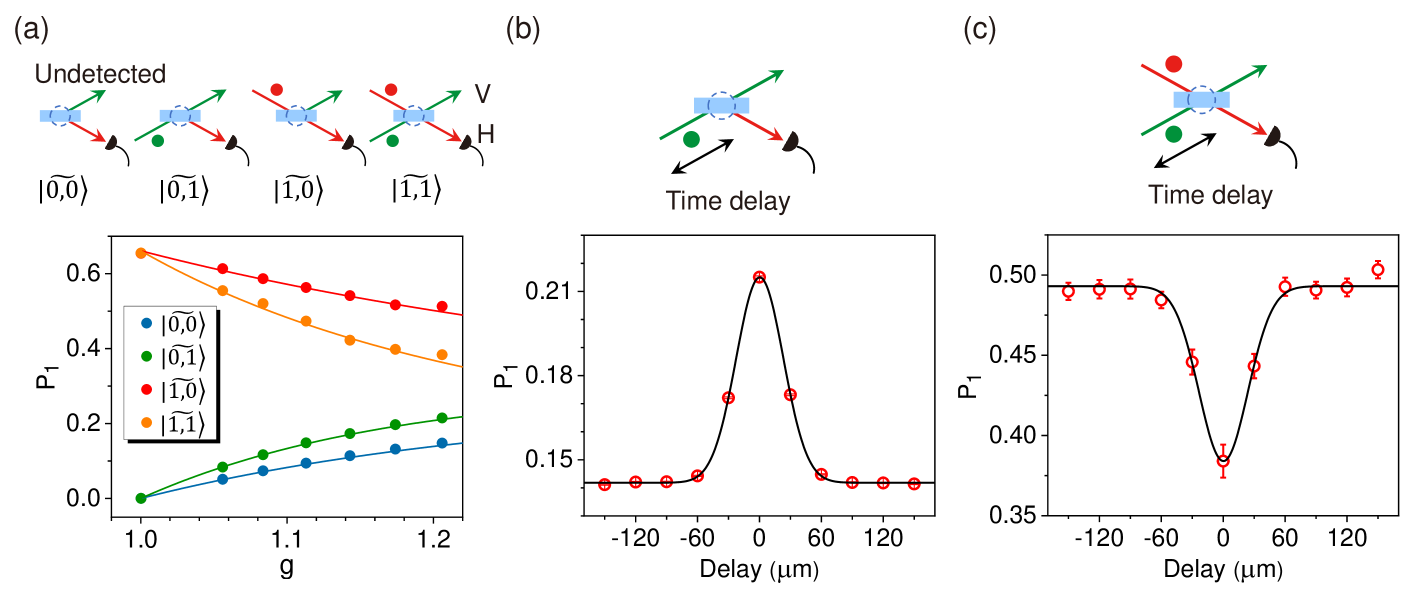
For different input states, the measured probability of outputting one H-polarized photon $P_{1}$ is shown in Fig. 3(a). Depending on whether the heralded H- or V-polarized single photon are blocked or not, we label the input state as $\ket{\widetilde{0,0}}$ , $\ket{\widetilde{0,1}}$ , $\ket{\widetilde{1,0}}$ , and $\ket{\widetilde{1,1}}$ . The tilde are used to stress that, due to imperfect mode match, these states could deviate from the ideal input states denoted as $\ket{0,0}$ , $\ket{0,1}$ , $\ket{1,0}$ , and $\ket{1,1}$ . The parametric gain $g$ ranges from 1 to 1.21, corresponding to increase the pump power from 0 to \qty700mW. When no single photons are input ( $\ket{\widetilde{0,0}}$ ), it is common to see that the larger pump power gives rise to higher generation rate of down-converted photons, i.e., $P_{1}$ increases with $g$ . As expected, $P_{1}$ increases even faster when inputting a V-polarized single photon ( $\ket{\widetilde{0,1}}$ ) as a result of stimulated emission. In contrast, if inputting a H-polarized photon ( $\ket{\widetilde{1,0}}$ ), $P_{1}$ decreases with $g$ because the probability of outputting more than one photons emerges in the active PDC process. Note that for $g=1$ (when the pump laser of PPKTP3 is blocked and no interaction occurs), we have $P_{1}\approx 0.65$ , deviating from the theoretical value $P_{1}=1$ as expected for ideal single-photon input state $\ket{1,0}$ . This is mainly due to the limited mode match between the heralded single photon and the PDC modes in PPKTP3, which leads to mix some state $\ket{0,0}$ together with states $\ket{1,0}$ in the initial state $\ket{\widetilde{1,0}}$ (see Supplementary Information).

Now, the key observation is that $P_{1}$ decays even further with $g$ when both H- and V-polarized heralded single photons are inputted ( $\ket{\widetilde{1,1}}$ ). It is indeed counterintuitive that inputting an extra V-polarized photon results in the decline (instead of the enhancement) of the probability of outputting a single H-polarized photon. This indicates that a two-photon destructive quantum interference is at play when single photons are injected in pair. In Fig. 3(b) and (c), we compare the measured $P_{1}$ for single-photon stimulation and photon pair suppression (corresponding, respectively, to inputs $\ket{\widetilde{0,1}}$ and $\ket{\widetilde{1,1}}$ ) when the injected photons arrive at PPKTP3 together with the pump pulse. When the V-polarized single photon is gradually temporally mismatched by changing the time delay, the input state deviates to $\ket{\widetilde{0,0}}$ ( $\ket{\widetilde{1,0}}$ ) so that the stimulated peak (suppressed dip) subsides, as shown in Fig. 3 (b) (Fig. 3(c)).

Discussion.

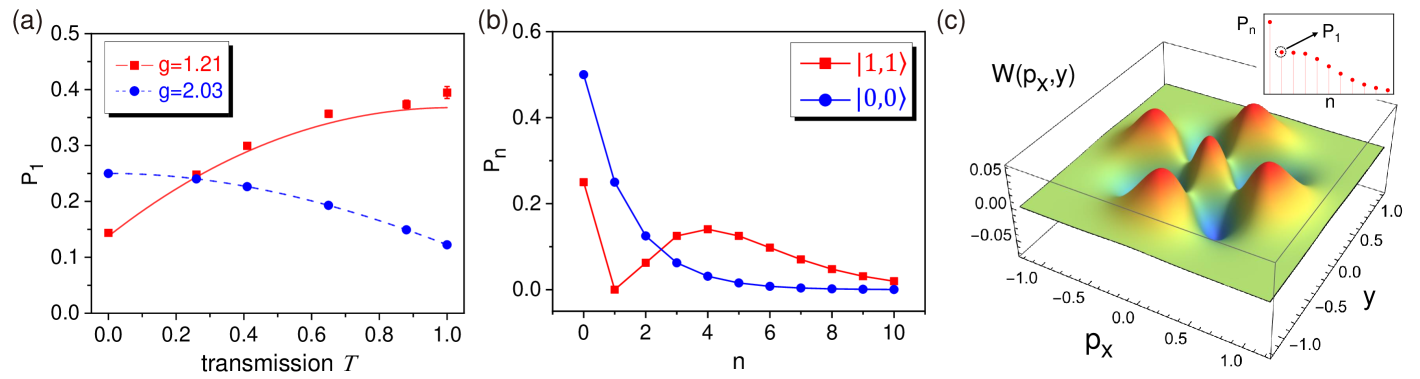
We now focus on the two-photon CJ interference in a PDC crystal and analyze its main features in Fig. 4. First, the impact of the quality of the injected photon pair is analyzed and compared at different values of the parametric gain $g$ , which is the analogue of the split ratio of the BS affecting the visibility of the HOM dip, as shown in Fig. 4(a). A neutral density filter with step-variable transmission $\mathrm{\it{T}}$ is introduced in the front of PPKTP3 to adjust the heralding efficiency of the input single photon pairs. For $\mathrm{\it{T}}=1$ , the input state mostly consists of $\ket{1,1}$ ; for $\mathrm{\it{T}}=0$ , the input state is a vacuum state although the detectors Trig-1 and Trig-2 count single photons. At small gain ( $g=1.21$ ), $P_{1}$ consistently increases with $\mathrm{\it{T}}$ as more single photon pairs are inputted, because the directly transmitted photon pairs dominate those interacting with the PDC crystal. Amazingly, this explains why the two-photon CJ nonlinear quantum interference had remained unsuspected in all previous experiments with moderate pump power. Here, we promote the gain to $g=2.03$ and observe that inputting more photon pairs instead comes with outputting less photon pairs, demonstrating the destructive nonlinear quantum interference in the PPKTP crystal. In practice, the residual value of $P_{1}\approx 0.1$ at $\mathrm{\it{T}}=1$ mainly results from the limited mode matching, as mentioned before.

Importantly, together with the interferometric suppression of $P_{1}$ , the entire photon-number distribution of the output state is impacted by the CJ effect [30]. In Fig. 4(b), we show the theoretically simulated photon-number distribution $P_{n}$ of the $H$ -polarized mode. For the $\ket{0,0}$ input, the output is a two-mode squeezed vacuum state, exhibiting an exponential decay of $P_{n}$ with $n$ as expected. With ideal one-photon-pair input state $\ket{1,1}$ , the output photon number distribution shows a dip at $n=1$ due to the two-photon CJ nonlinear quantum interference. In Fig. 4(c), we also plot the reconstructed output two-mode state in phase space, together with the corresponding photon-number distribution retrieved from the experiment. Although experimental imperfections lead to some leftover probability $P_{1}$ , the output state still remains quite non-Gaussian, with the presence of Wigner negativity. The non-Gaussianity of the output state stems from the input single photons, in contrast with the reported photon addition/subtraction protocols [41, 42, 43, 44]. When increasing the pump power to $g=3$ , four-photon destructive interference in the PDC crystal results in the suppression of $P_{2}$ (see Supplementary Information).

Conclusion.

We experimentally demonstrate a surprising quantum interference mechanism by impinging two single photons on a highly-pumped PDC crystal, which is the nonlinear counterpart to the well-known HOM interference when timelike indistinguishability is at play. We observe a depletion of the probability of detecting precisely one pair of photons at the output, witnessing the destructive interference between the transmitted photons and their reborn substitutes due to the nonlinear interaction when the gain reaches 2. Aside from the fundamentally new mechanism that it unveils, our work unambiguously verifies the two-photon rebirth (a combination of generating and annihilating photons in pairs) and pushes nonlinear quantum interference to genuine multi-photon regime, which could enrich the toolkit for nonlinear interaction between single photons and matter [45, 46]. The resulting ability to control the photon-number distribution of the output two-mode state provides an alternative powerful scheme to engineer non-Gaussian entangled states [43, 44, 47] of light by utilizing such a PDC-based nonlinear quantum interference. Two-photon interference serves as the basic element for large scale photonic quantum systems. Thus, by generalizing to multiple photons and multiple modes [48, 49, 50], we anticipate that two-photon nonlinear quantum interference may have enormous applications in optical quantum computation and quantum information processing.

References

Mandel [1999] L. Mandel, Quantum effects in one-photon and two-photon interference, Rev. Mod. Phys. 71, S274 (1999).
Yurke et al. [1986] B. Yurke, S. L. McCall, and J. R. Klauder, SU(2) and SU(1,1) interferometers, Phys. Rev. A 33, 4033 (1986).
Wang et al. [1991] L. J. Wang, X. Y. Zou, and L. Mandel, Induced coherence without induced emission, Phys. Rev. A 44, 4614 (1991).
Zou et al. [1991] X. Y. Zou, L. J. Wang, and L. Mandel, Induced coherence and indistinguishability in optical interference, Phys. Rev. Lett. 67, 318 (1991).
Heuer et al. [2015] A. Heuer, R. Menzel, and P. W. Milonni, Induced Coherence, Vacuum Fields, and Complementarity in Biphoton Generation, Phys. Rev. Lett. 114, 053601 (2015).
Ono et al. [2019] T. Ono, G. F. Sinclair, D. Bonneau, M. G. Thompson, J. C. F. Matthews, and J. G. Rarity, Observation of nonlinear interference on a silicon photonic chip, Opt. Lett., OL 44, 1277 (2019).
Hochrainer et al. [2022] A. Hochrainer, M. Lahiri, M. Erhard, M. Krenn, and A. Zeilinger, Quantum indistinguishability by path identity and with undetected photons, Rev. Mod. Phys. 94, 025007 (2022).
Feng et al. [2023] L.-T. Feng, M. Zhang, D. Liu, Y.-J. Cheng, G.-P. Guo, D.-X. Dai, G.-C. Guo, M. Krenn, and X.-F. Ren, On-chip quantum interference between the origins of a multi-photon state, Optica 10, 105 (2023).
Simon et al. [2000] C. Simon, G. Weihs, and A. Zeilinger, Optimal Quantum Cloning via Stimulated Emission, Phys. Rev. Lett. 84, 2993 (2000).
Lamas-Linares et al. [2002] A. Lamas-Linares, C. Simon, J. C. Howell, and D. Bouwmeester, Experimental Quantum Cloning of Single Photons, Science 296, 712 (2002).
Sun et al. [2007] F. W. Sun, B. H. Liu, Y. X. Gong, Y. F. Huang, Z. Y. Ou, and G. C. Guo, Stimulated Emission as a Result of Multiphoton Interference, Phys. Rev. Lett. 99, 043601 (2007).
Lemos et al. [2014] G. B. Lemos, V. Borish, G. D. Cole, S. Ramelow, R. Lapkiewicz, and A. Zeilinger, Quantum imaging with undetected photons, Nature 512, 409 (2014).
Qian et al. [2023a] G. Qian, X. Xu, S.-A. Zhu, C. Xu, F. Gao, V. V. Yakovlev, X. Liu, S.-Y. Zhu, and D.-W. Wang, Quantum Induced Coherence Light Detection and Ranging, Phys. Rev. Lett. 131, 033603 (2023a).
Qin et al. [2023] J. Qin, Y.-H. Deng, H.-S. Zhong, L.-C. Peng, H. Su, Y.-H. Luo, J.-M. Xu, D. Wu, S.-Q. Gong, H.-L. Liu, H. Wang, M.-C. Chen, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W. Pan, Unconditional and Robust Quantum Metrological Advantage beyond N00N States, Phys. Rev. Lett. 130, 070801 (2023).
Hong et al. [1987] C. K. Hong, Z. Y. Ou, and L. Mandel, Measurement of subpicosecond time intervals between two photons by interference, Phys. Rev. Lett. 59, 2044 (1987).
Santori et al. [2002] C. Santori, D. Fattal, J. Vučković, G. S. Solomon, and Y. Yamamoto, Indistinguishable photons from a single-photon device, Nature 419, 594 (2002).
Patel et al. [2010] R. B. Patel, A. J. Bennett, I. Farrer, C. A. Nicoll, D. A. Ritchie, and A. J. Shields, Two-photon interference of the emission from electrically tunable remote quantum dots, Nature Photon 4, 632 (2010).
Kobayashi et al. [2016] T. Kobayashi, R. Ikuta, S. Yasui, S. Miki, T. Yamashita, H. Terai, T. Yamamoto, M. Koashi, and N. Imoto, Frequency-domain Hong–Ou–Mandel interference, Nature Photon 10, 441 (2016).
Fakonas et al. [2014] J. S. Fakonas, H. Lee, Y. A. Kelaita, and H. A. Atwater, Two-plasmon quantum interference, Nature Photon 8, 317 (2014).
Lopes et al. [2015] R. Lopes, A. Imanaliev, A. Aspect, M. Cheneau, D. Boiron, and C. I. Westbrook, Atomic Hong–Ou–Mandel experiment, Nature 520, 66 (2015).
Toyoda et al. [2015] K. Toyoda, R. Hiji, A. Noguchi, and S. Urabe, Hong–Ou–Mandel interference of two phonons in trapped ions, Nature 527, 74 (2015).
Wang et al. [2016] X.-L. Wang, L.-K. Chen, W. Li, H.-L. Huang, C. Liu, C. Chen, Y.-H. Luo, Z.-E. Su, D. Wu, Z.-D. Li, H. Lu, Y. Hu, X. Jiang, C.-Z. Peng, L. Li, N.-L. Liu, Y.-A. Chen, C.-Y. Lu, and J.-W. Pan, Experimental Ten-Photon Entanglement, Phys. Rev. Lett. 117, 210502 (2016).
Menssen et al. [2017] A. J. Menssen, A. E. Jones, B. J. Metcalf, M. C. Tichy, S. Barz, W. S. Kolthammer, and I. A. Walmsley, Distinguishability and Many-Particle Interference, Phys. Rev. Lett. 118, 153603 (2017).
Broome et al. [2013] M. A. Broome, A. Fedrizzi, S. Rahimi-Keshari, J. Dove, S. Aaronson, T. C. Ralph, and A. G. White, Photonic Boson Sampling in a Tunable Circuit, Science 339, 794 (2013).
Tillmann et al. [2013] M. Tillmann, B. Dakić, R. Heilmann, S. Nolte, A. Szameit, and P. Walther, Experimental boson sampling, Nature Photon 7, 540 (2013).
Crespi et al. [2013] A. Crespi, R. Osellame, R. Ramponi, D. J. Brod, E. F. Galvão, N. Spagnolo, C. Vitelli, E. Maiorino, P. Mataloni, and F. Sciarrino, Integrated multimode interferometers with arbitrary designs for photonic boson sampling, Nature Photon 7, 545 (2013).
Wang et al. [2017] H. Wang, Y. He, Y.-H. Li, Z.-E. Su, B. Li, H.-L. Huang, X. Ding, M.-C. Chen, C. Liu, J. Qin, J.-P. Li, Y.-M. He, C. Schneider, M. Kamp, C.-Z. Peng, S. Höfling, C.-Y. Lu, and J.-W. Pan, High-efficiency multiphoton boson sampling, Nature Photon 11, 361 (2017).
Zhong et al. [2018] H.-S. Zhong, Y. Li, W. Li, L.-C. Peng, Z.-E. Su, Y. Hu, Y.-M. He, X. Ding, W. Zhang, H. Li, L. Zhang, Z. Wang, L. You, X.-L. Wang, X. Jiang, L. Li, Y.-A. Chen, N.-L. Liu, C.-Y. Lu, and J.-W. Pan, 12-Photon Entanglement and Scalable Scattershot Boson Sampling with Optimal Entangled-Photon Pairs from Parametric Down-Conversion, Phys. Rev. Lett. 121, 250505 (2018).
Zhong et al. [2020] H.-S. Zhong, H. Wang, Y.-H. Deng, M.-C. Chen, L.-C. Peng, Y.-H. Luo, J. Qin, D. Wu, X. Ding, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W. Pan, Quantum computational advantage using photons, Science 370, 1460 (2020).
Cerf and Jabbour [2020] N. J. Cerf and M. G. Jabbour, Two-boson quantum interference in time, Proceedings of the National Academy of Sciences 117, 33107 (2020).
Chekhova and Ou [2016] M. V. Chekhova and Z. Y. Ou, Nonlinear interferometers in quantum optics, Adv. Opt. Photon., AOP 8, 104 (2016).
Lvovsky [2016] A. I. Lvovsky, Squeezed light, arXiv:1401.4118 [physics, physics:quant-ph] (2016), arxiv:1401.4118 [physics, physics:quant-ph] .
Paterova and Krivitsky [2020] A. V. Paterova and L. A. Krivitsky, Nonlinear interference in crystal superlattices, Light Sci Appl 9, 82 (2020).
Luo et al. [2021] K.-H. Luo, M. Santandrea, M. Stefszky, J. Sperling, M. Massaro, A. Ferreri, P. R. Sharapova, H. Herrmann, and C. Silberhorn, Quantum optical coherence: From linear to nonlinear interferometers, Phys. Rev. A 104, 043707 (2021).
Mari and Eisert [2012] A. Mari and J. Eisert, Positive Wigner Functions Render Classical Simulation of Quantum Computation Efficient, Phys. Rev. Lett. 109, 230503 (2012).
Veitch et al. [2013] V. Veitch, N. Wiebe, C. Ferrie, and J. Emerson, Efficient simulation scheme for a class of quantum optics experiments with non-negative Wigner representation, New J. Phys. 15, 013037 (2013).
Rahimi-Keshari et al. [2016] S. Rahimi-Keshari, T. C. Ralph, and C. M. Caves, Sufficient Conditions for Efficient Classical Simulation of Quantum Optics, Phys. Rev. X 6, 021039 (2016).
Zhong et al. [2021] H.-S. Zhong, Y.-H. Deng, J. Qin, H. Wang, M.-C. Chen, L.-C. Peng, Y.-H. Luo, D. Wu, S.-Q. Gong, H. Su, Y. Hu, P. Hu, X.-Y. Yang, W.-J. Zhang, H. Li, Y. Li, X. Jiang, L. Gan, G. Yang, L. You, Z. Wang, L. Li, N.-L. Liu, J. J. Renema, C.-Y. Lu, and J.-W. Pan, Phase-Programmable Gaussian Boson Sampling Using Stimulated Squeezed Light, Phys. Rev. Lett. 127, 180502 (2021).
Christ et al. [2011] A. Christ, K. Laiho, A. Eckstein, K. N. Cassemiro, and C. Silberhorn, Probing multimode squeezing with correlation functions, New J. Phys. 13, 033027 (2011).
Qian et al. [2023b] K. Qian, K. Wang, L. Chen, Z. Hou, M. Krenn, S. Zhu, and X.-s. Ma, Multiphoton non-local quantum interference controlled by an undetected photon, Nat Commun 14, 1480 (2023b).
Wenger et al. [2004] J. Wenger, R. Tualle-Brouri, and P. Grangier, Non-Gaussian Statistics from Individual Pulses of Squeezed Light, Phys. Rev. Lett. 92, 153601 (2004).
Jeong et al. [2014] H. Jeong, A. Zavatta, M. Kang, S.-W. Lee, L. S. Costanzo, S. Grandi, T. C. Ralph, and M. Bellini, Generation of hybrid entanglement of light, Nature Photon 8, 564 (2014).
Ra et al. [2020] Y.-S. Ra, A. Dufour, M. Walschaers, C. Jacquard, T. Michel, C. Fabre, and N. Treps, Non-Gaussian quantum states of a multimode light field, Nat. Phys. 16, 144 (2020).
Walschaers [2021] M. Walschaers, Non-Gaussian Quantum States and Where to Find Them, PRX Quantum 2, 030204 (2021).
Hübel et al. [2010] H. Hübel, D. R. Hamel, A. Fedrizzi, S. Ramelow, K. J. Resch, and T. Jennewein, Direct generation of photon triplets using cascaded photon-pair sources, Nature 466, 601 (2010).
Guerreiro et al. [2014] T. Guerreiro, A. Martin, B. Sanguinetti, J. S. Pelc, C. Langrock, M. M. Fejer, N. Gisin, H. Zbinden, N. Sangouard, and R. T. Thew, Nonlinear Interaction between Single Photons, Phys. Rev. Lett. 113, 173601 (2014).
Zhang et al. [2022] K. Zhang, J. Jing, N. Treps, and M. Walschaers, Maximal entanglement increase with single-photon subtraction, Quantum 6, 704 (2022).
Jabbour and Cerf [2021] M. G. Jabbour and N. J. Cerf, Multiparticle quantum interference in Bogoliubov bosonic transformations, Phys. Rev. Res. 3, 043065 (2021).
Salazar et al. [2023] W. E. Salazar, O. Calderón-Losada, and J. H. Reina, Linear-nonlinear duality for circuit design on quantum computing platforms (2023), arxiv:2310.20416 [quant-ph] .
Bezerra and Shchesnovich [2023] M. E. O. Bezerra and V. Shchesnovich, Families of bosonic suppression laws beyond the permutation symmetry principle, https://arxiv.org/abs/2301.02192v3 (2023).

Methods

Determination of $P_{1}$ from multi-channel coincidence measurement. For an arbitrary state with photon number distribution $P_{n}$ , the probability that $m$ detectors respond simultaneously is

	$\displaystyle C_{m}$	$\displaystyle=\sum_{n=m}^{\infty}P_{n}*P^{(n)}_{m}$		(2)
		$\displaystyle=\sum_{n=m}^{\infty}P_{n}\sum_{r=0}^{m}(-1)^{r}\frac{m!}{r!(m-r)!}(1-r\eta)^{n}$		(2)

Since the detection efficiency $\eta$ can be measured experimentally, there is a deterministic relationship between $C_{m}$ and $P_{n}$ . Therefore, $P_{1}$ also can be calculated by measured $C_{m}$ (see Supplementary Information). In realistic experiment, the number of detectors is limited. For example, $m$ detectors enable the measurement of $C_{1},C_{2},\cdots,C_{m}$ . We select $C_{1},C_{2},\cdots,C_{5}$ to approximate $P_{1}$ , which is the upper bound of real $P_{1}$ . This approximation is valid when $g\lesssim 1.2$ . In this case, the response probability of $m$ detectors, $C_{m}$ , is negligible small for $m\geq 6$ , i.e., the $n~(n\geq 6)$ -photon component is insignificant.

To resolve $P_{1}$ when $g>1.2$ , we create a model characterized by parameters – gain $g$ , mode match and detection efficiency to describe two-photon CJ nonlinear interference experiments (see Supplementary Information). All the parameters are fitted in auxiliary experiments, where the input states for PPKTP3 are changed. Then we substitute the fitted parameters into the model to calculate the $P_{1}$ of the output state for two-photon nonlinear interference experiment when $g\approx 2$ . The deduced $P_{1}$ from the fitted model agrees well with the approximated $P_{1}$ from multi-channel coincidence measurement for experiments of $g\approx 1.2$ , confirming the validity of our fitted model.

Data availability
The data supporting the study and figures are available upon request, which should be addressed to Chao Chen.

Acknowledgements
We thank the team of Jiuzhang quantum computer for technical support of vital importance. This work was supported financially by the National Natural Science Foundation of China (Grants No. 12234009, No. 12274215 and No. 12304398); the National Key R&D Program of China (Grants No. 2019YFA0308700 and No. 2020YFA0309500); the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0301400); the Program for Innovative Talents and Entrepreneurs in Jiangsu; Key R&D Program of Jiangsu Province (Grant No. BE2023002); the Key R&D Program of Guangdong Province (Grant No. 2020B0303010001); the Natural Science Foundation of Jiangsu Province (Grant No. BK20220759); the China Postdoctoral Science Foundation (2023T160297). MGJ acknowledges support by the Fonds de la Recherche Scientifique – FNRS, as well as by the Carlsberg Foundation. NJC acknowledges support from the European Union under project ShoQC within the ERA-NET Cofund in Quantum Technologies (QuantERA) program, as well as from the Fonds de la Recherche Scientifique – FNRS under project CHEQS within the Excellence of Science (EOS) program.

Author contributions
Xi-Lin Wang and Hui-Tian Wang designed the research and supervised the project; Chao Chen, Shu-Tian Xue, Yu-Peng Shi, Xi-Lin Wang and Hui-Tian Wang performed the experiment and implemented the numerics; Nicolas J. Cerf, Chao Chen, Shu-Tian Xue, Xi-Lin Wang and Hui-Tian Wang analyzed the results and wrote the manuscript; all authors discussed the results and reviewed the manuscript.

Competing interests
The authors declare no competing interests.

Additional information
Further material and details on the calculations are provided in Supplementary Information.

Two-particle quantum interference in a nonlinear optical medium: a witness of timelike indistinguishability