Ultracold Bose Mixtures with Spin-Dependent Fermion-Mediated Interactions

Mediated-interactions are ubiquitous in nature. In high energy physics, all fundamental interactions are mediated by gauge bosons [1]. In solid state physics, phonon-mediated electron-electron attractions are responsible for the formation of Cooper pairs, whose condensation leads to the phenomena of conventional superconductivity [2]. Ultracold atomic gases have emerged as a versatile platform to investigate quantum many-body physics [3, 4, 5]. Excitingly, it allows one to create controllable long-range interactions between atoms [6, 7], including direct electric and magnetic dipole interactions [8, 9, 10, 11, 12, 13, 14], phonon-mediated coupling in trapped ions [15, 16, 17], and photon-mediated interactions in optical cavities [18, 19, 20, 21, 22, 23]. Very recently, adding to the new excitements are the observations of fermion-mediated long-range interactions between bosons in Bose-Fermi mixtures [24, 25, 26]. There exist some theoretical efforts [27, 28, 29] for understanding such fermion-mediated interactions based on the linear response theory.

Binary Bose-Einstein condensates (BECs) have been the focus of both theoretical [30, 31, 32, 33, 34, 35, 36, 37, 38] and experimental [39, 40, 41, 42, 43, 44, 45] research over the past years. One of the key questions to ask is how this newly-achieved interaction reshapes our understanding of these exciting systems. Since homogeneous quantum gases have been realized in experiments [46, 47], theoretical understanding on the effects of fermion-mediated interactions upon homogeneous binary Bose mixtures becomes an experimentally interesting and urgent task.

In this work, we shall carry out a systematic study on a homogenous Bose-Fermi mixture, with the aim of laying down a solid and decent framework to treat such problems, fully characterizing fermion-induced interactions, and identifying new features arising from spin-dependent fermion-mediated interactions on binary BECs. First, we shall start from the functional representation of the partition function. By tracing out the fermions, we obtain an effective action entirely in terms of bosonic degrees of freedom, so that we can isolate the effects of fermion-mediated interactions upon the BECs. Second, we shall obtain the induced interactions in the static limit, where an analytic result for the effective interaction potential in real space exists. Third, we will examine how the induce interactions modify the Bogoliubov spectrum and lead to the damping of quasiparticles. Finally, we will explore the quantum fluctuation effects of the effective interaction potential on the density and spin density response of the binary BECs.

We consider a homogeneous mixture of two-species Bose gases and spin-polarized Fermi gases, described by the following grand canonical Hamiltonian

	$\displaystyle H$	$\displaystyle=$	$\displaystyle\int d^{3}\mathbf{r}\left(\mathcal{H}_{B}+\mathcal{H}_{F}+\mathcal{H}_{I}\right),$		(1a)
	$\displaystyle\mathcal{H}_{B}$	$\displaystyle=$	$\displaystyle\sum_{\sigma=\uparrow,\downarrow}\phi_{\sigma}^{\dagger}\left(-\frac{\hbar^{2}\nabla^{2}}{2m_{B}}-\mu_{\sigma}\right)\phi_{\sigma},$		(1b)
	$\displaystyle\mathcal{H}_{F}$	$\displaystyle=$	$\displaystyle\psi^{\dagger}(-\frac{\hbar^{2}\nabla^{2}}{2m_{F}}-\mu_{F})\psi,$		(1c)
	$\displaystyle\mathcal{H}_{I}$	$\displaystyle=$	$\displaystyle\sum_{\sigma=\uparrow,\downarrow}\left(g_{F\sigma}\psi^{\dagger}\psi n_{\sigma}+\frac{g_{\sigma\sigma}}{2}n_{\sigma}^{2}\right)+g_{\uparrow\downarrow}n_{\uparrow}n_{\downarrow}.$		(1d)

Here, $\phi_{\sigma}$ is the field operator for bosons with hyperfine state $\sigma=\{\uparrow,\downarrow\}$, $\mu_{\sigma}$ is the associated chemical potential, and $m_{B}$ is the mass of the atoms. For fermions, $\psi$ is the field operator and $\mu_{F}$ is the chemical potential. In the interaction term $\mathcal{H}_{I}$, $n_{\sigma}=\phi_{\sigma}^{\dagger}\phi_{\sigma}$ is the number operator for bosons of species $\sigma$, the coupling $g_{F\sigma}$ accounts for the interactions between the fermions and the bosons of species $\sigma$, and $g_{\sigma\sigma}$ accounts for the intraspecies interactions between bosons of species $\sigma$, while $g_{\uparrow\downarrow}=4\pi\hbar^{2}a_{\uparrow\downarrow}/m_{B}$ characterizes the interspecies interaction between bosons, where $a_{\uparrow\downarrow}$ is the s-wave interspecies scattering length. For convenience, we define the Fermi momentum $k_{F}=(6\pi^{2}n_{F})^{1/3}$ with $n_{F}$ being the number density of Fermi gases, the Fermi velocity $v_{F}=\hbar k_{F}/m_{F}$ and the corresponding Fermi energy $E_{F}=\hbar^{2}k_{F}^{2}/2m_{F}$. For brevity, we shall adopt natural units $k_{B}=\hbar=1$ hereafter.

Within the framework of imaginary-time field integral, the partition function of the system can be cast as $\mathcal{Z}=\int d[\bar{\psi},\psi]d[\phi_{\sigma}^{*},\phi_{\sigma}]e^{-S}$ with the action given by [48] $S=\int_{0}^{\beta}d\tau\left[H+\int d^{3}\mathbf{r}(\bar{\psi}\partial_{\tau}\psi+\sum_{\sigma}\phi_{\sigma}^{*}\partial_{\tau}\phi_{\sigma})\right]$, where $\beta=1/k_{B}T$ is the inverse temperature. To single out the fermion-mediated effects, we carry out the integration over the fermionic degrees of freedom, resulting in an effective action solely in terms of bosonic degrees of freedom $S_{eff}=\int d\tau d^{3}\mathbf{r}\mathcal{L}_{B}-Tr\ln\mathcal{M}$, where

	$\displaystyle\!\mathcal{L}_{B}$	$\displaystyle=$	$\displaystyle\sum_{\sigma}\left[\phi_{\sigma}^{*}(\partial_{\tau}-\frac{\nabla^{2}}{2m_{B}}-\mu_{\sigma})\phi_{\sigma}+\frac{g_{\sigma\sigma}}{2}n_{\sigma}^{2}\right]\!+g_{\uparrow\downarrow}n_{\uparrow}n_{\downarrow},$
	$\displaystyle\mathcal{M}$	$\displaystyle=$	$\displaystyle\partial_{\tau}-\frac{\nabla^{2}}{2m_{F}}-\mu_{F}+\sum_{\sigma}g_{F\sigma}\phi_{\sigma}^{*}\phi_{\sigma}.$		(2)

Up to this level, the formal manipulation of the partition function is exact. To distill low energy physics, we shall resort to some sorts of approximations to be addressed.

To proceed, we write $\phi_{\sigma}^{*}\phi_{\sigma}=\rho_{0\sigma}+\sum_{q\neq 0}\rho_{q\sigma}e^{iqx}$ with $x$ being spacetime coordinate and $q\equiv(\mathbf{q},iw_{m})$, and set $\mathcal{M}=-\mathcal{G}^{-1}+\mathcal{M}_{1}$ with $\mathcal{G}^{-1}=-\partial_{\tau}+\hbar^{2}\nabla^{2}/2m_{F}+\mu_{F}-\sum_{\sigma}g_{F\sigma}\rho_{0\sigma}$ being the inverse fermion Green’s function and $\mathcal{M}_{1}=\sum_{q\neq 0}\sum_{\sigma}g_{F\sigma}\rho_{q\sigma}e^{iqx}$. This allows one to write $Tr\ln\mathcal{M}=Tr\ln(-\mathcal{G}^{-1})+Tr\ln{(1-\mathcal{GM}_{1})}$ and to perform series expansions $-Tr\ln(1-\mathcal{GM}_{1})=\sum_{l=1}Tr\left[(\mathcal{G}\mathcal{M}_{1})^{l}\right]/l$. To fully exploit the translational invariance of the system, we shall evaluate the trace in the momentum-frequency representation. We expand the series up to the quadratic order ($l\leq 2$), resulting in

	$\displaystyle Tr(\mathcal{GM}_{1})=\mathcal{M}_{1}(0)\sum_{k}\mathcal{G}(k)=0,$		(3a)
	$\displaystyle\!Tr\left[(\mathcal{GM}_{1})^{2}\right]=\beta V\sum_{q\neq 0,\sigma\sigma^{\prime}}g_{F\sigma}g_{F\sigma^{\prime}}\Pi_{q}\rho_{q\sigma}\rho_{-q\sigma^{\prime}},\!$		(3b)
	$\displaystyle\Pi_{q}=\frac{1}{\beta V}\sum_{k}\mathcal{G}(k)\mathcal{G}(k+q).$		(3c)

Several comments are in order: For the series expansion, the $l=1$ term vanishes due to $\mathcal{M}_{1}(0)=0$ by definition, as can be seen from Eq. $(\ref{eq:one})$; The $l=2$ term corresponds to fermion-induced spin-dependent two-body interactions between bosons, as can be seen from Eq. $(\ref{eq:two})$ and Eq. $(\ref{eq:three})$, where we have defined $\Pi_{q}$, the so-called polarization function; We will neglect $l\geq 3$ terms, as they represent induced three-body or more interactions among bosons, which are usually irrelevant for dilute gases. By collecting the relevant terms, we arrive at the approximated effective action $S_{eff}=\int d\tau d\mathbf{r}\mathcal{L}_{B}-Tr\ln{(-\mathcal{G}^{-1})}+S_{ind}$, with the induced action given by $S_{ind}=\sum_{\sigma\sigma^{\prime}}g_{F\sigma}g_{F\sigma^{\prime}}/2\sum_{q\neq 0}\Pi_{q}\rho_{q\sigma}\rho_{-q\sigma^{\prime}}$. Remarkably, the induced action is purely a quantum fluctuating effect as the classical $q=0$ component is explicitly excluded.

In the spirit of the Bogoliubov theory, we split the bosonic field $\phi_{\sigma}$ into a mean-field part $\phi_{0\sigma}$ and a fluctuating part $\varphi_{\sigma}$. By retaining the fluctuating fields up to the quadratic order, we approximate the effective action as $S_{eff}\approx S_{0}+S_{g}$, where $S_{0}$ is the mean-field action and $S_{g}$ is the gaussian action with quadratic orders of the fluctuating fields $\varphi_{\sigma}^{*}$ and $\varphi_{\sigma}$. The grand potential density at mean-field level is given by $\Omega^{(0)}=S_{0}/\beta V$. The saddle point condition $\delta\Omega^{(0)}/\delta\phi_{0\sigma}^{*}=0$ leads to the Hugenholz-Pines theorem [49] determining the chemical potential $\mu_{\sigma}=g_{F\sigma}n_{F\sigma}+g_{\sigma\sigma}\left|\phi_{0\sigma}\right|^{2}+g_{\uparrow\downarrow}|\phi_{0\bar{\sigma}}|^{2}$. Without loss of generality, we set $\phi_{0\sigma}=\sqrt{n_{\sigma}}$, where $n_{\sigma}$ is the condensate density for bosons of species $\sigma$. The self-consistent condition for the fermion density is determined via $n_{F}=-\partial\Omega^{(0)}/\partial\mu_{F}$, which gives the chemical potential for the Fermi gases: $\mu_{F}=E_{F}+\sum_{\sigma}g_{F\sigma}n_{\sigma}$.

At the mean-field level, the ground-state energy density can be obtained via $E_{G}^{(0)}=\Omega^{(0)}+\mu_{F}n_{F}+\sum_{\sigma}\mu_{\sigma}n_{\sigma}$, yielding

$\displaystyle E_{G}^{(0)}=\frac{3}{5}n_{F}E_{F}+\sum_{\sigma}\left(\frac{g}{2}n_{\sigma}^{2}+g_{I}n_{\sigma}n_{F}\right)+g_{\uparrow\downarrow}n_{\uparrow}n_{\downarrow}.$

(4)

For the system to be stable, we naturally requires that the Hessian matrix constructed for the ground state energy to be positive definite, which leads to an extra constraint for a stable miscible phase

$\displaystyle n_{F}^{1/3}<\frac{(6\pi^{2})^{2/3}\left(g_{\uparrow\uparrow}g_{\downarrow\downarrow}-g_{\uparrow\downarrow}^{2}\right)}{3m_{F}\left(g_{F\uparrow}^{2}g_{\downarrow\downarrow}+g_{F\downarrow}^{2}g_{\uparrow\uparrow}-2g_{F\uparrow}g_{F\downarrow}g_{\uparrow\downarrow}\right)},$

(5)

in addition to the traditional miscible condition $g_{\uparrow\uparrow}g_{\downarrow\downarrow}-g_{\uparrow\downarrow}^{2}>0$ where $g_{\sigma\sigma}>0$ for a binary mixtures of Bose-Einstein condensates [30, 31, 32, 33].

Derived from $S_{ind}$, the Hamiltonian describing the induced two-body interactions between bosons through coupling with fermions reads $H_{ind}=\sum_{\sigma\sigma^{\prime}}g_{F\sigma}g_{F\sigma^{\prime}}/2\sum_{\mathbf{q\neq 0}}\Pi(\mathbf{q})\sum_{\mathbf{k,p}}\phi_{\mathbf{k+q}\sigma}^{\dagger}\phi_{\mathbf{p-q}\sigma^{\prime}}^{\dagger}\phi_{\mathbf{p}\sigma^{\prime}}\phi_{\mathbf{k}\sigma}$. Here, $\Pi_{\mathbf{q}}\equiv\Pi_{(\mathbf{q},0)}$ is the polarization function evaluated at the static limit at zero temperature, which reads

$\displaystyle\Pi_{\mathbf{q}}=-\frac{d(E_{F})}{4}\left[1+\frac{k_{F}^{2}-q^{2}/4}{k_{F}q}\ln\left|\frac{q+2k_{F}}{q-2k_{F}}\right|\right],$

(6)

where $d(E_{F})=m_{F}k_{F}/\pi^{2}$ is the density of states at the Fermi energy.

Performing the Fourier transform of $H_{ind}$ to real space, we obtain an induced pairwise spin-dependent interaction potential between two Bose atoms of species $\sigma$ and $\sigma^{\prime}$ with relative coordinate $\mathbf{r}$, given by

	$\displaystyle V_{ind}^{\sigma\sigma^{\prime}}(\mathbf{r})$	$\displaystyle=$	$\displaystyle-\frac{d(E_{F})g_{F\sigma}g_{F\sigma^{\prime}}}{4}V_{RKKY}(r),$		(7a)
	$\displaystyle V_{RKKY}(r)$	$\displaystyle=$	$\displaystyle\frac{\sin{(2k_{F}r)}-2k_{F}r\cos{(2k_{F}r)}}{2\pi k_{F}r^{4}}.$		(7b)

The induced spin-dependent attractive long-range interaction is of the RKKY type [50] in real space, where it decays at $1/r^{3}$ at large spatial separation and shows the Friedel oscillations at a period of $1/2k_{F}$, imprinted by the density of the Fermi gases.

Let us examine how the fermion-mediated interactions plays its role in the cerebrated Bogoliubov theory. For ease of notation, we focus on the situation where both boson species possess same number density and same intraspecies interaction strength: $n_{\uparrow}=n_{\downarrow}\equiv n_{B}$, $g_{\uparrow\uparrow}=g_{\downarrow\downarrow}\equiv g=4\pi\hbar^{2}a_{BB}/m_{B}$ and $g_{F\uparrow}=g_{F\downarrow}\equiv g_{FB}=2\pi\hbar^{2}a_{FB}(m_{F}^{-1}+m_{B}^{-1})$, where $a_{BB}$ and $a_{FB}$ are the respective s-wave scattering lengths. By defining a column vector $\Phi_{q}=(\varphi_{q\uparrow},\varphi_{q\downarrow},\varphi_{-q\uparrow}^{\dagger},\varphi_{-q\downarrow}^{\dagger})^{T}$, the gaussian action can be written in a compact form $S_{g}=(1/2)\sum_{q}\Phi_{q}^{\dagger}\mathcal{G}_{B}^{-1}\Phi_{q}$, with the inverse Green’s function $\mathcal{G}_{B}^{-1}(\mathbf{q},i\omega_{m})$ defined as follows

$\displaystyle\mathcal{G}_{B}^{-1}(\mathbf{q},z)=\begin{pmatrix}-z+a&b_{1}&b_{2}&b_{1}\\ b_{1}&-z+a&b_{1}&b_{2}\\ b_{2}&b_{1}&z+a&b_{1}\\ b_{1}&b_{2}&b_{1}&z+a\end{pmatrix},$

(8)

where $a=\epsilon_{\mathbf{q}}+(g+g_{FB}^{2}\Pi_{q})n_{B}$ with $\epsilon_{\mathbf{q}}=\mathbf{q}^{2}/2m_{B}$, $b_{1}=(g_{\uparrow\downarrow}+g_{FB}^{2}\Pi_{q})n_{B}$, and $b_{2}=(g+g_{FB}^{2}\Pi_{q})n_{B}$. The quasiparticle spectrum $\omega(\mathbf{q})$ and the damping rate $\gamma(\mathbf{q})$ can be found by solving the secular equation $det\mathcal{G}_{B}^{-1}(\mathbf{q},\omega-i\gamma)=0$ with the substitution of $\Pi_{q}|{i\omega_{m}\rightarrow\omega+i0^{\dagger}}$. This substitution corresponds to analytic continuation to real frequency ($i\omega\rightarrow\omega+i0^{\dagger}$), yielding the real and imaginary part of the polarization function, so-called the Lindhard function [51]

	$\displaystyle Re\Pi$	$\displaystyle=$	$\displaystyle-\frac{d(E_{F})}{4}\left[1+\sum_{s=\pm}s\frac{1-u_{s}^{2}}{2q/k_{F}}\ln{\left|\frac{1+u_{s}}{1-u_{\bar{s}}}\right|}\right],$		(9a)
	$\displaystyle Im\Pi$	$\displaystyle=$	$\displaystyle d(E_{F})\frac{\pi k_{F}}{8q}\left[\sum_{s=\pm}s(1-u_{s}^{2})\Theta(1-u_{s}^{2})\right],$		(9b)

where $u_{\pm}=\omega/qv_{F}\pm q/2k_{F}$ and $\bar{s}=-s$. The system accommodates two branches of excitations $\omega_{\pm}(\mathbf{q})$, where the upper branch is given by $\omega_{+}(\mathbf{q})=Re\sqrt{\epsilon_{\mathbf{q}}\left[\epsilon_{\mathbf{q}}+2(g+g_{\uparrow\downarrow}+2g_{FB}^{2}\Pi_{q})n_{B}\right]}$ and the lower branch is given by $\omega_{-}(\mathbf{q})=\sqrt{\epsilon_{\mathbf{q}}\left[\epsilon_{\mathbf{q}}+2(g-g_{\uparrow\downarrow})n_{B}\right]}$. It is evident that the upper branch gets modified by the induced interaction, while the lower branch is left intact.

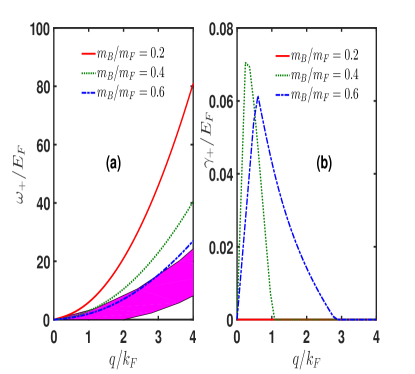
The quasiparticle spectrum for the upper branch $\omega_{+}(\mathbf{q})$ and the associated damping rates $\gamma_{+}(\mathbf{q})$ for three typical mass ratios $m_{B}/m_{F}=0.2$, $0.4$, and $0.6$ are shown in Fig. 1. On panel (a), the shade region has nonzero damping rates. This is found by requiring $Im\Pi\neq 0$, which leads to an inequality constraint $(q/k_{F})^{2}-2q/k_{F}<\omega/E_{F}<(q/k_{F})^{2}+2q/k_{F}$ in the $(\mathbf{q},\omega)$ plane. For a small mass ratio $m_{B}/m_{F}=0.2$, the excitation spectrum lies outside the shade region, indicating that it is well-defined and long-lived. With a large mass ratio, the excitation gets damped, propagating with a finite lifetime $1/\gamma$. As shown in panel (b), the damping rate remains zero for varying momentum amplitude at $m_{B}/m_{F}=0.2$. For a larger mass ratio, the damping rate features a sharp peak, with the momentum amplitude at which the maximum damping occurs shifts to a higher value.

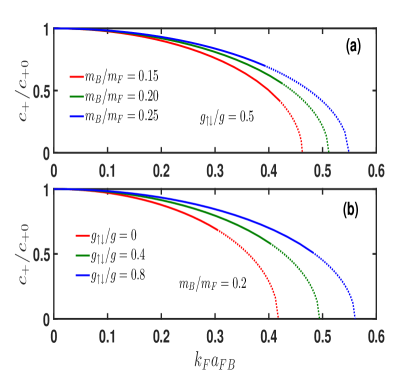
At long wavelength, the excitation spectrum is phonon-like with characteristic dispersion $\omega(\mathbf{q})=cq$, where $c$ is the sound velocity. We show the sound velocity $c_{+}$ for the upper branch of the excitation spectrum in Fig. 2. In the absence of Bose-Fermi coupling $k_{F}a_{FB}=0$, the sound velocity reduces to $c_{+0}=\sqrt{(g+g_{\uparrow\downarrow})n_{B}/m_{B}}$. As the coupling parameter $k_{F}a_{FB}$ increases, the sound velocity decreases monotonically, first with a solid line (undamped mode), then with a dotted line (damped mode), before it terminates at zero when reaching a phase boundary separating miscible and immiscible phases. Interestingly, one can verify that the positivity of the sound velocity ($g+g_{\uparrow\downarrow}+2g_{BF}^{2}\Pi_{0}>0$) leads to a constraint consistent with Eq. (5), which can be translated as $(k_{F}a_{FB})^{2}<\pi k_{F}(a_{BB}+a_{\uparrow\downarrow})m_{F}m_{B}/(m_{F}+m_{B})^{2}$. Increasing the mass ratio $m_{B}/m_{F}$ leads to an increase of the sound velocity, as shown in panel (a). The larger interspecies coupling between bosons $g_{\uparrow\downarrow}/g$, the bigger the sound velocity, as indicated in panel (b).

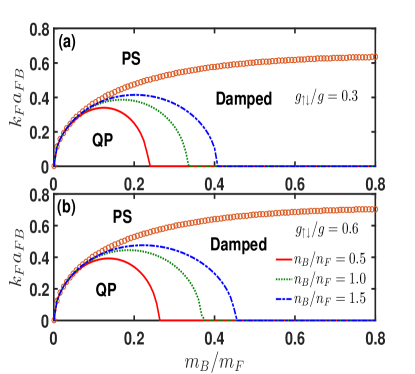
We are now in a position to construct a ground-state phase diagram, spanned by mass ratio $m_{B}/m_{F}$ and Bose-Fermi coupling parameter $k_{F}a_{FB}$. The phase stability constraint provided by Eq. (5) marks the phase boundary separating stable miscible phase and phase separation (PS) into bosons and fermions or a purely boson phase coexisting with a mixed phase [52, 53, 54], shown in Fig. 3, which stays intact for varying number density ratio $n_{B}/n_{F}$. In the stable miscible phase, we can further classify it into region accommodating long-lived quasiparticle excitations and region residing quasiparticle excitations of finite lifetime due to the Landau damping. To search for well-behaved, long-lived excitations, we consider the region satisfying $Im\Pi(\mathbf{q},\omega)=0$, which occurs at $\omega/qv_{F}>1+q/2k_{F}$ [see Eq. (9b)]. At long wavelength, this becomes $c_{+}/E_{F}>2k_{F}$, yielding $(k_{F}a_{FB})^{2}<\pi m_{F}m_{B}/(m_{F}+m_{B})^{2}\left[k_{F}(a_{BB}+a_{\uparrow\downarrow})-3\pi n_{F}m_{B}^{2}/(2n_{B}m_{F}^{2})\right]$. As shown in Fig. 3, tuning up the number density ratio $n_{B}/n_{F}$ expands the region of quasiparticle excitations with infinite lifetime (QP). Increasing the interspecies coupling $g_{\uparrow\downarrow}/g$ contributes to a broadened region of QP, and a shrinkage of damped region. The reason behind the fact that we have focused on the Landau damping of the collective long-wavelength excitations is that Beliaev damping is strongly suppressed at low momenta [55].

Now we turn to examine the effects of quantum fluctuation arising from the effective interaction potential on the properties of the binary BECs. The static structure factor $S(\mathbf{q})$ probes density fluctuations of a system. It provides information both on the spectrum of collective excitations and the momentum distribution. We can evaluate the static structure at the Bogoliubov level as follows:

	$\displaystyle S(\mathbf{q})$	$\displaystyle=$	$\displaystyle\frac{1}{2N_{B}}<\delta\rho_{\mathbf{q}}^{\dagger}\delta\rho_{\mathbf{q}}>=\frac{1}{2}\sum_{i\omega_{m}}\sum_{i,j=1}^{4}\mathcal{G}_{Bij}(\mathbf{q},i\omega_{m})$		(10)
		$\displaystyle=$	$\displaystyle\frac{\epsilon_{\mathbf{q}}}{\omega_{+}(\mathbf{q})}\cot{\frac{\beta\omega_{+}(\mathbf{q})}{2}}.$

This corresponds to the Feynman relation [56] for the upper branch, which connects the static structure factor to the excitation spectrum for a Bose superfluid enjoys time-reversal symmetry. The Bragg spectroscopy can be employed to measure the zero-temperature structure factor of the system [57].

Similarly, the spin density structure factor $S_{\sigma}(\mathbf{q})$ can be determined as follows:

	$\displaystyle S_{\sigma}(\mathbf{q})$	$\displaystyle=$	$\displaystyle\frac{1}{2N_{B}}<\delta(\rho_{\mathbf{q}\uparrow}-\rho_{\mathbf{q}\downarrow})^{\dagger}\delta(\rho_{\mathbf{q}\uparrow}-\rho_{\mathbf{q}\downarrow})>$		(11)
		$\displaystyle=$	$\displaystyle\frac{1}{2}\sum_{i\omega_{m}}\sum_{i,j=1}^{4}(-1)^{i+j}\mathcal{G}_{Bij}(\mathbf{q},i\omega_{m})$
		$\displaystyle=$	$\displaystyle\frac{\epsilon_{\mathbf{q}}}{\omega_{-}(\mathbf{q})}\cot{\frac{\beta\omega_{-}(\mathbf{q})}{2}}.$

This is precisely the Feynman relation for the lower branch, which connects the spin structure factor to the excitation spectrum of the Bose superfluid. Since the lower branch is left intact for the induced interaction, we deduce that the spin density structure factor is immune to the Bose-Fermi coupling. The spin structure factor can be measured from noise correlations or Bragg scattering of light [58, 59].

In summary, we find that spin-dependent fermion-mediated interactions dramatically modify the properties of the binary BECs. The upper branch is affected by the induced interactions, while the lower branch is clearly not. We map out the phase diagram based on the phase stability condition and Landau damping of the excitations of the upper branch. It consists of the phase boundary separating stable region of miscible phases and unstable region toward phase separation. Due to the fermion-mediated interactions, we find that the stable region can be further classified into two parts based on the damping of the excitations. The predicted damping rate can be probed experimentally via two-phonon Bragg spectroscopy [60]. We find that both the density structure factor and spin density structure factor satisfy the Feynman relation, reflecting density and spin excitations respectively. Experimental verifications of new features predicted in this work is expected to provide a significant advance to our understanding of emergent phenomena associated with spin-dependent fermion-mediated interactions.