Unbounded Slice Sampling

Daichi Mochihashi
The Institute of Statistical Mathematics
daichi@ism.ac.jp

( 2020-1-5 (Sun) )

Abstract

Slice sampling is an efficient Markov Chain Monte Carlo algorithm to sample from an unnormalized density with acceptance ratio always $1$ . However, when the variable to sample is unbounded, its “stepping-out” heuristic works only locally, making it difficult to uniformly explore possible candidates. This paper proposes a simple change-of-variable method to slice sample an unbounded variable equivalently from $[\kern 1.1pt0,1)$ .

1 Introduction

Slice sampling [1] is one of the Markov Chain Monte Carlo (MCMC) methods to sample from one-dimensional distribution. Because its acceptance probability is always $1$ as opposed to famous Metropolis-Hastings algorithm [2], slice sampling is widely employed in modern statistics and machine learning problems, especially for sampling hyperparameters of a statistical model where each hyperparameter is often univariate but has a nontrivial likelihood surface.

When the variable to sample is not bounded, an algorithm called “stepping-out” [3] is usually employed to adaptively adjust the interval to sample from based on the current value of the variable. However, this “stepping-out” works only locally, thus will be potentially trapped to local modes in multimodal likelihoods. In contrast, in this paper we propose a simple method to uniformly sample from an unbounded variable through an appropriate reparametrization with a unit interval $[\kern 1.1pt0,1)$ .

2 Slice sampling

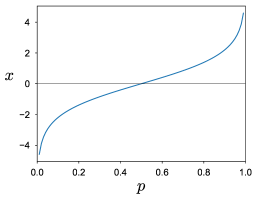
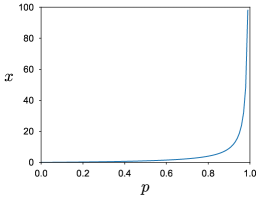
Refer to caption — (a) Sigmoid map $\displaystyle p=\frac{1}{1+e^{-x}}$

Slice sampling iteratively draws $x$ from a probability distribution

p(x)=\frac{f(x)}{Z}

(1)

without knowing the normalizing constant $\displaystyle Z\!=\!\int\!f(x)dx$ by the following general algorithm, starting from an initial value $x^{(0)}$ :

Algorithm 1 General slice sampling

1: for

t=1\cdots T

\ell=f(x^{(t-1)})

\rho\sim{\rm Uniform}[0,\ell)

x^{(t)}\sim{\rm Uniform}(\{x:f(x)>\rho\})

5: end for

In practice, Step $4$ of the Algorithm 1 is not trivial, and usually “stepping-out” heuristic [1] is employed to determine the interval from which $x$ is uniformly drawn, starting from an initial interval enclosing $x$ that is adaptively expanded.

However, the efficiency of “stepping-out” depends on setting the initial interval whose appropriate scale for the problem is not known in advance. Moreover, it works only locally: if $f(x)$ has multiple and distant modes, it tends to wander around a single mode and will spend a very long time to explore different modes that might have higher probabilities.

On the other hand, if $x$ is bounded and known to always reside in the interval $[{\it st},{\it ed}]$ , slice sampling is very easy using the following algorithm:

Algorithm 2 Bounded slice sampling

1: for

t=1\cdots T

\ell=f(x^{(t-1)})

\rho\sim{\rm Uniform}[0,\ell)

4: while true do

x\sim{\rm Uniform}[{\it st},{\it ed}]

/* generate a candidate */

6: if

f(x)>\rho

then

x^{(t)}=x

; break

8: else /* modify interval */

9: if

x<x^{(t-1)}

then

10:

{\it st}:=x

11: else

12:

{\it ed}:=x

13: end if

14: end if

15: end while

16: end for

This is an efficient binary search that quickly draws $x$ uniformly over the region $[{\it st},{\it ed}]$ where $f(x)>\rho$ .

3 Unbounded slice sampling

Algorithm 2 is effective for a bounded $x$ that is known to reside in $[{\it st},{\it ed}]$ . However, even when $x$ is unbounded, we can sample $x$ through an one-to-one map between $[\kern 1.1pt0,1)$ and $\mathbb{R}$ .

General unbounded variate:

For example, using a sigmoid map

	$\displaystyle p$	$\displaystyle=\frac{1}{1+e^{-x}}$		(2)
	$\displaystyle\text{\it i.e.}\qquad x$	$\displaystyle=-\log\left(\frac{1}{\,p\,}-1\right)$		(3)

for $p\in[\kern 1.1pt0,1)$ shown in Figure 1(a), for each $x\in\mathbb{R}$ we can associate $p\in[\kern 1.1pt0,1)$ and vice versa.

Since

\frac{dx}{dp}=\frac{1}{p(1-p)}~{},

(4)

we can alternatively sample $p$ in place of $x$ using the exchange of variables:

f(x)dx=f(x)\frac{dx}{dp}dp=f\left(-\log\left(\frac{1}{\,p\,}-1\right)\right)\frac{1}{p(1-p)}dp

(5)

Using (5) for the Algorithm 2 in place of $f(x)$ can sample $p\in[\kern 1.1pt0,1)$ , from which we can recover $x$ by the relationship (3).

Positive variate:

When $x>0$ , for example we can exploit a map

x=\frac{p}{1-p}

(6)

therefore

\frac{dx}{dp}=\frac{1}{(1-p)^{2}}~{},

(7)

leading

f(x)dx=f(x)\frac{dx}{dp}dp=f\left(\frac{p}{1-p}\right)\frac{1}{(1-p)^{2}}dp

(8)

to sample $p\in[\kern 1.1pt0,1)$ and obtain $x$ by the relationship (6).

Using this reparameterization, we can slice sample an unbounded $x$ essentially by a “probabilistic binary search” always on $[\kern 1.1pt0,1)$ . We included sample of MATLAB and C codes for our unbounded slice sampling in Appendix B and C.

In practice, sometimes we cannot compute a corresponding $p$ for very large (or small) $x$ using equation (2). Therefore, instead of (2) we can use

p=\sigma(x/A)=\frac{1}{1+e^{-x/A}}

(9)

for some constant $A>0$ as shown in Figure 2. While every $x\in\mathbb{R}$ is mathematically equivalent, notice that usually the parameter to sample from a statistical model roughly¹¹1 This is important, because we do not enforce a strict interval to sample $x$ in this paper. resides in this regime; even if $x$ will exceed over this regime, we can safely rescale $x$ to fit into a decent interval. We empirically confirmed that $A=100$ usually works fine for $-1000<x<1000$ (see Section 4).

4 Experiments

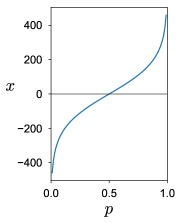
We conducted some experiments to confirm that our unbounded slice sampler correctly samples from a given distribution. Using the C code shown in Appendix A, we can easily sample from $p(x)$ .

For a general unbounded case $x\in\mathbb{R}$ , Figure 3 shows the plots of sampled $x$ from (a) $f(x)=\exp(-(x\!-\!500)^{2}/10)$ , (b) $f(x)=\exp(-(x\!-\!500)^{2}/10)$ , and (c) $f(x)=\exp(-(x\!-\!1000)^{2}/100)$ . Note that $p(x)$ will be high on different regimes for each case: roughly $0<x<4$ for (a), $x\approx 500$ for (b), and $x\approx 1000$ for (c), while these regimes are not known in advance, and they have different variances. Figure 3 clearly shows we can correctly sample from $p(x)$ , even when $x$ is very large using the map (9) with $A\!=\!100$ . The average step of “binary search”, i.e. the number of function evaluations for the loop in Step 4 of the Algorithm 2, is $11.44$ for (a), $16.48$ for (b), and $9.34$ for (c).

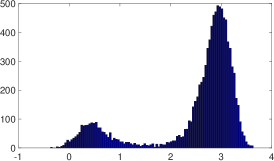
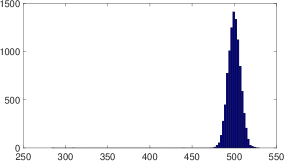
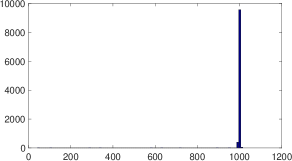
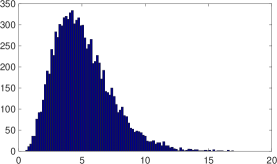
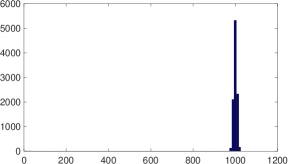
For a positive case $x\in\mathbb{R}^{+}$ , Figure 4 shows the results for (a) $f(x)=x^{4}e^{-x}$ and (b) $f(x)=\exp(-(x\!-\!1000)^{2}/100)$ ; (a) means $p(x)\sim{\rm Gamma}(5,1)$ .

Comparison with stepping-out

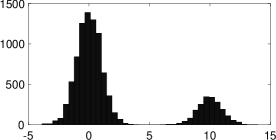
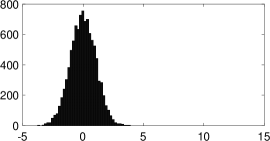
To confirm the advantage of our unbounded slice sampling, we also conducted an experiment to sample from a multimodal distribution. Specifically, Figure 5 shows a draw of $10,000$ samples from a Gaussian mixture model $p(x)=0.8\mathcal{N}(x|0,1^{2})+0.2\mathcal{N}(x|10,1^{2})$ using unbounded slice sampler and “stepping-out” algorithm, respectively.

Clearly, “stepping-out” is stuck into the first mode because the sampling starts from $x=1$ , and this tendency remained the same over multiple simulations. Moreover, because “stepping-out” linearly increases the interval to sample from, sampling from a distant density shown in Figure 3(c) required about $2,000$ function evaluations at first to reach the mode, while unbounded slice sampling required only $9.34$ as described before, thanks to the efficient “probabilistic binary search” on $\mathbb{R}$ .

References

[1] Radford M. Neal. Slice sampling. Annals of Statistics, pages 705–741, 2003.
[2] W. R. Gilks, S. Richardson, and D. J. Spiegelhalter. Markov Chain Monte Carlo in Practice. Chapman & Hall / CRC, 1996.
[3] David J. C. MacKay. Information Theory, Inference, and Learning Algorithms. Cambridge University Press, 2003.

Appendix

Appendix A C code of easy slice sampling

#include "slice.h"

double
f (double x, void *arg)
{
        return - x * (x - 1) * (x - 2) * (x - 3.5);
}

main () {
        int i, N = atoi (argv[1]);
        double x = 1;

        for (i = 0; i < N; i++) {
                x = slice_sample (x, f, NULL);
                printf("%lf\n", x);
        }
}

Appendix B C code for unbounded slice sampling

/*
 *    slice.c
 *    Unbounded slice sampling with ease.
 *    $Id: unbounded.tex,v 1.17 2020/01/03 01:23:08 daichi Exp $
 *
 */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "random.h"

static double A = 100.0;
typedef double (*likfun)(double x, void *args);

static double
expand (double p)        /* p -> x */
{
        return - A * log (1 / p - 1);
}

static double
shrink (double x)        /* x -> p */
{
        return 1 / (1 + exp(- x / A));
}

static double
expandp (double p)        /* p -> (x > 0) */
{
        return p / (1 - p);
}

static double
shrinkp (double x)        /* (x > 0) -> p */
{
        return  x / (1 + x);
}

double
slice_sample (double x, likfun loglik, void *arg)
{
        double st = 0, ed = 1;
        double r, rnew, slice, newlik;
        int iter, maxiter = 1000;

        r = shrink (x);
        slice = (*loglik)(x, arg) - log (A * r * (1 - r)) + log (RANDOM);

        for (iter = 0; iter < maxiter; iter++)
        {
                rnew = unif (st, ed);
                newlik = (*loglik)(expand(rnew), arg)
                                        - log (A * rnew * (1 - rnew));

                if (newlik > slice)
                        return expand (rnew);
                else if (rnew > r)
                        ed = rnew;
                else if (rnew < r)
                        st = rnew;
                else
                        return x;
        }
        fprintf(stderr, "slice_sample: max iteration %d reached.\n", maxiter);
        return x;
}

double
slice_sample_positive (double x, likfun loglik, void *arg)
{
        double st = 0, ed = 1;
        double r, rnew, slice, newlik;
        int iter, maxiter = 1000;

        r = shrinkp (x);
        slice = (*loglik)(x, arg) - 2 * log (1 - r) + log (RANDOM);

        for (iter = 0; iter < maxiter; iter++)
        {
                rnew = unif (st, ed);
                newlik = (*loglik)(expandp(rnew), arg) - 2 * log (1 - rnew);

                if (newlik > slice)
                        return expandp (rnew);
                else if (rnew > r)
                        ed = rnew;
                else if (rnew < r)
                        st = rnew;
                else
                        return x;
        }
        fprintf(stderr, "slice_sample: max iteration %d reached.\n", maxiter);
        return x;
}

#if 1

double
f (double x, void *arg)
{
        return - x * (x - 1) * (x - 2) * (x - 3.5);
}

double
g (double x, void *arg)
{
        return - 10 * (x + 1000) * (x + 1000);
}

double
h (double p, void *arg)
{
        double a = 2, b = 3;
        return (a - 1) * log (p) + (b - 1) * log (1 - p);
}

int
main (int argc, char *argv[])
{
        int i, N = atoi(argv[1]);
        double x = 0.5;

        for (i = 0; i < N; i++)
        {
                x = slice_sample (x, g, NULL);
                // x = slice_sample_positive (x, f, NULL);
                printf("%.4lf\n", x);
        }
}

#endif

Appendix C MATLAB code for unbounded slice sampling

function xnew = slice_sample (x,likfun,varargin)
% xnew = slice_sample (x,likfun,varargin)
% Unbounded slice sampling in MATLAB.
% $Id: unbounded.tex,v 1.17 2020/01/03 01:23:08 daichi Exp $
global A;
A  = 100;
st = 0; ed = 1;
maxiter = 1000;
% function body
r = shrink (x);
slice = feval (likfun,x,varargin{:}) - log (A * r * (r - 1)) + log (rand());
% slice sampling
for iter = 1:maxiter
  rnew = unif (st,ed);
  xnew = expand (rnew);
  newlik = feval (likfun,xnew,varargin{:}) - log (A * rnew * (rnew - 1));
  if (newlik > slice)
    return;
  elseif (rnew > r)
    ed = rnew;
  elseif (rnew < r)
    st = rnew;
  else
    return;
  end
end
fprintf(stderr,’slice_sample: max iteration %d reached\n’,maxiter);
return;

function p = shrink(x)Ψ% x -> p
global A;
p = 1 / (1 + exp (- x / A));

function x = expand(p)Ψ% p -> x
global A;
x = - A * log (1 / p - 1);

function xnew = slice_sample_positive (x,likfun,varargin)
% xnew = slice_sample_positive (x,likfun,varargin)
% Unbounded slice sampling in MATLAB. (only positive)
% $Id: unbounded.tex,v 1.17 2020/01/03 01:23:08 daichi Exp $
st = 0; ed = 1;
maxiter = 1000;
% function body
r = shrinkp (x);
slice = feval (likfun,x,varargin{:}) - 2 * log (1 - r) + log (rand());
% slice sampling
for iter = 1:maxiter
  rnew = unif (st,ed);
  xnew = expandp (rnew);
  newlik = feval (likfun,xnew,varargin{:}) - 2 * log (1 - rnew);
  if (newlik > slice)
    return;
  elseif (rnew > r)
    ed = rnew;
  elseif (rnew < r)
    st = rnew;
  else
    return;
  end
end
fprintf(stderr,’slice_sample: max iteration %d reached\n’,maxiter);
return;

function p = shrinkp (x)Ψ% (x > 0) -> p
p = x / (1 + x);

function x = expandp (p)Ψ% p -> (x > 0)
x = p / (1 - p);