Uncertainty quantification by block bootstrap for differentially private stochastic gradient descent

In times where data is collected almost everywhere and anytime, privacy is an important issue that has to be addressed in any data analysis. In the past, successful de-anonymisation attacks have been performed (see, for example, Narayanan and Shmatikov,, 2006; Gambs et al.,, 2014; Eshun and Palmieri,, 2022) leaking private, possible sensitive data of individuals. Differential Privacy (DP) is a framework that has been introduced by Dwork et al., (2006) to protect an individuals data against such attacks while still learning something about the population. Nowadays, Differential Privacy has become a state-of-the-art framework which has been implemented by the US Census and large companies like Apple, Microsoft and Google (see Ding et al.,, 2017; Abowd,, 2018).
The key idea of Differential Privacy is to randomize the data or a data dependent statistic. This additional randomness guarantees that the exchange of one individual merely changes the distribution of the randomized output. In the last decade, numerous differentially private algorithms have been developed, see for example Wang et al., (2020); Xiong et al., (2020); Yang et al., (2023) and the references therein. In many cases differentially private algorithms are based on already known and well studied procedures such as empirical risk minimisation, where either the objective function (objective pertubation) or the minimizer of that function (output perturbation) is privatized, or statistical testing, where the statistic is privatized, see for example Chaudhuri et al., (2011); Vu and Slavkovic, (2009). Two different concepts of differential privacy are distinguished in the literature: the first one, called (global) Differential Privacy (DP) assumes the presence of a trusted curator, who maintains and performs computations on the data and ensures that a published statistic satisfies a certain privacy guarantee. The second one, which is considered in this paper, does not make this assumption and is called local Differential Privacy (LDP). Here it is required that the data is collected in a privacy preserving way.
Besides privacy there is a second issue which has to be addressed in the analysis of massive data, namely the problem of computational complexity. A common and widely used tool when dealing with large-scale and complex optimization problems in big data analysis is Stochastic Gradient Descent (SGD), which is already introduced in the early work of Robbins and Monro, (1951). This procedure computes data based, iteratively and in an online fashion an estimate of the minimizer

of a function $L$. The convergence properties of adaptive algorithms, such as SGD, towards $\theta_{\star}$ are well studied, see for example the monograph Benveniste et al., (1990) and the references therein. Mertikopoulos et al., (2020) investigate SGD in case of non convex functions and show convergence to a local minimizer.
There also exists a large amount of work on statistical inference based on SGD estimation starting with the seminal papers of Ruppert, (1988) and Polyak and Juditsky, (1992), who establish asymptotic normality of the averaged SGD estimator for convex functions. The covariance matrix of the asymptotic distribution has a sandwich form, say $G^{-1}SG^{-1}$, and Chen et al., (2020) propose two different approaches to estimate this matrix. An online version for one of these methods is proposed in Zhu et al., (2021), while Yu et al., (2021) generalize these results for SGD with constant stepsize and non convex loss functions. Recent literature on UQ for SDG includes Su and Zhu, (2018), who propose iterative sample splitting of the path of SGD, Li et al., (2018), who consider SGD with constant stepsize splitting the whole path into segments, and Chee et al., (2023), who construct a simple confidence interval for the last iterate of SGD.
Song et al., (2013) investigate SGD under DP and demonstrate that mini-batch SGD has a much better accuracy than estimators obtained with batch size $1$. However, mini-batch SGD with a batch size larger than $1$ only guarantees global DP and therefore requires the presence of a trusted curator. Among other approaches for empirical risk minimization, Bassily et al., (2014) derive a utility bound in terms of the excess risk for an $(\epsilon,\delta)$-DP SGD and Avella-Medina et al., (2023) investigate statistical inference for noisy gradient descent under Gaussian DP.
On the other hand, statistcial inference for SGD under LDP is far less explored. Duchi et al., (2018) show the minimax optimality of the LDP SGD median but do not provide confidence intervals for inference. The method of Chen et al., (2020) is not always applicable (for example, for quantiles) and requires an additional private estimate of the matrix $G$ in the asymptotic covariance matrix of the SDG estimate. Recently, Liu et al., (2023) propose a self-normalizing approach to obtain distribution free locally differentially private confidence intervals for quantiles. However, this method is tailored to a specific model and it is well known that the nice property of distribution free inference by self-normalization comes with the price of a loss in statistical efficiency (see Dette and Gösmann,, 2020, for an example in the context of testing).
A natural alternative is the application of bootstrap, and bootstrap for SGD in the non-private case has been studied by Fang et al., (2018); Zhong et al., (2023). These authors propose a multiplier approach where SGD is executed $B$ times multiplying the updates by non-negative random variables. However, to ensure $\epsilon$-LDP, the privacy budget must be split over all $B$ bootstrap versions, leading to large noise levels and high inaccuracy of the resulting estimators. There is also ongoing research on parametric Bootstrap under DP, (see Ferrando et al.,, 2022; Fu et al.,, 2023; Wang and Awan,, 2023) who assume that the parameter of interest characterizes the distribution of the data, which is not necessarily the case for SGD. Finally we mention Wang et al., (2022), who introduce a bootstrap procedure under Gaussian DP, where each bootstrap estimator is privately computed on a random subset.

Our Contribution: In this paper we propose a computational tractable method for statistical inference using SGD under LDP. Our approach provides a universally applicable and statistically valid method for uncertainty quantification for SDG and LDP-SGD. It is based on an application of the block bootstrap to the mean of the iterates obtained by SGD. The (multiplier) block bootstrap is a common principle in time series analysis (see Lahiri,, 2003). However, in contrast to this field, where the dependencies in the sequence of observations are quickly decreasing with an increasing lag, the statistical analysis of such an approach for SGD is very challenging. More precisely, SGD produces a sequence of highly dependent iterates, which makes the application of classical concepts from time series analysis such as mixing (see Bradley,, 2005) or physical dependence (see Wu,, 2005) impossible. Instead, we use a different technique and show the consistency of the proposed multiplier block bootstrap for the LDP-SGD under appropriate conditions on the block length and the learning rate. As a by-product our results also provide a new method of UQ for SGD and for mini-batch SGD in the non-private case.

Notations: $\lVert\cdot\rVert$ denotes a norm on $\mathbb{R}^{d}$ if not further specified. $\overset{d}{\to}$ denotes weak convergence and $\overset{\mathbb{P}}{\to}$ denotes convergence in probability.

Stochastic Gradient Descent (SGD). Define $L(\theta)=\mathbb{E}[\ell(\theta,X)]$, where $X$ is a $\mathbb{X}$-valued random variable and $\ell:\mathbb{R}^{d}\times\mathbb{X}\to\mathbb{R}$ is a loss function. We consider the optimization problem (1). If $L$ is differentiable and convex, then this minimization problem is equivalent to solving

where $R=\nabla L$ is the gradient of $L$. SGD computes an estimator $\bar{\theta}$ for $\theta_{\star}$ using noisy observations $g(X_{i},\cdot)$ of the gradient $R(\cdot)$ in an iterative way. Note that $g$ does not need to be differentiable with respect to $\theta$. The iterations of SGD are defined by

where $\eta_{i}=ci^{-\gamma}$ with parameters $c>0$ and $\gamma\in(0.5,1)$ is the learning rate and the quantity $\xi_{i}=g(X_{i},\theta_{i-1})-R(\theta_{i-1})$ is called measurement error in the $i$th iteration (note that we do not reflect the dependence on $\theta_{i-1}$ and $X_{i}$ in the definition of $\xi_{i}$). The estimator of $\theta_{\star}$ is finally obtained as the average of the iterates, that is

Note that the first representation in (2) can be directly used for implementation, while the second is helpful for proving probabilistic properties of SGD. For example Polyak and Juditsky, (1992) show that, under appropriate conditions, $\sqrt{n}(\bar{\theta}-\theta_{\star})$ is asymptotically normal distributed where the covariance matrix $\Sigma$ of the limit distribution depends on the optimization problem and the variance of the measurement errors $\xi_{t}$.

The use of only one observation $g(X_{i},\theta_{i-1})$ in SGD yields a relatively large measurement error in each iteration which might result in inaccurate estimation of the gradient $R(\theta_{i-1})$. Therefore, several authors have proposed a variant of SGD, called mini-batch SGD, where $s\geq 1$ observations $g(X_{i_{1}},\tilde{\theta}_{i-1}),\ldots,g(X_{i_{s}},\tilde{\theta}_{i-1})$ are used for the update. An estimator for $R(\tilde{\theta}_{i-1})$ is then given by the mean of this observations, yielding the recursion

where the measurement error is given by $\tilde{\xi}_{i}=\frac{1}{s}\sum_{j=1}^{s}g(X_{i_{j}},\tilde{\theta}_{i-1})-R(\tilde{\theta}_{i-1})$, see for example Cotter et al., (2011); Khirirat et al., (2017).

In this paper we work under the constraints of local differential privacy (LDP).

The following result is well known (see, for example Dwork and Roth,, 2014).

Two well known privacy mechanism are the following:

Local Differential Private Stochastic Gradient Descent (LDP-SGD). By Theorem˜2.1 it follows that SGD is $\epsilon$-ldp if the noisy observations $g(X_{i},\theta_{i-1})$ in (2) are computed in a way that preserves $\epsilon$-LDP. Let $\mathcal{A}$ be such an $\epsilon$-ldp mechanism for computing $g$. The LDP-SGD updates are then given by

where

captures the error due to measurement and

captures the error due to privacy. Analog to (3), the final ldp SDG estimate is defined by

In this section, we will develop a multiplier block bootstrap approach to obtain the distribution of the LDP-SGD estimate $\bar{\theta}^{LDP}$ defined in (9) by resampling. We also prove that this method is statistically valid in the sense that the bootstrap distribution converges weakly (conditional on the data) to the limit distribution of the estimate $\bar{\theta}^{LDP}$, which is derived first.

Our first result is a direct consequence of Theorem 2 in Polyak and Juditsky, (1992) which can be applied to LDP-SGD.

In principle ldp statistical inference based on the statistic $\bar{\theta}^{LDP}$ can be made using the asymptotic distribution in Theorem 3.1 with an ldp estimator of the covariance matrix $\Sigma$ in (10). For this purpose the matrices $G$ and $S$ have to be estimated in an ldp way. While $S$ can be estimated directly from the ldp observations $\mathcal{A}(g(X_{i},\theta_{i-1}^{LDP}))$ in (6) by

the matrix $G$ has to be estimated separately. Therefore, the privacy budget has to be split on the estimation of $G$ and on the iterations of SGD. As a consequence this approach leads to high inaccuracies since all components need to be estimated in a ldp way. Furthermore, common estimates of $G$ are based on the derivative of $g$ (with respect to $\theta$), and therefore $g$ needs to be differentiable. This excludes important examples such as quantile regression. Additionally, the computation of the inverse of $G$ can become computationally costly in high dimensions.

As an alternative we will develop a multiplier block bootstrap, which avoids these problems. Before we explain our approach in detail we note that the bootstrap method proposed in Fang et al., (2018) for non private SGD is not applicable in the present context. These authors replace the recursion in (2) by $\theta_{i}^{\star}=\theta_{i-1}^{\star}-\eta_{i}w_{i}g(X_{i},\theta_{i-1}^{\star})$ where $w_{1},\ldots,w_{n}$ are independent identically distributed non-negative random variables with $Var(w_{i})=1=\mathbb{E}[w_{i}]$. By applying SGD in this way $B$ times they calculate SGD estimates $\bar{\theta}^{\star(1)},\ldots,\bar{\theta}^{\star(B)}$, which are used to estimate the distribution of $\bar{\theta}$. However, for the implementation of this approach under LDP the privacy budget $\epsilon$ must be split onto these $B$ versions. In other words, for the calculation of each bootstrap replication $\bar{\theta}^{\star(b)}$ there is only a privacy budget of $\epsilon/B$ left, resulting in highly inaccurate estimators.
To address these problems we propose to apply the multiplier block bootstrap principle to the iterations $\theta_{1}^{LDP},\ldots,\theta_{n}^{LDP}$ of LDP-SGD in order to mimic the strong dependencies in this data. To be precise let $l=l(n)$ be the block length and $m=\lfloor\frac{n}{l}\rfloor$ the number of blocks. Let $\epsilon_{1},\ldots,\epsilon_{m}$ be bounded, real-valued, independent and identically distributed random variables with $\mathbb{E}[\epsilon_{i}]=0$ and equal to ${\rm Var}(\epsilon_{i})=1$. For the given iterates $\theta_{1}^{LDP},\ldots,\theta_{n}^{LDP}$ by LDP-SGD in (6) we calculate a bootstrap analog of $\bar{\theta}^{LPD}-\theta_{\star}$ as

where $\bar{\theta}^{LDP}$ is the LDP-SGD estimate defined in (9). We will show below that under appropriate assumptions the distribution of $\bar{\theta}^{\star}$ is a reasonable approximation of the distribution of $\bar{\theta}^{LDP}-\theta_{\star}$. In practice this distribution can be obtained by generating $B$ samples of the form (11). Details are given in Algorithm˜2, where the multiplier block bootstrap is used to construct an $\alpha$-quantile for the distribution of $\bar{\theta}^{LDP}-\theta_{\star}$, say $q_{\alpha}$. With these quantiles we obtain an $(1-2\alpha)$ confidence interval for $\theta_{\star}$ as

We will consider LDP-SGD for the estimation of a quantile and of the parameters in a quantile regression model. We investigate these models because here the gradient is not differentiable and the plug-in estimator from Chen et al., (2020) can not be used. In each scenario, we consider samples of size $n=10^{6},10^{7},10^{8}$ and privacy parameter $\epsilon=1$. The stepsize of the SGD is chosen as $\eta_{i}=i^{-0.51}$. The $90\%$ confidence intervals (12) for the quantities of interest are computed by $B=500$ bootstrap replications. The block length is chosen as $l=\lfloor n^{\beta}\rfloor$, where $\beta=0.75$. The distribution of multiplier is chosen as $\epsilon_{i}\sim\operatorname{Unif}(-\sqrt{3},\sqrt{3})$. The empirical coverage probability and average length of the interval $\hat{C}$ are estimated by $500$ simulation runs. All simulations are run in R (R Core Team,, 2023) and executed on an internal cluster with an AMD EPYC 7763 64-Core processor under Ubuntu 22.04.4.

Quantiles: Let $X_{1},\ldots,X_{n}$ be independent and identically distributed $\mathbb{R}$ valued random variables with distribution function $F_{X}$ and density $p_{X}$. Denote by $x_{\tau}$ the $\tau$-th quantile of $X_{1}$ i.e. $F_{X}(x_{\tau})=\tau$. We assume that $p_{X}(x)>0$ in a neighborhood of $x_{\tau}$, then $x_{\tau}$ is the (unique) root of the equation $R(\theta)=-\tau+F_{X}(\theta).$ The noisy gradient is given by $g(X_{i},\theta)=-\tau+\mathbb{I}\{X_{i}\leq\theta\},$ which can be privatized using Randomized Response, that is

where $\mathcal{A}_{RR}$ is defined in Example 2.2 and $p=\frac{e^{\epsilon}}{1+e^{\epsilon}}$. Note that the re-scaling ensures that $\mathbb{E}[\mathcal{A}(g(X_{i},\theta))|X_{i}]=g(X_{i},\theta)$ for all $\theta\in\mathbb{R}$. The measurement error and the error due to privacy in (7) and (8) are given by

respectively, which define indeed martingale difference processes with respect to the filtration $\{\mathcal{F}_{i}\}_{i\geq 1}$, where $\mathcal{F}_{i}=\sigma(\theta_{1}^{LDP},\ldots,\theta_{i}^{LDP})$ and $\sigma(Y)$ denotes the sigma algebra generated by the random variable $Y$. The assumptions of Theorems˜3.2 and 3.1 can be verified with $\Sigma=(S_{SGD}+S_{LDP})/(p_{X}(x_{\tau}))^{2}$ where

In Table˜1 we display the simulated coverage probabilities and length of the confidence intervals for the $50\%$ and $90\%$ quantile of a standard normal distribution calculated by block bootstrap (BB). We also compare our approach with the batch mean (BM) introduced in Chen et al., (2020) and the self normalisation (SN) approach suggested in Liu et al., (2023). We observe that BB and BM behave very similar with respect to the empirical coverage and the length of the computed confidence intervals while the confidence intervals obtained by SN are slightly larger.
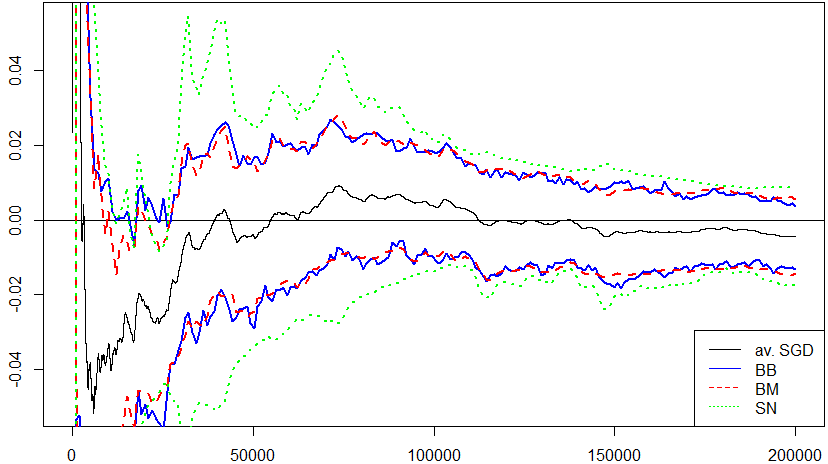
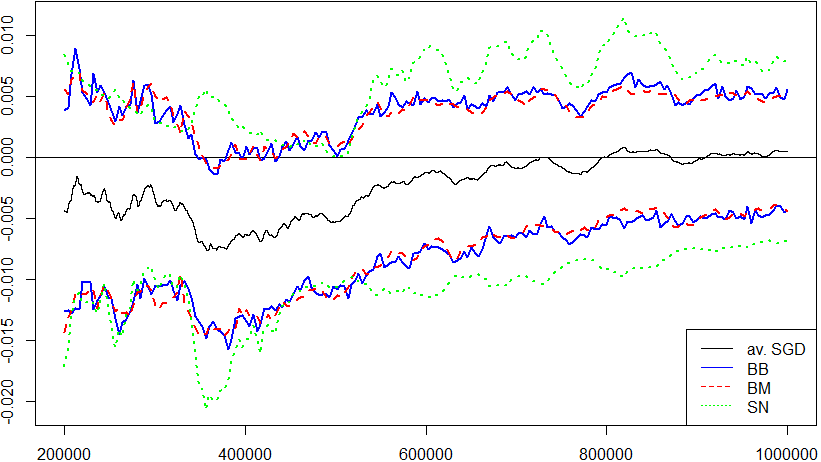
In Figure˜1 we display the trajectory of the upper and lower boundaries of a $90\%$ confidence interval for the $50\%$ quantile of a standard normal distribution for the BB, BM and SN approach. Again, we observe that the confidence intervals obtained by BB and BM are quite similar and the confidence intervals obtained by SN are wider.

Quantile Regression: Let $Z_{1},\ldots,Z_{n}$ be iid random vectors where $Z_{i}=(X_{i},y_{i})$, $X_{i}\in\mathbb{R}^{d}$ with $\Sigma_{X}=\mathbb{E}[X_{i}X_{i}^{T}]$ and $y_{i}=X_{i}^{T}\beta_{\tau}+\varepsilon_{i}$ where $\varepsilon_{i}$ is independent of $X_{i}$ with distribution function $F_{\varepsilon}$. We further assume that $F_{\varepsilon}$ has a density in a neighbourhood of $0$, say $p_{\varepsilon}$, with $p_{\varepsilon}(0)>0$, that $F_{\varepsilon}(0)=\tau$ and that there exists a constant $m>0$ such that $|X_{i}|\leq m$ for all $i=1,\ldots,d$. If $Q_{y|X}(\tau)$ is the conditional quantile of $y$ given $X$, it follows that $Q_{y|X}(\tau)=X^{T}\beta_{\tau}$ and $R(\beta_{\tau})=0$, where

which can be linearly approximated by $G=\Sigma_{X}p_{\varepsilon}(0)$, since a Taylor expansion at $\beta_{\tau}$ yields

The noisy observations are given by $g(Z_{j},\beta)=(-\tau+\mathbb{I}\{y_{j}-X_{j}^{T}\beta\leq 0\})X_{j}$ and can be privatized by the Laplace mechanism (see Example 2.1)

where $\mathbf{L}_{j}=(L_{1},\ldots,L_{d})^{T}$ is a vector of independent and identical distributed Laplacian random variables, i.e. $L_{i}\sim\operatorname{Lap}(0,2\max(\tau,1-\tau)md/\epsilon)$.
The measurement error and the error due to privacy in (7) and (8) are given by

which are indeed martingale difference processes with respect to the filtration $\{\mathcal{F}_{i}\}_{i\geq 1}$, where $\mathcal{F}_{i}=\sigma(\beta_{1}^{LDP},\ldots,\beta_{i}^{LDP})$. The assumptions from Theorems˜3.2 and 3.1 can be verified with $\Sigma=\Sigma_{X}^{-1}(S_{SGD}+S_{LDP})\Sigma_{X}^{-1}/p_{\varepsilon}(0)^{2}$ and

We compare the confidence intervals obtained by BB and BM where $X=(1,X_{1},X_{2},X_{3})$, $(X_{1},X_{2},X_{3})$ follows a truncated standard normal distribution on the cube $[-1,1]^{3}$ and $\varepsilon_{i}$ is normal distributed with variance $1$. For the generation of the truncated normal and the Laplace distribution we used the package of Botev and Belzile, (2021) and Wu et al., (2023), respectively. The simulation results are displayed in Table˜2. We observe that for $n=10^{6}$ BB yields too small and BM yields too large coverage probabilities, while the lengths of the confidence intervals from BB are smaller. If $n=10^{7}$ and $n=10^{8}$ the coverage probabilities from BB and BM are increasing and decreasing respectively.