Uncovering Optimal Attached Eddies in Wall-bounded Turbulence

We begin with a short description of the attached eddy hypothesis and modeling. This presentation generally follows W&M with a slightly different pedagogy. Consider a collection of $n$ eddies (Figure 1) of length scale $h_{e,i}$ that are placed on the wall at locations $\mathbf{x}_{e,i}$. Since these are attached eddies, it is implicit that only the streamwise and spanwise components of $\mathbf{x}_{e,i}$ are variable. Define $\mathbf{h}_{e}\triangleq\{h_{e,1},h_{e,2},..,h_{e,n}\}$ and $\mathbf{X}\triangleq\{\mathbf{x}_{e,1},\mathbf{x}_{e,2},..,\mathbf{x}_{e,n}\}$. Assuming self-similarity and linearity, a quantity $q$ (e.g. spanwise velocity) evaluated at a location $\mathbf{x}$ can be determined using the superposition $q(\mathbf{x},\mathbf{X}_{e},\mathbf{h}_{e},n)\triangleq\sum_{i=1}^{n}q\left(\frac{\mathbf{x}-\mathbf{x}_{e,i}}{h_{e,i}}\right).$

Restricting our attention to a streamwise and spanwise square wall patch of side $2L$ in which the eddies are assumed to be idependently and uniformly distributed, and assuming that the range of eddy length scales follows a probability density function $p(h)$, the expectation of $q$ in this region is given by

$$q(\mathbf{x},n)\triangleq\mathbb{E}_{\mathbf{X}_{e},\mathbf{h}_{e}}[q(\mathbf{x},\mathbf{X}_{e},\mathbf{h}_{e},n)]=\frac{1}{4L^{2}}\int_{h_{min}}^{h_{max}}\int_{-L}^{L}\int_{-L}^{L}\sum_{i=1}^{n}q\left(\frac{\mathbf{x}-\mathbf{x}_{e,i}}{h}\right)p(h)d\mathbf{x}_{e,i}dh.$$

(1)

Homogenizing in the $x,y$ directions, assuming $L$ is large enough that each eddy centered at the origin has a negligible induced contribution outside an area $4L^{2}$ (Refer Campbell’s theorem  Rice (1944) and appendix of W&M), it can be shown that

$$q(z,n)\triangleq\mathbb{E}_{x,y}[q(\mathbf{x},n)]\approx\frac{n}{4L^{2}}\int_{h_{min}}^{h_{max}}\int_{-L}^{L}\int_{-L}^{L}q\left(\frac{\mathbf{x}}{h}\right)p(h)dxdydh.$$

Note that in the above equation, the entire field is written as a function of one prototypical eddy, which is scaled by the probability density function of the eddy sizes $p(h)$ and the eddy density $n/(4L^{2})$. If the mean eddy density is $\beta$, then using Poisson’s law, the expected value (over all numbers of eddies) is

$$Q(z)\triangleq\mathbb{E}_{n}[q(z,n)]=\beta\int_{h_{min}}^{h_{max}}\int_{-L}^{L}\int_{-L}^{L}q\left(\frac{\mathbf{x}}{h}\right)p(h)dxdydh.$$

(2)

Note that all the $q$’s defined above are random variables, yet $Q(z)$ is a deterministic quantity. Now we are in a position to define the mean streamwise velocity $U(z)$ as a superposition of eddies of various sizes $h$. This can be written in terms of the induced velocity field $u_{1}(\cdot)$ of one prototypical eddy.

	$\displaystyle U(z)$	$\displaystyle\triangleq\beta\int_{h_{min}}^{h_{max}}\int_{-L}^{L}\int_{-L}^{L}u_{1}\left(\frac{\mathbf{x}}{h}\right)p(h)dxdydh+U_{\infty}$
		$\displaystyle=\beta\int_{h_{min}}^{h_{max}}p(h)h^{2}\left[\int_{-L/h}^{L/h}\int_{-L/h}^{L/h}u_{1}\left(\frac{\mathbf{x}}{h}\right)d\left(\frac{x}{h}\right)d\left(\frac{y}{h}\right)\right]dh+U_{\infty}$
		$\displaystyle=\beta\int_{h_{min}}^{h_{max}}p(h)h^{2}I_{1}\left(\frac{z}{h}\right)dh+U_{\infty},$		(3)

where the mean flow eddy contribution function is

$\displaystyle I_{1}\left(\frac{z}{h}\right)$

$\displaystyle\triangleq\int_{-L/h}^{L/h}\int_{-L/h}^{L/h}u_{1}\left(\frac{\mathbf{x}}{h}\right)d\left(\frac{x}{h}\right)d\left(\frac{y}{h}\right).$

(4)

Similarly, we can define the Reynolds stress tensor as

	$\displaystyle R_{ij}(z)$	$\displaystyle\triangleq\beta\int_{h_{min}}^{h_{max}}p(h)I_{ij}\left(\frac{z}{h}\right)dh,$
	$\displaystyle\textrm{ where }I_{ij}\left(\frac{z}{h}\right)$	$\displaystyle\triangleq\int_{-L/h}^{L/h}\int_{-L/h}^{L/h}u_{i}\left(\frac{\mathbf{x}}{h}\right)u_{j}\left(\frac{\mathbf{x}}{h}\right)d\left(\frac{x}{h}\right)d\left(\frac{y}{h}\right).$

Note the presence of an additional freestream velocity in the definition of $U(z)$. This is required because we are working with induced velocity fluctuations. The final piece we need is the probability distribution of the eddy sizes. Using insight from Townsend (1976) and  Perry & Chong (1982), W&M propose that $p(h)\propto 1/h^{3}$ and thus $p(h)=\frac{2/h^{3}}{1/h_{\min}^{2}-1/h_{\min}^{2}}$, with the note that $h_{\max}=\delta$ (i.e.) the boundary layer thickness and $h_{\min}$ is set by the friction Reynolds number $Re_{\tau}$. For notational simplicity, all length and velocity scales should be assumed to be in wall units henceforth.

We now address the following question: How should the ’perfect’ eddy contribution function look like? Townsend and Perry & Chong have provided insight into the behavior of the eddy distribution function, but the current objective is to be precise. Towards this end, consider a discrete set of eddy sizes $\tilde{\mathbf{h}}=\{h_{1},h_{2},h_{3},..,h_{m}\}=\{h_{\min},h_{\min}+\Delta h,h_{\min}+2\Delta h,..,h_{\max}\}$ and a similar discretization of the wall-normal coordinate $\tilde{\mathbf{z}}=\{z_{1},z_{2},z_{3},..,z_{m}\}=\{h_{\min},h_{\min}+\Delta h,h_{\min}+2\Delta h,..,h_{\max}\}$. Then, the discretized velocity moments are

	$\displaystyle U(z_{r};\mathbf{d})$	$\displaystyle=\beta\sum_{l=1}^{m}p(h_{l})\left[\sum_{q}\sum_{p}u_{1}\left(\frac{{x_{p},y_{q},z_{r}}}{h_{l}};\mathbf{d}\right)\left(\frac{\Delta x}{h_{l}}\right)\left(\frac{\Delta y}{h_{l}}\right)\right]\Delta h+U_{\infty}$
	$\displaystyle R_{ij}(z_{r};\mathbf{d})$	$\displaystyle=\beta\sum_{l=1}^{m}p(h_{l})\left[\sum_{q}\sum_{p}u_{i}\left(\frac{{x_{p},y_{q},z_{r}}}{h_{l}};\mathbf{d}\right)u_{j}\left(\frac{{x_{p},y_{q},z_{r}}}{h_{l}};\mathbf{d}\right)\left(\frac{\Delta x}{h_{l}}\right)\left(\frac{\Delta y}{h_{l}}\right)\right]\Delta h.$

This can be represented as a matrix vector product in the form $\mathbf{U}(\tilde{\mathbf{z}})-U_{\infty}=\mathbf{A}\mathbf{b},$ where $A_{ij}=I_{1}(z_{i}/h_{j})$ and $b_{i}=\beta p(h_{i})h_{i}^{2}\Delta h.$ We would now like to extract these coefficients. Towards this end, we define the eddy contribution function at selected locations, and interpolate for the values in other locations in a piecewise linear fashion. In other words

$$\mathbf{A}=\begin{bmatrix}I_{1}(1)&I_{1}(h_{1}/h_{2})&I_{1}(h_{1}/h_{3})&..&I_{1}(h_{1}/h_{m-1})&I_{1}(h_{1}/h_{m})\\ I_{1}(h_{2}/h_{1})&I_{1}(1)&I_{1}(h_{2}/h_{3})&..&I_{1}(h_{2}/h_{m-1})&I_{1}(h_{2}/h_{m})\\ ..&..&..&..&..&..\\ I_{1}(h_{m}/h_{1})&I_{1}(h_{m}/h_{2})&I_{1}(h_{m}/h_{3})&..&I_{1}(h_{m}/h_{m-1})&I_{1}(1)\end{bmatrix}$$

$$\triangleq\begin{bmatrix}c_{1}&c_{m+1}&c_{m+2}&..&c_{2m-2}&c_{2m-1}\\ c_{2}&c_{1}&I_{1}(h_{2}/h_{3})&..&I_{1}(h_{2}/h_{m-1})&I_{1}(h_{2}/h_{m})\\ ..&..&..&..&..&..\\ c_{m}&I_{1}(h_{m}/h_{2})&I_{1}(h_{m}/h_{3})&..&I_{1}(h_{m}/h_{m-1})&c_{1}\\ \end{bmatrix}.$$

The unknown $I_{1}(\cdot)$ values are then interpolated ²²2For instance, if $h_{\min}=186$ and $h_{\max}=5186$ and $m=11$, then $I_{1}(h_{2}/h_{3})=0.42106c_{1}+0.57894c_{12}$ from the nodal locations $\mathbf{c}$. Note that there are more unknowns ($2m$) than equations ($m$), and so while it is possible to determine the unknowns that lead to perfect match of a reference (DNS or experiment) velocity profiles, a choice has to be made on the problem formulation. We choose to define the following least norm problem:

$$\{\mathbf{c}_{\textrm{opt}},\beta_{\textrm{opt}}\}=\min_{\mathbf{c},\beta}||\mathbf{U}_{ref}(\tilde{\mathbf{z}})-U_{\infty}-\mathbf{A}\mathbf{b}||_{2}^{2}.$$

Figure 2 shows the optimal eddy contribution functions inferred from the channel flow data (Lee & Moser, 2015) at friction Reynolds number $Re_{\tau}\approx 5200$. Figure 3 confirms that the first and second velocity moments are perfectly reproduced.

Consider a collection of attached eddies that result in a simple function as shown in Fig. 4.

It will be shown below that it is indeed possible to construct an attached eddy that corresponds to such a function. Using this influence function, one can reconstruct the mean streamwise velocity as

	$\displaystyle U(z)$	$\displaystyle=\frac{2\beta}{1/h_{\min}^{2}-1/h_{\max}^{2}}\int_{h_{min}}^{h_{max}}\frac{I_{1}\left({z}/{h}\right)}{h}dh+U_{\infty}$
		$\displaystyle=\frac{2\beta}{1/h_{\min}^{2}-1/h_{\max}^{2}}\int_{z/h_{max}}^{z/h_{min}}\frac{I_{1}\left({z}/{h}\right)}{z/h}d(z/h)+U_{\infty}$
		$\displaystyle\approx\frac{2\beta}{1/h_{\min}^{2}-1/h_{\max}^{2}}\left[\int_{z/h_{max}}^{1}\frac{-a_{0}}{z/h}d(z/h)+\int_{1}^{a_{1}/a_{2}}\frac{a_{1}-a_{2}z/h}{z/h}d(z/h)\right]+U_{\infty}$
		$\displaystyle=\frac{2\beta}{1/h_{\min}^{2}-1/h_{\max}^{2}}\left[\int_{z/h_{max}}^{1}\frac{-a_{0}}{z/h}d(z/h)+\int_{1}^{a_{1}/a_{2}}\frac{a_{1}-a_{2}z/h}{z/h}d(z/h)\right]+U_{\infty}$
		$\displaystyle=\frac{2\beta}{1/h_{\min}^{2}-1/h_{\max}^{2}}\left[a_{0}\log[z/h_{\max}]+a_{1}\log[a_{1}/a_{2}]-a_{1}+a_{2}\right]+U_{\infty}.$

It is thus clear that the Karman constant can be constructed as

$$\kappa=\frac{1/h_{\min}^{2}-1/h_{\max}^{2}}{2a_{0}\beta}.$$

Note that $W\&M$ use a Taylor series approximation on a generic eddy to derive an alternate expression for $\kappa$.

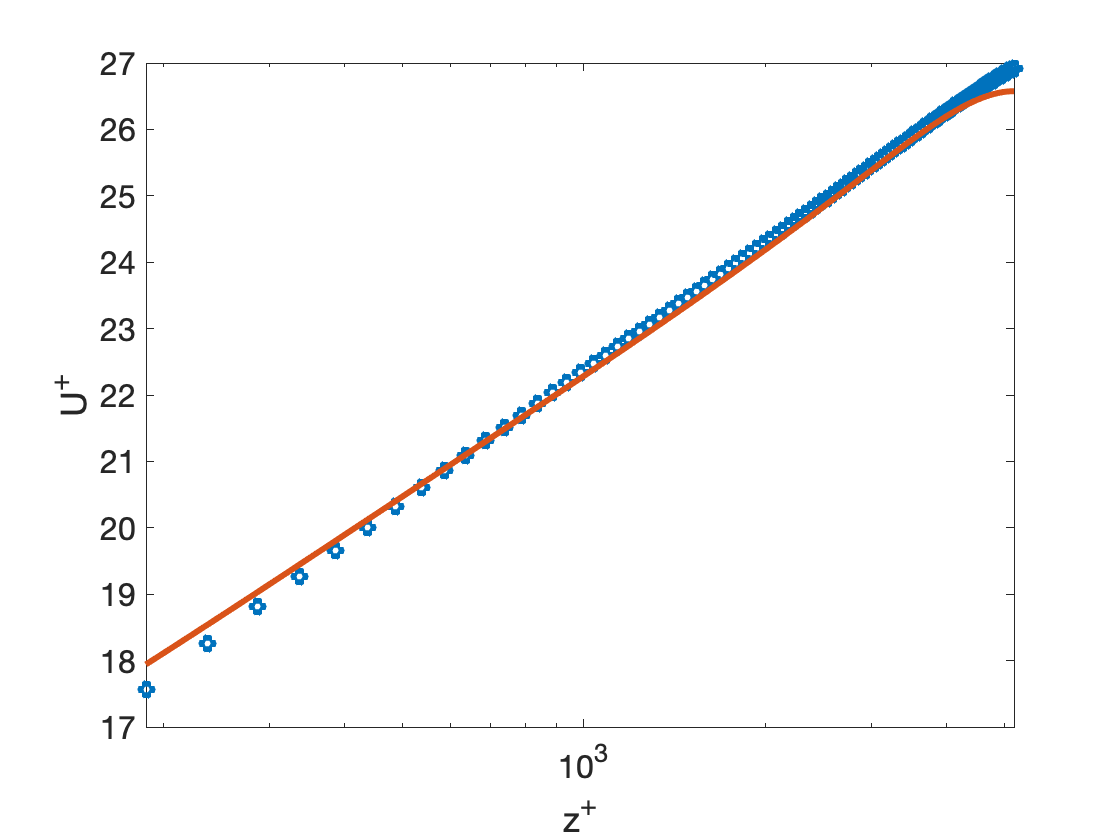
Now, we answer the question whether it is possible to recreate the above hypothetical influence function using an attached eddy. Consider a square hairpin (Figure 5) with unit circulation as the attached eddy, along with its image across the $z=0$ plane to enforce no-penetration. It is remarked that this eddy has a square structure, yet the leg of the eddy aligned with the wall is canceled by an equal and opposite image vortex pair, and is thus consistent with the kinematics. Using the Biot-savart law to compute the induced velocity $u_{1}$ in Eqn. 4, Figure 6 shows that such a simple attached eddy can reproduce the mean streamwise velocity extremely accurately. Further, the second moments are also seen to be reasonably well-predicted as shown in Figure 6.

To assess whether the above attached eddy shape can be improved to yield more accurate statistics, we pose a constrained optimization problem. The prototypical attached eddy is now represented using 20 parameters as shown in Fig. 7. It is noted that the shape is symmetric across the $y=0$ plane, and a mirror image is used across the $z=0$ plane to satisfy inviscid boundary conditions.

The following optimization problem is solved

	$\displaystyle\mathbf{d}_{\textrm{opt}}$	$\displaystyle=\min_{\mathbf{d},\beta}(||\mathbf{U}_{ref}(\tilde{\mathbf{z}})-\mathbf{U}(\tilde{\mathbf{z}};\mathbf{d})||_{2}^{2}+||\mathbf{R}_{11,ref}(\tilde{\mathbf{z}})-\mathbf{R}_{11}(\tilde{\mathbf{z}};\mathbf{d})||_{2}^{2}+||\mathbf{R}_{22,ref}(\tilde{\mathbf{z}})-\mathbf{R}_{22}(\tilde{\mathbf{z}};\mathbf{d})||_{2}^{2}$
		$\displaystyle+||\mathbf{R}_{33,ref}(\tilde{\mathbf{z}})-\mathbf{R}_{33}(\tilde{\mathbf{z}};\mathbf{d})||_{2}^{2}+||\mathbf{R}_{13,ref}(\tilde{\mathbf{z}})-\mathbf{R}_{13}(\tilde{\mathbf{z}};\mathbf{d})||_{2}^{2})$
		$\displaystyle\textrm{s.t. }\mathbf{C}\mathbf{d}\leq\mathbf{f}\textrm{ and }\mathbf{d}_{l}\leq\mathbf{d}\leq\mathbf{d}_{u},$

where the constraints $\mathbf{C}$ and $\mathbf{f}$ are designed to ensure that $d_{20}>d_{17}>d_{14}>d_{11}>d_{8}>d_{5}>d_{2}>0$, and $1>d_{19}>d_{16}>d_{13}>d_{10}>d_{7}>d_{4}>0$. The bounds $\mathbf{d}_{l},\mathbf{d}_{u}$ ensure that the x and y extents of the prototypical eddy is bounded. Sequential quadratic programming is used to solve the above constrained optimization problem. The results of the optimization is shown in Figures 8, 9, and improvement is noticeable over the simpler eddy (Figure 6) .

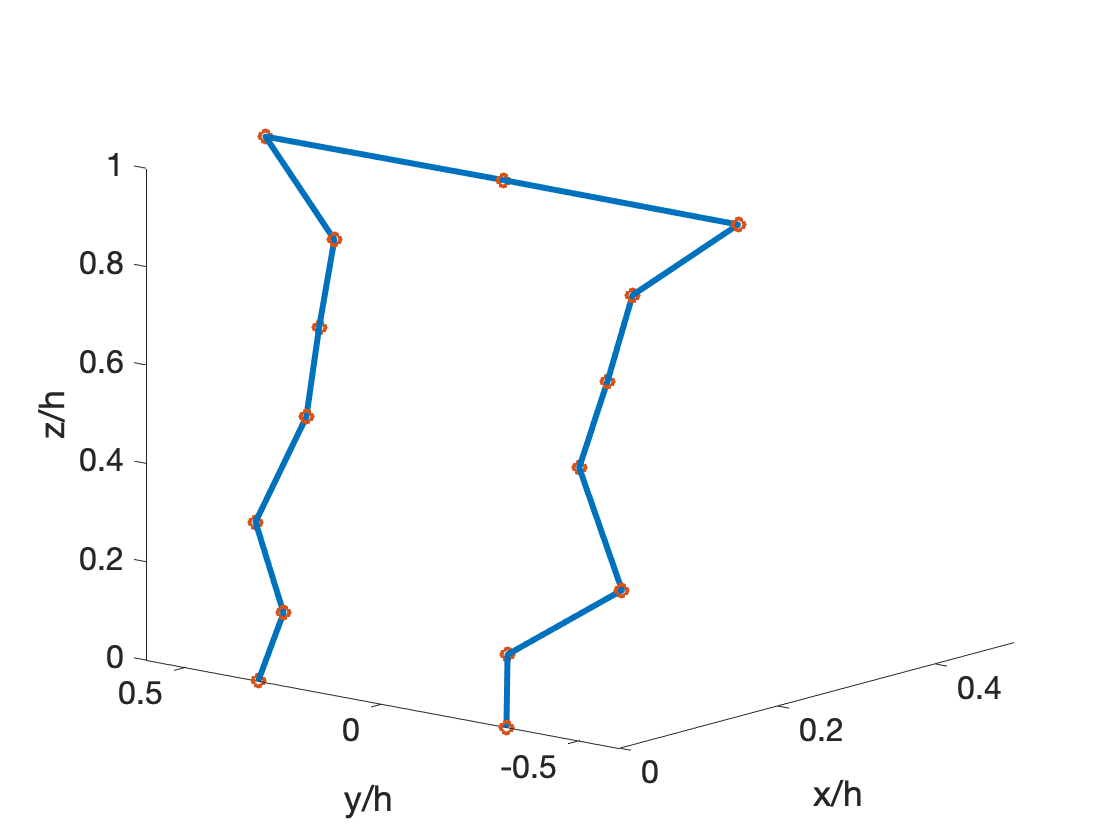
At this juncture, we remark that the AEM is a statistical and non-dynamic model, and thus prototypical eddies cannot be considered to be physical structures. However, from a conceptual and aesthetic standpoint, the eddy shape in Figure 9 may be unsatisfactory. Indeed, analyses and observations from experiments and numerical simulations have suggested the following features of dynamically-important eddies: a) Hairpin-type structures are present the form of eddy packets (rather than individual eddies ), and b) A preferential alignment of approximately $45^{\circ}$ to the wall. Simply stacking the hairpins of Figure 5 with equal circulation strengths did not yield meaningful results, and thus the circulation strength of the individual hairpins in the packet (Figure 9) were optimized and found to follow a roughly quadratic distribution with hairpin size. It is noted that - in contrast to the above square hairpins, single / stacked lambda vortices did not yield accurate predictions of the statistics.

We conclude by stating that there are several directions for future work, including a) a more complete consideration of statistics such as the structure function, high-order moments, and the energy spectrum; b) assessment of the impact of the prototypical eddy in explaining physical characteristics of the flow; c) use of more sophisticated topological optimization and richer parametrizations of the eddies; and d) extension to other scenarios including boundary layers with pressure gradients and in combination with detached eddies. Further we note that opportunities exist in modeling flow regions beyond the log layer. In fact, the current inference approach and predictions already include the outer layer.