Understanding Negative Sampling in Graph Representation Learning
Abstract.
11footnotetext: Equal contribution. Ming Ding proposed the theories and method. Zhen Yang conducted the experiments. Codes are available at https://github.com/zyang-16/MCNS.44footnotetext: Corresponding Authors.Graph representation learning has been extensively studied in recent years, in which sampling is a critical point. Prior arts usually focus on sampling positive node pairs, while the strategy for negative sampling is left insufficiently explored. To bridge the gap, we systematically analyze the role of negative sampling from the perspectives of both objective and risk, theoretically demonstrating that negative sampling is as important as positive sampling in determining the optimization objective and the resulted variance. To the best of our knowledge, we are the first to derive the theory and quantify that a nice negative sampling distribution is . With the guidance of the theory, we propose MCNS, approximating the positive distribution with self-contrast approximation and accelerating negative sampling by Metropolis-Hastings. We evaluate our method on 5 datasets that cover extensive downstream graph learning tasks, including link prediction, node classification and recommendation, on a total of 19 experimental settings. These relatively comprehensive experimental results demonstrate its robustness and superiorities.
1. Introduction
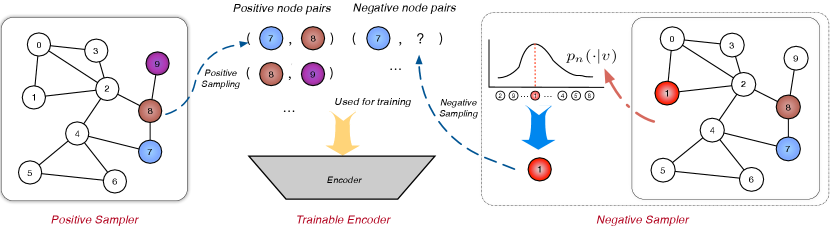
Recent years have seen the graph representation learning gradually stepping into the spotlight of data mining research. The mainstream graph representation learning algorithms include traditional Network Embedding methods (e.g. DeepWalk (Perozzi et al., 2014), LINE (Tang et al., 2015)) and Graph Neural Networks (e.g. GCN (Kipf and Welling, 2017), GraphSAGE (Hamilton et al., 2017)), although the latter sometimes are trained end-to-end in classification tasks. These methods transform nodes in the graph into low-dimensional vectors to facilitate a myriad of downstream tasks, such as node classification (Perozzi et al., 2014), link prediction (Zhou et al., 2017) and recommendation (Ying et al., 2018).
Most graph representation learning can be unified within a Sampled Noise Contrastive Estimation (SampledNCE) framework (§ 2), comprising of a trainable encoder to generate node embeddings, a positive sampler and a negative sampler to sample positive and negative nodes respectively for any given node. The encoder is trained to distinguish positive and negative pairs based on the inner products of their embeddings (See Figure 1 for illustration).
Massive network embedding works have investigated good criteria to sample positive node pairs, such as by random walk (Perozzi et al., 2014), the second-order proximity (Tang et al., 2015), community structure (Wang et al., 2017a), etc. Meanwhile, the line of GNN papers focuses on advanced encoders, evolving from basic graph convolution layers (Kipf and Welling, 2017) to attention-based (Veličković et al., 2018), GAN-based (Ding et al., 2018), sampled aggregator (Hamilton et al., 2017) and WL kernel-based (Xu et al., 2018) layers. However, the strategy for negative sampling is relatively unexplored.
Negative sampling (Mikolov et al., 2013) is firstly proposed to serve as a simplified version of noise contrastive estimation (Mnih and Kavukcuoglu, 2013; Gutmann and Hyvärinen, 2012), which is an efficient way to compute the partition function of an unnormalized distribution to accelerate the training of word2vec. Mikolov et al. (2013) set the negative sampling distribution proportional to the power of degree by tuning the power parameter. Most later works on network embedding (Perozzi et al., 2014; Tang et al., 2015) readily keep this setting. However, results in several papers (Zhang and Zweigenbaum, 2018; Caselles-Dupré et al., 2018; Ying et al., 2018) demonstrate that not only the distribution of negative sampling has a huge influence on the performance, but also the best choice varies largely on different datasets (Caselles-Dupré et al., 2018).
To the best of our knowledge, few papers systematically analyzed or discussed negative sampling in graph representation learning. In this paper, we first examine the role of negative sampling from the perspectives of objective and risk. Negative sampling is as important as positive sampling to determine the optimization objective and reduce the variance of the estimation in real-world graph data. According to our theory, the negative sampling distribution should be positively but sub-linearly correlated to their positive sampling distribution. Although our theory contradicts with the intuition “positively sampling nearby nodes and negatively sampling the faraway nodes”, it accounts for the observation in previous works (Ying et al., 2018; Zhang and Zweigenbaum, 2018; Gao and Huang, 2018) where additional hard negative samples improve performance.
We propose an effective and scalable negative sampling strategy, Markov chain Monte Carlo Negative Sampling (MCNS), which applies our theory with an approximated positive distribution based on current embeddings. To reduce the time complexity, we leverage a special Metropolis-Hastings algorithm (Metropolis et al., 1953) for sampling. Most graphs naturally satisfy the assumption that adjacent nodes share similar positive distributions, thus the Markov chain from neighbors can be continued to skip the burn-in period and finally accelerates the sampling process without degradations in performance.
We evaluate MCNS on three most general graph-related tasks, link prediction, node classification and recommendation. Regardless of the network embedding or GNN model used, significant improvements are shown by replacing the original negative sampler to MCNS. We also collect many negative sampling strategies from information retrieval (Weston et al., 2011; Wang et al., 2017b), ranking in recommendation (Hu et al., 2008; Zhang et al., 2013) and knowledge graph embeddings (Cai and Wang, 2018; Zhang et al., 2019). Our experiments in five datasets demonstrate that MCNS stably outperforms these negative sampling strategies.
2. Framework
In this section, we introduce the preliminaries to understand negative sampling, including the unique embedding transformation, the SampledNCE framework and how the traditional network embeddings and GNNs are unified into the framework.
2.1. Unique Embedding Transformation
Many network embedding algorithms, such as DeepWalk (Perozzi et al., 2014), LINE (Tang et al., 2015) and node2vec (Grover and Leskovec, 2016), actually assign each node two embeddings 111Others, for example GraphSAGE (Hamilton et al., 2017) use a unique embedding., node embedding and contextual embedding. When sampled as context, the contextual embedding, instead of its node embedding is used for inner product. This implementation technique stems from word2vec (Mikolov et al., 2013), though sometimes omitted by following papers, and improves performance by utilizing the asymmetry of the contextual nodes and central nodes.
We can split each node into central node and contextual node , and each edge becomes . Running those network embedding algorithms on the transformed bipartite graph is strictly equivalent to running on the original graph.222For bipartite graphs, always take nodes from part as central node and sample negative nodes from part. According to the above analysis, we only need to anaylze graphs with unique embeddings without loss of generality.
2.2. The SampledNCE Framework
We unify a large part of graph representation learning algorithms into the general SampledNCE framework, shown in Algorithm 1. The framework depends on an encoder , which can be either an embedding lookup table or a variant of GNN, to generate node embeddings.
In the training process, positive nodes and negative nodes are sampled. In Algorithm 1, we use the cross-entropy loss to optimize the inner product where . And the other choices of loss function work in similar ways. In link prediction or recommendation, we recall the top nodes with largest for each node . In classification, we evaluate the performance of logistic regression with the node embeddings as features.
2.3. Network Embedding and GNNs
Edges in natural graph data can be assumed as sampled from an underlying positive distribution . However, only a few edges are observable so that numerous techniques are developed to make reasonable assumptions to better estimate , resulting in various in different algorithms to approximate .
Network embedding algorithms employ various positive distributions implicitly or explicitly. LINE (Tang et al., 2015) samples positive nodes directly from adjacent nodes. DeepWalk (Perozzi et al., 2014) samples via random walks and implicitly defines as the stationary distribution of random walks (Qiu et al., 2018). node2vec (Grover and Leskovec, 2016) argues that homophily and structural equivalence of nodes and indicates a larger . These assumptions are mainly based on local smoothness and augment observed positive node pairs for training.
Graph neural networks are equipped with different encoder layers and perform implicit regularizations on positive distribution. Previous work (Li et al., 2018) reveals that GCN is a variant of graph Laplacian smoothing, which directly constrains the difference of the embedding of adjacent nodes. GCN, or its sampling version GraphSAGE (Hamilton et al., 2017), does not explicitly augment positive pairs but regularizes the output embedding by local smoothness, which can be seen as an implicit regularization of .
3. Understanding Negative Sampling
In contrast to elaborate estimation of the positive sampling distribution, negative sampling has long been overlooked. In this section, we revisit negative sampling from the perspective of objective and risk, and conclude that “the negative sampling distribution should be positively but sub-linearly correlated to their positive sampling distribution”.
3.1. How does negative sampling influence the objective of embedding learning?
Previous works (Qiu et al., 2018) interpret network embedding as implicit matrix factorization. We discuss a more general form where the factorized matrix is determined by estimated data distribution and negative distribution . According to (Levy and Goldberg, 2014) (Qiu et al., 2018), the objective function for embedding is
| (1) |
where are embeddings for node and and is the sigmoid function. We can separately consider each node and show the objective for optimization as follows:
Theorem 1.
(Optimal Embedding) The optimal embedding satisfies that for each node pair ,
| (2) |
Proof Let us consider the conditional data and the negative distribution of node . To maximize is equivalent to minimize the following objective function for each ,
For each pair, if we define two Bernoulli distributions where and where , the equation above is simplified as follows:
where is the cross entropy between two distributions. According to Gibbs Inequality, the maximizer of satisfies for each pair, which gives
| (3) | ||||
The above theorem clearly shows that the positive and negative distributions and have the same level of influence on optimization. In contrast to abundant research on finding a better to approximate , negative distribution is apparently under-explored.
3.2. How does negative sampling influence the expected loss (risk) of embedding learning?
The analysis above shows that with enough (possibly infinite) samples of edges from , the inner product of embedding has an optimal value. In real-world data, we only have limited samples from , which leads to a nonnegligible expected loss (risk). Then the loss function to minimize empirical risk for node becomes:
| (4) |
where are sampled from and are sampled from .
In this section, we only consider optimization of node , which can be directly generalized to the whole embedding learning. More precisely, we equivalently consider as the parameters to be optimized, where are all the N nodes in the graph. Suppose the optimal parameter for and are and respectively. The gap between and is described as follows:
Theorem 2.
The random variable asymptotically converges to a distribution with zero mean vector and covariance matrix
| (5) |
where and .
Proof Our analysis is based on the Taylor expansion of around . As is the minimizer of , we must have , which gives
| (6) |
Up to terms of order , we have
| (7) |
Next, we will analyze and respectively by the following lemmas.
Lemma 0.
The negative Hessian matrix converges in probability to .
Proof First, we calculate the gradient of and Hessian matrix . Let be the parameter in for modeling and be the one-hot vector which only has a 1 on this dimension.
| (8) | ||||
According to equation (3), at . Therefore,
| (9) |
Lemma 0.
The expectation and variance of satisfy
| (10) | ||||
| (11) |
3.3. The Principle of Negative Sampling
To determine an appropriate for a specific , a trade-off might be needed to balance the rationality of the objective (to what extent the optimal embedding fits for the downstream task) and the expected loss, also known as risk (to what extent the trained embedding deviates from the optimum).
A simple solution is to sample negative nodes positively but sub-linearly correlated to their positive sampling distribution, i.e. .
(Monotonicity) From the perspective of objective, if we have ,
where is a constant. The sizes of inner products is in accordance with positive distribution , facilitating the task relying on relative sizes of for different s, such as recommendation or link prediction.
(Accuracy) From the perspective of risk, we mainly care about the scale of the expected loss. According to equation (13), the expected squared deviation is dominated by the smallest one in and . If an intermediate node with large is negatively sampled insufficiently (with small ), the accurate optimization will be corrupted. But if , then
The order of magnitude of deviation only negatively related to , meaning that with limited positive samples, the inner products for high-probability node pairs are estimated more accurate. This is an evident advantage over evenly negative sampling.
4. Method
4.1. The Self-contrast Approximation
Although we deduced that , the real is unknown and its approximation is often implicitly defined. – How can the principle help negative sampling?
We therefore propose a self-contrast approximation, replacing by inner products based on the current encoder, i.e.
The resulting form is similar to a technique in RotatE (Sun et al., 2019), and very time-consuming. Each sampling requires time, making it impossible for middle- or large-scale graphs. Our MCNS solves this problem by our adapted version of Metropolis-Hastings algorithm.
4.2. The Metropolis-Hastings Algorithm
As one of the most distinguished Markov chain Monte Carlo (MCMC) methods, the Metropolis-Hastings algorithm (Metropolis et al., 1953) is designed for obtaining a sequence of random samples from unnormalized distributions. Suppose we want to sample from distribution but only know . Meanwhile the computation of normalizer is unaffordable. The Metropolis-Hastings algorithm constructs a Markov chain that is ergodic and stationary with respect to —- meaning that, .
The transition in the Markov chain has two steps:
(1) Generate where the proposal distribution is arbitrary chosen as long as positive everywhere.
(2) Pick as at the probability , or . See tutorial (Chib and
Greenberg, 1995) for more details.
4.3. Markov chain Negative Sampling
The main idea for MCNS is to apply the Metropolis-Hastings algorithm for each node with . Then we are sampling from the self-contrast approximated distribution. However, a notorious disadvantage for the Metropolis-Hastings is a relatively long period, i.e. the distribution of only when is large, which heavily affects its efficiency.
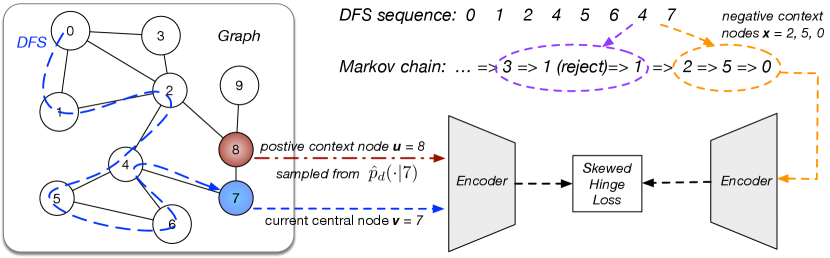
Fortunately, the connatural property exists for graphs that nearby nodes usually share similar , as evident from triadic closure in social network (Huang et al., 2014), collaborative filtering in recommendation (Linden et al., 2003), etc. Since nearby nodes have similar target negative sampling distribution, the Markov chain for one node is likely to still work well for its neighbors. Therefore, a neat solution is to traverse the graph by Depth First Search (DFS, See Appendix A.6) and keep generating negative samples from the last node’s Markov chain (Figure 2).
The proposal distribution also influences convergence rate. Our is defined by mixing uniform sampling and sampling from the nearest nodes with probability each. The hinge loss pulls positive node pairs closer and pushes negative node pairs away until they are beyond a pre-defined margin. Thus, we substitute the binary cross-entropy loss as a -skewed hinge loss,
| (14) |
where is a positive node pair and is negative. is a hyperparameter. The MCNS is summarized in Algorithm 2.
5. Experiments
To demonstrate the efficacy of MCNS, we conduct a comprehensive suite of experiments on 3 representative tasks, 3 graph representation learning algorithms and 5 datasets, a total of 19 experimental settings, under all of which MCNS consistently achieves significant improvements over 8 negative sampling baselines collected from previous papers (Ying et al., 2018; Perozzi et al., 2014) and other relevant topics (Zhang et al., 2013; Wang et al., 2017b; Cai and Wang, 2018; Weston et al., 2011).
5.1. Experimental Setup
5.1.1. Tasks and Dataset.
The statistics of tasks and datasets are shown in Table 1. Introductions about the datasets are in Appendix A.4.
| Task | Dataset | Nodes | Edges | Classes |
| Recommendation | MovieLens | 2,625 | 100,000 | / |
| Amazon | 255,404 | 1,689,188 | / | |
| Alibaba | 159,633 | 907,470 | / | |
| Link Prediction | Arxiv | 5,242 | 28,980 | / |
| Node Classification | BlogCatalog | 10,312 | 333,983 | 39 |
5.1.2. Encoders.
To verify the adaptiveness of MCNS to different genres of graph representation learning algorithms, we utilize an embedding lookup table or a variant of GNN as encoder for experiments, including DeepWalk, GCN and GraphSAGE. The detailed algorithms are shown in Appendix A.2.
| MovieLens | Amazon | Alibaba | ||||||
| DeepWalk | GCN | GraphSAGE | DeepWalk | GraphSAGE | DeepWalk | GraphSAGE | ||
| 0.025.001 | 0.062.001 | 0.063.001 | 0.041.001 | 0.057.001 | 0.037.001 | 0.064.001 | ||
| WRMF | 0.022.001 | 0.038.001 | 0.040.001 | 0.034.001 | 0.043.001 | 0.036.001 | 0.057.002 | |
| RNS | 0.031.001 | 0.082.002 | 0.079.001 | 0.046.003 | 0.079.003 | 0.035.001 | 0.078.003 | |
| PinSAGE | 0.036.001 | 0.091.002 | 0.090.002 | 0.057.004 | 0.080.001 | 0.054.001 | 0.081.001 | |
| WARP | 0.041.003 | 0.114.003 | 0.111.003 | 0.061.001 | 0.098.002 | 0.067.001 | 0.106.001 | |
| DNS | 0.040.003 | 0.113.003 | 0.115.003 | 0.063.001 | 0.101.003 | 0.067.001 | 0.090.002 | |
| IRGAN | 0.047.002 | 0.111.002 | 0.101.002 | 0.059.001 | 0.091.001 | 0.061.001 | 0.083.001 | |
| KBGAN | 0.049.001 | 0.114.003 | 0.100 .001 | 0.060.001 | 0.089.001 | 0.065.001 | 0.087.002 | |
| MCNS | 0.053.001 | 0.122.004 | 0.114.001 | 0.065.001 | 0.108.001 | 0.070.001 | 0.116.001 | |
| 0.115.002 | 0.270.002 | 0.270.001 | 0.161.003 | 0.238.002 | .003 | 0.249.004 | ||
| WRMF | 0.110.003 | 0.187.002 | 0.181.002 | 0.139.002 | 0.188.001 | 0.121.003 | 0.227.004 | |
| RNS | 0.143.004 | 0.362.004 | 0.356.001 | 0.171.004 | 0.317.004 | 0.132.004 | 0.302.005 | |
| PinSAGE | 0.158.003 | 0.379.005 | 0.383.005 | 0.176.004 | 0.333.005 | 0.146.003 | 0.312.005 | |
| WARP | 0.164.005 | 0.406.002 | 0.404.005 | 0.181.004 | 0.340.004 | 0.178.004 | 0.342.004 | |
| DNS | 0.166.005 | 0.404.006 | 0.410.006 | 0.182.003 | 0.358.004 | 0.186.005 | 0.336.004 | |
| IRGAN | 0.207.002 | 0.415.004 | 0.408.004 | 0.183.004 | 0.342.003 | 0.175.003 | 0.320.002 | |
| KBGAN | 0.198.003 | 0.420.003 | 0.401.005 | 0.181.003 | 0.347.003 | 0.181.003 | 0.331.004 | |
| MCNS | 0.230.003 | 0.426 .005 | 0.413.003 | 0.207.003 | 0.386.004 | 0.201.003 | 0.387.002 | |
5.1.3. Baselines.
Baselines in our experiments generally fall into the following categories. The detailed description of each baseline is provided in Appendix A.3.
- •
-
•
Hard-samples Negative Sampling. Based on the observation that “hard negative samples” – the nodes with high positive probabilities – helps recommendation, methods are proposed to mine the hard negative samples by rejection (WARP (Zhao et al., 2015)), sampling-max (DNS (Zhang et al., 2013)) and personalized PageRank (PinSAGE (Ying et al., 2018)).
- •
5.2. Results
In this section, we demonstrate the results in the 19 settings. Note that all values and standard deviations reported in the tables are from ten-fold cross validation. We also leverage paired t-tests (Hsu and Lachenbruch, 2007) to verify whether MCNS is significantly better than the strongest baseline. The tests in the 19 settings give a max p-value (Amazon, GraphSAGE) of 0.0005 , quantitatively proving the significance of our improvements.
5.2.1. Recommendation
Recommendation is the most important technology in many E-commerce platforms, which evolved from collaborative filtering to graph-based models. Graph-based recommender systems represent all users and items by embeddings, and recommend items with largest inner products for a given user.
In this paper, (Cremonesi et al., 2010) and mean reciprocal ranking () (Sugiyama and Kan, 2010) serve as evaluation methodologies, whose definitions can be found in Appendix A.5. Moreover, we only use observed positive pairs to train node embeddings, which can clearly demonstrate that the improvement of performance comes from the proposed negative sampling. We summarize the performance of MCNS as well as the baselines in Table 2.
The results show that Hard-samples negative samplings generally surpass degree-based strategies with performance leaps in MRR. GAN-based negative sampling strategies perform even better, owing to the evolving generator mining hard negative samples more accurately. In the light of our theory, the proposed MCNS accomplishes significant gains of over the best baselines.
5.2.2. Link Prediction
Link prediction aims to predict the occurrence of links in graphs, more specifically, to judge whether a node pair is a masked true edge or unlinked pair based on nodes’ representations. Details about data split and evaluation are in Appendix A.5.
The results for link prediction are given in Table 3. MCNS outperforms all baselines with various graph representation learning methods on the Arxiv dataset. An interesting phenomenon about degree-based strategies is that both WRMF and commonly-used outperform uniform RNS sampling, completely adverse to the results on recommendation datasets. The results can be verified by examining the results in previous papers (Mikolov et al., 2013; Zhang and Zweigenbaum, 2018), reflecting the different network characteristics of user-item graphs and citation networks.
| Algorithm | DeepWalk | GCN | GraphSAGE | |
| AUC | 64.60.1 | 79.60.4 | 78.90.4 | |
| WRMF | 65.30.1 | 80.30.4 | 79.10.2 | |
| RNS | 62.20.2 | 74.30.5 | 74.70.5 | |
| PinSAGE | 67.20.4 | 80.40.3 | 80.10.4 | |
| WARP | 70.50.3 | 81.60.3 | 82.70.4 | |
| DNS | 70.40.3 | 81.50.3 | 82.60.4 | |
| IRGAN | 71.10.2 | 82.00.4 | 82.20.3 | |
| KBGAN | 71.60.3 | 81.70.3 | 82.10.3 | |
| MCNS | 73.10.4 | 82.60.4 | 83.50.5 |
5.2.3. Node Classification
Multi-label node classification is a usual task to assess graph representation algorithms. The one-vs-rest logistic regression classifier(Fan et al., 2008) is trained in a supervised way with graph representations as the features of nodes. In this experiment, we keep the default setting as the DeepWalk’s original paper for fair comparison on the BlogCatalog dataset.
Table 4 summarizes the Micro-F1 result on the BlogCatalog dataset. MCNS stably outperforms all baselines regardless of the training set ratio . The trends are similar for Macro-F1, which is omitted due to the space limitation.
| Algorithm | DeepWalk | GCN | GraphSAGE | |||||||
| 10 | 50 | 90 | 10 | 50 | 90 | 10 | 50 | 90 | ||
| Micro -F1 | 31.6 | 36.6 | 39.1 | 36.1 | 41.8 | 44.6 | 35.9 | 42.1 | 44.0 | |
| WRMF | 30.9 | 35.8 | 37.5 | 34.2 | 41.4 | 43.3 | 34.4 | 41.0 | 43.1 | |
| RNS | 29.8 | 34.1 | 36.0 | 33.4 | 40.5 | 42.3 | 33.5 | 39.6 | 41.6 | |
| PinSAGE | 32.0 | 37.4 | 40.1 | 37.2 | 43.2 | 45.7 | 36.9 | 43.2 | 45.1 | |
| WARP | 35.1 | 40.3 | 42.1 | 39.9 | 45.8 | 47.7 | 40.1 | 45.5 | 47.5 | |
| DNS | 35.2 | 40.4 | 42.5 | 40.4 | 46.0 | 48.6 | 40.5 | 46.3 | 48.5 | |
| IRGAN | 34.3 | 39.6 | 41.8 | 39.1 | 45.2 | 47.9 | 38.9 | 45.0 | 47.6 | |
| KBGAN | 34.6 | 40.0 | 42.3 | 39.5 | 45.5 | 48.3 | 39.6 | 45.3 | 48.5 | |
| MCNS | 36.1 | 41.2 | 43.3 | 41.7 | 47.3 | 49.9 | 41.6 | 47.5 | 50.1 | |
5.3. Analysis
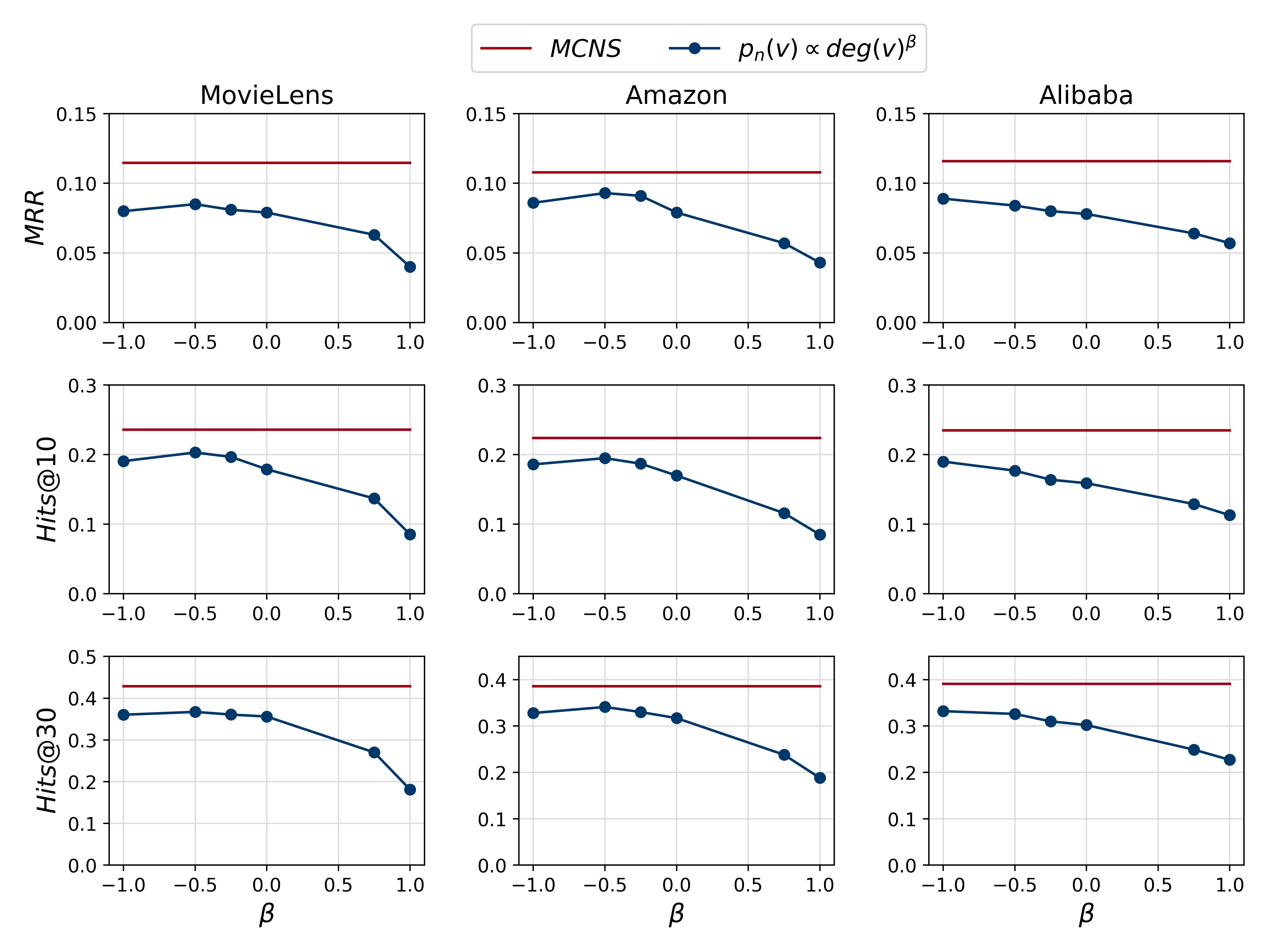
Comparison with Power of Degree. To thoroughly investigate the potential of degree-based strategies , a series of experiments are conducted by varying from -1 to 1 with GraphSAGE. Figure 3 shows that the performance of degree-based is consistently lower than that of MCNS, suggesting that MCNS learns a better negative distribution beyond the expressiveness of degree-based strategies. Moreover, the best varies between datasets and seems not easy to determine before experiments, while MCNS naturally adapts to different datasets.
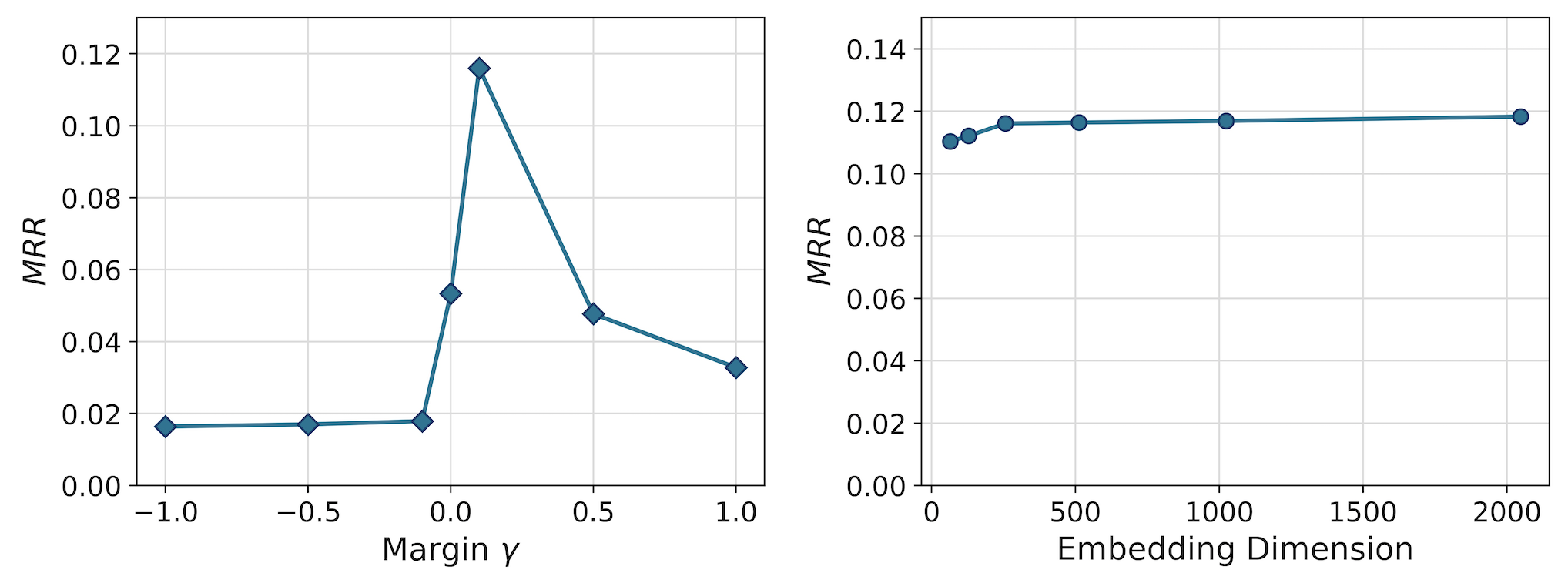
Parameter Analysis. To test the robustness of MCNS quantitively, we visualize the MRR curves of MCNS by varying two most important hyperparameters, embedding dimension and margin . The results with GraphSAGE on Alibaba dataset are shown in Figure 4.
The skewed hinge loss in Equation (14) aims to keep at least distance between the inner product of the positive pair and that of the negative pair. controls the distance between positive-negative samples and must be positive in principle. Correspondingly, Figure 4 shows that the hinge loss begins to take effect when and reaches its optimum at , which is a reasonable boundary. As the performance increases slowly with a large embedding dimension, we set it due to the trade-off between the performance and time consumption.
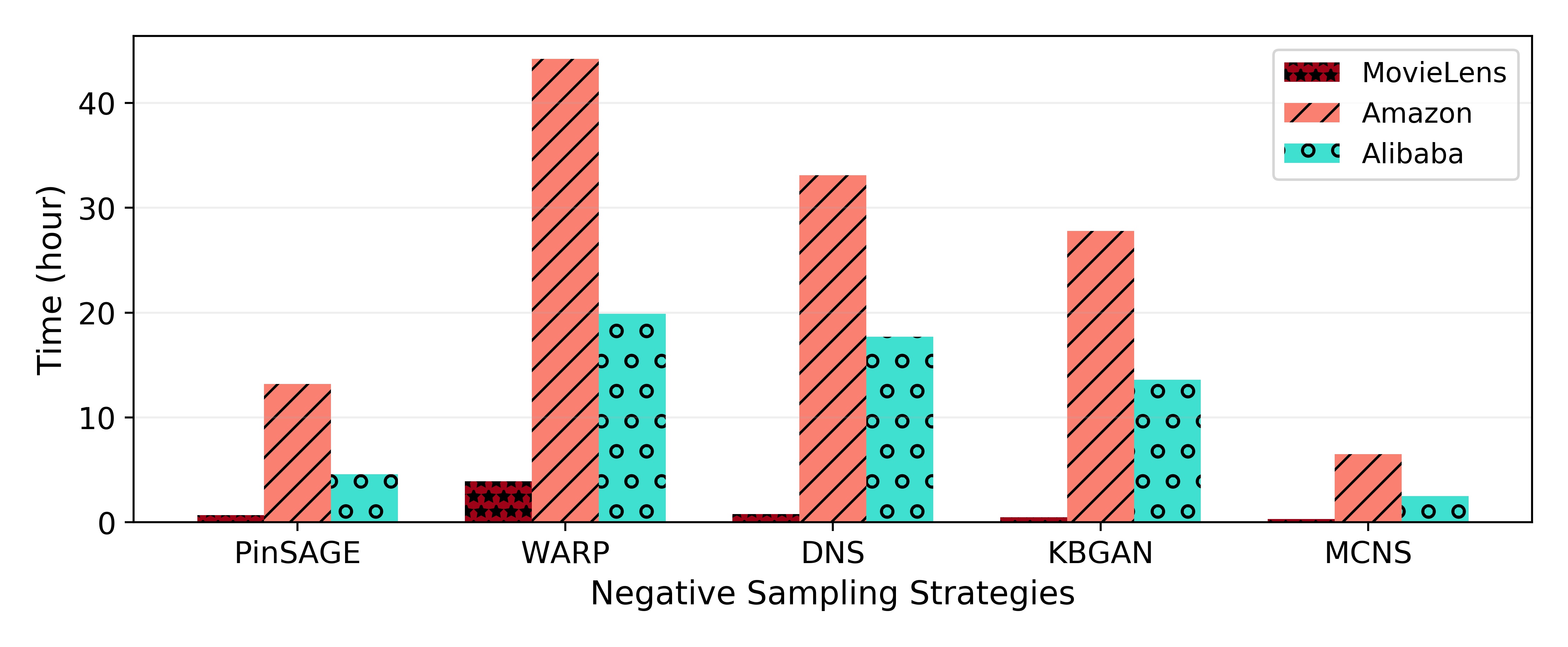
Efficiency Comparison. To compare the efficiency of different negative sampling methods, we report the runtime of MCNS and hard-samples or GAN-based strategies (PinSAGE, WARP, DNS, KBGAN) with GraphSAGE encoder in recommendation task in Figure 5. We keep the same batch size and number of epochs for a fair comparison. WARP might need a large number of tries before finding negative samples, leading to a long running time. PinSAGE utilizes PageRank to generate “hard negative items”, which increases running time compared with uniformly sampling. DNS and KBGAN both first sample a batch of candidates and then select negative samples from them, but the latter uses a lighter generator. MCNS requires 17 mins to complete ten-epochs training while the fastest baseline KBGAN is at least 2 slower on the MovieLens dataset.
5.4. Experiments for Further Understanding
In section 3, we have analyzed the criterion about negative sampling from the perspective of objective and risk. However, doubts might arise about (1) whether sampling more negative samples is always helpful, (2) why our conclusion contradicts with the intuition “positively sampling nearby nodes and negatively sampling faraway nodes ”.
To further deepen the understanding of negative sampling, we design two extended experiments on MovieLens with GraphSAGE encoder to verify our theory and present the results in Figure 6.
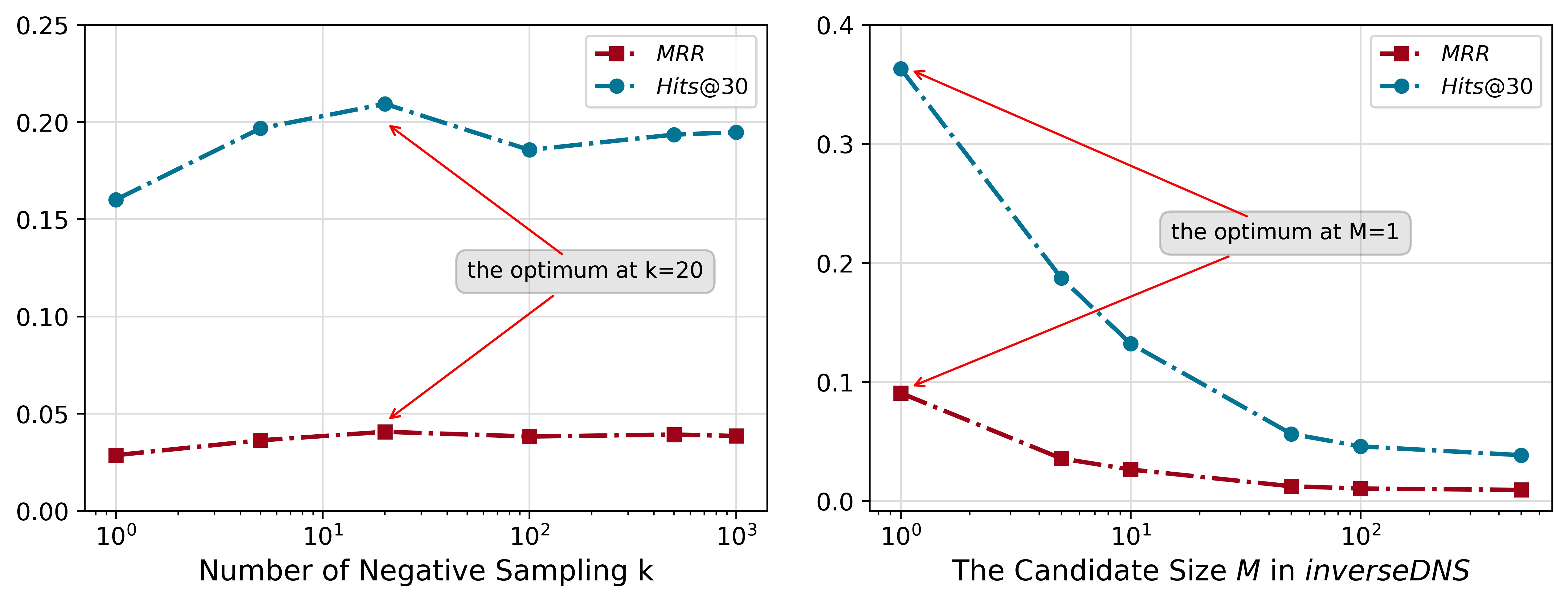
If we sample more negative samples, the performance increases with subsequently decrease. According to Equation (13), sampling more negative samples always decrease the risk, leading to an improvement in performance at first. However, performance begins to decrease after reaching the optimum, because extra bias is added to the objective by the increase of according to Equation (2). The bias impedes the optimization of the objective from zero-centered initial embeddings.
The second experiment in Figure 6 shows the disastrous consequences of negatively sampling more distant nodes, the nodes with small . To test the performances with varying degrees of the mismatching of and , we design a strategy, inverseDNS, by selecting the one scored lowest in the candidate items. In this way, not only the negative sampling probabilities of the items are sampled negatively correlated to , but also we can control the degree by varying candidate size . Both MRR and go down as increases, hence verifies our theory.
6. Related Work
Graph Representation Learning. The mainstream of graph representation learning on graphs diverges into two main topics: traditional network embedding and GNNs. Traditional network embedding cares more about the distribution of positive node pairs. Inspired by the skip-gram model (Mikolov et al., 2013), DeepWalk (Perozzi et al., 2014) learns embeddings via sampling “context” nodes for each vertex with random walks, and maximize the log-likelihood of observed context nodes for the given vertex. LINE (Tang et al., 2015) and node2vec (Grover and Leskovec, 2016) extend DeepWalk with various positive distributions. GNNs are deep learning based methods that generalize convolution operation to graph data. (Kipf and Welling, 2017) design GCNs by approximating localized 1-order spectral convolution. For scalability, GraphSAGE (Hamilton et al., 2017) employs neighbor sampling to alleviate the receptive field expansion. FastGCN (Chen et al., 2018) adopts importance sampling in each layer.
Negative Sampling. Negative sampling is firstly proposed to speed up skip-gram training in word2vec (Mikolov et al., 2013). Word embedding models sample negative samples according to its word frequency distribution proportional to the 3/4 power. Most later works on network embedding (Grover and Leskovec, 2016; Tang et al., 2015) follow this setting. In addition, negative sampling has been studied extensively in recommendation. Bayesian Personalized Ranking (Rendle et al., 2009) proposes uniform sampling for negative samples. Then, dynamic negative sampling (DNS) (Zhang et al., 2013) is proposed to sample informative negative samples based on current prediction scores. Besides, the PinSAGE (Ying et al., 2018) adds “hard negative items” to obtain fine enough “resolution” for recommender system. The negative samples are sampled uniformly with the rejection in WARP (Weston et al., 2011). Recently, GAN-based negative sampling method has also been adopted to train better node representations for information retrieval (Wang et al., 2017b), recommendation (Wang et al., 2018), word embeddings (Bose et al., 2018), knowledge graph embeddings (Cai and Wang, 2018). Another lines of research focus on exploiting sampled softmax (Bengio and Senécal, 2008) or its debiasing variant (Zhou et al., 2020) for extremely large scale link prediction tasks.
7. Conclusion
In this paper, we study the effect of negative sampling, a practical approach adopted in the literature of graph representation learning. Different from the existing works that decide a proper distribution for negative sampling in heuristics, we theoretically analyze the objective and risk of the negative sampling approach and conclude that the negative sampling distribution should be positively but sub-linearly correlated to their positive sampling distribution. Motivated by the theoretical results, we propose MCNS, approximating the ideal distribution by self-contrast and accelerating sampling by Metropolis-Hastings. Extensive experiments show that MCNS outperforms 8 negative sampling strategies, regardless of the underlying graph representation learning methods.
Acknowledgements
The work is supported by the NSFC for Distinguished Young Scholar (61825602), NSFC (61836013), and a research fund supported by Alibaba Group.
References
- (1)
- Bengio and Senécal (2008) Yoshua Bengio and Jean-Sébastien Senécal. 2008. Adaptive importance sampling to accelerate training of a neural probabilistic language model. IEEE Transactions on Neural Networks 19, 4 (2008), 713–722.
- Bose et al. (2018) Avishek Joey Bose, Huan Ling, and Yanshuai Cao. 2018. Adversarial Contrastive Estimation. (2018), 1021–1032.
- Cai and Wang (2018) Liwei Cai and William Yang Wang. 2018. KBGAN: Adversarial Learning for Knowledge Graph Embeddings. In NAACL-HLT‘18. 1470–1480.
- Caselles-Dupré et al. (2018) Hugo Caselles-Dupré, Florian Lesaint, and Jimena Royo-Letelier. 2018. Word2vec applied to recommendation: Hyperparameters matter. In RecSys’18. ACM, 352–356.
- Chen et al. (2018) Jie Chen, Tengfei Ma, and Cao Xiao. 2018. FastGCN: fast learning with graph convolutional networks via importance sampling. ICLR’18 (2018).
- Chib and Greenberg (1995) Siddhartha Chib and Edward Greenberg. 1995. Understanding the metropolis-hastings algorithm. The american statistician 49, 4 (1995), 327–335.
- Cremonesi et al. (2010) Paolo Cremonesi, Yehuda Koren, and Roberto Turrin. 2010. Performance of recommender algorithms on top-n recommendation tasks. In Proceedings of the fourth ACM conference on Recommender systems. ACM, 39–46.
- Ding et al. (2018) Ming Ding, Jie Tang, and Jie Zhang. 2018. Semi-supervised learning on graphs with generative adversarial nets. In CIKM’18. ACM, 913–922.
- Fan et al. (2008) Rong-En Fan, Kai-Wei Chang, Cho-Jui Hsieh, Xiang-Rui Wang, and Chih-Jen Lin. 2008. LIBLINEAR: A library for large linear classification. Journal of machine learning research 9, Aug (2008), 1871–1874.
- Gao and Huang (2018) Hongchang Gao and Heng Huang. 2018. Self-Paced Network Embedding. (2018), 1406–1415.
- Grover and Leskovec (2016) Aditya Grover and Jure Leskovec. 2016. node2vec: Scalable feature learning for networks. In KDD’16. ACM, 855–864.
- Gutmann and Hyvärinen (2012) Michael U Gutmann and Aapo Hyvärinen. 2012. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics. Journal of Machine Learning Research 13, Feb (2012), 307–361.
- Hamilton et al. (2017) Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. In NIPS’17. 1024–1034.
- Hsu and Lachenbruch (2007) Henry Hsu and Peter A Lachenbruch. 2007. Paired t test. Wiley encyclopedia of clinical trials (2007), 1–3.
- Hu et al. (2008) Yifan Hu, Yehuda Koren, and Chris Volinsky. 2008. Collaborative filtering for implicit feedback datasets. In ICDM’08. Ieee, 263–272.
- Huang et al. (2014) Hong Huang, Jie Tang, Sen Wu, Lu Liu, and Xiaoming Fu. 2014. Mining triadic closure patterns in social networks. In WWW’14. 499–504.
- Kipf and Welling (2017) Thomas N Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks. ICLR’17 (2017).
- Leskovec et al. (2007) Jure Leskovec, Jon Kleinberg, and Christos Faloutsos. 2007. Graph evolution: Densification and shrinking diameters. TKDD’07 1, 1 (2007), 2–es.
- Levy and Goldberg (2014) Omer Levy and Yoav Goldberg. 2014. Neural word embedding as implicit matrix factorization. In NIPS’14. 2177–2185.
- Li et al. (2018) Qimai Li, Zhichao Han, and Xiao-Ming Wu. 2018. Deeper insights into graph convolutional networks for semi-supervised learning. In AAAI’18.
- Linden et al. (2003) Greg Linden, Brent Smith, and Jeremy York. 2003. Amazon. com recommendations: Item-to-item collaborative filtering. IEEE Internet computing 7, 1 (2003), 76–80.
- McAuley et al. (2015) Julian McAuley, Christopher Targett, Qinfeng Shi, and Anton Van Den Hengel. 2015. Image-based recommendations on styles and substitutes. In SIGIR’15. ACM, 43–52.
- Metropolis et al. (1953) Nicholas Metropolis, Arianna W Rosenbluth, Marshall N Rosenbluth, Augusta H Teller, and Edward Teller. 1953. Equation of state calculations by fast computing machines. The journal of chemical physics 21, 6 (1953), 1087–1092.
- Mikolov et al. (2013) Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013. Distributed representations of words and phrases and their compositionality. In NIPS’13. 3111–3119.
- Mnih and Kavukcuoglu (2013) Andriy Mnih and Koray Kavukcuoglu. 2013. Learning word embeddings efficiently with noise-contrastive estimation. In NIPS’13. 2265–2273.
- Pan et al. (2008) Rong Pan, Yunhong Zhou, Bin Cao, Nathan N Liu, Rajan Lukose, Martin Scholz, and Qiang Yang. 2008. One-class collaborative filtering. In ICDM’08. IEEE, 502–511.
- Perozzi et al. (2014) Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. 2014. Deepwalk: Online learning of social representations. In KDD’14. ACM, 701–710.
- Qiu et al. (2018) Jiezhong Qiu, Yuxiao Dong, Hao Ma, Jian Li, Kuansan Wang, and Jie Tang. 2018. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In WSDM’18. ACM, 459–467.
- Rendle et al. (2009) Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. 2009. BPR: Bayesian personalized ranking from implicit feedback. In UAI’09. AUAI Press, 452–461.
- Sugiyama and Kan (2010) Kazunari Sugiyama and Min-Yen Kan. 2010. Scholarly paper recommendation via user’s recent research interests. In JCDL’10. ACM, 29–38.
- Sun et al. (2019) Zhiqing Sun, Zhi-Hong Deng, Jian-Yun Nie, and Jian Tang. 2019. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv preprint arXiv:1902.10197 (2019).
- Tang et al. (2015) Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. 2015. Line: Large-scale information network embedding. In WWW’15. 1067–1077.
- Tu et al. (2017) Cunchao Tu, Han Liu, Zhiyuan Liu, and Maosong Sun. 2017. Cane: Context-aware network embedding for relation modeling. In ACL’17. 1722–1731.
- Veličković et al. (2018) Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. 2018. Graph attention networks. ICLR’18 (2018).
- Wang et al. (2017b) Jun Wang, Lantao Yu, Weinan Zhang, Yu Gong, Yinghui Xu, Benyou Wang, Peng Zhang, and Dell Zhang. 2017b. Irgan: A minimax game for unifying generative and discriminative information retrieval models. In SIGIR’17. ACM, 515–524.
- Wang et al. (2018) Qinyong Wang, Hongzhi Yin, Zhiting Hu, Defu Lian, Hao Wang, and Zi Huang. 2018. Neural memory streaming recommender networks with adversarial training. In KDD’18. ACM, 2467–2475.
- Wang et al. (2017a) Xiao Wang, Peng Cui, Jing Wang, Jian Pei, Wenwu Zhu, and Shiqiang Yang. 2017a. Community preserving network embedding. In AAAI’17.
- Weston et al. (2011) Jason Weston, Samy Bengio, and Nicolas Usunier. 2011. Wsabie: Scaling up to large vocabulary image annotation. In IJCAI’11.
- Xu et al. (2018) Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2018. How powerful are graph neural networks? arXiv preprint arXiv:1810.00826 (2018).
- Ying et al. (2018) Rex Ying, Ruining He, Kaifeng Chen, Pong Eksombatchai, William L Hamilton, and Jure Leskovec. 2018. Graph convolutional neural networks for web-scale recommender systems. In KDD’18. ACM, 974–983.
- Zhang et al. (2013) Weinan Zhang, Tianqi Chen, Jun Wang, and Yong Yu. 2013. Optimizing Top-N Collaborative Filtering via Dynamic Negative Item Sampling. In SIGIR’13. ACM, 785–788.
- Zhang et al. (2019) Yongqi Zhang, Quanming Yao, Yingxia Shao, and Lei Chen. 2019. NSCaching: Simple and Efficient Negative Sampling for Knowledge Graph Embedding. (2019), 614–625.
- Zhang and Zweigenbaum (2018) Zheng Zhang and Pierre Zweigenbaum. 2018. GNEG: Graph-Based Negative Sampling for word2vec. In ACL’18. 566–571.
- Zhao et al. (2015) Tong Zhao, Julian McAuley, and Irwin King. 2015. Improving latent factor models via personalized feature projection for one class recommendation. In CIKM’15. ACM, 821–830.
- Zhou et al. (2017) Chang Zhou, Yuqiong Liu, Xiaofei Liu, Zhongyi Liu, and Jun Gao. 2017. Scalable graph embedding for asymmetric proximity. In AAAI’17.
- Zhou et al. (2020) Chang Zhou, Jianxin Ma, Jianwei Zhang, Jingren Zhou, and Hongxia Yang. 2020. Contrastive Learning for Debiased Candidate Generation in Large-Scale Recommender Systems. arXiv:cs.IR/2005.12964
Appendix A Appendix
In the appendix, we first report the implementation notes of MCNS, including the running environment and implementation details. Then, the encoder algorithms are presented. Next, the detailed description of each baseline is provided. Finally, we present datasets, evaluation metrics and the DFS algorithm in detail.
A.1. Implementation Notes
Running Environment. The experiments are conducted on a single Linux server with 14 Intel(R) Xeon(R) CPU E5-268 v4 @ 2.40GHz, 256G RAM and 8 NVIDIA GeForce RTX 2080TI-11GB. Our proposed MCNS is implemented in Tensorflow 1.14 and Python 3.7.
Implementation Details. All algorithms can be divided into three parts: negative sampling, positive sampling and embedding learning. In this paper, we focus on negative sampling strategy. A negative sampler selects a negative sample for each positive pair and feeds it with a corresponding positive pair to the encoder to learn node embeddings. With the exception of PinSAGE, the ratio of positive to negative pairs is set to for all negative sampling strategies. PinSAGE uniformly selects 20 negative samples per batch and adds 5 “hard negative samples” per positive pair. Nodes ranked at top-100 according to PageRank scores are randomly sampled as “hard negative samples”. The candidate size in DNS is set to 5 for all datasets. The value of in KBGAN is set to 200 for Amazon and Alibaba datasets, and 100 for other datasets.
For recommendation task, we evenly divide the edges in each dataset into 11 parts, 10 for ten-fold cross validation and the extra one as a validation set to determine hyperparameters. For recommendation datasets, the node types contain and representing user and item respectively. Thus, the paths for information aggregation are set to and for GraphSAGE and GCN encoders. All the important parameters in MCNS are determined by a rough grid search. For example, the learning rate is the best among [,,,]. Adam with serves as the optimizer for all the experiments. The values of hyperparameters in different datasets are listed as follows:
| MovieLens | Amazon | Alibaba | |
| learning rate | |||
| embedding dim | 256 | 512 | 512 |
| margin | 0.1 | 0.1 | 0.1 |
| batch size | 256 | 512 | 512 |
| in Hits@k | ALL | 500 | 500 |
For link prediction task, we employ five-fold cross validation to train all methods. The embedding dimension is set to 256, and the margin also be set to 0.1 for all strategies. The model parameters are updated and optimized by stochastic gradient descent with Adam optimizer.
In multi-label classification task, we first employ all the edges to learn node embeddings. Then, these embeddings serve as features to train the classifier. Embedding dimension is set to 128 and the margin is set as 0.1 on the BlogCatalog dataset for all negative sampling strategies. The optimizer also adopts Adam updating rule.
A.2. Encoders
We perform experiments on three algorithms as follows.
-
•
DeepWalk (Perozzi et al., 2014) is the most representative graph representation algorithm. According to the Skip-gram model (Mikolov et al., 2013), DeepWalk samples nodes co-occurring in the same window in random-walk paths as positive pairs, which acts as a data augmentation. This strategy serves as “sampling from ” in the view of SampledNCE (§2.2).
-
•
GCN (Kipf and Welling, 2017) introduces a simple and effective neighbor aggregation operation for graph representation learning. Although GCN samples positive pairs from direct edges in the graph, the final embeddings of nodes are implicitly constrained by the smoothing effect of graph convolution. However, due to its poor scalability and high memory consumption, GCN cannot handle large graphs.
-
•
GraphSAGE (Hamilton et al., 2017) is an inductive framework of graph convolution. A fixed number of neighbors are sampled to make the model suitable for batch training, bringing about its prevalence in large-scale graphs. The mean-aggregator is used in our experiments.
A.3. Baselines
We give detailed negative sampling strategies as follows. For each encoder, the hyperparameters for various negative sampling strategies remain the same.
- •
-
•
RNS (Caselles-Dupré et al., 2018). RNS means sampling negative nodes at uniform random. Previous work (Caselles-Dupré et al., 2018) mentions that in recommendation, RNS performs better and more robust than during tuning hyperparameters. This phenomenon is also verified in our recommendation experiments by using this setting as a baseline.
-
•
WRMF (Hu et al., 2008; Pan et al., 2008). Weighted Regularized Matrix Factorization is an implicit MF model, which adapts a weight to reduce the impact of unobserved interactions and utilizes an altering-least-squares optimization process. To solve the high computational costs, WRMF proposes three negative sampling schemes, including Uniform Random Sampling (RNS), Item-Oriented Sampling (ItemPop), User-Oriented Sampling (Unconsider in our paper).
-
•
DNS (Zhang et al., 2013). Dynamic Negative Sampling (DNS) is originally designed for sampling negative items to improve pair-wise collaborative filtering. For each user , DNS samples negative items and only retains the one with the highest scoring function . DNS can be applied to graph-based recommendation by replacing in BPR (Rendle et al., 2009) with the inner product of embedding .
-
•
PinSAGE (Ying et al., 2018). In PinSAGE, a technique called “hard negative items” is introduced to improve its performance. The hard negative items refer to the high ranking items according to users’ Personalized PageRank scores. Finally, negative items are sampled from top-K hard negative items.
- •
-
•
IRGAN (Wang et al., 2017b). IRGAN is a GAN-based IR model that unify generative and discriminative information retrieval models. The generator generates adversarial negative samples to fool the discriminator while the discriminator tries to distinguish them from true positive samples.
-
•
KBGAN (Cai and Wang, 2018). KBGAN proposed a adversarial sampler to improve the performances of knowledge graph embedding models. To reduce computational complexity, KBGAN uniformly randomly selects nodes to calculate the probability distribution for generating negative samples. Inspired by it, NMRN (Wang et al., 2018) employed a GAN-based adversarial training framework in streaming recommender model.
A.4. Datasets
The detailed descriptions for five datasets are listed as follows.
-
•
MovieLens333https://grouplens.org/datasets/movielens/100k/ is a widely-used movie rating dataset for evaluating recommender systems. We choose the MovieLens-100k version that contains 100,000 interaction records generated by 943 users on 1682 movies.
-
•
Amazon444http://jmcauley.ucsd.edu/data/amazon/links.html is a large E-commerce dataset introduced in (McAuley et al., 2015), which contains purchase records and review texts whose time stamps span from May 1996 to July 2014. In the experiments, we take the data from the commonly-used “electronics” category to establish a user-item graph.
-
•
Alibaba555we use Alibaba dataset to represent the real data we collected. is constructed based on the data from another large E-commerce platform, which contains user’s purchase records and items’ attribute information. The data are organized as a user-item graph for recommendation.
-
•
Arxiv GR-QC (Leskovec et al., 2007) is a collaboration network generated from the e-print arXiv where nodes represent authors and edges indicate collaborations between authors.
-
•
BlogCatalog is a network of social relationships provided by blogger authors. The labels represent the topic categories provided by the authors and each blogger may be associated to multiple categories. There are overall 39 different categories for BlogCatalog.
A.5. Evaluation Metrics
Recommendation. To evaluate the performance of MCNS for recommendation task, (Cremonesi et al., 2010) and mean reciprocal ranking () (Sugiyama and Kan, 2010) serve as evaluation methodologies.
-
•
Hits@k is introduced by the classic work (Sugiyama and Kan, 2010) to measure the performance of personalized recommendation at a coarse granularity. Specifically, we can compute of a recommendation system as follows:
-
(1)
For each user-item pair in the test set , we randomly select additional items which are never showed to the queried user .
-
(2)
Form a ranked list of in descending order.
-
(3)
Examine whether the rank of is less than (hit) or not (miss).
-
(4)
Calculate according to .
-
(1)
-
•
MRR is another evaluation metric for recommendation task, which measures the performance at a finer granularity than . assigns different scores to different ranks of item in the ranked list mentioned above when querying user , which is defined as follows:
In our experiment, we set as , and is set to 500 for the Alibaba and Amazon datasets. For the MovieLens dataset, we use all unconnected items for each user as items to evaluate the hit rate.
Link Prediction. The standard evaluation metric AUC is widely applied to evaluate the performance on link prediction task (Grover and Leskovec, 2016; Tu et al., 2017; Zhou et al., 2017). Here, we utilize rocaucscore function from scikit-learn to calculate prediction score. The specific calculation process is demonstrated as follows.
-
(1)
We extract of true edges and remove them from the whole graph while ensuring the residual graph is connected.
-
(2)
We sample 30 false edges, and then combine of true edges and false edges into a test set.
-
(3)
Each graph embedding algorithm with various negative sampling strategies is trained using the residual graph, and then the embedding for each node is obtained.
-
(4)
We predict the probability of a node pair being a true edge according to the inner product. We finally calculate AUC score according to the probability via rocaucscore function.
Multi-label Classification. In the multi-label classification, we adopt Micro-F1 and Macro-F1 as evaluation metrics, which are widely used in many previous works (Mikolov et al., 2013; Grover and Leskovec, 2016). In our experiments, the F1 score is calculated by scikit-learn. In detail, we randomly select a percentage of labeled nodes, %%% to learn node embeddings. Then the learned embeddings is used as features to train the classifier and predict the labels of the remaining nodes. For fairness in comparison, we used the same training set to train the classifier for all negative sampling strategies. For each training ratio, we repeat the process 10 times and report the average scores.
A.6. DFS
Here we introduce a DFS strategy to generate traversal sequence where adjacent nodes in the sequence is also adjacent in the graph.