Unfolding Conformal Geometry
Abstract
Conformal geometry is studied using the unfolded formulation à la Vasiliev. Analyzing the first-order consistency of the unfolded equations, we identify the content of zero-forms as the spin-two off-shell Fradkin-Tseytlin module of . We sketch the nonlinear structure of the equations and explain how Weyl invariant densities, which Type-B Weyl anomaly consist of, could be systematically computed within the unfolded formulation. The unfolded equation for conformal geometry is also shown to be reduced to various on-shell gravitational systems by requiring additional algebraic constraints.
1 Introduction
Conformal geometry plays an important role in many areas of gravitational and high energy physics as well as in certain fields of geometry. It extends the diffeomorphism invariant Riemannian geometry with local rescaling symmtery, namely the Weyl (rescaling) symmetry. Conformal geometry can be also viewed as the geometry of the asymptotic boundary of the bulk spacetime with negative cosmological constant [1], and hence it can be used in the AdS/CFT correspondence [2]. Conformal gravity in four dimensions is an alternative gravitational theory enjoying Weyl symmetry besides diffeomorphism. Since its introduction by Weyl and Bach, many studies were devoted to it (see e.g. [3, 4, 5] and references therein). As a four-derivative gravitational theory in four dimensions, it is power-counting renormalizable as opposed to Einstein gravity and has many interesting features which might be relevant in phenomenological models of gravity: notably, it has the conformal symmetry which the early universe seems to exhibit, and hence conformal gravity or its variant may replace Einstein gravity in the very early time of the universe (see e.g. recent works [5, 6] and references therein). More generally, when we consider various modifications of gravity, conformal geometry also plays a distinguished role since the diffeomorphism plus Weyl rescaling is the maximum gauge symmetry that a theory of symmetric rank-two tensor field can afford.
Another prominent use of conformal geometry is in conformal field theories where it appears as Weyl anomaly (see e.g. [7] for an historical overview). Like the other anomalies, Weyl anomaly is subjected to the Wess-Zumino consistency condition, and the classification of Weyl anomalies by the relevant cohomological analysis has been innitiated in [8, 9] with results up to dimension six. The structure in general dimensions, postulated already in [9], was confirmed first by using the technics of dimensional regularization on the effective gravitational action [10] and later by a cohomological analysis [11, 12]. According to these results, a Weyl anomaly in dimensions is the spacetime integral of a linear combination of the following densities multiplied by the Weyl rescaling parameter .
-
•
Type-A anomaly, associated with -coefficient: Euler density, , where is the Riemann curvature two-forms.
-
•
Type-B anomaly, associated with -coefficient: strictly Weyl invariant density, which is a specific contraction of (covariant derivatives of) Riemann tensors, including any full contraction of Weyl tensors.
The explicit form or even the number of the non-trivial Weyl invariant densities — by “non-trivial Weyl invariant densities”, we mean Weyl invariant densities which are not contractions of Weyl tensors — are not known in general dimensions but up to dimensions eight. In six dimensions, it was shown in [9, 13, 10] that there exists only one non-trivial Weyl invariant density (see also [2]). In eight dimensions, the authors of [14] showed, by employing purely algebraic methods based on a Weyl covariant tensor calculus [15] and with a help of computer program, that there exists five non-trivial Weyl invariant densities. The covariant derivative and the calculus used in [15] is closely related (see [16] for the relation) to the Thomas D operator and the tractor calculus for conformal geometry [17]. See e.g. [18] for more background in this topic. The current work originated from the attempt of understanding the above structure from a different angle.
As Riemaniann geometry can be understood as the gauge theory of an isometry group, such as Poincaré or (Anti) de Sitter group, conformal geometry can be viewed as the gauge theory of conformal group . Such algebraic approaches to geometries have been pioneered by Cartan and Weyl, and known as Cartan geometry (see e.g. [19]). It incorporates not only Riemaniann, but also parabolic geometry of which conformal geometry is an example. In physics, there have been several attempts to obtain conformal gravity actions using -gauge fields. Analogously to the re-derivation of Einstein action using the isometry-algebra-valued gauge field [20] (see also [21]), four-dimensional conformal gravity action has been expressed as an action of -gauge field subject to certain off-shell constraints [22, 23, 24] (see also the review [25]). In three dimensions, the Chern-Simons theory of -gauge field provides a Weyl invariant theory with all necessary constraints integrated in it [26]. It has been also shown that conformal gravity actions can be obtained from an ambient space formulation [27] and from a dimensional reduction [28].
Yet another framework intimately related to the Cartan geometry is the Vasiliev’s unfolded formulation [29, 30, 31, 32, 33]. It is basically the zero-form extension of free differential algebra introduced in the context of supergravity [34]. Thanks to the zero-forms, dynamical equations can be expressed in an integrable first-derivative form, and the consistency of dynamical system becomes purely algebraic. The unfolded formulation has been originally introduced for higher spin gravity [33, 35, 36] but can be applied to any dynamical system. In particular, a huge variety of free dynamical systems governed by the conformal algebra have been analyzed in the unfolded formulation [37, 38], and it has been shown that the structure of the representations appearing there matches that of the Bernstein-Gelfand-Gelfand resolution (see e.g. [39]). In [40], Fefferman-Graham ambient construction has been integrated into the unfolded system as Hamiltonian constraints.
In this work, we unfold conformal geometry starting from the gauge connection. As mentioned above, the merit of the unfolding procedure lies in the zero-form sector and we closely look into this part and fill the details which are not delineated in the literature. By explicitly analyzing the first-order consistency of the unfolded equation, we find that the content of zero-forms corresponds to the spin-two off-shell Fradkin-Tseyltin module [37, 41] (see also [42]), that is the module associated with the off-shell spin-two Fradkin-Tseytlin field [25]. In this paper, we are primarily interested in the unfolding of the off-shell system. Indeed, the unfolding formulation can be applied not only to dynamical systems but also systems without prescribed dynamics, namely, off-shell systems [38]. See [43, 44] for recent works on the off-shell extension of higher spin gravity. An interesting point of off-shell unfolding is that it can be posteriorly reduced to an on-shell system by imposing additional algebraic constraints on the zero-form sector. In this way, once we unfold conformal geometry, we can reduce it to the on-shell conformal gravity, namely Bach-flat geometry, by eliminating some zero-forms with additional algebraic constraints. Moreover, by imposing additional constraints on both of the one-form and zero-form sectors, one can reduce it even to Einstein gravity or various modifications of it. If we restrict to the linear equation, then the unfolded off-shell spin-two Fradkin-Tseytlin system can be reduced to on-shell Fradkin-Tseytlin system, as well as partially massless or massive spin-two systems [45, 46]. In this paper, we mostly consider the spin-two cases, but clearly, many of the above reductions can be generalized to higher spins. Let us note — to avoid a potential confusion of interpreting the above statements in the AdS/CFT context — that all these theories are defined in the same dimensional spacetime.
Another merit of the unfolding of conformal geometry is that it allows to revisit the classification of Weyl anomalies, which was our original motivation. As we shall show below, the classification of Weyl anomalies à la unfolding is essentially the same as the method proposed in [14]. The latter makes use of Weyl-covariant derivatives of Weyl tensors, which carry reducible Lorentz representations, to make an ansatz for Weyl invariant density. Instead, the unfolded equation is equipped with the zero-forms carrying irreducible Lorentz representations, and the ansatz for a Weyl invariant density is made by these zero-forms. Unfortunately, the unfolding does not gain sizable computational efficiency, and to revisit the eight dimensional classification or even to attack the ten dimensional problem, it would be inevitable to use a computer programming, like in [14], which was beyond the scope of the current work. Despite this limitation, we still find it useful in understanding the general structure of unfolding conformal geometry and the essence of the Weyl anomaly classification problem. The explicit knowledge of the zero-form content and their first-order gauge transformation allows us to do a few preliminary assessments of the classification.
The organization of paper is as follows. In Section 2, we begin with a review of the gauge formulation of conformal gravity and set the problem of unfolding conformal geometry, which can be approached perturbatively in the power of zero-forms. In Section 3, we explain how the linear part of the unfolded equation in the zero-form expansion defines a representation in the space of zero-form fields. This differs from the analysis of linearized equations around a specific background as the latter captures only the isometry part of . We solve the consistency conditions of the linear part by using cell operators and find explicit form of the equation up to linear order in the zero-form. In Section 4, we review the spin-two off-shell Fradkin-Tseyltin module, and show its decomposition coincides with the content of the zero-form fields. We comment also on the subtle points on the active and passive actions and the role of dual representation. In Section 5, we sketch the structure of the unfolding at nonlinear orders and show how the nonlinear equations can be systematically determined by moving up from the zero-form field equation of the lowest conformal weight. In Section 6, we review the gauge symmetry of an unfolded system, and show how the non-trivial Weyl invariants could be determined as gauge invariant -forms. In particular, we determine the unique quadratic part of the Weyl invariants in eight and ten dimensions. We also provide discussions on higher order parts. In Section 7, we show how various on-shell systems can be obtained by requiring certain algebraic constraints which are invariant under special conformal transformations. We also discuss how the off-shell conformal system itself can be viewed as a constrained system.
2 Unfolding conformal geometry
In this section, first we review the gauge formulation of conformal geometry, which has been known since [22, 23, 24] (see also [47] for a recent use of it). Then, we introduce the unfolding scheme to conformal geometry with a rather pedagogical account.
2.1 Gauge formulation of conformal geometry
Let us begin with setting the convention for the conformal algebra: the Lie algebra is generated by anti-Hermitian generators with the Lie bracket,
| (2.1) |
where is the flat metric with signature . Taking the basis with indices and where and is the -dimensional flat metric with signature , the Lie bracket of , , and read
| (2.2) | |||||
From now on, all the Latin indices are lowered and raised by and .
Let us review now the gauge formulation of conformal geometry. We consider the gauge one-form taking value in algebra,
| (2.3) |
where are one-form fields which are all independent at this stage. For geometric interpretation, we assume the one-form has components which are invertible, and the inverse is denoted by , which define vector fields . The curvature two form,
| (2.4) |
has the components,
| (2.5) | |||||
Here, is the Lorentz covariant differential,
| (2.6) |
and is given by
| (2.7) |
This system has gauge symmetry,
| (2.8) |
Labeling the components of the gauge parameter as
| (2.9) |
the one-forms transform as
| (2.10) | |||
| (2.11) | |||
| (2.12) | |||
| (2.13) |
We would need a partial gauge fixing as well as imposing constraints to recover the usual geometry based on metric tensor.
Let us review the set of constraints which bring the -gauge theory to conformal geometry. First, we impose the torsionless constraint,
| (2.14) |
which is modified by the presence of . Here, we use the notation to emphasize that it is a constraint that we decided to impose. We also impose the curvature for dilation to vanish
| (2.15) |
From the Bianchi identity , we find
| (2.16) | |||||
| (2.17) | |||||
| (2.18) | |||||
| (2.19) |
where we implemented the constraints C (2.14) and C (2.15). Let us express
| (2.20) |
Then and are given in terms of and with (or and ) as
| (2.21) | |||||
| (2.22) |
where . The first two identities, namely, the algebraic Bianchi identities are equivalent to
| (2.23) |
| (2.24) |
so they are irreducible tensors:
| (2.25) |
Moreover if we impose the trace-free constraint on ,
| (2.26) |
the trace of the differential Bianchi identity (2.18) requires to be trace-free as well:
| (2.27) |
In fact, the constraints and are not independent, and the former is a consequence of the latter together with other constraints. To recapitulate, we impose the following set of constraints,111In parabolic geometry [19], these constraints are what define “normal connection”. See Section 7 for further discussions.
| (2.28) |
and the resulting algebraic Bianchi identities are
| (2.29) |
The differential Bianchi identities (2.18) and (2.19) read
| (2.30) |
The above is the starting point of the unfolding machinery. Before moving to that, let us review how the usual conformal geometry can be recovered from this setting.
Reduction to metric formulation
All the constraints can be solved algebraically:
-
•
The constraint C determines (or ) in terms of and as
(2.31) -
•
The constraint C determines in terms of :
(2.32) where .
-
•
The constraint C determines in terms of : from (2.21), we find
(2.33)
After solving all the constraints, the -gauge symmetry reduces to222In fact, the constraints are not invariant under the gauge transformation (2.13) with the parameter : (2.34) However, the gauge symmetries can be properly modified by a “non-geometrical” curvature term [23] so as to leave all the constraints invariant. In fact, this modification naturally arises in the unfolded formulation. See Section 6.1 for the details.
| (2.35) | |||
| (2.36) |
We can fix the gauge symmetries associated with and as follows.
-
•
The gauge symmetry of allows us to set to zero:
(2.37) Note that in this gauge, the symmetry must transformation under the symmetry with the parameter,
(2.38) -
•
The gauge symmetry of is
(2.39) which allows us to fix the degrees of freedom of besides those in
(2.40)
The residual gauge symmetries are those of and ,
-
•
The gauge symmetry of gives the Weyl rescaling,
(2.41) -
•
The gauge symmetry of gives the diffeomorphism,
(2.42)
After the reduction, we find that and coincide with the usual Riemann and Weyl tensor, and and with the Schouten and Cotton tensors.
2.2 Unfolding conformal geometry
Let us now consider the unfolding of conformal geometry. Remind that we have used the equations,
| (2.43) |
with
| (2.44) |
In the former set of equations, we slightly simplified the expressions by introducing or 333The maximal compact subalgebra of is not but . However, the two subalgebras are intimately related as we shall comment later in Section 4.1. covariant derivative , which acts on a -tensor with conformal dimension as
| (2.45) |
and assigning the conformal dimensions to , respectively.444Assigning the conformal dimension to , the fields have conformal dimensions identical to the numbers of derivatives of the corresponding fields in the metric formulation. Note here that the eigenvalue of the dilation operator is . This reflects that the fields carry in fact a dual (or contragredient) representation which is obtained by the anti-involution . See Section 4.2 for more discussions on this point.
In the following, we sketch the key reasoning of the unfolding scheme.
-
•
The system (2.43) can be regarded as a set of equations for one-forms and as well as zero-forms and . Note that and have conformal dimensions and , respectively. The zero-forms are completely, namely algebraically, determined by the equations, and hence no new degrees of freedom are introduced by employing them. About the one-forms, basically the equations tell how the (covariant) derivatives of the one-forms are determined by the other fields without any derivatives. Consequently, the one-forms are subject to certain conditions which are necessary for the system to be equivalent to conformal geometry.
-
•
Viewing (2.43) as a dynamical system for the associated fields, that is, the one-forms and and the zero-forms and , it is more natural to introduce a new set of equations which determine the evolution—that is, the (covariant) derivatives—of and :
(2.46) On the right hand side of the equations, we have introduced a new set of zero-form fields and besides what can be expressed in terms of pre-existing fields. The new fields and should be subject to a proper set of conditions so that the new equations (2.46) with the new fields neither introduce any new degrees of freedom nor remove any pre-existing degrees of freedom. For this, one need to examine the compatibility of the new equations (2.46) with the Bianchi identities (2.30).
- •
-
•
This procedure can be continued iteratively, and introduces infinitely many zero-form fields with infinitely many equations in a way that such an extension of the fields and equations does not alter the content of degrees of the freedom of the system.
In order to work with an infinite number of additional zero-form fields, we need to label them efficiently, and the subalgebra can provide such a good label:555At this stage, it is not clear whether the -label would be sufficient without necessitating an additional label to distinguish two fields of the same -label. As we will show below, the -label is sufficient to describe all the fields in the system. In other words, in the decomposition of the zero-form module into -irreps, there is no multiplicty. in the following any zero-form fields will be labeled as traceless fiberwise tensors with two groups of totally symmetric indices,
| (2.47) |
subject to the Young projection condition,
| (2.48) |
In this way, the fiberwise tensor carries an irrep under corresponding to a two-row Young diagram. We adopt the following common short-hand notation,
| (2.49) |
Sometimes, it will be more convenient to use what we will refer to as “depth” , than the conformal dimension :
| (2.50) |
The zero-form fields and should be identified with the usual Weyl and Cotton tensors:
| (2.51) |
If we relax the above identification condition, the zero-form equations that we will elaborate below has the capacity to describe a system of any integral spin.
The infinite amount of the -covariant equations for zero-forms that we need to identify will take the following form,
| (2.52) |
where and are functions of the zero-forms with total conformal weight and . Let us recall that the conformal dimensions of and are and 0. We can consider the Taylor expansion of ,
| (2.53) |
where the expansion coefficients and are made only by Kronecker delta symbols so that they only rearrange or contract indices. The function can be expanded analogously. Identifying the general form of and is a highly non-trivial task, and hence we first identify the linear parts, which will determine the content of the zero-forms. The identification of non-linear terms can be worked out, in principle, order by order in . Due to the boundness of , will involve at most order terms.
3 First order unfolding of conformal geometry
3.1 First order unfolding
Let us consider the system only up to the linear order,
| (3.1) |
where we have used the notation,666Note that denotes the components of the tensor . Here, is not a tenor of type but is.
| (3.2) |
Remark that the linear terms of and are denoted by the actions of and , respectively. It will become shortly clearly that they indeed correspond to the action of translation and special conformal transformation. Remind also that the action of and on the space of zero-form fields is not yet defined. The equation (3.1) suggests to combine the linear terms with the -covariant derivative as
| (3.3) |
with
| (3.4) |
The Bianchi identity is the consistency of the equation (3.3) associated with
| (3.5) | |||||
Since the action of on is at least quadratic in , the following should hold.
| (3.6) |
and, we find that the consistency of the equation requires the operators and coincide with the actions of translation and special conformal transformation. Therefore, the linear part of can be viewed as a -covariant derivative.
The most general form of a action on the space of tensors with two-row Young symmetry is simply
| (3.7) | |||||
where the operators and are the operators which map the tensors with the Young symmetry , and to the tensor with the Young symmetry . Since these operators are unique up to overall factors (see Section 3.3 for the details), the unknowns are only the proportionality constants which depend and . Similarly, the most general form of a action can be written as
| (3.8) | |||||
with similarly defined operators and .
3.2 Linearization around (A)dS background
Before moving to solve the conditions (3.6), let us consider the linearization around a (A)dS background where the zero-forms all vanish:
| (3.9) |
and the one-forms satisfy
| (3.10) |
and hence,
| (3.11) |
Repeating the analysis for the linear fluctuation, we find that the background -covariant derivative reduces to a background -covariant derivative
| (3.12) |
where is the subgroup for , for and for generated by and . In this case, the Bianchi identity gives the condition,
| (3.13) |
Since the above, being identities, should not impose any relation between fields of different , the three terms should separately vanish we can recover the three conditions among the ones in (3.6). When the cosmological constant vanishes, we have only one consistency condition, , which determines only the action, then the action alone defines the zero-form field content of linearized conformal geometry around flat spacetime (that is, the spin-two off-shell Fradkin-Tseyltin system). Since the field content of the linearized system should be the same as the field content of non-linear one, the action should be enough to determine the zero-form field content of conformal geometry. However, when we consider an on-shell reduction of the system, it is necessary to have the information of the action, which cannot be obtained from the linearization around flat space.
It would be instructive to rewrite the linearized zero-form equation using the depth (2.50) instead of the conformal weight :
| (3.14) |
Remark that the half of terms in the action above preserve the depth, but not the conformal dimension, of the fields. If we impose the condition,
| (3.15) |
then the system can rely on fields of a single depth:
| (3.16) |
The resulting system is nothing but a non-conformal system such as massless, partially-massless or even massive spin two. These systems are studied in [45, 46]. The and operators used therein correspond in our case to
| (3.17) |
Furthermore, if we impose the restriction,
| (3.18) |
then we end up with only two operators and , which describe the massless spin- dynamics. Therefore, the system (3.14) encompasses the dynamics of (partially-)massless and massive as well as conformal fields—the goal of the current paper—with a consistent choice of and . We will come back to this point later in Section 7.
3.3 Cell operators and Recurrence relations
As mentioned earlier, the operators and are proportional to the cell operators which adds or removes one box with index to a two-row Young diagram [45, 48, 49, 46]. These operators are unique up to proportionality and their precise expressions and properties are given in the latter references. Here, we use their realizations as differential operators acting on auxiliary variables: we contract the zero-form fiberwise tensors with two set of auxiliary variables and as
| (3.19) |
Then, the irreducibility and traceless conditions of the tensors read
| (3.20) |
and the Lorentz generators act as the differential operator,
| (3.21) |
The one-cell operators, denoted henceforth by , can be defined as777 More explicitly, the one-cell operators, when acted on tensors, have the form, (3.22) (3.23)
| (3.25) |
where is the projection operator onto the space of traceless tensors of two-row Young diagram symmetry. Beside the one-cell operators, let us also introduce ‘two-cell operators’ defined by
| (3.26) | |||||
| (3.27) |
and
| (3.28) | |||||
| (3.29) |
We can express the product of two one-cell operators as two-cell operators as
| (3.30) |
| (3.32) |
| (3.33) | |||||
| (3.34) | |||||
where are the eigenvalues of and , that is, the length of the first and second rows of the Young diagram on which the operators act. Since the two-cell operators are independent, we can solve the Bianchi identities by expressing all the operators appearing there as linear combinations of the two-cell operators. In particular, the Lorentz generator can be expressed as
| (3.35) |
The operators and are both proportional to :
| (3.36) |
where and are the proportionality constants. We will determine these constants by asking the operators and , defined by (3.7), (3.8) and (3.36), satisfy the conditions (3.6) which arose from the Bianchi identities of the zero-form equations and implies that the operators and form a representation of conformal algebra together with and . Note that and can be viewed as differential operators acting on , whereas and cannot because they alter the conformal dimensions .
Firstly, the condition gives
| (3.37) | |||||
| (3.38) | |||||
| (3.39) | |||||
| (3.40) | |||||
| (3.41) | |||||
| (3.42) |
Secondly, the condition gives two kinds of equations: homogeneous ones and inhomogeneous ones. The homogeneous equations are
| (3.43) | |||
| (3.44) |
and
| (3.45) | |||||
| (3.46) | |||||
| (3.47) | |||||
| (3.48) | |||||
| (3.49) |
The inhomogeneous equations are
| (3.50) |
| (3.51) |
| (3.52) |
and
| (3.53) |
Finally, gives
| (3.54) | |||||
| (3.55) | |||||
| (3.56) | |||||
| (3.57) | |||||
| (3.58) | |||||
| (3.59) |
When identifying consistent sets of equations for zero-form fields , one needs to take into account the ambiguities (or redundancies) of field redefinitions,
| (3.60) |
This would affect the action of and as
| (3.61) |
and
| (3.62) |
3.4 Solutions
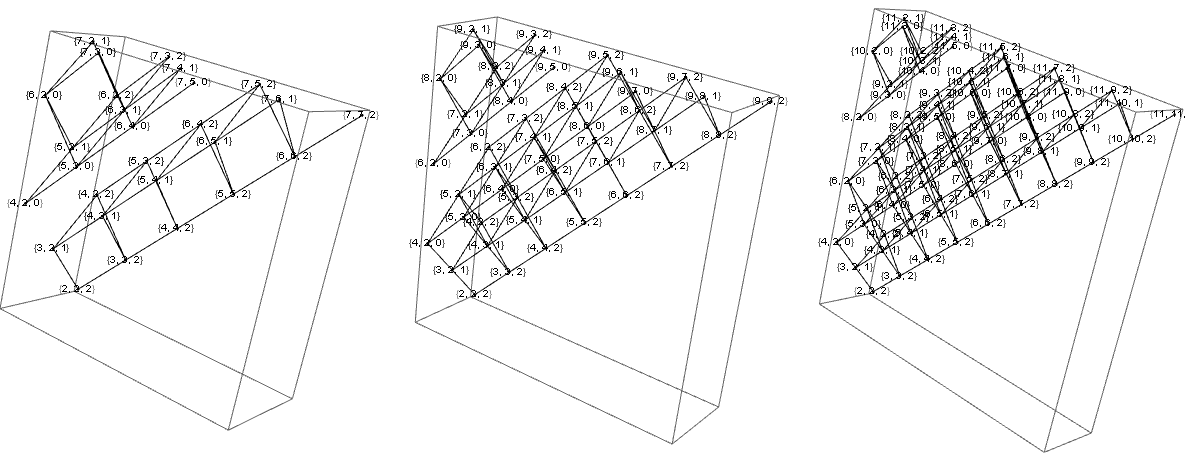
We can first consider the equations (3.37)–(3.42) from , which are homogeneous equations for the coefficients. One can first observe that the ‘seed’ zero-form generate other zero-forms with integer and their Lorentz label are restricted since they should be related to by actions of one-cell operators. A simple reasoning reveals the following. For even and odd , the admissible Lorentz labels of zero-forms are depicted as the black bullets in the lattice of Figure 1 and Figure 2, respectively.
In other words, the conformal dimension of the zero-forms with Lorentz label is restricted to the ones with non-negative integer depth (2.50):
| (3.63) |
In the following we shall label the conformal dimension in terms of the depth . The above content of zero-forms coincides with the basis tensors of Weyl invariants used in [15].
When we build the and action, we assumed that there exist one zero-form for each label, which is now restricted to admissible ones. This ‘multiplicity-one’ assumption can be verified by demonstrating that the recurrence relations arising from uniquely determines after fixing all field redefinition ambiguities. As mentioned before, the content of zero-form is determined solely by the action because if we linearize the system around the flat background, we only obtain the condition . The other consistency conditions will be served to determine the action together with the value .
Let us demonstrate how the recurrence relations (3.37)–(3.42) can be solved. First, using the field redefinitions with , we fix all with to 1. Note that this leaves out the field redefinitions as the corresponding coefficients already vanish. Then, the equations (3.37) and (3.39) determine in terms of as
| (3.64) | |||||
The remaining equations (3.40)–(3.42) determine also in terms of as
| (3.65) |
and impose the constraint on ,
| (3.66) |
In the end, we are left with subject to the above equations. For , we have only two non-zero coefficients and and they can be fixed by the field redefinitions and , respectively. If all the coefficients and field redefinitions, except for , are fixed up to an order with , we can determine the four coefficients by using the equation (3.66) and the three field redefinitions . By induction, we can determine all the coefficients and hence the action. In doing this, we used all the field redefinitions except for . The latter field redefinition corresponds to the overall rescaling of the homogeneous equation, and hence it is trivial. To recapitulate, we have shown that the recurrence relations (3.37)–(3.42) determine uniquely the coefficients, namely the action, by making use of the freedom of field redefinition. This proves the correctness of the ‘multiplicity-one’ assumption. Let us restate the zero-form field content of the conformal geometry:
| (3.67) |
If we do not aim for conformal geometry, then there are more possibilities: instead of determining with field redefinitions, we can set some of them to zero and solve the conditions (3.66) as . In this case, the fields whose redefinition could fix such coefficients simply decouple from the theory, and hence we can remove them. Since we have less zero-form fields compared to the off-shell system, the resulting system will be an on-shell theory. See Appendix A for more details.
Next we can move to the inhomogeneous equations (3.50)–(3.53) arising from . They uniquely determine the following quadratics: for we obtain
| (3.68) |
and for we obtain
| (3.69) |
Since the are already determined to be non-vanishing numbers, the above equations alone determine all the coefficients. One can check that such readily satisfy the remaining equations (3.43)–(3.49) and (3.54)–(3.59) arising respectively from and . Therefore, both and action is entirely determined and hence the linear part of the unfolded equation for conformal geometry.
At this point, one can observe from (3.68) and (3.69) that and never vanish but and can vanish for some . Since are not zero, we find that the coefficients (depicted as orange arrows in Figure 3) should vanish.
For a generic , the black bullets, which have vanishing coefficients, still keeps non-vanishing coefficients (depicted as green arrows in Figure 3), and hence the corresponding zero-forms can be still obtained from or by the action. On the contrary, for , the zero-forms can never be obtained from by the action: See Figure 4.
Therefore, the field cannot be obtained from a action. In fact, the tensor corresponds to the Bach tensor, and the decoupling of under action assures that one can consistently impose the Bach-flat condition . As mentioned earlier, the zero-form fields carry certain dual representations of highest weight representations of . The decoupling of implies that its dual state is a lowest state and generates an invariant sub-representation, which can be quotiented out to get an “on-shell” representation. In order to understand better the relation between the zero-form module and the highest weight representation of , we review a few results of the representation theory in the following section.
4 Representation
4.1 Off-shell Fradkin-Tseytlin module
The actions of and identified in the previous section, together with those of and , define a -representation realized on the space of zero-forms with field content (3.67). In this section, we demonstrate how one can recover the same field contents from an analysis of representations. For that, let us review a few basics: the (generalized) Verma module of is given by
| (4.1) |
where is the lowest-weight representation (or primary state),
| (4.2) |
which carries a finite-dimensional irrep of . We denote the Young diagram as a row vector,
| (4.3) |
The Bernstein-Gelfand-Gelfand resolution provides various (non-unitary) representations of as a successive quotient of Verma modules [37, 41] (see also [42]). The spin- Fradkin-Tseytlin (FT) module,
| (4.4) |
with
| (4.5) |
is the one related to the on-shell conformal spin- field, but what we need is the module related to the off-shell conformal spin , in particular the off-shell conformal spin two, namely conformal geometry. Above, is the module of the spin- conformal Killing tensors. Note that the module associated with an on-shell system is the quotient of the module associated with its off-shell system by the module associated with the equation of motion. For the conformal geometry with , the equation of motion is the -derivative Bach equation. Therefore, conformal geometry must be associated with the module which does not involve any dependent quotient. The logic extends to other spins, and is the off-shell FT module, also sometimes referred to as the shadow module. Let us decompose into modules for . The spin-two conformal Killing tensors are nothing but the adjoint representation,
| (4.6) |
and hence we find
| (4.7) | |||
The same result can be also obtained from
| (4.8) |
where the successive quotients represent the implementation of the Bianchi identity and the Bianchi identity of the Bianchi identity etc. The decomposition of the above into modules are shown, in Appendix B, to reproduce the result (4.7).
In (4.7), the lowest conformal weight state is , which is the representation of the Weyl tensor, and the space coincides with the zero-form field content (3.67). Remark that in the unfolded equation, the zero-form fields carry finite-dimensional representations of , which is different from . However, they are related by the “Wick rotation” on the -th and -th components, which maps the generators to and to . To repeat, the Wick rotation maps the Lie algebras and into the Lie algebras and , respectively. It is important to note here that the Wick rotation does not alter the vector space on which the generators act, and the same vector space carries a representation of as well as a representation of . In a vector space carrying an irreducible unitary representation of , has a real eigenvalue , and and are represented as finite-dimensional Hermitian matrices. The same vector space carries a finite but non-unitary representation of , which was used to label the zero-form fields. Let us note also that the decomposition of a representation into (infinitely many) non-unitary finite-dimensional representations of does not imply that the -representation is a non-unitary one. In fact, a state in the -representation is not a finite but an infinite linear combination of finite-dimensional -representations. If we adopt the standard norm of finite-dimensional representations (which is not positive definite since is non-compact), the norm of a state in the -representation may diverge. Therefore, we need to introduce a new scalar product for the -representation, which will be singular for a finite-dimensional -representation. This new scalar product can be positive definite, though the Fradkin-Tseytlin module is not of this type. What we discussed just above is analogous to what happens in the Taylor expansion of space: each Taylor coefficient has a divergent norm, whereas a state may have a divergent norm with respect to a well-defined scalar product in the space of Taylor coefficients.
Before moving to the next section, let us make a remark on the relation between and , namely the relation between the off-shell spin-2 FT module (or the spin-2 shadow module) and the on-shell massless spin-2 module. In terms of nonlinear system, such a relation is about the interplay between the -dimensional conformal geometry and the -dimensional Einstein gravity with negative cosmological constant. The massless spin-2 module can be branched into as
| (4.9) | |||
Comparing (4.9) with (4.7), one can see that the two vector spaces are isomorphic as representations, but have different eigenvalues. One can obtain the same result (4.9) via the decomposition of ,
| (4.10) |
which is the zero-form content of massless spin-2 field in its unfolded formulation. Here, one need to remind that the expansion in should be considered as a Taylor expansion of a function even though it is not normalizable in Taylor basis but in a harmonic basis. Each of the module can be further branched into irreps as
| (4.11) |
The expansion (4.10) with (4.11) reproduces the decomposition (4.9) with , but without the labels.
4.2 Zero-form module
In this section, we provide a more detailed explanation about the connection between the representations of zero-form fields and the off-shell FT module. All zero-form fields of conformal geometry can be packed into
| (4.12) |
by contracting them with the basis vectors, denoted by , of the underlying representation, denoted by . Then, all zero-form equations can be obtained from
| (4.13) |
and the gauge symmetry simply reads
| (4.14) |
with
| (4.15) | |||||
The basis vector can be realized various ways, for instance as we have introduced earlier in the paper, as a function of auxiliary variables:
| (4.16) |
with . Note here that we have introduce also a Lorentz scalar auxiliary variable to generate fields of different conformal dimensions. The above realization is compatible with the grading,
| (4.17) |
In terms of these, all the generators of will be realized as differential operators acting on the auxiliary variables:
| (4.18) |
where and are defined in (3.36). Therefore, we constructed an oscillator representation which is realized on the space of functions ,
| (4.19) |
subject to the conditions and . It will be interesting to relate the above representation to the one that can be obtained from the reductive dual pair correspondence of (see [50] for a review of the correspondence).
Note that has vectors with negative conformal weights, which are bounded from above (). The representation is in fact isomorphic to the dual representation (aka contragredient representation) of the off-shell FT model . The isomorphism is given by the anti-involution,888The anti-involution flips only the sign of generators. If we take at the place of , then the anti-involution would correspond to minus the Cartan anti-involution. Note that is different from the Chevallay anti-involution , (4.20) used in [37]. They are related by through the involution given by (4.21)
| (4.22) |
More precisely, we can define a non-degenerate bi-linear form for as
| (4.23) |
where is the projection operator onto the space , and and are the basis vectors of and , respectively. Then, for any and , the actions of an element on each spaces satisfy
| (4.24) |
The duality between and implies that is the subspace of (generalized) highest weight states annihilated by , if and only if there is no such that :
| (4.25) |
This shows that the field is dual to an invariant highest-weight representation generated by as it cannot be obtained from by actions.
So far, we have considered only the passive transformation of , which acts only on the basis vectors but not on the coefficients . We can also consider the active transformation of , which acts only on but not on , as the linear part of the gauge transformation with constant parameters, namely the global transformation: the active action of an element in can be defined as
| (4.26) |
Here, should not be viewed as the coefficients, but as the dual basis vectors. Indeed, the active representation of the zero-form fields is dual to the passive representation, . Therefore, the active representation of the zero-form fields is simply the off-shell FT module . What is noteworthy in the active representation is that it is related to the gauge transformation which is in fact nonlinear in . We will come back to this point in Section 7.
5 Higher order unfolding of conformal geometry
5.1 General structure
Let us discuss the structure of the nonlinear unfolded equations for the zero-form fields. For that, let us label the zero-form fields by a collective index as
| (5.1) |
In this notation, the nonlinear unfolded equations read simply999One may think that it could be more useful to express the equation as (5.2) then, act on it to get the Bianchi identity. However, such a computation could lead to an inconsistency: the LHS of the Bianchi identity is quadratic in since , whereas the RHS is cubic in . The mistake is due to the incorrect assumption of the -covariance of the multi-linear forms hidden in the RHS of (5.2). More formally, the cocyle of the corresponding Chevalley-Eilenberg complex is covariant under but not under .
| (5.3) |
where the conformal weight of and are and , respectively. Using the relations,
| (5.4) |
we can simplify the action of on (5.3) as
| (5.5) | |||||
We require the above equation to hold identically — it becomes the Bianchi identity for the zero-form fields. Moreover, each line should vanish separately since the equation should hold independently of the choice of and . This requirement, together with the Bianchi identities (2.30) of the one-form fields, determines the functions and , up to (nonlinear) field redefinitions of .
Since the identity should hold for any value of , we can expand the functions in the powers of as
| (5.6) |
and the equation (5.5) should hold identically order by order in powers of . The first order part of the equation,
| (5.7) |
is what we have worked out in the previous section, and and are determined by the actions of and . Moving to the second order, we find
| (5.8) |
Since and are already determined, the above defines inhomogeneous linear equations for and . Finally, at the order , we have
| (5.9) |
which define again inhomogeneous linear equations for and where the coefficients are given by with . In this way, one can iteratively determine all power series coefficients and by solving the linear equations. The index takes infinitely many values, but at a fixed order only finitely many can appear because the conformal dimensions is additive and bounded from below () :
| (5.10) |
Moreover, for a finite , finitely many tensors appear. Therefore, the procedure of determining the functions and — that is, the unfolded equations for the zero-forms — can be decomposed into finite-dimensional linear equations.
We have seen that the linear part of the unfolded equation for conformal geometry defines the representation of conformal group , but the system is not consistent without higher order completion. In general the unfolded equations can be viewed as a Lie algebroid with an infinite-dimensional base manifold corresponding to the zero-forms. In the conformal geometry case, the structure constant of the Lie algebroid is at most linear in , whereas the anchor, given by and , are higher order polynomials in .
5.2 A few lowest
Let us show more explicitly, but still schematically, how the nonlinear part of the consistency equations (5.8) and (5.9) can be organized as a series of finite-dimensional linear equations by arranging them in the total conformal dimensions .
-
•
: We have only one non-trivial condition from ,
(5.11) which is an equation for . Here, we suppressed the Lorentz label in the tensors for simplicity of the expressions, and one should note that there are more than one tensors for a given . Since is at most quadratic in , by solving the above equations, we can determine completely.
-
•
: We still have only one equation from , which reads,
(5.12) and it determines . Since is at most quadratic in , it is also determined.
-
•
: In this case, we find two non-trivial conditions from and .
-
–
First, from , we obtain two quadratic and one cubic conditions. The first quadratic condition is proportional to ,
(5.13) and it determines . The second quadratic condition is proportional to ,
(5.14) and it determines . The cubic condition is
(5.15) and it determines . With these, is completely determined as it is at most cubic in .
-
–
From , we find one condition,
(5.16) which determines , and hence as it is at most quadratic.
-
–
Even though that the above sets of equations are finite-dimensional linear equations, they are tedious to solve and hence it would be more desirable to use a computer program code, which is beyond the scope of the current paper.
6 Weyl invariant densities
In this section we discuss how Weyl invariants can be classified within the unfolded formulation of conformal geometry.
6.1 Gauge symmetry
Let us consider our system within the general framework of the unfolded formulation. Our system has two kinds of differential forms, the one-forms taking values in the adjoint representation of and the zero-forms taking (infinitely many) values in the off-shell FT module of ,
| (6.1) |
Their equations have the general structure,
| (6.2) |
with the (generalized) Jacobi identity,
| (6.3) |
The system is invariant under the gauge transformations,
| (6.4) |
where are the -form gauge parameters associated with the -form field . Applying this to our system, we find the “standard” gauge transformations for and as
| (6.5) |
and “deformed” gauge transformations for and as
| (6.6) |
The modification terms are proportional to the curvatures and corresponds to the “non-geometrical” terms considered in [23].
The zero-forms transform as
| (6.7) |
involving nonlinear functions and .
As we discussed earlier, the gauge transformations by and can be used to reduce the system to the metric form, whereas the transformations generated by and become the diffeomorphisms and Weyl transformations.
6.2 Constructing Weyl invariants à la unfolding
Let us revisit the classification of Weyl invariants, which consist of the type-B Weyl anomalies, within the unfolded formulation of conformal geometry. Weyl invariants are the scalar densities made by curvatures, which are strictly invariant under Weyl rescaling, without relying on a total derivative term.
The Weyl invariants should correspond to a gauge invariant -form within the unfolded formulation. The invariance under and requires the basis for the -form to be made by and only. The gauge symmetry is the diffeomorphism, so its invariance can be achieved only up to a total derivative term. On the contrary, the gauge symmetry is related to a Weyl rescaling, so we require the strict invariance without relying on an integration by part. From this, we can rule out the dependency of as it transforms with derivatives, which can never be compensated if integrations by part are not allowed. In the end, the ansatz for the Weyl invariants is
| (6.8) |
The invariance under the Lorentz and dilatation is guaranteed by considering where all the Lorentz indices of are fully contracted without using any external tensors and the total conformal dimension is . The gauge variation under translation and special conformal transformations give
| (6.9) | |||||
With a total derivative term, the above can be expressed as
| (6.10) | |||||
The first line is a total derivative term proportional to the translation gauge parameter . The second line vanishes identically:
| (6.11) |
due to the properties of antisymmetrizations. Only the third line poses as a non-trivial condition,
| (6.12) |
which ensures the gauge invariance under translation and special conformal transformation at the same time. In the end, it is sufficient to ask the special conformal invariance of the density :
| (6.13) |
To find an explicit form of Weyl invariants, one needs to begin with a general ansatz
| (6.14) |
with a certain finite number of undetermined coefficients . For instance, for we have only one term,
| (6.15) |
whereas for , we have three terms,
| (6.16) | |||||
In the last line, we used the convention,
| (6.17) |
By checking the special conformal transformations of and , we find is already conformally invariant:
| (6.18) |
whereas the conformal invariance of requires
| (6.19) | |||||
The above defines the system of linear equations for ,
| (6.20) |
In any , the above has one-dimensional solution space,
| (6.21) |
where we fixed using field redefinition freedoms (we will keep this choice in the following analysis). Likewise, once the form of is determined, the problem of finding Weyl invariants becomes a pure algebraic exercise.
6.3 Quadratic Weyl invariants
As we have seen in case, the ansatz for quadratic Weyl invariants are easy to handle so it allowed to determine the invariant using the explicit expression of action. Let us extend this analysis to and . In these cases, the quadratic Lorentz scalars that are invariant under the linear part of action should be complemented by cubic (and also quartic for ) terms to compensate the nonlinear part of action.
In the following, we determine the quadratic part of Weyl invariants, that is, the quadratic Lorentz scalars invariant under the linear part of action. In , there are 3 quadratic Lorentz scalars with , and 2 quadratic Lorentz vectors with , so a generic action of would have left one dimensional solution space for quadratic Weyl invariant. This is to be contrasted with the situations in higher dimensions: as shown in Appendix C, there are 7 quadratic Lorentz scalars with , and 8 quadratic Lorentz vectors with ; and there are 12 quadratic Lorentz scalars with , and 19 quadratic Lorentz vectors with . See Table 6.3 for the summary.
| 6 | 8 | 10 | |
|---|---|---|---|
| Number of quadratic scalars with | 3 | 7 | 12 |
| Number of quadratic vectors with | 2 | 8 | 19 |
Because of the “inversion of numbers” in and , we need explicit computations to identify the kernel of action in these cases.
Eight dimensions
As mentioned above, there are 7 quadratic Lorentz scalar with leading to the ansatz,
| (6.22) | |||||
The invariance of under transformation requires
| (6.23) |
With explicit values of , we find the solution space is one-dimensional:
| (6.24) |
Ten dimensions
We have 12 dimensional ansatz,
| (6.25) | |||
The invariance of gives
| (6.26) |
which has one-dimensional solution space,
| (6.27) |
Let us note that the densities and are invariant under action in any dimensions. Multiplied by the volume form, they become Weyl invariants in 8 and 10 dimensions.
6.4 Higher order Weyl invariants
In the previous section, we identified the quadratic part of Weyl invariants in and , and this analysis can be straightforwardly extended to any even dimensions as we know the linear part of the action explicitly. In principle, to identify higher order parts, we would need explicit expressions of up to , which requires many steps even for as we have seen in Section 5.2. However, even without the nonlinear part of action being identified, one can still guess the number of Weyl invariants. Let us explain this point in the following. The gauge transformation is a linear differential operator on the space of and hence can be expanded as powers of as
| (6.28) |
where . The commutativity of transformation implies
| (6.29) |
In example, the Weyl invariants have at most cubic terms:
| (6.30) |
and the invariance of the above is equivalent to
| (6.31) |
The first equation is what we have solved in the previous section, and we already identified . Turning to the second equation, we need to solve again linear equations for with inhomogeneous term , which obscures the existence of the solution . By taking the antisymmetrized variation of the second equation, we find
| (6.32) |
This tells that the inhomogeneous term is closed. If is not in the cohomology of the space of vectors with , then we know the solution will exist, and it will be sufficient to identify the kernel of in the space of scalars with . We know from [14] this is indeed the case and the dimension of the kernel is four: the number of scalars and vectors are 11 and 7, and hence is surjective.
Let us consider also the example, where the Weyl invariants have at most quartic terms:
| (6.33) |
The invariance gives
| (6.34) |
where the inhomogeneous terms in the second and third equations are closed:
| (6.35) |
Again, if the inhomogeneous terms are not in the cohomology of the space of and vectors with , then the solution will exist for and , respectively. Therefore, in such case, one can just identify the kernel of in the space of and scalars with .
Let us discuss more about the underlying algebraic structure. At a fixed order , the variation defines the cochain complex where and is the subalgebra of generated by . By introducing the co-differential from the action, the associated homotopy operator is given by
| (6.36) |
We find that the cohomology is trivial if as it lies in the kernel of . Weyl invariants precisely concern the other cases with and we need more detalied analysis. For explicit computations of the cohomology, it will be useful to recast all higher-order forms of as differential operators in auxiliary variables. If we combine different , we have and the differential and co-differential and are deformed to the full gauge variations and which are nonlinear in . This can be viewed as a deformation of Lie algebra cohomology to a Lie algebroid one.
7 Reduction by constraints
So far, we have considered the unfolded equation for conformal geometry, that is, the off-shell system for conformal gravity. In this section, we discuss how an off-shell system can be reduced to various on-shell systems. The reduction can be achieved by imposing certain algebraic constraints on the fields,
| (7.1) |
A constraint generates infinitely many consequent algebraic constraints through (successive) gauge variations,
| (7.2) |
where each gauge variation makes use of different gauge parameters, and they are not nilpotent operators. If the constraints are Lorentz tensors, Lorentz transformation will not generate any consequent constraint. If the constraints can be decomposed into homogeneous ones under dilatation, dilatation will also leave the constraints invariant. On the contrary, translation always generates additional algebraic constraints at the level of the unfolded system, but they are related to the derivatives of original constraints. Therefore, we can disregard the constraints which can be obtained by a transformation. We will refer to this class of constraints as descendant constraint. In this way, we are left with an assessment of the effect of special conformal transformation on the constraints. Below, we consider two cases of non-descendant constraints.
-
•
Primary constraint:101010This is not to be confused with the primary constraint of Hamiltonian system. We use this term because this class of constraints generalizes the concept of primary fields. the constraints which are left invariant under dilatation and special conformal transformation. If we further restrict to the constraints which contain linear term in fields, we find only two possibilities because only and satisfy the primary field condition and , respectively. The former case corresponds to the conformally flat geometry,
(7.3) The latter case corresponds to the Bach flat geometry,
(7.4) where we have included non-linear terms , which is necessary in compensating . This nonlinear term in (7.4) can be removed by a nonlinear field redefinition of . If we consider primary constraints which are at least quadratic in fields, then the Weyl invariant densities belong to this class. They are all scalars, but one could equally consider tensor analogues of these nonlinear constraints. These constraints generalize the concept of primary fields to a nonlinear level because the transformation acts nonlinearly on the field and the constraints are in general nonlinear functions of .
-
•
Section constraint: the constraints which are neither primary nor generate new constraints under action. In this case, the variation necessarily constrains the gauge parameters and breaks a part of conformal symmetry. A simple example is the Einstein equation,
(7.5) whose gauge variation, dropping the local Lorentz part, is
(7.6) The above results in the symmetry breaking,
(7.7) and will be reduced to either or depending on the parameter . Another example is
(7.8) where is a rank-two tensor function of . The simplest non-trivial case is , and it leads to a four-derivative theory. Therefore, in the unfolded system of conformal geometry, the dynamical equations of various on-shell gravitational systems can be treated as algebraic constraints.
In order to obtain conformal geometry, we have used the constraints (2.28). These constraints can be also regarded as primary constraints imposed on an even larger system, where none of two form curvatures are constrained:
| (7.9) | |||||
Here, the zero-form fields are reducible Lorentz tensors (no Young symmetry condition is imposed on them)111111For more concrete analysis, it would be better to decompose into irreducible tensors, but for the current discussion it is enough to deal with reducible tensors. with two groups of fully antisymmetric indices, and . They are subject to the Bianchi identities,
| (7.10) | |||
| (7.11) | |||
| (7.12) | |||
| (7.13) |
Here, the nonlinearities are due to non-vanishing torsion . In order to obtain the gauge transformation , we need to determine their unfolded equations. But since they are equivalent to these Bianchi identities, we can read off the relevant information from (7.10)–(7.13) directly. First, the field , being the lowest field, does not have any term in its equation (7.10). This means that its transformation vanishes and hence it is primary. From the antisymmetrization in (7.10), we find that the descendants of do not contain the traceful projection . The projection of (7.11) to such components of contains term, and hence these fields are neither descendant nor primary. We may call these constraints “secondary” since their variations vanish upon imposing primary constraints. Finally, all the components of are descendants of the primary or the secondary constraints. Therefore, imposing all the secondary constraints would trivialize the system and imposing only the traceful part of the secondary constraints gives conformal geometry. To recapitulate, in this enlarged unfolded system, which is nothing but the off-shell gauge theory with invertible , conformal geometry is obtained by imposing all the primary and a part of secondary constraints.
The unfolded system asks us to work with the space of functions in the zero-form fields. The vector space that the zero-form fields take value in carry an infinite-dimensional representation, which can be viewed as the Hilbert space of the corresponding quantum system. Then, it is natural to interpret the space of functions in the zero-form fields as the Fock space of the corresponding quantum field theory. In this regard, it would be tempting to understand whether and how a suitable quantization of the unfolded system can actually associate the space of functions in the zero-forms with the Fock space. After such a quantization, the Fock space will be endowed with nonlinear actions of . It will be equally interesting to understand the physical meaning of this nonlinear actions and the associated representations in the context of conformal field theory.
Acknowledgments
We thank Thomas Basile and Nicolas Boulanger for useful discussions and helpful comments on our first draft. This work was supported by National Research Foundation (Korea) through the grant NRF-2019R1F1A1044065.
Appendix A Unfolding free fields
As shown in Section 3, the action is determined by the coefficients , , and subject to the condition (3.66). We also showed that all these coefficients can be determined by field redefinitions leading to the off-shell system (conformal geometry) or some of them can be set to zero and solve the condition (3.66) as . In the latter cases, the corresponding fields decouple from the system. In the following, we provide a few solutions of this kind.
Let us begin with the off-shell system where none of , , and vanish: in Figure 6, the coefficients and are depicted as the lines which start from the Young diagrams and ends at and , respectively.
Let us examine the consequences of setting some of , , and to zero. At the lowest depth, we find that the possibility which gives massless system since the zero-form content depicted in Figure 7(a) matches that of massless system. Moving to the next depth , we can consider where the condition (3.66) reduces to . If we take the possibility , then the zero-form content in Figure 7(b) matches that of the on-shell Fradkin-Tseyltin system (on-shell conformal spin two). If we take the other possibility , then we find yet another system with a scalar degrees of freedom. We can impose also together with , and get a system (see Figure 7(c)) with one helicity-two and one helicity-one degrees of freedom, which match the degrees of freedom of partially-massless spin-two field. Moving to the third depth, we find many possibilities, among which the condition gives the spectra (see Figure 7(d)) which match the system given by , where is the four-derivative linearized Bach tensor.
Appendix B Decomposition of the off-shell spin-2 Fradkin-Tseytlin module
Let us decompose each Verma modules appearing in the off-shell FT module (4.8) into irreps,
| (B.1) |
The tensor product of irreps are given by
| (B.2) |
where has three irreducible pieces,
| (B.3) |
whereas with is
| (B.4) | |||||
Using these results, the Verma module can be expressed as
| (B.5) |
Finally, using the above result in (4.8) and redefining the summation variable, we find
| (B.6) |
which can be simplified as
| (B.7) |
Appendix C Number of ansatz for Weyl invariants
Since each zero-form fields correspond to a modules inside of the spin 2 FT module , the number of possible contractions of the zero-forms can be obtained from multiple symmetrized tensor products of . The latter can be conveniently handled in terms of Lie algebra character, and all symmetrized tensor products are generated by the plethystic exponential,
where and . The above can be expanded as a series of characters, and the number of all possible contractions of zero-forms, which is a Lorentz tensor of dimension , is equal to the coefficient of the character corresponding to the irrep . Therefore, the numbers and are the coefficients of the character and in the expansion of (C). Using the expression of the character,
| (C.1) |
where is the Vandermonde determinant, one can extract the number, namely the multiplicity, of the module as the multiple integral,
| (C.2) |
It is also useful to expand as
| (C.3) |
where we used the compact notation and . The -th order part corresponds to symmetrized tensor product of the copies of the relevant representation. First few reads
| (C.4) | |||
For our purpose — computing the numbers of the dimension scalars and the dimension vectors — it is sufficient to consider since has minimum conformal dimension . The last piece corresponds to the contractions of copies of , which are trivially Weyl invariant. Therefore, we consider only , and the expressions (C) are sufficient up to .
Eight dimensions
In , the relevant ’s are the and . From
| (C.5) | |||||
we find and , which simply coincide to the numbers of terms. From
| (C.6) | |||||
we find and from the integral.
Ten dimensions
In , the relevant ’s are the , and . From
| (C.7) | |||||
we find and . From
| (C.8) | |||||
we find and . From
| (C.9) | |||||
we find and .
References
- [1] C. Fefferman and C. R. Graham, The ambient metric, Ann. Math. Stud. 178 (2011) 1–128, [0710.0919].
- [2] M. Henningson and K. Skenderis, The Holographic Weyl anomaly, JHEP 07 (1998) 023, [hep-th/9806087].
- [3] J. T. Wheeler, Weyl gravity as general relativity, Phys. Rev. D 90 (2014) 025027, [1310.0526].
- [4] E. Scholz, The unexpected resurgence of Weyl geometry in late 20-th century physics, Einstein Stud. 14 (2018) 261–360, [1703.03187].
- [5] M. P. Hobson and A. N. Lasenby, Conformal gravity does not predict flat galaxy rotation curves, 2103.13451.
- [6] A. Kehagias and A. Riotto, Topological Early Universe Cosmology, 2105.10669.
- [7] M. J. Duff, Twenty years of the Weyl anomaly, Class. Quant. Grav. 11 (1994) 1387–1404, [hep-th/9308075].
- [8] L. Bonora, P. Cotta-Ramusino and C. Reina, Conformal Anomaly and Cohomology, Phys. Lett. B 126 (1983) 305–308.
- [9] L. Bonora, P. Pasti and M. Bregola, WEYL COCYCLES, Class. Quant. Grav. 3 (1986) 635.
- [10] S. Deser and A. Schwimmer, Geometric classification of conformal anomalies in arbitrary dimensions, Phys. Lett. B 309 (1993) 279–284, [hep-th/9302047].
- [11] N. Boulanger, Algebraic Classification of Weyl Anomalies in Arbitrary Dimensions, Phys. Rev. Lett. 98 (2007) 261302, [0706.0340].
- [12] N. Boulanger, General solutions of the Wess-Zumino consistency condition for the Weyl anomalies, JHEP 07 (2007) 069, [0704.2472].
- [13] T. Parker and S. Rosenberg, Invariants of conformal Laplacians, Journal of Differential Geometry 25 (1987) 199 – 222.
- [14] N. Boulanger and J. Erdmenger, A Classification of local Weyl invariants in D=8, Class. Quant. Grav. 21 (2004) 4305–4316, [hep-th/0405228].
- [15] N. Boulanger, A Weyl-covariant tensor calculus, J. Math. Phys. 46 (2005) 053508, [hep-th/0412314].
- [16] J. Francois, S. Lazzarini and T. Masson, Becchi-rouet-stora-tyutin structure for the mixed weyl-diffeomorphism residual symmetry, J. Math. Phys. 57 (2016) 033504, [1508.07666].
- [17] S. Curry and A. R. Gover, An introduction to conformal geometry and tractor calculus, with a view to applications in general relativity, 1412.7559.
- [18] J. Erdmenger, Conformally covariant differential operators: Properties and applications, Class. Quant. Grav. 14 (1997) 2061–2084, [hep-th/9704108].
- [19] R. Sharpe, Differential Geometry: Cartain’s generalization of Klein’s Erlangen program, vol. 166 of Graduate Texts in Mathematics. Springer-Verlag, 1997.
- [20] S. W. MacDowell and F. Mansouri, Unified Geometric Theory of Gravity and Supergravity, Phys. Rev. Lett. 38 (1977) 739.
- [21] K. S. Stelle and P. C. West, Spontaneously Broken De Sitter Symmetry and the Gravitational Holonomy Group, Phys. Rev. D 21 (1980) 1466.
- [22] J. Crispim Romao, A. Ferber and P. G. O. Freund, Unified Superconformal Gauge Theories, Nucl. Phys. B 126 (1977) 429–435.
- [23] M. Kaku, P. K. Townsend and P. van Nieuwenhuizen, Gauge Theory of the Conformal and Superconformal Group, Phys. Lett. B 69 (1977) 304–308.
- [24] J. Crispim-Romao, CONFORMAL AND SUPERCONFORMAL GRAVITY AND NONLINEAR REPRESENTATIONS, Nucl. Phys. B 145 (1978) 535–546.
- [25] E. S. Fradkin and A. A. Tseytlin, CONFORMAL SUPERGRAVITY, Phys. Rept. 119 (1985) 233–362.
- [26] J. H. Horne and E. Witten, Conformal Gravity in Three-dimensions as a Gauge Theory, Phys. Rev. Lett. 62 (1989) 501–504.
- [27] C. R. Preitschopf and M. A. Vasiliev, Conformal field theory in conformal space, Nucl. Phys. B 549 (1999) 450–480, [hep-th/9812113].
- [28] R. Aros and D. E. Diaz, AdS Chern-Simons Gravity induces Conformal Gravity, Phys. Rev. D 89 (2014) 084026, [1311.5364].
- [29] M. A. Vasiliev, Free Massless Fields of Arbitrary Spin in the De Sitter Space and Initial Data for a Higher Spin Superalgebra, Fortsch. Phys. 35 (1987) 741–770.
- [30] M. A. Vasiliev, Linearized Curvatures for Auxiliary Fields in the De Sitter Space, Nucl. Phys. B 307 (1988) 319.
- [31] V. E. Lopatin and M. A. Vasiliev, Free Massless Bosonic Fields of Arbitrary Spin in -dimensional De Sitter Space, Mod. Phys. Lett. A 3 (1988) 257.
- [32] M. A. Vasiliev, Equations of Motion of Interacting Massless Fields of All Spins as a Free Differential Algebra, Phys. Lett. B 209 (1988) 491–497.
- [33] M. A. Vasiliev, Consistent Equations for Interacting Massless Fields of All Spins in the First Order in Curvatures, Annals Phys. 190 (1989) 59–106.
- [34] R. D’Auria, P. Fre, P. K. Townsend and P. van Nieuwenhuizen, Invariance of Actions, Rheonomy and the New Minimal Supergravity in the Group Manifold Approach, Annals Phys. 155 (1984) 423.
- [35] M. A. Vasiliev, Consistent equation for interacting gauge fields of all spins in (3+1)-dimensions, Phys. Lett. B 243 (1990) 378–382.
- [36] M. A. Vasiliev, Nonlinear equations for symmetric massless higher spin fields in (A)dS(d), Phys. Lett. B567 (2003) 139–151, [hep-th/0304049].
- [37] O. V. Shaynkman, I. Y. Tipunin and M. A. Vasiliev, Unfolded form of conformal equations in M dimensions and o(M + 2) modules, Rev. Math. Phys. 18 (2006) 823–886, [hep-th/0401086].
- [38] M. A. Vasiliev, Bosonic conformal higher-spin fields of any symmetry, Nucl. Phys. B 829 (2010) 176–224, [0909.5226].
- [39] J. E. Humphreys, Representations of Semisimple Lie Algebras in the BGG Category O, vol. 94 of Graduate Studies in Mathematics. American Mathematical Society, 2008.
- [40] X. Bekaert, M. Grigoriev and E. D. Skvortsov, Higher Spin Extension of Fefferman-Graham Construction, Universe 4 (2018) 17, [1710.11463].
- [41] M. Beccaria, X. Bekaert and A. A. Tseytlin, Partition function of free conformal higher spin theory, JHEP 08 (2014) 113, [1406.3542].
- [42] T. Basile, X. Bekaert and E. Joung, Conformal Higher-Spin Gravity: Linearized Spectrum = Symmetry Algebra, JHEP 11 (2018) 167, [1808.07728].
- [43] N. Misuna, On unfolded off-shell formulation for higher-spin theory, Phys. Lett. B 798 (2019) 134956, [1905.06925].
- [44] N. G. Misuna, Off-shell higher-spin fields in and external currents, 2012.06570.
- [45] E. D. Skvortsov and M. A. Vasiliev, Geometric formulation for partially massless fields, Nucl. Phys. B 756 (2006) 117–147, [hep-th/0601095].
- [46] D. S. Ponomarev and M. A. Vasiliev, Frame-Like Action and Unfolded Formulation for Massive Higher-Spin Fields, Nucl. Phys. B 839 (2010) 466–498, [1001.0062].
- [47] S. M. Kuzenko and M. Ponds, Conformal geometry and (super)conformal higher-spin gauge theories, JHEP 05 (2019) 113, [1902.08010].
- [48] N. Boulanger, C. Iazeolla and P. Sundell, Unfolding Mixed-Symmetry Fields in AdS and the BMV Conjecture: I. General Formalism, JHEP 07 (2009) 013, [0812.3615].
- [49] N. Boulanger, C. Iazeolla and P. Sundell, Unfolding Mixed-Symmetry Fields in AdS and the BMV Conjecture. II. Oscillator Realization, JHEP 07 (2009) 014, [0812.4438].
- [50] T. Basile, E. Joung, K. Mkrtchyan and M. Mojaza, Dual Pair Correspondence in Physics: Oscillator Realizations and Representations, 2006.07102.