Unitary Designs of Symmetric Local Random Circuits

Introduction.— Symmetry is one of the most foundational and ubiquitous principles that affect natural phenomena. It not only puts constraints on static or dynamic properties of systems on microscopic and macroscopic scales, but also give rise to new physics as in spontaneous symmetry breaking [1, 2, 3], symmetry-enhanced topological phenomena [4, 5, 6, 7, 8, 9, 10], and quantum memories [11, 12, 13, 14]. The concept has an intriguing interplay with yet another fundamental notion, locality, in both spacial and temporal ways. The former emerges for instance in the hydrodynamic transport [15, 16] and quantum chaos [17, 18], whereas the latter includes the universality of unitary evolution, i.e., the ability to generate arbitrary unitary operations. This is a crucial concept in quantum information science including quantum computing, quantum control, and quantum cryptography.

In the absence of any symmetry, it is well-understood that the universality regarding the global unitary group is achieved by layers of locally universal gate sets [19, 20, 21]. While one may naturally deduce that such a connection between globalness and locality is robust, it was shown that symmetric local gates are not universal for symmetric global gates [22]. This counterintuitive no-go theorem of universality casts light on the impact of symmetry on the practicality of quantum information processing and quantum computing [23], as well as statistical and dynamical properties of quantum many-body systems [24, 25, 26, 27, 28]. An outstanding question we must ask is the following: to what extent the globalness of unitary evolution is allowed under the presence of symmetry for individual quantum operation?

A first key step was made by introducing a weaker version of the universality called semi-universality, which means the relaxed tunability up to the relative phases between symmetry sectors [29]. Such a property is indeed shown to be satisfied in some non-universal cases including 2-local circuits obeying symmetries such as $\mathbb{Z}_{2}$, U(1) or SU(2) with $2$-local interaction [30, 31] and $\mathrm{SU}(d)$ with $3$-local gates [32].

A complementary approach to such a qualitative picture is to examine the expressibility in a quantitative manner via the randomness of local circuits. As known in the non-symmetric cases, this allows us to assess the applicability to quantum tomography [33], quantum device benchmarking [34, 35, 36], variational quantum computation [37], and so on. In this direction, Refs. [38, 39] lower-bounded the expressibility of symmetric circuits with specific locality via the ability to compose symmetric unitary $t$-design, or, mimic the symmetric Haar random unitary distribution up to the $t$th moment  [34, 40, 41]. However, in sharp contrast to the non-symmetric case, it remains an open question to establish a unified theory that provides the maximal order of unitary designs achievable with symmetric local random circuits for general symmetry and locality.

In this work, we fill this void by establishing a formula to characterize the randomness of random circuits under arbitrary symmetry and locality constraints. Concretely, we prove that finding the tight bound on the achievable order of unitary designs can be reduced to a simple integer optimization problem. By using this result, we explicitly obtain the maximal order of unitary designs generated by local random circuits under physically important symmetries $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, and $\mathrm{SU}(2)$.

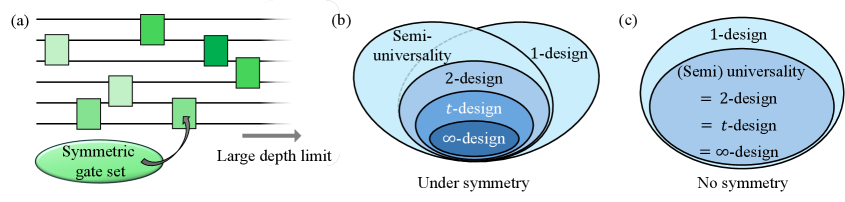
Setup.— We consider random circuits consisting of symmetric and local gates on $n$ qudits, as shown in Fig 1 (a). We first explain the symmetry constraint and next, introduce the locality constraint. By using the pair of a group $G$ and its unitary representation $R$, we say that an operator is $(G,R)$-symmetric if it commutes with $R(g)$ for all $g\in G$, and we denote the set of all $(G,R)$-symmetric unitary gates on $n$ qudits by $\mathcal{U}_{n,G,R}$. Specifically, the representations of the physically plausible $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, and $\mathrm{SU}(2)$ symmetries on $n$ qubits are respectively given by

	$\displaystyle R(0)=\mathrm{I}^{\otimes n},\ R(1)=\mathrm{Z}^{\otimes n},$		(1)
	$\displaystyle R(e^{i\theta})=e^{i\theta\mathrm{Z}^{\mathrm{tot}}},$		(2)
	$\displaystyle R(e^{i(\theta_{\mathrm{X}}\mathrm{X}+\theta_{\mathrm{Y}}\mathrm{Y}+\theta_{\mathrm{Z}}\mathrm{Z})})=e^{i(\theta_{\mathrm{X}}\mathrm{X}^{\mathrm{tot}}+\theta_{\mathrm{Y}}\mathrm{Y}^{\mathrm{tot}}+\theta_{\mathrm{Z}}\mathrm{Z}^{\mathrm{tot}})},$		(3)

where $\mathrm{X}$, $\mathrm{Y}$, and $\mathrm{Z}$ are the Pauli operators, and the superscript “tot” means the sum of the Pauli operators acting on every single qubit. These symmetries appear in the transverse-field Ising model, the Heisenberg XXZ model, and the XXX model, for example.

Next, by adding the locality constraints, we define symmetric local random circuits. Given $\gamma$ representing a set of labels for qudits, we denote the set of all $(G,R)$-symmetric unitary gates nontrivially acting on the qudit set $\gamma$ by $\mathcal{U}_{n,G,R}^{\gamma}$. We construct a random circuit by taking $\gamma$ from the set $\Gamma$ of qudit sets with nonzero probability $p^{\gamma}>0$ and randomly drawing a unitary gate $U$ from $\mathcal{U}_{n,G,R}^{\gamma}$, i.e., the distribution of unitary gates at each time step is given by

$\displaystyle\zeta=\sum_{\gamma\in\Gamma}p^{\gamma}\mu_{\mathcal{U}_{n,G,R}^{\gamma}},$

(4)

where $\mu_{\mathcal{U}_{n,G,R}^{\gamma}}$ is the normalized Haar measure on $\mathcal{U}_{n,G,R}^{\gamma}$. For example, when we express the nearest neighbor gate sets on a one-dimensional system consisting of $n$ qudits labeled as $1$, $2$, …, $n$ with the open boundary condition, $\Gamma$ is given by $\{\{j,j+1\}|j=1,2,...,n-1\}$, which corresponds to the circuit shown in Fig. 1 (a).

In order to investigate the randomness of symmetric random circuits specified by the distribution $\zeta$, we rely on a notion called approximate unitary design, defined as follows.

This condition implies that the behavior of the distribution $\nu$ asymptotically coincides with the symmetric global random distribution up to the $t$th order in the infinite depth. We note that even if we assume the infinite depth, the problem of finding the maximal order of $t$ is still highly nontrivial in the presence of symmetry, because there are rich structures in the classes of designs in the presence of symmetry unlike in the absence of symmetry (see Fig. 1 (b)(c)). In the following, we assume that $\Gamma$ is inseparable, i.e., we cannot decompose the qudits into two disjoint parts $C_{1}$ and $C_{2}$ such that every $\gamma\in\Gamma$ satisfies $\gamma\subset C_{1}$ or $\gamma\subset C_{2}$. This is because if $\Gamma$ is separable, the gate set $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$ does not scramble between the two qudit regions, and does not generate unitary designs.

Results for concrete symmetries.— We focus on the $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, and $\mathrm{SU}(2)$ symmetries in our first main result, which explicitly gives the maximal order of approximate unitary design.

We note that this result depends only on the locality $k$ of $\Gamma$, and not on other information of $\Gamma$ such as the connectivity between qubits, because every symmetric $k$-local operator can be generated with some symmetric $k$-local operator and swap operators in $\mathcal{U}_{n,G,R}^{\gamma}$ with some $\gamma$ satisfying $\#\gamma=k$. This result is also independent of the detailed probability $p^{\gamma}$. We present the result for $k=2,3,4$ and the range of $n$ in Table 1. As for the maximal order $t$ for small $n$, there are some exceptions in the $\mathrm{SU}(2)$ case (see Theorem 6 of Ref. [42]). We note that although Eq. (7) holds for all $n\geq k+1$ when $k=2$, $3$ and $4$ in the $\mathrm{U}(1)$ symmetry, this relation does not hold for all $n\geq k+1$.

Result for general case.— Next, we present the result for general symmetries. For stating the result, we prepare two notions: semi-universality and symmetric operator decomposition. The semi-universality is a weaker version of universality, defined as follows:

We note that this definition means that a semi-universal gate set can generate all operators in $\mathcal{U}_{n,G,R}$ up to $Z(\mathcal{U}_{n,G,R})$, which is the relative phase group between symmetry sectors explained below. When the symmetry is trivial, i.e., $G=\{I\}$, the condition of semi-universality reduces to the ordinary universality up to the global phase, because the center of unitary group $\mathcal{U}_{n}$ is the global phase group $\{e^{i\theta}I\}_{\theta\in\mathbb{R}}$. The semi-universality was first considered in the context of decoherence-free subspaces [29], and it is known that the $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, or $\mathrm{SU}(2)$-symmetric $2$-local gate sets satisfy semi-universality but do not satisfy universality [30, 31].

As for the relation to unitary designs, it is known that if the gate set $\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma}$ is not semi-universal for $\mathcal{U}_{n,G,R}$, the distribution $\zeta$ defined by Eq. (4) is not an approximate $(G,R)$-symmetric unitary $2$-design, which follows from the combination of Theorem 16 of Ref. [43] (see below Definition 2 in Ref. [42] for details). We note that this statement holds because $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$ are continuous gate sets, and it does not generally hold for discrete gate sets such as the Clifford gates. On the other hand, the semi-universality does not even imply $\zeta$ being an approximate $1$-design. As a counterexample, for the $\mathbb{Z}_{2}$ symmetry on a single qubit, the trivial gate set $\{I\}$ is semi-universal for $\mathcal{U}_{1,G,R}$, but does not generate a $1$-design.

As the second notion for stating our general result, we introduce the decomposition of symmetric operators. We note that every unitary representation $R$ can be decomposed into inequivalent irreducible representations:

$\displaystyle R(g)\cong\bigoplus_{\lambda\in\Lambda}R_{\lambda}(g)\otimes\mathrm{id}(\mathbb{C}^{m_{\lambda}}),$

(10)

where $\Lambda$ is the set of all labels $\lambda$ for the irreducible representations $R_{\lambda}$ appearing in the decomposition of $R$, $m_{\lambda}$ is the multiplicity of $R_{\lambda}$, $\mathrm{id}(\mathbb{C}^{m})$ is the identity operator on $\mathbb{C}^{m}$, and $\cong$ means isomorphism. Then, by Schur’s lemma, every $(G,R)$-symmetric operator $A$ can be shown to be written as [44]

$\displaystyle A\cong\bigoplus_{\lambda\in\Lambda}\mathrm{id}(\mathbb{C}^{r_{\lambda}})\otimes A_{\lambda}$

(11)

with some uniquely determined operator $A_{\lambda}$ acting on the multiplicity space $\mathbb{C}^{m_{\lambda}}$, where $r_{\lambda}$ is the dimension of the representation space of $R_{\lambda}$. By using this decomposition, we can confirm that $Z(\mathcal{U}_{n,G,R})\cong\bigoplus_{\lambda\in\Lambda}e^{i\theta_{\lambda}}\mathrm{id}(\mathbb{C}^{r_{\lambda}})\otimes\mathrm{id}(\mathbb{C}^{m_{\lambda}})$ is the relative phase group, and that the semi-universality of $\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma}$ for $\mathcal{U}_{n,G,R}$ is equivalent to the following condition: every unitary operator in the form of $\bigoplus_{\lambda\in\Lambda}\mathrm{id}(\mathbb{C}^{r_{\lambda}})\otimes U_{\lambda}$ with $U_{\lambda}\in\mathrm{SU}(m_{\lambda})$ is generated by $\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma}$.

We illustrate the decomposition by taking the $\mathrm{U}(1)$ symmetry. Since $\mathrm{U}(1)$ is commutative, every irreducible representation is one-dimensional and corresponds to the eigenvalue of $\mathrm{Z}^{\mathrm{tot}}$. Concretely, it is decomposed into $n+1$ irreducible representations $R_{\lambda}(e^{i\theta})=e^{i(n-2\lambda)\theta}$ with $\lambda\in\{0,1,...,n\}$, and the multiplicity $m_{\lambda}$ is given by $\binom{n}{\lambda}$, which corresponds to the dimension of the eigenspace of $\mathrm{Z}^{\mathrm{tot}}$ with eigenvalue $n-2\lambda$.

We are now ready to state our general theorem.

This theorem applies to arbitrary symmetries including noncommutative ones as long as the semi-universality condition holds. We note that Eq. (12) means $t<\infty$ when $(\mathcal{V}^{\perp}\cap\mathbb{Z})\backslash\{\bm{0}\}=\varnothing$, which consists with the fact that $\zeta$ is an approximate $(G,R)$-symmetric unitary $t$-design for all $t\in\mathbb{N}$ when $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$ is universal for $\mathcal{U}_{n,G,R}$. We show that this theorem also implies the converse below. We also note that when the representation $R$ is given by $T^{\otimes n}$ with a single qudit representation $T$ of $G$, $\mathcal{V}$ is given by $\{\bm{f}(A\otimes\mathrm{I}^{\otimes n-k})|A\in\mathcal{L}_{k,G,T^{\otimes k}}\}$, where $\mathcal{L}_{k,G,T^{\otimes k}}$ is the set of all linear operators on $k$ qubits commuting with $T^{\otimes k}(g)$ for all $g\in G$. In this case, the dimension of $\mathcal{V}$ is constant with respect to the qudit count $n$, because it is no greater than the dimension of $\mathcal{L}_{k,G,T^{\otimes k}}$.

We explain how we can confirm that $\zeta$ is an approximate unitary $t$-design for all $t\in\mathbb{N}$ if and only if $\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma}$ is universal for $\mathcal{U}_{n,G,R}$. The “if” part is trivial because we can apply the same argument in the absence of symmetry. For the converse part, whenever $\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma}$ is not universal, we can give a not necessarily tight upper bound $u$ on $t$. We can get such $u$ by $u:=(\bm{m},\bm{c}^{+})$ with some $\bm{c}\in(\mathcal{V}^{\perp}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}$ (see below Theorem 1 of Ref. [42] for the proof of the existence of $\bm{c}$).

We also remark that the (not necessarily tight) upper bound $u$ is useful for the numerical computation of the tight bound, because Eq. (12) is equivalent to

$\displaystyle t<\min\left\{u,\min_{\bm{x}\in(\mathcal{V}^{\perp}\cap\mathcal{F}_{u}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}}(\bm{m},\bm{x}^{+})\right\}$

(13)

with $\mathcal{F}_{u}:=\{\bm{x}\in\mathbb{R}^{\Lambda}||x_{\lambda}|<u/m_{\lambda}\ \forall\lambda\in\Lambda\}$, and the r.h.s. of Eq. (13) can be computed by enumeration. For the proof of Eq. (13), it is sufficient to show that $\min_{\bm{x}\in\overline{\mathcal{F}_{u}}\cap\mathbb{Z}^{\Lambda}}(\bm{m},\bm{x}^{+})\geq u$ by noting that $[(\mathcal{V}^{\perp}\cap\mathcal{F}_{u}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}]\cup(\overline{\mathcal{F}_{u}}\cap\mathbb{Z}^{\Lambda})\supset(\mathcal{V}^{\perp}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}$. For arbitrary $\bm{x}\in\overline{\mathcal{F}_{u}}\cap\mathbb{Z}^{\Lambda}$, we can take some $\lambda\in\Lambda$ such that $|x_{\lambda}|\geq u/m_{\lambda}$. We can suppose that $x_{\lambda}>0$ without loss of generality, since $\bm{x}\in\overline{\mathcal{F}_{u}}\cap\mathbb{Z}^{\Lambda}$ implies $-\bm{x}\in\overline{\mathcal{F}_{u}}\cap\mathbb{Z}^{\Lambda}$. Then, we get $(\bm{m},\bm{x}^{+})\geq m_{\lambda}x_{\lambda}\geq u$.

Although we present the complete proof of Theorem 2 in Ref. [42], we briefly explain the proof idea. First, we give an intuitive explanation. Since we consider the case when the set of symmetric local gates is semi-universal, the expressibility of symmetric local gate set and that of symmetric global gate set are different only in terms of the relative phases. Therefore, the notion of approximate unitary $t$-design is related to the controllability of the $t$-fold relative phase Such condition is equivalently rephrased as the condition for a certain set of equations having no nontrivial integer solution, which can also be expressed as integer optimization.

Next, we comment on the technical perspective of the proof. By a standard argument, the distribution $\zeta$ is an approximate $(G,R)$-symmetric $t$-design if and only if the commutants of $\Omega_{t}(\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma})$ and $\Omega_{t}(\mathcal{U}_{n,G,R})$ are identical, where $\Omega_{t}$ is the $t$-fold channel defined by $\Omega_{t}(U):=U^{\otimes t}$. Thus for the proof of the “if” part, we prove that every element in $\Omega_{t}(\mathcal{U}_{n,G,R})$ can be generated by $\bigcup_{\gamma\in\Gamma}\Omega_{t}({\mathcal{U}_{n,G,R}^{\gamma}})$ in the sense of algebra. Since the semi-universality is assumed, it is sufficient to show that every element in $\Omega_{t}(Z(\mathcal{U}_{n,G,R}))$ can be generated. For that purpose, we take a certain map from a set of real numbers to $\braket{\Omega_{t}(\bigcup_{\gamma\in\Gamma}\mathcal{U}_{n,G,R}^{\gamma})}$ and conduct an integration like the Fourier transformation. For the proof of the “only if” part, we prove that we can construct an operator that commutes with $\bigcup_{\gamma\in\Gamma}\Omega_{t}(\mathcal{U}_{n,G,R}^{\gamma})$ but not with $\Omega_{t}(\mathcal{U}_{n,G,R})$. For the construction, we use the totally antisymmetric state defined as $\ket{\chi(\mathbb{C}^{m})}:=\sum_{\sigma\in\mathfrak{S}_{m}}\mathrm{sgn}(\sigma)\bigotimes_{j=1}^{m}\ket{\sigma(j)}/\sqrt{m!}$ with the symmetric group $\mathfrak{S}_{m}$ of degree $m$. This state is useful because it satisfies $A^{\otimes m}\ket{\chi(\mathbb{C}^{m})}=\mathrm{det}(A)\ket{\chi(\mathbb{C}^{m})}$ for all operators $A$ on $\mathbb{C}^{m}$.

Derivation of Theorem 1 from Theorem 2.— We explain the general procedure to obtain the explicit tight bound on $t$ for a given symmetry such as Theorem 1 by using the general result of Theorem 2. This process consists of three steps. In the first step, we find the concrete expression of $m_{\lambda}$ for the symmetry, and take the basis $\{\bm{v}_{j}\}_{j=1}^{J}$ of $\mathcal{V}$. The multiplicity $m_{\lambda}$ can be obtained by using the representation theory, as we have mentioned just above Theorem 2. As for taking the basis of $\mathcal{V}$, it is important to know the dimension $J$. We can show that $J=1$, $k+1$, and $\lfloor k/2\rfloor+1$ in the $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, and $\mathrm{SU}(2)$ cases, respectively.

In the second step, we get a not-necessarily tight upper bound $u^{\prime}$ on $t$ by taking a certain $\bm{x}\in(\mathcal{V}^{\perp}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}$. We consider the case when the size of $\Lambda$ is larger than the dimension $J$ of $\mathcal{V}$, because otherwise the gate set $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$ is universal, and thus $\zeta$ is an approximate $(G,R)$-symmetric unitary $t$-design for all $t$. We label the elements of $\Lambda$ as $\lambda_{1}$, $\lambda_{2}$, …, $\lambda_{\#\Lambda}$ such that $m_{\lambda_{1}}\leq m_{\lambda_{2}}\leq\cdots\leq m_{\lambda_{\#\Lambda}}$ and restrict the region of $\bm{x}$ to $\mathcal{D}:=\{\bm{x}\in\mathbb{R}^{\Lambda}|x_{\lambda_{j}}=0\ \forall j\geq J+2\}$. Then, $\mathcal{V}^{\perp}\cap\mathcal{D}$ is one-dimensional, and we can take $\bm{p}\in\mathbb{Z}^{\Lambda}$ such that $\mathcal{V}^{\perp}\cap\mathcal{D}\cap\mathbb{Z}^{\Lambda}=\{a\bm{p}|a\in\mathbb{Z}\}$. We define $u^{\prime}:=(\bm{m},\bm{p}^{+})$, which gives an upper bound on $t$.

In the third step, we show that $u^{\prime}$ is the tight bound under the assumption that $u^{\prime}\leq m_{\lambda_{j}}$ for all $j\geq J+2$, which holds for sufficiently large $n$ in the $\mathrm{U}(1)$ and $\mathrm{SU}(2)$ cases. By applying Eq. (13), it is sufficient to show that $\min_{\bm{x}\in(\mathcal{V}^{\perp}\cap\mathcal{F}_{u^{\prime}}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}}(\bm{m},\bm{x}^{+})\geq u^{\prime}$. By using the assumption above, we get the inclusion relation $\mathcal{F}_{u^{\prime}}\cap\mathbb{Z}^{\Lambda}\subset\mathcal{D}\cap\mathbb{Z}^{\Lambda}$. We thus have $\min_{\bm{x}\in(\mathcal{V}^{\perp}\cap\mathcal{F}_{u}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}}(\bm{m},\bm{x}^{+})\geq\min_{\bm{x}\in(\mathcal{V}^{\perp}\cap\mathcal{D}\cap\mathbb{Z}^{\Lambda})\backslash\{\bm{0}\}}(\bm{m},\bm{x}^{+})=u^{\prime}$.

We illustrate these steps in the $\mathrm{U}(1)$-symmetric and $2$-local case. First, as we have mentioned just above Theorem 2, we have $\Lambda=\{0,1,...,n\}$, and the multiplicity $m_{\lambda}$ is given by $\binom{n}{\lambda}$. In order to take the basis of $\mathcal{V}$, we note that every U(1)-symmetric 2-local operator $A\in\mathcal{L}_{2,G,T^{\otimes 2}}$ can be written in a block diagonal form $A_{0}\oplus A_{1}\oplus A_{2}$ with $A_{j}$’s acting on the eigenspaces of $\mathrm{Z}\otimes\mathrm{I}+\mathrm{I}\otimes\mathrm{Z}$ with eigenvalues $2-2j$, respectively. Then, $f_{\lambda}(A\otimes\mathrm{I}^{\otimes n-2})$ is given by $\sum_{j=0}^{2}\mathrm{tr}(A_{j})\binom{n-2}{\lambda-j}$, which implies that we can take $\bm{v}_{j}=(\binom{n-2}{\lambda-j})_{\lambda\in\Lambda}$ with $j=0,1,2$ as a basis of $\mathcal{V}$, where we define $\binom{a}{b}:=0$ when $b\not\in\{0,1,...,a\}$. Next, we define $\mathcal{D}:=\{\bm{x}\in\mathbb{R}^{\Lambda}|x_{\lambda}=0\ \forall\lambda\in\{2,3,...,n-2\}\}$. Then, $\mathcal{V}^{\perp}\cap\mathcal{D}\cap\mathbb{Z}^{\Lambda}$ can be expressed as $\{a\bm{p}|a\in\mathbb{Z}\}$ with $\bm{p}\in\mathbb{Z}^{\Lambda}$ defined by $(p_{0},p_{1},p_{n-1},p_{n})=(1,-(n-2),n-2,-1)$ and $p_{\lambda}=0$ for all $\lambda\in\{2,3,...,n-2\}$. We thus define $u^{\prime}:=2(n-1)$, which is an upper bound on $t$. Finally, we note that the assumption holds for all $n\geq 3$, i.e. $u^{\prime}=2(n-1)\leq\binom{n}{2}\leq m_{\lambda_{j}}$ for all $j\geq 5$, where we note that there does not exist an element $\lambda_{j}$ with $j\geq 5$ when $n=3$. We therefore conclude that $u^{\prime}=2(n-1)$ is the tight bound on $t$ for all $n$. We can deal with general $k$-local cases with a similar method.

Discussion.— In this work, we presented a formula for finding the maximal order of unitary design generated with symmetric local random circuits for general symmetries and general localities in Theorem 2. By applying this result to the $\mathbb{Z}_{2}$, $\mathrm{U}(1)$, and $\mathrm{SU}(2)$ symmetries, we have explicitly shown the maximal order of unitary designs for general localities in Theorem 1. Although we have focused on a continuous gate set $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$, our results are also applicable to random circuits with an arbitrary gate set as long as the gate set can generate the continuous unitary ensemble $\{\mathcal{U}_{n,G,R}^{\gamma}\}_{\gamma\in\Gamma}$. Since Theorem 2 is given in a general form, we can derive the results for other symmetries and localities.

As a future research direction, it is important to investigate the convergence speed of the approximate unitary designs on symmetric and local circuits. Moreover, the conserved quantity in $t$ copies of a system under symmetric local unitaries, which we have constructed in the proof of the “only if” part of Theorem 2, may lead to the discovery of some limitation in the process of thermalization under symmetric local Hamiltonians.

Acknowledgements.— The authors wish to thank Iman Marvian, Hiroyasu Tajima, and Janek Denzler for insightful discussions. Y.M. is supported by JSPS KAKENHI Grant No. JP23KJ0421. R.S. is supported by the BMBF (PhoQuant, Grant No. 13N16103). This research is funded in part by the Gordon and Betty Moore Foundation’s EPiQS Initiative, Grant GBMF8683 to T.S. N.Y. wishes to thank JST PRESTO No. JPMJPR2119, JST ASPIRE Grant Number JPMJAP2316, and the support from IBM Quantum. This work was supported by JST Grant Number JPMJPF2221, JST ERATO Grant Number JPMJER2302, and JST CREST Grant Number JPMJCR23I4, Japan.

Note Added: During the preparation of this article, we became aware of independent work by Austin Hulse, Hanqing Liu, and Iman Marvian  [45], which studies similar questions and was posted on arXiv concurrently with the present paper. Both have arrived at the same result on the maximal order of unitary designs under the $\mathrm{U}(1)$ and $\mathrm{SU}(2)$ symmetries. Ref. [45] has assumed conjectures about combinatorial identities, which are introduced as Eqs. (86) and (120) of the version 1 of their manuscript for the proof of general $k$-local cases. In our work, we have provided a proof that is independent of any conjectures.