Unmasking Transformers: A Theoretical Approach to Data Recovery via Attention Weights

We state our result as follows:

We used $\mathbb{R}$ to denote real numbers. We use $A\in\mathbb{R}^{n\times d}$ to denote an $n\times d$ size matrix where each entry is a real number. For any positive integer $n$, we use $[n]$ to denote $\{1,2,\cdots,n\}$. For a matrix $A\in\mathbb{R}^{n\times d}$, we use $a_{i,j}$ to denote the an entry of $A$ which is in $i$-th row and $j$-th column of $A$, for each $i\in[n]$, $j\in[d]$. We use $A_{i,j}\in\mathbb{R}^{n\times d}$ to denote a matrix such that all of its entries equal to $0$ except for $a_{i,j}$. We use ${\bf 1}_{n}$ to denote a length-$n$ vector where all the entries are ones. For a vector $w\in\mathbb{R}^{n}$, we use $\operatorname{diag}(w)\in\mathbb{R}^{n\times n}$ denote a diagonal matrix where $(\operatorname{diag}(w))_{i,i}=w_{i}$ and all other off-diagonal entries are zero. Let $D\in\mathbb{R}^{n\times n}$ be a diagonal matrix, we use $D^{-1}\in\mathbb{R}^{n\times n}$ to denote a diagonal matrix where $i$-th entry on diagonal is $D_{i,i}$ and all the off-diagonal entries are zero. Given two vectors $a,b\in\mathbb{R}^{n}$, we use $(a\circ b)\in\mathbb{R}^{n}$ to denote the length-$n$ vector where $i$-th entry is $a_{i}b_{i}$. For a matrix $A\in\mathbb{R}^{n\times d}$, we use $A^{\top}\in\mathbb{R}^{d\times n}$ to denote the transpose of matrix $A$. For a vector $x\in\mathbb{R}^{n}$, we use $\exp(x)\in\mathbb{R}^{n}$ to denote a length-$n$ vector where $\exp(x)_{i}=\exp(x_{i})$ for all $i\in[n]$. For a matrix $X\in\mathbb{R}^{n\times n}$, we use $\exp(X)\in\mathbb{R}^{n\times n}$ to denote matrix where $\exp(X)_{i,j}=\exp(X_{i,j})$. For any matrix $A\in\mathbb{R}^{n\times d}$, we define $\|A\|_{F}:=(\sum_{i=1}^{n}\sum_{j=1}^{d}A_{i,j}^{2})^{1/2}$. For a vector $a,b\in\mathbb{R}^{n}$, we use $\langle a,b\rangle$ to denote $\sum_{i=1}^{n}a_{i}b_{i}$.

A model inversion attack is a type of adversarial attack in which a malicious user attempts to recover the private dataset used to train a supervised machine learning model . The goal of a model inversion attack is to generate realistic and diverse samples that accurately describe each class in the private dataset.

The attacker typically has access to the trained model and can use it to make predictions on input data . By carefully crafting input data and observing the model’s predictions, the attacker can infer information about the training data.

Model inversion attacks can be a significant privacy concern, as they can potentially reveal sensitive information about individuals or organizations. These attacks exploit vulnerabilities in the model’s behavior and can be used to extract information that was not intended to be disclosed.

Model inversion attacks can be formulated as an optimization problem. Given the output $Y$, the model function $f_{\theta}$ with parameters $\theta$, and the loss function $\mathcal{L}$, the objective of a model inversion attack is to find an input data $X^{*}$ that minimizes the loss between the model’s prediction $f_{\theta}(X)$ and the target output $Y$. Mathematically, this can be expressed as:

Since the loss function $\mathcal{L}(f_{\theta}(X),Y)$ is convex with respect to optimizing $X$, we can employ a specific method for model inversion attack, which involves the following steps:

1. 1.

   Initialize an input data $X$.

2. 2.

   Compute the gradient $\nabla_{X}\mathcal{L}(f_{\theta}(X),Y)$.

3. 3.

   Optimize $X$ using a learning rate $\eta$ by updating $X=X-\eta\nabla_{X}\mathcal{L}(f_{\theta}(X),Y)$.

This iterative process aims to find an input $X$ that minimizes the loss between the model’s prediction and the target output. By updating $X$ in the direction opposite to the gradient, the attack can potentially converge to an input that generates a prediction close to the desired output, thereby inverting the model. In this work, we focus our effort on the Attention models (which is natural due to the explosive development of LLMs). In this case, the parameters $\theta$ in our model are considered to consist of $\{Q,K,V\}$. During the script, to avoid the abuse of notations, we use $B=Y$ to denote the ground truth label.

In this paper, we extend the prior work of [37] and focus on the training process of the attention mechanism in the context of the Transformer model. We decompose the training procedure into a regression form based on the insights provided by [27].

Specifically, we investigate the training process for a specific layer, denoted as the $l$-th layer, and consider the case of single-headed attention. In this setting, we have an input matrix represented as $X\in\mathbb{R}^{d\times n}$ and a target matrix denoted as $B\in\mathbb{R}^{d\times n}$. Given $Q\in\mathbb{R}^{d\times d},K\in\mathbb{R}^{d\times d},V\in\mathbb{R}^{d\times d}$ as the trained weights of attention architecture. The objective of the training process in the Transformer model is to minimize the loss function by utilizing back-propagation.

The loss function, denoted as $L(X)$, is defined as follows:

where $D:=\text{diag}(\exp(X^{\top}K^{\top}QX)\mathbf{1}_{n})$ and each row of $D^{-1}\exp()$ corresponds to a softmax function.

The goal of minimizing this loss function is to align the predicted output, obtained by applying the attention mechanism, with the target matrix $B$.

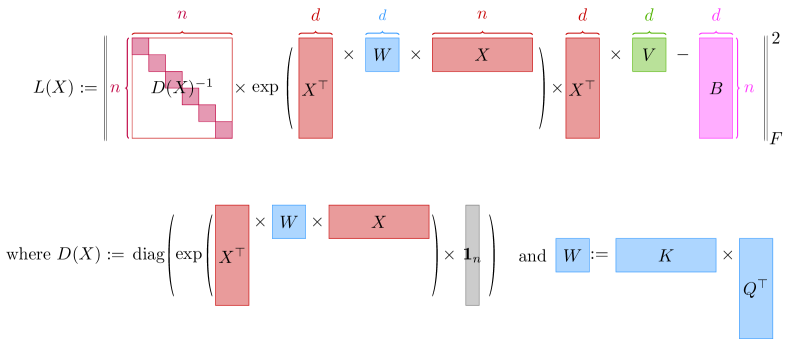
In this study, we propose a novel technique for inverting the attention weights of a transformer model using Hessian decomposition. Our aim is to find the input $X\in\mathbb{R}^{d\times n}$ that minimizes the Frobenius norm of the difference between $D(X)^{-1}\exp(X^{\top}WX)V$ and $B$, where $W=KQ^{\top}\in\mathbb{R}^{d\times d}$ represents the attention weights, $B\in\mathbb{R}^{n\times d}$ is the desired output, and $D(X)=\operatorname{diag}(\exp(X^{\top}WX))\in\mathbb{R}^{n\times n}$ is a diagonal matrix.

To achieve this, we introduce an algorithm that minimizes the loss function $L(X)$, defined as follows:

where $V\in\mathbb{R}^{d\times d}$ is a matrix of values, and $L_{\rm reg}$ captures any additional regularization terms. This loss function quantifies the discrepancy between the expected output and the actual output of the transformer.

In our approach, we leverage Hessian decomposition to efficiently compute the Hessian matrix and apply a second-order method to approximate the optimal input $X$. By utilizing the Hessian, we can gain insights into the curvature of the loss function and improve the efficiency of optimization. This approach enables us to efficiently find an approximate solution for the input $X$ that minimizes the loss function, thereby inverting the attention weights of the transformer model.

By integrating Hessian decomposition and second-order optimization techniques ([5, 62, 19, 50, 44, 35, 41]), our proposed algorithm provides a promising approach for addressing the challenging task of inverting attention weights in transformer models.

Due to the complexity of the loss function (Eq. (1)), directly computing its Hessian is challenging or even impossible. To simplify the computation, we introduce several notations (See Figure 2 for visualization):

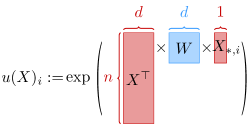
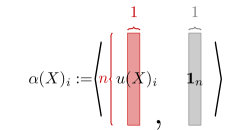
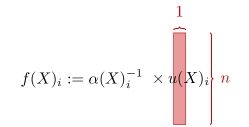
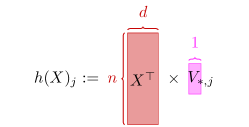
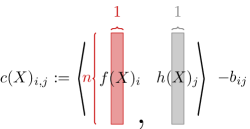
Using these terms, we can express the loss function $L(X)$ as the sum over all elements:

This allows us to break down the computation into several steps. Specifically, we start by computing the gradients of the predefined terms. Given two integers $i_{0}\in[n]$ and $j_{0}\in[d]$, we define $c(X)_{i_{0},j_{0}}$ as a matrix where all entries are zero except for the entry $c_{i_{0},j_{0}}$. Additionally, we denote $i_{1}\in[n]$ and $j_{1}\in[d]$ as two other integers, and use $x_{i_{1},j_{1}}$ to represent the entry in $X$ corresponding to the $i_{1}$-th row and $j_{1}$-th column.

We can now express $\frac{\mathrm{d}c(X)_{i_{0},j_{0}}}{\mathrm{d}x_{i_{1},j_{1}}}$ (the gradient of $c(X)_{i_{0},j_{0}}$) in two cases:

• •

  Case 1: The situation when $i_{0}=i_{1}$.

• •

  Case 2: The situation when $i_{0}\neq i_{1}$.

By decomposing the Hessian into several cases (See Section F for details), we can calculate the final Hessian. Similar to the approach used when computing the gradients, we introduce two additional integers $i_{2}\in[n]$ and $j_{2}\in[d]$. The Hessian can then be expressed as $\frac{\mathrm{d}^{2}c(X)_{i_{0},j_{0}}}{\mathrm{d}x_{i_{1},j_{1}}\mathrm{d}x_{i_{2},j_{2}}}$. We can further break down the computation into four cases to handle different scenarios:

• •

  Case 1: The situation when $i_{0}=i_{1}=i_{2}$.

• •

  Case 2: The situation when $i_{0}=i_{1}\neq i_{2}$.

• •

  Case 3: The situation when $i_{0}\neq i_{1}$, $i_{0}\neq i_{2}$ and $i_{1}=i_{2}$.

• •

  Case 4: The situation when $i_{0}\neq i_{1}$, $i_{0}\neq i_{2}$ and $i_{1}\neq i_{2}$.

It is worth mentioning that there is a case that $i_{0}\neq i_{1}$, $i_{0}=i_{2}$, is equivalent to the case that $i_{0}=i_{1}\neq i_{2}$. By considering these four cases, we can calculate the Hessian for each element in $X$. This allows us to gain further insights into the curvature of the loss function and optimize the parameters more effectively.

By considering different conditions of Hessian, we have the following decomposition.

Utilizing above definitions, we split the Hessian to a $n\times n$ partition with its $i_{1},i_{2}$-th component being $H_{i}{(i_{1},i_{2})}$.

We present our findings that establish the Lipschitz continuity property of the Hessian of $L(X)$, which is a highly desirable characteristic in optimization. This property signifies that the second derivatives of $L(X)$ exhibit smooth changes within a defined range. Leveraging this Lipschitz property enables us to employ gradient-based methods with guaranteed convergence rates and enhanced stability. Consequently, our results validate the feasibility of utilizing the proposed training objective to achieve convergence in the model inversion attack. This finding holds significant promise for the development of efficient and effective optimization strategies in this context.

After computing the Hessian of $L(X)$, we now show our result that can confirm it is positive definite under proper regularization. Therefore, we can apply a modified Newton’s method to approach the optimal solution.

Therefore, we define the regulatization term as follows to have the PSD guarantee.

With above properties of the loss function, we have the convergence result in Theorem 1.3.