Unravelling the origin of the peculiar transition in the magnetically ordered phase of the Weyl semimetal Co3Sn2S2
Abstract
Recent discovery of topologically non-trivial behavior in Co3Sn2S2 stimulated a notable interest in this itinerant ferromagnet ( K). The exact magnetic state remains ambiguous, with several reports indicating the existence of a second transition in the range 125 – 130 K, with antiferromagnetic and glassy phases proposed to coexist with the ferromagnetic phase. Using detailed angle-dependent DC and AC magnetization measurements on large, high-quality single crystals we reveal a highly anisotropic behavior of both static and dynamic response of Co3Sn2S2. It is established that many observations related to sharp magnetization changes when are influenced by the demagnetization factor of a sample. On the other hand, a genuine transition has been found at K, with the magnetic response being strictly perpendicular to the c-axis and several orders of magnitude smaller than for . Calculations using density-functional theory indicate that the ground state magnetic structure consist of magnetic moments canted away from the c-axis by a small angle (). We argue that the second transition originates from a small additional canting of moments within the kagome plane, with two equivalent orientations for each spin.
Topology and topological properties of matter have recently gained a lot of attention due to the realization of their importance in various exotic phases like topological insulators [1], Dirac and Weyl (semi)metals [2] and spin-liquids [3]. The band structure of topologically non-trivial compounds is strongly influenced by spin-orbit coupling (SOC), leading to band-inversion and relativistic fermions with linear dispersions. Depending on whether the spatial () and time-reversal () symmetries are preserved or broken, the crossing points of such inverted bands are called Dirac or Weyl nodes, respectively. If Weyl nodes are found close to the Fermi energy they can strongly affect the transport properties due to the fact that the nodes act as sources of Berry curvature [4]. The control of topological properties using external parameters is highly sought-after, offering a novel type of topological phase transitions. In systems with broken this is hard to realize, as they are intrinsically linked to the underlying crystal structure. On the other hand, -breaking is related to the appearance of magnetic order, allowing temperature or magnetic field to tune topological invariants and drive the system across a topological phase transition.
It has been recently suggested that Co3Sn2S2 is a Weyl semimetal [5, 6], exhibiting ferromagnetic (FM) order below K [7]. Evidence of topologically non-trivial behavior includes the anomalous Hall effect [5], the visualisation of surface Fermi arcs [6, 8] and the giant magneto-optical response [9]. These are considered to arise from the existence of Weyl nodes with opposite chirality [2], whose number and the position relative to the Fermi energy are strongly influenced by the details of the magnetic order. It has been established that the value of the magnetic moment on Co ions is directly linked to the separation of Weyl nodes in the k-space [10] while controlling the direction of magnetization allows to shift, create and annihilate Weyl nodes [11].
The FM order is associated with itinerant electrons originating from d-orbitals of Co ions (/Co), arranged in kagome layers (sketched in Figure 1a) and stacked along the c-axis in the A-B-C pattern [7]. Such a reduced value of the magnetic moment has recently been explained within the local triangular Co cluster, giving rise to a state () over three Co ions. It has been indicated numerically [12] and experimentally [13] that the moment is aligned parallel to the c-axis, with a field of 23 T needed to fully orient the moment parallel to the kagome plane [13].
This simple configuration has been recently challenged by a muon-spin rotation (SR) study, indicating that just below the FM order is accompanied by a second phase, interpreted as an antiferromagnetic (AFM) arrangement of in-plane moments forming a type of a 120∘ configuration [14]. The second phase appears above 90 K, reaching almost 70% of the volume fraction just below . Those conclusions have been called into question by a recent polarized neutron study [15], severely limiting the extent of a coherent AFM phase. Additionally, a second transition has been suggested to appear in the range 125 – 130 K based on DC and AC magnetization measurements [16]. Further experimental evidence for its presence has been accumulated by resistivity and magnetization [17], magneto-optical Kerr effect studies [18] and neutron diffraction [15], although the exact temperature of the transition has been shown to differ from one study to the other. The observation of shifted, magnetic-field-driven hystereses at low temperatures has been ascribed to exchange bias mechanism and associated with the appearance of a glassy state below 125 K [17].
In this Letter, we aim to clarify several confusing, and often contradicting findings related to the magnetic order in Co3Sn2S2. We clearly establish strongly direction-dependent magnetic response and reveal that for it is largely dominated by the demagnetization factor. For a second transition is found at K, with the magnetic component strictly confined to the kagome plane, indicating small canting of magnetic moments on Co ions. We confirm the canting scenario by performing careful density-functional theory (DFT) calculations, revealing the umbrella structure where moments on a triangle tilt towards its center.
High-quality single crystals were grown by the self-flux method and characterized in previous publications [6, 19, 15]. DC and AC magnetization were measured on a SQUID-based magnetometer (MPMS3, Quantum Design) equipped with a horizontal rotator, allowing the angular precision better than 0.1∘. Three samples have been used throughout this study, cut from the same large single crystal, their dimensions and masses are detailed in Supplementary Material [20]. DFT calculations were performed using the Vienna Ab Initio Simulation Package (VASP) [21, 22] on periodic models of the experimental crystal structure [23]. Electron-core interactions were described with the projector-augmented wave method, while the Kohn-Sham wave-functions for the valence electrons were expanded in a plane wave basis with a cutoff of 500 eV on the kinetic energy. We used a mesh of 11 11 11 -points and the PBE variant [24] of the GGA functional while setting the convergence limit of energy to eV. SOC was included in all calculations in a self-consistent manner.
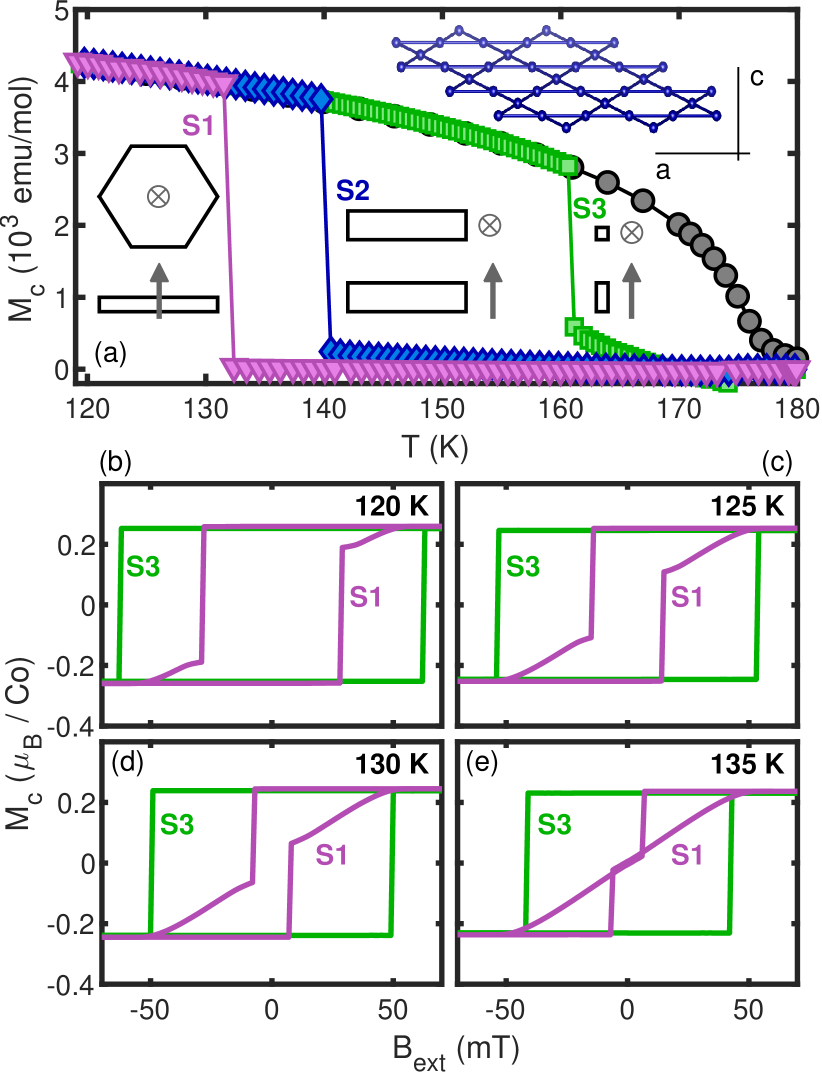
In several publications [17, 18, 15] the appearance of the second transition has been reported as a jump in magnetization following a protocol in which the sample is cooled down to the lowest temperatures in magnetic field () large enough to ensure the magnetization is completely saturated, after which has been measured while warming in a nominally zero field (FC/ZFW). In Figure 1a we present our results following the same protocol for three different samples, with three markedly different temperatures at which the jump occurs. The observed variation can be associated with shapes of the prepared samples (sketched alongside the respective curves) and their demagnetization factors [25, 26]. During a ZFW protocol, although , a fully saturated sample experiences a demagnetization field whose effect is to cause a reversal at a lower temperature when is larger. In the same way one can shift the reversal to lower or higher temperatures if or , respectively [20]. Therefore, the jumps in magnetization during the FC/ZFW protocols cannot be taken as an evidence of a thermodynamic transition occurring around 125 K while their observation in that range of temperatures is a simple consequence of a specific sample geometry, typical for thin samples of Co3Sn2S2. Additional evidence can be found in Figure 1b-e where hystereses loops are presented for and samples in the range of temperatures spanning the purported transition. In Ref. [17] it has been suggested that one of the characteristic features is the change from the square-shaped loop into a more elongated one, with triangular wings. To the contrary, our results clearly show that neither (large ) nor (small ) change their behavior across 125 K. exhibits a square-loop only below 115 K while up to 155 K. The only qualitative change occurs between 130 K and 135 K where the reversal field for goes from negative to positive, which agrees with the observed reversal temperature in the ZFW protocol of 132 K. Together with a lack of any feature seen in the AC response within the same temperature range (see below), we argue that there is no thermodynamic transition associated with below .
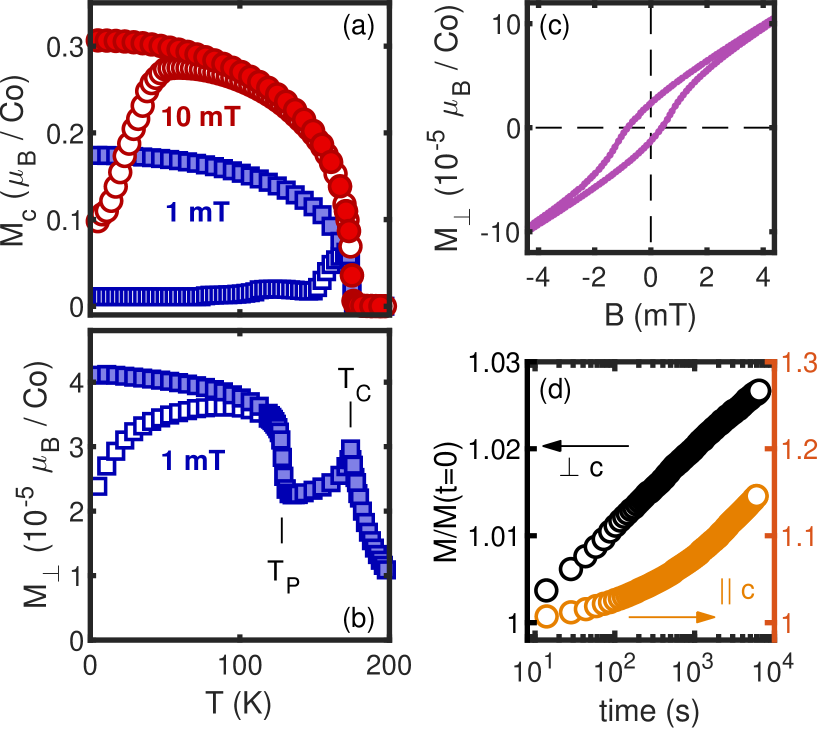
On the other hand, evidence presented by Kassem et al. [16] and especially recent reports [17, 27] for unequivocally point to an intrinsic feature related to the magnetism of Co3Sn2S2. In order to directly compare contributions to magnetization along different crystallographic directions we plot in Figure 2 for and following standard zero-field cooled (ZFC)/field-cooled (FC) protocols. The main transition at causes a sharp increase in , followed by a ZFC/FC splitting stemming from the appearance of domains and pinning of domain walls. At the same time a clear maximum is observed in at . On the other hand, a clear indication of a second transition is seen only in . In a similar fashion as increases and splits into separate ZFC and FC branches at , follows the same behavior below K, with values approximately four orders of magnitude smaller than . The associated hysteresis loop, presented in Figure 2c, reveals that the splitting collapses already at 2 mT, significantly lower than for . An unequivocal decoupling of two directions can also be seen following a ZFC protocol to and observing a time dependence of magnetization after magnetic field is turned on. Figure 2d reveals that the in-plane magnetization process cannot be seen as a simple projection of a (much larger) signal in but it reflects a separate physical mechanism.
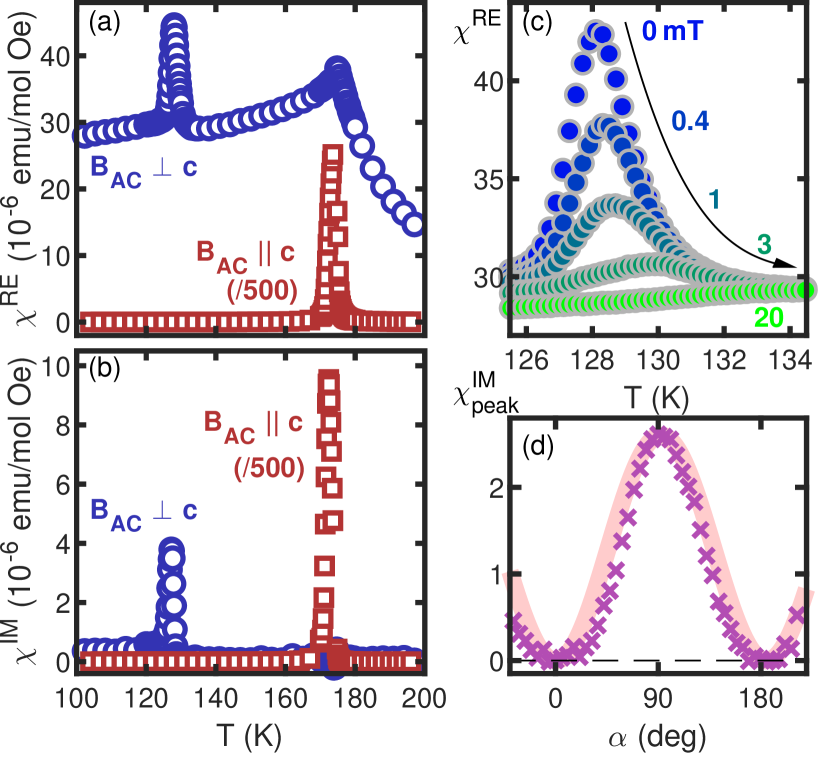
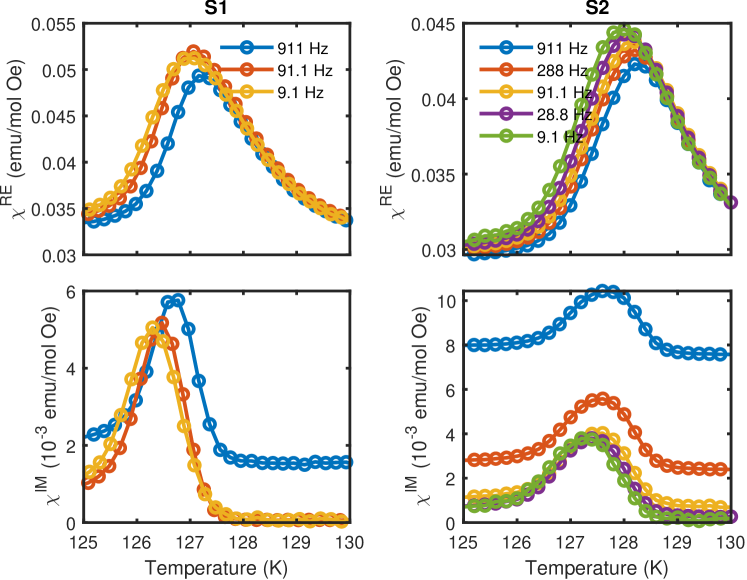
In Figures 3a and 3b we demonstrate the overall behavior of AC susceptibility, the real and the imaginary component , for two directions in zero DC magnetic field. For both and show a sharp peak at but no visible trace of the second transition. With shows a maximum at , similar in shape to , without any sizeable feature in . At both components reveal a sharp, narrow peak, below which continues a slow decrease while remains near zero. Again the scale of response is orders of magnitude smaller for but the features all remain well defined. There is a very weak frequency dependence of the maximum at , similar in magnitude to the previous report [17].
One of the factors that strongly impacts the magnitude of the response at is DC magnetic field. As seen in Figure 3c, the peak is more than halved at 1 mT, while practically completely vanishes at 20 mT. One should note that a superconducting magnet, after being ramped down to a nominal zero field, still contains stray fields from pinned vortices, which can reach several mT (and cause a negative signal in nominally ZFC measurement conditions [5, 16]). Combined with a typical sample mass of a couple of milligrams, it is easy to understand why in most cases the transition is hard to observe.
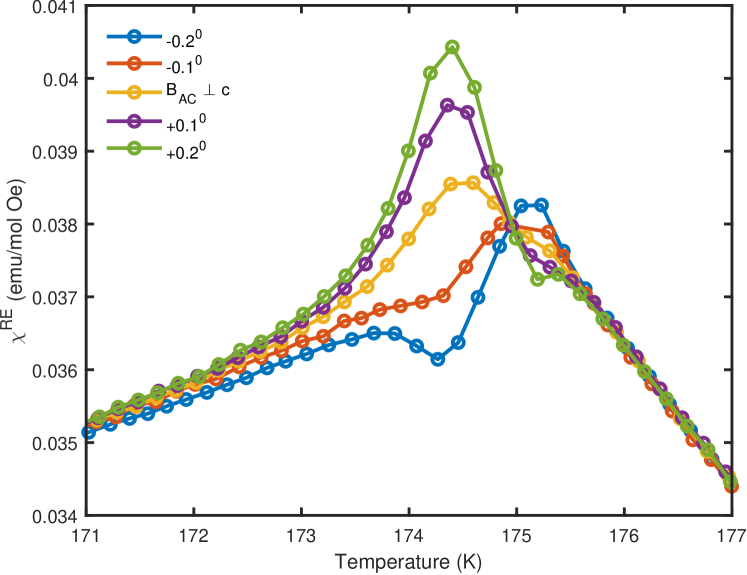
In order to reveal the angular dependence of the magnetic response around , we turn to . As displayed in Figure 3d, the amplitude of the peak closely follows a dependence, where is the angle between the AC magnetic field and the c-axis. Such a type of a behavior is typical for projection-based vectors: one comes from the projection of the magnetic field onto a given axis, the second one comes from the projection of magnetic moments back to the axis of the magnetic field. This indicates that the dissipation induced around , and thus the order developing below revealed by in Figure 2b, comes from the component of magnetic moments strictly perpendicular to the c-axis. Note that completely vanishes for , unlike which remains non-zero in the whole temperature range below (Figure 3a). The lack of the imaginary component is a direct evidence against the idea of a thermodynamic transition occurring at since crossing from the low-temperature phase into a ferromagnetic phase above would involve a reconfiguration of moments and a substantial, more isotropic .
Such a strictly in-plane component is incompatible with any known spin-glass scenario, which has been suggested solely based on a weak frequency dependence at . It is left unclear how this state would emerge from an FM state with a strong spin anisotropy or where is disorder needed for a glassy state coming from. On the other hand, the weak in-plane dynamics can arise if the dominantly c-axis oriented magnetic moments are canted by a small angle. The question of canting of the moments in Co3Sn2S2 has been addressed in several publications. Xu et al. [12] were first to use DFT calculations to calculate the total energy vs the canting angle, suggesting . Ghimire et al. [11] studied the magnetic field-induced canting and its effect on the position and the total number of Weyl nodes. This was followed up by the SR study [14] which suggested a sizeable in-plane component forming a separate AFM phase, coexisting with the main (FM) one. Finally, recent DFT calculations by Solovyev et al. [28] addressed the stability of the FM order and again concluded that the lowest energy configuration corresponds to moments being strictly parallel to the c-axis. Contrary to those results is the more general, symmetry-based discussion about complex noncollinear structures in itinerant magnets with non-negligible SOC [29], which helped explain the emergence of canting in several systems, including Mn3Sn and U3P4. The main conclusion is that the ferromagnetic structure with is not symmetry-protected, allowing for SOC-induced, small-angle canting of moments.
Motivated by these considerations, we performed self-consistent non-collinear magnetic calculations with VASP. We find that the magnetic moments in the resulting ferromagnetic ground state deviate from the -axis by a rather small angle forming the “umbrella structure” sketched in Figure 4a. The magnetic moment vector obtained from the self-consistent calculations for the three Co sites are , and in Bohr magneton units. We find that the in-plane components of the moments are quite small, but very robust to the changes in -space mesh and initial electron density guess. Additionally, we calculated the total energy of the system with respect to the canting angle (focusing especially on the small-angle region), by constraining the direction of the moments at the three Co sites while allowing the size of the moments to evolve self-consistently. As shown in Figure 4b, the results of these calculations confirm that the deviation of moments from the c-axis by an angle of , yields lower total energy per Co ion. It should be remarked that both previous reports [12, 28] considered a relatively sparse grid, with steps in the range 5 – 10∘. Additionally, Solovyev et al. [28] performed the calculations without SOC, therefore our results represent the first detailed numerical investigation of the full SOC-driven magnetic structure in Co3Sn2S2. Note that the umbrella structure is fully compatible with a single irreducible representation [15].
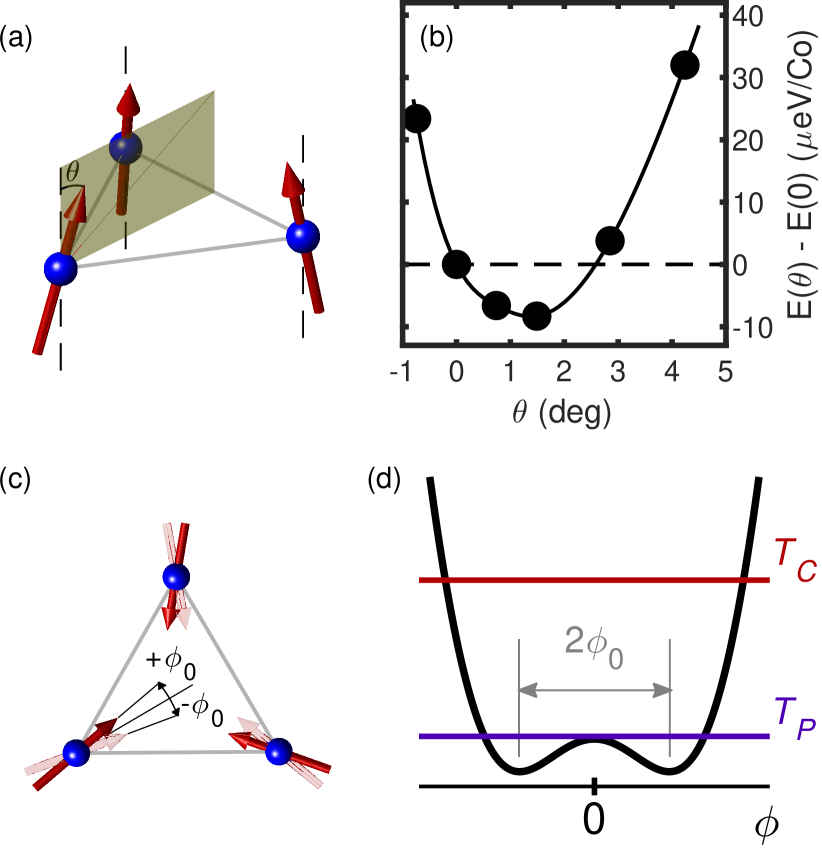
We can return now to the question of the second transition at and the development of the FM-like behavior of below . It is evident that the FM component cannot arise from the umbrella structure as presented in Figure 4a, since the spin projections onto the kagome plane are forming a 120∘ structure, which is a fully compensated AFM arrangement. Instead, we propose a further modification which involves the rotation of moments around the c-axis by an angle , Figure 4c. Given that the transition at is described within [15], such a rotation is forbidden by symmetry. However, once the temperature is lowered below and the ordered state has been established, there are no symmetry-related constraints imposed on this type of a rotation. A simple model, presented in Figure 4d, encapsulates both of these aspects. It consists of a double-well potential with a barrier height significantly lower than . Because the potential is symmetric in , the fluctuations of the order parameter within the critical region around are still described by since . Once the temperature is lowered to , the -rotations start to randomly freeze into and , giving rise to the peak in AC susceptibility and its weak frequency dependence. A very small magnetic field can switch and eventually completely polarize those projections, ultimately giving rise to the dynamic completely different from the one observed for domain walls for . Alternatively, the double-well potential could arise at , implying an additional energy scale for which there is no immediate evidence.
The value of can be estimated from the in-plane FM component which is given by . Taking that and , the amount of rotation perpendicular to the c-axis is . Such a small value of agrees with the model’s assumption of a very small energy barrier while on the other hand represents a significant challenge for DFT and can even arise from contributions not considered in our calculations. It also explains the lack of any feature in specific heat, since the entropy change across would be negligibly small compared to phonon and magnon contributions.
Our findings are based on a careful control of all experimental parameters using large, high-quality single crystals. As such, they pose severe limits to hypotheses about the coexistence of secondary phases [14, 17]. Note that those two proposals are mutually contradictory: the in-plane, AFM phase has been suggested to occur above K [14], reaching almost 70% volume fraction close to and having a different ordering temperature . On the other hand, the spin-glass phase has been hypothesized to exist below . No indication of could be found below , nor were there any evidence of the dynamics of the phase boundary between the FM and AFM volume fractions. We confirmed the weak frequency dependence at but for a true spin-glass phase the response would be expected to be more isotropic. We emphasize that many observations presented in those studies could find a natural explanation in a peculiar behavior of domain walls [7, 18].
In summary, our results resolve several outstanding issues in Co3Sn2S2. The second transition occurs at K and is related to the freezing of a small component of magnetic moments perpendicular to the -axis. The jumps observed in magnetization parallel to the -axis are revealed to be sample dependent through the effect of demagnetization. Our SOC-based DFT calculations found that the moments are slightly canted away from the c-axis, forming the umbrella configuration. The additional canting along the -angle is needed to account for the in-plane component, whose origin at the moment remains unknown.
I. Ž. acknowledges fruitful discussions with V. Ivanov, S. Savrasov, S. Acharya and M. I. Katsnelson. J.-R. Soh acknowledges support from the Singapore National Science Scholarship, Agency for Science Technology and Research. I. Ž. and J.-R. Soh acknowledge support from the ERC Synergy grant HERO (Grant ID: 810451). C.Y. and Y.S. were supported by the National Natural Science Foundation of China (No. 12004416, No. U2032204) and the Informatization Plan of the Chinese Academy of Sciences (CAS-WX2021SF-0102). R.Y. was supported by the Swiss National Science Foundation (SNSF) Sinergia network ‘NanoSkyrmionics’ (grant No. CRSII5-171003). H. M. R. acknowledges the support from SNSF Projects No. 200020-188648 and 206021-189644. First-principles calculations were performed at the Swiss National Supercomputing Centre (CSCS) under project s1008.
References
- Yan and Zhang [2012] B. Yan and S. C. Zhang, Rep. Prog. Phys 75, 096501 (2012).
- Armitage et al. [2018] N. P. Armitage, E. J. Mele, and A. Vishwanath, Rep. Mod. Phys 90, 015001 (2018).
- Savary and Balents [2016] L. Savary and L. Balents, Rep. Prog. Phys. 80, 016502 (2016).
- Nagaosa et al. [2010] N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald, and N. P. Ong, Rep. Mod. Phys 82, 1539 (2010).
- Liu et al. [2018] E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S.-Y. Yang, D. Liu, A. Liang, Q. Xu, J. Kroder, V. Süß, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Wirth, Y. Chen, S. T. B. Goennenwein, and C. Felser, Nat. Phys. 14, 1125 (2018).
- Liu et al. [2019] D. F. Liu, A. J. Liang, E. K. Liu, Q. N. Xu, Y. W. Li, C. Chen, D. Pei, W. J. Shi, S. K. Mo, P. Dudin, T. Kim, C. Cacho, G. Li, Y. Sun, L. X. Yang, Z. K. Liu, S. S. P. Parkin, C. Felser, and Y. L. Chen, Science 365, 1282 (2019).
- Schnelle et al. [2013] W. Schnelle, A. Leithe-Jasper, H. Rosner, F. M. Schappacher, R. Pöttgen, F. Pielnhofer, and R. Weihrich, Phys. Rev. B 88, 144404 (2013).
- Morali et al. [2019] N. Morali, R. Batabyal, P. K. Nag, E. Liu, X. Xu, Y. Sun, B. Yan, C. Felser, N. Avraham, and H. Beidenkopf, Science 365, 1286 (2019).
- Okamura et al. [2020] Y. Okamura, S. Minami, Y. Kato, Y. Fujishiro, Y. Kaneko, J. Ikeda, J. Muramoto, R. Kaneko, K. Ueda, V. Kocsis, N. Kanazawa, Y. Taguchi, T. Koretsune, K. Fujiwara, A. Tsukazaki, R. Arita, Y. Tokura, and Y. Takahashi, Nat. Commun. 11, 4619 (2020).
- Wang et al. [2018] Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang, and H. Lei, Nat. Commun. 9, 3681 (2018).
- Ghimire et al. [2019] M. P. Ghimire, J. I. Facio, J.-S. You, L. Ye, J. G. Checkelsky, S. Fang, E. Kaxiras, M. Richter, and J. van den Brink, Phys. Rev. Research 1, 032044 (2019).
- Xu et al. [2018] Q. Xu, E. Liu, W. Shi, L. Muechler, J. Gayles, C. Felser, and Y. Sun, Phys. Rev. B 97, 235416 (2018).
- Shen et al. [2019] J. Shen, Q. Zeng, S. Zhang, W. Tong, L. Ling, C. Xi, Z. Wang, E. Liu, W. Wang, G. Wu, and B. Shen, Appl. Phys. Lett. 115, 212403 (2019).
- Guguchia et al. [2020] Z. Guguchia, J. A. T. Verezhak, D. J. Gawryluk, S. S. Tsirkin, J.-X. Yin, I. Belopolski, H. Zhou, G. Simutis, S.-S. Zhang, T. A. Cochran, G. Chang, E. Pomjakushina, L. Keller, Z. Skrzeczkowska, Q. Wang, H. C. Lei, R. Khasanov, A. Amato, S. Jia, T. Neupert, H. Luetkens, and M. Z. Hasan, Nat. Commun. 11, 559 (2020).
- Soh et al. [2022] J.-R. Soh, C. Yi, I. Zivkovic, N. Qureshi, A. Stunault, B. Ouladdiaf, J. A. Rodríguez-Velamazán, Y. Shi, H. M. Rønnow, and A. T. Boothroyd, Phys. Rev. B 105, 094435 (2022).
- Kassem et al. [2017] M. A. Kassem, Y. Tabata, T. Waki, and H. Nakamura, Phys. Rev. B 96, 014429 (2017).
- Lachman et al. [2020] E. Lachman, R. A. Murphy, N. Maksimovic, R. Kealhofer, S. Haley, R. D. McDonald, J. R. Long, and J. G. Analytis, Nat. Commun. 11, 560 (2020).
- Lee et al. [2021] C. Lee, P. Vir, K. Manna, C. Shekhar, J. E. Moore, M. A. Kastner, C. Felser, and J. Orenstein, Observation of a phase transition within the domain walls of the magnetic Weyl semimetal (2021), arXiv:2104.13381 .
- Xu et al. [2020] Y. Xu, J. Zhao, C. Yi, Q. Wang, Q. Yin, Y. Wang, X. Hu, L. Wang, E. Liu, G. Xu, L. Lu, A. A. Soluyanov, H. Lei, Y. Shi, J. Luo, and Z.-G. Chen, Nat. Commun. 11, 3985 (2020).
- [20] See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.XXX.
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Phys. Rev. B 54, 11169 (1996).
- Kresse and Hafner [1993] G. Kresse and J. Hafner, Phys. Rev. B 47, 558 (1993).
- Vaqueiro and Sobany [2009] P. Vaqueiro and G. G. Sobany, Solid State Sci. 11, 513 (2009).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
- Chen et al. [1991] D.-X. Chen, J. Brug, and R. Goldfarb, IEEE Trans. Magn 27, 3601 (1991).
- Chen et al. [2002] D.-X. Chen, E. Pardo, and A. Sanchez, IEEE Trans. Magn 38, 1742 (2002).
- Zhang et al. [2021] Q. Zhang, S. Okamoto, G. D. Samolyuk, M. B. Stone, A. I. Kolesnikov, R. Xue, J. Yan, M. A. McGuire, D. Mandrus, and D. A. Tennant, Phys. Rev. Lett. 127, 117201 (2021).
- Solovyev et al. [2022] I. V. Solovyev, S. A. Nikolaev, A. V. Ushakov, V. Y. Irkhin, A. Tanaka, and S. V. Streltsov, Phys. Rev. B 105, 014415 (2022).
- Sandratskii [1998] L. Sandratskii, Adv. Phys. 47, 91 (1998).
I SUPPLEMENTARY MATERIAL
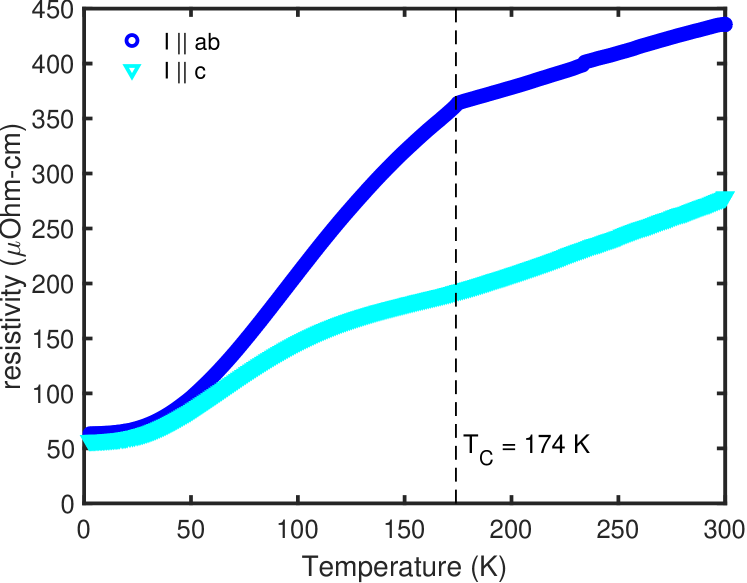
II Resistivity
Resistivity was measured with a 4-point contact method on a well defined geometry for both directions: 3 x 0.9 x 0.6 mm3 for and 2 x 1 x 0.5 mm3 for .
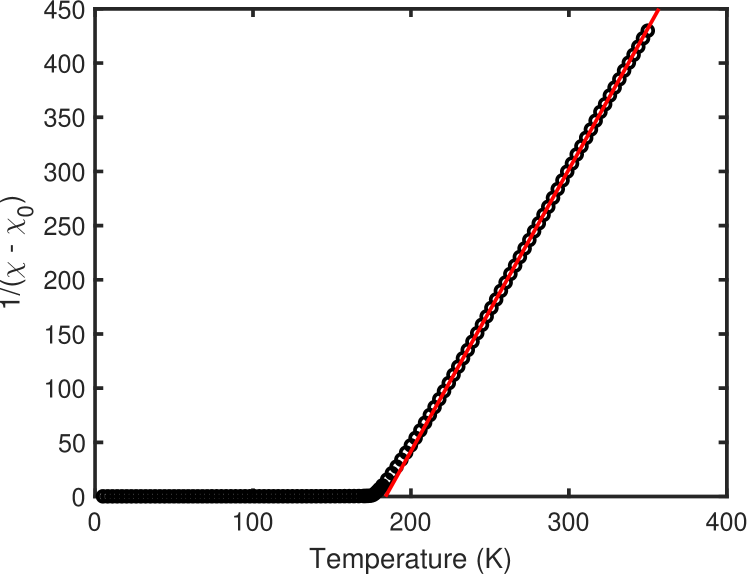
III Curie-Weiss behavior
The magnetization of the sample has been measured in T. A fit to the Curie-Weiss formula has been performed above the ordering temperature. The extracted values are emu K/mol, K and emu/mol. Here we have normalized the magnetization to the full formula unit (3 Co ions). The value of /(3 Co) should result in with , in excellent agreement with our measurements.
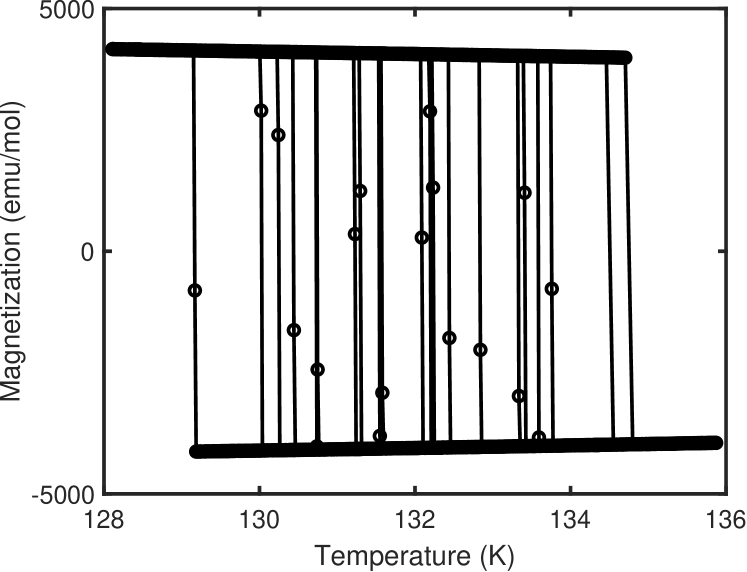
IV Magnetization reversal
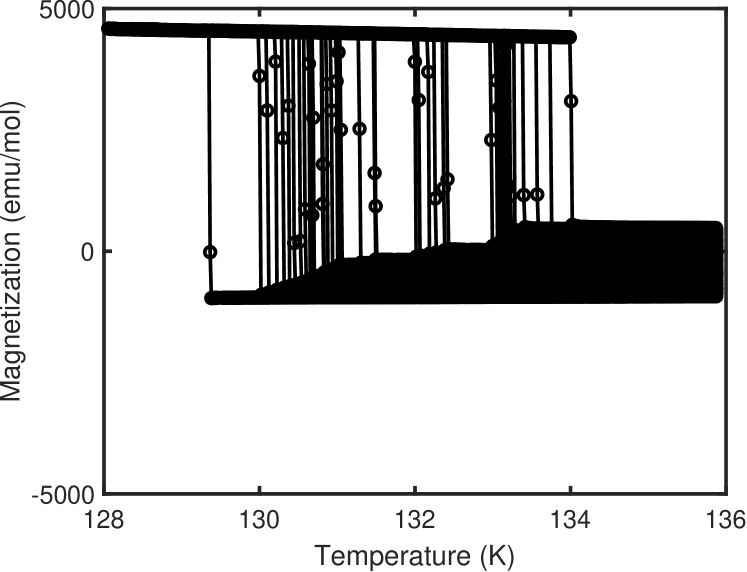
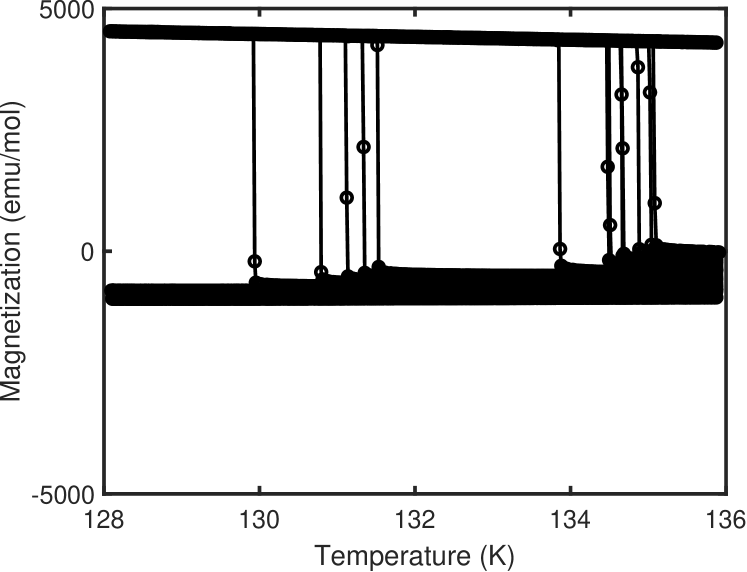
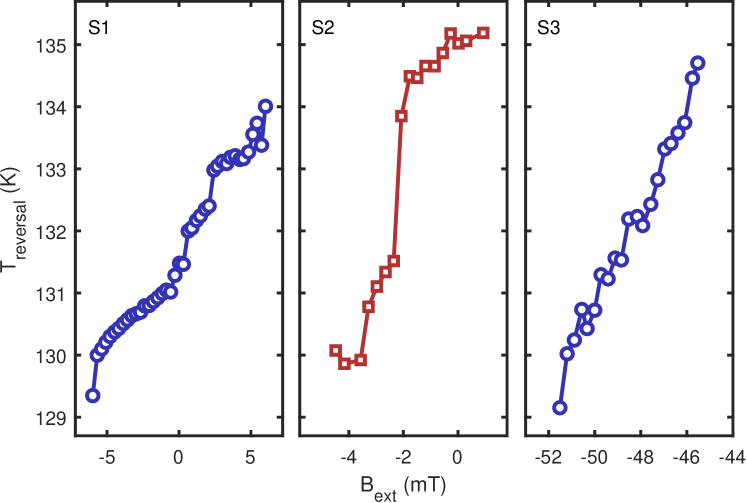
V Comparison between three samples
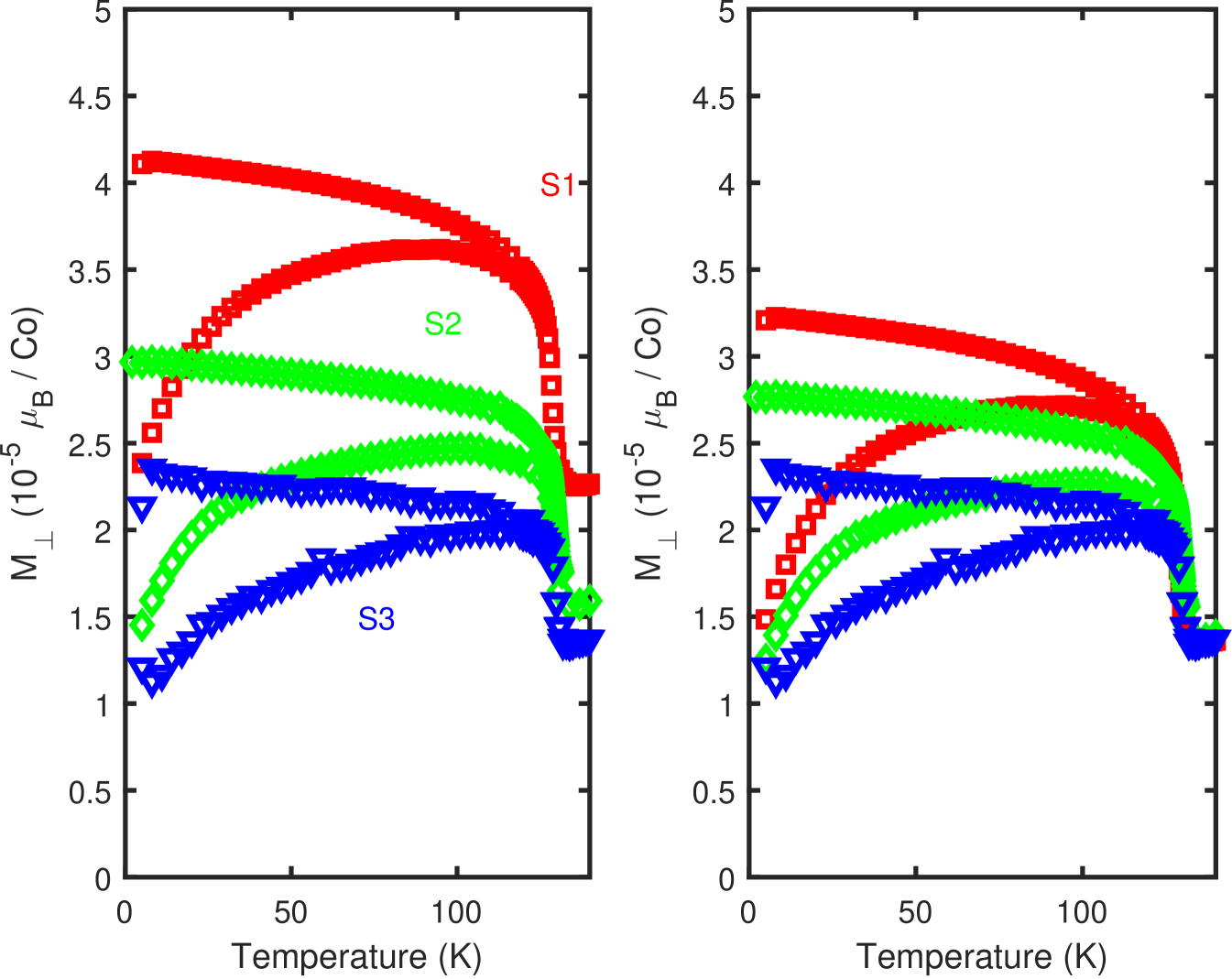
VI Angular dependence around the main transition