Unveiling the Unexplored Decay Mode of a Light Charged Higgs Boson to an Off-Shell Top Quark and a Bottom Quark
Abstract
The charged Higgs boson () with a mass below the top quark mass remains a viable possibility within the type-I two-Higgs-doublet model under current constraints. While previous LHC searches have primarily focused on the decay mode, the decay channel into an off-shell top quark and a bottom quark, , is leading or subleading for masses between 130 and 170 GeV. This study investigates the discovery potential of future colliders for this off-shell decay mode through pair-produced charged Higgs bosons decaying via . We perform signal-to-background analyses at the HL-LHC and a prospective 100 TeV proton-proton collider, employing cut-flow strategies and the Boosted Decision Tree method. However, due to the softness of the jets, signal significances fall below detection thresholds at these facilities. Extending our study to a multi-TeV muon collider (MuC), we demonstrate that a 3 TeV MuC achieves high signal significance, surpassing the threshold with an integrated luminosity of 1 ab-1, assuming a 10% background uncertainty. Specifically, for , 150, and 170 GeV, the significances are 13.7, 13.5, and 6.06, respectively. In contrast, a 10 TeV MuC requires 10 ab-1 to achieve similar results. Our findings highlight the critical role of the MuC in probing the new signal channel , offering a promising avenue for future charged Higgs boson searches involving off-shell top quarks.
I Introduction
The milestone discovery of the Higgs boson at the LHC ATLAS:2012yve ; CMS:2012qbp seemingly completes the Standard Model (SM), yet the quest for a new particle physics theory beyond the SM (BSM) continues. This pursuit is driven by unresolved fundamental questions of the Universe, such as the naturalness problem, fermion mass hierarchy, baryogenesis, non-zero neutrino masses, and the identity of dark matter. High-energy collider experiments are indispensable in this quest, offering the ability to directly study fundamental particles in a highly controlled environment and providing complementary insights to cosmological and dark matter searches.
One of the most promising BSM signals at high-energy colliders is the presence of a light charged Higgs boson with a mass below the top quark mass . This possibility remains viable under current constraints within the type-I and type-X111In type-II and type-Y 2HDM, the charged Higgs boson is tightly constrained to be as heavy as due to the measurements of the inclusive -meson decay into Misiak:2020vlo . two-Higgs-doublet model (2HDM) Aoki:2009ha ; Branco:2011iw ; Craig:2013hca ; Wang:2022yhm ; Shen:2022yuo ; Kanemura:2022ldq ; Lee:2022gyf , three-Higgs doublet model Akeroyd:2018axd , next-to-2HDM Abouabid:2021yvw , lepton-specific Inert doublet model Han:2021gfu , and scalar-triplet model Ferreira:2021bdj .
Significant efforts have been made to search for the light charged Higgs boson at the LHC and future lepton colliders. For the decay , various production channels have been explored, such as Abbaspour:2018ysj ; Demir:2018iqo ; ATLAS:2018gfm ; Sanyal:2019xcp ; Sirunyan:2019hkq ; Ghosh:2022wbe , Kim:2023lxc , Kanemura:2011kx , Duarte:2024zeh , Hernandez-Sanchez:2012vxa ; Hernandez-Sanchez:2020vax , and Aiko:2019mww . Here, denotes a new CP-even neutral Higgs boson. For the mode, the production channel of has been considered ATLAS:2013uxj ; CMS:2015yvc ; Akeroyd:2018axd ; CMS:2018dzl ; ATLAS:2021zyv ; CMS:2020osd ; Akeroyd:2022ouy . The modes have been extensively studied for production channels such as Dermisek:2012cn ; Arhrib:2020tqk ; Hu:2022gwd ; Fu:2023sng , Arhrib:2017wmo ; Mondal:2021bxa ; Arhrib:2022inj ; Kim:2022hvh ; Kim:2022nmm ; Bhatia:2022ugu ; Li:2023btx ; Mondal:2023wib , Arhrib:2021xmc ; Arhrib:2021yqf , Kausar:2020ims , Arhrib:2021xmc ; Arhrib:2021yqf ; Shen:2022yuo , Arhrib:2019ywg , Krab:2022lih , and Kang:2022mdy .
However, one important decay mode has been largely overlooked: the decay of a light charged Higgs boson into an off-shell top quark (denoted as ) and a bottom quark. In the type-I 2HDM, where the Yukawa couplings of are inversely proportional to , the decay becomes the leading mode for , with as the second leading mode. Thus, it is of great significance to investigate the discovery potential of future high-energy colliders for this decay mode. For the production of charged Higgs bosons, we consider pair production, yielding the final state of . This approach is necessitated by the stringent constraints from searches for , which limit the branching ratio to below in the type-I 2HDM.
We will rigorously investigate the discovery potential of the HL-LHC and a 100 TeV collider for the signal , employing both cut-flow strategies and the Boosted Decision Tree (BDT) method. The analysis reveals that these efforts are unfortunately unsuccessful due to the softness of the jets. Given these challenges, the focus of our research then shifts to the multi-TeV Muon Collider (MuC). This facility promises to offer a higher boost for the jets, potentially enhancing their detectability and opening new avenues for exploration.
The MuC stands out as a powerful tool for BSM searches Capdevilla:2020qel ; Bandyopadhyay:2021pld ; Sen:2021fha ; Asadi:2021gah ; Huang:2021nkl ; Choi:1999kn ; Han:2020uak ; Han:2021udl ; Jueid:2021avn ; Han:2022edd ; Black:2022qlg ; Belfkir:2023vpo ; Jueid:2023zxx , thanks to its clean collision environment, higher energy reach, reduced beamstrahlung, and efficient energy use. The prospects of the MuC program have been significantly enhanced by recent advancements in addressing critical challenges, such as cooling muon beams Antonelli:2013mmk ; Antonelli:2015nla and reducing beam-induced backgrounds (BIB) Collamati:2021sbv ; Ally:2022rgk .
Our study will conduct a signal-to-background analysis for two collider configurations: with a total integrated luminosity of and with a total integrated luminosity of . The analysis aims to demonstrate that the entire mass range of can achieve a high signal significance, surpassing the discovery threshold. These findings represent our main contributions to the study of the light charged Higgs boson.
The paper is organized as follows. In Sec. II, we briefly review the type-I 2HDM with CP invariance and softly broken parity. Based on the results of random scans incorporating theoretical and experimental constraints, we investigate the characteristic features of the allowed parameters and suggest the golden channel to probe the unexplored decay mode, . Section III deals with the signal-to-background analysis at the HL-LHC and a 100 TeV collider, incorporating comprehensive cut-based analysis and the BDT. In Sec. IV, we turn to the multi-TeV MuC and perform the signal-to-background analysis. Conclusions are presented in Sec. V.
II Brief review of the light charged Higgs boson in type-I 2HDM
The 2HDM introduces two complex Higgs doublet scalar fields, and , with hypercharge Branco:2011iw :
| (3) |
where and denote the non-zero vacuum expectation values of and , respectively. The ratio of to defines the mixing angle through . The electroweak symmetry is spontaneously broken by .
To prevent flavor-changing neutral currents at the tree level, a discrete symmetry is imposed, under which and Glashow:1976nt ; Paschos:1976ay . Assuming CP invariance and allowing for softly broken parity, the scalar potential is defined as follows:
In 2HDM, there are five distinct physical Higgs bosons: the lighter CP-even scalar , the heavier CP-even scalar , the CP-odd pseudoscalar , and a pair of charged Higgs bosons . The relationships between these Higgs states and the weak eigenstates described in Equation 3 are determined by two mixing angles, and , which can be found in Ref. Song:2019aav . The SM Higgs boson is a linear combination of and , specifically as .
According to the assignment of parity to the right-handed fermions, the model has four variants, type-I, type-II, type-X, and type-Y. The mass of in type-II and type-Y is heavily constrained by the measurements of the inclusive -meson decay into , requiring Misiak:2020vlo . Only type-I and type-X allow for the existence of charged Higgs bosons lighter than the top quark. Therefore, we focus on type-I in this study.
We employ two popular conditions: the Higgs alignment limit for the SM-like Higgs boson Carena:2013ooa ; Celis:2013rcs ; Cheung:2013rva ; Bernon:2015qea ; Chang:2015goa ; Das:2015mwa ; Kanemura:2021dez and the mass degeneracy of and for the electroweak precision data Kanemura:2011sj ; Chang:2015goa ; Chen:2019pkq . The Higgs alignment limit precludes the decay channel . Furthermore, we restrict our analysis to scenarios where the charged Higgs boson is lighter than and . Under this condition, the charged Higgs boson decays exclusively into fermion pairs, ensuring that the mode maintains a significant branching ratio. Conversely, if , the decay modes become accessible222For a detailed phenomenological study of the scenario where , see Ref. Sanyal:2023pfs ., suppressing the branching ratio of .
In summary, our model configuration is as follows:
| (5) |
The Yukawa couplings of the charged Higgs boson to the SM fermions in type-I 2HDM are given by
| (6) |
where . Because these Yukawa couplings have a common factor of , the branching ratio of is independent of .
We also present the gauge interactions of a pair of charged Higgs bosons, crucial for the pair production at high-energy colliders Branco:2011iw :
| (7) | ||||
where , , and is the electroweak mixing angle.
To study the characteristics of the permissible parameter space for the light charged Higgs boson that predominantly decays into , we set and perform a random scan within the following parameter ranges:
| (8) |
The scan is conducted while imposing both theoretical requirements and experimental constraints.
For the theoretical requirements, we enforce conditions ensuring vacuum stability Ivanov:2008cxa ; Barroso:2012mj ; Barroso:2013awa , a bounded-from-below Higgs potential Ivanov:2006yq , tree-level unitarity in scalar-scalar scatterings Branco:2011iw ; Arhrib:2000is , and perturbativity of the Higgs quartic couplings Chang:2015goa . These conditions are evaluated using the public code 2HDMC Eriksson:2009ws . Additionally, we require that the cutoff scale exceed , where the cutoff scale is defined as the energy level at which any of the conditions for tree-level unitarity, perturbativity, or vacuum stability is violated Kim:2023lxc . The evolution of the model parameters via the renormalization group equations is facilitated using the public code 2HDME Oredsson:2018yho ; Oredsson:2018vio .
For the experimental constraints, we incorporated measurements at the 95% confidence level, encompassing inclusive -meson decay into Arbey:2017gmh ; Sanyal:2019xcp ; Misiak:2017bgg and direct search bounds from LEP, Tevatron, and LHC experiments. For the direct search constraints, we have employed the public code HiggsBounds-v5.10.2 Bechtle:2013wla . Notably, our adoption of the Higgs alignment limit ensures that the Higgs precision data at the LHC are inherently satisfied.
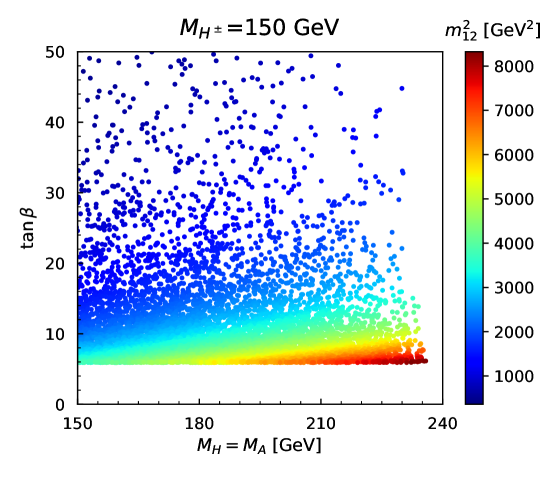
In Figure 1, we present the allowed parameter points in the plane for the given . The color code denotes . A notable feature is the upper bound on the masses of and , with . Although our focus in this paper is on the charged Higgs boson, the relatively low upper bounds on suggest promising discovery prospects for the heavy neutral Higgs bosons at high-energy colliders. Additionally, we observe lower bounds on , specifically .
Now, let us identify the optimal production mechanism at the LHC for the light charged Higgs boson. LHC searches have primarily focused on its production through top quark decay, , followed by ATLAS:2018gfm ; Sirunyan:2019hkq because the Yukawa couplings of are proportional to the fermion mass with a common coupling modifier . Despite comprehensive searches, no new signals have been observed, leading to stringent upper limits on the product of the two branching ratios, . As depends solely on for the given , the observed upper bound strictly limits . For , must be below . Consequently, leveraging top quark decay for production proves ineffective.
Given this constraint, the production channels of via the decay of heavier Higgs states, such as , have been extensively investigated Arhrib:2017wmo ; Mondal:2021bxa ; Arhrib:2021xmc ; Cheung:2022ndq ; Bhatia:2022ugu ; Kim:2022hvh ; Kim:2022nmm ; Arhrib:2022inj ; Kim:2023lxc ; Li:2023btx ; Mondal:2023wib . The production of or occurs through gluon fusion () or associated production (, ). However, the signal rates are sensitive to model parameters, such as and . Furthermore, the allowed parameter space shown in Figure 1 does not permit the on-shell decay , preventing the effective suppression of backgrounds by exploiting the boson mass constraint.
A more promising production mechanism is the pair production of charged Higgs bosons via the Drell-Yan process. This channel offers a straightforward and model-independent avenue for production, as the production cross section is exclusively determined by the mass of the charged Higgs boson. Although this production channel has been studied for the decays Duarte:2024zeh and Arhrib:2021xmc ; Arhrib:2021yqf ; Shen:2022yuo , it has not been explored for our target decay mode . Therefore, we focus our analysis on the pair production channel for the decay mode.
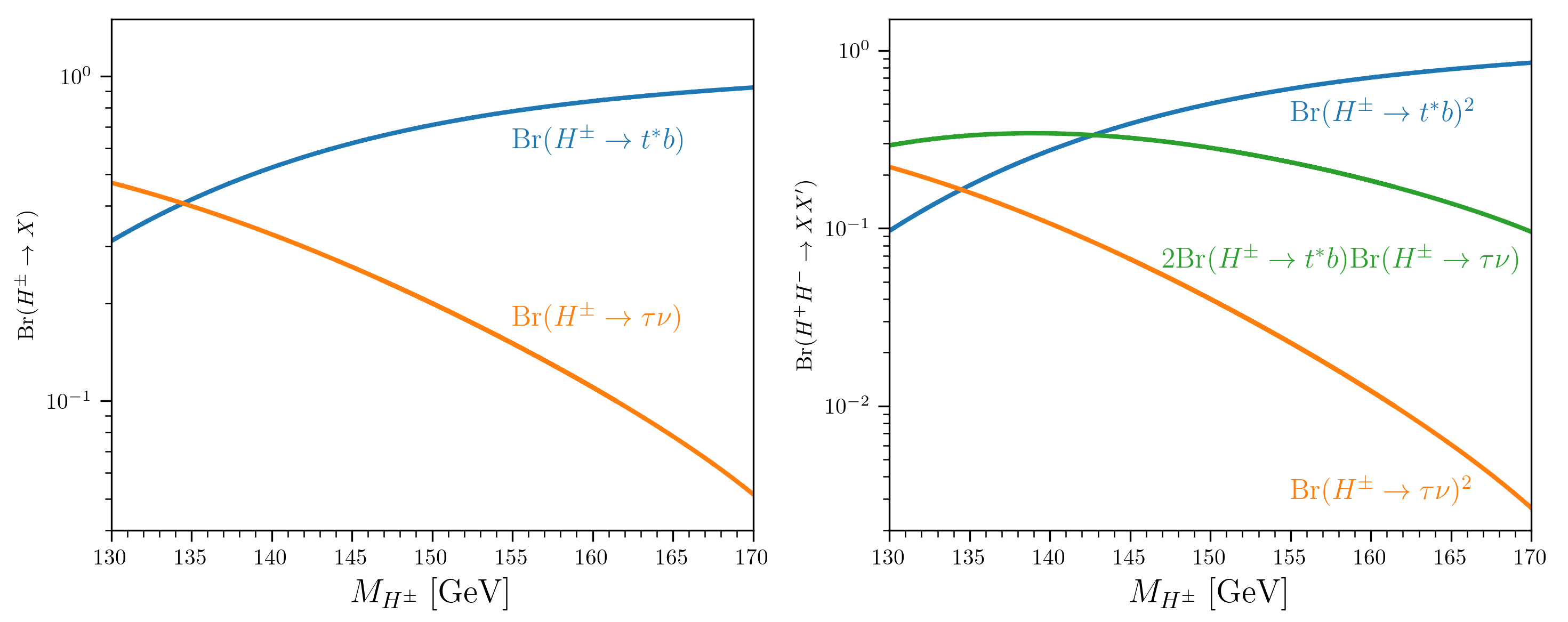
Let us delve into the decay of the light charged Higgs boson in the mass range between 130 GeV and 170 GeV. There are two dominant decay channels, and . Figure 2 depicts their branching ratios as functions of , comparing scenarios with a single charged Higgs boson (left panel) and a pair of charged Higgs bosons (right panel). Note that these results are independent of , , or . For the decay, we incorporate QCD radiative corrections to order in the scheme, employing the 2HDMC Eriksson:2009ws . This includes adjustments for running fermion masses in the Higgs couplings, applying leading logarithmic corrections across all orders with the renormalization scale .
The decay mode exhibits significant branching ratios throughout the target range and becomes dominant if GeV. For GeV, becomes the subleading decay channel, with being the leading one. In the pair production of charged Higgs bosons, plays a more significant role. The mode is leading for GeV. Interestingly, the process emerges as the most prominent for GeV and remains the second most dominant for GeV, which benefits from a combinatorial factor of two. In contrast, the final state, heavily emphasized in prior studies for lighter , exhibits markedly reduced branching ratios.
The results in Figure 2 strongly support investigating the off-shell mode as a potential discovery channel for the light charged Higgs boson within the mass range in 130 to . Since the final state faces challenges from the combinatoric complications and the larger QCD backgrounds at the LHC, our investigation targets the following discovery channel for the light charged Higgs boson in the mass range of 130 to 170 GeV:
| (9) |
III at the HL-LHC and a 100 TeV collider
In the preceding section, we identified the pair production of charged Higgs bosons, followed by , as a key channel for probing the light charged Higgs boson in the mass range of . This section explores the discovery potential of the HL-LHC and a prospective 100 TeV collider, focusing on the case with . For the decay of the off-shell top quark, we consider the hadronic decay channel of the boson. Our signal process is summarized as:
| (10) |
where , denotes a light quark jet, and the particles in a square bracket represent decay products originating from the same parent particle. The resultant final state includes two jets, two jets, a tau lepton, and missing transverse energy. The primary background originates from top quark pair production:
| (11) |
For the simulation of the signal and background, we followed a comprehensive procedure. We first calculated parton-level cross sections at the 14 TeV LHC using MadGraph5-aMC@NLO Alwall:2011uj version 3.5.0 with the PDF set to NNPDF31_nlo_as_0118, setting both the renormalization and factorization scales as . We generated signal events and background events. Next, we applied NLO corrections for the signal and approximate N3LO corrections for the background by incorporating the -factor Kim:2024ppt . The parton-level cross sections were determined to be for the signal and for the background.
Parton showering and hadronization were performed using Pythia version 8.309 Bierlich:2022pfr . For the detector-level analysis, a fast detector response simulation was employed with Delphes deFavereau:2013fsa using the high-luminosity LHC card, delphes_card_HLLHC.tcl. Jet clustering was conducted with FastJet version 3.3.4 Cacciari:2011ma using the anti- algorithm with a jet radius of .
Accurate identification of the final state in Equation 10 critically depends on -tagging and -tagging procedures. A jet is designated as a jet if a hadron with is detected within a radius of the jet. Candidate jets are required to meet the threshold of and , after which the -tagging efficiency is applied. Charm and other light quark jets can be mistagged as jets. The efficiencies for tagging and mistagging depend on the jet’s kinematics and are approximately ATL-PHYS-PUB-2016-026 ; ATL-PHYS-PUB-2017-001 :
| (12) |
Identification of the tau lepton is feasible when it decays hadronically, denoted as , marked by a collimated jet with a sparse number of hadrons CMS:2007sch ; Bagliesi:2007qx ; CMS:2018jrd . The Delphes default settings for tagging and mistagging efficiencies were applied, which are approximately
| (13) |
After completing the detector simulation, the following basic selection criteria are imposed:
-
•
, , and , where , , and satisfy GeV and ;
-
•
GeV.
The presence of neutrinos in the decay chain of necessitates a minimum threshold for the missing transverse energy .
Despite the relatively loose selection criteria, the basic selection results in an exceedingly low acceptance rate for the signal, approximately 1%. In contrast, the background acceptance rate is substantially higher, around 2.7%. With the suppressed signal cross section after the basic selection being only , even the final projected luminosity of at the HL-LHC would result in merely a few hundred signal events. This scarcity of signal events severely limits the ability to devise an effective strategy using kinematic cuts to disentangle the signal from the backgrounds, irrespective of their efficiency.
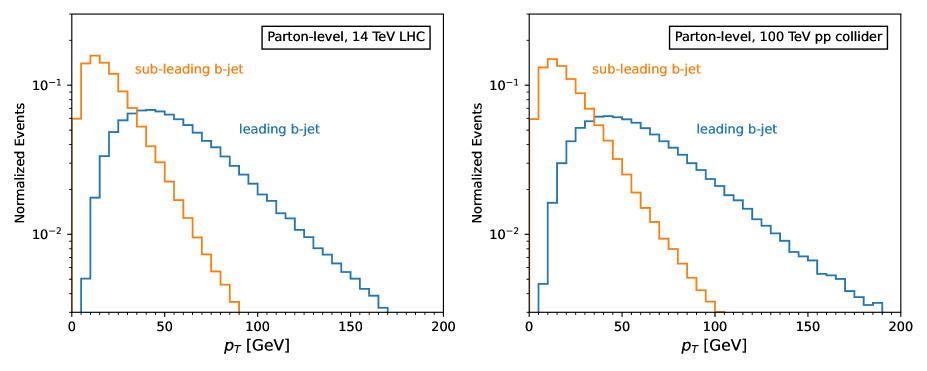
A primary factor contributing to the low signal acceptance after basic selection is the low transverse momentum (softness) of the jets originating from the decay . This softness is due to the small mass difference between and , which is crucial for ensuring a substantial branching ratio for the decay mode, as depicted in Figure 2. Additionally, the quark from the decay of the off-shell top quark, , also exhibits lower transverse momentum compared to its on-shell counterpart. The challenge with these soft jets is that the majority of the subleading jets fail to meet the minimum transverse momentum threshold () required for jet clustering.
To illustrate the softness of the jets, we present in Figure 3 the parton-level distributions of the leading and subleading jets for the signal process. We order jets by their descending . The left panel shows the results at the 14 TeV LHC, while the right panel displays the results for a 100 TeV collider. It is evident that approximately 70% of the subleading jets fail to surpass the threshold. This minimum threshold for jets cannot be relaxed because it plays a pivotal role in jet clustering algorithms, primarily aimed at reducing noise from low-energy particles, suppressing background, and enhancing computational efficiency. Moreover, lowering this threshold is counterproductive for the signal-to-background analysis, as the background acceptance would increase more than the signal acceptance.
Even at a higher collision energy of 100 TeV, as shown in the right panel, both the leading and subleading jets remain as soft as those at the HL-LHC. The jets do not receive a substantial boost because parton-parton collisions at hadron colliders do not fully utilize the beam energy.
Given the limited number of signal events after the basic selection, we need to devise a strategic approach using kinematic cuts that retain as many signal events as possible while effectively suppressing the backgrounds. With this goal in mind, we examined various kinematic distributions and identified key variables that could discriminate the signal from the background.
One set of crucial discriminating variables are the angular separations, defined by , among jets and light jets. These variables are efficient because the signal channel results in a smaller angular separation within the grouping. In contrast, the background channel forms a back-to-back topology between and , leading to a larger between two jets as well as a larger between and the in the system.
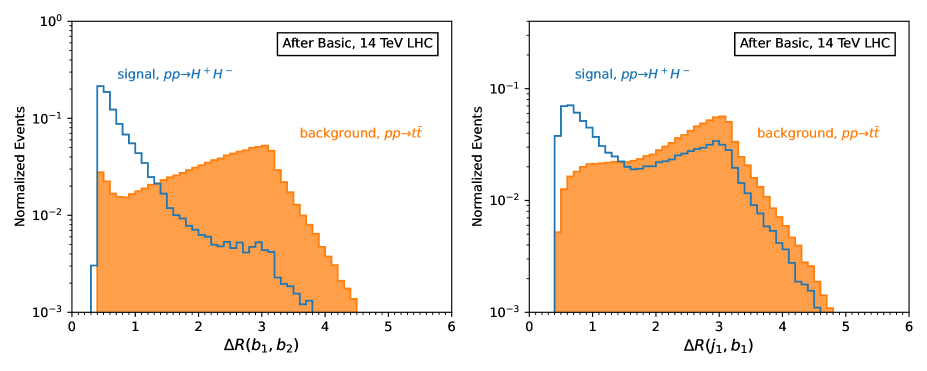
In Figure 4, we present normalized distributions of two representative angular separations: in the left panel and in the right panel. For the signal , the distribution peaks near 0.4, indicating the close proximity of the two jets originating from the same parent particle . In contrast, the background exhibits a broader distribution with a dominant peak near 3. This reflects the back-to-back motion of two jets, each originating from a different parent top quark. Moreover, the distributions further highlight differences between the signal and background. The signal’s distribution peaks at a lower value of approximately 0.8, whereas the background peaks at higher values near 3.
Based on these distinct features in the angular separation distributions, we impose the following cuts to suppress the background while retaining a significant fraction of the signal events:
| (14) |
Other crucial discriminating variables pertain to the reconstruction of the charged Higgs boson mass . In the signal process , can be measured in two complementary ways: through the invariant mass of the system and the transverse mass derived from the system. The transverse mass is a useful variable defined for a visible particle and the missing transverse energy , where covers all observed particles:
| (15) |
where .
For the signal process , with the visible particle being the tau lepton, is expected to peak at the charged Higgs boson mass . Since both the invariant mass and the transverse mass should reconstruct the same for the signal events, we define an asymmetry variable to quantify the difference between these two mass observables:
| (16) |
By imposing an appropriate upper bound on , we can efficiently separate the signal from the background.
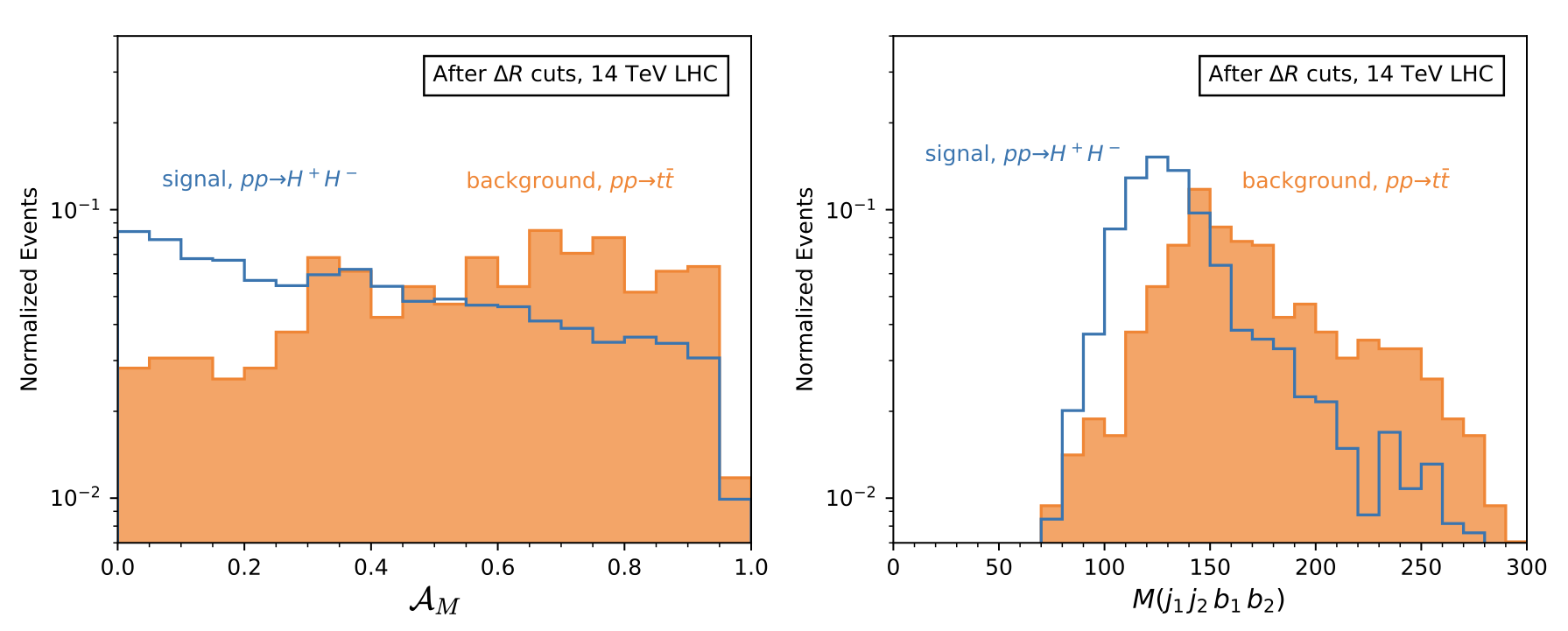
In Figure 5, we present the normalized distributions of (left) and the invariant mass (right) for the signal with (blue) and the background (orange), after imposing the cuts in Equation 14. Two distinct features are evident. First, as expected, the distribution for the signal peaks sharply at , while the background prefers larger values above 0.2. Imposing an upper bound on will efficiently separate the signal events from the background.
The second notable feature is observed in the invariant mass distribution . For the signal, it exhibits a resonance peak around 130 GeV, which is lower than the true charged Higgs boson mass of 150 GeV. This discrepancy is attributed to several factors, including neutrinos in meson decays, imperfect jet energy resolution, and gluon radiation not fully captured within the jet clustering cone. Despite this shift, the resonance peak in the distribution provides a distinct signature for the signal process.
| Cut-flow for at the 14 TeV LHC | |||
| [fb] | [fb] | ||
| Basic Selection | |||
To evaluate the discovery potential for this channel, we present in Table 1 the cut-flow for the signal process at the 14 TeV LHC. The table shows the cross sections of the signal and background after each cut, as well as the significance considering a 10% background uncertainty for an integrated luminosity of . The significance is defined as:
| (17) |
where denotes the number of signal events, the number of background events, and the background uncertainty yield.
Despite applying the key kinematic cuts, the final significance reaches only 0.19. While our final selection cut boosts the signal significance by approximately 300-fold relative to the basic selection phase, the significance remains substantially below a detectable level. Moreover, the signal cross section after the final selection, approximately , precludes any further refinements through cuts. This cut-based analysis highlights the challenges in probing the charged Higgs boson through the channel at the HL-LHC using kinematic cuts alone, due to the extremely small signal cross section and overwhelming backgrounds.
To assess if the BDT method can enhance sensitivity to the decay mode of the light charged Higgs boson, we employed the Extreme Gradient Boosting (XGBoost) package Chen:2016btl . XGBoost has seen increasing use in the particle physics community for a variety of analyses, including studies on the SM Higgs boson ATLAS:2017ztq ; CMS:2020tkr ; ATLAS:2021ifb ; CMS:2020cga ; CMS:2021sdq , dark matter ATLAS:2021jbf , vectorlike quarks Dasgupta:2021fzw , a composite pseudoscalar Cornell:2020usb , and innovative strategies for faster event generation Bishara:2019iwh . In our study, XGBoost was used as a binary classifier, aimed at more effectively distinguishing between signal and background events.
We initialized the XGBoost classifier with the objective set to binary and the evaluation metric set to logloss. The learning rate was configured at 0.1. For training the model, we generated signal events and background events, all of which met the basic selection criteria. We divided the dataset into three parts: 50% for training, 20% for validating the algorithm, and 30% for testing. As inputs for the XGBoost model, we used the following 50 variables:
-
1.
Angular distance: , , , , , , , , , , , , , , , , , , , .
-
2.
Invariant mass : , , , .
-
3.
Transverse mass of : , , .
-
4.
Four momentum of for each of , , , , .
-
5.
Missing transverse energy and Missing energy azimuthal angle: , .
-
6.
Mass asymmetry: .
Here, the multiple particle symbol represents the system consisting of the constituent particles. For example, the term refers to a system whose momentum is the vector sum of the momenta of and .
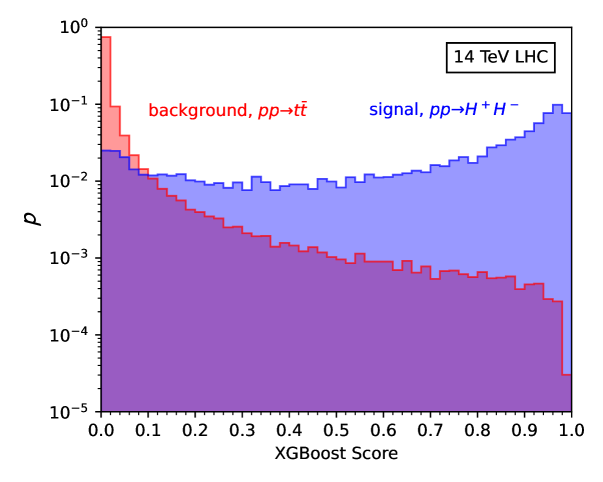
In Figure 6, we illustrate the distributions of BDT scores for both the signal (in blue) and the background (in red). These results are derived exclusively from the testing dataset, which the model did not encounter during its training and validation phases. The BDT score distributions reveal a discernible separation between the signal and background. Applying a threshold of 0.98 for the XGBoost score results in cross sections of for the signal and for the background. Considering a 10% background uncertainty and an integrated luminosity of , the signal significance reaches 1.35.
Although the signal significance in the BDT analysis shows a roughly sevenfold increase compared to the significance in the cut-based analysis, it remains below the threshold for a confident detection. This challenge is primarily due to the soft jets in the signal events, which fail to satisfy the basic selection.
To explore whether a 100 TeV collider could offer higher discovery potential for the signal, we conducted signal-to-background analyses for the same process, , using the Delphes card FCChh.tcl. Unfortunately, the issue of excessively soft -jets persists even at a 100 TeV collider, failing to yield a significance above the detection threshold.
Our cut-based analysis, employing sequential kinematic cuts of (with ), , , , , , and , results in a significance of only 0.38 at a 100 TeV collider. Moreover, the BDT analysis underperforms compared to the HL-LHC, with the signal significance reaching merely about 0.75.
In conclusion, high-energy hadron colliders, such as the HL-LHC and a prospective 100 TeV collider, cannot effectively probe the decay mode of the light charged Higgs boson due to the inherent softness of the -jets in this channel. This limitation highlights the need for alternative approaches or collider technologies to investigate this particular decay mode of the light charged Higgs boson.
IV at a Multi-TeV Muon Collider
In the previous section, we demonstrated that the proposed signal process at the HL-LHC yields very low significance, reaching only 1.35 even with BDT analysis. This low significance is primarily due to the jets from the decay being too soft for effective reconstruction. Additionally, a 100 TeV collider cannot adequately boost the jets as the beam energy is not fully transferred to the parton-parton collision. Consequently, we shift our focus to a multi-TeV MuC, which fully harnesses the beam energy in collisions between two fundamental particles. We target two configurations: with an integrated luminosity of and with an integrated luminosity of Han:2021udl ; AlAli:2021let .
For the production of charged Higgs bosons, we consider their pair production with the following final state:
| (18) |
At the MuC, there are three different production channels relevant to this final state:
| (19) | ||||
| (20) | ||||
| (21) |
where and include all three neutrino flavors, and denotes a forward muon with .
The first process in Equation 19 is the Drell-Yan process mediated by the boson and photon. The second process in Equation 20 involves pair production associated with a pair of neutrinos. Since these additional neutrinos manifest as missing transverse energy, they create the same phenomenological signature as the final state with a single neutrino, making it indistinguishable from the first process. For this process, there are numerous Feynman diagrams, including those involving and . Additionally, Vector Boson Scattering (VBS) processes such as , VBS processes through the quartic vertex --- in Equation 7, and VBS processes through the -channels mediated by and also contribute.
The third process in Equation 21 involves pair production associated with two forward muons. In the conventional detector design of a multi-TeV MuC, forward muons are not detectable333Recently, the integration of forward muon detectors into the MuC’s design has been initiated within the MuC community, as the energetic forward muons can penetrate the tungsten nozzles. This forward muon detector is highly expected to play a crucial role in probing various BSM models Accettura:2023ked ; Ruhdorfer:2023uea ; Forslund:2023reu ; Bandyopadhyay:2024plc . because they fall outside the pseudorapidity coverage limit of . This limitation is due to tungsten nozzles designed to shield the detector from BIB particles Collamati:2021sbv ; Ally:2022rgk . This neutral-current VBS process occurs through , the quartic vertex ---, and the -channels mediated by and .
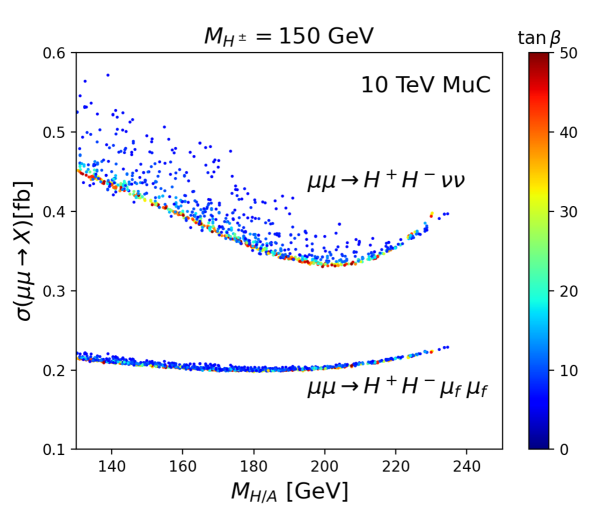
Let us discuss the dependence of cross sections for and on model parameters. Unlike the Drell-Yan process, these two associated production processes include contributions mediated by and , making their cross sections potentially sensitive to . Additionally, VBS contributions through to and to , though not dominant, introduce dependences on .
Figure 7 illustrates parton-level cross sections as a function of for the processes and with at . The color codes denote . The analysis considers parameter points allowed by theoretical and experimental constraints discussed in Sec. II. For forward muons , we apply the condition . The lower bound of ensures that forward muons fall outside the conventional pseudorapidity coverage limit. The upper bound of is implemented to manage cross section divergence that occurs as the scattering angle approaches 0 or , a consequence of -channel photon-mediated diagrams. Typically, this divergence is canceled by higher-order QED corrections, particularly from soft photon emissions. In practice, such divergences are often handled by imposing a minimum scattering angle cut during data analysis. Considering the high collision energy at the MuC, we constrain the scattering angle to , which corresponds to .
Figure 7 clearly demonstrates that both processes exhibit modest dependence of cross sections on the model parameters and . Notably, the cross section for remains nearly constant across the allowed parameter space, varying by only about 10%. In contrast, the cross section for shows a more pronounced dependence on the model parameters, with variations of approximately 70%. For a given , the cross section initially decreases as increases, reaches a minimum at , and then rises again.
Given these observations, we adopt a conservative approach by selecting , , and for our signal-to-background analysis. This choice represents a pessimistic scenario, ensuring that if we achieve signal significance above the discovery potential, it would guarantee the accessibility of the entire parameter space through our target signal .
| Cross sections of the pair production of charged Higgs bosons at the MuC | ||||||
We now compare the cross sections of the three production channels for the charged Higgs mass:
| (22) |
Table 2 presents the parton-level cross sections at 3 TeV and 10 TeV MuC for , , and . We used MadGraph5_aMC@NLO version 3.5.0.
The Drell-Yan process exhibits nearly constant cross sections for different values at a given : approximately 3 fb at and 0.3 fb at . This consistency is due to the relatively light compared to the multi-TeV collision energy. The marked decrease in cross sections from to illustrates the typical behavior of Drell-Yan cross sections, which are inversely proportional to the square of the beam energy. In contrast, the cross sections for the second and third processes moderately increase with increasing . This opposing trend is characteristic of VBS processes, whose cross sections increase according to Han:2021udl .
The relative importance of the three production channels varies with collision energy. At , the Drell-Yan process dominates, yielding the highest cross section. Meanwhile, the processes involving two forward muons and those with two neutrinos exhibit comparable cross sections. However, this hierarchy changes at . In this higher energy regime, emerges as the dominant process, exhibiting the largest cross section. The Drell-Yan process becomes the second most significant, while now shows the smallest cross section among the three channels. Despite this, we will demonstrate that even at , the Drell-Yan production remains dominant after the final selection.
Next, we present the signal-to-background analysis at the detector level. We conducted showering with Pythia version 8.307. A rapid detector simulation was performed using Delphes version 3.5.0, utilizing the delphes_card_MuonColliderDet.tcl card.444It is accessible at https://github.com/delphes/delphes/blob/master/cards/delphes_card_MuonColliderDet.tcl the MuC Delphes card accommodates slightly different values for the tagging and mistagging rates compared to those for the HL-LHC: for , , , and .
For jet clustering, we employed the exclusive Valencia algorithm Boronat:2014hva ; Boronat:2016tgd , implemented in FastJet. This algorithm is particularly well-suited for high-energy lepton colliders due to its adept handling of initial state radiation and beam-induced backgrounds by incorporating beam jets. We chose the exclusive clustering setting for two primary reasons. First, it is more efficient for signals with a predefined number of jets, such as our signal , which requires five jets. The exclusive algorithm terminates jet clustering when the jet count matches the specified number of jets. Second, the inclusive algorithm is often ineffective for our signal jets since it can easily miss very close jets due to its requirement for a minimum distance between any two jets. Our signal jets, originating from the decay of the same parent particle produced at the multi-TeV MuC, tend to have a small jet radius and thus can fail to be selected by the inclusive algorithm. To overcome this, we implemented the exclusive Valencia Algorithm with a jet radius of and .
To discuss the potential SM backgrounds for the final state at the MuC, we first note that producing the system requires the presence of a boson. Since the boson must be pair-produced at the MuC, the two light jets in the final state originate from the decay of the other boson. Considering the possibility of light quark jets being misidentified as jets, we identify two primary background processes: and . It is worth noting that the process encompasses top quark pair production, whereas includes the contribution from . After applying -jet mistagging rates, we found that the contribution from the process is negligible. Therefore, we identify as the main background for the final state.
Brief comments on BIB are in order here. Beam-induced backgrounds arise from the decay of muons in the beam, which produces electrons and positrons. As these interact with machine components, various secondary particles such as photons, electron-positron pairs, hadrons, and neutrinos are generated. Many of these secondary particles result from forward scattering, causing most BIB particles to be directed along the beam and to have low energies, typically below 1 GeV Bartosik:2024ulr . Given that our final state requires five hard jets in the central region, BIB are of negligible concern. Thus, we do not consider BIB a significant background for our analysis of the final state at the MuC.
We establish the following basic selection criteria:
-
•
Jet multiplicity: Exactly 2 light jets and 2 -jets, along with one hadronically decaying tau lepton, with transverse momentum GeV and pseudorapidity for all QCD jets and the tau jet.
-
•
Missing transverse energy: GeV.
-
•
Lepton veto: Events containing any electrons or muons with GeV and are vetoed to suppress backgrounds from leptonic decays of bosons.
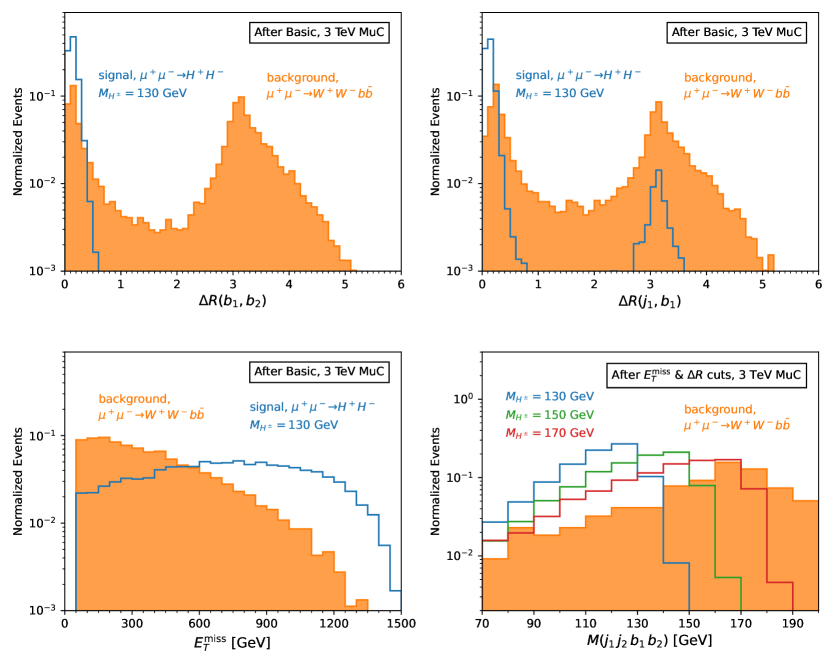
To establish an effective cut-flow, we begin with a detailed analysis of the key kinematic variables that differentiate signal from background. The normalized distributions of the most critical variables are presented in Figure 8: in the upper-left panel, in the upper-right panel, in the lower-left panel, and in the lower-right panel. The signal distributions are depicted as solid lines, while the background distributions are shown as orange histograms. The and distributions are presented after applying the basic selection criteria, for the representative case of GeV. For the distribution, we show the results for (blue), 150 GeV (green), and 170 GeV (red) after imposing , , and .
The distribution in Figure 8 clearly shows that this variable is highly discriminating for separating the signal from the background. In the signal events, the two -jets are typically adjacent, originating from the decay of the same parent . In contrast, the background exhibits a broader distribution with larger angular separations between the two -jets. A stringent criterion of is effective in isolating the signal from the background.
Similarly, the angular separation between the leading light jet and the leading -jet, , exhibits a distinct pattern for the signal compared to the background. The signal distribution shows a prominent primary peak at , reflecting the fact that and originate from the same decay. This feature is consistently observed in other combinations, such as , , and , as expected from the kinematics of the signal process. Unexpectedly, a secondary peak is observed at higher values around in the signal distribution. We found that it arises from occasional misidentification between light jets and tau-jets. Despite the presence of this small secondary peak, a loose cut of for is still effective in enhancing the signal over the background by retaining the prominent primary peak region.
Another crucial discriminating variable is the missing transverse energy, shown in the lower-left panel of Figure 8. The signal exhibits a significantly higher distribution compared to the background, attributed to the different production mechanisms and mother particles of the neutrino. In the signal process, the system originates from the decay of a charged Higgs boson produced through a scattering process at the MuC. The large energy transfer to the results in a highly energetic neutrino from its subsequent decay, leading to substantial missing transverse energy in the final state. In contrast, the background process involves a boson produced through a scattering process, which inherently results in a softer energy transfer to the and, consequently, a less energetic neutrino from its decay. As a result, a stringent cut of GeV is highly effective in enhancing the signal significance.
Finally, we present the invariant mass distribution constructed from the two leading -jets and two leading light quark jets in the lower-right panel of Figure 8 for GeV (blue), 150 GeV (green), and 170 GeV (red). To demonstrate the efficiency of our proposed cuts on and in revealing the invariant mass peaks over the background distributions, we show the distributions after imposing the requirements , for , and GeV. We observe distinct resonance peaks in the signal distributions, although the peak positions appear slightly below the true charged Higgs boson mass, primarily due to smearing effects in reconstructing the two -jets and two light jets from the decays. The background distribution also exhibits a peak marginally above the top quark mass, largely attributable to contributions from top quark pair production.
| Cut-flow for at a 3 TeV MuC with | |||||||
| Cut | [fb] | ||||||
| [fb] | [fb] | [fb] | |||||
| Basic | 0.600 | ||||||
| 1.19 | |||||||
| 6.23 | 2.50 | ||||||
| 8.38 | 3.50 | ||||||
| 8.50 | 3.57 | ||||||
| 11.2 | 4.95 | ||||||
| 11.3 | 4.99 | ||||||
| 13.5 | 6.06 | ||||||
Based on the observations from the key kinematic variable distributions, we propose an effective cut-flow strategy to achieve the high discovery potential at the 3 TeV MuC, as summarized in Table 3. Although we do not present the cut-flow for the negligible , their contributions are included in calculating the significance. In the following discussion, the selection efficiency of each specific cut is measured relative to the preceding cut in the cut-flow.
For the signal process, we set , , and , and consider three benchmark scenarios with charged Higgs boson masses of , 150, and 170 GeV. After applying the basic selection criteria, the signal cross sections show similar values across the three cases, with a slight decrease as increases.
The first effective kinematic cut is on the missing transverse energy, with a threshold of GeV. This cut results in approximately 70% selection efficiency for the signal and only about 30% for the background, providing an initial suppression of the background while retaining a substantial fraction of the signal events.
The most crucial cut is on the angular distance between the leading and subleading -jets, . Among the events that satisfy the cut, almost all the signal events survive under this cut, while only about 30% of the background events remain. At this stage, we already achieve substantial signal significances: for GeV and GeV, and for GeV. The smaller significance for GeV is attributed to the reduced production cross section due to the heavier charged Higgs boson mass.
Subsequently, we impose a series of angular distance cuts between a jet and a light jet, collectively denoted as . Each of these cuts consistently reduces the background while retaining almost all of the signal events. The selection efficiency of this series of cuts is about 20% for the background and about 90% for the signal.
Finally, we impose a condition on the invariant mass of the two -jets and two light jets, such that GeV. Note that we apply an upper bound on rather than a mass window. This approach is designed to retain as many signal events as possible, since the signal cross sections after the final selection are only of the order of ab, resulting in dozens of signal events with a total integrated luminosity of ab-1. Additionally, the relatively broad resonance peak, due to smearing effects in reconstructing the two -jets and two light jets, is another reason for not imposing a narrow mass window (see Figure 8). This final selection ensures a significant discovery potential for all three benchmark cases. For , 150, and 170 GeV, the final signal significances are 13.7, 13.5, and 6.06, respectively.
To investigate the impacts of higher collision energy on probing the mode, we consider the 10 TeV MuC with a total integrated luminosity of . One might naively expect that the 10 TeV MuC would yield higher signal sensitivity than the 3 TeV MuC, as the 10 TeV MuC benefits from the VBS processes of , which have parton-level cross sections more than two times larger than that of the Drell-Yan process (see Table 2).
| Cut-flow for at a 10 TeV MuC with | |||||||
| Cut | [fb] | ||||||
| [fb] | [fb] | [fb] | [fb] | ||||
| Basic | 2.17 | 0.677 | |||||
| 2.24 | 0.773 | ||||||
| 3.65 | 1.28 | ||||||
| 12.2 | 5.17 | ||||||
| 14.8 | 6.26 | ||||||
In Table 4, we present the cut-flow of the cross sections for and at the 10 TeV MuC. The results for are omitted as they are very similar to those for , with differences below 1%. The significances are calculated for a total integrated luminosity of and a 10% background uncertainty. For , we present the cut-flow for all three production channels: the Drell-Yan process, , and , with their respective cross sections denoted by , , and . After the basic selection, the cross sections for the three processes are of the same order of magnitude. However, the cut substantially suppresses and , leaving less than 10% of events. In contrast, the Drell-Yan process maintains a high selection efficiency, around 83%. In the case of , we present only the Drell-Yan cross sections since the non-Drell-Yan signal processes are negligible after the final selection. However, the signal significances are calculated based on the total cross section from all three processes.
The most decisive cuts for suppressing the background are the series of , which results in a background selection efficiency of about 5.7%. These cuts achieve a significance well above the discovery threshold. Our final selection on the invariant mass of two jets and two light jets further enhances the significance. For , , and , the significances are 14.8, 14.4, and 6.26, respectively.
Despite these results, we conclude that the 3 TeV MuC is more efficient than the 10 TeV MuC for probing the new physics signal of . Although both the 3 TeV and 10 TeV MuCs achieve similar signal significances, the 3 TeV MuC requires only luminosity, whereas the 10 TeV MuC demands a much higher luminosity of .
V Conclusions
In this study, we explored an unexplored decay channel of the light charged Higgs boson into an off-shell top quark and a bottom quark, , within the context of the type-I two-Higgs-doublet model. We focused on the mass range of 130 to 170 GeV, where the decay becomes significant. To probe this new physics signal without resorting to specific model parameters, we proposed the pair production of charged Higgs bosons as a golden production channel, followed by the decay .
We conducted a detailed signal-to-background analysis at the High-Luminosity Large Hadron Collider and a prospective 100 TeV proton-proton collider, employing comprehensive cut-flow strategies and the Boosted Decision Tree method. However, we found that the signal significance remains far below the threshold for a confident detection at these colliders, primarily due to the inherent softness of the jets in the decay process, which fail to meet the basic threshold for jet clustering.
Recognizing the constraints of hadron colliders, we extended our analysis to explore the discovery potential of a multi-TeV muon collider (MuC) for the signal process. The MuC offers a significant advantage by fully exploiting the beam energy in collisions between fundamental particles. Our analysis demonstrated that the MuC, particularly at a center-of-mass energy of 3 TeV, provides a promising environment for probing the decay mode. The cut-flow analysis at the 3 TeV MuC yielded a high signal significance, surpassing the discovery threshold, with a total integrated luminosity of 1 ab-1. Specifically, for , 150, and 170 GeV, the signal significances were 13.7, 13.5, and 6.06, respectively. In contrast, the 10 TeV MuC, despite its higher collision energy, requires a substantially larger integrated luminosity of 10 ab-1 to achieve comparable results. This is due to the reduced signal cross sections of the Drell-Yan production process at higher collision energies.
The results of our study underscore the challenges and potential in searching for the light charged Higgs boson via the decay mode. While high-energy hadron colliders face significant obstacles due to the soft jets, the multi-TeV MuC emerges as a highly effective platform. The detailed simulation and cut-flow strategy developed in this work provide a robust framework for future experimental searches for this promising new signal, emphasizing the critical role of a multi-TeV MuC in exploring beyond the Standard Model physics.
Acknowledgements.
We thank Kingman Cheung and Chih-Ting Lu for useful discussions. And the work of D.W., J.K., P.S., and J.S. is supported by the National Research Foundation of Korea, Grant No. NRF-2022R1A2C1007583. The work of S.L. is supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education(RS-2023-00274098).References
- (1) ATLAS collaboration, G. Aad et al., Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC, Phys. Lett. B 716 (2012) 1–29, [1207.7214].
- (2) CMS collaboration, S. Chatrchyan et al., Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC, Phys. Lett. B 716 (2012) 30–61, [1207.7235].
- (3) M. Misiak, A. Rehman and M. Steinhauser, Towards at the NNLO in QCD without interpolation in mc, JHEP 06 (2020) 175, [2002.01548].
- (4) M. Aoki, S. Kanemura, K. Tsumura and K. Yagyu, Models of Yukawa interaction in the two Higgs doublet model, and their collider phenomenology, Phys. Rev. D 80 (2009) 015017, [0902.4665].
- (5) G. C. Branco, P. M. Ferreira, L. Lavoura, M. N. Rebelo, M. Sher and J. P. Silva, Theory and phenomenology of two-Higgs-doublet models, Phys. Rept. 516 (2012) 1–102, [1106.0034].
- (6) N. Craig, J. Galloway and S. Thomas, Searching for Signs of the Second Higgs Doublet, 1305.2424.
- (7) L. Wang, J. M. Yang and Y. Zhang, Two-Higgs-doublet models in light of current experiments: a brief review, Commun. Theor. Phys. 74 (2022) 097202, [2203.07244].
- (8) X.-M. Shen, Y. Hu, C. Sun and J. Gao, Decay of the charged Higgs boson and the top quark in two-Higgs-doublet model at NNLO in QCD, JHEP 05 (2022) 157, [2201.08139].
- (9) S. Kanemura, M. Kikuchi and K. Yagyu, Next-to-leading order corrections to decays of the heavier CP-even Higgs boson in the two Higgs doublet model, Nucl. Phys. B 983 (2022) 115906, [2203.08337].
- (10) S. Lee, K. Cheung, J. Kim, C.-T. Lu and J. Song, Status of the two-Higgs-doublet model in light of the CDF mW measurement, Phys. Rev. D 106 (2022) 075013, [2204.10338].
- (11) A. G. Akeroyd, S. Moretti and M. Song, Light charged Higgs boson with dominant decay to quarks and its search at the LHC and future colliders, Phys. Rev. D 98 (2018) 115024, [1810.05403].
- (12) H. Abouabid, A. Arhrib, D. Azevedo, J. E. Falaki, P. M. Ferreira, M. Mühlleitner et al., Benchmarking di-Higgs production in various extended Higgs sector models, JHEP 09 (2022) 011, [2112.12515].
- (13) X.-F. Han, T. Li, H.-X. Wang, L. Wang and Y. Zhang, Lepton-specific inert two-Higgs-doublet model confronted with the new results for muon and electron g-2 anomalies and multilepton searches at the LHC, Phys. Rev. D 104 (2021) 115001, [2104.03227].
- (14) P. M. Ferreira, B. L. Gonçalves and F. R. Joaquim, The hidden side of scalar-triplet models with spontaneous CP violation, JHEP 05 (2022) 105, [2109.13179].
- (15) S. Abbaspour, S. M. Moosavi Nejad and M. Balali, Indirect search for light charged Higgs bosons through the dominant semileptonic decays of top quark , Nucl. Phys. B 932 (2018) 505–528, [1806.02546].
- (16) G. K. Demir, N. Sönmez and H. Dogan, Deep-Learning in Search of Light Charged Higgs, 1803.01550.
- (17) ATLAS collaboration, M. Aaboud et al., Search for charged Higgs bosons decaying via in the +jets and +lepton final states with 36 fb-1 of collision data recorded at TeV with the ATLAS experiment, JHEP 09 (2018) 139, [1807.07915].
- (18) P. Sanyal, Limits on the Charged Higgs Parameters in the Two Higgs Doublet Model using CMS TeV Results, Eur. Phys. J. C 79 (2019) 913, [1906.02520].
- (19) CMS collaboration, A. M. Sirunyan et al., Search for charged Higgs bosons in the H± decay channel in proton-proton collisions at 13 TeV, JHEP 07 (2019) 142, [1903.04560].
- (20) S. Ghosh, Fermionic decay of charged Higgs boson in low mass region in Georgi Machacek Model, 2205.03896.
- (21) J. Kim, S. Lee, P. Sanyal, J. Song and D. Wang, and to probe the fermiophobic Higgs boson with high cutoff scales, JHEP 04 (2023) 083, [2302.05467].
- (22) S. Kanemura, K. Tsumura and H. Yokoya, Multi-tau-lepton signatures at the LHC in the two Higgs doublet model, Phys. Rev. D 85 (2012) 095001, [1111.6089].
- (23) L. Duarte, V. P. Goncalves, D. E. Martins and T. B. de Melo, Single charged Higgs pair production in exclusive processes at the LHC, 2403.01953.
- (24) J. Hernandez-Sanchez, S. Moretti, R. Noriega-Papaqui and A. Rosado, Off-diagonal terms in Yukawa textures of the type-III 2-Higgs doublet model and light charged Higgs boson phenomenology, JHEP 07 (2013) 044, [1212.6818].
- (25) J. Hernández-Sánchez, C. G. Honorato, S. Moretti and S. Rosado-Navarro, Charged Higgs boson production via -fusion at the Large Hadron Collider, Phys. Rev. D 102 (2020) 055008, [2003.06263].
- (26) M. Aiko, S. Kanemura and K. Mawatari, Exploring the global symmetry structure of the Higgs potential via same-sign pair production of charged Higgs bosons, Phys. Lett. B 797 (2019) 134854, [1906.09101].
- (27) ATLAS collaboration, G. Aad et al., Search for a light charged Higgs boson in the decay channel in events using pp collisions at = 7 TeV with the ATLAS detector, Eur. Phys. J. C 73 (2013) 2465, [1302.3694].
- (28) CMS collaboration, V. Khachatryan et al., Search for a light charged Higgs boson decaying to in pp collisions at TeV, JHEP 12 (2015) 178, [1510.04252].
- (29) CMS collaboration, A. M. Sirunyan et al., Search for a charged Higgs boson decaying to charm and bottom quarks in proton-proton collisions at TeV, JHEP 11 (2018) 115, [1808.06575].
- (30) ATLAS collaboration, Search for a light charged Higgs boson in decays, with , in the lepton+jets final state in proton-proton collisions at TeV with the ATLAS detector, ATLAS-CONF-2021-037.
- (31) CMS collaboration, A. M. Sirunyan et al., Search for a light charged Higgs boson in the H± cs channel in proton-proton collisions at 13 TeV, Phys. Rev. D 102 (2020) 072001, [2005.08900].
- (32) A. G. Akeroyd, S. Moretti and M. Song, Slight excess at 130 GeV in search for a charged Higgs boson decaying to a charm quark and a bottom quark at the Large Hadron Collider, J. Phys. G 49 (2022) 085004, [2202.03522].
- (33) R. Dermisek, E. Lunghi and A. Raval, Trilepton Signatures of Light Charged and CP-odd Higgs Bosons in Top Quark Decays, JHEP 04 (2013) 063, [1212.5021].
- (34) A. Arhrib, R. Benbrik, H. Harouiz, S. Moretti, Y. Wang and Q.-S. Yan, Implications of a light charged Higgs boson at the LHC run III in the 2HDM, Phys. Rev. D 102 (2020) 115040, [2003.11108].
- (35) Y. Hu, C. Fu and J. Gao, Signature of a light charged Higgs boson from top quark pairs at the LHC, Phys. Rev. D 106 (2022) L071701, [2206.05748].
- (36) C. Fu and J. Gao, Constraint for a light charged Higgs boson and its neutral partners from top quark pairs at the LHC, Phys. Rev. D 108 (2023) 035007, [2304.07782].
- (37) A. Arhrib, R. Benbrik, R. Enberg, W. Klemm, S. Moretti and S. Munir, Identifying a light charged Higgs boson at the LHC Run II, Phys. Lett. B 774 (2017) 591–598, [1706.01964].
- (38) T. Mondal and P. Sanyal, Same sign trilepton as signature of charged Higgs in two Higgs doublet model, JHEP 05 (2022) 040, [2109.05682].
- (39) A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti, Y. Wang et al., Light charged Higgs boson in associated production at the LHC, in 1st Pan-African Astro-Particle and Collider Physics Workshop, 5, 2022, 2205.14274.
- (40) J. Kim, S. Lee, P. Sanyal and J. Song, CDF W-boson mass and muon g-2 in a type-X two-Higgs-doublet model with a Higgs-phobic light pseudoscalar, Phys. Rev. D 106 (2022) 035002, [2205.01701].
- (41) J. Kim, S. Lee, J. Song and P. Sanyal, Fermiophobic light Higgs boson in the type-I two-Higgs-doublet model, Phys. Lett. B 834 (2022) 137406, [2207.05104].
- (42) D. Bhatia, N. Desai and S. Dwivedi, Discovery prospects of a light charged Higgs near the fermiophobic region of type-I 2HDM, JHEP 06 (2023) 100, [2212.14363].
- (43) Z. Li, A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti et al., Discovering a light charged Higgs boson via + 4 final states at the LHC, 2305.05788.
- (44) T. Mondal, S. Moretti, S. Munir and P. Sanyal, Electroweak Multi-Higgs Production: A Smoking Gun for the type-I Two-Higgs-Doublet Model, Phys. Rev. Lett. 131 (2023) 231801, [2304.07719].
- (45) A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti, Y. Wang et al., New discovery modes for a light charged Higgs boson at the LHC, JHEP 10 (2021) 073, [2106.13656].
- (46) A. Arhrib, R. Benbrik, M. Krab, B. Manaut, S. Moretti, Y. Wang et al., New Light H Discovery Channels at the LHC, Symmetry 13 (2021) 2319, [2110.04823].
- (47) N. Kausar, I. Ahmed, W. Sagheer and A. M. W., Charged Higgs observability via charged Higgs pair production at future lepton collider, Eur. Phys. J. Plus 137 (2022) 603, [2011.11131].
- (48) A. Arhrib, K. Cheung and C.-T. Lu, Same-sign charged Higgs boson pair production in bosonic decay channels at the HL-LHC and HE-LHC, Phys. Rev. D 102 (2020) 095026, [1910.02571].
- (49) M. Krab, M. Ouchemhou, A. Arhrib, R. Benbrik, B. Manaut and Q.-S. Yan, Single charged Higgs boson production at the LHC, Phys. Lett. B 839 (2023) 137705, [2210.09416].
- (50) S. K. Kang, J. Kim, S. Lee and J. Song, Disentangling the high- and low-cutoff scales via the trilinear Higgs couplings in the type-I two-Higgs-doublet model, Phys. Rev. D 107 (2023) 015025, [2210.00020].
- (51) R. Capdevilla, D. Curtin, Y. Kahn and G. Krnjaic, Discovering the physics of at future muon colliders, Phys. Rev. D 103 (2021) 075028, [2006.16277].
- (52) P. Bandyopadhyay, A. Karan, R. Mandal and S. Parashar, Distinguishing signatures of scalar leptoquarks at hadron and muon colliders, Eur. Phys. J. C 82 (2022) 916, [2108.06506].
- (53) C. Sen, P. Bandyopadhyay, S. Dutta and A. KT, Displaced Higgs production in type-III seesaw at the LHC/FCC, MATHUSLA and muon collider, Eur. Phys. J. C 82 (2022) 230, [2107.12442].
- (54) P. Asadi, R. Capdevilla, C. Cesarotti and S. Homiller, Searching for leptoquarks at future muon colliders, JHEP 10 (2021) 182, [2104.05720].
- (55) G.-y. Huang, F. S. Queiroz and W. Rodejohann, Gauged at a muon collider, Phys. Rev. D 103 (2021) 095005, [2101.04956].
- (56) S. Y. Choi and J. S. Lee, S-channel production of MSSM Higgs bosons at a muon collider with explicit CP violation, Phys. Rev. D 61 (2000) 111702, [hep-ph/9909315].
- (57) T. Han, Z. Liu, L.-T. Wang and X. Wang, WIMPs at High Energy Muon Colliders, Phys. Rev. D 103 (2021) 075004, [2009.11287].
- (58) T. Han, S. Li, S. Su, W. Su and Y. Wu, Heavy Higgs bosons in 2HDM at a muon collider, Phys. Rev. D 104 (2021) 055029, [2102.08386].
- (59) A. Jueid, J. Kim, S. Lee and J. Song, type-X two-Higgs-doublet model in light of the muon g-2: Confronting Higgs boson and collider data, Phys. Rev. D 104 (2021) 095008, [2104.10175].
- (60) T. Han, S. Li, S. Su, W. Su and Y. Wu, BSM Higgs Production at a Muon Collider, in Snowmass 2021, 5, 2022, 2205.11730.
- (61) K. Black, T. Bose, Y. Chen, S. Dasu, H. Jia, D. Pinna et al., Prospects for Heavy WIMP Dark Matter Searches at Muon Colliders, in Snowmass 2021, 5, 2022, 2205.10404.
- (62) M. Belfkir, A. Jueid and S. Nasri, Boosting dark matter searches at muon colliders with machine learning: The mono-Higgs channel as a case study, PTEP 2023 (2023) 123B03, [2309.11241].
- (63) A. Jueid and S. Nasri, Lepton portal dark matter at muon colliders: Total rates and generic features for phenomenologically viable scenarios, Phys. Rev. D 107 (2023) 115027, [2301.12524].
- (64) M. Antonelli and P. Raimondi, Snowmass Report: Ideas for Muon Production from Positron Beam Interaction on a Plasma Target, in Snowmass 2013: Snowmass on the Mississippi, 11, 2013, INFN-13-22/LNF.
- (65) M. Antonelli, M. Boscolo, R. Di Nardo and P. Raimondi, Novel proposal for a low emittance muon beam using positron beam on target, Nucl. Instrum. Meth. A 807 (2016) 101–107, [1509.04454].
- (66) F. Collamati, C. Curatolo, D. Lucchesi, A. Mereghetti, N. Mokhov, M. Palmer et al., Advanced assessment of beam-induced background at a muon collider, JINST 16 (2021) P11009, [2105.09116].
- (67) D. Ally, L. Carpenter, T. Holmes, L. Lee and P. Wagenknecht, Strategies for Beam-Induced Background Reduction at Muon Colliders, in Snowmass 2021, 3, 2022, 2203.06773.
- (68) S. L. Glashow and S. Weinberg, Natural Conservation Laws for Neutral Currents, Phys. Rev. D 15 (1977) 1958.
- (69) E. A. Paschos, Diagonal Neutral Currents, Phys. Rev. D 15 (1977) 1966.
- (70) J. Song and Y. W. Yoon, decay of the elusive charged Higgs boson in the two-Higgs-doublet model with vectorlike fermions, Phys. Rev. D 100 (2019) 055006, [1904.06521].
- (71) M. Carena, I. Low, N. R. Shah and C. E. M. Wagner, Impersonating the Standard Model Higgs Boson: Alignment without Decoupling, JHEP 04 (2014) 015, [1310.2248].
- (72) A. Celis, V. Ilisie and A. Pich, LHC constraints on two-Higgs doublet models, JHEP 07 (2013) 053, [1302.4022].
- (73) K. Cheung, J. S. Lee and P.-Y. Tseng, Higgcision in the Two-Higgs Doublet Models, JHEP 01 (2014) 085, [1310.3937].
- (74) J. Bernon, J. F. Gunion, H. E. Haber, Y. Jiang and S. Kraml, Scrutinizing the alignment limit in two-Higgs-doublet models: mh=125 GeV, Phys. Rev. D 92 (2015) 075004, [1507.00933].
- (75) S. Chang, S. K. Kang, J.-P. Lee and J. Song, Higgs potential and hidden light Higgs scenario in two Higgs doublet models, Phys. Rev. D 92 (2015) 075023, [1507.03618].
- (76) D. Das and I. Saha, Search for a stable alignment limit in two-Higgs-doublet models, Phys. Rev. D 91 (2015) 095024, [1503.02135].
- (77) S. Kanemura, M. Takeuchi and K. Yagyu, Probing double-aligned two-Higgs-doublet models at the LHC, Phys. Rev. D 105 (2022) 115001, [2112.13679].
- (78) S. Kanemura, Y. Okada, H. Taniguchi and K. Tsumura, Indirect bounds on heavy scalar masses of the two-Higgs-doublet model in light of recent Higgs boson searches, Phys. Lett. B 704 (2011) 303–307, [1108.3297].
- (79) N. Chen, T. Han, S. Li, S. Su, W. Su and Y. Wu, type-I 2HDM under the Higgs and Electroweak Precision Measurements, JHEP 08 (2020) 131, [1912.01431].
- (80) P. Sanyal and D. Wang, Probing the electroweak [inline-graphic not available: see fulltext] final state in type I 2HDM at the LHC, JHEP 09 (2023) 076, [2305.00659].
- (81) I. P. Ivanov, General two-order-parameter Ginzburg-Landau model with quadratic and quartic interactions, Phys. Rev. E 79 (2009) 021116, [0802.2107].
- (82) A. Barroso, P. M. Ferreira, I. P. Ivanov, R. Santos and J. P. Silva, Evading death by vacuum, Eur. Phys. J. C 73 (2013) 2537, [1211.6119].
- (83) A. Barroso, P. M. Ferreira, I. P. Ivanov and R. Santos, Metastability bounds on the two Higgs doublet model, JHEP 06 (2013) 045, [1303.5098].
- (84) I. P. Ivanov, Minkowski space structure of the Higgs potential in 2HDM, Phys. Rev. D 75 (2007) 035001, [hep-ph/0609018]. [Erratum: Phys.Rev.D 76, 039902 (2007)].
- (85) A. Arhrib, Unitarity constraints on scalar parameters of the standard and two Higgs doublets model, in Workshop on Noncommutative Geometry, Superstrings and Particle Physics, 12, 2000, hep-ph/0012353.
- (86) D. Eriksson, J. Rathsman and O. Stal, 2HDMC: Two-Higgs-Doublet Model Calculator Physics and Manual, Comput. Phys. Commun. 181 (2010) 189–205, [0902.0851].
- (87) J. Oredsson and J. Rathsman, breaking effects in 2-loop RG evolution of 2HDM, JHEP 02 (2019) 152, [1810.02588].
- (88) J. Oredsson, 2HDME : Two-Higgs-Doublet Model Evolver, Comput. Phys. Commun. 244 (2019) 409–426, [1811.08215].
- (89) A. Arbey, F. Mahmoudi, O. Stal and T. Stefaniak, Status of the Charged Higgs Boson in Two Higgs Doublet Models, Eur. Phys. J. C 78 (2018) 182, [1706.07414].
- (90) M. Misiak and M. Steinhauser, Weak radiative decays of the B meson and bounds on in the Two-Higgs-Doublet Model, Eur. Phys. J. C 77 (2017) 201, [1702.04571].
- (91) P. Bechtle, O. Brein, S. Heinemeyer, O. Stål, T. Stefaniak, G. Weiglein et al., : Improved Tests of Extended Higgs Sectors against Exclusion Bounds from LEP, the Tevatron and the LHC, Eur. Phys. J. C 74 (2014) 2693, [1311.0055].
- (92) K. Cheung, A. Jueid, J. Kim, S. Lee, C.-T. Lu and J. Song, Comprehensive study of the light charged Higgs boson in the type-I two-Higgs-doublet model, Phys. Rev. D 105 (2022) 095044, [2201.06890].
- (93) J. Alwall, M. Herquet, F. Maltoni, O. Mattelaer and T. Stelzer, MadGraph 5 : Going Beyond, JHEP 06 (2011) 128, [1106.0522].
- (94) D. Kim, S. Lee, H. Jung, D. Kim, J. Kim and J. Song, A panoramic study of K-factors for 111 processes at the 14 TeV LHC, J. Korean Phys. Soc. 84 (2024) no.12, 914-926, [2402.16276].
- (95) C. Bierlich et al., A comprehensive guide to the physics and usage of PYTHIA 8.3, SciPost Phys. Codeb. 2022 (2022) 8, [2203.11601].
- (96) DELPHES 3 collaboration, J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens et al., DELPHES 3, A modular framework for fast simulation of a generic collider experiment, JHEP 02 (2014) 057, [1307.6346].
- (97) M. Cacciari, G. P. Salam and G. Soyez, FastJet User Manual, Eur. Phys. J. C 72 (2012) 1896, [1111.6097].
- (98) ATLAS collaboration, Expected performance for an upgraded ATLAS detector at High-Luminosity LHC, ATL-PHYS-PUB-2016-026.
- (99) ATLAS collaboration, Study of the double Higgs production channel with the ATLAS experiment at the HL-LHC, ATL-PHYS-PUB-2017-001.
- (100) CMS collaboration, G. L. Bayatian et al., CMS technical design report, volume II: Physics performance, J. Phys. G 34 (2007) 995–1579.
- (101) G. Bagliesi, Tau tagging at Atlas and CMS, in 17th Symposium on Hadron Collider Physics 2006 (HCP 2006), 7, 2007, 0707.0928.
- (102) CMS collaboration, A. M. Sirunyan et al., Performance of reconstruction and identification of leptons decaying to hadrons and in pp collisions at 13 TeV, JINST 13 (2018) P10005, [1809.02816].
- (103) T. Chen and C. Guestrin, XGBoost: A Scalable Tree Boosting System, 1603.02754
- (104) ATLAS collaboration, M. Aaboud et al., Evidence for the associated production of the Higgs boson and a top quark pair with the ATLAS detector, Phys. Rev. D 97 (2018) 072003, [1712.08891].
- (105) CMS collaboration, A. M. Sirunyan et al., Search for nonresonant Higgs boson pair production in final states with two bottom quarks and two photons in proton-proton collisions at = 13 TeV, JHEP 03 (2021) 257, [2011.12373].
- (106) ATLAS collaboration, G. Aad et al., Search for Higgs boson pair production in the two bottom quarks plus two photons final state in collisions at TeV with the ATLAS detector, Phys. Rev. D 106 (2022) 052001, [2112.11876].
- (107) CMS collaboration, A. M. Sirunyan et al., Measurements of Production and the CP Structure of the Yukawa Interaction between the Higgs Boson and Top Quark in the Diphoton Decay Channel, Phys. Rev. Lett. 125 (2020) 061801, [2003.10866].
- (108) CMS collaboration, A. Tumasyan et al., Analysis of the structure of the Yukawa coupling between the Higgs boson and leptons in proton-proton collisions at = 13 TeV, JHEP 06 (2022) 012, [2110.04836].
- (109) ATLAS collaboration, G. Aad et al., Search for dark matter in events with missing transverse momentum and a Higgs boson decaying into two photons in pp collisions at = 13 TeV with the ATLAS detector, JHEP 10 (2021) 013, [2104.13240].
- (110) S. Dasgupta, R. Pramanick and T. S. Ray, Broad toplike vector quarks at LHC and HL-LHC, Phys. Rev. D 105 (2022) 035032, [2112.03742].
- (111) A. S. Cornell, A. Deandrea, B. Fuks and L. Mason, Future lepton collider prospects for a ubiquitous composite pseudoscalar, Phys. Rev. D 102 (2020) 035030, [2004.09825].
- (112) F. Bishara and M. Montull, Machine learning amplitudes for faster event generation, Phys. Rev. D 107 (2023) L071901, [1912.11055].
- (113) H. Al Ali et al., The muon Smasher’s guide, Rept. Prog. Phys. 85 (2022) 084201, [2103.14043].
- (114) C. Accettura et al., Towards a muon collider, Eur. Phys. J. C 83 (2023) 864, [2303.08533]. [Erratum: Eur.Phys.J.C 84, 36 (2024)].
- (115) M. Ruhdorfer, E. Salvioni and A. Wulzer, Invisible Higgs boson decay from forward muons at a muon collider, Phys. Rev. D 107 (2023) 095038, [2303.14202].
- (116) M. Forslund and P. Meade, Precision Higgs width and couplings with a high energy muon collider, JHEP 01 (2024) 182, [2308.02633].
- (117) P. Bandyopadhyay, S. Parashar, C. Sen and J. Song, Probing Inert Triplet Model at a multi-TeV muon collider via vector boson fusion with forward muon tagging, 2401.02697.
- (118) M. Boronat, J. Fuster, I. Garcia, E. Ros and M. Vos, A robust jet reconstruction algorithm for high-energy lepton colliders, Phys. Lett. B 750 (2015) 95–99, [1404.4294].
- (119) M. Boronat, J. Fuster, I. Garcia, P. Roloff, R. Simoniello and M. Vos, Jet reconstruction at high-energy electron–positron colliders, Eur. Phys. J. C 78 (2018) 144, [1607.05039].
- (120) International Muon Collider collaboration, N. Bartosik, D. Calzolari, L. Castelli, A. Lechner and D. Lucchesi, Machine-Detector interface for multi-TeV Muon Collider, PoS EPS-HEP2023 (2024) 630.
- (121) International Muon Collider collaboration, M. Casarsa et al., Higgs physics prospects at a 3 TeV muon collider, PoS EPS-HEP2023 (2024) 408.