Using Capsule Networks to Classify Digitally Modulated Signals with Raw I/Q Data
Abstract
Machine learning has become a powerful tool for solving problems in various engineering and science areas, including the area of communication systems. This paper presents the use of capsule networks for classification of digitally modulated signals using the I/Q signal components. The generalization ability of a trained capsule network to correctly classify the classes of digitally modulated signals that it has been trained to recognize is also studied by using two different datasets that contain similar classes of digitally modulated signals but that have been generated independently. Results indicate that the capsule networks are able to achieve high classification accuracy. However, these networks are susceptible to the datashift problem which will be discussed in this paper.
Index Terms:
Capsule Networks, Deep Learning, Neural Networks, Digital Communications, Modulation Recognition, Signal Classification.I Introduction
In recent years, machine learning has emerged as a powerful tool in solving complex engineering problems and has been applied to diverse areas ranging from image processing and computer vision to speech recognition and internet search engines. Machine learning techniques have also been applied to wireless communication systems and networks in various settings that involve the different layers of wireless networks to solve problems related to signal classification and recognition of digital modulation schemes at the physical layer [1, 2, 3], to resource and mobility management at the data link (MAC) and network layers, to localization at the application layer [4].
Blind classification of digitally modulated signals has usually been accomplished using signal processing techniques that include likelihood-based approaches [5, 6] or cyclostationary signal processing (CSP) [7]. We note that, unlike the likelihood- or CSP-based approaches, which require the implementation of complex algorithms to extract features that distinguish different digital modulation schemes and then use these features for signal classification, machine learning implements neural networks and relies on their extensive training to make the distinction among different classes of digitally modulated signals. In this direction, recent approaches use convolutional and residual neural networks with the I/Q signal components for training and signal recognition/classification [2, 1, 3] or with alternative signal features such as the amplitude/phase or frequency domain representations of digitally modulated signals [8, 9, 10, 11, 12].
In this paper we explore the use of capsule networks [13] to classify digitally modulated signals using raw I/Q signal data. As discussed in [13], capsule networks are a version of convolutional neural networks that emphasize learning desirable characteristics of the training dataset by means of capsules, which are multiple parallel and independent nodes that learn class specific characteristics. Capsule networks have been used for digital modulation classification in [14, 7], and in our paper we pursue a variant of capsule networks which classifies with high accuracy modulated signals corresponding to several commonly used digital modulation schemes.
We compare the classification performance of the capsule network to that of the convolutional neural network (CNN) and the residual network (RESNET) used for classification of digitally modulated signals in [3], and similar to [3], we also explore the problem of the dataset shift, also referred to as out-of-distribution generalization [15]. This is an important problem in machine-learning-based approaches, which occurs when the training and testing data sets are distinct, implying that data from the testing environment is not used for training the classifier. In this direction we use two datasets that are publicly available from [16]:
- •
-
•
DataSet2: This dataset is similar to DataSet1 in terms of signal types included and their characteristics, and the key difference between signals in DataSet1 and DataSet2 is that they have different carrier frequency offset (CFO) intervals, which will be used to study the effects of the dataset shift on the capsule network performance.
Additional details about these two data sets will be provided in section III.
The paper is organized as follows: Section II includes a brief introduction to capsule networks along with a description of the specific capsule network used for classification of digitally modulated signals in our work. This is followed by a description of the data sets used for training the capsule network and for testing its classification performance in Section III, with performance results displayed in Section IV. The paper concludes with final remarks in Section V.
II Capsule Networks for Digital Modulation Classification
The aim of capsule networks is to focus on learning desirable characteristics of the input pattern or signal, which correspond to a specific input class, and they have been used in attempts to emulate human vision. We note that, when an eye receives visual stimulus, the eye does not focus on all available inputs, instead points of fixation are established and these points are used to identify or reconstruct a mental image of the object of focus [13]. This specificity is achieved by means of capsules, which are multiple parallel and independent nodes that learn class specific characteristics and represent points of fixation in the form of a capsule vector. In the context of classifying digitally modulated signals, the capsules are expected to discover excursion characteristics that are intrinsic to a modulation type [7, 14].
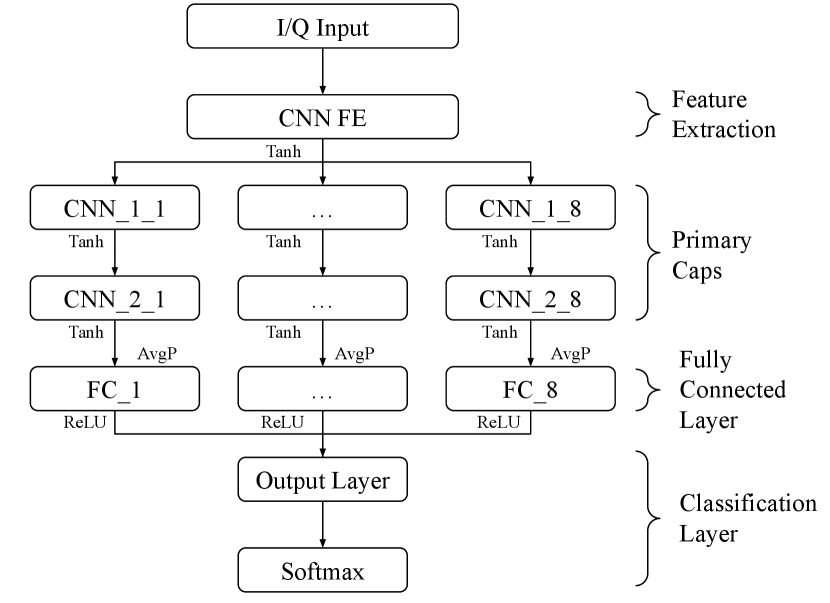
In general, a capsule network is a shallow convolutional neural network (CNN) that consists of a feature extracting layer followed by parallel CNN layers referred to as primary caps. Each of the parallel primary cap layers has a “capsule vector” as the output, which is referred to as digit capsule (or digit caps), and has dimension neurons. We note that this is different than in the case of CNN approaches, which rely on a single output neuron per class. The value of is a design parameter and corresponds to the points of fixation that the capsule network may learn, which are class specific attributes discovered by the network during training. Ideally, the magnitude of the capsule vector corresponds to the probability that the input matches the output corresponding to this capsule node and its orientation carries information related to the input properties. The neurons in the digit caps have connections to neurons in the primary caps layers and can be determined iteratively using the dynamic routing by agreement algorithm in [13], which has also been applied for modulation classification in digitally modulated signals [7, 14].
In this paper we consider the capsule network with topology illustrated in Fig. 1, and we study its use in the context of classification of digitally modulated signals. Furthermore, instead of using dynamic routing by agreement algorithm to update connections between a given capsule vector and higher layer neurons, all higher layer neurons are fully connected to each neuron in a neuron vector. These neurons will discover desirable attributes in the previous primary caps and activate on these characteristics. We note that, the considered topology allows for easy implementation from a design perspective and for efficient training as matrix operations are efficiently processed by graphic processing units (GPUs), whereas iterative learning through dynamic routing by agreement may result in increased computational complexity.
The capsule network shown in Fig. 1 takes as input sampled versions of the normalized in-phase (I) and quadrature (Q) components of a digitally modulated signal, which must be classified as corresponding to one of the following eight digital modulation schemes: BPSK, QPSK, 8-PSK, DQPSK, MSK, 16-QAM, 64-QAM, and 256-QAM. The various components of the capsule network considered in Fig. 1 include:
-
•
Feature Extraction Layer: This is the first layer of the network that performs a general feature mapping of the input signal, and its parameters are inspired from those of the CNNs used for classification of digitally modulated signals in [2, 17, 3], to include a convolutional layer followed by a batch normalization layer and an activation function.
-
•
Primary Caps: This layer consists of a number of primary caps that is equal to the number of digital modulation classes considered, which are operating in parallel using as inputs the output from the feature extraction layer. Each primary cap in this layer includes two convolutional layers with customized filter and stride, and an activation function, and is followed by a fully connected layer.
-
•
Fully Connected Layer: This layer consists of a neuron vector with the weights connecting to the previous layer. Each neuron in the last layer of the primary caps layer will be fully connected to each neuron in this layer, which are expected to, ideally, discover characteristics specific to the capsules class. To make the output of the network be compatible with a softmax classification layer, each neuron within this layer is fully connected to a single output neuron, and the output neurons for all primary caps will be combined depth wise to produce an 8-dimensional vector n, which is passed to the classification layer. The value of each respective element of n will be representative of the likelihood that its corresponding modulation type is present in the I/Q input data.
-
•
Classification Layer: This vector n is passed to the softmax layer, which will map each element , , in n to a value that is between , with each element representing the probability of occurrence, such that the sum of elements in n adds up to [18].
(1) This provides a convenient way to determine which modulation type is most likely to correspond to the signal with the I/Q data at the input of the capsule network.
More specific details on the capsule network parameters, such as filter sizes, strides, output dimensions, etc., are given in Table I.
| Layer | Filter | Stride | Size/Weights |
|---|---|---|---|
| Input | 2x32,768 | ||
| Conv | [1,22] | [1,9] | 22x2x64 |
| Batch Normalization | |||
| Tanh | |||
| Conv-1-(i) | [1 23] | [1,7] | 23x64x48 |
| Batch Normalization-1-(i) | |||
| Tanh-1-(i) | |||
| Conv-2-(i) | [1 22] | [1,8] | 22x48x64 |
| Batch Normalization-2-(i) | |||
| Tanh-2-(i) | |||
| Average Pool (i) | [1,8] | [1,1] | |
| FC-(i) | 32 | ||
| Batch Normalization-3-(i) | |||
| ReLu-1-(i) | |||
| Point FC-(i) | 1 | ||
| Depth Concatenation(i=1:8) | 8 | ||
| SoftMax |
III Datasets for Capsule Network
Training and Testing
A capsule network with the structure outlined in Section II is trained and tested using digitally modulated signals in two distinct datasets that are publicly available for general use [16]. These are referred to as DataSet1 and DataSet2, respectively, and each of them contains collections of the I/Q data corresponding to a total of computer generated digitally modulated signals that include BPSK, QPSK, 8-PSK, DQPSK, 16-QAM, 64-QAM, 256-QAM, and MSK modulation schemes. Signals employ square-root raised-cosine (SRRC) pulse shaping with roll off factor in the interval and a total of samples for each signal are included in the datasets.
We note that the listed signal-to-noise ratios (SNRs) for the signals in both DataSet1 and DataSet2 correspond to in-band SNR values, and that a band-of-interest (BOI) detector [19] was used to validate the labeled SNRs, CFOs, and SRRC roll-off values for the signals in both datasets.
III-A DataSet1
DataSet1 is available for download as CSPB.ML.2018 from [16], and additional characteristics for signals in this dataset include:
-
•
Symbol rates vary between and samples/symbol.
-
•
The in-band SNR varies between and dB.
III-B DataSet2
DataSet2 is available for download as CSPB.ML.2022 from [16], and for this dataset the additional signal characteristics include:
-
•
Symbol rates vary between and samples/symbol.
-
•
The in-band SNR varies between and dB.
The symbol rates and CFOs differ between the two datasets, and this difference will be used to study the generalization ability of the trained capsule networks. We note that the CFOs are distributed over disjoint intervals.
III-C Data Augmentation
It is expected that the trained digital modulation classifier will perform well at classifying high in-band SNR signals and perform less desirably as the SNR decreases. This is visible in similar digital modulation classification approaches [3, 1, 2, 17]. However, as noted in [20], for the two datasets used there are few samples for the lower SNR values, and the small sample size for the lower SNR values is not meaningful in evaluating the capsule network performance for the lower SNR values. To overcome this aspect, a process of data augmentation was used. The process, which is discussed in [20], consists of adding random noise to higher SNR signals to reduce the overall in-band SNR and implies after data augmentation the following in-band ranges:
-
•
From dB to dB for DataSet1.
-
•
From dB to dB for DataSet2.
IV Capsule Network Training
and Numerical Results
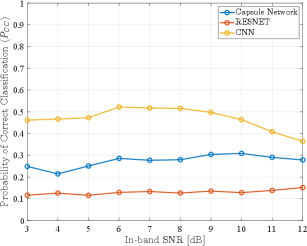
To illustrate the performance of the chosen capsule network for classifying digitally modulated signals we have trained and tested it with signals from the two datasets available. Each dataset was divided into three subsets that were used for training, validation, and testing, such that for both DataSet1 and DataSet2, 70% of the data is used for training, 5% of the data is used for validation and 25% is used for testing. All data is normalized to unit power before training begins, and the stochastic gradient descent with momentum (SGDM) algorithm [21] was used for training with a mini-batch size of 250. The capsule networks have been implemented in MATLAB and trained on a high-performance computing cluster with NVidia V100 graphical processing unit (GPU) nodes available, with each node having GB of memory. We note that training is computationally intensive however, if the resources are leveraged correctly and the entire dataset is loaded into RAM, training can be completed in several hours.
The classification performance of the capsule network is compared to that of the alternative deep learning approaches for classifying digitally modulated signals in [3], which also use the I/Q signal data but employ a convolutional neural network (CNN) and a residual network (RESNET) for signal classification. We note that the CNN and RESNET used in [3] are similar to the neural network structures considered in [2] and yield similar results those in [2] when tested with signals that come from the same dataset as the one used for training. However, as discussed in [3], these NNs do not display meaningful generalization ability, and both the CNN and the RESNET fail to identify most digital modulation schemes which they have been trained to recognize when tested with signals from a dataset that was generated independently from the training one.
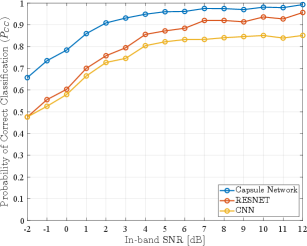
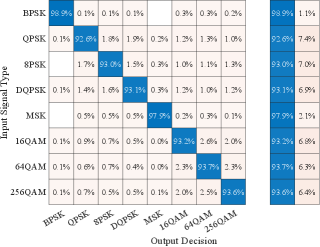
In the first experiment performed, the capsule network outlined in Fig. 1 is trained using DataSet1. Results from this experiment showing the probability of correct classification and the confusion matrix are given in Fig. 2 and Fig. 3, respectively, from which we note an overall performance of correct classification with probabilities of correct classification of individual modulation schemes ranging from for 16-QAM to for BPSK.
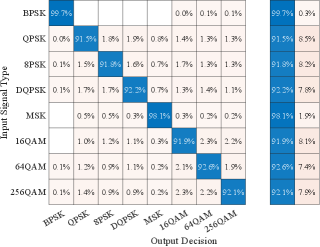
In a following experiment, the capsule network is re-trained using DataSet2, and similar results are obtained as can be seen from Fig. 4 and Fig. 5, showing the probability of correct classification and the confusion matrix, respectively, that are achieved when DataSet2 is used. In this case we note an overall performance of correct classification with probabilities of correct classification of individual modulation schemes ranging from for 8-PSK to for BPSK. The slight improvement in classification performance displayed in this case due to the fact that the SNR range for signals in DataSet2 is more favorable than the SNR range for signals in DataSet1.
Next, we studied the generalization ability of the capsule network, by using signals in DataSet1 for training the network followed by testing with signals in DataSet2. Results from this experiment are shown in Fig. 6 and Fig. 7 from where we note that when the capsule network trained using signals in DataSet1 was tested with signals in DataSet2, the classification performance degraded significantly to an overall probability of correct classification of only as can be observed from Fig. 6, indicating that the capsule network trained using DataSet1 does not appear to generalize training to a different dataset.
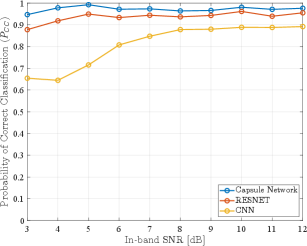
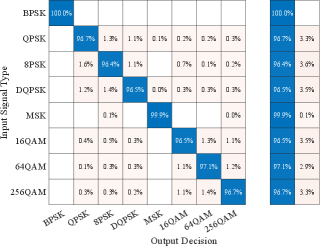
The lack of ability to generalize training is also observed if the capsule network is re-trained using signals from DataSet2 and then tested using signals in DataSet1, in which case a similar overall probability of correct classification of is obtained. Due to space constraints we omit the plots showing the variation of probability of correct classification vs. SNR and the confusion matrix for this experiment, as these are similar to the ones shown in Fig. 6 and Fig. 7, respectively. Thus, we conclude that, while the capsule network is able to adapt well to the dataset change and re-learn to correctly classify modulation types in a new dataset with high accuracy, it is not able to generalize its training to maintain good classification performance when presented with signals in a different dataset. Nevertheless, we note that the capsule network does appear to learn some baseline signal features that are common to both DataSet1 and DataSet2, as the overall probability of correct classification in both cases is more than double that of a random guess111With digital modulation schemes to be classified there is a chance of a random guess being correct., but that the classification performance is sensitive to the different CFOs or symbol rates in the two datasets.

In a final experiment, we combined the signals in DataSet1 and DataSet2 and trained the capsule network with this new, mixed dataset. We note that, while a total of signals are available in the two datasets, due to storage and memory constraints imposed by the high-performance cluster hardware and operation, we included only signals in the combined dataset, randomly taking signals from DataSet1 and from DataSet2 to make up the mixed dataset containing digitally modulated signals. Following a similar approach as for previous experiments, the signals in the combined dataset were divided into three categories, with of signals used for training, for validation, and the remaining of the signals used for testing. The results of this experiment are shown in Fig. 8 and Fig. 9, from which we note an overall performance of correct classification, with probabilities of correct classification of individual modulation schemes ranging from for QPSK to for BPSK.
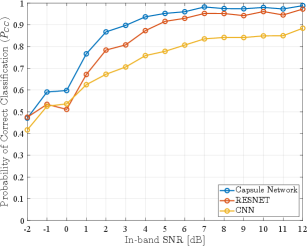
V Conclusions
This paper explored the use of capsule networks for classification of digitally modulated signals using the raw I/Q components of the modulated signal. The overall classification performance implied by capsule networks is on a par or exceeds that obtained in related work where CNNs or residual networks (RESNETs) are used [2, 3], indicating that capsule networks are a meaningful alternative for machine learning approaches to digitally modulated signal classification. We note that, similar to CNNs and RESNETs, when trained with the raw I/Q signal data, capsule networks are able to learn characteristics of the signals in the dataset used for training, but they are not able to generalize their learning to new datasets, which contain similar types of digitally modulated signals but with differences in some of their characteristics such as the CFO or symbol period.
To overcome the problem of generalization, the capsule network was also trained with a mix of datasets, which provided additional training data that contains desired learnable characteristics. This approach improved overall performance of the capsule network when tested with signals from the mixed datasets, acknowledging the expectation that given sufficient training data the overall classification performance improves. To further improve the generalization ability of capsule networks in classifying digitally modulated signals, future work will consider training them using specific features of digitally modulated signals that can be extracted from the raw I/Q signal data, such as those based on cyclostationary signal processing.
Acknowledgment
The authors would like to acknowledge the use of Old Dominion University High-Performance Computing facilities for obtaining numerical results presented in this work.
References
- [1] T. O’Shea and J. Hoydis, “An Introduction to Deep Learning for the Physical Layer,” IEEE Transactions on Cognitive Communications and Networking, vol. 3, no. 4, pp. 563–575, 2017.
- [2] T. J. O’Shea, T. Roy, and T. C. Clancy, “Over-the-Air Deep Learning Based Radio Signal Classification,” IEEE Journal of Selected Topics in Signal Processing, vol. 12, no. 1, pp. 168–179, 2018.
- [3] J. A. Snoap, D. C. Popescu, and C. M. Spooner, “On Deep Learning Classification of Digitally Modulated Signals Using Raw I/Q Data,” in Proceedings Annual IEEE Consumer Communications and Networking Conference – CCNC 2022, Las Vegas, NV, January 2022.
- [4] Y. Sun, M. Peng, Y. Zhou, Y. Huang, and S. Mao, “Application of Machine Learning in Wireless Networks: Key Techniques and Open Issues,” IEEE Communications Surveys Tutorials, vol. 21, no. 4, pp. 3072–3108, 2019.
- [5] F. Hameed, O. A. Dobre, and D. C. Popescu, “On the Likelihood-Based Approach to Modulation Classification,” IEEE Transactions on Wireless Communications, vol. 8, no. 12, pp. 5884–5892, December 2009.
- [6] J. L. Xu, W. Su, and M. Zhou, “Likelihood-Ratio Approaches to Automatic Modulation Classification,” IEEE Transactions on Systems, Man, and Cybernetics – Part C: Applications and Reviews, vol. 41, no. 4, pp. 3072–3108, July 2011.
- [7] L. Li, J. Huang, Q. Cheng, H. Meng, and Z. Han, “Automatic modulation recognition: A few-shot learning method based on the capsule network,” IEEE Wireless Communications Letters, vol. 10, no. 3, pp. 474–477, 2020.
- [8] J. Sun, G. Wang, Z. Lin, S. G. Razul, and X. Lai, “Automatic Modulation Classification of Cochannel Signals using Deep Learning,” in Proceedings 23rd IEEE International Conference on Digital Signal Processing (DSP), 2018, pp. 1–5.
- [9] D. Zhang, W. Ding, C. Liu, H. Wang, and B. Zhang, “Modulated Autocorrelation Convolution Networks for Automatic Modulation Classification Based on Small Sample Set,” IEEE Access, vol. 8, pp. 27 097–27 105, 2020.
- [10] M. Kulin, T. Kazaz, I. Moerman, and E. De Poorter, “End-to-End Learning From Spectrum Data: A Deep Learning Approach for Wireless Signal Identification in Spectrum Monitoring Applications,” IEEE Access, vol. 6, pp. 18 484–18 501, 2018.
- [11] S. Rajendran, W. Meert, D. Giustiniano, V. Lenders, and S. Pollin, “Deep Learning Models for Wireless Signal Classification With Distributed Low-Cost Spectrum Sensors,” IEEE Transactions on Cognitive Communications and Networking, vol. 4, no. 3, pp. 433–445, 2018.
- [12] K. Bu, Y. He, X. Jing, and J. Han, “Adversarial Transfer Learning for Deep Learning Based Automatic Modulation Classification,” IEEE Signal Processing Letters, vol. 27, pp. 880–884, 2020.
- [13] S. Sabour, N. Frosst, and G. E. Hinton, “Dynamic Routing Between Capsules,” in Proceedings International Conference on Neural Information Processing Systems – NIPS’17, Long Beach, CA, December 2017, pp. 3859–3869.
- [14] Y. Sang and L. Li, “Application of novel architectures for modulation recognition,” in 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS). IEEE, 2018, pp. 159–162.
- [15] J. Djolonga, J. Yung, M. Tschannen, and et al., “On Robustness and Transferability of Convolutional Neural Networks,” accessed: Feb. 18, 2021. [Online]. Available: https://arxiv.org/pdf/2007.08558.pdf.
- [16] The CSP Blog, “Data Sets for the Machine Learning Challenge,” accessed May 16, 2022. [Online]. Available: https://cyclostationary.blog/data-sets/.
- [17] M. Zhou, Z. Yin, Z. Wu, C. Y., N. Zhao, and Z. Yang, “A Robust Modulation Classification Method Using Convolutional Neural Networks,” EURASIP Journal on Advances in Signal Processing, vol. 2019, March 2019.
- [18] R. D. Luce, “Luce’s choice axiom,” Scholarpedia, vol. 3, no. 12, p. 8077, 2008.
- [19] C. M. Spooner, “Multi-Resolution White-Space Detection for Cognitive Radio,” in Proceedings 2007 IEEE Military Communications Conference (MILCOM), 2007, pp. 1–9.
- [20] J. A. Latshaw, “Machine Learning Classification of Digitally Modulated Signals,” Master’s thesis, Old Dominion University, Department of Electrical and Computer Engineering, 2022, thesis director: Prof. Dimitrie C. Popescu.
- [21] N. Qian, “On the Momentum Term in Gradient Descent Learning Algorithms,” Neural Networks, vol. 12, no. 1, pp. 145–151, 1999.