Variable-Length Sparse Feedback Codes for Point-to-Point, Multiple Access, and Random Access Channels

The benefits of feedback increase for codes with multiple decoding times (called variable-length or rateless codes). In [7], Burnashev shows that feedback significantly improves the optimal error exponent of variable-length codes for DM-PPCs. In [8], Polyanskiy et al. extend the work of Burnashev to the finite-length regime with non-vanishing error probabilities, introducing variable-length feedback (VLF) codes and deriving achievability and converse bounds on their performance. Tchamkerten and Telatar [9] show that Burnashev’s optimal error exponent is achieved for a family of BSCs and $Z$ channels, where the cross-over probability of the channel is unknown. For the BSC, Naghshvar et al. [10] propose a VLF coding scheme with a novel encoder called the small-enough-difference (SED) encoder and derive a non-asymptotic achievability bound. Their scheme is an alternative to Burnashev’s scheme to achieve the optimal error exponent. Yang et al. [11] extend the SED encoder to the binary asymmetric channel, of which the BSC is a special case, and derive refined non-asymptotic achievability bounds for the binary asymmetric channel. Guo and Kostina [12] propose an instantaneous SED code for a source whose symbols progressively arrive at the encoder in real time.

The feedback in VLF codes can be limited in its amount and frequency. Here, the amount refers to how much feedback is sent from the receiver at each time feedback is available; the frequency refers to how many times feedback is available throughout the communication epoch. The extreme cases in the frequency are no feedback and feedback after every channel use. The extreme cases in the amount are full feedback and stop feedback. With full feedback, at time $n_{i}$, the receiver sends all symbols received until that time, $Y^{n_{i}}$, which can be used by the transmitter to encode the $(n_{i+1})$-th symbol. With stop feedback, the receiver sends a single bit of feedback to inform the transmitter whether or not to stop transmitting. Unlike full-feedback codes, variable-length stop-feedback (VLSF) codes employ codewords that are fixed when the code is designed; that is, feedback affects how much of a codeword is sent but does not affect the codeword’s value.

In [8], Polyanskiy et al. define VLSF codes with feedback after every channel use. The result in [8, Th. 2] shows that variable-length coding improves the first-order term in the asymptotic expansion of the maximum achievable message set size from $NC$ to $\frac{NC}{1-\epsilon}$, where $C$ is the capacity of the DM-PPC, $N$ is the average decoding time (averaging is with respect to both the random message and the random noise), and $\epsilon$ is the average error probability. The second-order term achievable for VLF codes is $O(\log N)$, which means that VLF codes have zero dispersion and that the convergence to the capacity is much faster than that achieved by the fixed-length codes [13, 14]. In [15], Altuğ et al. modify the VLSF coding paradigm by replacing the average decoding time constraint with a constraint on the probability that the decoding time exceeds a target value; the benefit in the first-order term does not appear under this probabilistic delay constraint, and the dispersion is no longer zero. A VLSF scenario with noisy feedback and a finite largest available decoding time is studied in [16]. For VLSF codes, Forney [17] shows an achievable error exponent that is strictly better than that of fixed-length, no-feedback codes and is strictly worse than Burnashev’s error exponent for variable-length full-feedback codes. Ginzach et al. [18] derive the exact error exponent of VLSF codes for the BSC.

Bounds on the performance of VLSF codes that allow feedback after every channel use are derived for several network communication problems. Truong and Tan [19, 20] extend the results from [8] to the Gaussian multiple access channel (MAC) under an average power constraint. Trillingsgaard et al. [21] study the VLSF scenario where a common message is transmitted across a $K$-user discrete memoryless broadcast channel. Heidari et al. [22] extend Burnashev’s work from the DM-PPC to the DM-MAC, deriving lower and upper bounds on the error exponents of VLF codes for the DM-MAC. Bounds on the performance of VLSF codes for the DM-MAC with an unbounded number of decoding times appear in [23]. The achievability bounds for $K$-transmitter MAC in [20] and [23] employ $2^{K}-1$ simultaneous information density threshold rules.

While high rates of feedback are impractical for many applications — especially wireless applications on half-duplex devices — most prior work on VLSF codes (e.g., [8, 15, 19, 20, 21, 22, 23]) considers the densest feedback possible, using feedback at each of the (at most) $n_{\max}$ time steps before decoding, where $n_{\max}$ is the largest blocklength used by a given VLSF code. To consider more limited feedback scenarios, let $L$ denote the number of potential decoding times in a VLSF code, a number that we assume to be independent of the blocklength. We further assume that feedback is available only at the $L$ fixed decoding times $n_{1},\dots,n_{L}$, which are fixed in the code design and known by the transmitter and receiver before the start of transmission. In [24], Kim et al. choose the decoding time for each message from the set $\{d,2d,\dots,Ld\}$ for some positive integer $d$ and $L<\infty$, In [25], Williamson et al. numerically optimize the values of $L$ decoding times and employ punctured convolutional codes and a Viterbi algorithm. In [26], Vakilinia et al. introduce a sequential differential optimization (SDO) algorithm to optimize the choices of the $L$ potential decoding times $n_{1},\dots,n_{L}$, approximating the random decoding time $\tau$ by a Gaussian random variable. Vakilinia et al. apply the SDO algorithm to non-binary low-density parity-check codes over binary-input, additive white Gaussian channels; the mean and variance of $\tau$ are determined through simulation. Heidarzadeh et al. [27] extend [26] to account for the feedback rate and apply the SDO algorithm to random linear codes over the binary erasure channel. In [28], we develop a communication strategy for a random access scenario with a total of $K$ transmitters; in this scenario, neither the transmitters nor the receiver knows the set of active transmitters, which can vary from one epoch to the next. The code in [28] is a VLSF code with decoding times $n_{0}<n_{1}<\dots<n_{K}$. The decoder decodes messages only if it decides at that time that $k$ out of total $K$ transmitters are active at time $n_{k}$. It informs the transmitters about its decision by sending a one-bit signal at each time $n_{i}$ until the time at which it decodes. We show that our random access channel (RAC) code with sparse stop feedback achieves performance identical in the capacity and dispersion terms to that of the best-known code without feedback for a MAC in which the set of active transmitters is known a priori. An extension of [28] to low-density parity-check codes appears in [29]. Building upon an earlier version of the present paper [1], Yang et al. [30] construct an integer program to minimize the upper bound on the average blocklength subject to constraints on the average error probability and the minimum gap between consecutive decoding times. By employing a combination of the Edgeworth expansion [31, Sec. XVI.4] and the Petrov expansion (Lemma 2), that paper develops an approximation to the cumulative distribution function of the information density random variable $\imath(X^{n};Y^{n})$; the numerical comparison of their approximation and the empirical cumulant distribution function shows that the approximation is tight even for small values of $n$. Their analysis uses this tight approximation to numerically evaluate the non-asymptotic achievability bound (Theorem 1, below) for the BSC, binary erasure channel, and binary-input Gaussian PPC for all $L\leq 32$. The resulting numerical results show performance that closely approaches Polyanskiy’s VLSF achievability bound [8] with a relatively small $L$. For the binary erasure channel, [30] also proposes a new zero-error code that employs systematic transmission followed by random linear fountain coding; the proposed code outperforms Polyanskiy’s achievability bound.

Sparse feedback is known to achieve the optimal error exponent for VLF codes. Yamamoto and Itoh [32] construct a two-phase scheme that achieves Burnashev’s optimal error exponent [7]. Although their scheme allows an unlimited number of feedback instances and decoding times, it is sparse in the sense that feedback is available only at times $\alpha n,n,(1+\alpha)n,2n,\dots$ for some $\alpha\in(0,1)$ and integer $n$. Lalitha and Javidi [33] show that Burnashev’s optimal error exponent can be achieved by only $L=3$ decoding times by truncating the Yamamoto–Itoh scheme.

Decoding for VLSF codes can be accomplished by running a sequential hypothesis test (SHT) on each possible message. At each increasingly larger stopping times, the SHT compares a hypothesis $H_{0}$ corresponding to a particular transmitted message to the hypothesis $H_{1}$ corresponding to the marginal distribution of the channel output. In [34], Berlin et al. derive a bound on the average stopping time of an SHT. They then use this bound to derive a non-asymptotic converse bound for VLF codes. This result is an alternative proof for the converse of Burnashev’s error exponent [7].

Like [26, 25, 27], this paper studies VLSF codes under a finite constraint $L$ on the number of decoding times. While [26, 25, 27] focus on practical coding and performance, our goal is to derive new achievability bounds on the asymptotic rate achievable by VLSF codes between $L=1$ (the fixed-length regime analyzed in [13, 35]) and $L=n_{\max}$ (the classical variable-length regime defined in [8, Def. 1] where all decoding times 1, 2, $\dots,n_{\max}$ are available).

Our contributions are summarized as follows.

1. 1.

   We derive second-order achievability bounds for VLSF codes over DM-PPCs, DM-MACs, DM-RACs, and the Gaussian PPC with maximal power constraints. These bounds are presented in Theorems 2, 5, 6, and 7, respectively. In our analysis for each problem, we consider the asymptotic regime where the number of decoding times $L$ is fixed while the average decoding time $N$ grows without bound, i.e., $L=O(1)$ with respect to $N$. Each of our asymptotic bounds follows from the corresponding non-asymptotic bound that employs an information-density threshold rule with a stop-at-time-zero procedure. Asymptotically optimizing the values of the $L$ decoding times yields the given results. By viewing the proposed decoder as a special case of SHT-based decoders, we show a more general non-asymptotic achievability bound; Theorem 8 employs an arbitrary SHT to decide whether a message is transmitted.

2. 2.

   Linking the error probability of any given VLSF code to that of an SHT, in Theorem 9, we prove a converse bound in the spirit of the meta-converse bound from [13, Th. 27]. Analyzing the new bound with infinitely many uniformly-spaced decoding times over Cover–Thomas symmetric channels, in Theorem 3, we prove a converse bound for VLSF codes; the resulting bound is tight up to its second-order term. Unfortunately, since analyzing our meta-converse bound is challenging in the general case of an arbitrary DM-PPC and an arbitrary number $L$ of decoding times (see [36, Th. 3.2.3] for the structure of optimal SHTs with finitely many decoding times), whether or not the second-order term is tight in the general case remains an open question.

Below, we detail these contributions. Our main result shows that for VLSF codes with $L=O(1)\geq 2$ decoding times over a DM-PPC, message set size $M$ satisfying

is achievable. Here $\log_{(L)}(\cdot)$ denotes the $L$-fold nested logarithm, $N$ is the average decoding time, $\epsilon$ is the average error probability, and $C$ and $V$ are the capacity and dispersion of the DM-PPC, respectively. Similar formulas arise for the DM-MAC and DM-RAC, where $C$ and $V$ are replaced by the sum-rate mutual information and the sum-rate dispersion. The speed of convergence to $\frac{C}{1-\epsilon}$ depends on $L$. It is slower than the convergence to $C$ in the fixed-length scenario, which has second-order term $O(\sqrt{N})$ [13]. The $L=2$ case in (1) recovers the rate of convergence for the variable-length scenario without feedback, which has second-order term $O(\sqrt{N\log N})$ [8, Proof of Th. 1]; that rate is achieved with $n_{1}=0$. The nested logarithm term in (1) arises because after writing the average decoding time as $\mathbb{E}\left[\tau\right]=n_{1}+\sum_{i=1}^{L-1}(n_{i+1}-n_{i})\mathbb{P}\left[\tau>n_{i}\right]$, the decoding time choices in (22), below, satisfy $(n_{i+1}-n_{i})\mathbb{P}\left[\tau>n_{i}\right]=o(\sqrt{n_{1}})$ for $i\in[L-1]$, making the effect of each decoding time on the average decoding time asymptotically similar. We then use the SDO algorithm introduced in [26] to show that our particular choice of $n_{1},\dots,n_{L}$ is second-order optimal (see Appendix B.II). Despite the order-wise dependence of the rate of convergence on $L$, (1) grows so slowly with $L$ that it suggests little benefit to choosing a large $L$. For example, when $L=4$, $\sqrt{N\log_{(L-1)}(N)}$ behaves very similarly to $O(\sqrt{N})$ for practical values of $N$ (e.g., $N\in[10^{3},10^{5}]$). Notice, however, that the given achievability result provides a lower bound on the benefit of increasing $L$; bounding the benefit from above requires a converse result. We note, however, that the numerical results in [30] support our conclusion from the asymptotic achievability bound (1) that indicates that the improvement over achievable $\log M$ from $L$ to $L+1$ decoding times diminishes as $L$ increases.

For the PPC and MAC, the feedback rate of our code is $\frac{\ell}{n_{\ell}}$ if the decoding time is $n_{\ell}$; for the RAC, that rate becomes $\frac{(k-1)L+\ell+1}{n_{k,\ell}}$ if the decoding time is $n_{k,\ell}$. In both cases, our feedback rate approaches 0 as the decoding time grows. In contrast, VLSF codes like in [8, 17] use feedback rate 1 bit per channel use. In VLSF codes for the RAC, the decoder decodes at one of the available times $n_{k,1},n_{k,2},\dots,n_{k,L}$ if it estimates that the number of active transmitters is $k\neq 0$; we reserve a single decoding time $n_{0}$ for decoding the possibility that no active transmitters are active. Theorem 6 extends the RAC code in [28] from $L=1$ to any $L\geq 2$.

The converse result in Theorem 3 shows that in order to achieve (1) with evenly spaced decoding times, one needs at least $L=\Omega\left(\sqrt{\frac{N}{\log_{(L-1)}(N)}}\right)$ decoding times. In contrast, our optimized codes achieve (1) with a finite $L$ that does not grow with the average decoding time $N$, which highlights the importance of optimizing the values of decoding times in a VLSF code.

Table I summarizes the literature on VLSF codes and the new results from this work, showing how they vary with the number of decoding times and the channel type.

In what follows, Section II gives notation and definitions. Sections III–VI introduce variable-length sparse stop-feedback codes for the DM-PPC, DM-MAC, DM-RAC, and the Gaussian PPC, respectively, and present our main theorems for those channel models; Section VII concludes the paper. The proofs appear in the Appendix.

For any positive integers $k$ and $n$, $[k]\triangleq\{1,\dots,k\}$, $x^{n}\triangleq(x_{1},\dots,x_{n})$, and $x^{a:b}\triangleq(x_{a},x_{a+1},\dots,x_{b})$. The collection of length-$n$ vectors from the transmitter index set $\mathcal{A}$ is denoted by $x_{\mathcal{A}}^{n}\triangleq(x_{a}^{n}\colon a\in\mathcal{A})$; we drop the superscript $n$ if $n=1$, i.e., $x^{1}_{\mathcal{A}}=x_{\mathcal{A}}$. The collection of non-empty strict subsets of a set $\mathcal{A}$ is denoted by $\mathcal{P}(\mathcal{A})\triangleq\{\mathcal{B}\colon\mathcal{B}\subseteq\mathcal{A},0<|\mathcal{B}|<|\mathcal{A}|\}.$ All-zero and all-one vectors are denoted by $\mathbf{0}$ and $\mathbf{1}$, respectively; dimension is determined from the context. The sets of positive integers and non-negative integers are denoted by $\mathbb{Z}_{+}$ and $\mathbb{Z}_{\geq}$, respectively. We write $x^{n}\stackrel{{\scriptstyle\pi}}{{=}}y^{n}$ if there exists a permutation $\pi$ of $x^{n}$ such that $\pi(x^{n})=y^{n}$, and $x^{n}\stackrel{{\scriptstyle\pi}}{{\neq}}y^{n}$ if such a permutation does not exist. The identity matrix of dimension $n$ is denoted by $\mathsf{I}_{n}$. The Euclidean norm of vector $x^{n}$ is denoted by $\left\lVert x^{n}\right\rVert\triangleq\sqrt{\sum_{i=1}^{n}x_{i}^{2}}$. Unless specified otherwise, all logarithms and exponents have base $e$. Information is measured in nats. The standard $O(\cdot)$, $o(\cdot)$, and $\Omega(\cdot)$ notations are defined as $f(n)=O(g(n))$ if $\limsup_{n\to\infty}|f(n)/g(n)|<\infty$, $f(n)=o(g(n))$ if $\lim_{n\to\infty}|f(n)/g(n)|=0$, and $f(n)=\Omega(g(n))$ if $\lim_{n\to\infty}|f(n)/g(n)|>0$. The distribution of a random variable $X$ is denoted by $P_{X}$; $\mathcal{N}(\bm{\mu},\mathsf{V})$ denotes the Gaussian distribution with mean $\bm{\mu}$ and covariance matrix $\mathsf{V}$, $Q(\cdot)$ represents the complementary standard Gaussian cumulative distribution function $Q(x)\triangleq\frac{1}{\sqrt{2\pi}}\int_{x}^{\infty}\exp\left\{-\frac{t^{2}}{2}\right\}dt$, and $Q^{-1}(\cdot)$ is its functional inverse. We define the nested logarithm function

$\log_{(L)}(x)$ is undefined for all other $(L,x)$ pairs.

We denote the Radon-Nikodym derivative of distribution $P$ with respect to distribution $Q$ by $\frac{\mathrm{d}P}{\mathrm{d}Q}$. We denote the relative entropy and relative entropy variance between $P$ and $Q$ by $D(P\|Q)=\mathbb{E}\left[\log\frac{\mathrm{d}P}{\mathrm{d}Q}(X)\right]$ and $V(P\|Q)=\mathrm{Var}\left[\log\frac{\mathrm{d}P}{\mathrm{d}Q}(X)\right]$, respectively, where $X\sim P$. The $\sigma$-algebra generated by random variable $X$ is denoted by $\mathcal{F}(X)$. A random variable $X$ is called arithmetic if there exists some $d>0$ such that $\mathbb{P}\left[X\in d\mathbb{Z}\right]=1$. The largest $d$ that satisfies this condition is called the span. If such a $d$ does not exist, then the random variable is non-arithmetic. Denote $X^{+}\triangleq\max\{0,X\}$ and $X^{-}\triangleq-\min\{0,X\}$ for any random variable $X$.

A DM-PPC is defined by the triple $(\mathcal{X},P_{Y|X},\mathcal{Y})$, where $\mathcal{X}$ is the finite input alphabet, $P_{Y|X}$ is the channel transition kernel, and $\mathcal{Y}$ is the finite output alphabet. The $n$-letter input-output relationship of the channel is given by $P_{Y^{n}|X^{n}}(y^{n}|x^{n})=\prod_{i=1}^{n}P_{Y|X}(y_{i}|x_{i})$ for all $n$, $x^{n}$, and $y^{n}$.

The $n$-letter information density of a channel $P_{Y|X}$ under input distribution $P_{X^{n}}$ is defined as

where $P_{Y^{n}}$ is the $Y^{n}$ marginal of $P_{X^{n}}P_{Y^{n}|X^{n}}$. If the inputs $X_{1},X_{2},\dots,X_{n}$ are independently and identically distributed (i.i.d.) according to $P_{X}$, then

where the single-letter information density is given by

The mutual information and dispersion are defined as

respectively, where $(X,Y)\sim P_{X}P_{Y|X}$.

Let $\mathcal{P}$ denote all distributions on the alphabet $\mathcal{X}$. The capacity of the DM-PPC is

and the dispersion of the DM-PPC is

We consider VLSF codes with a finite number of potential decoding times $n_{1}<n_{2}<\cdots<n_{L}$ over a DM-PPC. The receiver chooses to end the transmission at the first time $n_{\ell}\in\{n_{1},\ldots,n_{L}\}$ that it is ready to decode. The transmitter learns of the receiver’s decision via a single bit of feedback at each of times $n_{1},\ldots,n_{\ell}$. Feedback bit “0” at time $n_{i}$ means that the receiver is not yet ready to decode, and transmission should continue; feedback bit “1” means that the receiver can decode at time $n_{i}$, which signals the transmitter to stop. Using this feedback, the transmitter and the receiver are synchronized and aware of the current state of the transmission at all times. Since $n_{L}$ is the last decoding time available, the receiver always makes a final decision if time $n_{L}$ is reached. Unlike [7, 32, 25], we do not allow re-transmission of the message after time $n_{L}$. Since the transmitter and the receiver both know the values of decoding times, the receiver does not need to send feedback at the last available time $n_{L}$. We assume that the transmitter and the receiver know the channel transition kernel $P_{Y|X}$. We employ average decoding time and average error probability constraints. Definition 1, below, formalizes our code description.

Recall that Definition 1 with $L=1$ recovers the fixed-length no-feedback codes in [13]. As in [8, 28, 21], we here need common randomness because the traditional random-coding argument does not prove the existence of a single (deterministic) code that simultaneously satisfies conditions (11) and (12) on the code. Therefore, randomized codes are necessary for our achievability argument; here, $|\mathcal{U}|\leq 2$ suffices [28, Appendix D].

We define the maximum achievable message set size $M^{*}(N,L,\epsilon)$ with $L$ decoding times, average decoding time $N$, and average error probability $\epsilon$ as

The maximum achievable message set size for VLSF codes with $L$ decoding times $n_{1},\dots,n_{L}$ that are restricted to belong to a subset $\mathcal{N}\subseteq\mathbb{Z}_{\geq}$ is denoted by $M^{*}(N,L,\epsilon,\mathcal{N})$.

The following discussion summarizes prior asymptotic expansions of the maximum achievable message set size for the DM-PPC.

1. a)

   $M^{*}(N,1,\epsilon)$: For $L=1$ and $\epsilon\in(0,1/2)$, Polyanskiy et al. [13, Th. 49] show that

   $\displaystyle\log M^{*}(N,1,\epsilon)=NC-\sqrt{NV}Q^{-1}(\epsilon)+O(\log N).$

   (14)

   For $\epsilon\in[1/2,1)$, the dispersion $V$ in (9) is replaced by the maximum dispersion $V_{\max}\triangleq\max\limits_{P_{X}\colon\imath(X;Y)=C}V(X;Y)$. The $O(\log N)$ term is lower bounded by $O(1)$ and upper bounded by $\frac{1}{2}\log N+O(1)$. For nonsingular DM-PPCs, i.e., the channels that satisfy $\mathbb{E}\left[\mathrm{Var}\left[\imath(X;Y)|Y\right]\right]>0$ for the distributions that achieve the capacity $C$ and the dispersion $V$, the $O(\log N)$ term is equal to $\frac{1}{2}\log N+O(1)$ [40]. Moulin [41] derives lower and upper bounds on the $O(1)$ term in the asymptotic expansion when the channel is nonsingular with non-lattice information density.

2. b)

   $M^{*}(N,\infty,\epsilon)$: For VLSF codes with $L=n_{\max}=\infty$, Polyanskiy et al. [8, Th. 2] show that for $\epsilon\in(0,1)$,

   	$\displaystyle\log M^{*}(N,\infty,\epsilon)$	$\displaystyle\geq\frac{NC}{1-\epsilon}-\log N+O(1)$		(15)
   	$\displaystyle\log M^{*}(N,\infty,\epsilon)$	$\displaystyle\leq\frac{NC}{1-\epsilon}+\frac{h_{b}(\epsilon)}{1-\epsilon},$		(16)

   where $h_{b}(\epsilon)\triangleq-\epsilon\log\epsilon-(1-\epsilon)\log(1-\epsilon)$ is the binary entropy function (in nats). The bounds in (15)–(16) indicate that the $\epsilon$-capacity (the first-order achievable term) is

   $\displaystyle\lim\inf_{N\to\infty}\frac{1}{N}\log M^{*}(N,\infty,\epsilon)=\frac{C}{1-\epsilon}.$

   (17)

   The achievable dispersion term is zero, i.e., the second-order term in the fundamental limit in (15)–(16) is $o(\sqrt{N})$.

Theorem 1, below, is our non-asymptotic achievability bound for VLSF codes with $L$ decoding times.

Theorem 2, stated next, is our second-order achievability bound for VLSF codes with $L=O(1)$ decoding times over the DM-PPC. The proof of Theorem 2 builds upon the non-asymptotic bound in Theorem 1.

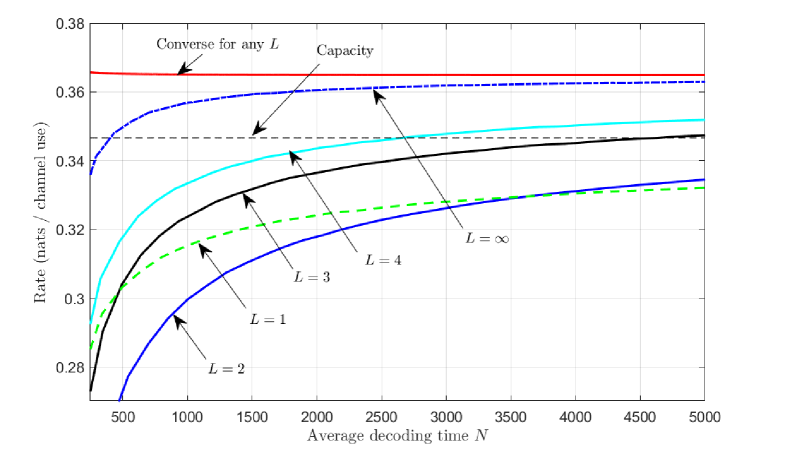
The non-asymptotic achievability bounds obtained from the coding scheme described in the proof sketch of Theorem 2 are illustrated for the BSC in Fig. 1. For $L\in\{2,3,4\}$, the decoding times $n_{1},\dots,n_{L}$ are chosen as described in (22) with the $O(1)$ term ignored, and $\epsilon_{N}^{\prime}$ in the stop-at-time-zero procedure is replaced with the right-hand side of (18). For $L=1$, Fig. 1 shows the random coding union bound in [13, Th. 16], which is a non-asymptotic achievability bound for fixed-length no-feedback codes. For $L=\infty$, Fig. 1 shows the non-asymptotic bound in [8, eq. (102)]. The curves for $L=1$ and $L=2$ cross because the choice of decoding times in (22) requires $\epsilon\gg\frac{1}{\sqrt{N\log N}}$ and is optimal only as $N\to\infty$. In [30], Yang et al. construct a computationally intensive integer program for the numerical optimization of the decoding times for finite $N$. If such a precise optimization is desired, our approximate decoding times in (22) can be used as starting locations for that integer program.

Replacing the information-density-based decoding rule in the proof sketch with the optimal SHT would improve the performance achieved on the right-hand side of (21) by only $O(1)$.

Since any $(N,L,M,\epsilon)$-VLSF code is also an $(N,\infty,M,\epsilon)$-VLSF code, (16) provides an upper bound on $\log M^{*}(N,L,\epsilon)$ for an arbitrary $L$. The order of the second-order term, $-\sqrt{N\log_{(L-1)}(N)\frac{V}{1-\epsilon}}$, depends on the number of decoding times $L$. The larger $L$, the faster the achievable rate converges to the capacity. However, the dependence on $L$ is weak since $\log_{(L-1)}(N)$ grows very slowly in $N$ even if $L$ is small. For example, for $L=4$ and $N=1000$, $\log_{(L-1)}(N)\approx 0.659$. For a finite $L$, this bound falls short of the $-\log N$ achievability bound in (16) achievable with $L=\infty$. Whether the second-order term achieved in Theorem 2 is tight remains an open problem.

The following theorem gives achievability and converse bounds for VLSF codes with decoding times uniformly spaced as $\{0,d_{N},2d_{N},\dots\}$.

Theorem 3 establishes that when $\frac{d_{N}}{\log N}\to\infty$, the second-order term of the logarithm of maximum achievable message set size among VLSF codes with uniformly spaced decoding times is $-\frac{d_{N}C}{2}$. Theorem 3 implies that in order to achieve the same performance as achieved in (21) with $L$ decoding times, one needs on average $\Omega\left(\sqrt{\frac{N}{\log_{(L-1)}(N)}}\right)$ uniformly spaced stop-feedback instances, suggesting that the optimization of available decoding times considered in Theorem 2 is crucial for attaining the second-order term in (21).

The case where $d_{N}=\Omega(N)$ is not as interesting as the case where $d_{N}=o(N)$ since analyzing Theorem 9 using Chernoff bound would yield a bound on the probability that the optimal SHT makes a decision at times other than $n_{1}=0$ and $\frac{N}{1-\epsilon}(1+o(1))$. Since that probability decays exponentially with $N$, the scenario where $L$ is unbounded and $d_{N}=\Omega(N)$ is asymptotically equivalent to $L=2$. For example, for $d_{N}=\frac{1}{\ell}\frac{N}{1-\epsilon}\left(1+O\left(\frac{1}{\sqrt{N\log N}}\right)\right)$ for some $\ell\in\mathbb{Z}_{+}$, the right-hand side of (21) is tight up to the second-order term.

A $K$-transmitter DM-MAC is defined by a triple $\left(\prod_{k=1}^{K}\mathcal{X}_{k},P_{Y_{K}|X_{[K]}},\mathcal{Y}_{K}\right)$, where $\mathcal{X}_{k}$ is the finite input alphabet for transmitter $k\in[K]$, $\mathcal{Y}_{K}$ is the finite output alphabet of the channel, and $P_{Y_{K}|X_{[K]}}$ is the channel transition probability.

In what follows, the subscript and superscript indicate the corresponding transmitter indices and the codeword lengths, respectively. Let $P_{Y_{K}}$ denote the marginal output distribution induced by the input distribution $P_{X_{[K]}}$. The unconditional and conditional information densities are defined for each non-empty $\mathcal{A}\subseteq[K]$ as

where $\mathcal{A}^{c}=[K]\setminus\mathcal{A}$. Note that in (28)–(29), the information density functions depend on the transmitter set $\mathcal{A}$ unless further symmetry conditions are assumed (e.g., in some cases we assume that the components of $P_{X_{[K]}}$ are i.i.d., and $P_{Y_{K}|X_{[K]}}$ is invariant to permutations of the inputs $X_{[K]}$).

The corresponding mutual informations under the input distribution $P_{X_{[K]}}$ and the channel transition probability $P_{Y_{K}|X_{[K]}}$ are defined as

The dispersions are defined as

For brevity, we define