Vector-Like Leptons and Inert Scalar Triplet: Lepton Flavor Violation, and Collider Searches
Abstract
We investigate simplified models involving an inert scalar triplet and vector-like leptons that can account for the muon anomaly. These simplified scenarios are embedded in a model that features W’ and Z’ bosons, which are subject to stringent collider bounds. The constraints coming from the muon anomaly are put into perspective with collider bounds, as well as bounds coming from lepton flavor violation searches. The region of parameter space that explains the anomaly is shown to be within reach of lepton flavor violation probes and future colliders such as HL-LHC and HE-LHC.
pacs:
95.35.+d, 14.60.Pq, 98.80.Cq, 12.60.FrI Introduction
The Dirac Equation predicts that the muon has a magnetic moment equal to , where is the gyromagnetic ratio. Quantum corrections to the -factor are parametrized by the muon anomalous magnetic moment () defined as,
| (1) |
Theoretical calculations of the Standard Model (SM) contributions to represent a remarkable success of quantum field theory. Since is the target of increasingly precise theoretical prediction on the one hand and vigorous experimental measurement on the other, it serves as a golden channel by which the SM can be tested at quantum loop level. Any deviation between theory and experiment would imply the existence of new physics.
Indeed, such a discrepancy between theory and experiment has been found and has persisted over many years Bennett et al. (2002, 2006). The precise extent of the anomaly may be mitigated or exacerbated by the still significant theoretical uncertainties Crivellin et al. (2020); Borsanyi et al. (2020). For example, the anomaly goes from up to depending on the hadronic corrections:
| (2) |
The current value adopted by the Particle Data Group (PDG) is Tanabashi et al. (2018), which is the value used in our work.
Highly anticipated experimental results from FERMILAB Grange et al. (2015), Al-Binni et al. (2013) and the J-PARC Abe et al. (2019) facility in Japan will further shed light on this anomaly. Recent theoretical progress in conjunction with the anticipated increase in experimental precision holds the promise of giving a unique window into beyond SM physics in the near future. It is thus extremely important to explore new physics scenarios which may potentially explain the anomaly, if it does indeed become stronger.
Many scenarios to address the muon anomaly have been put forward in the context of simplified models and supersymmetry Padley et al. (2015); Yamaguchi and Yin (2018); Yin and Yokozaki (2016); Endo and Yin (2019); Endo et al. (2020); Endo and Ueda (2019); Cox et al. (2019); Konar et al. (2018); Un and Ozdal (2016); An and Wang (2015); Chakraborty and Chakraborty (2016); Jana et al. (2020). We refer to Lindner et al. (2018) and references therein for a recent overview of the status of this vast literature.
In this work, we discuss simplified models for the anomaly containing vector-like leptons and an inert scalar triplet, and explore correlations with lepton flavor violation and constraints coming from collider physics. For earlier work on vector-like leptons in the context of , we refer to Dermisek and Raval (2013), Poh and Raby (2017), Barman et al. (2019). We embed our simplified scenarios into a model with the extended gauge group structure (3-3-1 for short) Pisano and Pleitez (1992); Foot et al. (1993); Long (1996a) which has been widely studied in the literature. Our focus is twofold: firstly, to study the confluence of diverse experimental constraints on our simplified models and their capacity to explain the anomaly; and secondly, to assess the possibility of addressing the anomaly within the broader architecture of the 3-3-1 models.
We briefly describe these two aspects of our work. Firstly, the confluence of various experimental results, especially those coming from lepton flavor violation, turns out to be quite restrictive on the prospects of addressing the anomaly within our simplified scenarios. We focus in particular on the rare muon decay , on which the MEG collaboration Baldini et al. (2016) currently imposes the bound . There is an ongoing effort to push this bound down to Mori (2017). Using the bound from the MEG collaboration restricts large portions of parameter space where the anomaly can be addressed; this can be seen from our results in FIG. 4, FIG. 5, and FIG. 6.
Secondly, our work is also relevant for attempts to address the anomaly within 3-3-1 models, since stringent collider bounds severely constrain such efforts in most avatars of these scenarios. The masses of the and bosons in these models are proportional to the energy scale at which . The LHC places strong lower bounds on the masses of these gauge bosons and typically, one finds that the energy scale of 3-3-1 symmetry breaking needs to be too small to explain the anomaly. As we shall see, embedding our simplified scenarios within the 3-3-1 models helps alleviate these tensions.
Our work is structured as follows: in Section II, we describe the simplified models; in Section III, we introduce 3-3-1 models and we present our results for 3-3-1 models that feature an inert scalar triplet and exotic charged leptons; in Section IV, we explore the connection between and collider searches; in Section V, we make the link between and lepton flavor violation, and in Section VI, we draw our conclusions.
II Simplified Models
Several simplified models have been proposed to explain but many of them are excluded by LEP and LHC data Freitas and Westhoff (2014). In this section, we will discuss two possible simplified models that invoke the presence of exotic charged leptons and an inert scalar doublet.
Inert scalar
An inert scalar doublet () under with hypercharge can be introduced to the Standard Model via,
| (3) |
where is the Standard Model lepton doublet, is the Yukawa coupling. Such a scalar doublet is subject to several constraints Freitas and Westhoff (2014). The couplings to Standard Model fermions also give rise a set of model-dependent bounds, which depend on whether this new doublet also interacts with quarks, the strength of its couplings to charged leptons, and if it represents a possible dark matter candidate Wang and Han (2015); Hektor et al. (2015); Cherchiglia et al. (2018); Wang et al. (2019); Iguro et al. (2019). The contribution to is found to be Lindner et al. (2018),
| (4) |
where and .
Such an inert scalar can also induce a sizeable branching ratio which is severely constrained by data. From Eq.(3) we get,
| (5) |
where is a form factor that accounts for the loop correction and carries information about the couplings and masses with,
| (6) |
where,
| (7) |
This general result can be used in all scenarios explored in this work.
Heavy Charged Leptons
Heavy charged leptons () represent an interesting class of models to explain the anomaly Queiroz and Shepherd (2014). Anomaly cancellation requires the introduction of a vector-like lepton with mass arising from a term like . If is a singlet under it will have interactions of the form,
| (8) |
where is now a scalar singlet under . Another way to generate a correction to via an exotic charged lepton is through the introduction of an inert doublet with,
| (9) |
One could also introduce exotic charged leptons () which are doublets under with,
| (10) |
As stated previously, these exotic charged leptons are required to be vector-like to ensure gauge anomaly cancellation. The contributions to are determined by Eq.(4) and arise from an interaction between the muon and a scalar, and an exotic charged lepton, if present. The key differences between these models are the phenomenological constraints they are subject to. While there are important bounds on exotic charged leptons Altmannshofer et al. (2014), these bounds will turn out to be less stringent than the collider bounds we will consider in this work.
We have reviewed possible simplified models that could accommodate the anomaly through the presence of an inert scalar and exotic charged leptons. We now outline how these simplified models can be embedded in 3-3-1 models.
III 3-3-1 Models
3-3-1 models are based on the gauge symmetry and were originally introduced since they offer a plausible answer to the number of generations in the Standard Model. These models have been extensively studied in contexts such as dark matter Fregolente and Tonasse (2003); Long and Lan (2003); de S. Pires and Rodrigues da Silva (2007); Mizukoshi et al. (2011); Profumo and Queiroz (2014); Dong et al. (2013a, b); Cogollo et al. (2014); Dong et al. (2014a, b); Carvajal et al. (2017); Montero et al. (2018); Huong et al. (2019), flavor physics Cabarcas et al. (2012, 2012); Santos and Vasconcelos (2018); Barreto et al. (2018); Wei and Chong-Xing (2017); Hue et al. (2018), neutrino masses Cogollo et al. (2010, 2008); Okada et al. (2016); Vien et al. (2019); Cárcamo Hernández et al. (2018); Nguyen et al. (2018); de Sousa Pires et al. (2019); Carcamo Hernandez et al. (2019a, b); Cárcamo Hernández et al. (2020), and collider physics Meirose and Nepomuceno (2011); Coutinho et al. (2013); Nepomuceno et al. (2016); Nepomuceno and Meirose (2020).
Since is promoted to , the fermion generations are arranged in the fundamental (or antifundamental) representation of . After the symmetry is spontaneously broken via the vacuum expectation value of a scalar triplet, a remnant arises Borges and Ramos (2016). The presence of an triplet implies the existence of new leptons and quarks that contribute to the new non-trivial gauge anomalies. The electric charge operator that preserves the vacuum is found to be,
| (11) |
where and are the generators of and , respectively. The parameters and N are in principle free parameters.
Nevertheless, as we need to recover the Standard Model spectrum, the first two components of the triplet should be a neutrino and a charged lepton. Therefore, . The third component of the triplet should have a quantum number equal to . If one takes , then the third component of the triplet would be a positively charged field. The Minimal 3-3-1 model Pisano and Pleitez (1992) and the 3-3-1 model with exotic charged leptons Ponce et al. (2002a, b); Anderson and Sher (2005); Cabarcas et al. (2014) are based on this choice. However, if one instead chooses then the third field component of the lepton triplet would be either a right-handed neutrino () or a heavy lepton (). These possibilities are known as 3-3-1 models with right-handed neutrinos Long (1996b, a) and 3-3-1 models with a left-handed neutral lepton Mizukoshi et al. (2011); Catano et al. (2012). The popular Economical 3-3-1 model is essentially the 3-3-1 model with right-handed neutrinos where two scalar triplets form the scalar sector Dong et al. (2006); Dong and Long (2008); Berenstein et al. (2009); Martinez and Ochoa (2014).
It has been recently shown that none of these models are capable of accommodating the anomaly due to the existence of stringent collider bounds (see Ky et al. (2000); Kelso et al. (2014); Binh et al. (2015); Cogollo (2017); De Conto and Pleitez (2017) for studies in the context of 3-3-1 models). The masses of the gauge bosons are proportional to the energy scale at which . Since the LHC places strong lower bounds on the masses of the gauge bosons, one can convert these bounds into limits on the energy scale of the 3-3-1 symmetry breaking. A common feature among all these models is that the energy scale of 3-3-1 symmetry breaking needs to be too low ( TeV) to explain . This is forbidden by collider searches. In summary, the most popular 3-3-1 models in the literature cannot address .
We now discuss the embedding of the simplified Lagrangians presented previously within the 3-3-1 model. We will take the 3-3-1 model with neutral heavy leptons as a benchmark, but our results can be easily extended to all five models mentioned earlier. In the 3-3-1 model with heavy neutral leptons, the leptons are arranged as follows,
| (12) |
where runs from one to three and are heavy neutral leptons. We do not consider the hadronic sector since it is not relevant to our discussion. The fermion masses are generated by spontaneous symmetry breaking governed by the three scalar triplets:
| (13) |
One could also successfully generate the fermion masses with two scalar triplets as occurs in the Economical 3-3-1 model Dong et al. (2006); Dong and Long (2008). We stress that the details are not relevant because our results can still be applied to this model. The leptons acquire mass via the Yukawa term in the Lagrangian,
| (14) |
When the neutral fields and develop a non-zero vacuum expectation value, the leptons acquire a mass term. Here we label and . The neutral and vector currents involving new gauge bosons are found to be Long (1996a, b),
| (15) |
with
and,
| (16) |
where,
and
| (18) |
The largest corrections to come from interactions involving new gauge bosons. It has been shown that the most popular 3-3-1 models are incapable of addressing due to the existence of collider bounds as we describe below.
III.1 Collider Bounds
The most important bounds on 3-3-1 models come from LHC searches for new gauge bosons. These limits rely on dilepton resonance searches. Assuming that the decays only into charged leptons the lower mass bound imposes TeV Lindner et al. (2018), which translates into TeV using Eq.III. For easy comparison between and , we note that .
We note that the heavy neutral lepton may be sufficiently light and become kinematically accessible for decays for the boson. The 3-3-1 models typically feature exotic quarks which can also be lighter than . Assuming that all exotic quarks and heavy neutral leptons represent kinematically accessible decay channels, the LHC bounds significantly weaken. Our implementation of the model takes the branching ratio into charged leptons to be between 50%-60% in agreement with de Jesus et al. (2020). The bounds derived from dilepton resonance searches are proportional to the branching ratio into charged leptons. Therefore, we can conservatively state that in light of these new decay modes a conservative LHC bound should read,
| (19) |
As stated in the Introduction, we have assumed the conservative PDG value and for this reason, we will also assume this conservative LHC bound. We stress that our overall conclusions will not change if one decides to alter the LHC bound ( TeV) because there is enough freedom to change other parameters and still obtain qualitatively similar results in regard to .
We now go on to discuss projected constraints coming from the High-Luminosity (HL-LHC) and High-Energy LHC (HE-LHC) on these scenarios. HL-LHC refers to LHC configuration at TeV center-of-mass energy with of integrated luminosity. The HE-LHC denotes a TeV center-of-mass energy with of integrated luminosity. For dilepton resonance searches the number of signal and background events scale equally with energy and luminosity. Thus, the bounds on the number of signal events at each value of the mass can be obtained in terms of the number of background events. We note that there are implicit assumptions about the event acceptance and efficiency rate, which are assumed to be independent of the dilepton invariant mass. It has been shown that these assumptions are reasonable for resonance searches under the narrow width approximation Cid Vidal et al. (2018) and as long as null results are reported. Therefore, one can use the code described in Thamm et al. (2015) to determine the HL-LHC and HE-LHC reach and conclude that
| (20) | |||
| (21) |
IV Muon Anomalous Magnetic Moment and Collider Physics
In this Section, we embed the simplified scenarios involving an inert scalar and exotic leptons introduced earlier into the 3-3-1 models. Our purpose is to study the anomaly and correlate that with potential positive signals in decay, in agreement with existing and future collider bounds.
Inert Scalar Triplet
Since the relevant symmetry is , an inert scalar triplet can be trivially added. Its contribution to is proportional to the mass of the muon, which would imply a suppressed correction to . Thus, we can add
| (22) |
The inert scalar triplet acquires a mass term from the quartic scalar potential term that goes as . Therefore, .
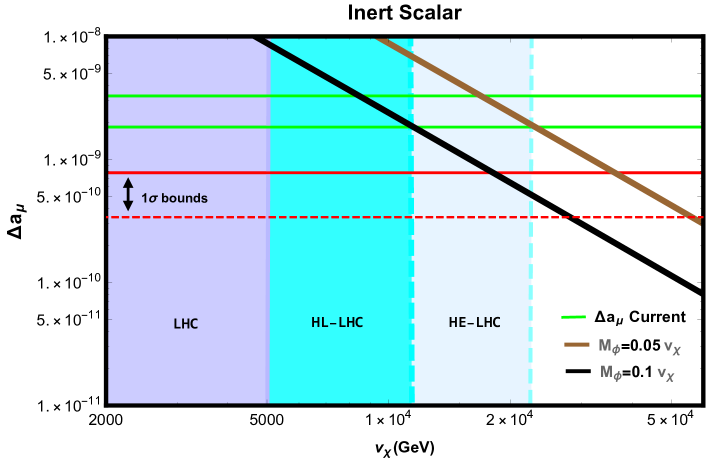
We display our results for . We exhibit the correction to in FIG.1 for (black curve) and (brown curve) and overlay the current and projected collider bounds. In this plot, we considered the Yukawa coupling of the muon with the scalar triplet as , obeying the limits from unitarity, which implies that . The green lines delimit the region of parameter space that explains . The LHC, HL-LHC and HE-LHC limits are superimposed according to Eqs.(19)-(21). The horizontal red lines represent the bounds by requiring the correction to be within the current () and projected () error. From FIG.1 we conclude that a scale of symmetry breaking around TeV is necessary to accommodate . It is important to stress that our choices for and are not random. We found that should be around to be able to explain while still resulting in an energy scale accessible by future colliders. Other values for are possible but then this complementarity with collider searches is lost.
Exotic Charged Lepton
We now explore the addition of vector-like charged leptons. Similar to the previous case, we can introduce a Lagrangian term of the type,
| (23) |
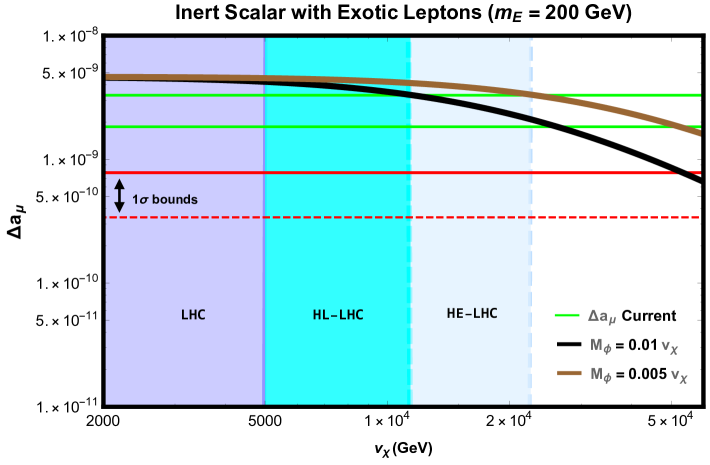
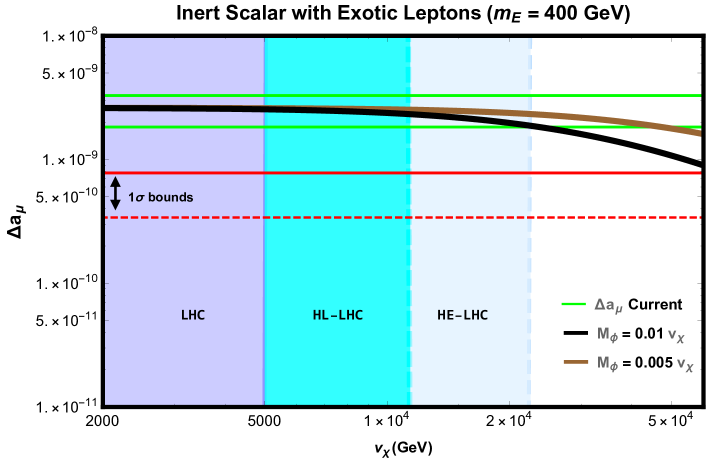
where is singlet scalar field and are vector-like charged leptons, which we assume to be mass degenerate for simplicity. The mass of the vector-like lepton arises from a bare mass term as described in Section II. The key difference between this scenario and the previous one is the presence of an additional free parameter, which is the mass of the vector-like lepton, . The mass of this scalar singlet will also be proportional to , i.e , where is the dimensionless quartic coupling in the scalar potential, similar to the previous case. We exhibit our findings for different values of in FIGs.2-3. A solution to via the introduction of a scalar singlet was also explored in Carcamo Hernandez et al. (2020), but in a different context.
From FIGs.2-3, we conclude that TeV and TeV are favored for and , respectively, where we considered the Yukawa couplings to the scalar singlet to be for the GeV case. Either way, it is interesting to see that there is a strong complementarity between future colliders and . Again notice that gives rise to stronger bounds than colliders by requiring the new physics corrections to be below the error bar.
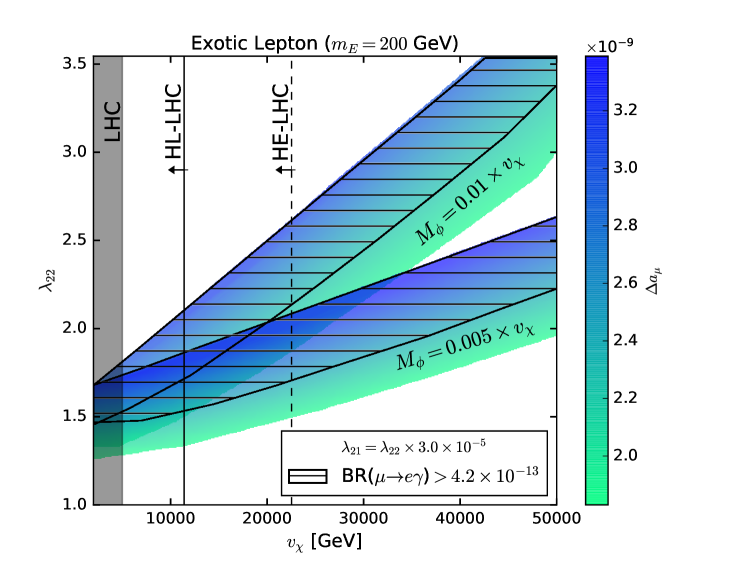
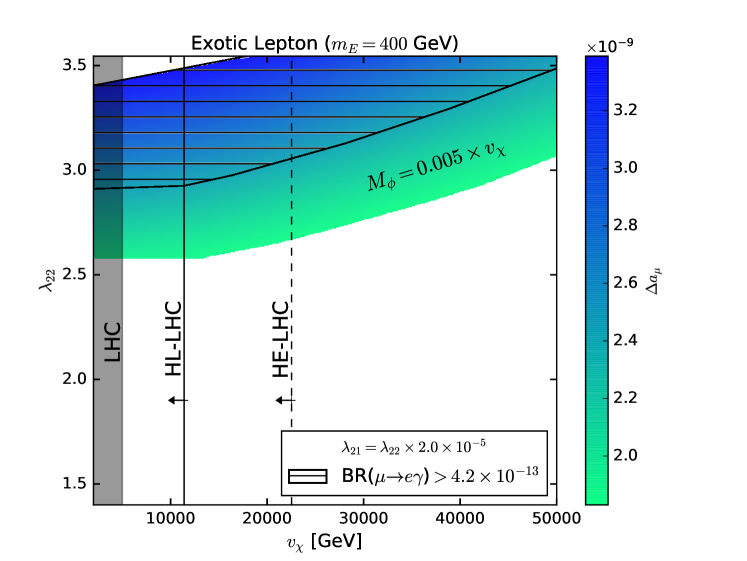
For GeV, the situation changes a bit as the scale of symmetry breaking explains up to higher values (), leaving an unexplored region above TeV to future colliders when we choose , and completely probed when we take , both for .
V Connection with Lepton Flavor Violation
The interplay between and collider bounds has been explored thus far. We now go on to a discussion of the complementarity of our results with lepton flavor violation.
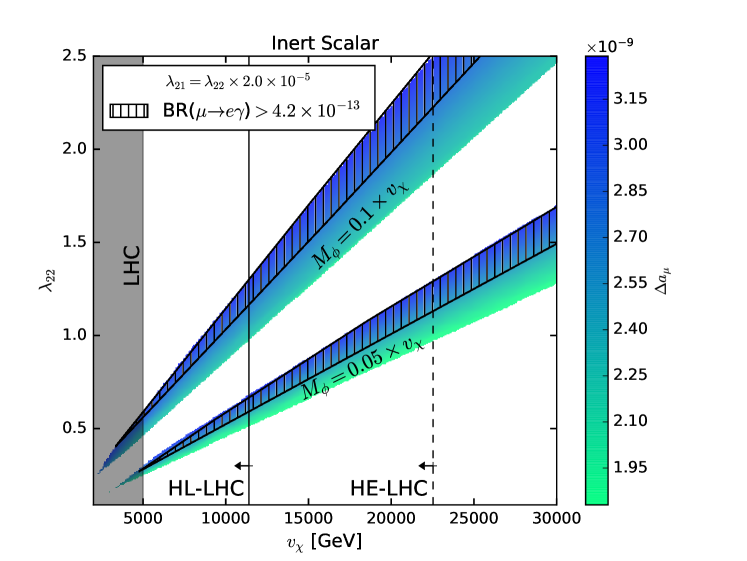
To correlate our findings with lepton flavor violation, we assume benchmark values for the off-diagonal Yukawa couplings. Our results are based on Eq.(5). In FIG.4, we show a contour plot for the inert scalar model in the - plane with the regions that address for and and superimpose the bounds on lepton flavor violation arising from future colliders. The hashed regions are excluded by and the black vertical lines delimit the HL-LHC (continuous) and HE-LHC (dashed) projected limits according to Eq.(21). To exhibit all these observables in the same plane we assumed . Notice that the diagonal coupling, , should be much larger than the off-diagonal coupling, , otherwise the bound coming from would rule out the entire region of parameter space in FIG.4. Notice that if we take TeV, we can explain and leave signatures at the HE-LHC and MEG II detectors. For any value chosen for the scale of symmetry breaking , we find similar conclusions. This is true because we chose a value for the ratio , to be able to show regions that are either excluded or consistent with . If we had adopted larger values for then the decay would have excluded the entire viable region for . We could draw a similar conclusion for . The relation between and was obtained by requiring that the parameter that resolves is testable at future collider and lepton flavor violation searches. Moreover, we can also conclude that exclusion region extends the HE-LHC one. Again, this demonstrates the importance of searching for new physics with complementarity between different observables and detectors.
In the presence of a vector-like exotic charged lepton the situation changes, as we have shown before. Now the connection to lepton flavor violation can be observed as well. In FIGs.5 and 6, we display contour plots in the region of parameter space that accommodates the anomaly and overlay that with projected collider and lepton flavor violation constraints. The only difference between these figures is the value adopted for the exotic charged lepton masses that goes from GeV in FIG.5 to GeV in FIG.6. Here we took , but now we explored the scenarios with and . We stress that these relations between and are obtained by requiring a strong degree of complementarity between , lepton flavor violation and collider physics. Focusing on Fig.5, we can easily conclude that the region with can be tested by future HL-LHC and HE-LHC colliders and decay searches. This conclusion holds true regardless of the exotic charged lepton mass. The quantitative predictions for and obviously change with the choice of the exotic lepton mass, as one can clearly see from FIG.6.
The scale of symmetry breaking that addresses and allows for a signal in is tied to the masses of the neutral () and charged gauge bosons . Therefore, if we observed positive signals in and , we would be able to predict the masses of the new gauge bosons to be observed at future LHC searches for dilepton resonances and charged lepton plus missing energy events which are the golden channel to search for these gauge bosons. This correlation could thus be used to discriminate our model from others in the literature.
VI Conclusions
We presented simplified scenarios that can accommodate the muon anomaly, and discussed their embedding into 3-3-1 models. In the augmented 3-3-1 models with charged vector-like leptons, we were able to accommodate while also being in agreement with collider bounds on the and bosons that appear in these models. This conclusion is valid for other avatars of the 3-3-1 model as well. Obviously, the quantitative results depend on the values assumed for the yukawa couplings and masses of the vector-like fermions, and we explored the possibility of non-zero off-diagonal couplings to exploit the complementarity between , collider searches and lepton flavor violation. If the yukawa couplings are taken to be suppressed the complementarity between different searches is lost. The confluence of various experimental results, especially those coming from the rare muon decay , turned out to be quite restrictive, as can be seen from FIG. 4, FIG. 5, and FIG.6. More optimistically, the solutions investigated here may explain anomaly and induce signals at upcoming searches for the rare decay and future colliders such as the HL-LHC and HE-LHC.
Acknowledgement
SK acknowledges support from CONICYT-Chile Fondecyt No. 1190845 and ANID-Chile PIA/APOYO AFB180002. ASJ acknowledges support from CAPES. CS is supported by MEC (Ministério da Educação) and UFRN. FSQ thanks CNPq grants 303817/2018-6 and 421952/2018-0, and ICTP-SAIFR FAPESP grant 2016/01343-7 for the financial support. FSQ thanks Andres Bello and UFRGS for the hospitality where part of this was partly done. This work was supported by the Serrapilheira Institute (grant number Serra-1912-31613). KS is supported by DOE Grant DE-SC0009956. We thank the High Performance Computing Center (NPAD) at UFRN for providing computational resources.
References
- Bennett et al. (2002) G. W. Bennett et al. (Muon g-2), Phys. Rev. Lett. 89, 101804 (2002), [Erratum: Phys. Rev. Lett.89,129903(2002)], arXiv:hep-ex/0208001 [hep-ex] .
- Bennett et al. (2006) G. W. Bennett et al. (Muon g-2), Phys. Rev. D73, 072003 (2006), arXiv:hep-ex/0602035 [hep-ex] .
- Crivellin et al. (2020) A. Crivellin, M. Hoferichter, C. A. Manzari, and M. Montull, (2020), arXiv:2003.04886 [hep-ph] .
- Borsanyi et al. (2020) S. Borsanyi et al., (2020), arXiv:2002.12347 [hep-lat] .
- Prades et al. (2009) J. Prades, E. de Rafael, and A. Vainshtein, Adv. Ser. Direct. High Energy Phys. 20, 303 (2009), arXiv:0901.0306 [hep-ph] .
- Tanabashi et al. (2018) M. Tanabashi et al. (Particle Data Group), Phys. Rev. D98, 030001 (2018).
- Benayoun et al. (2013) M. Benayoun, P. David, L. DelBuono, and F. Jegerlehner, Eur. Phys. J. C73, 2453 (2013), arXiv:1210.7184 [hep-ph] .
- Blum et al. (2013) T. Blum, A. Denig, I. Logashenko, E. de Rafael, B. L. Roberts, T. Teubner, and G. Venanzoni, (2013), arXiv:1311.2198 [hep-ph] .
- Benayoun et al. (2015) M. Benayoun, P. David, L. DelBuono, and F. Jegerlehner, Eur. Phys. J. C75, 613 (2015), arXiv:1507.02943 [hep-ph] .
- Jegerlehner (2018) F. Jegerlehner, Proceedings, KLOE-2 Workshop on Collision Physics at 1 GeV: Frascati, Italy, October , 2016, EPJ Web Conf. 166, 00022 (2018), arXiv:1705.00263 [hep-ph] .
- Keshavarzi et al. (2018) A. Keshavarzi, D. Nomura, and T. Teubner, Phys. Rev. D97, 114025 (2018), arXiv:1802.02995 [hep-ph] .
- Grange et al. (2015) J. Grange et al. (Muon g-2), (2015), arXiv:1501.06858 [physics.ins-det] .
- Al-Binni et al. (2013) U. Al-Binni et al., in Proceedings, 2013 Community Summer Study on the Future of U.S. Particle Physics: Snowmass on the Mississippi (CSS2013): Minneapolis, MN, USA, July 29-August 6, 2013, edited by A. S. Kronfeld and R. S. Tschirhart (2013) arXiv:1306.5009 [hep-ex] .
- Abe et al. (2019) M. Abe et al., PTEP 2019, 053C02 (2019), arXiv:1901.03047 [physics.ins-det] .
- Padley et al. (2015) B. P. Padley, K. Sinha, and K. Wang, Phys. Rev. D92, 055025 (2015), arXiv:1505.05877 [hep-ph] .
- Yamaguchi and Yin (2018) M. Yamaguchi and W. Yin, PTEP 2018, 023B06 (2018), arXiv:1606.04953 [hep-ph] .
- Yin and Yokozaki (2016) W. Yin and N. Yokozaki, Phys. Lett. B762, 72 (2016), arXiv:1607.05705 [hep-ph] .
- Endo and Yin (2019) M. Endo and W. Yin, JHEP 08, 122 (2019), arXiv:1906.08768 [hep-ph] .
- Endo et al. (2020) M. Endo, K. Hamaguchi, S. Iwamoto, and T. Kitahara, (2020), arXiv:2001.11025 [hep-ph] .
- Endo and Ueda (2019) M. Endo and D. Ueda, (2019), arXiv:1911.10805 [hep-ph] .
- Cox et al. (2019) P. Cox, C. Han, T. T. Yanagida, and N. Yokozaki, JHEP 08, 097 (2019), arXiv:1811.12699 [hep-ph] .
- Konar et al. (2018) P. Konar, T. Mondal, and A. K. Swain, JHEP 04, 024 (2018), arXiv:1710.08664 [hep-ph] .
- Un and Ozdal (2016) C. S. Un and O. Ozdal, Phys. Rev. D93, 055024 (2016), arXiv:1601.02494 [hep-ph] .
- An and Wang (2015) H. An and L.-T. Wang, Phys. Rev. Lett. 115, 181602 (2015), arXiv:1506.00653 [hep-ph] .
- Chakraborty and Chakraborty (2016) A. Chakraborty and S. Chakraborty, Phys. Rev. D93, 075035 (2016), arXiv:1511.08874 [hep-ph] .
- Jana et al. (2020) S. Jana, V. P. K., and S. Saad, (2020), arXiv:2003.03386 [hep-ph] .
- Lindner et al. (2018) M. Lindner, M. Platscher, and F. S. Queiroz, Phys. Rept. 731, 1 (2018), arXiv:1610.06587 [hep-ph] .
- Dermisek and Raval (2013) R. Dermisek and A. Raval, Phys. Rev. D88, 013017 (2013), arXiv:1305.3522 [hep-ph] .
- Poh and Raby (2017) Z. Poh and S. Raby, Phys. Rev. D96, 015032 (2017), arXiv:1705.07007 [hep-ph] .
- Barman et al. (2019) B. Barman, D. Borah, L. Mukherjee, and S. Nandi, Phys. Rev. D100, 115010 (2019), arXiv:1808.06639 [hep-ph] .
- Pisano and Pleitez (1992) F. Pisano and V. Pleitez, Phys. Rev. D46, 410 (1992), arXiv:hep-ph/9206242 [hep-ph] .
- Foot et al. (1993) R. Foot, O. F. Hernandez, F. Pisano, and V. Pleitez, Phys. Rev. D47, 4158 (1993), arXiv:hep-ph/9207264 [hep-ph] .
- Long (1996a) H. N. Long, Phys. Rev. D53, 437 (1996a), arXiv:hep-ph/9504274 [hep-ph] .
- Baldini et al. (2016) A. M. Baldini et al. (MEG), Eur. Phys. J. C76, 434 (2016), arXiv:1605.05081 [hep-ex] .
- Mori (2017) T. Mori (MEG), Proceedings, 30th Rencontres de Physique de La Vallée d’Aoste: La Thuile, Aosta Valley, Italy, March 6-12, 2016, Nuovo Cim. C39, 325 (2017), arXiv:1606.08168 [hep-ex] .
- Freitas and Westhoff (2014) A. Freitas and S. Westhoff, JHEP 10, 116 (2014), arXiv:1408.1959 [hep-ph] .
- Wang and Han (2015) L. Wang and X.-F. Han, JHEP 05, 039 (2015), arXiv:1412.4874 [hep-ph] .
- Hektor et al. (2015) A. Hektor, K. Kannike, and L. Marzola, JCAP 1510, 025 (2015), arXiv:1507.05096 [hep-ph] .
- Cherchiglia et al. (2018) A. Cherchiglia, D. Stöckinger, and H. Stöckinger-Kim, Phys. Rev. D98, 035001 (2018), arXiv:1711.11567 [hep-ph] .
- Wang et al. (2019) L. Wang, J. M. Yang, M. Zhang, and Y. Zhang, Phys. Lett. B788, 519 (2019), arXiv:1809.05857 [hep-ph] .
- Iguro et al. (2019) S. Iguro, Y. Omura, and M. Takeuchi, JHEP 11, 130 (2019), arXiv:1907.09845 [hep-ph] .
- Queiroz and Shepherd (2014) F. S. Queiroz and W. Shepherd, Phys. Rev. D89, 095024 (2014), arXiv:1403.2309 [hep-ph] .
- Altmannshofer et al. (2014) W. Altmannshofer, M. Bauer, and M. Carena, JHEP 01, 060 (2014), arXiv:1308.1987 [hep-ph] .
- Fregolente and Tonasse (2003) D. Fregolente and M. D. Tonasse, Phys. Lett. B555, 7 (2003), arXiv:hep-ph/0209119 [hep-ph] .
- Long and Lan (2003) H. N. Long and N. Q. Lan, Europhys. Lett. 64, 571 (2003), arXiv:hep-ph/0309038 [hep-ph] .
- de S. Pires and Rodrigues da Silva (2007) C. A. de S. Pires and P. S. Rodrigues da Silva, JCAP 0712, 012 (2007), arXiv:0710.2104 [hep-ph] .
- Mizukoshi et al. (2011) J. K. Mizukoshi, C. A. de S. Pires, F. S. Queiroz, and P. S. Rodrigues da Silva, Phys. Rev. D83, 065024 (2011), arXiv:1010.4097 [hep-ph] .
- Profumo and Queiroz (2014) S. Profumo and F. S. Queiroz, Eur. Phys. J. C74, 2960 (2014), arXiv:1307.7802 [hep-ph] .
- Dong et al. (2013a) P. V. Dong, T. P. Nguyen, and D. V. Soa, Phys. Rev. D88, 095014 (2013a), arXiv:1308.4097 [hep-ph] .
- Dong et al. (2013b) P. V. Dong, H. T. Hung, and T. D. Tham, Phys. Rev. D87, 115003 (2013b), arXiv:1305.0369 [hep-ph] .
- Cogollo et al. (2014) D. Cogollo, A. X. Gonzalez-Morales, F. S. Queiroz, and P. R. Teles, JCAP 1411, 002 (2014), arXiv:1402.3271 [hep-ph] .
- Dong et al. (2014a) P. V. Dong, D. T. Huong, F. S. Queiroz, and N. T. Thuy, Phys. Rev. D90, 075021 (2014a), arXiv:1405.2591 [hep-ph] .
- Dong et al. (2014b) P. V. Dong, N. T. K. Ngan, and D. V. Soa, Phys. Rev. D90, 075019 (2014b), arXiv:1407.3839 [hep-ph] .
- Carvajal et al. (2017) C. D. R. Carvajal, B. L. Sanchez-Vega, and O. Zapata, Phys. Rev. D96, 115035 (2017), arXiv:1704.08340 [hep-ph] .
- Montero et al. (2018) J. C. Montero, A. Romero, and B. L. Sanchez-Vega, Phys. Rev. D97, 063015 (2018), arXiv:1709.04535 [hep-ph] .
- Huong et al. (2019) D. T. Huong, D. N. Dinh, L. D. Thien, and P. Van Dong, JHEP 08, 051 (2019), arXiv:1906.05240 [hep-ph] .
- Cabarcas et al. (2012) J. M. Cabarcas, J. Duarte, and J. A. Rodriguez, Proceedings on 11th International Conference on Heavy Quarks and Leptons (HQL 2012): Prague, Czech Republic, Jun. 11-15, 2012, PoS HQL2012, 072 (2012), arXiv:1212.3586 [hep-ph] .
- Santos and Vasconcelos (2018) A. C. O. Santos and P. Vasconcelos, Adv. High Energy Phys. 2018, 9132381 (2018), arXiv:1708.03955 [hep-ph] .
- Barreto et al. (2018) E. R. Barreto, A. G. Dias, J. Leite, C. C. Nishi, R. L. N. Oliveira, and W. C. Vieira, Phys. Rev. D97, 055047 (2018), arXiv:1709.09946 [hep-ph] .
- Wei and Chong-Xing (2017) M. Wei and Y. Chong-Xing, Phys. Rev. D95, 035040 (2017), arXiv:1702.01255 [hep-ph] .
- Hue et al. (2018) L. T. Hue, L. D. Ninh, T. T. Thuc, and N. T. T. Dat, Eur. Phys. J. C78, 128 (2018), arXiv:1708.09723 [hep-ph] .
- Cogollo et al. (2010) D. Cogollo, H. Diniz, and C. A. de S. Pires, Phys. Lett. B687, 400 (2010), arXiv:1002.1944 [hep-ph] .
- Cogollo et al. (2008) D. Cogollo, H. Diniz, C. A. de S. Pires, and P. S. Rodrigues da Silva, Eur. Phys. J. C58, 455 (2008), arXiv:0806.3087 [hep-ph] .
- Okada et al. (2016) H. Okada, N. Okada, and Y. Orikasa, Phys. Rev. D93, 073006 (2016), arXiv:1504.01204 [hep-ph] .
- Vien et al. (2019) V. V. Vien, H. N. Long, and A. E. Carcamo Hernandez, Mod. Phys. Lett. A34, 1950005 (2019), arXiv:1812.07263 [hep-ph] .
- Cárcamo Hernández et al. (2018) A. E. Cárcamo Hernández, H. N. Long, and V. V. Vien, Eur. Phys. J. C78, 804 (2018), arXiv:1803.01636 [hep-ph] .
- Nguyen et al. (2018) T. P. Nguyen, T. T. Le, T. T. Hong, and L. T. Hue, Phys. Rev. D97, 073003 (2018), arXiv:1802.00429 [hep-ph] .
- de Sousa Pires et al. (2019) C. A. de Sousa Pires, F. Ferreira De Freitas, J. Shu, L. Huang, and P. Wagner Vasconcelos Olegário, Phys. Lett. B797, 134827 (2019), arXiv:1812.10570 [hep-ph] .
- Carcamo Hernandez et al. (2019a) A. E. Carcamo Hernandez, N. A. Perez-Julve, and Y. Hidalgo Velasquez, Phys. Rev. D100, 095025 (2019a), arXiv:1907.13083 [hep-ph] .
- Carcamo Hernandez et al. (2019b) A. E. Carcamo Hernandez, Y. Hidalgo Velasquez, and N. A. Perez-Julve, Eur. Phys. J. C79, 828 (2019b), arXiv:1905.02323 [hep-ph] .
- Cárcamo Hernández et al. (2020) A. E. Cárcamo Hernández, L. T. Hue, S. Kovalenko, and H. N. Long, (2020), arXiv:2001.01748 [hep-ph] .
- Meirose and Nepomuceno (2011) B. Meirose and A. A. Nepomuceno, Phys. Rev. D84, 055002 (2011), arXiv:1105.6299 [hep-ph] .
- Coutinho et al. (2013) Y. A. Coutinho, V. Salustino Guimarães, and A. A. Nepomuceno, Phys. Rev. D87, 115014 (2013), arXiv:1304.7907 [hep-ph] .
- Nepomuceno et al. (2016) A. Nepomuceno, B. Meirose, and F. Eccard, Phys. Rev. D94, 055020 (2016), arXiv:1604.07471 [hep-ph] .
- Nepomuceno and Meirose (2020) A. Nepomuceno and B. Meirose, Phys. Rev. D101, 035017 (2020), arXiv:1911.12783 [hep-ph] .
- Borges and Ramos (2016) J. S. Borges and R. O. Ramos, Eur. Phys. J. C76, 344 (2016), arXiv:1602.08165 [hep-ph] .
- Ponce et al. (2002a) W. A. Ponce, J. B. Florez, and L. A. Sanchez, Int. J. Mod. Phys. A17, 643 (2002a), arXiv:hep-ph/0103100 [hep-ph] .
- Ponce et al. (2002b) W. A. Ponce, Y. Giraldo, and L. A. Sanchez, Proceedings, 8th Mexican Workshop on Particles and Fields: Zacatecas, Mexico, November 14-20, 2001, AIP Conf. Proc. 623, 341 (2002b), arXiv:hep-ph/0201133 [hep-ph] .
- Anderson and Sher (2005) D. L. Anderson and M. Sher, Phys. Rev. D72, 095014 (2005), arXiv:hep-ph/0509200 [hep-ph] .
- Cabarcas et al. (2014) J. M. Cabarcas, J. Duarte, and J. A. Rodriguez, Int. J. Mod. Phys. A29, 1450015 (2014), arXiv:1310.1407 [hep-ph] .
- Long (1996b) H. N. Long, Phys. Rev. D54, 4691 (1996b), arXiv:hep-ph/9607439 [hep-ph] .
- Catano et al. (2012) M. E. Catano, R. Martinez, and F. Ochoa, Phys. Rev. D86, 073015 (2012), arXiv:1206.1966 [hep-ph] .
- Dong et al. (2006) P. V. Dong, H. N. Long, D. T. Nhung, and D. V. Soa, Phys. Rev. D73, 035004 (2006), arXiv:hep-ph/0601046 [hep-ph] .
- Dong and Long (2008) P. V. Dong and H. N. Long, Adv. High Energy Phys. 2008, 739492 (2008), arXiv:0804.3239 [hep-ph] .
- Berenstein et al. (2009) D. Berenstein, R. Martinez, F. Ochoa, and S. Pinansky, Phys. Rev. D79, 095005 (2009), arXiv:0807.1126 [hep-ph] .
- Martinez and Ochoa (2014) R. Martinez and F. Ochoa, Phys. Rev. D90, 015028 (2014), arXiv:1405.4566 [hep-ph] .
- Ky et al. (2000) N. A. Ky, H. N. Long, and D. Van Soa, Phys. Lett. B486, 140 (2000), arXiv:hep-ph/0007010 [hep-ph] .
- Kelso et al. (2014) C. Kelso, P. R. D. Pinheiro, F. S. Queiroz, and W. Shepherd, Eur. Phys. J. C74, 2808 (2014), arXiv:1312.0051 [hep-ph] .
- Binh et al. (2015) D. T. Binh, D. T. Huong, and H. N. Long, Zh. Eksp. Teor. Fiz. 148, 1115 (2015), [J. Exp. Theor. Phys.121,no.6,976(2015)], arXiv:1504.03510 [hep-ph] .
- Cogollo (2017) D. Cogollo, (2017), arXiv:1706.00397 [hep-ph] .
- De Conto and Pleitez (2017) G. De Conto and V. Pleitez, JHEP 05, 104 (2017), arXiv:1603.09691 [hep-ph] .
- de Jesus et al. (2020) A. S. de Jesus, S. Kovalenko, F. S. Queiroz, C. A. d. S. Pires, and Y. S. Villamizar, (2020), arXiv:2003.06440 [hep-ph] .
- Cid Vidal et al. (2018) X. Cid Vidal et al. (Working Group 3), (2018), arXiv:1812.07831 [hep-ph] .
- Thamm et al. (2015) A. Thamm, R. Torre, and A. Wulzer, JHEP 07, 100 (2015), arXiv:1502.01701 [hep-ph] .
- Carcamo Hernandez et al. (2020) A. E. Carcamo Hernandez, Y. H. Velasquez, S. Kovalenko, H. N. Long, N. A. Perez-Julve, and V. V. Vien, (2020), arXiv:2002.07347 [hep-ph] .