Vortex pair annihilation in arrays of photon cavities

Vladimir N. Gladilin Michiel Wouters TQC, Universiteit Antwerpen, Universiteitsplein 1, B-2610 Antwerpen, Belgium

Abstract

We investigate theoretically the evolution of the vortex number in an array of photon condensates that is brought from an incoherent low density state to a coherent high density state by a sudden change in the pumping laser intensity. We analyze how the recombination of vortices and antivortices depends on the system parameters such as the coefficients for emission and absorption of photons by the dye molecules, the rate of tunneling between the cavities, the photon loss rate and the number of photons in the condensate.

I Introduction

Vortex excitations of superfluids chaikin play a crucial role in a variety of phenomena such as the Berezinskii-Kosterlitz-Thouless (BKT) transition, the Kibble-Zurek (KZ) mechanism, the formation of Abrikosov vortex lattices and the the drag force on objects moving through a superfluid. These phenomena have been experimentally studied on a number of physical platforms such as superconductors, liquid helium and ultracold atoms bec_book . What all these systems have in common is that they are up to a very good approximation in (local) thermal equilibrium, a condition that is typically broken in experimental platforms that are based on optical systems carusotto13 ; carusotto21 . Optical Bose-Einstein condensates (BECs) have been experimentally achieved in optical cavities filled with a dye molecule solution and in microcavities where a photon is strongly coupled to an exciton resulting in exciton-polariton kavokin17 . While in the latter system, interactions between exciton-polaritons can lead to stimulated scattering into the ground state, in the photon-dye system it is repeated absorption and reemission of photons klaers_therm that enables a macroscopic occupation of the ground state klaers10 ; marelic16 ; greveling18 .

Due to photon losses, optical BECs need constant pumping by an excitation laser in order to reach a steady state where pumping balances the losses. Experimentally realized photon condensates are therefore driven-dissipative systems. The availability of several other experimental platforms, such as exciton-polaritons carusotto21 , superconducting circuits carusotto20 and Rydberg atoms bernien17 , for the study of driven-dissipative systems and their interest for quantum simulation and quantum computation has spurred substantial theoretical activity hartmann08 ; angelakis17 ; carusotto20 ; carusotto21 .

A typical photon condensation experiment starts from an empty cavity and optical excitations are created by turning on the pumping laser where the phase transition is crossed when the photon density exceeds threshold. Upon crossing the threshold, the system goes from the disordered to the ordered state, which according to the KZ mechanism may lead to the formation of vortex pairs. Vortices in nonequilibrium BECs have been the subject of both experimental Kasprzak06 ; lagoudakis08 ; lagoudakis2011 ; Liew15 ; caputo2016 and theoretical marchettiPRL10 ; cancellieriPRB14 ; ma2017 ; gladilin17 study in exciton-polariton systems, whereas in nonequilibrium photon condensates, vortices have only been studied theoretically gladilin20b .

The vortex pairs that are generated after a pump power quench are expected to disappear in a subsequent phase annealing stage, such that in the steady state above the critical density no vortices remain. The recombination of vortices and antivortices depends on their interactions, that has been shown to be crucially affected by the nonequilibrium condition giving rise to particle currents away from the vortex core. As a consequence, vortices, even of opposite signs, experience a long-range repulsion gladilin17 , that obviously hampers their recombination. This physics was theoretically investigated for exciton-polaritons and indeed it was found that the vortex pair annihilation is strongly affected by the nonequilibrium condition, where it was even observed that very long lived complexes of vortices and antivortices may form under certain conditions gladilin19 .

Photon condensates are even somewhat more peculiar for the study of vortex physics, because their negligible interactions imply that the core size tends to infinity in the equilibrium limit. This stands in contrast to polariton condensates, where the interactions always keep the vortex core size finite. It was however shown recently that a finite vortex core and therefore well defined vortex excitations do exist in lattices of coupled nonequilibrium photon condensates gladilin20b . Such lattices of photon condensates can be experimentally created by patterning the microcavity mirrors kassenberg20 ; dung17 , analogous to lattices for exciton-polaritons schneider16 . These vortices feature several unusual properties such as self acceleration and core deformation in addition to the aforementioned outward currents.

The twodimensional nature of polariton condensates implies that the phase transition between the normal and superfluid state at equilibrium is of the BKT type. Numerical simulations have provided evidence that a similar transition exists out of equilibrium dagdavorj ; caputo2016 ; gladilin19 ; comaron18 , even though studies based on the renormalization group have pointed out that the phase transition is crucially affected at long distances by the Kardar-Parisi-Zhang dynamics of the phase, that tends to destroy the ordered phase altman15 ; wachtel ; sieberer ; zamora . In practice, however, the KPZ physics can be limited to very large system sizes, so that in experimental 2D systems the BKT-like physics dominates dagdavorj ; caputo2016 ; gladilin19 ; comaron18 . Recently, we have shown by analytical arguments and numerical simulations that also photon condensates without interactions do feature a BKT like phase transition, that is stabilized by the driving and dissipation gladilin21 . The question of the dynamical formation of the ordered state after a rapid switching of the pumping intensity is therefore also relevant for photon condensates.

In the present paper, we address this issue. In particular, we investigate the annihilation of vortex pairs in a lattice of photon condensates where the pumping laser intensity is suddenly ramped up, starting from zero. After a short initial transient, the density goes relatively quickly to its steady state, but many phase defects, remnants of the random phases of the initial state, remain. By varying the system parameters (tunneling strength, emission/absorption coefficient, loss rate, photon number) around the range of their typical experimental values, we try to shed more light on the physics that governs the annihilation dynamics. We reveal a regime where the quasi-circular vortex trajectories together with the long range repulsion lead to a low mobility vortex-antivortex phase that shows very slow annihilation. In addition, we show that for very high emission/absorption rate the annihilation is fast and tends to the time dependence derived for the relaxational dynamics of the XY model yurke1993 ; jelic11 , a regime that was previously also obtained in numerical simulations for polariton condensates close to thermal equilibrium comaron18 ; gladilin19 .

The remainder of the paper is organized as follows. In Sec. II, we recapitulate our classical field model for photon condensates and describe the numerical simulations. In Sec. III, we discuss the various dependencies of the pair annihilation rate on the system parameters: the rates of emission/absorption, tunneling and losses and the photon number. Our conclusions are presented in Sec. IV.

II Model

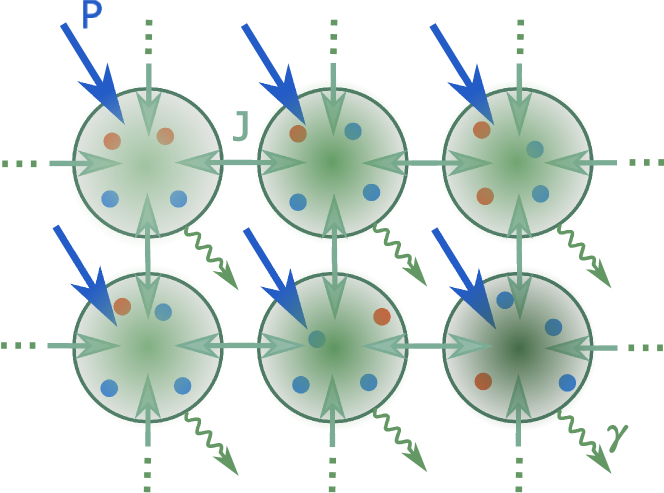
Refer to caption — Figure 1: Sketch of a part of the photon condensate array under study: the photonic cavity modes are coupled through tunneling with amplitude $J$ and are lost from the cavities at rate $\gamma$ . The dye molecules are localized in the cavities and can be in the ground state or excited state manifolds (indicated by different colors). The system is pumped by a laser with intensity $P$ , that excites the dye molecules.

At the semiclassical level, the system of coupled photon condensates can be described by a generalized Gross-Pitaevskii equation for the photon field $\psi(\mathbf{x})$ at each cavity position $\mathbf{x}$ gladilin20

	$\displaystyle i\hbar\frac{\partial\psi(\mathbf{x},t)}{\partial t}=$	$\displaystyle\frac{i}{2}\left[B_{21}M_{2}(\mathbf{x},t)-B_{12}M_{1}(\mathbf{x},t)-\gamma\right]\psi(\mathbf{x},t)$
		$\displaystyle-(1-i\kappa)J\sum_{\mathbf{x}^{\prime}\in\mathcal{N}_{\mathbf{x}}}\psi(\mathbf{x}^{\prime},t),$		(1)

where $\gamma$ is the photon loss rate and $J$ the coupling between the nearest-neighbor cavities kassenberg20 ; dung17 . The photons thermalize thanks to repeated absorption and emission by the dye molecules with respective rate coefficients $B_{12}$ and $B_{21}$ . The ground (excited) molecular state occupation is denoted by $M_{1(2)}$ and obeys $M_{1}(\mathbf{x})+M_{2}(\mathbf{x})=M$ , where $M$ is the number of dye molecules at each lattice site. The emission and absorption coefficients of the thermalized molecules satisfy the the Kennard-Stepanov relation kennard ; stepanov ; moroshkin14 $B_{12}=e^{\beta\Delta}B_{21}$ where $\Delta$ is the detuning between the cavity frequency and the dye zero-phonon transition frequency. The Kennard-Stepanov relation for the absorption and emission coefficients leads to energy relaxation with dimensionless strength $\kappa=B_{12}\bar{M}_{1}/(2T)$ (we set the Boltzmann constant $k_{B}=1$ ) gladilin20 .

The noise enters in the model due to fluctuations stemming from spontaneous emission that are described by adding a unit modulus complex number with random phase to the photon amplitude at the spontaneous emission rate $B_{21}M_{2}$ henry82 ; verstraelen19 . We have checked numerically that this way of introducing stochasticity yields the same results as a Langevin noise term representing the shot noise in the emission and absorption processes.

Equation (1) is coupled to a rate equation describing the evolution of the number of excited molecules due to emission and absorption processes and external pumping. The latter has to be applied to compensate for the photon losses. The steady-state average value $\bar{n}$ of the photon number in each cavity, $n=|\psi(\mathbf{x})|^{2}$ , results from the balance between the pumping rate $P$ and losses and satisfies $P=\gamma\bar{n}$ . Under the condition $J\ll T$ , which assures that the occupations of all momentum states are much larger than one, the generalized Gross Pitaevskii classical field model (1) is valid for all the modes and there is no need to use a more refined quantum optical approach kirton13 ; kirton15 ; kirton16 .

The noise, inherent to the spontaneous emission by the dye molecules, leads to the density and phase fluctuations. For the simplest case of a single cavity, a crossover in the density fluctuations between a ‘grandcanonical’ regime with large fluctuations ( $\delta n^{2}\sim\bar{n}^{2}$ ), for $\bar{n}^{2}\ll M_{\rm eff}$ , and a ‘canonical’ regime with small fluctuations ( $\delta n^{2}\ll\bar{n}^{2}$ ), for $\bar{n}^{2}\ll M_{\rm eff}$ , have been observed klaers12 ; schmitt14 . Here, the ‘effective’ number of molecules is given by $M_{\rm eff}=(M+\gamma e^{-\Delta/T}/B_{21})/[2+2\cosh(\Delta/T)]$ . For $e^{\Delta/T}\ll 1$ , one has $M_{\rm eff}\approx\bar{M}_{2}\approx\eta Me^{\Delta/T}$ with $\eta=1+{\gamma}/(2\kappa T)$ , while the energy relaxation parameter becomes $\kappa\approx B_{21}Me^{\Delta/T}/(2T)$ .

In our simulations, the following parameters are fixed: the temperature $T=25$ meV, the energy detuning $\Delta=-180$ meV, and the total number of molecules $M=5\times 10^{10}$ . With these dye molecule parameters, $M_{\rm eff}\approx 3.73\times 10^{7}$ and $n^{2}/M_{\rm eff}$ varies from 67 for $n=n_{0}$ down to 0.026 for $n=0.02n_{0}$ , where $n_{0}=5\times 10^{4}$ is our unit for the photon density. The other relevant parameters are expressed in the following units: $B_{0}=10^{-7}$ meV for the emission coefficient, $J_{0}=0.02$ meV for the coupling strength, and $\gamma_{0}=0.02$ meV for the loss rate. In each simulation, the initial state is formed by random values of the phase and (very small) number of photons ( $n<10^{-3}\bar{n}$ ) in each cavity, with no correlation between cavities. The pair annihilation dynamics are studied for an array of $200\times 200$ coupled photon cavities with periodic boundary conditions. Sample-averaged curves correspond to 10 to 32 runs.

III Discussion of the numerical results

III.1 The role of the emission-absorption rates

Photon condensates reach thermal equilibrium in the steady state when the loss rate is much smaller than the rates of absorption and re-emission. Even though in the present study, we do not investigate the steady state, one can still expect that the relative importance of emission-absorption with respect to losses has some influence on the phase relaxation dynamics. In our simulations, we have first kept the loss rate fixed at $\gamma_{0}=0.02$ meV and varied the emission coefficient $B_{21}$ and correspondingly the absorption coefficient according to $B_{12}=e^{\beta\Delta}B_{21}$ at fixed detuning.

Figure 2(a) shows the time evolution of the vortex-pair density $\sigma$ (the number of pairs per cavity) for various emission coefficients $B_{21}$ on a double logarithmic scale. Quite remarkably, we see a rich behavior in the evolution of the vortex pair density. Starting with the lowest value of $B_{21}$ (red full line), we see after an initial constant at very short times a fast decay up to $t\approx 10$ ns and a subsequently slower decay up to $t=100$ ns, when only two vortex pairs remain in the simulation region. The relatively slow time scale on which the vortex pair annihilation manifests itself is promising for its experimental detection: the observation of dynamics on the ns scale or slower is well within the domain of standard electronics.

The initial pair number annihilation rate increases when the emission coefficient $B_{12}$ is increased. There are two mechanisms that explain this dependence: (i) an increase of $B_{21}$ implies a more efficient interaction of cavity photons with the reservoir formed by dye molecules, and hence a more efficient role of pumping that tends to keep the condensate density close to its steady-state value $\bar{n}$ gladilin19 ; gladilin19b . Larger $B_{21}$ therefore more strongly disfavors states with many vortex cores, since in these states there are many cavities with photon densities much smaller than $\bar{n}$ . (ii) An increase in $B_{21}$ implies an increase in $\kappa\approx B_{21}Me^{\Delta/T}/(2T)$ . According to Eq. (1), the effect of $\kappa$ is to eliminate the photon field’s phase and density gradients. A larger value of $\kappa$ therefore leads to a faster recombination of vortices and antivortices.

Figure 3 illustrates that, at $\kappa>1$ , it is mainly the value of $\kappa$ that determines the vortex-pair annihilation rate. It shows the time evolution of the pair number for different values of $B_{21}$ with an independent variation of $\kappa$ (i.e. not according to $\kappa=B_{12}\bar{M}_{1}/(2T)$ ). Curves with the same $\kappa$ but with different $B_{21}$ are close to each other, clearly illustrating that the pair number dynamics is mainly governed by $\kappa$ . The thin solid line in Fig. 3 shows the analytical dependence for the number of vortices obtained for relaxation dynamics of the two-dimensional XY model $\sigma(t)\propto(t/t_{0})^{-1}\ln(t/t_{0})$ yurke1993 ; jelic11 and agrees well with the numerics for the largest values of $\kappa$ . This agreement is in analogy with simulations done for exciton-polariton condensates comaron18 ; gladilin19 . Also in line with the current observations, it was found in the polariton case that the vortex annihilation is accelerated when increasing $\kappa$ gladilin19 .

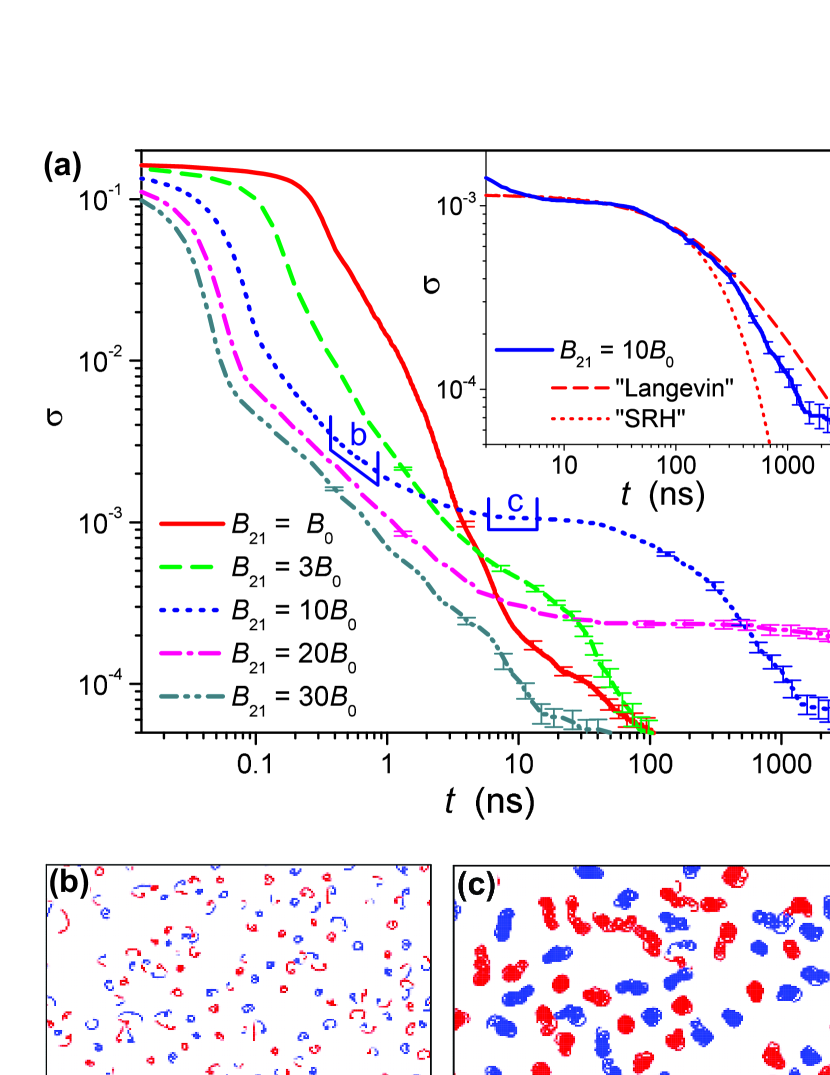
Going back to Fig. 2, one observes that the long-time behavior of $\sigma(t)$ varies non-monotonously with $B_{21}$ . For $B_{12}=10B_{0}$ , a clear plateau (on the used log-log scale) develops between $t=10$ ns and $t=100$ ns. We propose as the mechanism for the formation of the plateau the interplay between vortex-antivortex distances and the radius of the quasi-circular trajectories of self-accelerated vortices and antivortices, which decreases with increasing $B_{21}$ gladilin20b . Quasi-circular vortex trajectories with relatively small radius constitute an important distinctive feature of the system under consideration as compared to the exciton-polariton condensates analyzed in Refs. gladilin17 ; gladilin19 . The quasi-circular form of the trajectories leads to a localization of vortices, hampering their encounters when the vortex density becomes low. This is illustrated in panels (b) and (c) of Fig. 2, with their time intervals indicated in panel (a) as “b” and “c” respectively. In panel (b), with the higher vortex density, trajectories of vortices (red) and antivortices (blue) intersect quite frequently, leading to efficient annihilation. Within the corresponding subnanosecond time interval, as many as 70 vortex-antivortex pairs annihilate in the simulation region. In contrast, the low vortex density in panel (c) together with the well localized vortex orbits prevents annihilation during the longer time interval “c”. In addition to the self-acceleration that leads to circular orbits, the nonequilibrium situation leads to outward particle flows from vortex cores that cause - similarly to the case of exciton-polariton condensates gladilin17 - long-range repulsion of vortices independent of their mutual chirality gladilin20b . As a consequence, the localized orbits show very little overlap in the regime of low density. Furthermore, most of these orbits are seen to have a very low mobility, similar to a reduced transverse mobility of electrons in a magnetic field, so that vortex-antivortex collisions are rather rare. As a result, only 1 pair recombines in the simulation region in the time interval of about 13 ns. Increasing the emission rate $B_{21}$ both reduces the radius of the circular vortex trajectories and increases the long range repulsion gladilin20b , explaining why the plateau only develops for sufficiently large $B_{21}$ .

The subsequent decay of the pair density for $B_{12}=10B_{0}$ can be understood from the recombination of low mobility particles, analogous to particle-hole recombination in low mobility semiconductors. In the inset of Fig. 2(a), we compare $\sigma(t)$ with fits to the Langevin pairwise and Shockley-Read-Hall (SRH) single particle recombination, described by

	$\displaystyle\frac{d}{dt}n_{p}$	$\displaystyle=-\alpha\;n_{p}^{2}\hskip 14.22636pt{\rm(Langevin)},$		(2)
	$\displaystyle\frac{d}{dt}n_{p}$	$\displaystyle=-\alpha\;n_{p}\hskip 14.22636pt{\rm(SRH)}.$		(3)

The better fit to the Langevin model for times up to about 500 ns shows that pairwise annihilation is dominant when the pair density is sufficiently large. At later times, when the pair density has dropped, there is some deviation towards the SRH. The vortex density evolution is seen to be relatively close to the Langevin dynamics but with some deviation towards the SRH. Our tentative explanation of this deviation is that – as implied by Fig. 2(c) – not all vortices have the same mobility. Indeed, the exact SRH dependence would correspond to the limiting case where most of the vortices are pinned (have zero mobility) and some are mobile. Then it is natural to expect that less drastic but still significant differences in mobility result in some “intermediate” annihilation curve as compared to the purely Langevin and SRH dynamics.

As seen from Fig. 2(a), when increasing the emission coefficient from $B_{21}=10B_{0}$ to $B_{21}=20B_{0}$ , the plateau on the $\sigma(t)$ shifts down to lower pair densities and it fully disappears at $B_{21}=30B_{0}$ . At those large $B_{21}$ the energy relaxation parameter $\kappa$ exceeds 1 and the effect of its increase on the long-time pair-density dynamics dominates over that of the emission-absorption rates.

At the longest times, when only a few pairs remain ( $\sigma\lesssim 10^{-4}$ ), the slope of $\sigma(t)$ becomes flatter. In this regime, there is a formation of metastable low-density vortex-antivortex configurations. This interpretation is supported by the results of our simulations for finite arrays, where formation of metastable vortex-antivortex states, qualitatively resembling those obtained in gGPE simulations for exciton-polariton condensates gladilin19 , has been observed suppl .

III.2 The role of tunneling and losses

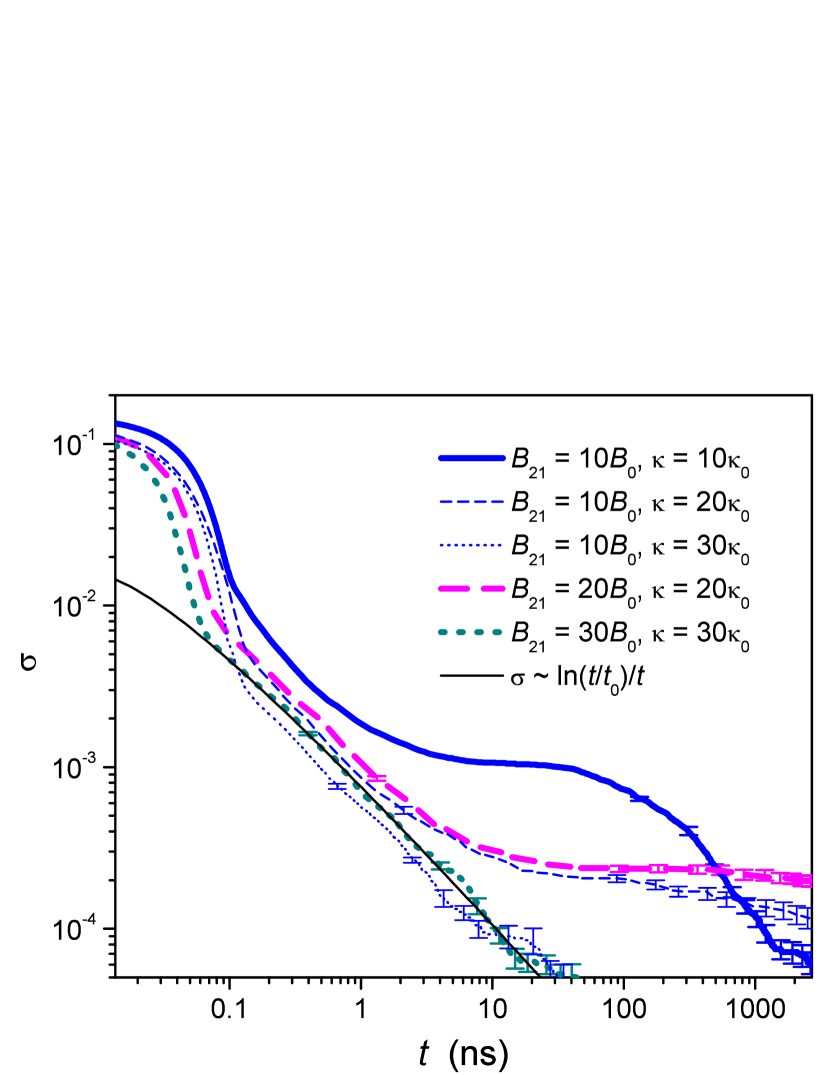
From the two parameters $J$ and $\gamma$ out of which the length scale $r_{v}\propto\sqrt{J/\gamma}$ has been argued to serve as a first estimate for the vortex core size gladilin20b , the effect of the tunneling on the pair relaxation dynamics is the most straightforward. Comparing in Fig. 4 the solid to the dotted curve, one sees that the pair relaxation rate is enhanced when $J$ is increased, a dependence that can be understood with the following “spatial resolution” argument. An increase of $J$ can be thought of as an increase in spatial resolution within the continuum limit of the lattice model gladilin20b . Correspondingly, the long-time behavior of $\sigma(t)$ at $J=2J_{0}$ is close to that of $\sigma(t)/2$ at $J=J_{0}$ , except at shortest $t$ , when the vortex cores strongly overlap and the structure of individual vortices is not well developed, so that the spatial resolution argument is not applicable.

In contrast to the dependence on $J$ , the effect of the loss rate $\gamma$ is more subtle. The comparison of the solid and dashed lines in Fig. 4 shows that for larger $\gamma$ , relaxation is faster at intermediate times, but slower at long times. Our interpretation of these dependencies is as follows. At earlier times, when the vortex density is large, it is mainly the enhanced stabilization of the density due to pump-loss dynamics that leads to a faster disappearance of vortex pairs. This argument is in line with the explanation of the role of $B_{21}$ on the very early time dynamics in the discussion of Fig. 2. At lower pair density however, the outward particle currents, leading to repulsion between vortices of opposite chirality, become important gladilin20b . These currents increase with the loss rate and therefore stronger losses suppress the pair annihilation rate. In general, the competition between the two different effects of losses on the annihilation rate results in a rather intricate influence of $\gamma$ on the shape of the annihilation curve. When $J$ and $\gamma$ are varied simultaneously, keeping the length scale $r_{v}=\sqrt{J/\gamma}$ fixed, the effect of $J$ on $\sigma(t)$ dominates, as illustrated in the inset of Fig. 4: the curve with larger $J$ (dotted) shows a faster decrease of $\sigma$ with respect to the one at lower $J$ (full line).

A remarkable feature of the curves $\sigma(t)$ , shown in the inset of Fig. 4 and corresponding to rather weak coupling $J$ , is their non-monotonous behavior at relatively low pair densities. This behavior reflects noise-induced generation of new vortex pairs, which becomes more pronounced with decreasing $J$ as the system gradually approaches the BKT transition point gladilin21 . These pair generation processes significantly slow down relaxation of the system towards a vortex-free state.

III.3 The influence of the photon number

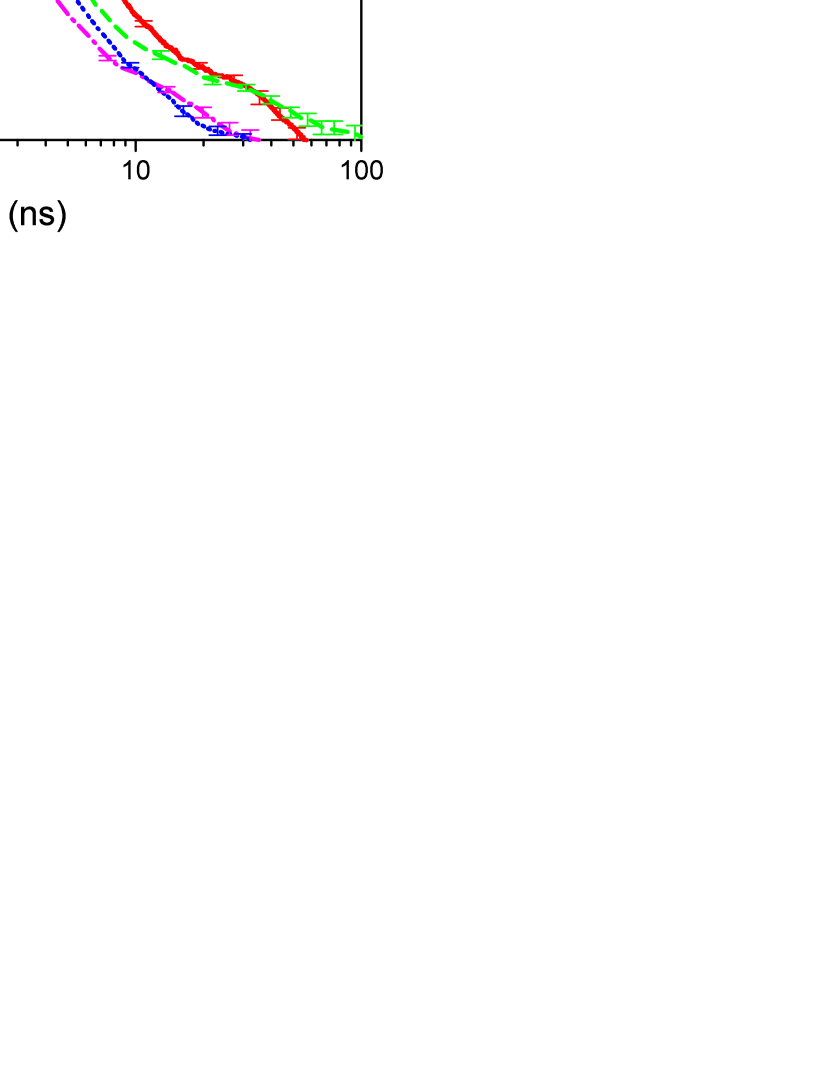
Let us finally discuss how the photon number affects the pair annihilation rate. In Fig. 5(a), we show $\sigma(t)$ for various photon numbers, that are smaller than the ones used in Figs. 2 - 4.

The first effect of a decreasing photon number is that it takes longer before the appreciably fast pair annihilation starts. This is the same trend as in Fig. 2 for decreasing emission rate. The reason is analogously that for lower photon number, it takes longer for the density to stabilize around its mean value, because of slower absorption-emission dynamics.

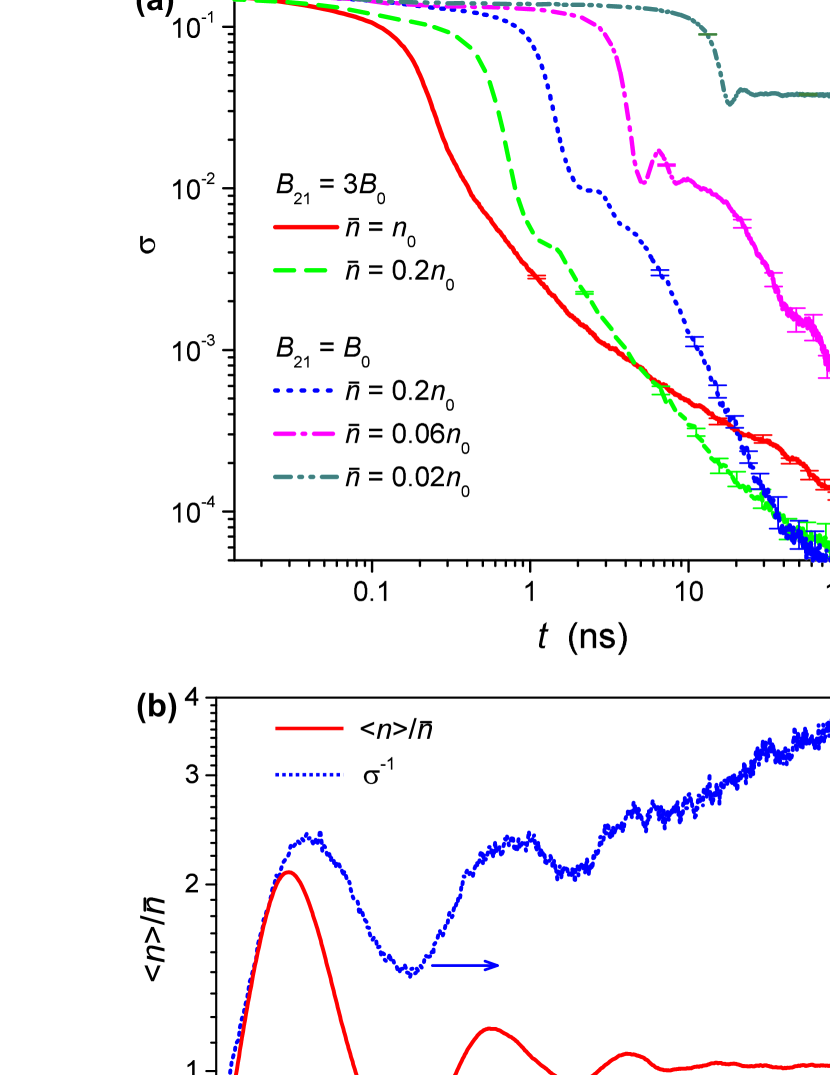
A second feature that stands out in Fig. 5(a) is that at the smallest photon number $n=0.02n_{0}=1000$ , the pair density does not decay to zero (dash-dot-dotted line). The reason is that the photon number is below the critical photon number for the Berezinskii-Kosterlitz-Thouless phase transition $n_{c}\approx 1200$ , estimated with the use of the numerical and analytical results from Ref. gladilin21 . The vortices present at late times (after $t\approx 30$ ns) are therefore spontaneous vortices caused by the noise in the system and are no longer due to the random initial condition of the photon field. For the dash-dotted curve at a the second lowest photon number $n=0.06n_{0}=3000$ , creation of new pairs by the noise leads to pronounced fluctuations of the pair density and strongly slows down its overall final decay. Since the photon number is much above the critical number for the BKT transition, we expect that the pair number will tend to zero at very long times.

A further notable feature of the two curves at the lowest photon numbers are the oscillations after the initial decay of $\sigma$ . These are related to the behavior of the photon number density [see Fig. 5(b)], that exhibits relaxation oscillations analogous to lasers svelto or perturbed photon condensates ozturk19 . At lower densities, the noise becomes relatively more important, leading to a more intense creation of new vortex pairs. Consequently, the vortex number shows oscillations, which decay together with the photon density oscillations and have the opposite phase (with some retardation).

Let us now turn to the difference between the solid and dashed lines in Fig. 5(a), that illustrate most clearly that far above the BKT transition, a lower photon number speeds up the decay of vortex pairs. We identify two reasons for this dependence. First, at lower photon number, the outward currents from each vortex core, which are responsible for the vortex-antivortex repulsion, decrease suppl , facilitating the annihilation of vortex pairs. Secondly, at lower photon numbers, the larger radius of the quasi-circular vortex trajectories and higher relative intensity of the noise suppl give the vortices a higher mobility, such that the formation of quasi-stable vortex patterns similar to that shown in Fig. 2(c) is less likely.

IV Conclusions and outlook

We have studied in this paper the phase annealing of a lattice of nonequilibrium photon condensates, that is created by a rapid switching of the pump laser intensity. The initial state shows very poor coherence, due to its random phases at each lattice site. After a transient with large density fluctuations, well defined vortices and antivortices are formed. The energy relaxation, that stems in the case of photon condensates from the Kennard-Stepanov relation, leads subsequently to the annihilation of vortex pairs. Our numerical simulations show that when the emission and absorption rates are very high, the vortices annihilate with the time dependence from XY model relaxational dynamics yurke1993 ; jelic11 .

At lower values of the emission/absorption rates, vortex repulsion, caused by outward currents from the vortex cores, in combination with quasi-circular motion of self-accelerated vortices can considerably slow down the pair annihilation. In this regime, a repulsive gas of vortices and antivortices with low mobility is formed, that survives for a significantly longer time. Its annihilation was shown to be in between Langevin and SRH-like dynamics.

For what concerns the influence of the tunneling and loss rates, the dependence on the former is the most straightforward. A modification of the tunneling rate can be seen as a change in spatial resolution with a corresponding effect on the vortex density (an increased tunneling leads to a decrease in the number of vortices). The dependence of the vortex annihilation on the loss rate is less pronounced and exhibits different trends at early and late times. Increasing the losses leads to an increase of the annihilation rate at early times and a slowing down at later times.

Finally, we have investigated the role of the photon number. Naturally, when the photon number is decreased below the critical number for the BKT transition, the vortex pairs no longer disappear at late times, but an equilibrium between their recombination and their noise-induced generation is established. Within the ordered phase however, increasing the photon number slows down the vortex pair annihilation due to an increase of outward currents and a reduction of the vortex mobility.

In the present work, we have focused on the presence/absence of vortices, the natural perspective from the phase annealing of 2D equilibrium condensates. It has been shown however that for sufficiently large systems, the phase dynamics of nonequilibrium condensates belongs to the KPZ universality class. It would be interesting to look for signatures of the KPZ physics on the phase annealing of nonequilibrium photon condensates.

Our simulations were performed for a translationally invariant system with equal tunnelings between all lattice sites, where the ground state is one with a uniform phase. The time needed to eliminate the vortices from the system is therefore the time that the system needs to reach the lowest energy state. It has been suggested to use photon condensates for analog computation by letting them find the ground state of a nontrivial classical XY model hamiltonian kassenberg20 . Our insights obtained here on the annihilation of vortex pairs are expected to be relevant for the estimation of the time needed to reach the ground state in such applications and the trends that were observed for the dependence on the system parameters may be useful in order to improve the performance of analog computing with photon BECs.

Acknowledgements

VG was financially supported by the FWO-Vlaanderen through grant nr. G061820N.

References

(1) P. M. Chaikin, Principles of Condensed Matter Physics (Cambride University Press, Cambridge, 2000).
(2) L. P. Pitaevski and S. Stringari, Bose-Einstein condensation (Oxford University Press, 2016).
(3) I. Carusotto and C. Ciuti, Rev. Mod. Phys. 85, 299 (2013).
(4) J. Bloch, I. Carusotto and M. Wouters, arXiv:2106.11137.
(5) A. V. Kavokin, J. J. Baumberg, G. Malpuech, and F. P.Laussy, Microcavities, Vol. 21 (Oxford university press,2017).
(6) J. Klaers, F. Vewinger and Martin Weitz, Nat. Phys. 6, 512 (2010).
(7) J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, Nature 468, 545 (2010).
(8) J. Marelic, L. F. Zajiczek, H. J. Hesten, K. H. Leung,E. Y. X. Ong, F. Mintert and R. A. Nyman, N. J. Phys. 18, 103012 (2016).
(9) S. Greveling, K. L. Perrier and D. van Oosten, Phys.Rev. A 98, 013810 (2018).
(10) I. Carusotto, A. A. Houck, A. J. Kollár, P. Roushan,D. I. Schuster, and J. Simon, Nature Physics16, 268 (2020).
(11) H. Bernien, S. Schwartz, A. Keesling, H. Levine, A. Omran, H. Pichler, S. Choi, A. S. Zibrov, M. Endres, M. Greiner, V. Vuletić and M. D. Lukin Nature 551, 579 (2017).
(12) M.J. Hartmann, F.G.S.L. Brandão, M.B. Plenio, Laser and Photon. Rev. 2, 553 (2008)
(13) D. G. Angelakis Ed. Quantum Simulations with Photons and Polaritons, Springer International Publishing AG 2017.
(14) J. Kasprzak, M. Richard, S. Kundermann, A. Baas, P. Jeambrun, J. Keeling, F. Marchetti, M. Szymańska, R. Andre, J. Staehli, V. Savona, P. B. Littlewood, B. Deveaud and Le Si Dang, Nature 443, 409 (2006).
(15) K. G. Lagoudakis, M. Wouters, M. Richard, A. Baas, I. Carusotto, R. André, L. S. Dang, and B. Deveaud-Plédran, Nat. Phys. 4, 706 (2008).
(16) K. G. Lagoudakis, F. Manni, B. Pietka, M. Wouters, T. C. H. Liew, V. Savona, A. V. Kavokin, R. André, and B. Deveaud-Plédran, Phys. Rev. Lett. 106, 115301 (2011).
(17) D. Caputo, D. Ballarini, G. Dagvadorj, C. S. Muñoz, M. De Giorgi,L. Dominici, K. West, L. N. Pfeiffer, G. Gigli, F. P. Laussy, M. H. Szymańska and D. Sanvitto, Nat. Mat. 17,145 (2018).
(18) T. C. H. Liew, O. A. Egorov, M. Matuszewski, O. Kyriienko, X. Ma, and E. A. Ostrovskaya, Phys. Rev. B 91, 085413 (2015).
(19) F. M. Marchetti, M. H. Szymańska, C. Tejedor, and D. M. Whittaker, Phys. Rev. Lett. 105, 063902 (2010).
(20) E. Cancellieri, T. Boulier, R. Hivet, D. Ballarini, D. Sanvitto, M. H. Szymanska, C. Ciuti, E. Giacobino, and A. Bramati, Phys. Rev. B 90, (2014).
(21) X. Ma and S. Schumacher, Phys. Rev. B , 235301 (2017).
(22) V. N. Gladilin and M. Wouters, New J. Phys. 19, 105005 (2017).
(23) V. N. Gladilin and M. Wouters, Phys. Rev. Lett. 125, 215301 (2020).
(24) V. N. Gladilin and M. Wouters, J. Phys. A 52, 1751 (2019).
(25) B. Kassenberg, M. Vretenar, S. Bissesar, J. Klaers, arXiv:2001.09828.
(26) D. Dung, C. Kurtscheid, T. Damm, J. Schmitt, F. Vewinger, M. Weitz and J. Klaers, Nat. Phot. 11, 565 (2017).
(27) C. Schneider, K. Winkler, M. Fraser, M. Kamp, Y. Ya-mamoto, E. Ostrovskaya, and S. Höfling, Exciton-polariton trapping and potential landscape engineering, Rep. Prog. Phys. 80, 016503 (2016).
(28) G. Dagvadorj, J. M. Fellows, S. Matyjaśkiewicz, F.?M. Marchetti, I. Carusotto, and M. H. Szymańska, Phys. Rev. X 5, 041028 (2015).
(29) P. Comaron, G. Dagvadorj, A. Zamora, I. Carusotto, N. P. Proukakis, and M. H. Szymańska, Phys. Rev. Lett. 121, 095302 (2018).
(30) E. Altman, L. M. Sieberer, L. Chen, S. Diehl and J. Toner, Phys. Rev. X 5, 011017 (2015).
(31) G. Wachtel, L. M. Sieberer, S. Diehl and E. Altman, Phys. Rev. B 94, 104520 (2016).
(32) L. M. Sieberer, G. Wachtel, E. Altman and S. Diehl, Phys. Rev. B 94, 104521 (2016).
(33) A. Zamora, L. M. Sieberer, K. Dunnett, S. Diehl, and M. H. Szymańska, Phys. Rev. X 7, 041006 (2017).
(34) V. N. Gladilin and M. Wouters, Phys. Rev. A 104, 043516 (2021).
(35) B. Yurke, A. N. Pargellis, T. Kovacs, and D. A. Huse, Phys. Rev. B 47, 1525 (1993).
(36) A. Jelić and L. F. Cugliandolo, J. Stat. Mech. 2011, P02032 (2011).
(37) V. N. Gladilin and M. Wouters, Phys. Rev. A 101, 043814 (2020).
(38) E. H. Kennard, Phys. Rev. 11, 29 (1918).
(39) B. I. Stepanov, Dokl. Akad. Nauk SSSR 112, 839 (1957). [Sov. Phys. Dokl. 2, 81 (1957)].
(40) P. Moroshkin, L. Weller, A. Saß, J. Klaers and M. Weitz, Phys. Rev. Lett. 113, 063002 (2014).
(41) C. Henry, IEEE Journal of Quantum Electronics 18, 259(1982).
(42) W. Verstraelen and M. Wouters, Phys. Rev. A 100, 013804 (2019).
(43) P. Kirton and J. Keeling, Phys. Rev. Lett. 111, 100404(2013).
(44) P. Kirton and J. Keeling, Phys. Rev. A 91, 033826 (2015).
(45) P. Kirton and J. Keeling, Phys. Rev. A 93, 013829 (2016).
(46) J. Klaers, J. Schmitt, T. Damm, F. Vewinger,and M. Weitz, Phys. Rev. Lett. 108, 160403 (2012).
(47) J. Schmitt, T. Damm, D. Dung, F. Vewinger, J. Klaers and M. Weitz, Phys. Rev. Lett. 112, 030401 (2014).
(48) V. N. Gladilin and M. Wouters, Phys. Rev. B 100, 214506 (2019).
(49) See Supplemental Material at [URL will be inserted by publisher] for examples of metastable vortex-antivortex states (Fig. s1) and for the effect of $\bar{n}$ on the single-vortex properties (Fig. s2).
(50) O. Svelto, Principles of lasers (Springer, New York, 2010).
(51) F. E. Ozturk, T. Lappe, G. Hellmann, J. Schmitt, J. Klaers, F. Vewinger, J. Kroha, and M. Weitz, Phys. Rev. A. A 100, 043803 (2019).