Vortex rings in fragmentation regions in heavy-ion collisions at 39 GeV
Abstract
Vorticity generated in heavy-ion collisions at energy of 39 GeV is studied. Simulations are performed within a model of the three-fluid dynamics. A peculiar structure consisting of two vortex rings is found: one ring in the target fragmentation region and another one in the projectile fragmentation region. These rings are also formed in central collisions. The matter rotation is opposite in this two rings. These vortex rings are already formed at the early stage of the collision together with primordial fragmentation regions. The average vorticity, responsible for the global polarization of the observed and , is also studied. In the semi-central collisions the average vorticity in the midrapidity region turns out to be more than an order of magnitude lower than the total one. The total vorticity is dominated by the contributions of the fragmentation regions and is produced because of asymmetry of the vortex rings in noncentral collisions. This suggests that in semi-central collisions the global polarization in the fragmentation regions should be at least an order of magnitude higher than that observed by the STAR collaboration in the midrapidity. This polarization should be asymmetrical in the reaction plain and correlate with the corresponding directed flow.
pacs:
25.75.-q, 25.75.Nq, 24.10.NzI Introduction
In peripheral collisions of high-energy heavy ions the system has a large angular momentum that results in observable consequences. In particular, it was proposed that hyperons can be polarized along the angular momentum of two colliding nuclei Liang:2004ph ; Betz:2007kg ; Gao:2007bc . Global polarization of and hyperons produced in heavy-ion collisions has been recently observed STAR:2017ckg by the STAR experiment in energy range of the Beam Energy Scan (BES) program at the at Relativistic Heavy Ion Collider (RHIC) at Brookhaven. It was measured in the midrapidity region of colliding nuclei. It was concluded that the observed rotational fluid has the largest vorticity, of the order of 1022 s-1, that ever existed in the universe. The measured polarization quantitatively agrees with the hydrodynamic Karpenko:2016jyx ; Xie:2017upb and kinetic Baznat:2017jfj ; Baznat:2017ars ; Kolomeitsev:2018svb ; Li:2017slc model calculations.
However, important questions still remain: Why does the global polarization decrease with the collision energy rise as the total angular momentum increases? Where is the huge angular momentum mainly accumulated? These questions were indirectly answered in Refs. Ivanov:2017dff ; Baznat:2015eca ; Baznat:2013zx . It was found that the vorticity, which is the driving force of the hadron polarization, is predominantly localized in a relatively thin layer at the boundary between participants and spectators. This implies that the hyperon polarization should be stronger at peripheral rapidities, corresponding to this border than in the midrapidity region. This enhancement at peripheral rapidities was illustrated in Ref. Baznat:2017ars at the example of Au+Au collision at 5 GeV. Although not all models predict the polarization minimum at the midrapidity Sun:2017xhx . The polarization enhancement at peripheral rapidities is not a direct explanation of the reduction of the midrapidity polarization with the collision energy rise but indicates that the hyperon polarization at peripheral rapidities may be very large as compared with that at the midrapidity in ultrarelativistic collisions and even higher than that at the lowest BEC-RHIC energy.
The study of the hyperon polarization at peripheral rapidities is not just of academic interest. Recent proposal Brodsky:2012vg to perform experiments at the Large Hadron Collider (LHC) at CERN in the fixed-target mode revived interest to the fragmentation regions in relativistic nucleus-nucleus collisions. The LHC beam of lead ions interacting on a fixed target would provide an opportunity to carry out precision measurements in the kinematical range of the target fragmentation region. If the LHC operates in a fixed-target mode at the beam energy of 2.76 GeV per nucleon for lead nuclei, this is equivalent to 72 GeV in terms the center-of-mass energy.
In the present paper we analyze the vorticity in Au+Au collisions at the energy of 39 GeV. A special emphasis is made on the vorticity in the fragmentation regions. The vorticity is simulated within the model of the three-fluid dynamics (3FD) 3FD . The 3FD model is quite successful in reproduction of the major part of bulk observables: the baryon stopping Ivanov:2013wha ; Ivanov:2012bh , yields of different hadrons, their rapidity and transverse momentum distributions Ivanov:2013yqa ; Ivanov:2013yla , and also the elliptic Ivanov:2014zqa and directed Konchakovski:2014gda flow excitation functions. In recent paper Ivanov:2018vpw it was demonstrated that the 3FD model successfully reproduces the extensive set of bulk observables at midrapidity recently presented by the STAR Collaboration Adamczyk:2017iwn . Therefore, the 3FD predictions for the fragmentation regions may be of interest.
II The 3FD Model
The 3FD approximation is a minimal way to simulate the early-stage nonequilibrium in the colliding nuclei at high incident energies. In contrast to the conventional hydrodynamics, a finite stopping power resulting in a counterstreaming regime of leading baryon-rich matter at early stage of the nuclear collision is taken into account in the 3FD description 3FD . This nonequilibrium state of the baryon-rich matter is modeled by two interpenetrating baryon-rich fluids initially associated with constituent nucleons of the projectile (p) and target (t) nuclei. At later stages these baryon-rich fluids may consist of any type of hadrons and/or partons (quarks and gluons), rather than only nucleons. Newly produced particles, which populate the midrapidity region, are associated with a fireball (f) fluid. Each of these fluids is governed by conventional hydrodynamic equations coupled by friction terms in the right-hand sides of the Euler equations. These friction terms describe energy–momentum loss of the baryon-rich fluids. A part of this loss is transformed into thermal excitation of these fluids, while another part gives rise to particle production into the fireball fluid.
The physical input of the present 3FD calculations is described in Ref. Ivanov:2013wha . The friction between fluids was fitted for each EoS to reproduce the observed stopping power, see Ref. Ivanov:2013wha for details. The simulations in Ivanov:2013wha ; Ivanov:2012bh ; Ivanov:2013yqa ; Ivanov:2013yla ; Ivanov:2014zqa ; Konchakovski:2014gda were performed with different equations of state (EoS’s)—a purely hadronic EoS gasEOS and two versions of the EoS involving the deconfinement transition Toneev06 , i.e. a first-order phase transition and a smooth crossover one. In the present paper we demonstrate results with only the first-order-phase-transition (1st-order-tr.) and crossover EoS’s as the most successful in reproduction of various observables, in particular, the recent data on bulk observables at 39 GeV Ivanov:2018vpw .
In semi-central Au+Au collisions at the energy of 39 GeV the counterstreaming of leading baryon-rich matter takes place only during short initial stage. After a short time 1 fm/c the p- and t-fluids are either spatially separated or mutually stopped and unified, thus forming a unified single baryon-rich fluid similarly to that happening in central collisions at this energy Ivanov:2017xee . Indeed, the corresponding unification measure
| (1) |
at fm/c is less than 0.01. Here
| (2) |
is the proper (i.e. in the local rest frame) baryon density of the unified baryon-rich fluid defined in terms of the baryon current , where and are the proper baryon densities and hydrodynamic 4-velocities of the p- and t-fluids, respectively. This unification measure is zero, when the p- and t-fluids are mutually stopped and unified, and has a positive value increasing with rise of the relative velocity of the p- and t-fluids.
The f-fluid also is entrained by the the unified baryon-rich fluid but is not that well unified with the latter. The local baryon-fireball relative velocity is 0.2, at 1 fm/c, i.e. it is small but not negligible. In particular, the friction between the baryon-rich and net-baryon-free fluids is the only source of dissipation at the expansion stage. Thus, at 1 fm/c the system is characterized by two hydrodynamical velocities, and , attributed to the baryon-rich and baryon-free fluids, respectively, and two corresponding temperatures and .
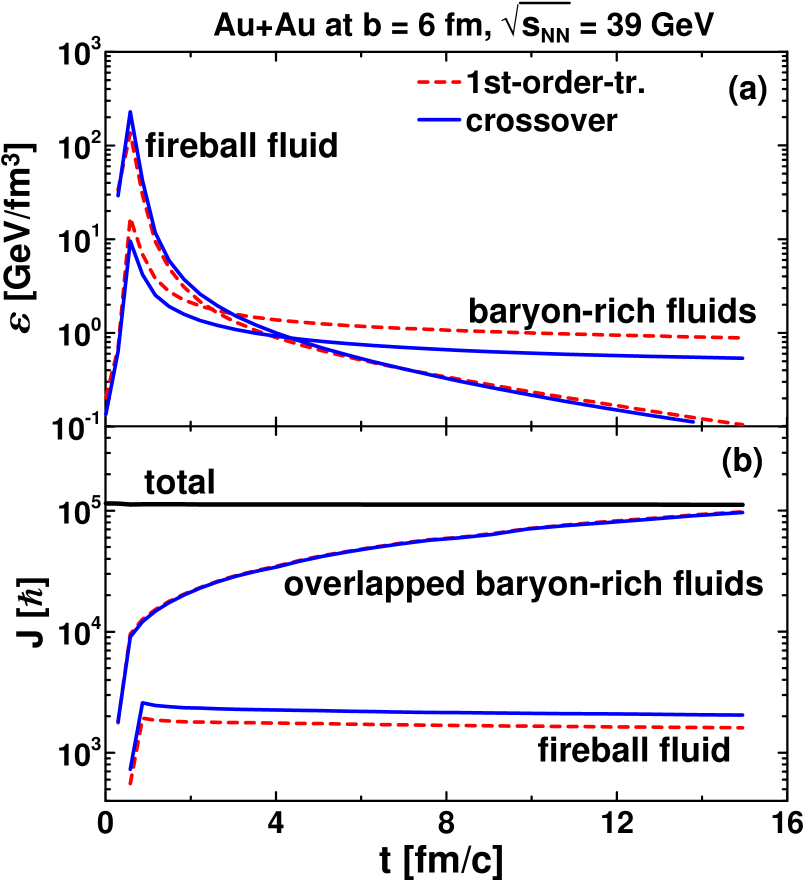
In Fig. 1 the time evolution of average proper energy densities of the baryon-rich and baryon-free fluids [panel (a)] and the total angular momentum, the angular momentum of the baryon-rich fluids in their overlap region and the angular momentum of the fireball fluid [panel (b)] in the semi-central ( 6 fm) Au+Au collision at 39 GeV are presented. As seen, at 4 fm/c the f-fluid dominates, i.e. its average energy density exceeds that of the baryon-rich fluid. Whereas at 4 fm/c, the situation is reversed – the baryon-rich fluid dominates. As seen from Fig. 2 (baryon-density and energy-density columns), it dominates in fragmentation regions where the baryon charge is concentrated.
The total angular momentum (that includes a contribution of spectators) is a conserved quantity. It is determined as
| (3) |
where is the energy-momentum tensor of the (=p,t,f) fluid that have the conventional hydrodynamical form, is the beam axis, is the reaction plane of the colliding nuclei. The constancy of the total angular momentum [Fig. 1, panel (b)] demonstrates the accuracy of the numeric scheme: is conserved with the accuracy of 1%. The overlap region of the baryon-rich fluids rises in the course of the expansion stage and includes more and more former spectators. Thus, the angular momentum of the baryon-rich fluid in their overlap almost accumulates the major part of the total angular momentum of the system at the final stage of the collision, cf. Fig. 1, panel (b). The angular momentum of the newly produced f-fluid is almost two orders of magnitude lower than that of the overlapped baryon-rich fluids at the final stage of the collision.
III Vorticity in the 3FD model
There are several definitions of the vorticity that are suitable for calculations of the hadron polarization in different approaches. In the present study we consider the relativistic kinematic vorticity
| (4) |
where is a collective local four-velocity of the matter. This type of the vorticity is directly relevant to the hadron polarization due to the chiral vortical effect Sorin:2016smp that was used in Refs. Baznat:2017jfj ; Baznat:2017ars . Another type of the vorticity is so-called thermal vorticity
| (5) |
where and with being the local temperature. Thus, is dimensionless. It is directly related to the polarization vector of a spin 1/2 particle in the thermodynamical approach Becattini:2013fla that was used in Refs. Karpenko:2016jyx ; Xie:2017upb ; Kolomeitsev:2018svb ; Li:2017slc .
As it was argued above, at 1 fm/c the system is characterized by two hydrodynamical velocities, and , and two corresponding temperatures, and , corresponding to the unified baryon-rich fluid (B) and the baryon-free fluid (f). Thus we deal with two sets of the vorticity attributed to to these baryon-rich and baryon-free fluids, respectively.
In order to suppress contributions of almost empty regions, where the matter is relatively thin, we consider a proper-energy-density weighted vorticity in the reaction () plane, i.e. at , similarly to that done in Ref. Ivanov:2017dff . Moreover, we sum the vorticity of the baryon-rich and baryon-free fluids with the weights of their energy densities in order to define a single quantity responsible for the vortical effects, in particular, the particle polarization. Thus, the proper-energy-density weighted kinematic vorticity is defined as
| (6) | |||||
| (7) |
where and are the proper energy densities of the the baryon-rich and baryon-free fluids, respectively. The total proper energy density of all three fluids in the local rest frame, , is strictly defined as follows
| (8) |
in terms of the total energy–momentum tensor being the sum of conventional hydrodynamical energy–momentum tensors of separate fluids, and the total collective 4-velocity of the matter
| (9) |
Note that definition (9) is, in fact, an equation determining . In general, this does not coincide with 4-velocities of separate fluids. However, in view of almost perfect unification of the baryon-rich fluids and small local baryon-fireball relative velocities, 0.2, at 1 fm/c, a very good approximation for is just
| (10) |
The average energy density in the plane in Eq. (6) is
| (11) |
Similarly to , we define the proper-energy-density weighted thermal vorticity in the reaction plane, though keep the same notation () for it.
The summation of and with the weights of their energy densities in Eq. (6) requires certain comments. Thus defined kinematic vorticity is very close to the true kinematic vorticity of the composed matter when the B- and f-velocities are close to each other. The latter is indeed the case at 1 fm/c. Although, for the thermal vorticity this is not true. It is impossible to unambiguously define an effective temperature of the composed matter. Therefore, the energy-density-weighted sum for the thermal vorticity of a thermally non-equilibrated system is a certain anzatz giving us a possibility to analyze a nonequilibrium system in equilibrium terms. Nevertheless, this anzatz is very close to the true thermal vorticity in certain cases. As it was mentioned above, the f-fluid energy density is lower than that of the unified baryon-rich fluid at 4 fm/c. Therefore, at 4 fm/c the f-fluid can be considered as small perturbation and hence this anzatz for the thermal vorticity of the composed matter is a good approximation.

The 3FD simulations of Au+Au collisions were performed without freeze-out. The freeze-out in the 3FD model removes the frozen out matter from the hydrodynamical evolution Russkikh:2006aa . Therefore, in order to keep all the matter in the consideration the freeze-out was turned off.
Figure 2 presents the time evolution of the proper-energy-density weighted relativistic kinematic vorticity of the composed matter, see Eq. (6), the similarly weighted thermal vorticity, the QGP fraction, and the proper baryon and energy densities, Eqs. (2) and (8), respectively, in the reaction plain () of central Au+Au collision at 39 GeV, where
| (12) |
is the longitudinal space-time rapidity and is the coordinate along the beam direction. The advantage of this longitudinal space-time rapidity is that it is equal to the kinematic longitudinal rapidity defined in terms of the longitudinal velocity in the self-similar one-dimensional expansion of the system. As already mentioned, the baryon-rich fluids are mutually stopped and unified at fm/c. As the f-fluid is not that well unified with the combined baryon-rich fluid, the evolution of the f-fluid is separately presented in Fig. 3. The baryon-rich fluid entrains the f-fluid. This is the reason for the smallness of .
Thus, the dissipation in the system is very moderate at fm/c because the system is almost kinetically equilibrated. This smallness of the dissipation was confirmed by the analysis of the entropy production in the 3FD simulations Ivanov:2016vkw . Therefore, it may seem that an additional conservation law, i.e. the circulation conservation (Kelvin’s circulation theorem), may be approximately valid. However, this is not the case. The Kelvin’s circulation theorem was originally formulated for a so-called barotropic fluid, i.e. the fluid with the EoS of the type of , where is the pressure. In fact, it is not important that depends on , it is important that depends on a single variable (it can also be the energy density ). In our case we have essentially because the system is essentially baryon-rich, as seen from Fig. 2. Therefore, the circulation is not conserved.
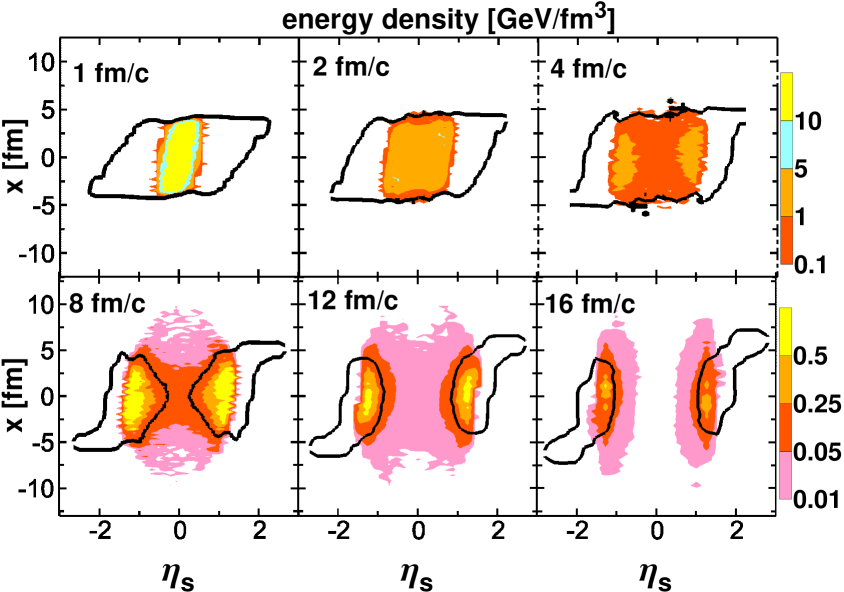
All major features of the collision dynamics are similar to those described in Ref. Ivanov:2017xee for the central collision at the same energy. As seen from Fig. 2, at 1 fm/c the thermalized central (see the central bumps in and ) and primordial fragmentation regions, i.e. the baryon-rich matter passed through the interaction region (see two bumps of baryon density near 1), have already been formed. The matter in all these regions is in the quark-gluon phase, see the QGP fraction in Fig. 2. There is a large fraction of the baryon charge stopped in the central region. This is in contrast to the ultra-relativistic scenario (at the top RHIC and LHC energies) where the major part of the baryon charge is assumed to be located in the fragmentation regions already at the initial stage. The proper baryon and energy densities in this central region approximately are 10 and 10 GeV/fm3, respectively. The proper baryon density is similar to that attained in the central collision Ivanov:2017xee while the energy one is considerably lower. The f-fluid dominates in this central energy density, as seen from Fig. 1.
In the course of time, the central region undergoes a rapid, practically self-similar one-dimensional (1D) expansion. In fact, the thermalized central region is produced in the state of this expansion. The matter, and in particular the baryon charge, is pushed out to the periphery of this central fireball, i.e. closer to the primordial fragmentation regions. The primordial fragmentation fireballs also expand in counter directions to the central one. The primordial fragmentation fireballs join with central contributions to the instant fm/c because of their counter expansion, see Fig. 2. Therefore, the final fragmentation regions consist of primordial fragmentation fireballs and baryon-rich regions of the central fireball pushed out to peripheral rapidities. However, complete mixing of these central and primordial fragmentation fireballs does not occur, as seen from Fig. 3.
At later time 8 fm/c, see Figs. 2 and 3, the central part of the system gets frozen out while the fragmentation regions continue to evolve being already separated in the configuration space. This longer evolution of the fragmentation regions is due to the relativistic time dilation caused by their high-speed motion with respect to the central region. Therefore, their evolution time in the c.m. frame of colliding nuclei lasts fm/c in the first-order-transition scenario and fm/c in the crossover one.
From the very beginning the vortical fields, both the kinematic and thermal ones, are predominately formed at the periphery of the system, i.e. at the border between the participant and spectator matter, see Fig. 2. This means that the vorticity is initially located at peripheral rapidities rather than at midrapidity. Later on, the vortical fields partially spread to the participant and spectator bulk though remain concentrated near the border. In the conventional hydrodynamics this extension into the bulk is an effect of the shear viscosity. In the 3FD dynamics it is driven by the 3FD dissipation which imitates the effect of the shear viscosity Ivanov:2016vkw . The spread into the bulk, i.e. into the midrapidity region, is stronger at lower collision energies Ivanov:2017dff because of the higher effective shear viscosity than that at higher energies Ivanov:2016vkw . This explains the drop of the vorticity value and consequently the observed hyperon polarization at the midrapidity with the collision energy rise.
At later times the maximum values in the vortical fields get more and more shifted to the fragmentation regions because of the 1D expansion of the system. At the same time, the vorticity in the participant bulk gradually dissolves and practically disappears in the center of the colliding system. This longer evolution of the fragmentation regions is a result of the above mentioned relativistic time dilation caused by their high-speed motion with respect to the central region.
It is peculiarly that four strong oppositely directed vortices are formed at the periphery of the fragmentation regions, see Fig. 2. These strong oppositely directed vortices pedominantely consist of the baryon-rich matter because the f-fluid lags behind the primordial fragmentation matter, see Fig. 3. Over time, these vortices capture ever larger areas. The vortex at the border with the spectator matter is an order of magnitude stronger than its counterpart. This is the structure as it is seen in the reaction plane.
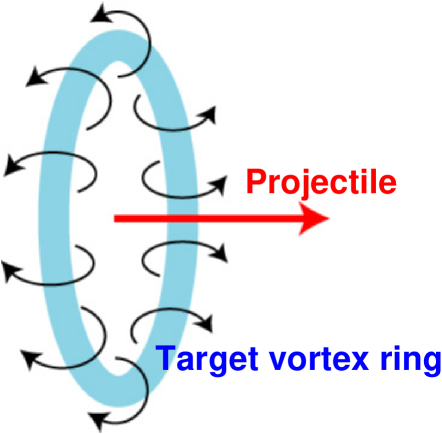
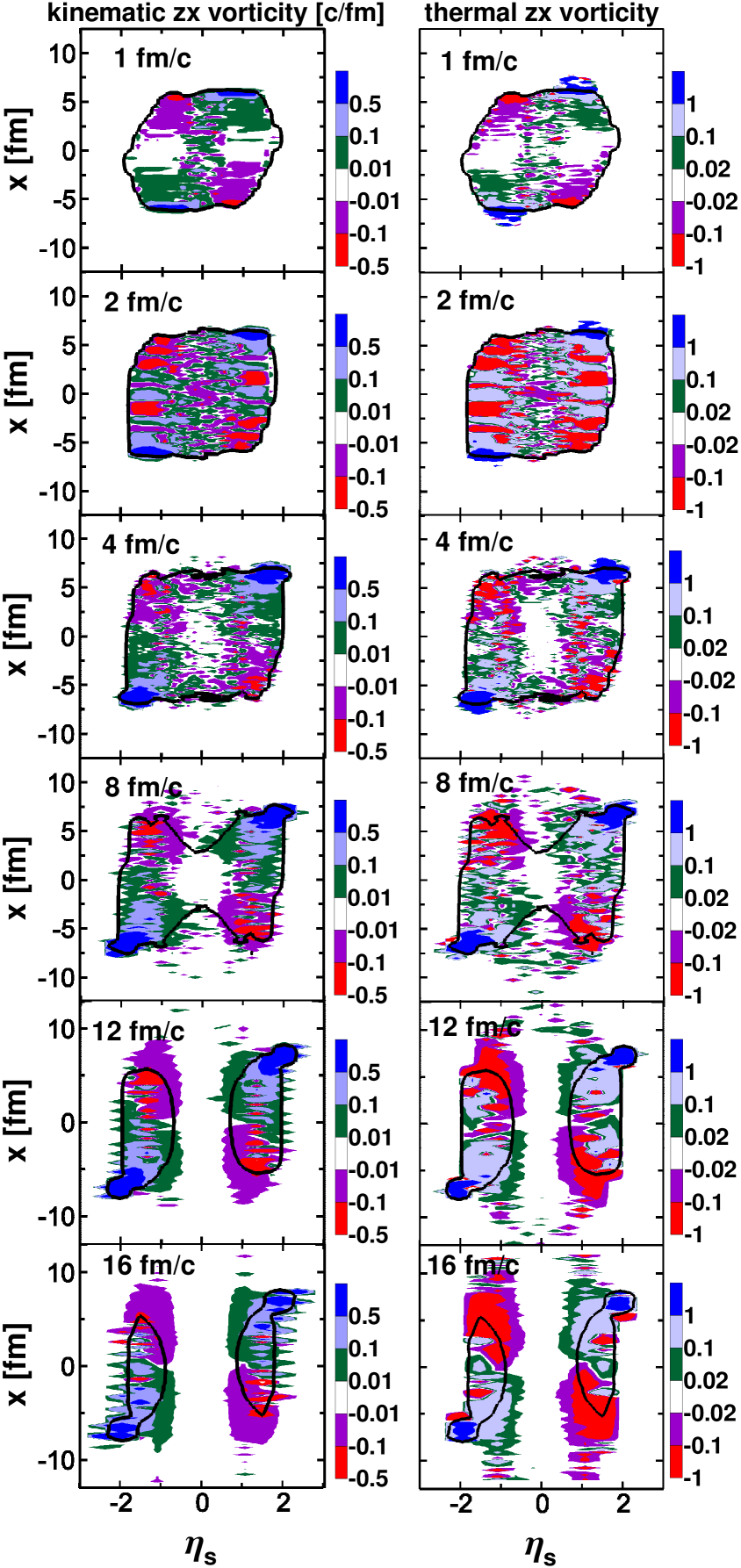
In fact, in three dimensions these are two vortex rings: one in the target fragmentation region and another in the projectile one. The matter rotation is opposite in this two rings. They are formed because the matter in the vicinity of the beam axis () is stronger decelerated because of thicker matter in the center than that at the periphery. Indeed, these rings are formed at the transverse periphery of the stopped matter in the central region, see the central bumps in and at 1 fm/c in Fig. 2. Thus, the peripheral matter acquires a rotational motion. A schematic picture of the vortex ring in the target fragmentation region is presented in Fig. 4.
A similar effect was noticed in the analysis of the vorticity field Ivanov:2017dff ; Baznat:2015eca ; Baznat:2013zx at energies of the Nuclotron-based Ion Collider fAcility (NICA) at the Joint Institute for Nuclear Research (JINR) in Dubna. The authors of Refs. Baznat:2015eca ; Baznat:2013zx called this specific toroidal structure as a femto-vortex sheet. This femto-vortex sheet is not a ring because the vorticity disappears in the plane, i.e. in the plane orthogonal to the reaction plane. At 39 GeV this femto-vortex sheet splits into two real rings, in which the vorticity does not disappear in the plane though is anisotropic in the direction in noncentral collisions.
These rings are also formed in central collisions, as seen from Fig. 5. In the case of 2 fm the distribution of the vorticity along the rings is more homogeneous than that at 6 fm, but still the vorticity reaches high values. As seen from Fig. 5, the vortex rings are already formed at 1 fm/c with the vorticity predominantly concentrated at the periphery of the fragmentation zone. In the course of time the vorticity spreads into the bulk of the fragmentation regions. In fact, the schematic picture of the completely symmetric vortex ring, see Fig. 4, corresponds to the exactly central collision at 0.
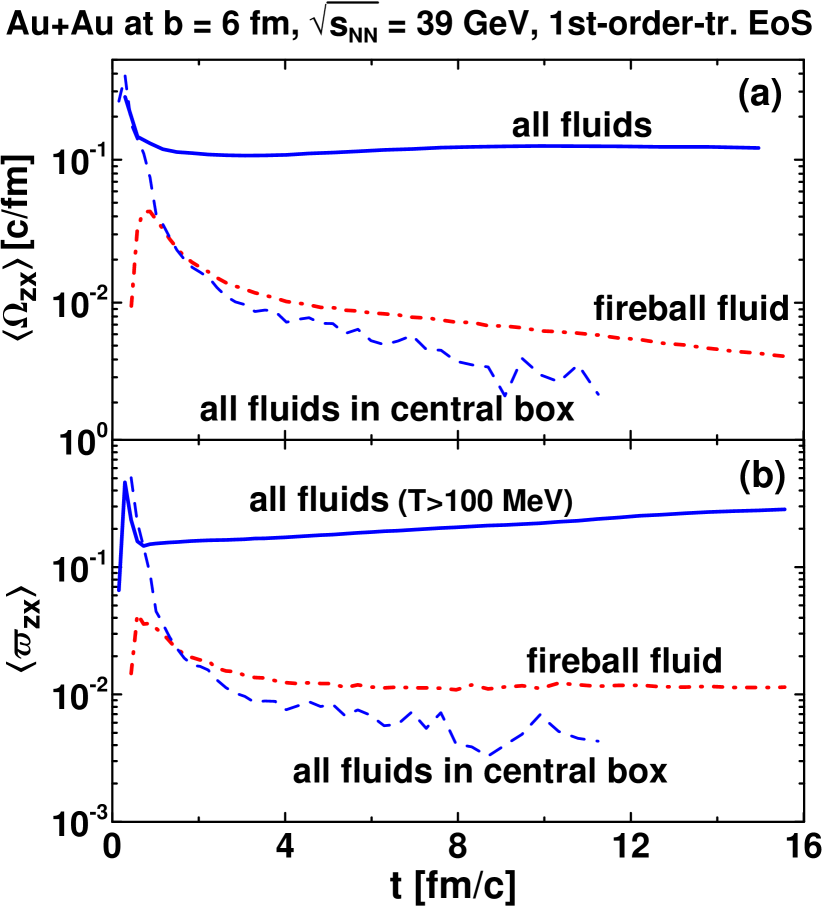
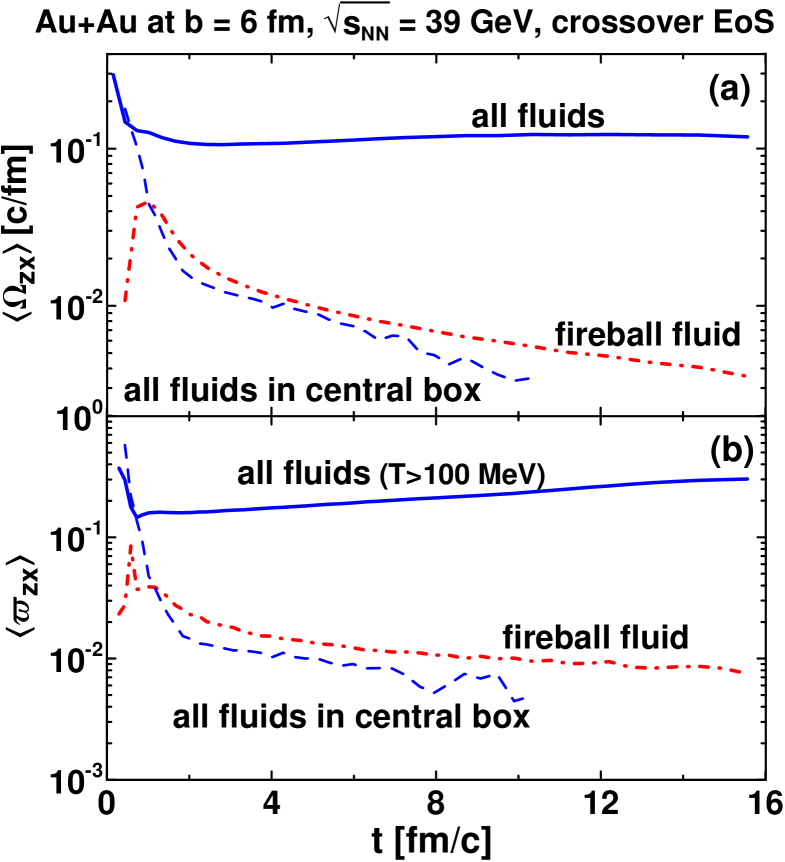
In order to perform a more quantitative comparison of the vorticity in the midrapidity and fragmentation regions we calculated (kinematic and thermal) vorticity of the composed matter [in the sense of the anzatz of Eq. (6)] in the semi-central ( 6 fm) Au+Au collision at 39 GeV averaged with the weight of the proper energy density over the whole system
| (13) | |||||
| (14) |
| (15) | |||||
| (16) |
where 100 MeV is the temperature constraint. This temperature constraint is introduced because the temperature gradients and hence the thermal vorticity are very high at the the spectator-participant border, where the temperature itself is not that high. At the same time, the hyperons are abundantly produced from the hottest regions of the system. Therefore, we applied this temperature constraint on this averaging, keeping in mind application the polarization. The average kinematic vorticity is not that strongly affected by the low-temperature contributions of the border regions Ivanov:2017dff . This is why this constraint is omitted in the case of the kinematic vorticity.
The above average values of the vorticity are dominated by that in the fragmentation regions. Therefore, we use them as an estimates of the vorticity in the fragmentation regions, keeping in mind that the true vorticity in the fragmentation regions is even higher. To estimate the vorticity in the midrapidity region we perform averaging over only the center region of the system , and , where is the radius of the Au nucleus and is the Lorentz factor associated with the initial nuclear motion in the c.m. frame. In fact, this center region is a central layer because it covers the whole participant region in the transverse direction.
Time evolution of the average relativistic kinematic and thermal vorticities calculated in the above described way is displayed in Figs. 6 and 7 for the two considered EoS’s. The kinematic and thermal vorticities manifest very similar behavior. The vorticity of the f-fluid averaged with the weight over the whole system is separately presented. The f-fluid vorticity is more than an order of magnitude lower than that of the baryon-rich fluid, as it is expected from the negligible fraction of the total angular momentum accumulated in the f-fluid, see Fig. 1. The contribution of the f-fluid only slightly reduces the vorticity of the composed matter as compared with the baryon-rich vorticity at 4 fm/c, when the energy density of the f-fluid becomes small compared to the that of the baryon-rich fluid, see Fig. 1.
The average vorticity in the central region rapidly drops with time. At the early stage the average vorticity in the central region practically coincides with the total one since this central region includes practically the whole system because of the Lorentz contraction of colliding nuclei. Already at 2 fm/c, the central vorticity is more than an order of magnitude lower than the total one. It means the vorticity moves to the fragmentation regions.
The vorticity is redistributed in the process of the collision: the vorticity of the f-fluid drops, the vorticity moves from the central region to the fragmentation ones. Nevertheless, the average vorticity of the matter remains approximately constant in the process of the collision. The average thermal vorticity even slightly rises with time.
It is worthwhile to mention that the average vorticity displayed in Figs. 6 and 7 does not coincide with that of the frozen-out system. The freeze-out in the 3FD model is a continuous in time process 3FD ; Russkikh:2006aa , as it is illustrated in Figs. 2 and 3. The actual vorticity of the frozen-out matter can be judged from the values of the vorticity field on the freeze-out contour in Figs. 2 and 3. As seen from Figs. 2 and 3, average values presented in Figs. 6 and 7 can be considered as order-of-magnitude estimates of the vorticity averaged over the frozen-out system at a fixed time instant.
IV Consequences for polarization
The above features of the vorticity imply certain consequences for the observable hyperon polarization. The vorticity cannot be presented as a function of the longitudinal rapidity because it is not an observable quantity. However, in the self-similar one-dimensional expansion of the system the longitudinal space-time rapidity (12) equals the kinematic longitudinal rapidity defined in terms of the longitudinal velocity. Thus, Fig. 2 gives an impression of the rapidity distribution of the vorticity and thereby the polarization. First of all, this distribution suggests that in semi-central collisions the polarization in the fragmentation regions should be at least an order of magnitude higher than that observed by the STAR collaboration STAR:2017ckg in the midrapidity.
The global polarization results from asymmetry of the vortex rings which also asymmetrically expand in the transverse direction. The asymmetrical expansion results in directed flow of emitted particles. Hence, the global polarization in the fragmentation regions should be asymmetrical in the reaction plain with the and polarizations correlating with the corresponding directed flow.
In view of the strong global and even stronger local polarization expected in the fragmentation regions one comment is in order. The experimental observation of the global polarization STAR:2017ckg indicates that a strong spin-orbital coupling of some kind is present in the system. This coupling transfers the initially collective angular momentum into that accumulated in aligned spins of constituents of the system. If this part accumulated in the aligned spins is large, it should affect the collective dynamics of the system because the collective angular momentum is respectively reduced. This means the need to incorporate the medium polarization into the collective dynamics, e.g. the hydrodynamics Montenegro:2017rbu ; Florkowski:2017ruc . The present 3FD simulations were performed without such feedback.
V Summary
Within the 3FD model we have studied vorticity evolution in Au+Au collisions at 39 GeV. We considered two definitions of the vorticity—relativistic kinematic and thermal vorticities—that are relevant in different approaches to the hyperon polarization. As found, the kinematic and thermal vorticities manifest very similar behavior. Moreover, this behavior is very similar within the first-order-transition and crossover scenarios.
The vortical fields, both the kinematic and thermal ones, are predominately formed at the periphery of the system, i.e. at the border between the participant and spectator matter. This means that the vorticity is initially located at peripheral rapidities rather than at midrapidity. Later on, the vortical fields partially spread to the participant and spectator bulk though remain concentrated near the border.
A peculiar structure of two vortex rings is formed: one in the target fragmentation region and another in the projectile one. The matter rotation is opposite in this two rings. They are formed because the matter in the vicinity of the beam axis is stronger decelerated than that at the periphery because of thicker matter in the center. Thus, the peripheral matter acquires a rotational motion, which is inhomogeneous along the rings in noncentral collisions.
These rings are also formed in central collisions. In this case the distribution of the vorticity is more homogeneous than that in semi-central collisions, but still the vorticity reaches high values. These vortex rings are already formed at the early stage of the collision ( 1 fm/c). The schematic picture of the completely symmetric vortex ring in presented in Fig. 4, corresponding to the exactly central collision.
The average vorticity is responsible for the global polarization of the observed and polarizations. In the semi-central collisions the average vorticity in the central region at 2 fm/c, when the central region can be associated with the midrapidity region, the central vorticity is more than an order of magnitude lower than the total one. The total vorticity is dominated contributions of the fragmentation regions and is produced because of the asymmetry of the above mentioned vortex rings.
The above features of the vorticity imply certain consequences for the observable hyperon polarization. First of all, they suggest that in semi-central collisions the global polarization in the fragmentation regions should be at least an order of magnitude higher than that observed by the STAR collaboration STAR:2017ckg in the midrapidity. This polarization should be asymmetrical in the reaction plain: the and polarizations should correlate with the corresponding directed flow.
Acknowledgements.
Fruitful discussions with D.N. Voskresensky are gratefully acknowledged. This work was carried out using computing resources of the federal collective usage center “Complex for simulation and data processing for mega-science facilities” at NRC ”Kurchatov Institute”, http://ckp.nrcki.ru/. Y.B.I. was supported by the Russian Science Foundation, Grant No. 17-12-01427. A.A.S. was partially supported by the Ministry of Education and Science of the Russian Federation within the Academic Excellence Project of the NRNU MEPhI under contract No. 02.A03.21.0005.References
- (1) Z. T. Liang and X. N. Wang, Phys. Rev. Lett. 94, 102301 (2005) Erratum: [Phys. Rev. Lett. 96, 039901 (2006)] doi:10.1103/PhysRevLett.94.102301, 10.1103/PhysRevLett.96.039901 [nucl-th/0410079].
- (2) B. Betz, M. Gyulassy and G. Torrieri, Phys. Rev. C 76, 044901 (2007) doi:10.1103/PhysRevC.76.044901 [arXiv:0708.0035 [nucl-th]].
- (3) J. H. Gao, S. W. Chen, W. t. Deng, Z. T. Liang, Q. Wang and X. N. Wang, Phys. Rev. C 77, 044902 (2008) doi:10.1103/PhysRevC.77.044902 [arXiv:0710.2943 [nucl-th]].
- (4) L. Adamczyk et al. [STAR Collaboration], Nature 548, 62 (2017) doi:10.1038/nature23004 [arXiv:1701.06657 [nucl-ex]].
- (5) I. Karpenko and F. Becattini, Eur. Phys. J. C 77, no. 4, 213 (2017) doi:10.1140/epjc/s10052-017-4765-1 [arXiv:1610.04717 [nucl-th]].
- (6) Y. Xie, D. Wang and L. P. Csernai, Phys. Rev. C 95, no. 3, 031901 (2017) doi:10.1103/PhysRevC.95.031901 [arXiv:1703.03770 [nucl-th]].
- (7) M. Baznat, K. Gudima, A. Sorin and O. Teryaev, Phys. Rev. C 97, no. 4, 041902 (2018) doi:10.1103/PhysRevC.97.041902 [arXiv:1701.00923 [nucl-th]]; M. Baznat, K. Gudima, G. Prokhorov, A. .Sorin, O. Teryaev and V. Zakharov, J. Phys. Conf. Ser. 938, no. 1, 012063 (2017). doi:10.1088/1742-6596/938/1/012063
- (8) M. Baznat, K. Gudima, A. Sorin and O. Teryaev, EPJ Web Conf. 138, 01008 (2017). doi:10.1051/epjconf/201713801008
- (9) E. E. Kolomeitsev, V. D. Toneev and V. Voronyuk, arXiv:1801.07610 [nucl-th].
- (10) H. Li, L. G. Pang, Q. Wang and X. L. Xia, Phys. Rev. C 96, no. 5, 054908 (2017) doi:10.1103/PhysRevC.96.054908 [arXiv:1704.01507 [nucl-th]].
- (11) Y. B. Ivanov and A. A. Soldatov, Phys. Rev. C 95, no. 5, 054915 (2017) doi:10.1103/PhysRevC.95.054915 [arXiv:1701.01319 [nucl-th]].
- (12) M. I. Baznat, K. K. Gudima, A. S. Sorin and O. V. Teryaev, Phys. Rev. C 93, no. 3, 031902 (2016) doi:10.1103/PhysRevC.93.031902 [arXiv:1507.04652 [nucl-th]].
- (13) M. Baznat, K. Gudima, A. Sorin and O. Teryaev, Phys. Rev. C 88, no. 6, 061901 (2013) doi:10.1103/PhysRevC.88.061901 [arXiv:1301.7003 [nucl-th]].
- (14) Y. Sun and C. M. Ko, Phys. Rev. C 96, no. 2, 024906 (2017) doi:10.1103/PhysRevC.96.024906 [arXiv:1706.09467 [nucl-th]].
- (15) S. J. Brodsky, F. Fleuret, C. Hadjidakis and J. P. Lansberg, Phys. Rept. 522, 239 (2013) doi:10.1016/j.physrep.2012.10.001 [arXiv:1202.6585 [hep-ph]].
- (16) Yu. B. Ivanov, V. N. Russkikh, and V.D. Toneev, Phys. Rev. C 73, 044904 (2006) [nucl-th/0503088].
- (17) Yu. B. Ivanov, Phys. Rev. C 87, 064904 (2013) [arXiv:1302.5766 [nucl-th]].
- (18) Y. B. Ivanov, Phys. Lett. B 721, 123 (2013) doi:10.1016/j.physletb.2013.02.038 [arXiv:1211.2579 [hep-ph]]; Y. B. Ivanov and D. Blaschke, Phys. Rev. C 92, no. 2, 024916 (2015) doi:10.1103/PhysRevC.92.024916 [arXiv:1504.03992 [nucl-th]].
- (19) Y. B. Ivanov, Phys. Rev. C 87, no. 6, 064905 (2013) doi:10.1103/PhysRevC.87.064905 [arXiv:1304.1638 [nucl-th]].
- (20) Y. B. Ivanov, Phys. Rev. C 89, no. 2, 024903 (2014) doi:10.1103/PhysRevC.89.024903 [arXiv:1311.0109 [nucl-th]].
- (21) Y. B. Ivanov and A. A. Soldatov, Phys. Rev. C 91, no. 2, 024914 (2015) doi:10.1103/PhysRevC.91.024914 [arXiv:1401.2265 [nucl-th]]; Y. B. Ivanov, Phys. Lett. B 723, 475 (2013) doi:10.1016/j.physletb.2013.05.053 [arXiv:1304.2307 [nucl-th]].
- (22) V. P. Konchakovski, W. Cassing, Y. B. Ivanov and V. D. Toneev, Phys. Rev. C 90, no. 1, 014903 (2014) doi:10.1103/PhysRevC.90.014903 [arXiv:1404.2765 [nucl-th]]; Y. B. Ivanov and A. A. Soldatov, Phys. Rev. C 91, no. 2, 024915 (2015) doi:10.1103/PhysRevC.91.024915 [arXiv:1412.1669 [nucl-th]]; Eur. Phys. J. A 52, no. 1, 10 (2016) doi:10.1140/epja/i2016-16010-9 [arXiv:1601.03902 [nucl-th]].
- (23) Y. B. Ivanov and A. A. Soldatov, Phys. Rev. C 97, no. 2, 024908 (2018) doi:10.1103/PhysRevC.97.024908 [arXiv:1801.01764 [nucl-th]].
- (24) L. Adamczyk et al. [STAR Collaboration], Phys. Rev. C 96, no. 4, 044904 (2017) doi:10.1103/PhysRevC.96.044904 [arXiv:1701.07065 [nucl-ex]].
- (25) V. M. Galitsky and I. N. Mishustin, Sov. J. Nucl. Phys. 29, 181 (1979).
- (26) A. S. Khvorostukhin, V. V. Skokov, K. Redlich, and V. D. Toneev, Eur. Phys. J. C48, 531 (2006) [nucl-th/0605069].
- (27) Y. B. Ivanov and A. A. Soldatov, Phys. Rev. C 97, no. 2, 021901 (2018) doi:10.1103/PhysRevC.97.021901 [arXiv:1711.03069 [nucl-th]].
- (28) A. Sorin and O. Teryaev, Phys. Rev. C 95, no. 1, 011902 (2017) doi:10.1103/PhysRevC.95.011902 [arXiv:1606.08398 [nucl-th]].
- (29) F. Becattini, V. Chandra, L. Del Zanna and E. Grossi, Annals Phys. 338, 32 (2013) doi:10.1016/j.aop.2013.07.004 [arXiv:1303.3431 [nucl-th]].
- (30) V. N. Russkikh and Yu. B. Ivanov, Phys. Rev. C 76, 054907 (2007) [nucl-th/0611094]; Yu. B. Ivanov and V. N. Russkikh, Phys. Atom. Nucl. 72, 1238 (2009) [arXiv:0810.2262 [nucl-th]].
- (31) Y. B. Ivanov and A. A. Soldatov, Eur. Phys. J. A 52, no. 5, 117 (2016) doi:10.1140/epja/i2016-16117-y [arXiv:1604.03261 [nucl-th]]; Eur. Phys. J. A 52, no. 12, 367 (2016) doi:10.1140/epja/i2016-16367-7 [arXiv:1605.02476 [nucl-th]].
- (32) D. Montenegro, L. Tinti and G. Torrieri, Phys. Rev. D 96, no. 5, 056012 (2017) Addendum: [Phys. Rev. D 96, no. 7, 079901 (2017)] doi:10.1103/PhysRevD.96.079901, 10.1103/PhysRevD.96.056012 [arXiv:1701.08263 [hep-th]].
- (33) W. Florkowski, B. Friman, A. Jaiswal and E. Speranza, Phys. Rev. C 97, no. 4, 041901 (2018) doi:10.1103/PhysRevC.97.041901 [arXiv:1705.00587 [nucl-th]].