WHERE IS PARTICLE PHYSICS GOING?
Abstract
The answer to the question in the title is: in search of new physics beyond the Standard Model, for which there are many motivations, including
the likely instability of the electroweak vacuum, dark matter, the origin of matter, the masses of neutrinos,
the naturalness of the hierarchy of mass scales, cosmological inflation and the search for quantum gravity.
So far, however, there are no clear indications about the theoretical solutions to these problems, nor the experimental
strategies to resolve them. It makes sense now to prepare various projects for possible future accelerators,
so as to be ready for decisions when the physics outlook becomes clearer.
Paraphrasing George Harrison, “ If you don’t yet know where you’re going,
any road may take you there.”
Contribution to the 2017 Hong Kong UST IAS Programme and Conference on High-Energy Physics.
KCL-PH-TH-2017-18, CERN-TH-2017-080
keywords:
Higgs boson; supersymmetry; dark matter; LHC; future colliders.PACS numbers: 12.15.-y, 12.60.Jv, 14.80.Bn, 14.80.Ly
1 Introduction
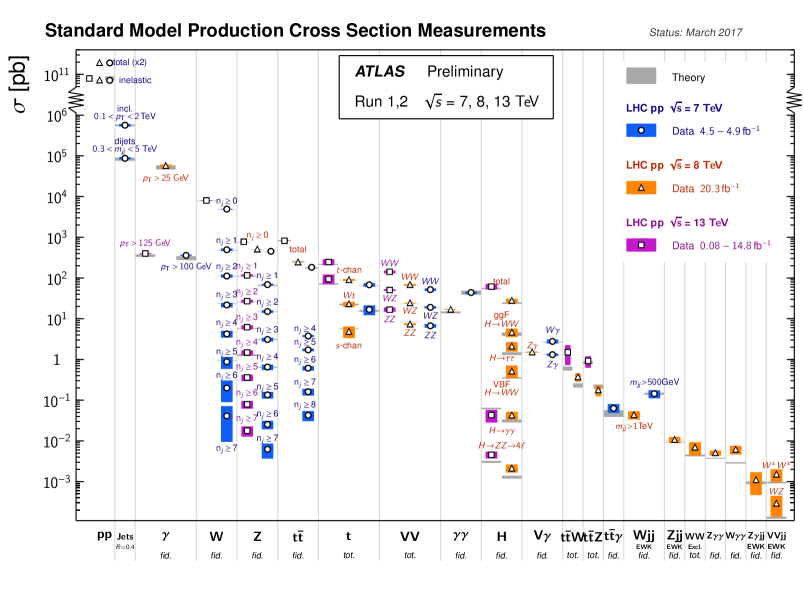
The bedrock upon which our search for new physics beyond the Standard Model (SM) is founded is our ability to make precise predictions within the Standard Model, notably for the LHC experiments. The predictions of many hard higher-order perturbative QCD calculations have been confirmed, as seen in Fig. 1, providing confidence in predictions for the production of the Higgs boson [1], and for the backgrounds to many searches for new physics.
2 The Flavour Sector
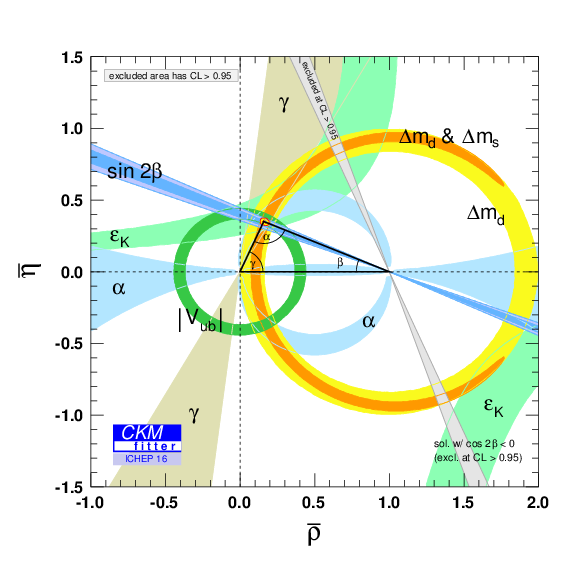
Many measurements in the flavour sector are also consistent with the predictions of the Cabibbo-Kobayashi-Maskawa (CKM) model [3, 4], e.g., there are many consistent measurements of the unitarity triangle, as seen in the left panel of Fig. 2. Historically, the angle has been the least constrained experimentally, but the LHCb Collaboration has recently published a combined measurement [5] that dominates the world average and is consistent with the other unitarity triangle measurements.
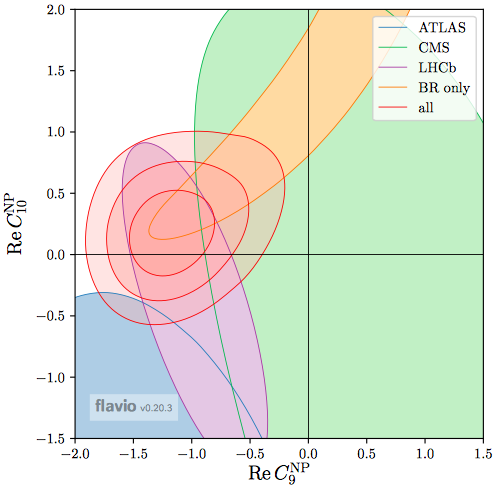
That said, there are several anomalies in the flavour sector of varying significance. For example, there are strengthening indications of violations of lepton universality in and decays, [6] and of or universality in decays [7] - to which my attitude is ‘wait and see’, as lepton non-universality has held up very well so far. Much attention has been attracted to the angular distribution in decay [8], which may be accompanied by an anomaly in the distribution in decay, leading to the constraints on possible new physics contributions to operator coefficients shown in the right panel of Fig. 2 [9]. These both appear at GeV2, and I do not know how seriously to take them, in view of my lack of understanding of the non-perturbative QCD corrections in this region. My ignorance also makes it difficult for me to judge the significance of the apparent discrepancy between theory [10, 11] and experiment for . Finally, a new kid on the flavour block has been the interesting search for decay [12] discussed below, though this may be reverting towards the SM with the latest Run 2 results [13].
3 Higgs Physics
3.1 The Higgs Mass
The most fundamental Higgs measurement is that of its mass. The combined LHC Run 1 results of ATLAS and CMS based on decays into and yielded [14]
| (1) |
and the preliminary CMS result from Run 2 is consistent with this, with slightly smaller errors [15]:
| (2) |
It is noteworthy that statistical uncertainties dominate, and we can look forward to substantial reductions in the future, determining at the per mille. Accurate knowledge of the Higgs mass is important for precision tests of Standard Model (and other) predictions and, as discussed later, is crucial for understanding the (in/meta)stability of the electroweak vacuum.
3.2 Higgs Couplings
The couplings of the Higgs boson to Standard Model particles are completely specified and, consequently, there are definite predictions for its production processes and decay branching ratios [16]. Concretely, one expects gluon-gluon fusion to dominate over vector-boson fusion, production in association with a vector boson and in association with a pair. The dominant decay mode is predicted to be into , with much smaller branching ratios for and .
Much progress was made in Run 1 probing these predictions [17], but much remains to be done. Higgs decays to and have been measured in gluon-gluon fusion, and there is solid evidence for vector-boson fusion, but the associated production mechanisms have yet to be confirmed. Moreover, there is no confirmation yet of the expected dominant decay mode: LHC evidence is at the level of 2.6 [18], and the Tevatron experiments have reported evidence at the 2.8- level. There is indirect evidence for the expected vertex via the measurements of gluon-gluon fusion and decay, but no significant evidence via associated or single production. Also on the agenda is the search for , which is predicted in the SM to appear at a level close to the current experimental sensitivity.
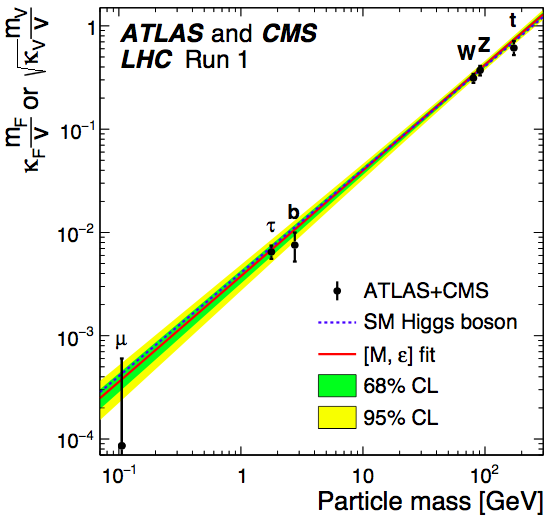
Fig. 3 is one way of displaying the available information on Higgs couplings [19, 17]. It is a characteristic prediction of the SM that the couplings to other particles should be related to their masses, for fermions and for massive vector bosons. The black solid line is a fit where in the couplings: we see that the combined ATLAS and CMS data are highly consistent with the SM expectation that , shown as the blue dashed line.
The couplings in Fig. 3 are all flavour-diagonal. The SM predicts that flavour-violating Higgs couplings should be very small, but measurements of flavour-violating processes at low energies would allow either or with branching ratio %, whereas the branching ratio for must be [20]. The was some excitement after Run 1 when the combined CMS and ATLAS data indicated a possible 2- excess [12]. This has not reappeared in early Run 2 data [13], but remains an open question.
4 Elementary Higgs Boson, or Composite?
There has been a long-running theoretical debate whether the Higgs boson could be as elementary as the other particles in the SM, or whether it might be composite. The elementary option encounters quadratically-divergent loop corrections to the mass of the Higgs boson, which are frequently (usually?) postulated to be cancelled by supersymmetric particles [21] appearing at the TeV scale [22] - which have not yet been seen.
On the other hand, the composite option has been favoured by many with memories of the (composite) Cooper pairs underlying superconductivity, and the (composite) pions associated with quark-antiquark condensation in QCD [23]. A composite Higgs would require a novel set of strong interactions, and early models tended to have a scalar particle much heavier than the Higgs that has been discovered, and to be in tension with the precision electroweak data. These difficulties can be circumvented by postulating that the Higgs is a pion-like pseudo-Nambu-Goldstone boson of a partially-broken larger symmetry that is restored at some higher energy scale [24].
A phenomenological framework that is convenient for characterizing the experimental constraints on such as possibility is provided by the following form of effective Lagrangian that preserves a custodial SU(2)V symmetry that guarantees up to quantum corrections [25]:
| (3) | |||||
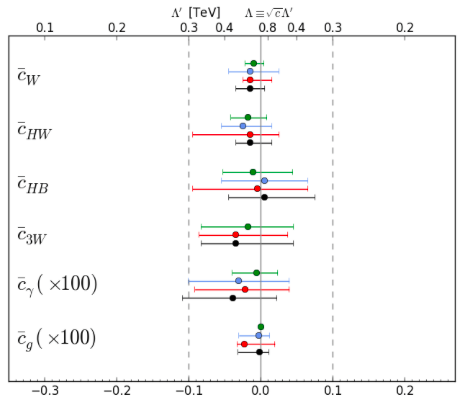
where is the field of the physical Higgs boson and the massive vector bosons are parametrized by the matrix . The terms in (3) are normalized so that the coefficients in the SM. The question for experiment is whether any of these coefficients exhibit a deviation that might be a signature of some composite Higgs model.
As seen in the left panel of Fig. 4, measurements of Higgs properties (yellow and orange ellipses) and precision electroweak data (blue ellipses) play complementary roles in constraining the couplings to vector bosons and fermions in (3) [26]. These constraints can be translated into lower limits on the possible compositeness scale in various models, as seen in the right panel of Fig. 4 [27].
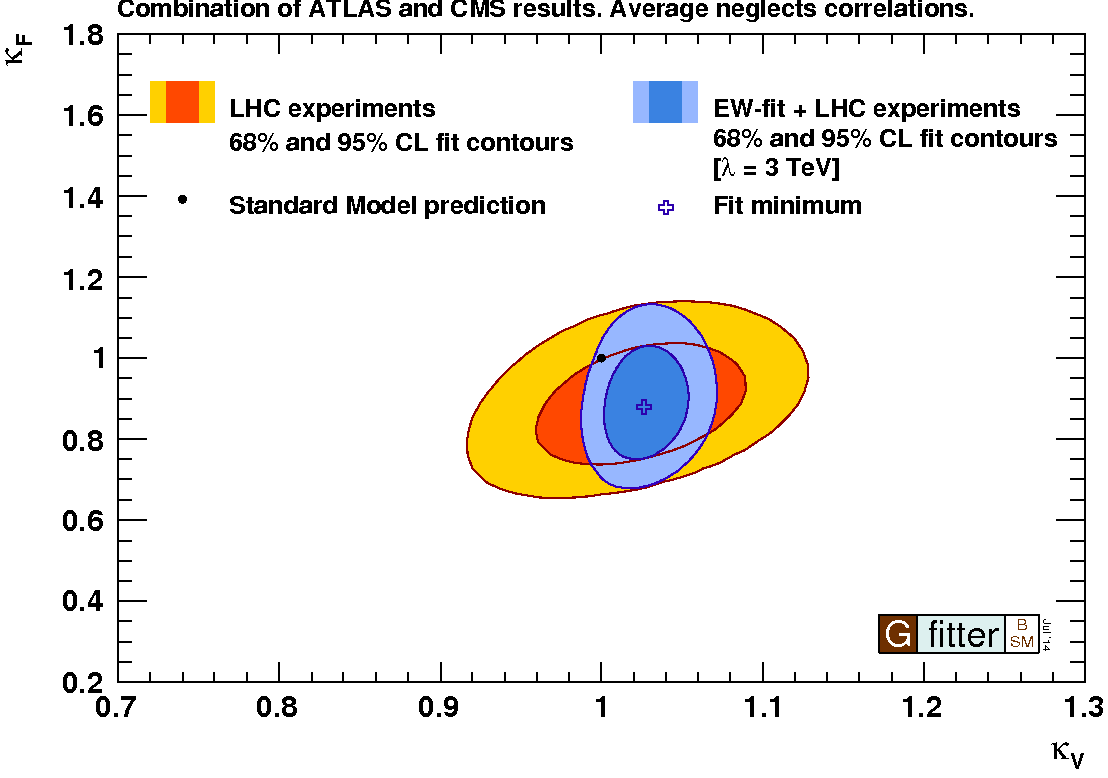
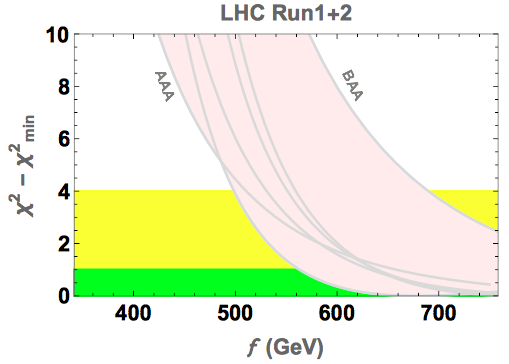
5 Stability of the Electroweak Vacuum
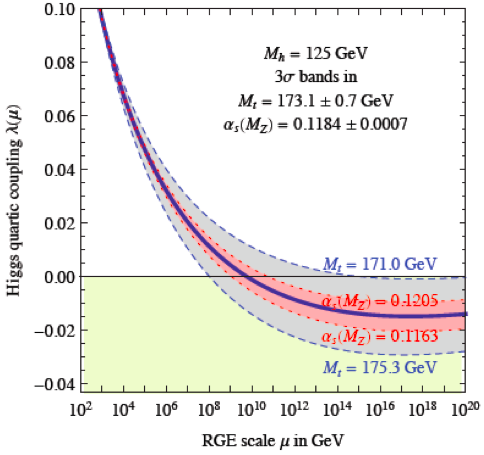
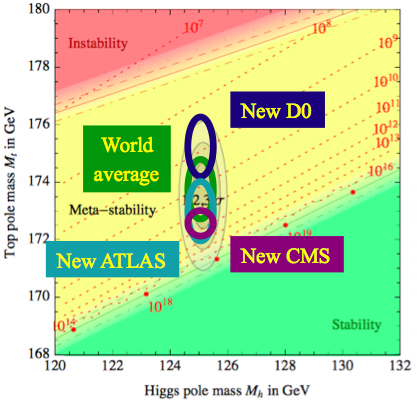
If the Higgs is indeed elementary, the measurements (1, 2) of , combined with those of , raise important questions about the stability and history of the electroweak vacuum, suggesting the necessity of new physics beyond the SM [28]. The issue is that the Higgs quartic self-coupling is renormalized not only by itself, which tends to increase it as the energy/mass scale increases, but also by the Higgs coupling to the top quark, which tends to drive it to smaller (even negative) values at higher scales , as seen in the left panel of Fig. 5GeV [29]. At leading order:
| (4) |
The right panel of Fig. 5 displays the results of one calculation of the regions of the plane where the electroweak vacuum is stable, metastable or unstable, and yields the following estimate of the ‘tipping point’ where goes negative [30]:
| (5) | |||||
The dominant uncertainty in the calculation of is due to that in , followed by that in (which enters in higher order in the calculation), the uncertainty due to the measurement of being relatively small. The final result is an estimate
| (6) |
indicating that we are (probably) doomed, unless some new physics intervenes.
Some people discount this ‘problem’ on the grounds that the prospective lifetime of the vacuum is much longer than its age. However, there is another issue, namely that fluctuations in the Higgs field in the very early Universe would have been much larger than now, and would probably have driven almost everywhere in the Universe into an anti-De Sitter phase from which there would have been no escape [31]. One could postulate that our piece of the Universe happened to be extraordinarily lucky and avoid this fate, but it seems more plausible that some new physics intervenes before the instability scale . Possible such remedies include higher-dimensional operators in the SM effective field theory (see the next Section), a non-minimal Higgs coupling to gravity, or a threshold for new physics such as supersymmetry [32] (see later).
6 The SM Effective Field Theory
An alternative way of analyzing the Higgs and other data is to assume that all the known particles (including the Higgs boson) are SM-like, and look for the effects of physics beyond the SM via an effective field theory (the SMEFT) containing higher-dimensional SU(2)U(1)-invariant operators constructed out of SM fields, e.g., of dimension 6 [33]:
| (7) |
where the characteristic scale of new physics is described by , with the being unknown dimensionless coefficients. Data on Higgs properties, precision electroweak data, triple-gauge couplings (TGCs), etc., can all be combined to constrain the SMEFT operator coefficients in a unified and consistent way. Table 6 shows which observables currently provide the greatest sensitivities to some of these operators [34].
Some of the relevant CP-even dimension-6 SMEFT operators in the basis. We display the types of observables that provide the greatest sensitivities to each operator. EWPTs Higgs Physics TGCs \colrule
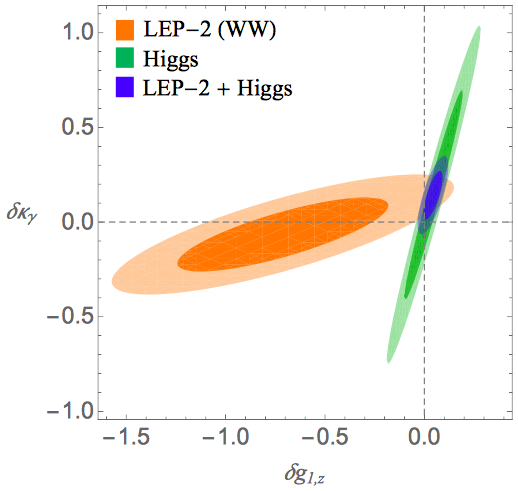
The left panel of Fig. 6 shows how the coefficients of the SMEFT operators in Table 6 were constrained by Run 1 Higgs data including kinematical variables (blue bar) and by Run 1 measurements of TGCs (red bar) [34]. The green bar gives the resulting ranges when each operator is switched on individually, and the black bar is for a global fit marginalizing over all the listed operators. The right panel of Fig. 6 manifests the complementarity between the Higgs and LEP-2 TGC data for constraining the anomalous couplings and [35]. Because of its power to constrain new physics appearing in many observables in a consistent way, the SMEFT is the preferred framework for assessing the sensitivities of future analyses of precision LHC measurements to physics beyond the SM, whose motivations are discussed in the next Section.
7 The Standard Model is not Enough [36]
There are many reasons to anticipate the existence of physics beyond the SM, of which I list just 7 here. 1) The prospective instability of the electroweak vacuum discussed earlier. 2) The astrophysical and cosmological necessity for dark matter. 3) The origin of matter itself, i.e., the cosmological baryon asymmetry. 4) The masses of neutrinos. 5) The naturalness of the hierarchy of mass scales in physics. 6) A mechanism (or replacement) for cosmological inflation to explain the great size and age of the Universe. 7) A quantum theory of gravity.
The good news is that LHC experiments are tackling most of these issues during Run 2. The bad news is that there is no consensus among theorists how to resolve them. Until recently, supersymmetry found the most theoretical favour, but the negative results from early Run 2 supersymmetry searches have caused some to waver. Not me, however - I still think that it is the most comprehensive and promising framework for new physics beyond the SM. In the words of the famous World War 1 cartoon [37] ”If you knows of a better ’ole, go to it.” I do not, so I will stay in the supersymmetric ’ole.
8 Supersymmetry
Indeed, I would even argue that Run 2 of the LHC has provided us with 3 new motivations for supersymmetry. i) It stabilizes the electroweak vacuum [32]. ii) It made a successful prediction for the Higgs mass, namely that it should weigh GeV in simple models [38]. iii) It predicted correctly that the Higgs couplings measured at the LHC should be within a few % of their SM values [39]. These new motivations are additional to the classic ones from the naturalness of the mass hierarchy [22], the availability of a natural dark matter candidate [40], the welcome help of supersymmetry in making grand unification possible [41], and its apparent necessity in string theory, which I regard as the only serious candidate for a quantum theory of gravity.
At this point, I must ’fess up to two pieces of bad news. One is that theorists have also not reached any consensus on the most promising supersymmetric model, largely because there is no favoured scenario for supersymmetry breaking. Alternatives range from models in which this is assumed to be universal at some GUT scale (such as the CMSSM) to models in which all the soft supersymmetry-breaking parameters are treated entirely phenomenologically as unknown parameters at the electroweak scale (the pMSSM). The other piece of bad news is that the LHC experiments have found not even a hint of supersymmetry, despite many searches making different assumptions about the supersymmetric spectrum 111On the other hand, they have found no hint of any other physics beyond the SM, despite a similar myriad of searches..
In the following, the negative results of the searches are combined with other measurements to constrain the parameter spaces of a couple of representative supersymmetric models.
8.1 Probing a Supersymmetric SU(5) GUT
The first model we study here is a supersymmetric SU(5) GUT in which the soft supersymmetry-breaking gaugino masses are assumed to be universal at the GUT scale, whereas the soft supersymmetry-breaking scalar masses are generation-independent but allowed to be different for the spartners of fermions in the and representations [42].
Fig. 6 displays the regions of the plane (left panel) and the plane (right panel) that are allowed in a global fit in this supersymmetric SU(5) GUT at the 95% CL (blue contours) and favoured at the 68% CL (red contours), as well as the best-fit point (green stars). The black lines are the nominal 95% CL limits set by LHC searches, assuming simplified decay patterns with 100% branching ratios, and the coloured shadings represent the actual dominant decays found in different regions of parameter space. We see in the left panel that gluino masses GeV are indicated, with a best-fit value of GeV, whereas the mass may be GeV lighter. One curiosity is a small strip in the right panel where is small and GeV. In this strip the dark matter (DM) density is brought into the range allowed by astrophysics and cosmology by squark-neutralino coannihilation, and this compressed-spectrum region is on the verge of exclusion by LHC searches.
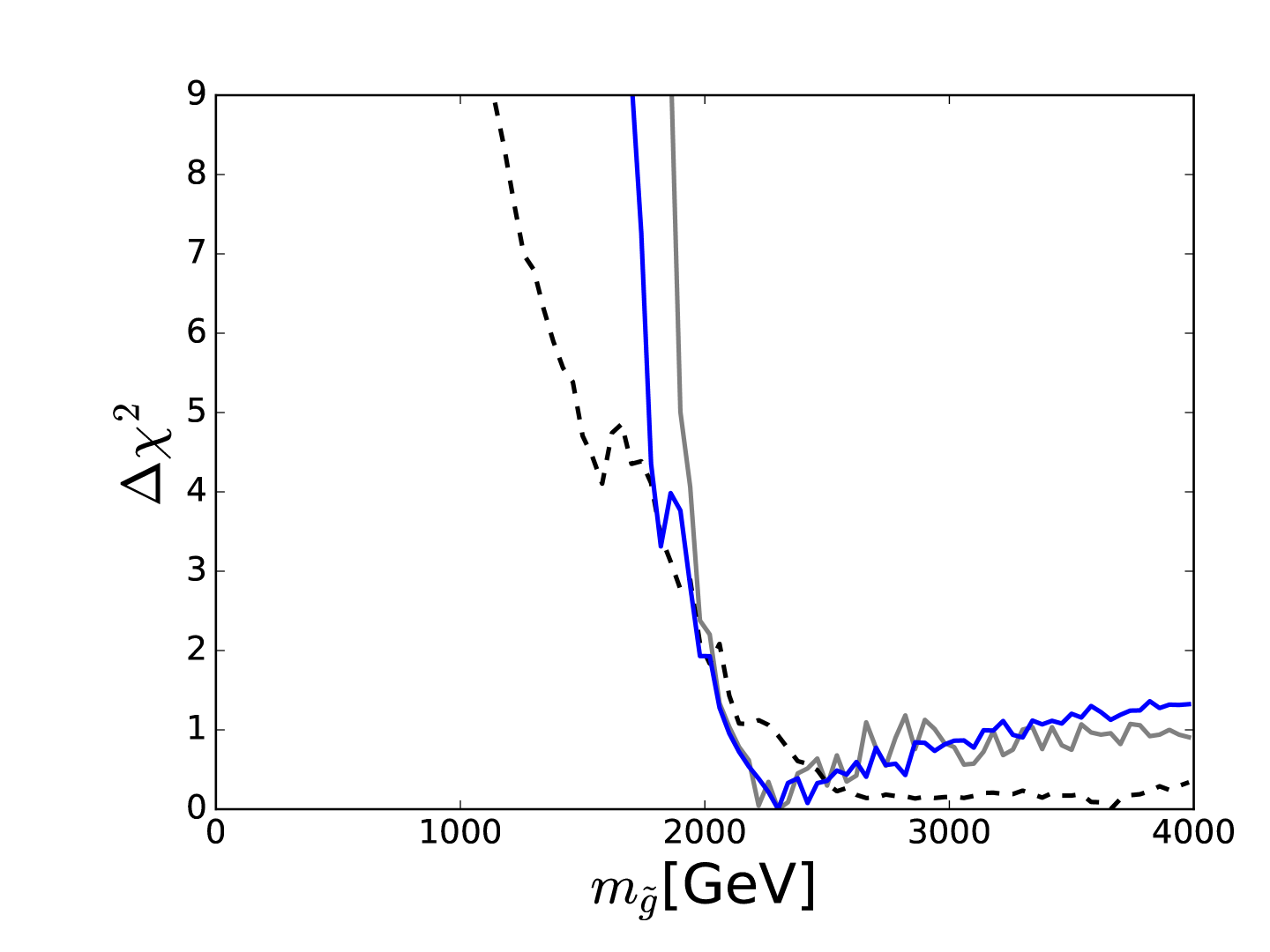
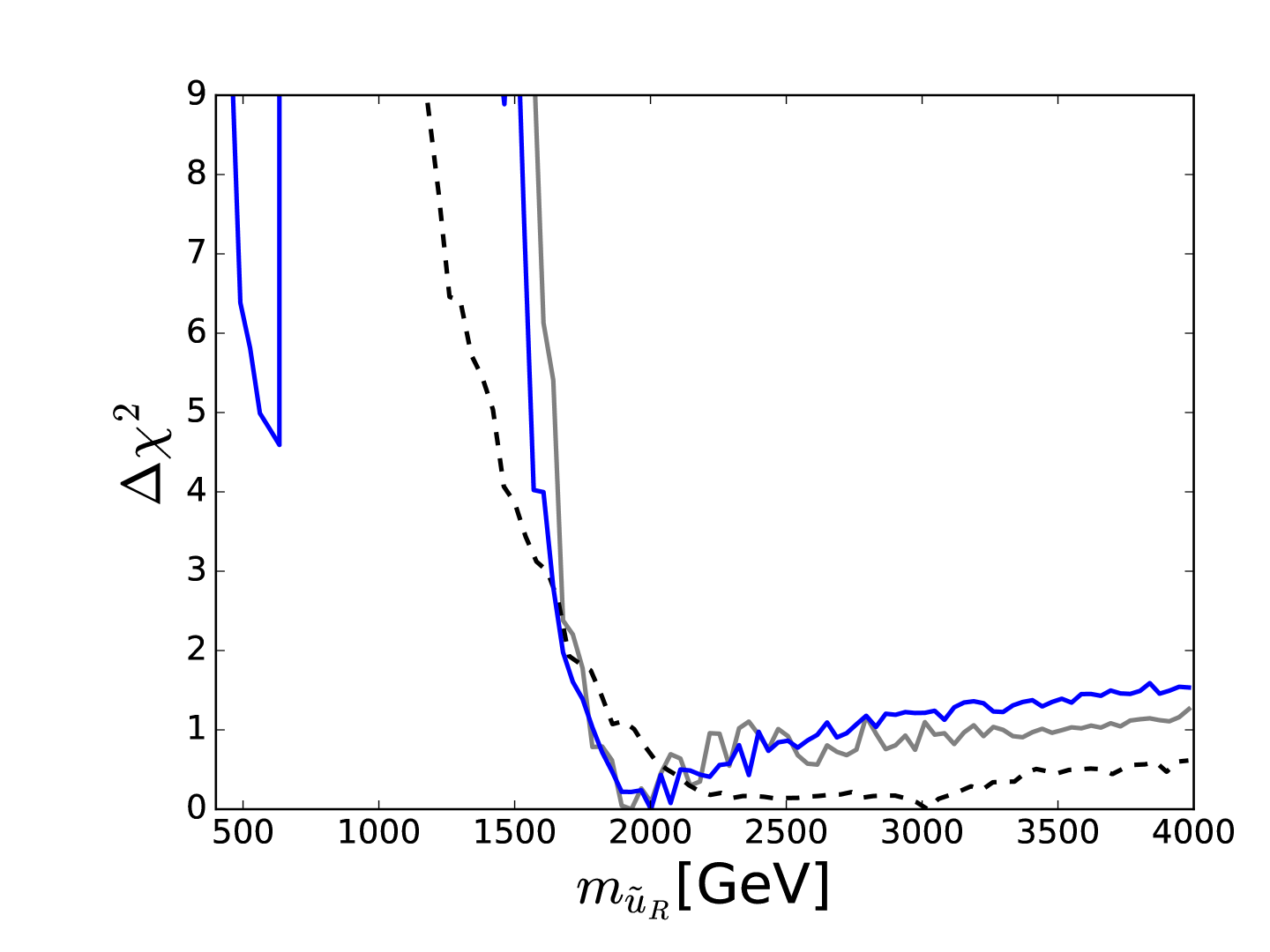
The best-fit spectrum in this SU(5) GUT model is shown in Fig. 8. We see that all the squarks have masses below GeV at the best-fit point, where they would be within the range of future LHC runs. This analysis included the results from the first /fb of LHC data at 13 TeV, and Fig. 9 compares the profiled likelihood functions for (left panel) and (right panel) found in this analysis (solid blue lines) with those found in an analysis restricted to 8 TeV data (dashed blue lines) 222The grey lines are for the NUHM2 model - see [42] for details.. We see that, whilst the 13 TeV have had a significant impact, they have not yet been a game-changer. There is still plenty of room for discovering supersymmetry in future LHC runs in this model, though there are no guarantees!
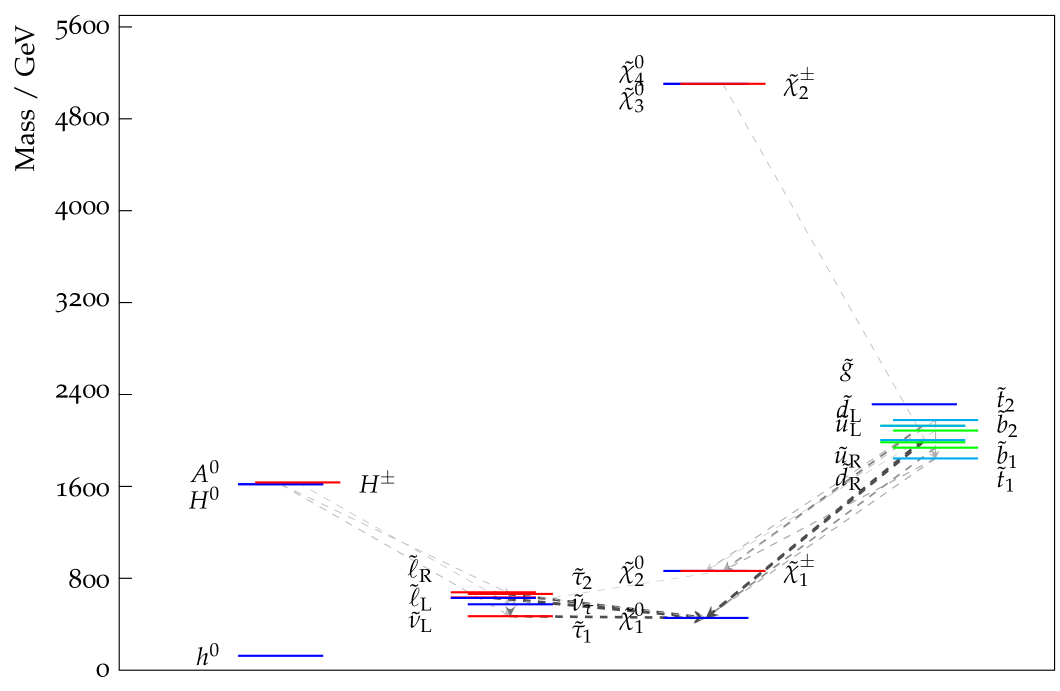
One of the interesting experimental possibilities in this and related models is that the next-to-lightest supersymmetric particle (NLSP) might be the lighter stau slepton, with a mass that could be so close to that of the that it might have a long enough lifetime to decay at a separated vertex, or even escape from the detector as a massive charged non-relativistic particle, as illustrated in Fig. 10 [42].

8.2 Probing the Minimal Anomaly-Mediated Supersymmetry-Breaking Model
Another model we have studied recently is the minimal anomaly-mediated supersymmetry-breaking (mAMSB) model [43]. In this case, the supersymmetric spectrum is relatively heavy. If one assumes that the lightest supersymmetric particle (LSP) is a wino that provides all the cosmological DM, it must weigh about 3 TeV, leading to a relatively heavy spectrum as seen in the left panel of Fig. 11, though the spectrum could be lighter if the LSP is a Higgsino, or if it provides only a fraction of the dark matter, as seen in the right panel of Fig. 11. We also see that the soft supersymmetry-breaking scalar mass in the mAMSB model must be quite large if the LSP provides all the dark matter, TeV, though it could be smaller if there is some other contribution to the dark matter.
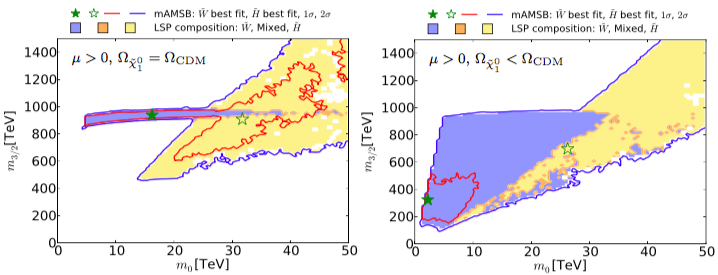
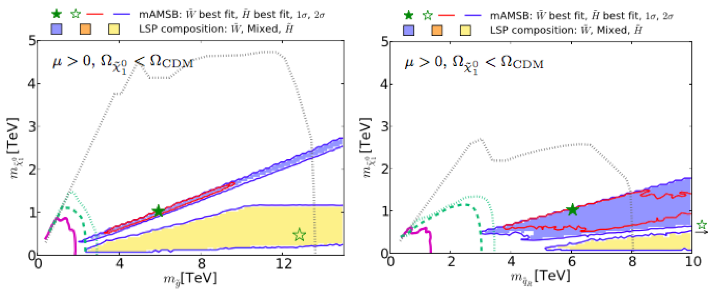
Fig. 12 displays the reaches of the LHC and a 100-TeV collider (FCC-hh) in the plane (left panel) and the plane (right panel) in the mAMSB [43]. We see that most of the allowed region of the mAMSB parameter space lies beyond the reach of the LHC, though it may be within reach of FCC-hh [44].
9 Direct Dark Matter Searches
Besides missing-energy searches at the LHC, the best prospects for exploring supersymmetry may be in the direct search for dark matter via scattering on nuclei in deep-underground laboratories [45]. Possible ranges of the LSP mass and the spin-independent cross section for LSP scattering on a proton target, , in the supersymmetric SU(5) and mAMSB models discussed above are shown in the left [42] and right [43] panels of Fig. 13, respectively. In both panels the range of excluded by the latest results from the PandaX [46] and LUX [47] experiments is shaded green. The estimated sensitivities of the planned LZ [48] and XENON1/nT [49] experiments are also shown, as is the neutrino ‘floor’ below which neutrino-induced backgrounds dominate. As in previous plots, the ranges allowed at the 95% CL (favoured at the 68% CL) are surrounded by blue and red contours, respectively, while the coloured shadings within them correspond to different mechanisms for bringing the LSP density into the cosmological range (discussed in [42, 43], and the best-fit points are marked by green stars.
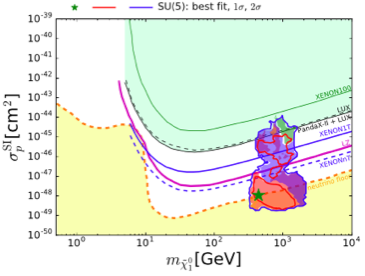
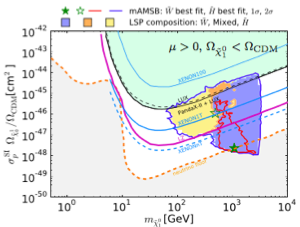
We see that values of anywhere from the present experimental limit down to below the neutrino ‘floor’ are possible in both the SU(5) and mAMSB cases. There are decent prospects for discovering direct DM scattering in the LZ and XENON1/nT experiments, but again no guarantees.
It is interesting to compare the sensitivities of LHC searches for mono-jet and other searches with those of direct searches for DM scattering, which can be done in the frameworks of simplified models for DM [50]. The results of the comparison depend, in particular, on the form of the coupling of the intermediate particle mediating the interactions between the DM and SM particles. Fig. 14 compares the sensitivities of LHC mono-jet and constraints in the case of a vector-like mediator (left panel) and LHC mono-jet searches and constraints on the spin-dependent scattering cross section, , in the case of an axial-vector mediator (right panel) [51]. We see that in the vector-like case the direct DM searches currently have more sensitivity except for small DM masses, whereas in the axial-vector case the LHC has greater sensitivity over a wide range of DM masses. These examples illustrate the complementarity of the LHC and direct searches in the quest for dark matter.
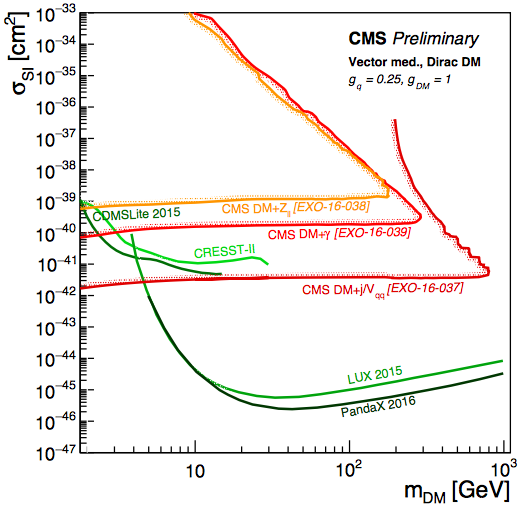
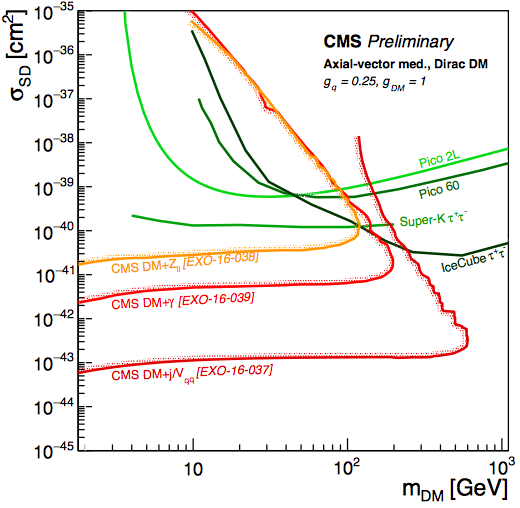
10 A Plea for Patience
The LHC will continue to operate for another 15 to 20 years, with the objective of gathering two orders of magnitude more data than those analyzed so far. Thus it has many opportunities to discover new physics beyond the Standard Model, e.g., in Higgs studies and in searches for new particles beyond the Standard Model such as supersymmetry and/or dark matter. Some lovers of superymmetry may be tempted to lose faith. However, it is worth remembering that the discovery of the Higgs boson came 48 years after it was postulated, whereas the first interesting supersymmetric models in four dimensions were written down at the end of 1973 [21], only just over 43 years ago! Moreover, the discovery of gravitational waves came just 100 years after they were predicted. Sometimes one must be patient.
In the mean time, what are the prospects for new accelerators to follow the LHC?
11 Electron-Positron Colliders
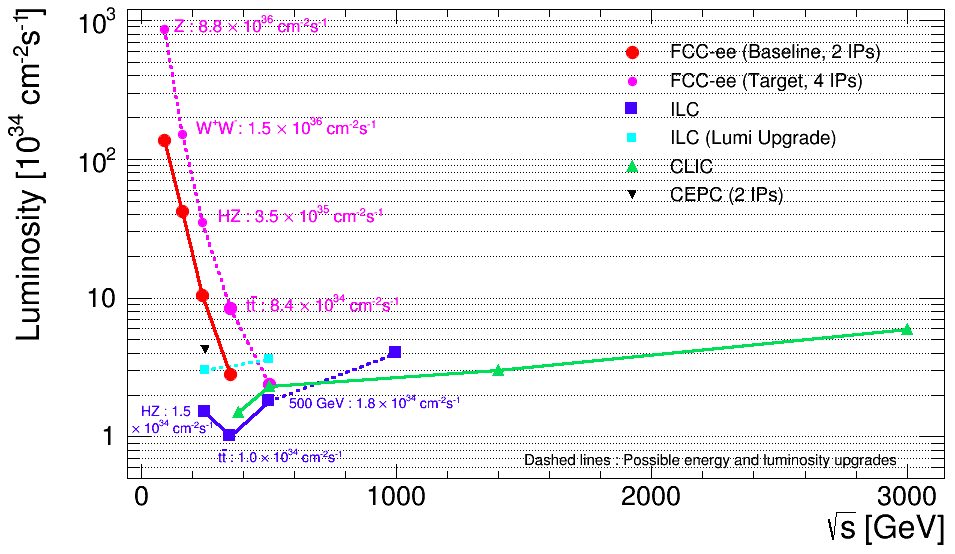
Fig. 15 shows the estimated luminosities as functions of the centre-of-mass energy for various projected colliders. We see that linear colliders (ILC [52], CLIC [53]) could reach higher energies, but circular colliders (CEPC [54], FCC-ee [55]) could provide higher luminosities at low energies. This means that CLIC, in particular, might be the accelerator of choice if future LHC runs reveal some new particles with masses TeV, or if the emphasis will be on probing decoupled new physics via SMEFT effects that grow with the centre-of-mass energy [56], whereas FCC-ee would be advantageous [57] if high-precision Higgs and measurements are to be prioritized.
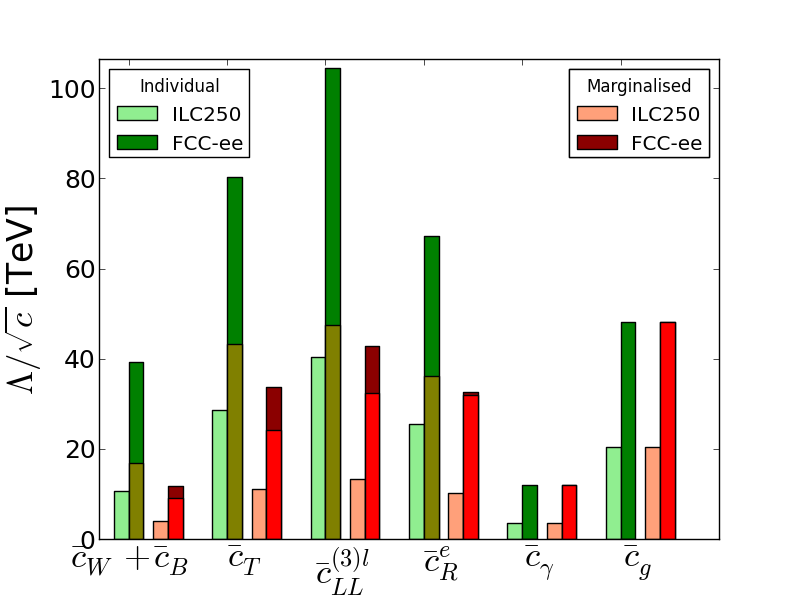
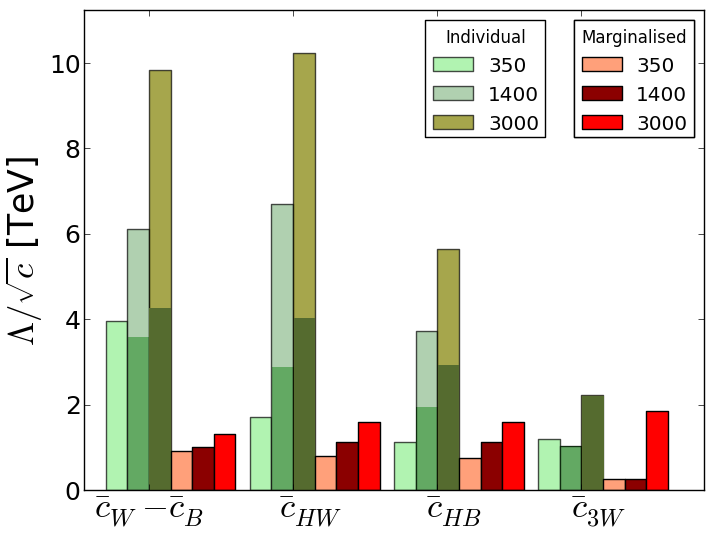
The left panel of Fig. 16 compares the estimated sensitivities of FCC-ee and ILC measurements of Higgs and electroweak precision measurements to the coefficients of some dimension-6 operators in the SMEFT [57]. The green bars are for fits to individual operator coefficients, and the red bars are after marginalization in global fits. We see that both FCC-ee (darker bars) and ILC (lighter bars) could reach far into the multi-TeV region. The right panel of Fig. 16 shows the estimated sensitivities of CLIC measurements to other combinations of dimension-6 SMEFT operators [56], highlighting the advantages conferred by high-energy running at CLIC.
12 Higher-Energy Proton-Proton Colliders
Circular colliders with circumferences approaching 100 km are being considered in China (CEPC/SppC [54]) and as a possible future CERN project (FCC-ee/hh [58]). One could imagine filling the tunnel with two successive accelerators, as was done with LEP and then the LHC in CERN’s present 27-km tunnel.
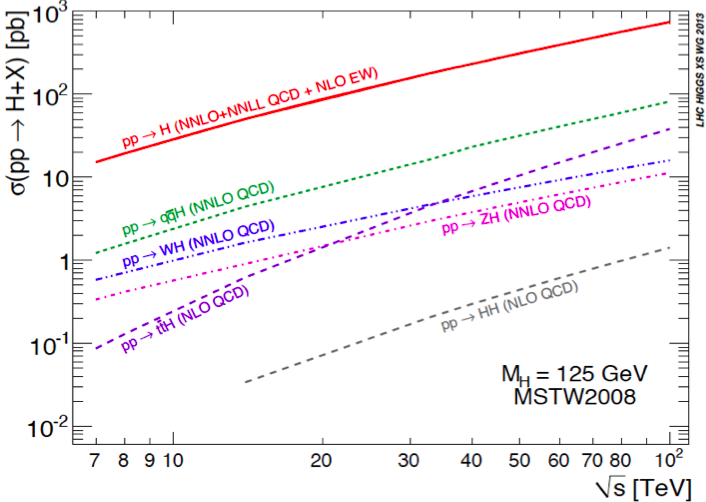
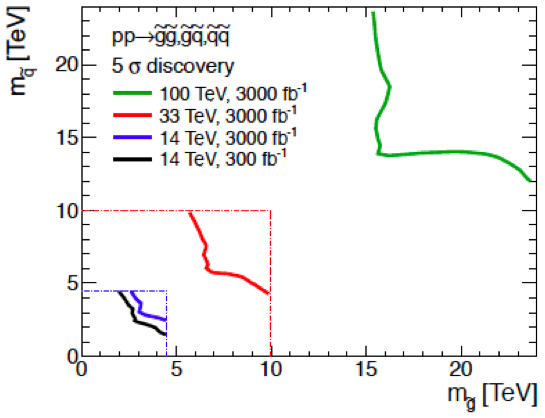
Fig. 17 provides two illustrations of the possible physics reach of the FCC-hh project for a collider. In the left panel we see the ways in which various Higgs production cross sections grow by almost two orders of magnitude with the centre-of-mass energy [59], offering many possibilities for high-precision measurements of Higgs production mechanisms and decay modes in collisions at 100 TeV. In particular, these might offer the opportunity to make the first accurate direct measurements of the triple-Higgs coupling. In the right panel we see the discovery reaches for squark and gluino discovery at FCC-pp [44]. The reaches for both these sparticles extend beyond 10 TeV and offer, e.g., the prospects for detecting the heavy spectrum of the mAMSB model shown in Fig. 12.
In my opinion, the combination of high precision and large kinematic reach offered by large circular colliders is unbeatable as a vision for the future of high-energy physics, offer the twin possibilities of exploring the 10 TeV scale directly in collisions at centre-of-mass energies up to 100 TeV and indirectly via the high-precision measurements mentioned in the previous Section.
13 Summary
Despite the impressive progress already made, many things are still to be learnt about the Higgs boson, including its expected dominant decay modes, rare decays into lighter particles and the triple-Higgs coupling. The best tool for interpreting Higgs and other electroweak measurements is the SMEFT, and possible future colliders offer good prospects for higher-precision measurements beyond the sensitivities of the LHC.
Like that of Mark Twain, rumours of the death of supersymmetry are exaggerated. I still think that it is the best framework for TeV-scale physics beyond the SM at the TeV scale. Simple supersymmetric models have been coming under increasing pressure from LHC searches, but other models with heavier spectra are still quite healthy. There are good prospects for discovering supersymmetry in future LHC runs and in direct dark matter detection experiments, but no guarantees. Maybe we will have to wait for a future higher-energy collider before discovering or abandoning supersymmetry?
In the mean time, we look forward to whatever indications the full LHC Run 2 date may provide before choosing what collider we would like to build next, but the answer to the question in the title may well be “round in circles”.
Acknowledgments
The author’s work was supported partly by the STFC Grant ST/L000326/1. He thanks his collaborators on topics discussed here, and thanks the Institute of Advanced Study of the Hong Kong University of Science and Technology for its kind hospitality.
References
- [1] For recent high points in this effort, see C. Anastasiou, C. Duhr, F. Dulat, F. Herzog and B. Mistlberger, Phys. Rev. Lett. 114 (2015) 212001 doi:10.1103/ PhysRevLett.114.212001 [arXiv:1503.06056 [hep-ph]]; J. Currie, E. W. N. Glover and J. Pires, Phys. Rev. Lett. 118 (2017) no.7, 072002 doi:10.1103/PhysRevLett.118.072002 [arXiv:1611.01460 [hep-ph]].
- [2] ATLAS Collaboration, https://twiki.cern.ch/twiki/bin/view/AtlasPublic/ StandardModelPublicResults; see also CMS Collaboration, https://twiki.cern.ch/ twiki/bin/view/CMSPublic/PhysicsResultsCombined.
- [3] J. Charles et al. [CKMfitter Collaboration], Phys. Rev. D 91 (2015) no.7, 073007 doi:10.1103/PhysRevD.91.073007 [arXiv:1501.05013 [hep-ph]], and http://ckmfitter.in2p3.fr.
- [4] UTfit Collaboration, http://www.utfit.org/UTfit/.
- [5] R. Aaij et al. [LHCb Collaboration], JHEP 1612 (2016) 087 doi:10.1007/JHEP12(2016)087 [arXiv:1611.03076 [hep-ex]].
- [6] For a recent review, see S. Bifani, https://indico.in2p3.fr/event/13763/ session/9/contribution/104/material/slides/0.pdf.
- [7] For a recent review, see G. Wormser, https://indico.in2p3.fr/event/13763/ session/9/contribution/105/material/slides/0.pdf.
- [8] S. Descotes-Genon, L. Hofer, J. Matias and J. Virto, JHEP 1606 (2016) 092 doi:10.1007/JHEP06(2016)092 [arXiv:1510.04239 [hep-ph]].
- [9] W. Altmannshofer, C. Niehoff, P. Stangl and D. M. Straub, arXiv:1703.09189 [hep-ph].
- [10] Z. Bai et al. [RBC and UKQCD Collaborations], Phys. Rev. Lett. 115 (2015) no.21, 212001 doi:10.1103/PhysRevLett.115.212001 [arXiv:1505.07863 [hep-lat]].
- [11] A. J. Buras, M. Gorbahn, S. J ger and M. Jamin, JHEP 1511 (2015) 202 doi:10.1007/JHEP11(2015)202 [arXiv:1507.06345 [hep-ph]].
- [12] V. Khachatryan et al. [CMS Collaboration], Phys. Lett. B 749 (2015) 337 doi:10.1016/j.physletb.2015.07.053 [arXiv:1502.07400 [hep-ex]]; G. Aad et al. [ATLAS Collaboration], JHEP 1511 (2015) 211 doi:10.1007/JHEP11(2015)211 [arXiv:1508.03372 [hep-ex]].
- [13] CMS Collaboration, https://cds.cern.ch/record/2159682/files/ HIG-16-005-pas.pdf.
- [14] G. Aad et al. [ATLAS and CMS Collaborations], Phys. Rev. Lett. 114 (2015) 191803 doi:10.1103/PhysRevLett.114.191803 [arXiv:1503.07589 [hep-ex]].
- [15] S. Oda, https://indico.in2p3.fr/event/13763/session/0/contribution/39/ material/slides/0.pdf.
- [16] D. de Florian et al. [LHC Higgs Cross Section Working Group], arXiv:1610.07922 [hep-ph].
- [17] G. Aad et al. [ATLAS and CMS Collaborations], JHEP 1608 (2016) 045 doi:10.1007/JHEP08(2016)045 [arXiv:1606.02266 [hep-ex]].
- [18] T. Aaltonen et al. [CDF and D0 Collaborations], Phys. Rev. D 88 (2013) no.5, 052014 doi:10.1103/PhysRevD.88.052014 [arXiv:1303.6346 [hep-ex]].
- [19] J. Ellis and T. You, JHEP 1306 (2013) 103 doi:10.1007/JHEP06(2013)103 [arXiv:1303.3879 [hep-ph]].
- [20] G. Blankenburg, J. Ellis and G. Isidori, Phys. Lett. B 712 (2012) 386 doi:10.1016/j.physletb.2012.05.007 [arXiv:1202.5704 [hep-ph]].
- [21] J. Wess and B. Zumino, Phys. Lett. 49B (1974) 52 doi:10.1016/0370-2693(74)90578-4; Nucl. Phys. B 70 (1974) 39 doi:10.1016/0550-3213(74)90355-1; Nucl. Phys. B 78 (1974) 1 doi:10.1016/0550-3213(74)90112-6.
- [22] L. Maiani, Proc. Summer School on Particle Physics, Gif-sur-Yvette, 1979 (IN2P3, Paris, 1980) p. 3; G. ’t Hooft, in: G. ’t Hooft et al., eds., Recent Developments in Field Theories (Plenum Press, New York, 1980); E. Witten, Nucl. Phys. B188 (1981) 513; R.K. Kaul, Phys. Lett. 109B (1982) 19.
- [23] See, for example: S. Weinberg, Phys. Rev. D 13 (1976) 974.
- [24] See, for example: N. Arkani-Hamed, A. G. Cohen, E. Katz and A. E. Nelson, JHEP 0207 (2002) 034 [arXiv:hep-ph/0206021].
- [25] G. F. Giudice, C. Grojean, A. Pomarol and R. Rattazzi, JHEP 0706 (2007) 045 doi:10.1088/1126-6708/2007/06/045 [hep-ph/0703164]; R. Contino, C. Grojean, M. Moretti, F. Piccinini and R. Rattazzi, JHEP 1005 (2010) 089 doi:10.1007/JHEP05(2010)089 [arXiv:1002.1011 [hep-ph]].
- [26] M. Baak et al. [Gfitter Group], Eur. Phys. J. C 74 (2014) 3046 doi:10.1140/epjc/s10052-014-3046-5 [arXiv:1407.3792 [hep-ph]].
- [27] V. Sanz and J. Setford, arXiv:1703.10190 [hep-ph].
- [28] J. Ellis, J. R. Espinosa, G. F. Giudice, A. Hoecker and A. Riotto, Phys. Lett. B 679 (2009) 369 doi:10.1016/j.physletb.2009.07.054 [arXiv:0906.0954 [hep-ph]].
- [29] G. Degrassi, S. Di Vita, J. Elias-Miro, J. R. Espinosa, G. F. Giudice, G. Isidori and A. Strumia, JHEP 1208 (2012) 098 [arXiv:1205.6497 [hep-ph]].
- [30] D. Buttazzo, G. Degrassi, P. P. Giardino, G. F. Giudice, F. Sala, A. Salvio and A. Strumia, JHEP 1312 (2013) 089 doi:10.1007/JHEP12(2013)089 [arXiv:1307.3536 [hep-ph]].
- [31] A. Hook, J. Kearney, B. Shakya and K. M. Zurek, JHEP 1501 (2015) 061 doi:10.1007/JHEP01(2015)061 [arXiv:1404.5953 [hep-ph]].
- [32] J. R. Ellis and D. Ross, Phys. Lett. B 506 (2001) 331 [arXiv:hep-ph/0012067].
- [33] W. Buchmuller and D. Wyler, Nucl. Phys. B 268 (1986) 621; A. Pomarol and F. Riva, JHEP 1401 (2014) 151 [arXiv:1308.2803 [hep-ph]].
- [34] J. Ellis, V. Sanz and T. You, JHEP 1503 (2015) 157 doi:10.1007/JHEP03(2015)157 [arXiv:1410.7703 [hep-ph]].
- [35] A. Falkowski, M. Gonzalez-Alonso, A. Greljo and D. Marzocca, Phys. Rev. Lett. 116 (2016), 011801 doi:10.1103/PhysRevLett.116.011801 [arXiv:1508.00581 [hep-ph]].
- [36] Paraphrasing J. Bond, http://www.imdb.com/title/tt0143145/fullcredits/.
- [37] B. Bairnsfather, http://www.independent.co.uk/news/uk/home-news/the- captain-who-gave-britain-its-ultimate-weapon-during-world-war-one- laughter-9833596.html.
- [38] J. R. Ellis, G. Ridolfi and F. Zwirner, Phys. Lett. B 257 (1991) 83; H. E. Haber and R. Hempfling, Phys. Rev. Lett. 66 (1991) 1815; Y. Okada, M. Yamaguchi and T. Yanagida, Prog. Theor. Phys. 85 (1991) 1.
- [39] J. R. Ellis, S. Heinemeyer, K. A. Olive and G. Weiglein, JHEP 0301 (2003) 006 doi:10.1088/1126-6708/2003/01/006 [hep-ph/0211206].
- [40] J. R. Ellis, J. S. Hagelin, D. V. Nanopoulos, K. A. Olive and M. Srednicki, Nucl. Phys. B 238 (1984) 453. doi:10.1016/0550-3213(84)90461-9
- [41] J. Ellis, S. Kelley and D.V. Nanopoulos, Phys. Lett. B260 (1991) 131; U. Amaldi, W. de Boer and H. Furstenau, Phys. Lett. B260 (1991) 447; P. Langacker and M. Luo, Phys. Review D44 (1991) 817; C. Giunti, C. W. Kim and U. W. Lee, Mod. Phys. Lett. A 6 (1991) 1745.
- [42] E. Bagnaschi et al., Eur. Phys. J. C 77 (2017) no.2, 104 doi:10.1140/epjc/s10052-017-4639-6 [arXiv:1610.10084 [hep-ph]].
- [43] E. Bagnaschi et al., arXiv:1612.05210 [hep-ph].
- [44] T. Golling et al., [arXiv:1606.00947 [hep-ph]].
- [45] P. Cushman et al. [WIMP Dark Matter Direct Detection Working Group], arXiv:1310.8327 [hep-ex].
- [46] A. Tan et al. [PandaX-II Collaboration], Phys. Rev. Lett. 117 (2016) no.12, 121303 doi:10.1103/PhysRevLett.117.121303 [arXiv:1607.07400 [hep-ex]].
- [47] D. S. Akerib et al. [LUX Collaboration], Phys. Rev. Lett. 118 (2017) no.2, 021303 doi:10.1103/PhysRevLett.118.021303 [arXiv:1608.07648 [astro-ph.CO]].
- [48] D. S. Akerib et al. [LZ Collaboration], arXiv:1509.02910 [physics.ins-det].
- [49] E. Aprile et al. [XENON Collaboration], JCAP 1604 (2016) no.04, 027 doi:10.1088/1475-7516/2016/04/027 [arXiv:1512.07501 [physics.ins-det]].
- [50] O. Buchmueller, M. J. Dolan and C. McCabe, JHEP 1401 (2014) 025 doi:10.1007/JHEP01(2014)025 [arXiv:1308.6799 [hep-ph]]; O. Buchmueller, S. A. Malik, C. McCabe and B. Penning, Phys. Rev. Lett. 115 (2015) no.18, 181802 doi:10.1103/PhysRevLett.115.181802 [arXiv:1505.07826 [hep-ph]]; S. A. Malik et al., White Paper from 2014 Brainstorming Workshop held at Imperial College London, Phys. Dark Univ. 9-10 (2015) 51 doi:10.1016/j.dark.2015.03.003 [arXiv:1409.4075 [hep-ex]]; J. Abdallah et al., Phys. Dark Univ. 9-10 (2015) 8 doi:10.1016/j.dark.2015.08.001 [arXiv:1506.03116 [hep-ph]]; M. Bauer et al., White Paper from 2016 Brainstorming Workshop held at Imperial College London, arXiv:1607.06680 [hep-ex]; D. Abercrombie et al. [ATLAS/CMS Dark Matter Forum], arXiv:1507.00966 [hep-ex]. A. Boveia et al. [LHC Dark Matter Working Group], arXiv:1603.04156 [hep-ex].
- [51] CMS Collaboration, https://cds.cern.ch/record/2208044/files/DP2016_057.pdf.
- [52] G. Aarons et al. [ILC Collaboration], arXiv:0709.1893 [hep-ph]; ILC TDR, H. Baer, T. Barklow, K. Fujii, Y. Gao, A. Hoang, S. Kanemura, J. List and H. E. Logan et al., arXiv:1306.6352 [hep-ph]; D. M. Asner et al., arXiv:1310.0763 [hep-ph].
- [53] CLIC CDR, eds. M. Aicheler, P. Burrows, M. Draper, T. Garvey, P. Lebrun, K. Peach, N. Phinney, H. Schmickler, D. Schulte and N. Toge, CERN-2012-007, http://project-clic-cdr.web.cern.ch/project-CLIC-CDR/; M. J. Boland et al. [CLIC and CLICdp Collaborations], doi:10.5170/CERN-2016-004 arXiv:1608.07537 [physics.acc-ph]; H. Abramowicz et al., arXiv:1608.07538 [hep-ex].
- [54] CEPC-SPPC Study Group, IHEP-CEPC-DR-2015-01, IHEP-TH-2015-01, IHEP-EP-2015-01.
- [55] M. Bicer et al. [TLEP Design Study Working Group Collaboration], JHEP 1401 (2014) 164[arXiv:1308.6176 [hep-ex]]; see also http://tlep.web.cern.ch/content/ machine-parameters.
- [56] J. Ellis, P. Roloff, V. Sanz and T. You, arXiv:1701.04804 [hep-ph].
- [57] J. Ellis and T. You, JHEP 1603 (2016) 089 doi:10.1007/JHEP03(2016)089 [arXiv:1510.04561 [hep-ph]].
- [58] FCC Collaboration, https://fcc.web.cern.ch/Pages/default.aspx.
- [59] R. Contino et al., arXiv:1606.09408 [hep-ph].