Words as block of notes and Zipf law in music using visibility algorithm.
Abstract
In this work we were aimed to study music using visibility algorithms. This algorithms are used as a way to get a network, from a time series. However the main idea of this paper was not to study music from the perspective of complex networks, but to studying it as a lenguage, basically the changes in wath we call words, between diferents ages in music. The visibility algorithm provide us a way to cut time series and generate the words, of the composers we where studying. We study clasical music composers from differents ages, from Bach to Schostakovish. Time series in this work came from MIDI archives and the series were generated by, the absolute diference between two adyacent notes, in the first voice in the MIDI archive. Once we had our series we apply the algorithm to generate words. The visibility algorihm was used also, as a way to get Zipf law becouse at first what we found was that when we used visibility algorithm we create a free-scale network, so we decided to take subgroup of this network that is going to be also free of scale, and make the musical words.
Introduction .
Music has been studied in several ways long ago. One of the first studies trying to see music behavior were made by , Voss and Clarke[10]. They observe a 1/f behaivor in music pitch. Since then there exist a number of works trying to study music, some from times series mesuring hurst exponent[9, 7, 8], treating music like a fractional Brownian motion (fBm), seeing and searching fractality and a lot of research related . Recently a new perspective has been used, transforming music into a complex networks in order to studying music, from the tools of complex networks[4, 3]. In contrast , in this work we try to see music in a different way, we are interested in see if music can be treated as a lenguage, from the point of view of a lenguage we need to define what our words are going to be. In order to form what we are going to call a word, we used the so called visibility algorithm[2]. Next what we are concerned, is to seeing if this words follow the Zipf’s law, like the rest of lenguages.
Visibility Algorithm
One algorithm that transform a time series into a network, is the Visibility Algorithms [2, 5, 6]. The natural visivility algorithm is a really easy way to transform a time series into a network. The main idea of the algorithm, is comparing two diferent points (A,B) in the time series. In order to decide, if this two are going to be conected in the network, wath visibility does is to compare the straight line that can be draw between this points and then check if all the points that lie between (A,B) are below the straight line, if does, then the algorithm says that the points A and B are conected in the network.
The Visibility Algorithm, is often written as the following inequality:
| (1) |
As we can see in figure LABEL:vix.
Recently it has been shown that the visiibility algorithm is a way to find motifs in time series [1].
Zipff Law.
In 1932 George Kingsley Zipf discover a new law concerning, the statistics properties of lenguages[11]. From this point it has been seen that humans lenguage follow the distribit
The zipff law was discoer in ….
Method.
In order to analyze music from diferent composers, we use MIDI files. In this files, we have information about duration and the note. Instead of having this information pictorically, as is often seeing in music scores, in our case is displayed with numerical values. So its relatively easy to extract the information and generate time series. Also we have the information related to the voices, all the pieces analyzed correspondo to piano works, and are from diferent composers.
Is good to clarify that, we only use the first voice in this study. Some times a chord comes out in the voice we are analyzing, in wich case we only used the higest note. Having extracted the information , its easy to made a time series from adyacent notes. In this work we were no worry about the duration of notes. We put every note the same duration in the time series.

What we see in the picture above, is the representation of notes as they are in a pentagram, normally one way of doing a time series of music notes, is to put the values of the notes acording to their corresponding value of the midi coding. Nevertheless, in this study we were aimed to do the semitone diference between adjacent notes. We can think that we are studying the discrete derivate of the original time series, becouse the diference in time is always one. So what we have pictorically in figure 1, once the diference in semitones between adjacent notes is done, is the next time series:
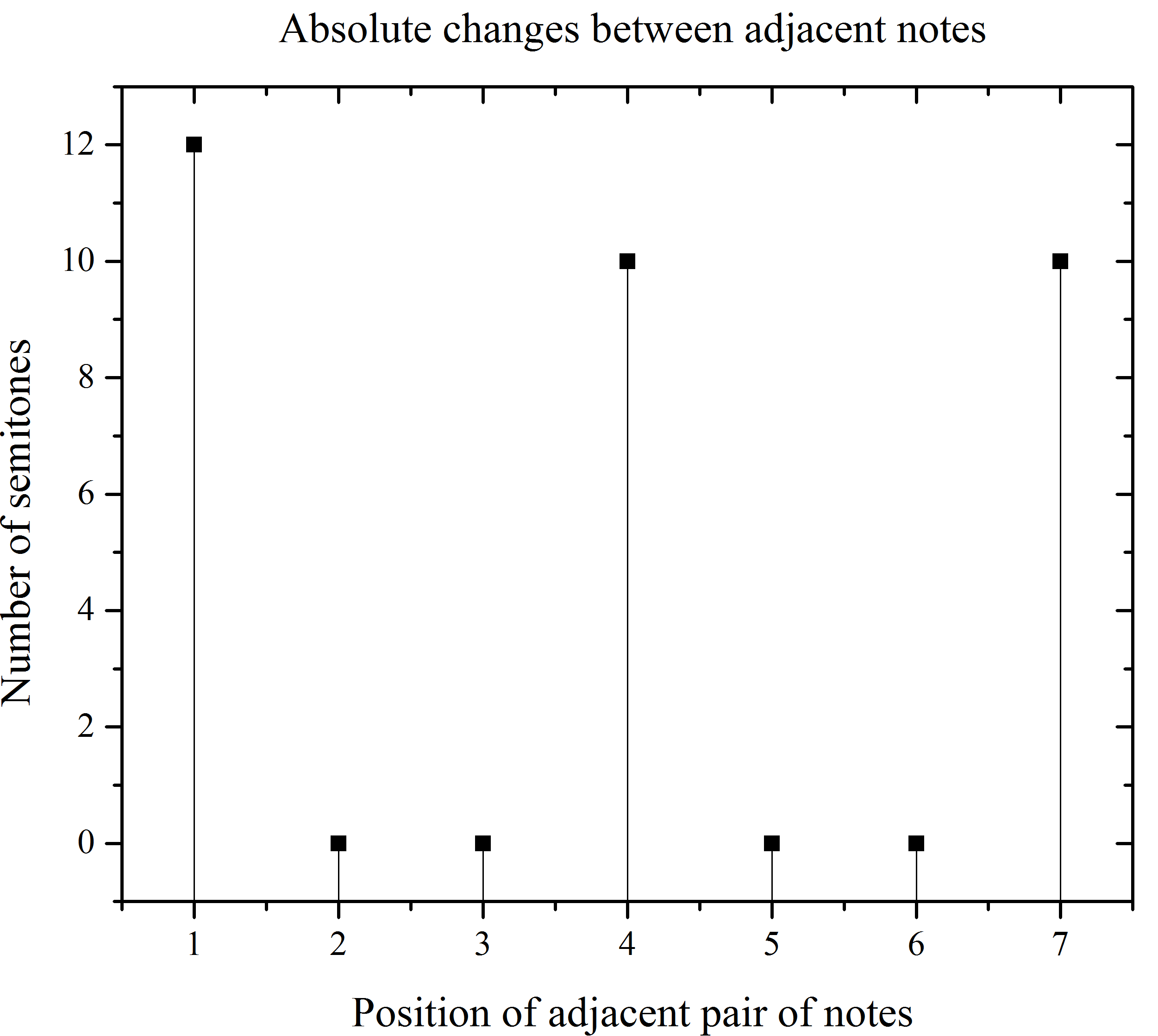
Once we have the rate of change series between adjacent semitones, then we apply the visibility algorithm. In spite of using the visibility rule we made some changes, instead of checking visibility between point A and the following points in the series, we stop once the visibility criteria isn’t satisfy between A and some other point C in the time series. In this point once we have stop the algorithm, a block is formed, this block contain information of the semintones in the interval [A,C), and the information is going to be codified using letters. For example in figure 3, is the time series we are studying under visibility. We start at event one in the series, we apply the algorithm rules. Then we find that under this rules we are unable to see event number five in the series, so we jump and restart the algorithm in event number 4, always one before the visibility being cutten. Once the the visibility criterion is not satisfy we do not check for other events, this mean that we do not check if the visibility criterion is true or false for event number six we simple move forward in the time series.
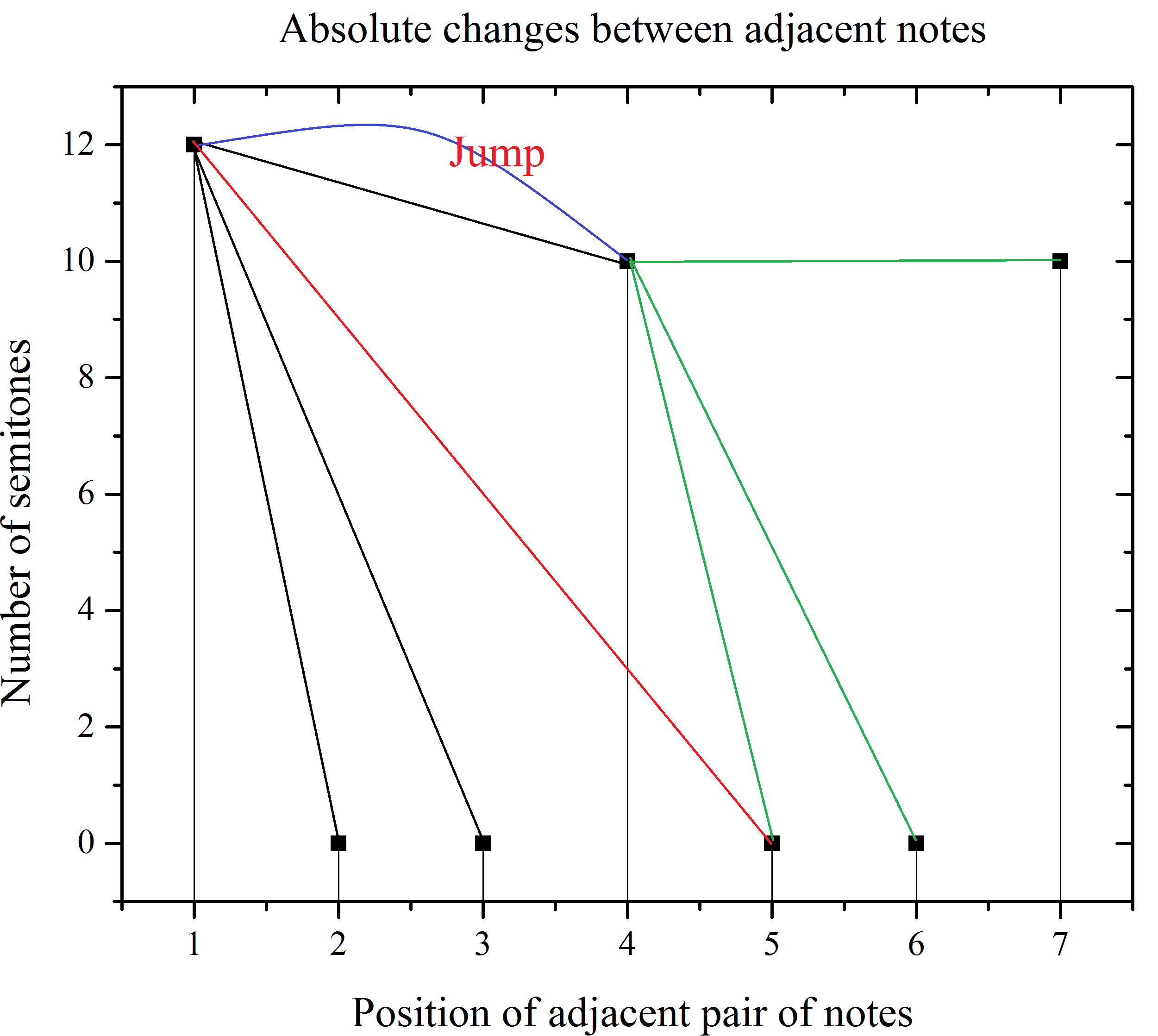
We mencioned before that we are aimed to formed words, so when the visibility is lost we create a block wich is going, from the event in wich the algoritm has been started, to one before the visibility has ben cutted. Neverteless in order to avoid confutions when reading the blocks, we put a labels to the diference in semitones, and obtaining a string of characters. Each caracter contain the information of the diference in semitones, acording to the following table.
| Nunmber of semitones | Letter representation |
|---|---|
| 0 | A |
| 1 | B |
| 2 | C |
| 3 | D |
| 4 | E |
With this, the information in figure 2 once is splitted is going to be coded as the next blocks: MAAL-LAAL. Also is worth it to mention, that if there is a difference above 25 semitones we put a d lowercase, re-starting the letters with the . For example if there is a 26 diference in semitones then we put . This doesn’t occur to often however it can occur. Also an importan thing is that we consider a block, the union of two consecutives blocks. So the final block above is going to be MAALAAL.
Results.
We analyzed pieces from diferent composers like Bach, Beethoven, Chopin, Scriabin, Satie among others. The majoritiy of ours files came from kunstderfuge web site, nearly 1300 pieces were analyzed. First we wanted to know if the difference series, transform as a scale free network. In order to know this we run the visibility algorithm with out any modification. What we saw was that the time series, was transformed into a scale free network. This can be seeing in the next graphs, we plot some of the reults found. The degree distribution follow a power law on most cases and is aproximated to this behavior.
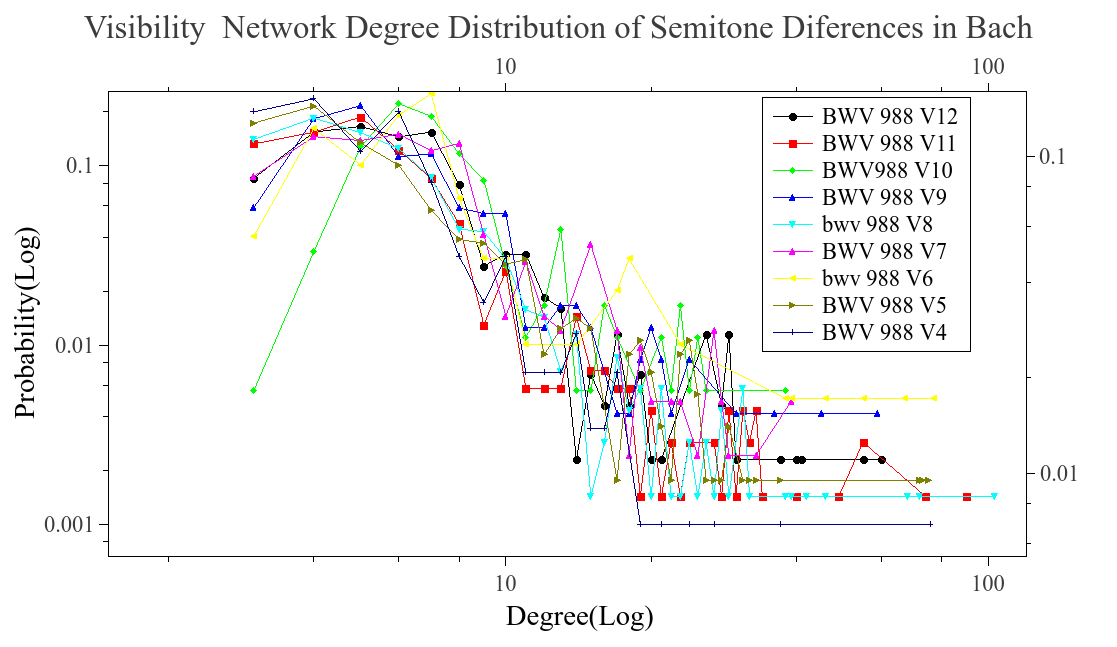
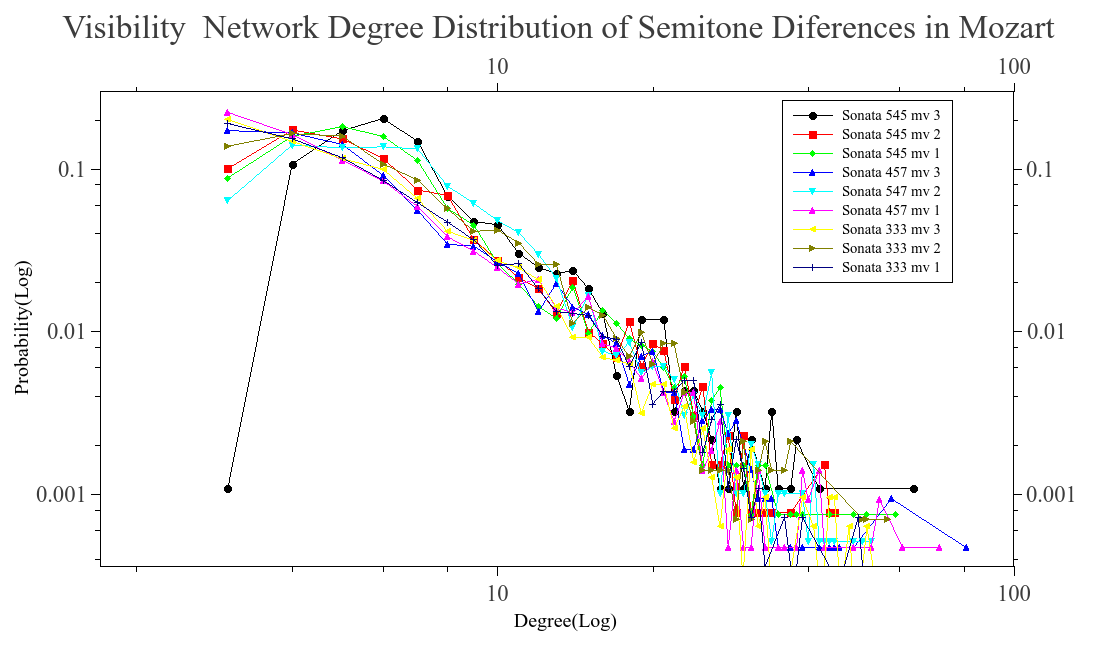
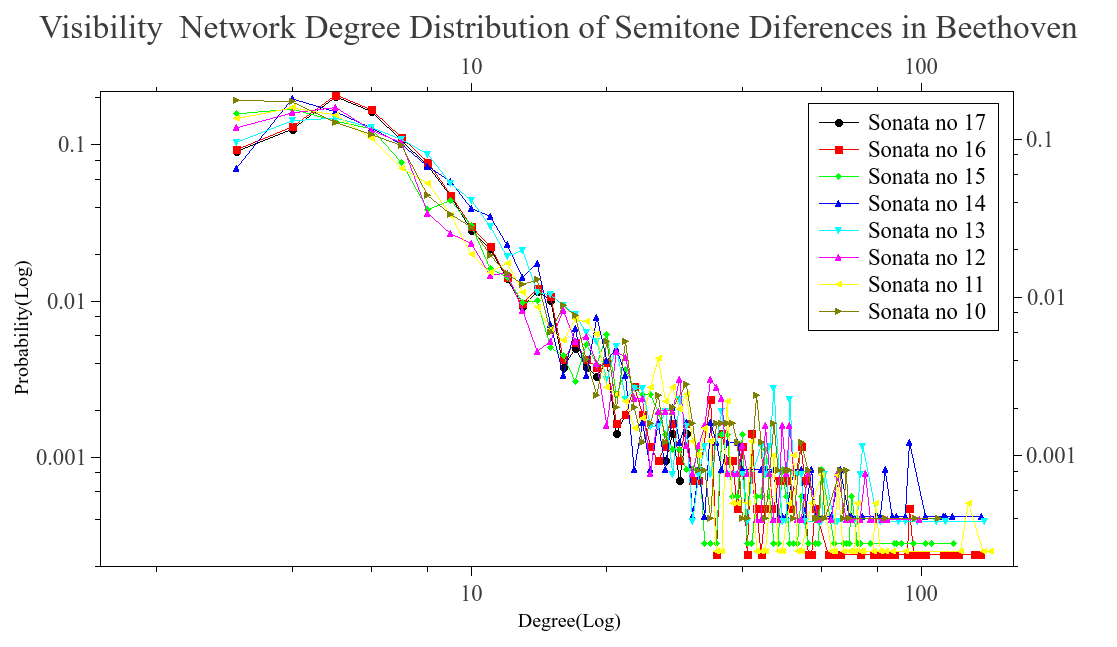
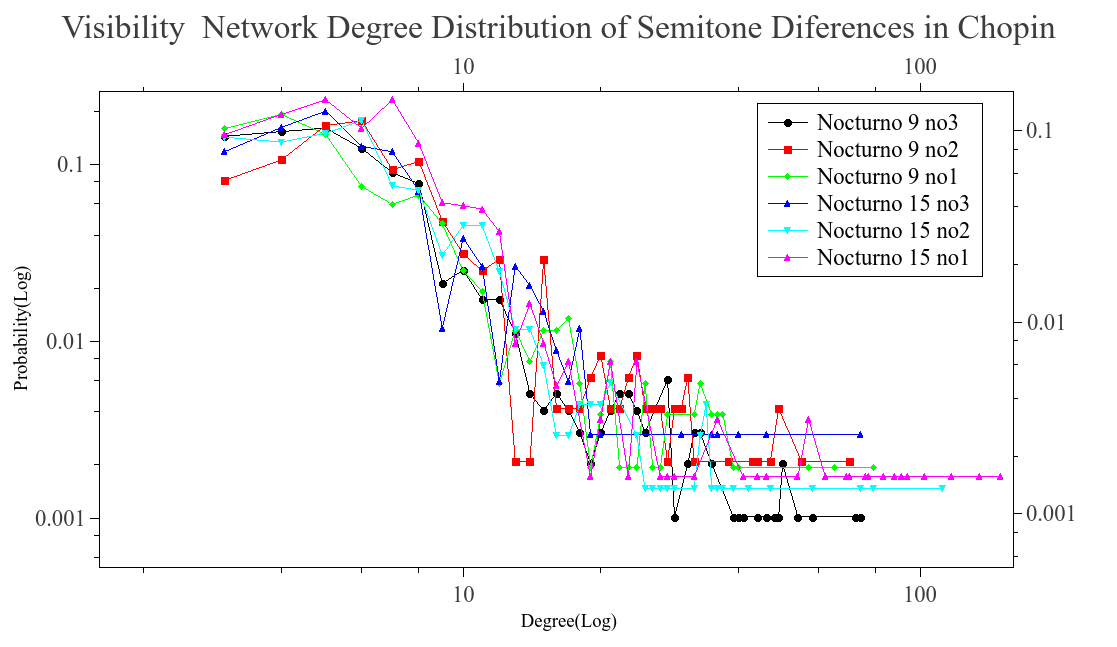
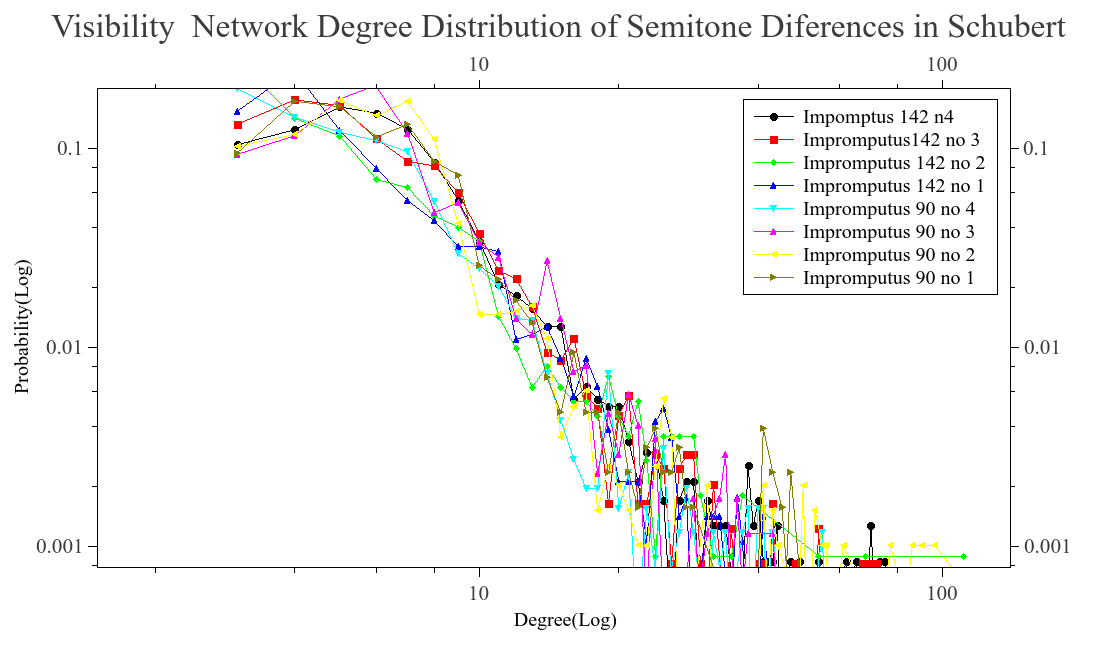
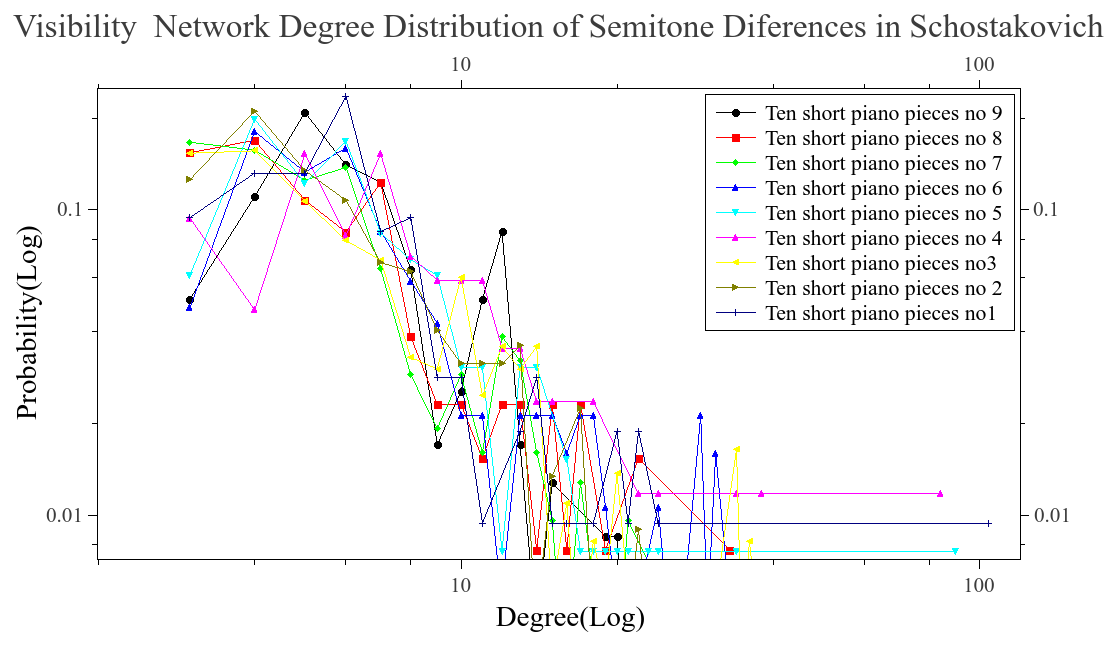
Once we know that the networks are scale free. We take a subgroup of the network, using the modifed algorithm. The blocks formed are conteined in the network but posibly with less conections, becouse of the modifications that were made when the visibility is lost. This blocks is what we call musical words, and as we know, the lenguages tent to follow Zipf’s law. Thats why we wanted to know if the whole network was scale free, as a maner to ensure that the words formed also have this behavior and result in a Zipf’s law when they are ranked.
In order to studie words, a data set was made. This data set contains the words used by a certain author, and how often are used by this composer. Thinking that every composer could be seen as a diferent musical lenguage with his own words. Again we used the 1300 files, and when we ploted, rank of the words used by the composer vs the probability for a certain word, we find the following graph
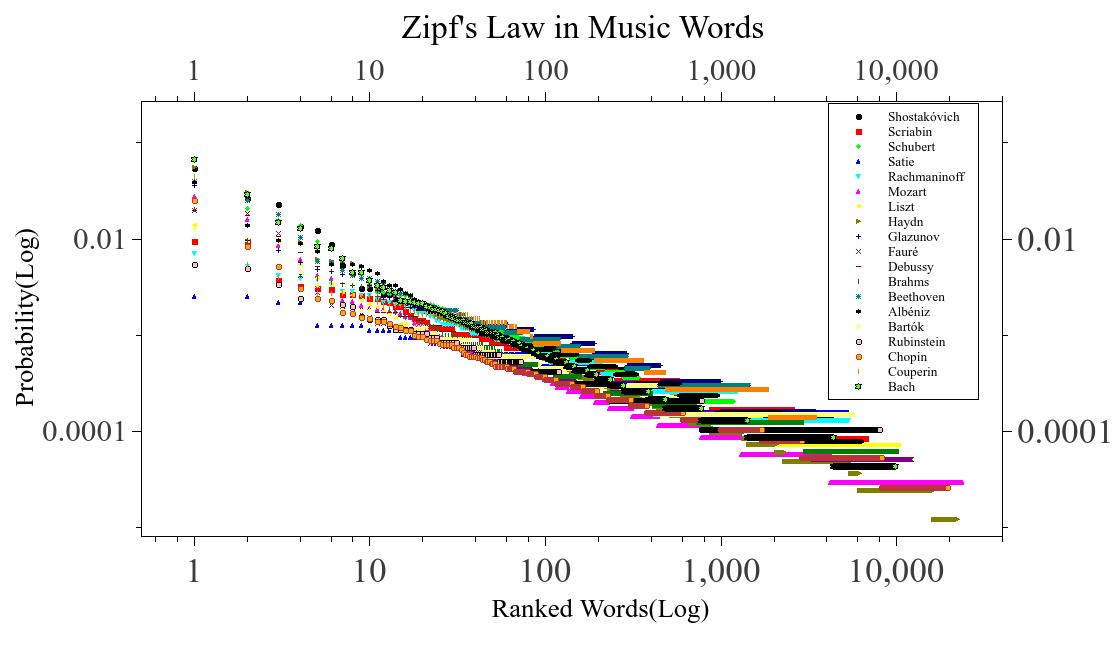
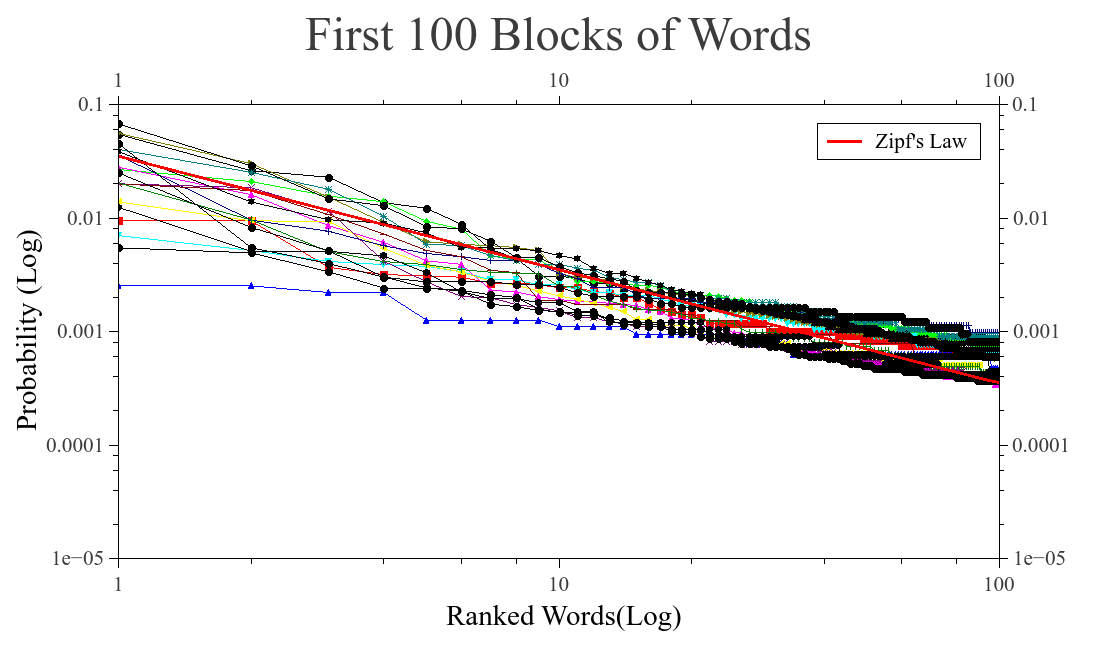
In the picture above we see that the blocks formed by the modified algorithm tent to follow a Zipf’s law, as lenguages does. With this result, we can think that every composer generate his own lenguage. The words in the lenguages are going to depend on the variations of the nearest notes, remembering that every character in the block is a mesure of the rate of change between adjacent notes in semitones. Having the words of the diferent composers, seems rasonable to find diferences among composers in the words formed. Meaning that we can construct a time series based, on how a fixed word, is probable for every composer. Thinking that every composer represent a diferent time in the series.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e20cfb94-b929-421a-ae03-6f255929676f/Bach.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e20cfb94-b929-421a-ae03-6f255929676f/couperin.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/e20cfb94-b929-421a-ae03-6f255929676f/Schubert.png)
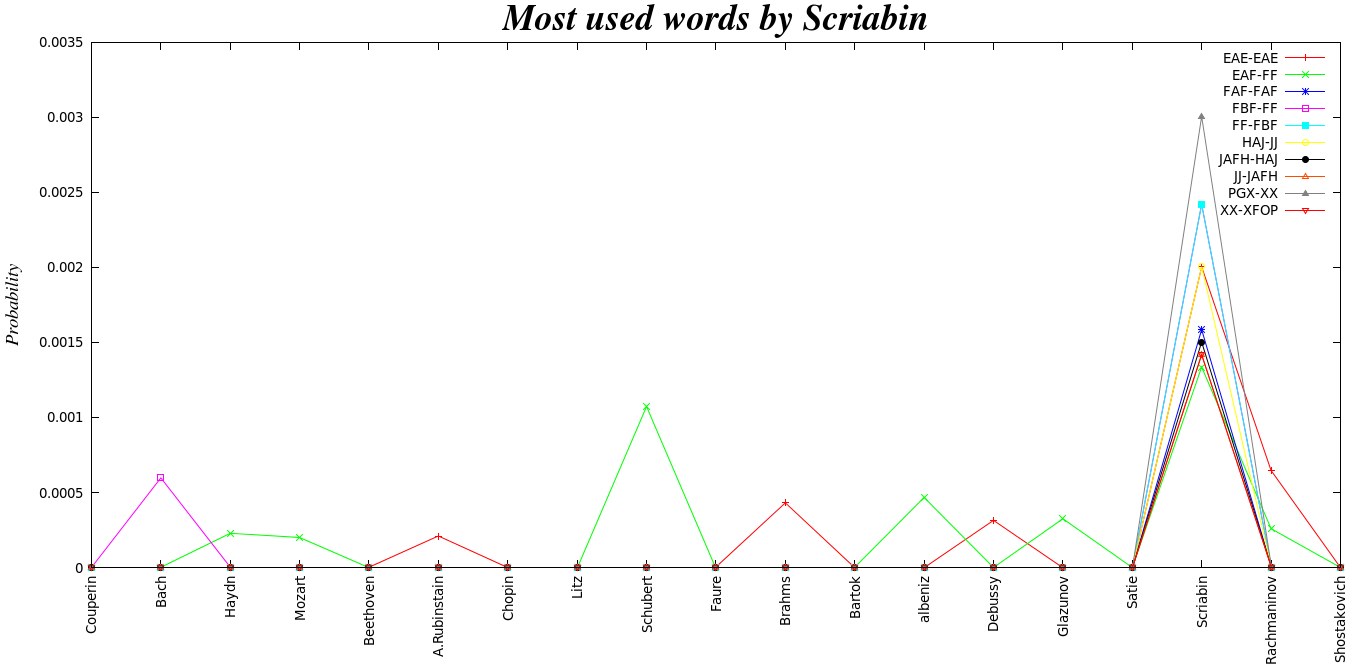
As we see above the words provides us a way to see how change the music from different times. For example, in early ages often we see that the words begin whit an C or a D, and also is not so common to find letters that are the last ones in the alphabet, among early composer. So waht we can think is that in early ages of music the jump between adjacent notes was really short in the majority of the times. Also when we compare the most often words use by this early composer, we can see that this words are used by more contemporany composers.The exeption it could be Couperin, in wich we found words with higer alphabet letters. When we see the graph of Couperin, we can see that most of their words died soon or are not longer used, others are used latrer on.

In contemporany composers we see that they like to introduce changes in adyacent notes that are above an octave, this make a contrast with early ages.Also among the most used words are some words that not were used before or after. This don’t ocure with early composers .

We can think that this most frequent words, are what makes the music composers differents between them.
References
- [1] Jacopo Iacovacci and Lucas Lacasa. Sequential visibility-graph motifs. Physical Review E, 93(4):042309, 2016.
- [2] Lucas Lacasa, Bartolo Luque, Fernando Ballesteros, Jordi Luque, and Juan Carlos Nuno. From time series to complex networks: The visibility graph. Proceedings of the National Academy of Sciences, 105(13):4972–4975, 2008.
- [3] Xiao Fan Liu, K Tse Chi, and Michael Small. Complex network structure of musical compositions: Algorithmic generation of appealing music. Physica A: Statistical Mechanics and its Applications, 389(1):126–132, 2010.
- [4] Xiaofan Liu, K Tse Chi, and Michael Small. Composing music with complex networks. In International Conference on Complex Sciences, pages 2196–2205. Springer Berlin Heidelberg, 2009.
- [5] Bartolo Luque, Lucas Lacasa, Fernando Ballesteros, and Jordi Luque. Horizontal visibility graphs: Exact results for random time series. Physical Review E, 80(4):046103, 2009.
- [6] Angel M Nuñez, Lucas Lacasa, Jose Patricio Gomez, and Bartolo Luque. Visibility algorithms: A short review. In New Frontiers in Graph Theory. InTech, 2012.
- [7] Zhi-Yuan Su and Tzuyin Wu. Multifractal analyses of music sequences. Physica D: Nonlinear Phenomena, 221(2):188–194, 2006.
- [8] Zhi-Yuan Su and Tzuyin Wu. Music walk, fractal geometry in music. Physica A: Statistical Mechanics and its Applications, 380:418–428, 2007.
- [9] Richard F Voss. Random fractals: Self-affinity in noise, music, mountains, and clouds. Physica D: Nonlinear Phenomena, 38(1-3):362–371, 1989.
- [10] Richard F Voss and John Clarke. 1/f noise in music: Music from 1/f noise. The Journal of the Acoustical Society of America, 63(1):258–263, 1978.
- [11] George Kingsley Zipf. Selected studies of the principle of relative frequency in language. 1932.