Wulff inequality for minimal submanifolds in Euclidean space
Abstract.
In this paper, we prove a Wulff inequality for -dimensional minimal submanifolds with boundary in , where we associate a nonnegative anisotropic weight to the boundary of minimal submanifolds. The Wulff inequality constant depends only on and , and is independent of the weights. The inequality is sharp if and is the support function of ellipsoids or certain type of centrally symmetric long convex bodies.
1. Introduction
The isoperimetric inequality is a fundamental geometric inequality that has been extensively studied throughout history since the ancient era of Queen Dido. It states that the round ball minimizes the boundary hypersurface area among all shapes with a given volume. There are several proofs of the isoperimetric inequality and readers can refer to the books and papers [BZ13, Oss78, Cha01]. Later, the isoperimetric inequality for general minimal submanifolds with nonzero codimension in Euclidean space was considered. It was conjectured in [AHO74] that
Conjecutre 1.1.
For any dimensional smooth minimal submanifold with smooth boundary , the following sharp isoperimetric inequality holds
| (1.1) |
and equality holds if and only if is an -dimensional ball in . Here, denotes the -dimensional volume (area) of , denotes the -dimensional volume (area) of the boundary , is the open unit ball in , and denotes its volume.
Carleman [Car21] proved that the conjecture holds for -dimensional minimal surfaces diffeomorphic to a disk in via Wirtinger inequality and Almgren [Alm86] showed that the conjecture holds for arbitrary codimensional area minimizing submanifolds in Euclidean space. In a recent breakthrough, Brendle [Bre21] verified the sharp isoperimetric inequality conjecture for minimal submanifolds in the cases of codimension one and two, adapting ideas from optimal mass transportation [MG13] and ABP method of Cabre [Cab08].
A natural generalization of the isoperimetric inequality considered by Wulff [Wul01] is the isoperimetric problem with weighted boundary density.
Definition 1.2.
Let be a positively one-homogeneous convex function in , and we define the -anisotropic perimeter
| (1.2) |
The set
| (1.3) |
is called the corresponding Wulff shape. The support function of is as follows:111It is well-known that support function and the Wulff shape are mutually determined and the Wulff shape induced by the support function of convex body is precisely the original convex body [Tay78].
| (1.4) |
Wulff considered the following question: Given a positive function , what shapes minimize the -anisotropic perimeter among the sets of finite perimeter with fixed volume. Wulff conjectured that the corresponding minimizers are homothetic to the Wulff shape generated by and the isoperimetric inequality can be extended to the following celebrated Wulff inequality.
Theorem 1.3 (Wulff Theorem [Wul01]).
Let be an -dimensional centrally symmetric convex body in , and be the corresponding support function. Then for any set of finite perimeter with , we have
| (1.5) |
Moreover, equality holds if and only if is homothetic to , namely for some and up to a set of measure zero.
This result was first stated without proof by Wulff in 1901 [Wul01]. A complete proof of Theorem 1.3 can be found in Taylor’s articles [Tay74, Tay75, Tay78]. Cabré, Ros-Oton and Serra in [CROS16] gave a new proof of Theorem 1.3 via the ABP method. Figalli, Maggi and Pratelli [FMP10] studied the quantitative version of the codimension zero anisotropic isoperimetric inequality. De Rosa, Kolasiński and Santilli [DRKS20] considered the uniqueness of critical points of the codimensional zero anisotropic isoperimetric problem and established Heintze-Karcher type inequality.
A natural question is whether the Wulff inequality holds for minimal submanifolds with nonzero codimension in Euclidean space 222Recently, De Philippis and Pigati [DPP] considered the Michael-Simon inequality for nonzero codimensional anisotropic minimal submanifolds in Euclidean space via ideas from multilinear Kakeya estimates, where the weight is put on the normal vectors of the submanifolds instead of relative normal vectors on the boundary of submanifolds.. To state the inequality, for each -dimensional affine subspace , we denote the projection of to and we let be any -dimensional affine subspace such that and denote any of them by .
Conjecutre 1.4 (Wulff inequality for minimal submanifolds).
In this paper, by adapting arguments of Brendle and Cabre, we first prove a boundary weighted isoperimetric inequality for minimal submanifolds in Euclidean space:
Theorem 1.5.
Let be centrally symmetric dimensional convex body in , and be the corresponding support function. Let be a minimal hypersurface with boundary embedded in . We have
| (1.7) |
where
| (1.8) |
and is the affine Grassmannian consisting of all -dimensional affine subspaces in
Remark 1.6.
By Fubini’s theorem we have the trivial upper bound
| (1.9) |
It is also clear that the supremum is always positive, as the function for sufficiently small is in . Later in (5.6), we will provide a better estimate of the quantity on left hand side of (1.9) for general Wulff shapes , and show that in some special cases the equality in (1.9) holds.
To state our next result, we define a class of convex bodies generated from ellipsoids using gluing and cutting operations. We refer to this class of convex bodies as long convex bodies, since a typical example of such shape is given by where is any -dimensional centrally symmetric convex body and .
Definition 1.7 (long convex body).
Let be the set of all -dimensional ellipsoids centering at origin. For , let be centrally symmetric convex bodies in , and some area-minimizing projection for . Let be an -dimensional affine subspace such that . The set of long convex bodies is the smallest set of centrally symmetric convex bodies satisfying the following conditions:
-
•
.
-
•
Gluing: if , and , then .
-
•
Cutting: if , and , then .
Remark 1.8.
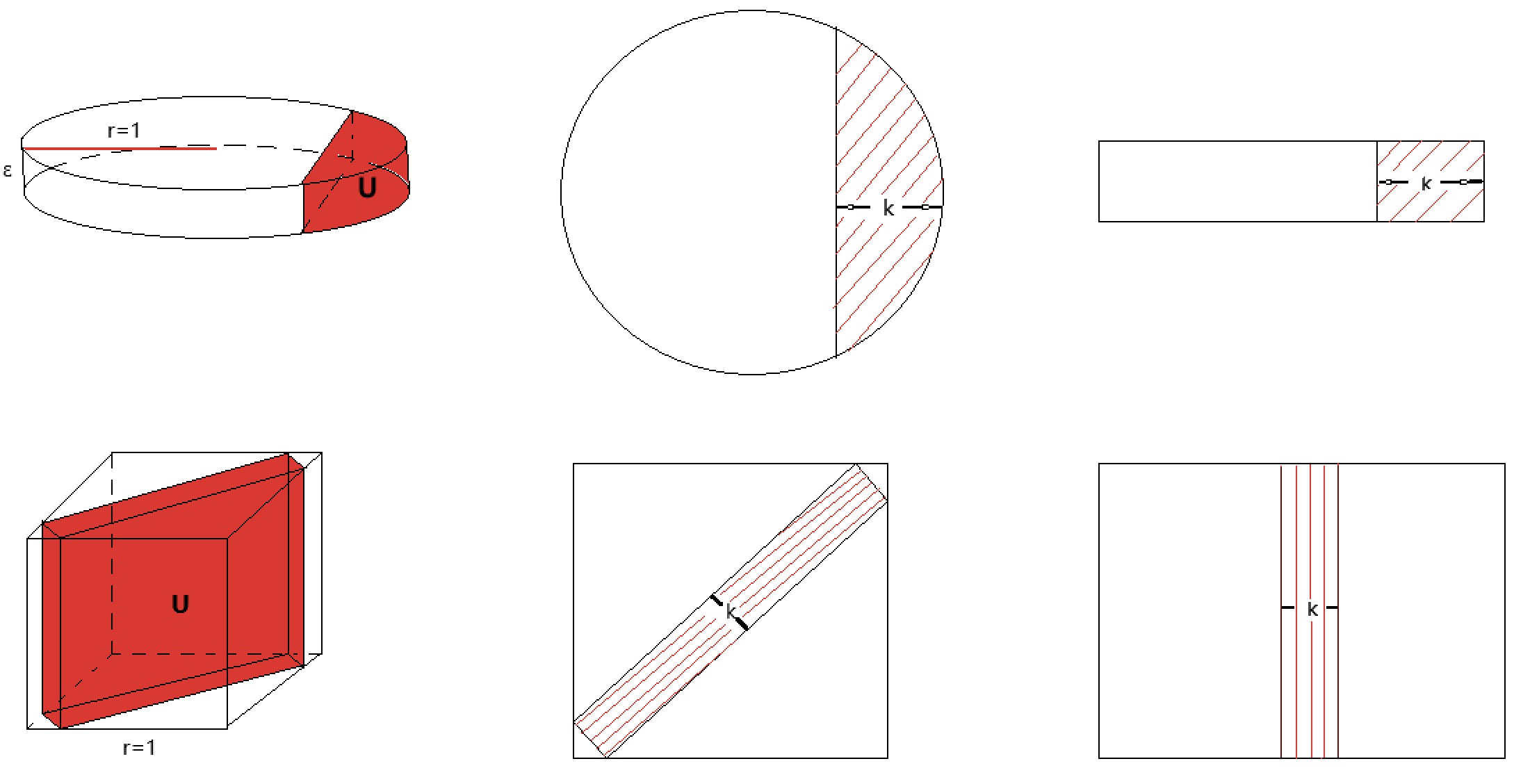
It is clear that consists of all centrally symmetric convex bodies that can be obtained by performing a finite number of gluing and cutting operations on an ellipsoid. Performing these operations repeatedly elongates the shape in the normal directions of the area-minimizing projection. These two operations provide necessary conditions for equality in (1.9), in the sense that performing gluing or cutting along some area-minimizing projection direction should preserve the fact that it is an area-minimizing projection direction. Specifically, if the equality in (1.9) holds for some , and (not necessarily centrally symmetric here) is generated from by gluing or cutting with respect to some such that is an area-minimizing projection for , then must also be an area-minimizing projection for , and the equality in (1.9) still holds for (see Lemma 4.3). For example, when is an -dimensional cube or a short cylinder of the form for small in Figure 1, it is possible to cut along some area-minimizing projection direction, such that after the cut, it is no longer the area-minimizing projection direction for the resulting shape. Hence, the equality in (1.9) must be strict for the cube and short cylinder.
In the cases of codimension one and two, by designing good candidates on ellipsoids and long convex bodies, we verify the above two conjectures when () and the weights are support functions of .
Theorem 1.9.
For , let and be the corresponding support function, then for being a minimal submanifold with boundary embedded in , we have
| (1.10) |
In particular, equality holds if and only if is homothetic to .
Remark 1.10.
More generally we prove a Wulff inequality for minimal submanifolds in the Euclidean space, where the constant depends only on dimension and codimension.
Theorem 1.11.
Let be centrally symmetric -dimensional convex body in and be the corresponding support function. Then for a minimal submanifold with boundary embedded in , we have
| (1.12) |
where
| (1.13) |
is a constant only depending on and but independent of the weight .555The Wulff inequality is scaling-invariant for weights or -dimensional Wulff shape, but the space of -dimensional Wulff shapes, after taking quotient by the scaling symmetry, is non-compact.
Remark 1.12.
It would be very interesting to improve the constant in (1.12) to some constant independent of and , which is expected to be 1. Another interesting direction is to prove sharp minimal submanifolds Wulff inequality for more general class of weights or the associated convex bodies.
The paper is organized as follows: in Section 2, we prove Theorem 1.5; in Section 3, we prove Theorem 1.9; and in Section 4, we prove Theorem 1.11.
Acknowledgments. The authors appreciate the funding and research environment support from MIT, UCSD, and ITS Westlake University, respectively.
2. Basic Convex Geometry
In this section, we first recall some basic properties of convex geometry that will be used in later sections.
Let be an -dimensional subspace passing through the origin. We now consider the following two sets in :
-
(1)
is the Wulff shape induced by ,
-
(2)
is the projection of onto ;
The following lemma shows that the two objects are the same.
Lemma 2.1.
If is the support function of , then , and is the support function of in .
Proof.
It suffices to show that is the support function of , since support functions and Wulff shapes uniquely determine each other (see [CROS16, page 2976]). For any and , we have , hence
| (2.1) |
∎
Remark 2.2.
Let be any -dimensional affine subspace such that is minimized, and let be the -dimensional subspace parallel to and passing through the origin. As a consequence of the lemma, is also the support function of in , so
| (2.2) |
where we used the fact that for almost every , the unit outward normal exists, and because it is the support function. According to (2.2), for any and such that both and are minimized, it follows that
| (2.3) |
Thus, the right-hand sides of (1.6), (1.10) and (1.12) are well defined for given .
3. Proof of Theorem 1.5
In this section, we prove Theorem 1.5. Let be a compact -dimensional minimal submanifold with boundary . We first consider the special case that is connected with boundary . By solving from the following Poisson equation with Neumann boundary condition
| (3.1) |
we can construct the map:
| (3.2) |
where is the normal bundle of . As in [Bre21], we define the following set:
| (3.3) |
where is the second fundamental form of
Lemma 3.1.
We have , thus is a surjective map from onto the interior of the Wulff shape .
Proof.
Let and we consider the map defined by
| (3.4) |
Denote the unit outward normal vector on the boundary relative to . Then, for any ,
| (3.5) |
Thus attains its minimum at some interior point . It follows that , which implies
| (3.6) |
for some . It remains to compute the determinant. Since achieves its minimum, we have
| (3.7) |
where the last equality holds from (3.6). Therefore, we obtain and . ∎
Lemma 3.2.
For all , the determinant of transport map satisfies
| (3.8) |
Proof.
Proof of Theorem 1.5.
We recall
| (3.11) |
and by Lemma 3.1 and Lemma 3.2, we have
| (3.12) | ||||
In particular, the above inequality gives
| (3.13) |
which implies (1.7). It remains to consider the case where is disconnected. In that case, we apply the inequality to each individual connected component of , sum over all connected components, and use the strict inequality
| (3.14) |
for all .
∎
4. Proof of Theorem 1.9
In this section, we prove Theorem 1.9. By Theorem 1.5 and (2.2), it suffices to show that there exists some such that
| (4.1) |
or there exists a sequence such that
| (4.2) |
In Proposition 4.1, Proposition 4.2 and Proposition 4.4, we demonstrate that when , equation (4.1) or (4.2) holds when is a centrally symmetric -dimensional ellipsoid and long convex body. In Proposition 4.2 we also obtain a weaker estimate for . Then in Proposition 4.5, we discuss the sharpness and rigidity when equality holds for ellipsoids and long bodies and .
Proposition 4.1.
If codimension and , there exists some such that (4.1) holds. Hence
| (4.3) |
Proof.
Suppose is an ellipsoid given by
| (4.4) |
where . Denote
| (4.5) |
Let the function be defined by
| (4.6) |
Consider a line that passes through the ellipsoid along unit vector direction. Then the end points () of the chord in the ellipsoid satisfies
| (4.7) |
This is a quadratic equation
| (4.8) |
where
| (4.9) |
Upon solving this, we obtain
| (4.10) |
Thus, the integral over the chord is given by
| (4.11) |
We notice that
| (4.12) |
and the equality holds if and only if , that is the line is parallel to the longest axis. We now define the function as
| (4.13) |
It satisfies its integral over any line that passes through the ellipsoid is at most 1, and achieves 1 when the line is parallel to the longest direction of ellipsoid, that is the axis corresponding to . Moreover, Fubini’s Theorem gives
| (4.14) |
Thus, and satisfies (4.1), and we have completed the proof. ∎
For codimension cases, we have following proposition.
Proposition 4.2.
If codimension and , then there exists a sequence of functions such that (4.2) holds. Hence when ,
| (4.15) |
If codimension and , then there exists a sequence of functions such that
| (4.16) |
Proof.
Denote the -dimensional ellipsoid
| (4.17) |
where , and for some .
Let be an -dimensional affine subspace which intersects with , where are orthonormal. The intersection region is the shell of two -dimensional homothetic ellipsoids (if is very close to the boundary, it would be fully outside of , so in that case is just an ellipsoid). Denote
| (4.18) |
Note that , so we can study the intersection between ellipsoid and lower dimensional plane by converting it to an intersection between ball and plane via , and converting everything back in the end by applying appropriate scaling. (For a detailed computation for and , see [Kle12].)
Specifically, the above computation yields that the length of the -th axis of the outer ellipsoid is
| (4.19) |
where is the squared distance between origin and . The length of -th axis of inner ellipsoid is
| (4.20) |
As discussed before, is the shell formed by two homothetic ellipsoids only when cuts through , which is the same as cuts through , or equivalently . Hence the intersection volume can be expressed as
| (4.21) |
Since is an orthonormal basis, we have
| (4.22) |
Then it follows
| (4.23) |
Now we consider
| (4.24) |
and it clearly satisfies and . For any -dimensional affine subspace in ,
| (4.25) |
On the other hand, the volume of the shell is given by the difference of two -dimensional ellipsoids, so
| (4.26) |
Taking the limit as , we obtain that
| (4.27) |
where we used for the ellipsoid. In particular, when , the coefficient simplifies to 1, and we have completed the proof of (4.2). ∎
Next we will prove a lemma about the necessary condition discussed in Remark 1.8. We will use this lemma and the and constructed above to verify (1.10) for general and .
Lemma 4.3.
Suppose and satisfies
| (4.28) |
and let be generated from via gluing or cutting with respect to an -dimensional affine subspace such that is an area-minimizing projection for . Then, must also be an area-minimizing projection for , and
| (4.29) |
Proof.
Suppose is obtained via a gluing operation. Then by Definition 1.7, . Moreover, we also have
| (4.30) |
Thus, we conclude that , and is an area-minimizing projection for . By assumption, we can thus find a sequence of such that
| (4.31) |
which finishes the proof for gluing operation.
Now suppose is obtained via a cutting operation. By Definition 1.7, . For any , denote the -dimensional affine subspace orthogonal to and passing through . By assumption, we can find a sequence such that
| (4.32) |
Use the fact that is an area-minimizing projection, we must have for a.e. ,
| (4.33) |
On the other hand, for any , by definition of cutting
| (4.34) |
Certainly , so for any . Therefore, satisfies
| (4.35) |
Combining with (1.9), we obtain
| (4.36) |
Hence must be area-minimizing projection, which finishes the proof for cutting operation. ∎
Proposition 4.4.
Proof.
By the discussion after Definition 1.7, any can be constructed through a finite number of gluing and cutting operations starting from an ellipsoid. It is also clear that Proposition 4.4 holds for ellipsoids by Proposition 4.1 and 4.2. Then for any long convex body, Proposition 4.4 directly follows from Lemma 4.3. In particular, let be the ellipsoid that generated , then for we can choose to be the one in Proposition 4.1, and for we can choose to be the sequence in Proposition 4.2, both restricted to . ∎
Next, we establish the sharpness and rigidity properties when equality holds for and codimension .
Proposition 4.5.
Let codimension and . Then the equality in (1.10) holds if and only if is homothetic to .
Proof.
It is clear from Remark 2.2 that if is homothetic to some then equality holds, so we only need to prove the converse.
First of all, if equality (1.10) holds for some , by (3.14) must be connected. Moreover, from Proposition 4.4 we know , and achieves the equality of (1.10) if and only if achieves the equality of (1.7).
When , let be the density function found in Proposition 4.4 such that
| (4.38) |
For such , the equalities in (3.12) must hold, meaning that
| (4.39) |
Moreover, we have where is the projection onto . Thus, the arithmetic-geometric mean inequality in Lemma 3.2 must be equality for a.e. points in , which only happens when is a constant multiple of identity matrix. Thus a.e. in , equivalent to a.e. in . Since is smooth, it is in some codimension affine subspace . By codimension zero Wulff inequality in Theorem 1.3, is homothetic to the Wulff shape corresponding to the restricted weight . Then by Lemma 2.1, must be homothetic to . By assumption achieves equality, so by Remark 2.2 we have
| (4.40) |
On the other hand, by (1.9) and the equality of (1.7), we also have
| (4.41) |
Therefore, and is homothetic to some area-minimizing projection in the codimension one case.
When , let the sequence be the corresponding approximating density functions defined in Proposition 4.4, these functions satisfy
| (4.42) |
Denote . If is an ellipsoid we simply have , and if is a general long convex body, , where is the original ellipsoid that generates . As shown in [Bre21, Section 3], we claim
Claim 4.6.
For all and all satisfying , the equality holds.
Proof.
Suppose that claim fails at some and satisfying and . Then we have . The arithmetic-geometric inequality and (3.1) imply
| (4.43) |
By continuity, there exists , and a neighborhood of such that for all , the following holds
| (4.44) |
Using Lemma 3.2, we deduce that on ,
| (4.45) |
Certainly in the case where not in , there exists a neighborhood of disjoint from , and (4.45) still holds. The inequality (3.12) becomes
| (4.46) |
For all sufficiently close to 1, the integral is bounded below by some positive constant independent on . Indeed, equality in (3.12) holds when taking the limit on both sides with respect to , which forces to converge to 1 for almost every . Thus, the integral is bounded below by the fact that the support of concentrates around by construction. Now taking the limit as on both side of (4), we obtain
| (4.47) |
where the last equality follows from Remark 2.2 and the assumption that achieves equality of (1.10). This leads to a contradiction with the equality of (1.7). ∎
From Claim 4.6, we obtain
| (4.48) |
for all satisfying . Note that the intersection is a -dimensional ellipse in the -dimensional plane . Indeed this is clear when is an ellipsoid; and when is some other long convex body, any such that is not a full ellipse would result in being strictly smaller than . In this case, equality cannot be achieved when taking limit on both sides of (3.12), so such forms at most a measure-zero set. Thus, we conclude from above that , which implies and for all . Arguing as codimension case, we conclude that is homothetic to some . This completes the proof of Proposition 4.5.
∎
5. Proof of Theorem 1.11
In this section, we prove Theorem 1.11 and we use the following lemma about John’s ellipsoid.
Lemma 5.1 (John’s ellipsoid [Sch14]).
If is a centrally symmetric convex body with interior points, then there exists an ellipsoid such that
| (5.1) |
Proof of Theorem 1.11.
Since is centrally symmetric, by Lemma 5.1 there is John’s ellipsoid such that
| (5.2) |
Denote as the projection that achieves minimal projection area for , then
| (5.3) |
Let and be the corresponding sets of functions from (1.8) for and , respectively. We note that implies .
Define to be
| (5.4) |
By Proposition 4.1 and Proposition 4.2 we have
| (5.5) |
Therefore
| (5.6) |
where the third inequality follows from (5.3). Then, by Theorem 1.5 and the fact that from (2.2), we conclude that
| (5.7) |
∎
References
- [AHO74] Herbert J. Alexander, David A. Hoffman, and Robert Osserman. Area estimates for submanifolds of euclidean space. In Symposia Mathematica, volume 14, pages 445–455, 1974.
- [Alm86] Frederick J. Almgren. Optimal isoperimetric inequalities. Indiana University mathematics journal, 35(3):451–547, 1986.
- [Bre21] Simon Brendle. The isoperimetric inequality for a minimal submanifold in Euclidean space. J. Amer. Math. Soc., 34(2):595–603, 2021.
- [BZ13] Yurii D. Burago and Viktor A. Zalgaller. Geometric inequalities, volume 285. Springer Science & Business Media, 2013.
- [Cab08] Xavier Cabré. Elliptic PDE’s in probability and geometry: Symmetry and regularity of solutions. Discrete Contin. Dyn. Syst., 20(3):425–457, 2008.
- [Car21] Torsten Carleman. Zur Theorie der Minimalflächen. Math. Z., 9:154–160, 1921.
- [Cha01] Isaac Chavel. Isoperimetric inequalities: differential geometric and analytic perspectives, volume 145. Cambridge University Press, 2001.
- [CROS16] Xavier Cabré, Xavier Ros-Oton, and Joaquim Serra. Sharp isoperimetric inequalities via the abp method. Journal of the European Mathematical Society (EMS Publishing), 18(12), 2016.
- [DPP] Guido De-Philippis and Alessandro Pigati. Michael-simon inequality for anisotropic varifolds. In prepration.
- [DRKS20] Antonio De Rosa, Sławomir Kolasiński, and Mario Santilli. Uniqueness of critical points of the anisotropic isoperimetric problem for finite perimeter sets. Archive for Rational Mechanics and Analysis, 238(3):1157–1198, 2020.
- [FMP10] Alessio Figalli, Francesco Maggi, and Aldo Pratelli. A mass transportation approach to quantitative isoperimetric inequalities. Inventiones mathematicae, 182(1):167–211, 2010.
- [Kle12] Peter Paul Klein. On the ellipsoid and plane intersection equation. Applied Mathematics, 3(11):1634–1640, 2012.
- [MG13] Robert J. McCann and Nestor Guillen. Five lectures on optimal transportation: geometry, regularity and applications. In Analysis and geometry of metric measure spaces. Lecture notes of the 50th Séminaire de Mathématiques Supérieures (SMS), Montréal, Canada, June 27 – July 8, 2011, pages 145–180. Providence, RI: American Mathematical Society (AMS), 2013.
- [Oss78] Robert Osserman. The isoperimetric inequality. Bulletin of the American Mathematical Society, 84(6):1182–1238, 1978.
- [Sch14] Rolf Schneider. Convex bodies: the Brunn-Minkowski theory, volume 151 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge, expanded edition, 2014.
- [Tay74] Jean E. Taylor. Existence and structure of solutions to a class of nonelliptic variational problems. In Symposia Mathematica, volume 14, pages 499–508, 1974.
- [Tay75] Jean E. Taylor. Unique structure of solutions to a class of nonelliptic variational problems. Differ. Geom., Proc. Symp. Pure Math. 27, Part 1, Stanford 1973, 419-427 (1975), 1975.
- [Tay78] Jean E. Taylor. Crystalline variational problems. Bulletin of the American Mathematical Society, 84(4):568–588, 1978.
- [Wul01] Georg. Wulff. Zur frage der geschwindigkeit des wachstums und der auflosung der kristall achen. Z. Kristallogr, 34:449–530, 1901.