YITP-23-163, J-PARC-TH-0301
Electromagnetic probes for critical fluctuations of phase transitions in dense QCD

In the high baryon-density region of Quantum Chromodynamics (QCD), rich phase structures are expected to exist. They will be revealed by various experimental programs of relativistic heavy-ion collisions (HIC) such as the beam-energy scan program at RHIC, HADES and NA61/SHINE, as well as the future experiments at FAIR, NICA and J-PARC-HI. In this proceeding, we discuss the possible observability of the color superconducting phase transition (CSC-PT) and the QCD critical point (QCD-CP) in these experiments through an anomalous enhancement of the dilepton production rate (DPR) caused by the soft modes associated with these phase transitions Nishimura:2022mku ; Nishimura:2023oqn . We also study the electric conductivity that is related to the low-energy limit of the DPR. We calculate them by extending the theory of metallic superconductors Larkin:book . It is shown that the soft modes lead to an anomalous enhancement of the DPR at low energy/momentum region and the conductivity near each phase transition. We argue that these enhancements are used for experimental observables to verify the existence of the second-order phase transition on the QCD phase diagram Nishimura:2023not .

To study the dense medium around the 2-flavor superconductivity (2SC) and QCD-CP at nonzero temperature ($T$) and quark chemical potential ($\mu$), we employ the 2-flavor NJL model

$\displaystyle\mathcal{L}$

$\displaystyle=\bar{\psi}i(\gamma^{\mu}\partial_{\mu}-m)\psi+\ G_{S}[(\bar{\psi}\psi)^{2}+(\bar{\psi}i\gamma_{5}\tau_{i}\psi)^{2}]+\ G_{D}(\bar{\psi}i\gamma_{5}\tau_{2}\lambda_{A}\psi^{C})(\bar{\psi}^{C}i\gamma_{5}\tau_{2}\lambda_{A}\psi),$

(1)

where $\tau_{i=1,2,3}$ is the Pauli matrix for the flavor $SU(2)_{f}$, $\lambda_{A=2,5,7}$ is the antisymmetric components of the Gell-Mann matrices for the color $SU(3)_{c}$ and $\psi^{C}(x)\equiv i\gamma_{2}\gamma_{0}\bar{\psi}^{T}(x)$. We use the scalar coupling $G_{S}=5.50\leavevmode\nobreak\ \rm{GeV^{-2}}$ and three-momentum cutoff $\Lambda=631\rm{MeV}$, which gives the pion mass $m_{\pi}=138\leavevmode\nobreak\ \rm{MeV}$ and pion decay constant $f_{\pi}=93\leavevmode\nobreak\ \rm{MeV}$ at the current quark mass $m=5.5\leavevmode\nobreak\ {\rm MeV}$ Hatsuda:1994pi , while the diquark coupling $G_{D}$ is treated as a free parameter.

It is known that the fluctuations of the diquark and chiral condensates form collective modes with significant strength near the 2SC-PT Kitazawa:2005vr and the QCD-CP Fujii:2004jt , respectively. The collective mode associated with the second-order phase transition is called the soft mode. In the random-phase approximation, the propagators of the respective soft modes in the imaginary-time formalism are evaluated as

	$\displaystyle\tilde{\Xi}_{D}(k)$	$\displaystyle=\frac{1}{{G_{D}}^{-1}+\mathcal{Q}_{D}(k)},\quad\mathcal{Q}_{D}(k)=\begin{minipage}[h]{43.36464pt} \centering\includegraphics[keepaspectratio,scale={0.034}]{qq-corr-crop.pdf} \@add@centering\end{minipage}=-2N_{f}(N_{c}-1)\int_{p}{\rm Tr}[\mathcal{G}_{0}(k-p)\mathcal{G}_{0}(p)],$		(2)
	$\displaystyle\tilde{\Xi}_{S}(k)$	$\displaystyle=\frac{1}{{G_{S}}^{-1}+\mathcal{Q}_{S}(k)},\quad\mathcal{Q}_{S}(k)=\begin{minipage}[h]{43.36464pt} \centering\includegraphics[keepaspectratio,scale={0.034}]{qqbar-corr-crop.pdf} \@add@centering\end{minipage}=2N_{f}N_{c}\int_{p}{\rm Tr}[\mathcal{G}_{0}(p-k)\mathcal{G}_{0}(p)],$		(3)

where $\mathcal{Q}_{D}(k)=\mathcal{Q}_{D}(\bm{k},i\nu_{n})$ and $\mathcal{Q}_{S}(k)=\mathcal{Q}_{S}(\bm{k},i\nu_{n})$ are the one-loop $qq$ and $q\bar{q}$ correlation function, respectively, with the free quark propagator $\mathcal{G}_{0}(p)=\mathcal{G}_{0}(\bm{p},i\omega_{m})=1/[(i\omega_{m}+\mu)\gamma_{0}-\bm{p}\cdot\bm{\gamma}-M]$, the Matsubara frequency for fermions (bosons) $\omega_{m}$ ($\nu_{n}$), the trace over Dirac indices ${\rm Tr}$, and $\smallint_{p}=T\sum_{m}\int d^{3}p/(2\pi)^{3}$. The retarded propagator $\Xi^{R}_{\gamma}(\bm{k},\omega)$ ($\gamma=D,S$) is obtained by the analytic continuation $i\nu_{n}\rightarrow\omega+i\eta$.

We remark that the propagators (2) and (3) satisfy the Thouless criterion, i.e. ${\Xi^{R}_{\gamma}}^{-1}(\bm{0},0)=0$ at the respective critical points. The criterion shows that a pole of the propagator approaches the origin of the complex energy plane as $T$ and $\mu$ goes toward the critical points, and hence the fluctuations of the condensates become soft near the critical points.

The DPR is related to the retarded photon self-energy $\Pi^{R\mu\nu}(k)$ as

$\displaystyle\frac{d^{4}\Gamma}{d^{4}k}=-\frac{\alpha}{12\pi^{4}}\frac{1}{k^{2}}\frac{1}{e^{\omega/T}-1}g_{\mu\nu}{\rm Im}\Pi^{R\mu\nu}(k),$

(4)

where $\alpha$ is the fine structure constant. The elecrtric conductivity is given in terms of the spectral density $\rho(\omega)=-\sum_{i}{\rm Im}\Pi^{Rii}(\bm{0},\omega)$ as

$\displaystyle\sigma=\frac{1}{3}\frac{\partial\rho(\omega)}{\partial\omega}\bigg{|}_{\omega=0}\leavevmode\nobreak\ .$

(5)

To construct the photon self-energy $\tilde{\Pi}^{\mu\nu}(k)$ that includes the soft modes, we start from the lowest contribution of the soft modes to the thermodynamic potential $\Omega_{\gamma}=\smallint_{p}\ln[G_{\gamma}\tilde{\Xi}_{\gamma}^{-1}(p)]$, which is the one-loop diagram of $\tilde{\Xi}_{\gamma}(p)$. The self-energy is then obtained by attaching electromagnetic vertices to two points of quark lines in $\Omega_{\gamma}$. From this procedure, one finds three types of diagrams which are called the Aslamazov-Larkin (AL), Maki-Thompson (MT) and density-of-states (DOS) terms in the theory of metallic superconductivity. Each contribution to the photon self-energy is given by

	$\displaystyle\tilde{\Pi}_{{\rm AL},D}^{\mu\nu}(k)$	$\displaystyle=3\int_{q}\tilde{\Gamma}_{D}^{\mu}(q,q+k)\tilde{\Xi}_{D}(q+k)\tilde{\Gamma}_{D}^{\nu}(q+k,q)\tilde{\Xi}_{D}(q),$		(6)
	$\displaystyle\tilde{\Pi}_{{\rm MT(DOS)},D}^{\mu\nu}(k)$	$\displaystyle=3\int_{q}\tilde{\Xi}_{D}(q)\mathcal{R}_{{\rm MT(DOS)},D}^{\mu\nu}(q,k),$		(7)
	$\displaystyle\tilde{\Pi}_{{\rm AL},S}^{\mu\nu}(k)$	$\displaystyle=\sum_{f=u,d}\int_{q}\tilde{\Gamma}_{f}^{\mu}(q,q+k)\tilde{\Xi}_{S}(q+k)\tilde{\Gamma}_{f}^{\nu}(q+k,q)\tilde{\Xi}_{S}(q),$		(8)
	$\displaystyle\tilde{\Pi}_{{\rm MT(DOS)},S}^{\mu\nu}(k)$	$\displaystyle=\sum_{f=u,d}\int_{q}\tilde{\Xi}_{S}(q)\mathcal{R}_{{\rm MT(DOS)},f}^{\mu\nu}(q,k),$		(9)

where the vertices $\tilde{\Gamma}_{D}^{\mu}(q,q+k)$, $\mathcal{R}^{\mu\nu}_{D}(q,k)=\mathcal{R}_{{\rm MT},D}^{\mu\nu}(q,k)+\mathcal{R}_{{\rm DOS},D}^{\mu\nu}(q,k)$, $\tilde{\Gamma}_{f}^{\mu}(q,q+k)$, and $\mathcal{R}^{\mu\nu}_{f}(q,k)=\mathcal{R}_{{\rm MT},f}^{\mu\nu}(q,k)+\mathcal{R}_{{\rm DOS},f}^{\mu\nu}(q,k)$ satisfy the Ward-Takahashi (WT) identities

	$\displaystyle k_{\mu}\tilde{\Gamma}_{D}^{\mu}(q,q+k)$	$\displaystyle=(e_{u}+e_{d})[\mathcal{Q}_{D}(q+k)-\mathcal{Q}_{D}(q)],$		(10)
	$\displaystyle k_{\mu}\mathcal{R}_{D}^{\mu\nu}(q,k)$	$\displaystyle=(e_{u}+e_{d})[\tilde{\Gamma}_{D}^{\nu}(q-k,q)-\tilde{\Gamma}_{D}^{\nu}(q,q+k)],$		(11)
	$\displaystyle k_{\mu}\tilde{\Gamma}_{f}^{\mu}(q,q+k)$	$\displaystyle=-e_{f}[\mathcal{Q}_{S}(q+k)-\mathcal{Q}_{S}(q)],$		(12)
	$\displaystyle k_{\mu}\mathcal{R}_{f}^{\mu\nu}(q,k)$	$\displaystyle=-e_{f}[\tilde{\Gamma}_{f}^{\nu}(q-k,q)-\tilde{\Gamma}_{f}^{\nu}(q,q+k)],$		(13)

with $e_{u}=2|e|/3$ ($e_{d}=-|e|/3$) being the electric charge of the up (down) quark. The total photon self-energy is then given by $\tilde{\Pi}^{\mu\nu}(k)=\tilde{\Pi}_{\rm free}^{\mu\nu}(k)+\tilde{\Pi}_{D}^{\mu\nu}(k)+\tilde{\Pi}_{S}^{\mu\nu}(k)$ with

	$\displaystyle\tilde{\Pi}_{D}^{\mu\nu}(k)=$	$\displaystyle\tilde{\Pi}_{{\rm AL},D}^{\mu\nu}(k)+\tilde{\Pi}_{{\rm MT},D}^{\mu\nu}(k)+\tilde{\Pi}_{{\rm DOS},D}^{\mu\nu}(k),$		(14)
	$\displaystyle\tilde{\Pi}_{S}^{\mu\nu}(k)=$	$\displaystyle\tilde{\Pi}_{{\rm AL},S}^{\mu\nu}(k)+\tilde{\Pi}_{{\rm MT},S}^{\mu\nu}(k)+\tilde{\Pi}_{{\rm DOS},S}^{\mu\nu}(k),$		(15)

where $\tilde{\Pi}_{\rm free}^{\mu\nu}(k)$ is the contribution of the massless free quark gases. One can explicitly check that $\tilde{\Pi}^{\mu\nu}(k)$ satisfies the WT identity $k_{\mu}\tilde{\Pi}^{\mu\nu}(k)=0$ using Eqs. (10)–(13).

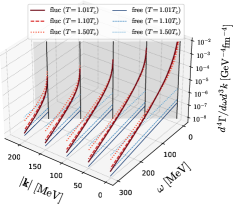
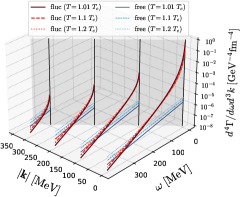
The left panel of Fig. 1 shows the DPR per unit energy $\omega$ and momentum $\bm{k}$ near the 2SC-PT for $T/T_{c}=1.01$, $1.1$ and $1.5$ at $\mu=350\leavevmode\nobreak\ {\rm MeV}$ and $G_{D}=0.7G_{S}$ with the critical temperature $T_{c}=42.94\leavevmode\nobreak\ {\rm MeV}$ Nishimura:2022mku . The thick lines are the contributions from the soft modes, while the thin lines are the ones of the free quark gas. One sees that the DPR from the soft modes is anomalously enhanced at small $\omega$ and $\bm{k}$ region in comparison with the free quark gas for $T\lesssim 1.5T_{c}$, and this enhancement is more pronounced as $T$ approaches $T_{c}$. This result is expected from the properties of the soft modes. Shown in the right panel of Fig. 1 is the DPR near the QCD-CP for $T/T_{\rm CP}=1.01$, $1.1$ and $1.2$ at $\mu=\mu_{\rm CP}$ with the location of the QCD-CP $(T_{\rm CP},\mu_{\rm CP})=(46.712,329.34)\leavevmode\nobreak\ {\rm MeV}$ Nishimura:2023oqn . One finds that the anomalous enhancement of the DPR is observed similarly to the case of the 2SC.

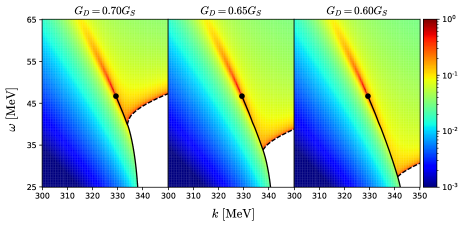
Figure 2 shows the contour maps of the electric conductivity $\sigma/T$ on the $T$–$\mu$ plane for $G_{D}/G_{S}=0.70$, $0.65$ and $0.60$ obtained from $\tilde{\Pi}^{\mu\nu}(k)$ with the effects of the 2SC-PT and QCD-CP. One sees that the conductivity is enhanced around these phase transitions. Since the effect of finite diquark condensate is not considered, our formalism is not applicable to the 2SC phase, i.e. the white region in the figure.

In Fig. 2, it is notable that the electric conductivity is enhanced at two distinct regions on the $T$–$\mu$ plane near the QCD-CP and 2SC-PT, whose separation is controlled by the value of $G_{D}$. Since the electric conductivity is related to the DPR at low-mass region through Eqs. (4) and (5), this result indicates that there are also two hot spots of the dilepton production on the QCD phase diagram. In the beam-energy scan of the HIC where different regions on the $T$–$\mu$ plane can be investigated by varying the collision energy $\sqrt{s_{{}_{NN}}}$, this behavior would result in two distinct enhancements of the dilepton yield as a function of $\sqrt{s_{{}_{NN}}}$, as recently demonstrated in Ref. Nishimura:2023not . It is quite interesting to pursue such behavior in the HIC, as it becomes strong collateral evidence for the existence of both the QCD-CP and 2SC-PT.

In this proceeding, we studied how the soft modes of the 2SC-PT and QCD-CP affect the DPR and electric conductivity around the phase transitions. The modifications of the photon self-energy due to the soft modes are incorporated through the Aslamazov-Larkin, Maki-Thompson, and density-of-states terms, in accordance with the WT identity of the photon self-energy. The characteristic structure of the enhancement of the DPR on the QCD phase diagram found in this study would allow us to detect the 2SC-PT and QCD-CP in future HIC experiments.