Zermelo deformation of Finsler metrics by Killing vector fields
Abstract
We show how geodesics, Jacobi vector fields and flag curvature of a Finsler metric behave under Zermelo deformation with respect to a Killing vector field. We also show that Zermelo deformation with respect to a Killing vector field of a locally symmetric Finsler metric is also locally symmetric.
1 Introduction
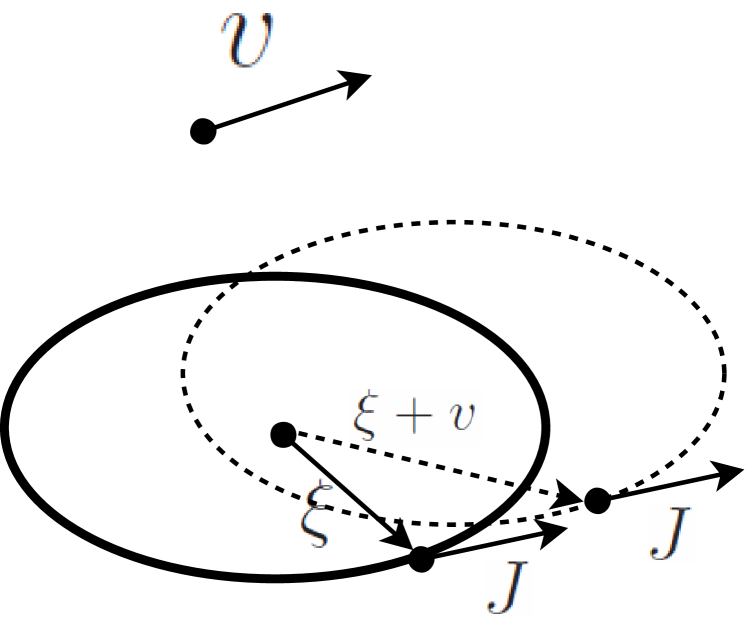
Let be a Finsler metric on and be a vector field such that for any . We will denote by the Zermelo deformation of by . That is, for each point , the unit -ball is the translation in along the vector of the unit -ball (see Fig. 1).
Equivalently, this can be reformulated as
| (1) |
Indeed, the equation (1) is positively homogeneous, and for any such that we have .
The first result of this note is a description of how geodesics, Jacobi vector fields and flag curvatures of and of are related, if the vector field is a Killing vector field for , that is, if the flow of preserves .
Theorem 1.
Let be a Finsler metric on admitting a Killing vector field such that for all . We denote by the flow of and by the -Zermelo deformation of .
Then, for any -arc-length-parameterized geodesic of , the curve which we denote by is a -arc-length-parameterized geodesic of .
Moreover, for any Jacobi vector field along such that it is orthogonal to in the metric , the pushforward is a Jacobi vector field for and is orthogonal to in
Moreover, flag curvatures and of and are related by the following formula: for any and any “flag” with flagpole and transverse edge , we have provided that and are linearly independent.
We do not pretend that the whole result is new and rather suggest that its certain parts are known. The first statement of Theorem 1 appears in [6]. We recall the arguments of A. Katok in Remark 1. The third statement was announced in [3] and follows from the recent paper [5]. Special cases when the metric is Riemannian were studied in details in e.g. [1, 8]. Though we did not find the second statement of Theorem 1, the one about the Jacobi vector fields, in the literature, we think it is known in folklore.
Unfortunately in all these references, the proof is by direct calculations, which are sometimes quite tricky and sometimes require a lot of preliminary work. One of the goals of this note is to show the geometry lying below Theorem 1 and to demonstrate that certain parts of Theorem 1 at least are almost trivial.
Our second result shows that Zermelo deformation with respect to a Killing vector field preserves the property of a Finsler metric to be a locally symmetric space. We will call a Finsler metric locally symmetric, if for any geodesic the covariant derivative of the Riemann curvature (=Jacobi operator) vanished:
| (2) |
Here stays for the covariant derivative along the geodesic: . Both most popular Finslerian connections, Berwald and Chern-Rund connections, can be used as the Finslerian connection in the last formula, see e.g. [9, §7.3], whose notation we partially follow.
Remark 1.
In Riemannian geometry there exist two equivalent definitions of locally symmetric spaces: according to the “metric” definition, a space is locally symmetric if for any point there exists a local isometry such that this point is a fixed point and the differential of the isometry at this point is minus the identity. By the other “curvature” definition, a space is locally symmetric if the covariant derivative of the curvature tensor is zero. The equivalence of these two definitions is a classical result of E. Cartan. We see that our definition above is the generalization to the Finsler metrics of the “curvature” definition; it was first suggested in [4].
In the Finsler setup, both “metric” and “curvature” definitions are used in the literature, but they are not equivalent anymore: the symmetric spaces with respect to the “metric” definition are symmetric spaces with respect to the “curvature” definition, but not vice versa.
In fact, the “metric” definition is much more restrictive; in particular locally symmetric metrics in the “metric” definition are automatically Berwaldian [7, Theorem 9.2] and are clearly reversible. On the other hand, all metrics of constant flag curvature, in particular all Hilbert metrics in a strictly convex domain, are locally symmetric in the “curvature” definition, and are symmetric with respect to the “metric” definition if and only if the domain is an ellipsoid.
In view of this, the name “locally symmetric” is slightly misleading, since locally symmetric manifolds may have no (local) isometries. We will still use this terminology because it was used in the literature before.
Theorem 2.
Suppose that is a locally symmetric Finsler metric and a Killing vector field satisfying for all . Then, the -Zermelo deformation of is also locally symmetric.
All Finsler metrics in our paper are assumed to be smooth and strictly convex but may be irreversible.
2 Proofs.
2.1 Proof of Theorem 1.
Let be an arc-length-parameterized -geodesic, we need to prove that the curve is an arc-length-parameterized -geodesic. In order to do it, observe that for any -arc-length-parameterized curve the -derivative of is given by . Since the flow preserves and , it preserves and therefore
The last equality in the formula above is true because, for any such that , we have by the definition of the Zermelo deformation. Thus, if the curve is -arc-length-parameterized, then the curve is -arc-length-parameterized.
This also implies that the integrals and coincide for all -arc-length-parameterized curves . Since geodesics are locally the shortest arc-length parameterized curves connecting two points, for each arc-length parameterized -geodesic the curve is a -arc-length-parameterized geodesic as we claimed.
Remark 2.
Alternative geometric proof of the statement that for each arc-length parameterized -geodesic the curve is a -arc-length-parameterized geodesic is essentially due to [6]: consider the Legendre-transformation corresponding to the function and denote by the pullback of to , . Next, view the vector field as a function on by the obvious rule . It is known that the Hamiltonian flow corresponding to the function is the natural lift of the flow of the vector field to . Since is assumed to be a Killing vector field, the Hamiltonian flows of and of commute. Next, consider the function . If satisfies , then the restriction of to is convex, consider the Legendre-transformation corresponding to the function and the pullback of to , it is a Finsler metric which we denote by . It is a standard fact in convex geometry that the Finsler metric is the -Zermelo-deformation of . Since the Hamiltonian flows of and of , which we denote by and , commute, the Hamiltonian flow of is simply given by
| (3) |
Then, for any point with , the projections of the orbits of and of starting at this point are arc-length parameterized geodesics of and of . By (3) we have as we claimed.
Let us now prove the second statement of Theorem 1. Consider a Jacobi vector field which are orthogonal to . We need to show that the pushforward is a Jacobi vector field for the -geodesic . By the definition of Jacobi vector field there exists a family of geodesics with such that , since is orthogonal to we may assume that all geodesics are arc-length parameterized. As we explained above, is a family of -geodesics; taking the derivative by at proves what we want.
Let us now show that is orthogonal to . First observe that the condition that is orthogonal to is equivalent to the condition that vanishes at for each . Indeed, consider the one-form . Because of the (positive) homogeneity of the function we have that at a point
| (4) |
Next, take Equation (1) and calculate the differential of the restriction of to the tangent space: its components are given by
| (5) |
In this formula, the derivatives of the function are taken at , and the derivatives of the function are taken at . By we denoted the function .
In view of (5), vanishes at , so is orthogonal to (the orthogonality is understood in the sense of ). Then, is orthogonal to
Remark 3.
Geometrically, the just proved statement that is orthogonal to , after the identification of and by the differential of the diffeomorphism , corresponds to the following simple observation: if is tangent to the unit -sphere at the point , then it is also tangent to the unit -sphere at the point , see Fig. 1.
Let us now prove the third statement of Theorem 1, we need to show that . We consider a -geodesic with and and the corresponding -geodesic since , we have .
We will assume that is -orthogonal to . As explained above this implies that is -orthogonal to . Then, by (6), the minimum of taken over all Jacobi vector fields along which are equal to at , is equal to . An analogous statement is clearly true also for , and : namely, the minimum of taken over all Jacobi vector fields along which are equal to at , is equal to . Here we used the relation . Finally, in order to show that it is sufficient to show that the function is proportional, with a constant coefficient, to the function
In order to prove this, let us first compare and
It is convenient to work in coordinates such that the entries of are constants, in these coordinates for each the differential of the diffeomorphism is given by the identity matrix, so in these coordinates and
Differentiating (5), we get the second derivatives of . They are given by
| (7) |
Again, all derivatives of the function are taken at , and of the function are taken at . Note that one term in the brackets in (7) appears because we differentiate , and the other appears because the derivatives of are taken at . When we differentiate it, we also need to take into account the additional term .
Now, in view of the formula we obtain from (7) the formula for :
| (8) |
Let us now compare the length of in with that of in . We multiply (8) by and sum with respect to and . Since by assumptions vanishes at , all terms in the sum but the first vanish. We thus obtain that the length of in is proportional to that of in with the coefficient which is the square root of .
But along the geodesic both and are constant. Indeed, is the “Noether” integral corresponding to the Killing vector field. Theorem 1 is proved.
2.2 Proof of Theorem 2.
First, observe that a Finsler metric is locally symmetric if and only if for any geodesic and any Jacobi vector field along the vector field is also a Jacobi vector field. Indeed, the equation for Jacobi vector fields is
| (9) |
-differentiating this equation, we obtain
If is a Jacobi vector field, vanishes so the equation above implies , and since it is fulfilled for all Jacobi vector fields we have as we claimed.
Thus, we assume that for any geodesic and for any Jacobi vector field for its derivative is also a Jacobi vector field, and our goal is to show the same for . Clearly, it is sufficient to show this only for Jacobi vector fields which are -orthogonal to . Note that for such Jacobi vector fields is also orthogonal to , since both and are -parallel.
Take a (arc-length-parameterized) -geodesic and a point on it. Consider the geodesic polar coordinated around this point, let us recall what they are and their properties which we use in the proof.
Consider the (local) diffeomorphism of to which sends to , where is the geodesic starting from with the velocity vector . As the local coordinate systems on we take the following one: we choose a local coordinate system on the unit -sphere and set the tuple to be the coordinates of . Combining it with the diffeomorphism , we obtain a local coordinate system on . By construction, in this coordinate system each arc-length parameterized geodesics starting at , in particular the geodesic , is a curve of the form .
Next, consider the following local Riemannian metric in a punctured neighborhood of : for a point of this neighborhood such that is a geodesic passing through we set .
It is known that in the polar coordinates the metric is block-diagonal with one block which is simply the identity and one -block which we denote by :
It is known, see e.g. [9, Lemma 7.1.4], that the geodesics passing through are also geodesics of , and that for each such geodesic the operator , where is the Levi-Civita connection of , coincides with .
Next, consider analogous objects for the metric . As the local coordinate system on the unit -sphere we take the following: as the coordinate tuple of with we take the coordinate tuple , where . (Recall that the -parallel-transport sends the unit -sphere to the unit -sphere.)
By Theorem 1, in these coordinate systems each Jacobi vector field along which is orthogonal to is also a Jacobi vector field along , which is the -geodesic such that and , and is orthogonal to . By (8), the corresponding block is given by . Since the function is constant along geodesics, the coefficients of the Levi-Civita connection of such that or coincide with that of for the analog for . A direct way to see the last claim is to use the formula , where of course all indices run from to and the summation convention is assumed.
Then, in our chosen coordinate system, the formula for the covariant derivative in along for vector fields which are orthogonal to simply coincides with that of the formula for the corresponding objects for . Then, for any -Jacobi vector field orthogonal to we have that - is again a Jacobi vector field. Theorem 2 is proved.
Acknowledgments. The authors thank Sergei Ivanov for useful comments. V.M. was partially supported by the University of Jena and by the DFG grant MA 2565/4.
References
- [1] D. Bao, C. Robles, Z. Shen, Zermelo Navigation on Riemannian manifolds. J. Diff. Geom. 66(2004), 377–435.
- [2] S.-S. Chern, Z. Shen, Riemann-Finsler geometry. Nankai Tracts in Mathematics, 6(2005). World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ. x+192 pp.
- [3] P. Foulon, Ziller-Katok deformations of Finsler metrics. 2004 International Symposium on Finsler Geometry, Tianjin, PRC, 2004. 22–24.
- [4] P. Foulon, Locally symmetric Finsler spaces in negative curvature. C. R. Acad. Sci. 324(1997), no. 10, 1127–1132.
- [5] L. Huang and X. Mo, On the Flag Curvature of a class of Finsler metrics produced by the Navigation problem. Pac. J. Math. 277(2015), 149–168.
- [6] A. B. Katok, Ergodic properties of degenerate integrable Hamiltonian systems. Izv. Akad. Nauk SSSR. 37(1973), 775–778, English translation in Math. USSR-Isv. 7(1973), 535–571.
- [7] V. S. Matveev and M. Troyanov, The Binet-Legendre metric in Finsler geometry. Geom. Topol. 16(2012), no. 4, 2135–2170.
- [8] Z. Shen, Finsler manifolds of constant positive curvature. In: Finsler Geometry, Contemporary Math. 196 (1996), 83֭–92.
- [9] Z. Shen, Differential Geometry of Spray and Finsler Spaces. Kluwer Academic Publishers, Dordrecht,
Patrick Foulon: Centre International de Rencontres Mathématiques-CIRM, 163 avenue de Luminy,
Case 916, F-13288 Marseille - Cedex 9, France.
Email: foulon@cirm-math.fr
Vladimir S. Matveev: Institut für Mathematik,
Fakultät für Mathematik und Informatik,
Friedrich-Schiller-Universität Jena,
07737 Jena, Germany.
Email: vladimir.matveev@uni-jena.de