11email: luharvey@tcd.ie 22institutetext: Oskar Klein Centre, Department of Astronomy, Stockholm University, SE-10691 Stockholm, Sweden 33institutetext: Oskar Klein Centre, Department of Physics, Stockholm University, SE-10691 Stockholm, Sweden 44institutetext: Institute of Physics, Humbolt-Universität zu Berlin, Newtonstr. 15, D-12489 Berlin, Germany 55institutetext: Univ Lyon, Univ Claude Bernard Lyon 1, CNRS, IP2I Lyon/IN2P3, UMR 5822, F-69622, Villeurbanne, France 66institutetext: Department of Physics, Lancaster University, Lancs LA1 4YB, UK 77institutetext: Université Clermont Auvergne, CNRS/IN2P3, LPCA, F-63000 Clermont-Ferrand, France 88institutetext: Instituto de Estudios Astrofísicos, Facultad de Ingeniería y Ciencias, Universidad Diego Portales, Av. Ejército Libertador 441, Santiago, Chile 99institutetext: Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot 7610001, Israel 1010institutetext: Institute of Astronomy and Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 1111institutetext: Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Can Magrans, s/n, E-08193, Barcelona, Spain 1212institutetext: Institut d’Estudis Espacials de Catalunya (IEEC), E-08034 Barcelona, Spain 1313institutetext: Department of Physics and Astronomy, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA 1414institutetext: Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), 1800 Sherman Ave., Evanston, IL 60201, USA 1515institutetext: Nordic Optical Telescope, Rambla José Ana Fernández Pérez 7, ES-38711 Breña Baja, Spain 1616institutetext: INAF - Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, I-35122 Padova, Italy 1717institutetext: Division of Physics, Mathematics, and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 1818institutetext: IPAC, California Institute of Technology, 1200 E. California Blvd, Pasadena, CA 91125, USA 1919institutetext: Caltech Optical Observatories, California Institute of Technology, Pasadena, CA 91125, USA
ZTF SN Ia DR2: High-velocity components in the Si ii
The Zwicky Transient Facility SN Ia Data Release 2 provides a perfect opportunity to perform a thorough search for, and subsequent analysis of, high-velocity components in the Si ii feature in the pre-peak regime. The source of such features remains unclear, with potential origins in circumstellar material or density/abundance enhancements intrinsic to the SN ejecta. Therefore, they may provide clues to the elusive progenitor and explosion scenarios of SNe Ia. We employ a Markov-Chain Monte Carlo fitting method followed by Bayesian Information Criterion testing to classify single and double Si ii components in the DR2. The detection efficiency of our classification method is investigated through the fitting of simulated features, allowing us to place cuts upon spectral quality required for reliable classification. These simulations were also used to perform an analysis of the recovered parameter uncertainties and potential biases in the measurements. Within the 329 spectra sample that we investigate, we identify 85 spectra exhibiting Si ii HVFs. We find that HVFs decrease in strength with phase relative to their photospheric counterparts – however, this decrease can occur at different phases for different objects. HVFs with larger velocity separations from the photosphere are seen to fade earlier leaving only the double components with smaller separations as we move towards maximum light. Our findings suggest that around three quarters of SN Ia spectra before d show high-velocity components in the Si ii with this dropping to around one third in the six days before maximum light. We observe no difference between the populations of SNe Ia that do and do not form Si ii HVFs in terms of SALT2 light-curve parameter , peak magnitude, decline rate, host mass, or host colour, supporting the idea that these features are ubiquitous across the SN Ia population.
Key Words.:
stars: supernovae: general1 Introduction
Believed to be the thermonuclear explosion of a white dwarf due to interactions with a binary companion, Type Ia supernovae (SNe Ia) are a well-studied class of transients. With the normal SNe Ia following a strict relationship between their absolute magnitude and their light curve shape (Pskovskii 1977; Phillips 1993), their application as standardised candles was key to the discovery of the accelerating expansion of the Universe and in turn, dark energy (Riess et al. 1998; Perlmutter et al. 1999).
The observational properties and evolution of SNe Ia have been well investigated in the literature, leading to further subdivision of the class into an ever growing number of subclasses (see Taubenberger 2017 for a review). Many diagnostics have been developed to explore this diversity, grouping together clusters of similar SNe Ia in various parameter spaces; many of which revolve around the Si ii absorption feature. The Branch classification scheme (Branch et al., 2006, 2009) divides the SN Ia population into four classes (core-normal, shallow-silicon, broad-line, and cool) based on the pseudo-equivalent widths of the Si ii and 5972 lines at maximum light, with the shallow-silicon and cool groups broadly aligning with the 91T- and 91bg-like subtypes respectively. Wang et al. (2009) also drew their classifications from maximum-light spectra, defining all objects with Si ii velocity below 12000 km s-1 as normal-velocity, with those above this threshold as high-velocity. Analysing not just the Si ii velocity from a single epoch, but the rate at which this velocity drops, Benetti et al. (2005) divide the population into low velocity-gradient (LVG) and high velocity-gradient (HVG), with the post peak velocity decline as less than or greater than 70 km s-1 day-1, respectively.
While the velocities and widths of the Si ii line have been well characterised, little focus has been given to the potential presence of high-velocity features (HVFs). Seen predominantly in the Ca ii NIR and Ca ii H&K absorption lines in spectra taken up to maximum light (Hatano et al., 1999; Kasen et al., 2003; Wang et al., 2003; Gerardy et al., 2004; Thomas et al., 2004; Mazzali et al., 2005a, b; Maguire et al., 2014; Marion et al., 2013), these features appear as secondary absorption components several thousands of km s-1 to the blue of the photospheric-velocity component (PV). While less common than in the calcium, a number of SNe Ia have been seen to possess these HV components in the Si ii (Quimby et al., 2006; Childress et al., 2013; Marion et al., 2013), with HVFs also having been reported in Si iii, S ii, and Fe ii lines (Hatano et al., 1999; Marion et al., 2013). The source of these HVFs remains uncertain, with potential origins in density or abundance enhancements in the ejecta or their formation due to circumstellar material (e.g. Mazzali et al., 2005a; Tanaka et al., 2006).
Few samples of HVF spectra have been constructed and studied in the past, with any discussion of HVFs being typically conducted on an object-by-object basis. Childress et al. (2014) studied a sample of 58 low-redshift (z 0.03) SNe Ia with maximum-light spectra to investigate the relation between the Si ii and Ca ii NIR features. Their analysis of the strengths of the HV components in the Ca ii NIR feature indicated that HVF strength decreases with increasing light-curve decline rate, being absent altogether in the rapidly-evolving targets. Ca ii NIR HVF strength was also shown to decrease with increasing silicon velocity at maximum light, with clearly ‘high-velocity’ SNe Ia (v 12000 km s-1 at peak; Wang et al., 2009) showing no HVFs. Maguire et al. (2014) investigated a sample of 264 SNe Ia from the Palomar Transient Factory (PTF), including spectra obtained more than two weeks before maximum light. They found that HVFs in Ca ii NIR line appear to be ubiquitous at early times, with 95 per cent of SNe Ia with a spectrum before 5 days from peak displaying a HV component.
Silverman et al. (2015) conducted a search for HVFs in 445 spectra from 210 objects in the Si ii , Ca ii NIR, and H&K features. Their results agreed with Childress et al. (2014) in finding underluminous objects to lack Ca ii NIR HVFs unlike the rest of the subclass. The less common Si ii HVFs were shown to only appear at earlier phases and are more commonly found accompanied by higher photospheric velocities. Silverman et al. (2015) also found stronger HV components in the Si ii in objects lacking early C ii absorption with redder colours around peak.
This work aims to identify spectra in the Zwicky Transient Facility (ZTF; Bellm et al., 2019; Graham et al., 2019; Masci et al., 2019; Dekany et al., 2020) Cosmology Data Release 2 (‘ZTF Cosmo DR2’ or simply ‘DR2’; Rigault et al. in prep.) possessing HV components in the Si ii feature and then analyse the resulting distributions of phase, component velocity separation (), and corresponding light curve properties, as well as investigate the correlations drawn from previous samples. In Sect. 2 we introduce the dataset, in Sect. 3 we present the fitting algorithm for the spectra and our simulations, the results of the fitting to the real data and presented in Sect. 4 and subsequently discussed in the context of the literature in Sect. 5.
2 Observations and sample definition
The ZTF Cosmo DR2 comprises the ZTF data for SNe Ia in the first three years of operations (2018 – 2020), which is the largest SN Ia sample to date from a single untargeted survey. This dataset consists of forced photometry light curves and spectroscopy for each SN Ia. A dataset overview containing statistics and technical details concerning the photometric and spectroscopic observations, as well as details on sub-classifications and host associations, can be found in Rigault et al. (2024), along with a list of accompanying analysis papers written by the ZTF Ia working group.
2.1 Data acquisition and reduction
The SN Ia spectra in our sample come from a variety of sources. In this section, we describe the instrument and telescope, as well as data reduction technique for each telescope and instrument setup. Our measurements are sensitive to the wavelength and relative flux calibration across the Si ii feature, but we do not make use of the absolute values so absolute flux calibration to photometric measurements is not performed. These spectra are publicly released as part of the ZTF DR2 data release, with details on how to access the spectra and metadata provided in Rigault et al. (2024). We perform a number of cuts on our sample to select pre-maxiumum light spectra that reliable phase estimates from their light curves and have sufficient signal to noise in the region of the Si ii feature (see Section 2.2).
Spectra from the European Southern Observatory’s (ESO) New Technology Telescope (NTT) were obtained with ESO Faint Object Spectrograph and Camera version 2 (EFOSC2; Buzzoni et al., 1984) as part of the ePESSTO/ePESSTO+ collaboration (Smartt et al., 2015) at the La Silla Observatory. These spectra were reduced using a custom built pipeline described in Smartt et al. (2015) to provide wavelength- and flux-calibrated spectra. A number of spectra come from the 2 m Liverpool Telescope (LT; Steele et al., 2004) using the Spectrograph for the Rapid Acquisition of Transients (SPRAT; Piascik et al., 2014) at the Observatorio del Roque de los Muchachos. The spectra were reduced with the pipeline of Barnsley et al. (2012), adapted for SPRAT, along with a custom Python pipeline (Prentice et al., 2018).
Spectra were obtained with the SuperNova Integral Field Spectrograph (Aldering et al., 2002) on the University of Hawai’i 88-inch Telescope (UH88) at the Mauna Kea Observatories. The spectra were reduced using the pipeline of the Spectroscopic Classification of Astronomical Transients (SCAT) Survey (Tucker et al., 2022). This pipeline is insufficient for studies involving absolute spectrophotometric calibration. However, our measurements involve velocities and relative line fluxes of the Si ii feature and so this is not an issue. We are also not concerned with the region affected by the dichroic crossover (5000 - 5200 Å) that require special flat field images that are not applied by this pipeline. Spectra were also obtained at the Las Cumbres Observatory’s FLOYDS Spectrograph on the Faulkes Telescope North (FTN) and on the Faulkes Telescope South (FTS) at Haleakala and Siding Spring, respectively (Brown et al., 2013). These spectra were reduced and calibrated using a custom pipeline111floydspipeline,https://github.com/svalenti/floydspipeline described in Valenti et al. (2014).
The KAST Spectrograph (Miller & Stone, 1993) on the Shane 3 m Telescope at the Lick Observatory was used to obtain spectra that were reduced and calibrated using a custom Python pipeline, as detailed in Dimitriadis et al. (2022). Spectra were obtained with the Low Resolution Imaging Spectrometer (LRIS; Oke et al., 1995; McCarthy et al., 1998; Rockosi et al., 2010) on the Keck I telescope and reduced and calibrated using lpipe (Perley, 2019). The spectrum obtained with DEIMOS on the Keck II telescope was reduced using the pypeit software package (Prochaska et al., 2020)222https://github.com/pypeit/PypeIt. The Double Beam Spectrograph (DBSP) on the 200-inch Telescope (P200) at Palomar Observatory was used to obtain a number of spectra, these were reduced used a PyRAF-based pipeline, ‘pyraf-dbsp’ (Bellm & Sesar, 2016).
Spectra were obtained with the Asiago Faint Objects Spectrograph and Camera (AFOSC) on the 1.82 m Copernico Telescope at the INAF Osservatorio Astronomico di Padova. They were reduced using standard tasks in iraf, including wavelength calibration with arc lamp spectra and flux calibration using spectrophotometric standard stars. The spectra obtained at Alhambra Faint Object Spectrograph and Camera (ALFOSC) on the Nordic Optical Telescope (NOT) at the Observatorio del Roque de los Muchachos was reduced using a custom pypeit (Prochaska et al., 2020) environment333https://gitlab.com/steveschulze/pypeitalfoscenv. Spectra were obtained using the Dual Imaging Spectrograph (DIS) on the Astrophysical Research Consortium 3.5m Telescope (ARC) at the Apache Point Observatory (APO) and reduced using standard routines in iraf, as in e.g. Sharma et al. (2023). Spectra obtained at the Goodman Spectrograph (Clemens et al., 2004) on the Southern Astrophysical Research Telescope (SOAR) at Cerro Tololo Inter-American Observatory were reduced and calibrated using a custom Python pipeline, as detailed in e.g. Dimitriadis et al. (2022). Spectra were obtained at the Very Large Telescope with the Focal Reducer and Low Dispersion Spectrograph 2 (FORS2) on UT1 of the Very Large Telescope (VLT) at the ESO Paranal Observatory. These spectra were reduced using a custom Python pipeline444forsify, https://github.com/afloers/forsify based on pypeit (Prochaska et al., 2020).
Spectra were observed with the Inamori-Magellan Areal Camera and Spectrograph (IMACS Dressler et al., 2011) mounted on the Magellan-Baade telescope at Las Campanas observatory. The data reduction was performed in iraf555IRAF was distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation. following standard reduction procedures. The Low Dispersion Survey Spectrograph 3 (LDSS-3; Stevenson et al., 2016) on the Magellan-Clay Telescope at Las Campanas Observatory was used to obtain one spectrum, which was reduced using standard iraf routines as described in Hamuy et al. (2006) using the same procedure as described for IMACS above.
Spectra were obtained with the Optical System for Imaging and low-Intermediate Resolution Integrated Spectroscopy (OSIRIS; Cepa et al., 2000) on the Gran Telescopio Canarias (GTC) at the Observatorio del Roque de los Muchachos. These data were reduced and calibrated following the method in Piscarrera (in prep.) using custom routines based on pypeit (Prochaska et al., 2020). Some spectra were obtained with the Device Optimized for the Low Resolution (DOLORES) on the Telescopio Nazionale Galileo (TNG) at the Observatorio del Roque de los Muchachos and reduced using pypeit (Prochaska et al., 2020), following Das et al. (2023).
Spectra were obtained with Gemini Multi-Object Spectrographs (GMOS) (Hook et al., 2004; Allington-Smith et al., 2002) on the Gemini North Telescope at the Mauna Kea Observatories. The spectra were reduced using standard iraf/pyraf and Python routines, following Dimitriadis et al. (2022). The Intermediate-Dispersion Spectrograph and Imaging System (ISIS) and the Auxiliary-port Camera (ACAM; Benn et al., 2008) on the William Herschel Telescope (WHT) at the Observatorio del Roque de los Muchachos were used to obtain spectra. These were reduced and calibrated using standard iraf routines. The Robert Stobie Spectrograph (RSS) (Kobulnicky et al., 2003) on the South African Large Telescope (SALT) (Buckley et al., 2006) at the South African Astronomical Observatory (SAAO) was used to obtain spectra. The spectra were reduced using the custom pipeline, PySALT (Crawford et al., 2010) to produce wavelength- and flux-calibrated spectra. Spectra were obtained with the DeVeny spectrograph on the 4.3 m Discovery Channel Telescope (DCT), which was reduced using standard iraf routines, including wavelength and flux calibration (Hung et al., 2017). The Spectral Energy Distribution Machine (SEDm; Blagorodnova et al., 2018; Kim et al., 2022; Lezmy et al., 2022) on the P60 (Cenko et al., 2006) was used to obtain spectra, which were subsequently reduced using pysedm (Rigault et al., 2019).
We do not require absolute flux calibration for our measurements but our measurements are impacted by the relative flux and the wavelength calibration. Not all the spectral reduction techniques used for our sample provide meaningful flux uncertainties. Therefore, as described in Section 3.1.1, we estimate the uncertainty on the flux using the standard deviation of the values in certain continuum regions near to the feature of interest. For SN Ia spectra, where flux uncertainties were available, we cross-checked against the uncertainty estimates from the standard deviation near the feature of interest and found them to be consistent. In Section 2.2, we describe how we performed a cut on the sample based on the signal to noise in the Si ii region. Each remaining spectrum after this cut was inspected manually while choosing the continuum regions and if any cosmic rays or host galaxy lines were identified they were masked out prior to fitting the Si ii feature. We include an uncertainty in our fitting of 200 km s-1 to account for additional velocity offsets associated with motions of the SNe Ia in their host galaxies.
2.2 Sample definition
The starting point for defining our sample is the subset of the 3628 confirmed SNe Ia in the DR2 with spectra from the aforementioned facilities for which sufficient data information and reliable reductions could be performed, amounting to 3585 targets with 5028 spectra. 43 SNe Ia that were included in the full DR2 data release are excluded from our sample due to a lack of sufficient information on the observations and data reduction techniques. As our analysis will be restricted to spectra in the pre-peak regime, we require sufficient photometry to produce a reliable estimate of spectral phase. We used the suggested cuts of Rigault et al. (2024) on the SALT2 light-curve fitter (Guy et al., 2007) outputs, of fit probability greater than 10-5 and uncertainties smaller than the quoted values for the light curve width parameter, (), color parameter, (), and the time of maximum light, ( d). We do not impose any constraints on the measured values of or .
To maximise our spectral sample, we investigated all SNe Ia that failed to meet these criteria in order to avoid cutting otherwise acceptable spectra solely due to poor phase estimates from sparse photometry. In many cases this involved fitting supplementary photometry obtained from other surveys. A summary of this investigation and the updated phase estimates can be found in Appendix A. Following this investigation we are left with 4572spectra for which we have reliable phase estimates. As we are specifically interested in the evolution of Si ii high-velocity components, we limit our search to the pre-peak regime when these features are expected to be present. Cutting any spectra with a phase post-peak, we are left with 2362spectra from 1801SNe Ia.
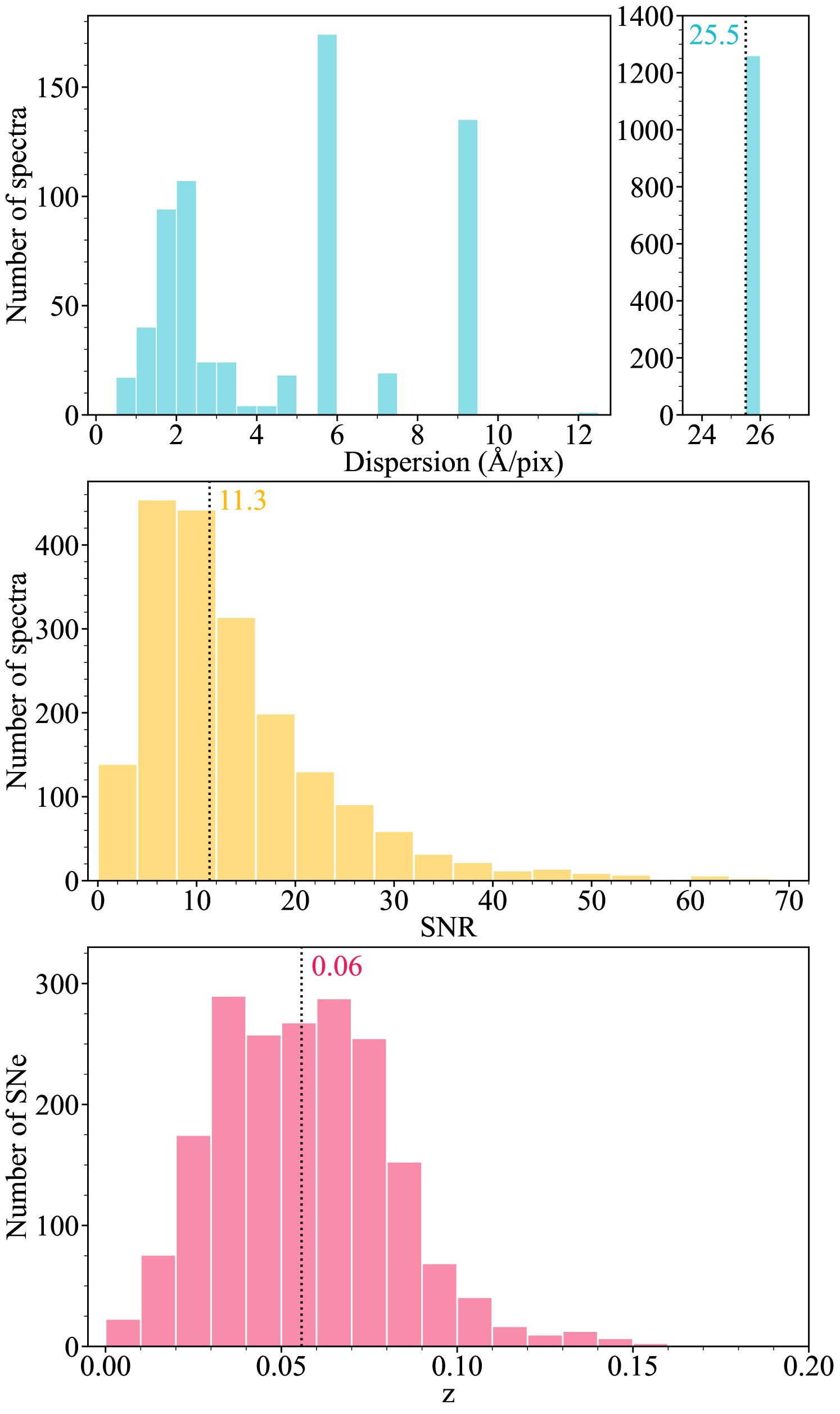
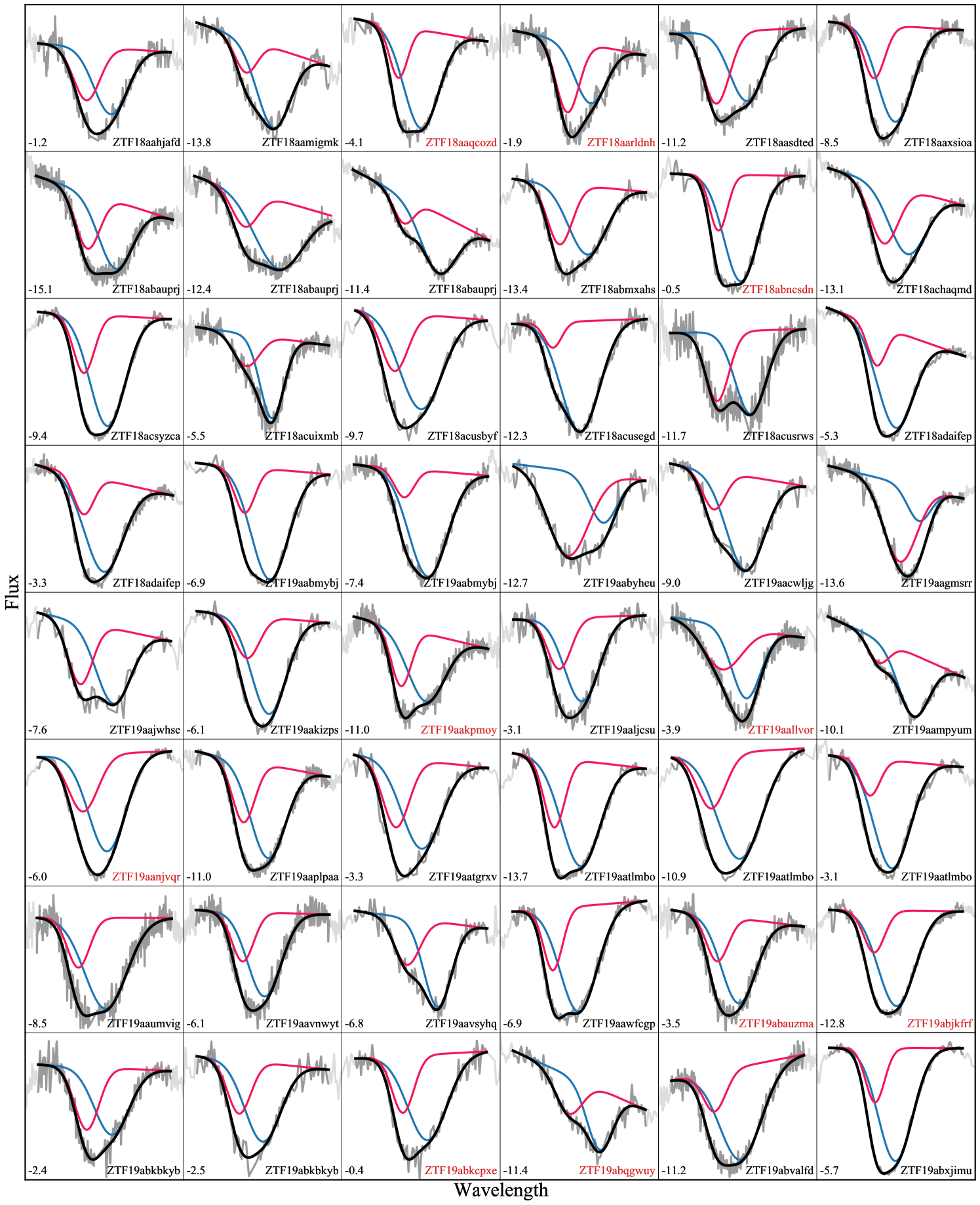
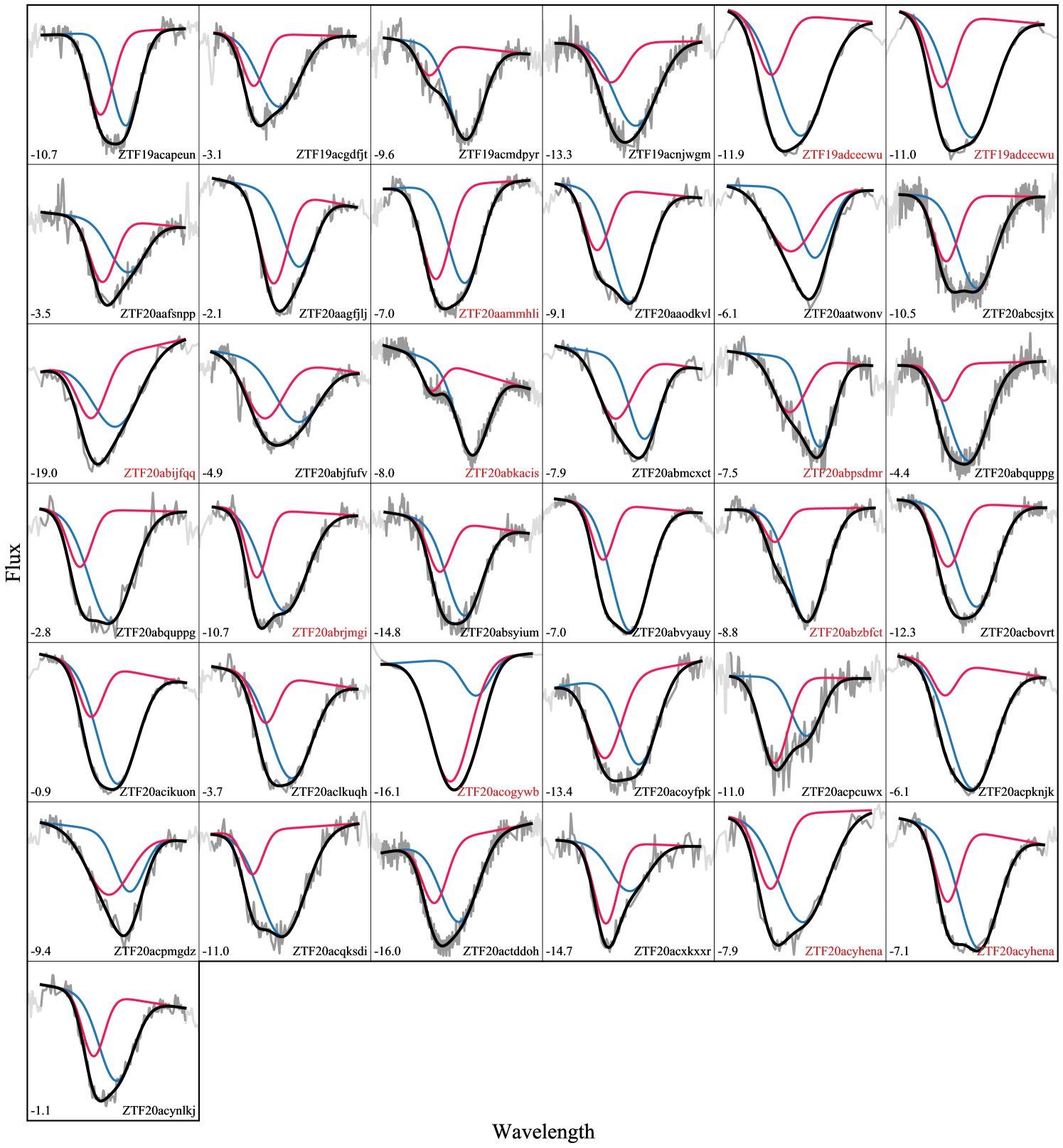
To assess the spectral quality in the vicinity of the Si ii we define a local signal-to-noise ratio (SNR) as the ratio of the depth of the Si ii to the standard deviation in the regions of the continuum to the red and blue (continuum region selection shall be discussed in detail in Sect. 3.1). This measurement is made once the continuum has been removed and is repeated 1000 times with different continuum selection points. The final SNR estimate is taken as the mean of these 1000 values. In making these estimates we identified 432 spectra that either did not cover the wavelength range of the Si ii feature, or did not have a clearly visible Si ii feature from which to compute an estimate of local SNR. These spectra were cut from the sample and the measurements of SNR for the remaining objects can be found in Fig. 1, along with the distribution of dispersion (average separation between pixels in Å) and the redshift distribution of the corresponding SNe. The large peak at 25 Å in the spectral dispersion panel corresponds to the spectra coming from the Spectral Energy Distribution Machine (SEDM; Blagorodnova et al., 2018; Rigault et al., 2019) on the P60 (Cenko et al., 2006) at the Palomar Observatory. The SEDM provides 60 per cent of the full DR2 spectral sample. The usefulness of the SEDM spectra in the search for HVFs will be determined by the simulations in Sect. 3.2, in which we will place a cut on both dispersion and SNR.
3 Method
In Section. 3.1, we detail the procedure for fitting the Si ii and our method of classifying high-velocity and non-high-velocity features. In Section 3.2, we describe the formulation of our synthetic Si ii features, as well as present the simulation results that test the ability of our method to identify HVFs. Based on these results, we can determine the dispersion and SNR that are required to identify HV components in observed spectra. We also investigate the simulation results to assess potential biases in our measurements of the feature parameters.
3.1 Identification of high-velocity components in the Si ii
Our aim is to distinguish between those SN Ia spectra that possess a HV component in the Si ii line and those that do not. The feature fitting with single and double component models shall be performed with an Markov-Chain Monte Carlo (MCMC) framework using the emcee package (Foreman-Mackey et al., 2013), treating the local continuum as linear and leaving the corresponding slope and intercept as free parameters in the fitting.
3.1.1 Spectral line fitting
As for the SNR estimation discussed in Section 2.2, the line fitting requires defined continuum regions to the blue and to the red of the Si ii absorption feature. The so-called ‘continuum’ in these photospheric phase spectra is in fact the overlapping of many different P-Cygni emission profiles and as such we are actually defining a pseudo-continuum. This pseudo-continuum region selection is more complex for the observed data than for the simulated features for reasons such as contamination by neighbouring features and noise spikes. The initial selections of these local pseudo-continuum regions were performed using a gradient method similar to previous studies (e.g. Blondin et al. 2011; Nordin et al. 2011; Silverman et al. 2012, 2015). Starting at the local minimum of the feature, gradients are calculated in wavelength bins successively moving outwards to the red and blue until the gradient changes sign, indicating a maximum. The wavelength bins corresponding to these sign changes are therefore taken as the initial pseudo-continuum regions selections. Each selection was subsequently checked over manually, with any necessary updates to the regions being made.
For each spectrum, we commence with a pre-processing step which involves the cutting of two small regions of the spectrum (6275–6307 Å and 6860–6890 Å) corresponding to telluric regions, as well as correcting for the host galaxy redshift. We then perform a normalisation step by dividing the flux of the spectrum by the maximum value found between 200 Å to the blue of the blue continuum region and 200 Å to the red of the red continuum region. This ensures that the slopes and offsets of all the features in the fitting will be of a similar order of magnitude.
The Si ii feature is a doublet comprised of two lines very close together in wavelength space at 6347.11 and 6371.37 Å. Our feature fitting assumes the two singlets of the Si ii doublet to be tied in all parameters (velocity, depth, and width) as is the case under the assumption of an optically thick regime at these pre-peak phases (see discussion in Childress et al., 2013). The single component model corresponds to one Si ii doublet, typically associated with the photosphere and therefore, we call this the photospheric-velocity (PV) component. The double-component model includes an additional Si ii doublet at higher velocity, which we refer to as the high-velocity (HV) component.
The single () and double () component models take the forms,
| (1) |
and
| (2) |
with as the flux, and as the continuum slope and intercept respectively, and being an indivdual Si ii doublet of the form:
| (3) |
where is the depth of one of the singlets, is the wavelength position of the minimum, with the 7.89 and 16.37 quantities as the offsets from 6355 Å for the 6347.11 Å and 6371.37 Å lines of the doublet, is the width, and the PV and HV subscripts refer to the photospheric- and high-velocity components of the model, respectively. The uncertainty on the flux values is taken as the standard deviation of the points in the continuum regions around the linear fit used for the initialisation of and .
We place a number of priors on the MCMC fitting to restrict the walkers to the relevant region of the parameter space. The depth parameters ( and ) and width parameters ( and ) are bound to be larger than 0.05 and 30 Å, respectively to avoid overfitting, especially in the noisier and lower resolution spectra. To ensure that the fitted components fall within the wavelength region of the feature we introduced the restrictions that the sum was smaller than the lower bound of the red continuum region and than was higher than the upper bound of the blue continuum region (or in the single component model).
Through preliminary testing with simulated features (see Section 3.2.1), we found that in most cases the slope from a linear fit to the continuum regions provided a smaller residual with the true value than that of the final output of the MCMC. This effect was counteracted by placing a uniform prior on the slope parameter, with dispersion-dependent limits away from this slope estimate derived empirically as
| (4) |
with as the dispersion in Å/pix.
The measured values for the parameters are taken as the medians of the posteriors, with the lower and upper uncertainties as the 16th and 84th percentiles, corresponding to a 68 per cent confidence interval. We use the MCMC chains to calculate parameters such as pseudo-equivalent widths (pEWs), pEW ratios, and velocity separations directly, drawing the median and lower and upper uncertainties from the resulting posteriors. The accuracy of these uncertainties shall be investigated with the simulated data in Section 3.2.
3.1.2 Deciding upon the preferred model
With single- and double-component posterior distributions derived from the MCMC, we now employ the Bayesian Information Criterion (BIC) - a goodness-of-fit metric that disfavours more complex models - to decide upon the preferred model. As there are three more free parameters in the double-component model than the single-component model, the corresponding fit has to significantly improve the goodness-of-fit in order to be preferred by the BIC. We employ the BIC as
| (5) |
with as the maximised value of the likelihood function, as the number of free parameters (5 for the single and 8 for the double component), and as the number of data points in the fitting. The model that produces the lowest BIC is provisionally deemed to be the best match, subject to two cuts explained below.
HV components that possess large velocity separations from their PV counterparts are easily distinguishable through fitting or visual inspection. However, as this velocity separation decreases, the components become increasingly more entangled and more difficult to detect. With the addition of noise, this has the potential to lead to high false-positive rates. Therefore, a cut upon the minimum velocity separation is necessary in the fitting, as below this limit we will not be able to reliably differentiate between single and double component features. A lower limit of 4500 km s-1 was adopted in Silverman et al. (2015). Our lower limit of 4000 km s-1 was set based on the performance of our classification method on simulated data (Section 3.2). Similarly to Silverman et al. (2015), we consider any two-component classifications with a PVF velocity km s-1 as unreliable, with the fitted PV component likely corresponding to contaminating C ii absorption. Therefore, in these cases we choose the single- over double-component classification, regardless of the BIC-based classification.
3.2 Simulations
To investigate the accuracy of the MCMC/BIC method described in Section 3.1 for identifying HV components, as well as its ability to recover the injected parameters, we generated synthetic Si ii features. The results from these simulations were also used to inform cuts on dispersion and SNR in the observed data. In Section 3.2.1, we describe the construction of our simulated data for testing our method, while in Section 3.2.2, we detail our detection efficiencies and in Section 3.2.3, we discuss the correction for biases in our fitting based on our simulations.
3.2.1 Constructing the simulated data
The synthetic features are comprised of two (PV and HV) doublet components, separated by a fixed velocity difference - with the exception of the simulations where we injected no HV component to assess the false-positive rate. We created a grid spanning four SNRs (4, 8, 15, and 25), four dispersions (2, 5, 10, and 25 Å/pix) to cover the range of values found for the DR2 subsample (Fig. 1), as well as seven velocity separations (no HVF, 3000, 4000, 5000, 6000, 7000, and 8000 km s-1) covering the range of separations expected from the data. For each of these parameter setups we generated 500 simulated features.
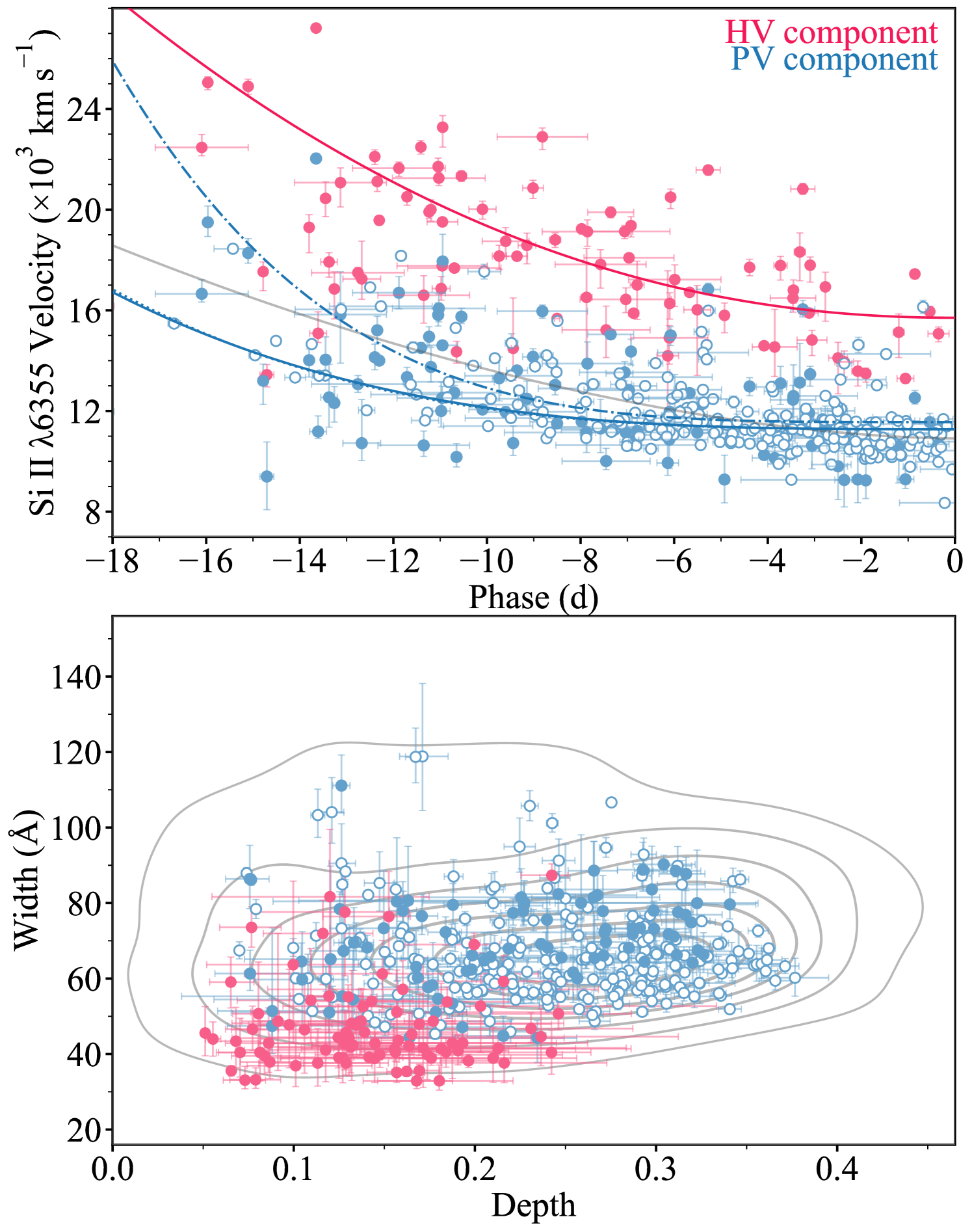
Measurements from PTF SNe Ia (Maguire et al., 2014) were used to inform our generation of Si ii line profiles. For each feature we generate a random phase between 17 and 0 d, which then gives a photospheric velocity probability distribution as the cross-section of the power-law fit to the PTF data seen in the top panel of Fig. 2. We draw a photospheric velocity from this resulting distribution, with the HVF velocity then defined by the fixed velocity separation in the simulation. The depths and widths of both components are drawn from a kernel density estimate (KDE) of the PTF measurements found in the bottom panel of Fig. 2. The modelling of the HV components in these simulations is rather simplistic, with the depths and widths assumed to follow the same distribution as those of the PV components. The photospheric velocity, width, and depth estimates based on Maguire et al. (2014) are also biased since these include contributions from high-velocity features. The validity and potential implications of these assumptions can be assessed with our final DR2 sample and shall be discussed in Section 4.2.
Noise was introduced to the simulated features and surrounding continuum based on the set SNR values defined by the simulation grid. Noise values for each wavelength bin were then drawn from a Gaussian distribution centered about zero with a standard deviation as the product of the SNR and the depth of the composite feature. The dispersion of each simulated feature is simply defined as the separation between the wavelength bins (the same definition as used for the observed spectra). With this simulated feature constructed, we introduced a simple linear continuum to each feature, varying the slope and intercept between them. The values for these slopes were drawn from the normal distribution with mean and standard deviation , chosen to match the range of initial slope estimates from the normalised DR2 spectra.
Our simulated spectra with the single- and double-component models were then fit following the procedure described in Section 3.1. The continuum region selection for the simulated data was performed in a similar fashion to that of the observed data but did not require manual checking for cosmic ray spikes or contamination by host lines.
3.2.2 Detection efficiencies
| Cut | Spectra | SNe |
| Initial cuts | ||
| ZTF Cosmo DR2 | 5028 | 3585 |
| Light curve quality cuts | 4572 | 3280 |
| Phase < 0 d | 2362 | 1801 |
| Si ii wavelength coverage | 2349 | 1793 |
| Visible Si ii | 1930 | 1557 |
| Spectral quality cuts | ||
| Dispersion 10 Å/pix | 660 | 605 |
| SNR 8 | 329 | 307 |
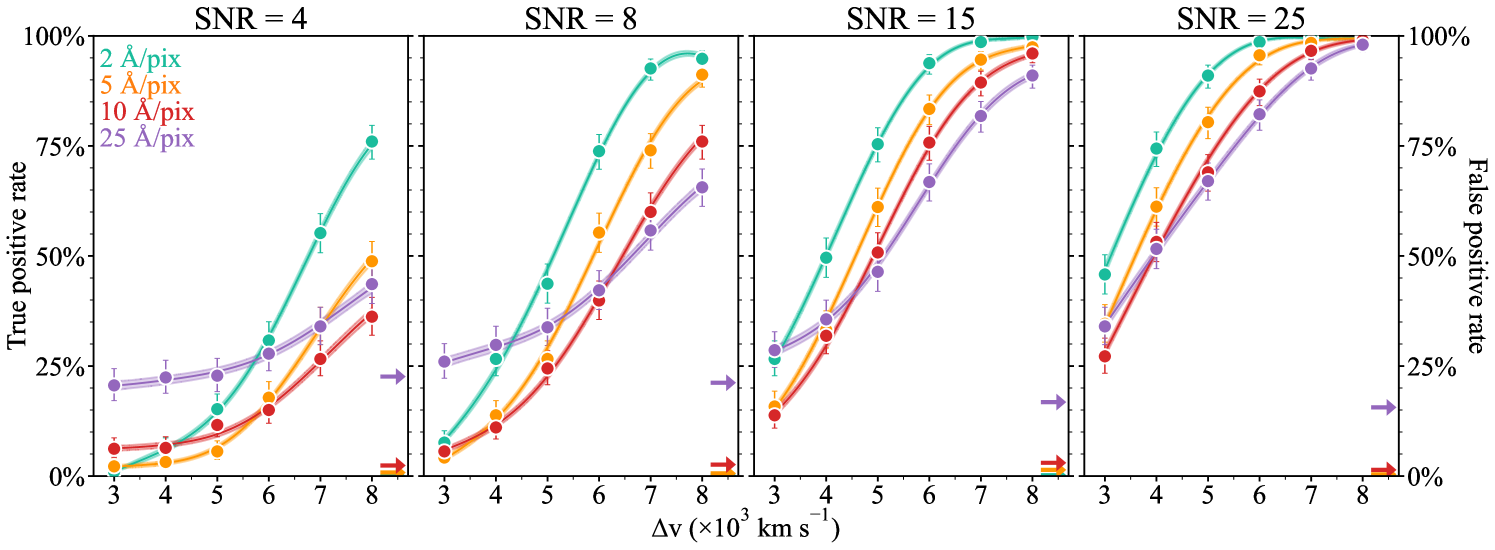
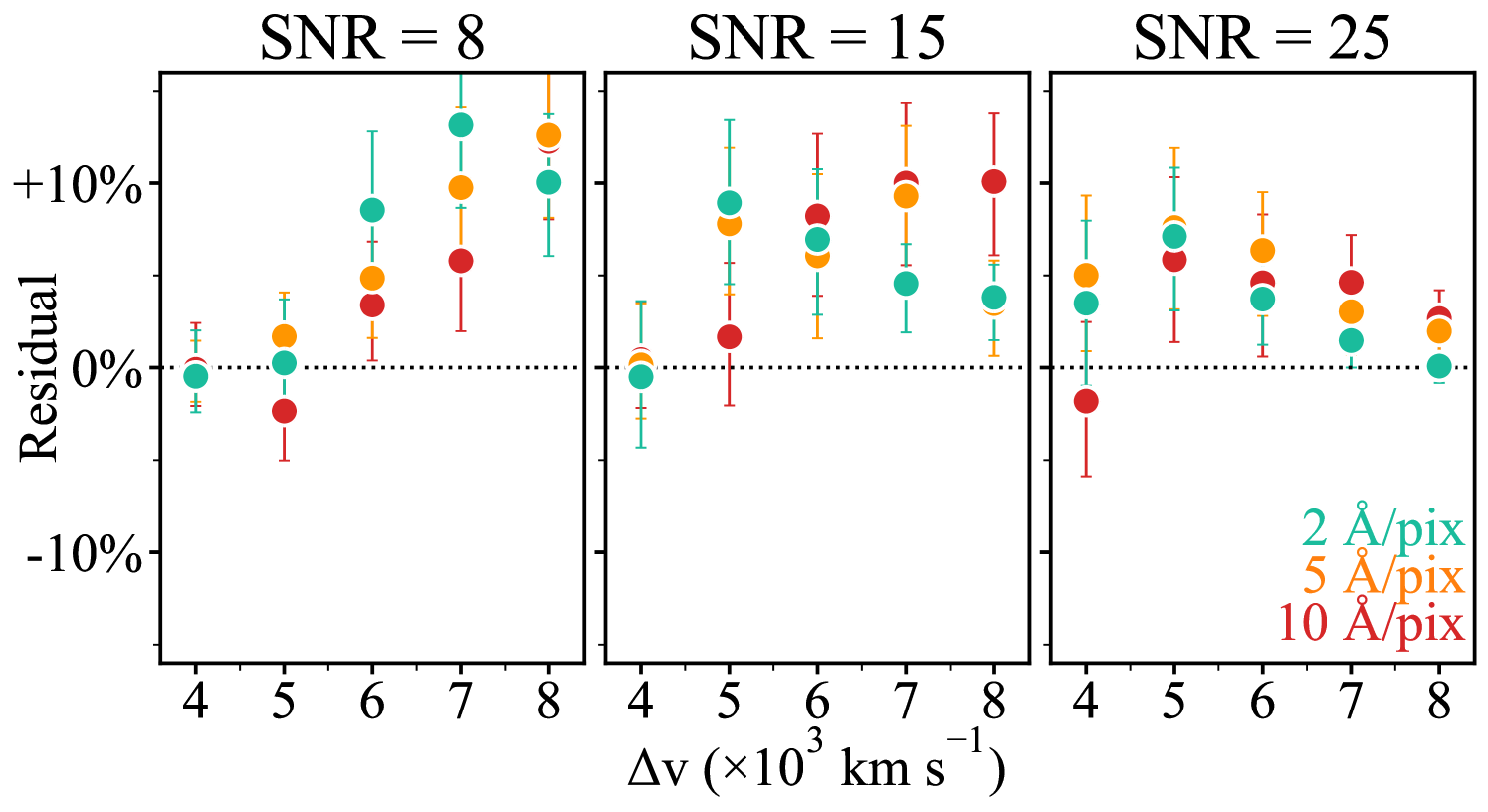
We have performed simulations of the Si ii region with different SNRs, dispersions and the presence (at different velocity separations between the low- and high-velocity components) or absence of a HV component. We present the resulting true- and false-positive rates for the detection of high-velocity features for each of the different simulation setups in Fig. 3. The panels display the four SNR ratios increasing from left to right, with the different colours indicating the four different dispersions. The circle markers correspond to the left axis and display the percentage of the 500 simulated features in that simulation that were correctly identified as possessing both a high-velocity and photospheric velocity component. The arrows correspond to the right axis and represent the percentage of the 500 simulated features without a HV component that were incorrectly identified as possessing two components. The uncertainties on these points are taken as binomial and calculated from the Clopper-Pearson method with a 95% confidence interval.
Each simulation setup in our grid can be thought of as a point in a 3D parameter space spanning SNR, dispersion, and velocity separation. At every point in this space there exists some true-positive rate which can be used to assess how probable it is to correctly identify a HV component with such properties. Using the Gaussian Process (GP) module within scikit-learn (Pedregosa et al., 2011) we perform a 3D interpolation of this discrete grid to obtain a continuous view of the changing detection efficiency. One-dimensional slices in velocity space are shown in Fig. 3.
Our aim is then to introduce cuts based on the velocity separation, SNR, and dispersion to keep the true-positive rate high and the false-positive rate to a minimum, while maximising our sample size. As one might expect, we see an increase in our ability to correctly identify HVFs as the noise is reduced, as we improve the spectral resolution (decrease the dispersion), and as we separate the components in velocity space. The highest dispersion simulations (purple in Fig. 3) have a separation of 25 Å between wavelength bins and represent the large percentage of DR2 spectra coming from the SEDm spectrograph. Accompanying the smaller true-positive rates for these features, we see large false-positive rates of the order 15 - 20%. These false-positive rates also stand as lower thresholds for the true-positive rates as we can see for the 25 Å/pix lines in the left hand panel, where the true-positive rates flatten off and plateau at the level of the false-positive rate as we approach smaller velocity separations. This leveling off of the true-positive rate as it becomes similar in magnitude to the false-positive rate causes an overlap effect between the 25 Å/pix simulations and those with smaller dispersions. The simulations with SNR of 4 exhibit the same overlap effect as seen for the 25 Å/pix dispersion simulations for the 10 Å/pix dispersion spectra for velocity separations up to 5000 km s-1.
Due to these issues with the lowest resolution and lowest SNR spectra, we cut all spectra from our observed sample with a dispersion greater than 10 Å/pix and SNR 8. With this dispersion cut, we remove all SEDm spectra from our sample, which due to its brighter limiting magnitude for targets compared to the other telescopes, may potentially remove brighter events from the sample. We test the impact of this on our demographic comparison in Section 4.3 but find no bias in SALT2 for our sample compared to the volume-limited DR2 sample. Our SNR cut could also potentially bias our sample, removing events with intrinsically shallower Si ii features. However, ‘shallow Silicon’ (Branch et al., 2006) SNe Ia have light curve widths (parameterised by e.g., SALT2 ) that are higher than mean of the SNe Ia sample (e.g. Blondin et al., 2011) and we find no bias relative to our comparison DR2 sample, again suggesting that this SNR cut does not introduce a significant bias to our final sample. With these two spectral quality cuts in place, we obtain our final sample of 329 observed spectra from 307 SNe ready for fitting. The breakdown of each of the cuts can be found in Table 1.
The final result to be drawn from Fig. 3 is a cut upon the measured velocity separation based on the simulations. Silverman et al. (2015) chose to disregard any classifications of features with separations less than 4500 km s-1, instead classifying these spectra as having single components. We chose a similar threshold of 4000 km s-1, as below this velocity we begin to see the previously discussed overlap effect below 4000 km s-1 for the 10 Å/pix simulations with SNR of 8 (lowest final resolution and SNR studied). This is further justified by closer inspection of the false positive rate. Averaging over all simulations passing the implemented dispersion and SNR cuts, we find a false positive rate of 1%, with 80% of these false positive classifications measured with velocity separations less than 4000 km s-1. Applying this velocity separation cut reduces the simulation false positive rate to 0.2% in the remaining simulations. Given that the simulations represent the ideal scenario with linear continua, generated Gaussian features, and Gaussian noise, this rate is optimistic; therefore, we assume a more conservative false positive rate of 2%. The false positives as measured in the DR2 are likely to be concentrated at smaller velocity separations up to 5000 km s-1 where there exists more degeneracy between the single and double component models.
3.2.3 Parameter recovery and uncertainty corrections
Along with estimating the detection efficiencies of our MCMC/BIC HVF classification method, the grid of simulations also allows us to test how the estimated uncertainties perform in terms of truly representing 68% confidence intervals, and identify potential biases in our measurements. The pull for some parameter is calculated as
| (6) |
with as the uncertainty taken from the posterior distribution. In the case of no biases and uncertainties that truly reflect 68% confidence intervals, these distributions should be Gaussian with a mean of zero and a standard deviation of unity.
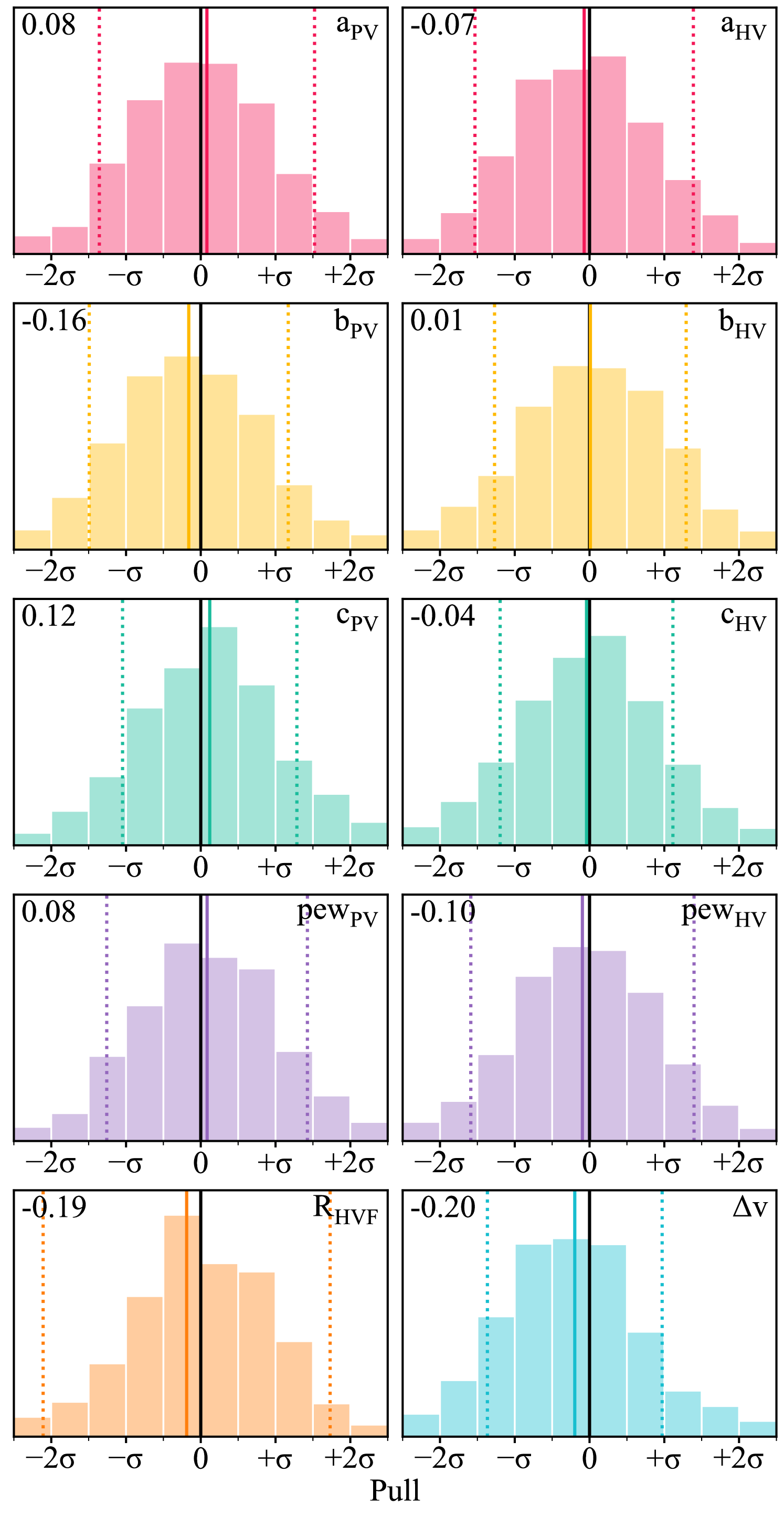
In Fig. 4 we show example distributions of the pulls in the six parameters describing the PV and HV components, as well as the pEWs, R (the ratio of pEW/pEW), and from a simulation with our middle remaining dispersion of 5 Å/pix and middle remaining SNR of 15, with a velocity separation of 5000 km s-1. As clearly visible for the majority of the measured parameters, the spread of the pull distribution is too large with a mean standard deviation of about the mean for this set of simulation parameters, indicating that the uncertainties from the MCMC posterior are times too small. A pull is also observed in most parameters where the means of the distributions do not lie exactly at zero.
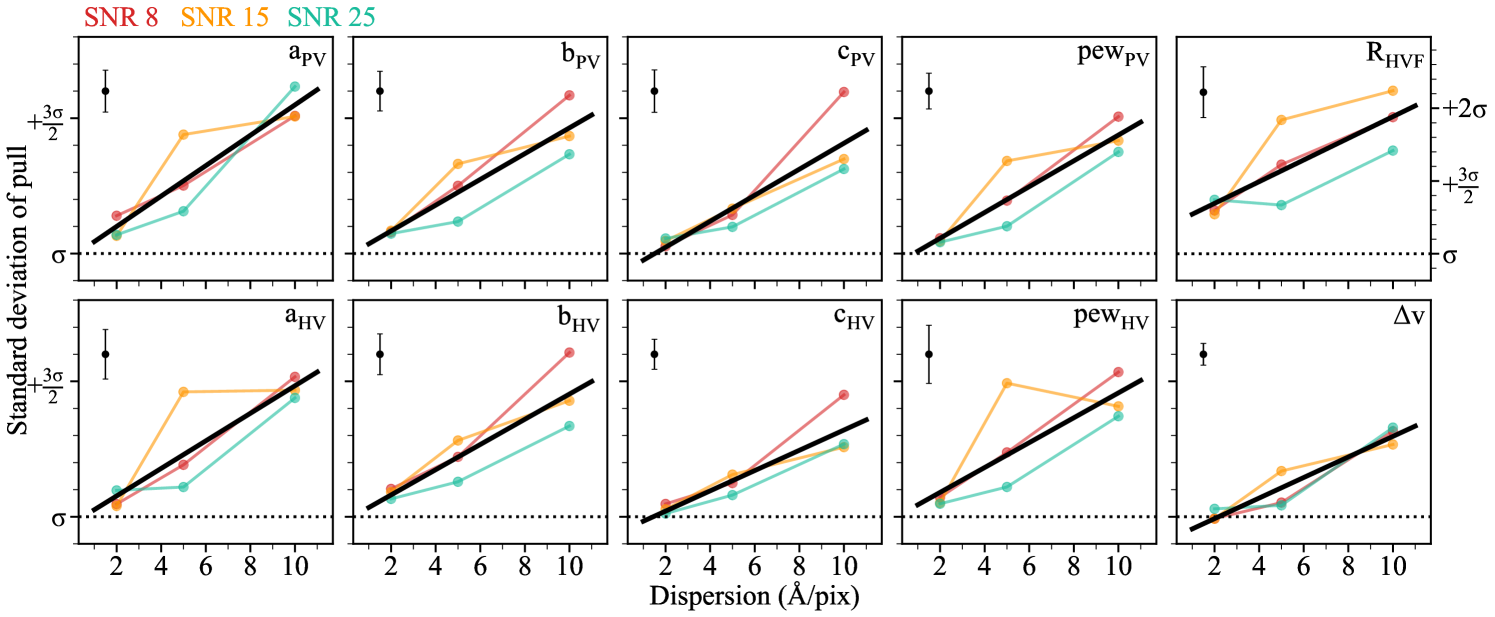
In Fig. 5, we present the standard deviations for each of the parameters as a function of dispersion and split into the three remaining SNR (8, 15 and 25). All two-component fits with resulting velocity separation measurements below the 4000 km s-1 threshold have been already removed. Most of the 2 Å/pix dispersion simulations exhibit standard deviations close to unity and therefore, require little to no correction. The standard deviations of the pull generally increase with increasing dispersion for all SNR simulations. The thick black lines present linear regressions to these combined SNR standard deviation trends and are used to compute scale factor corrections to the uncertainties to bring them in line with 68% confidence intervals.
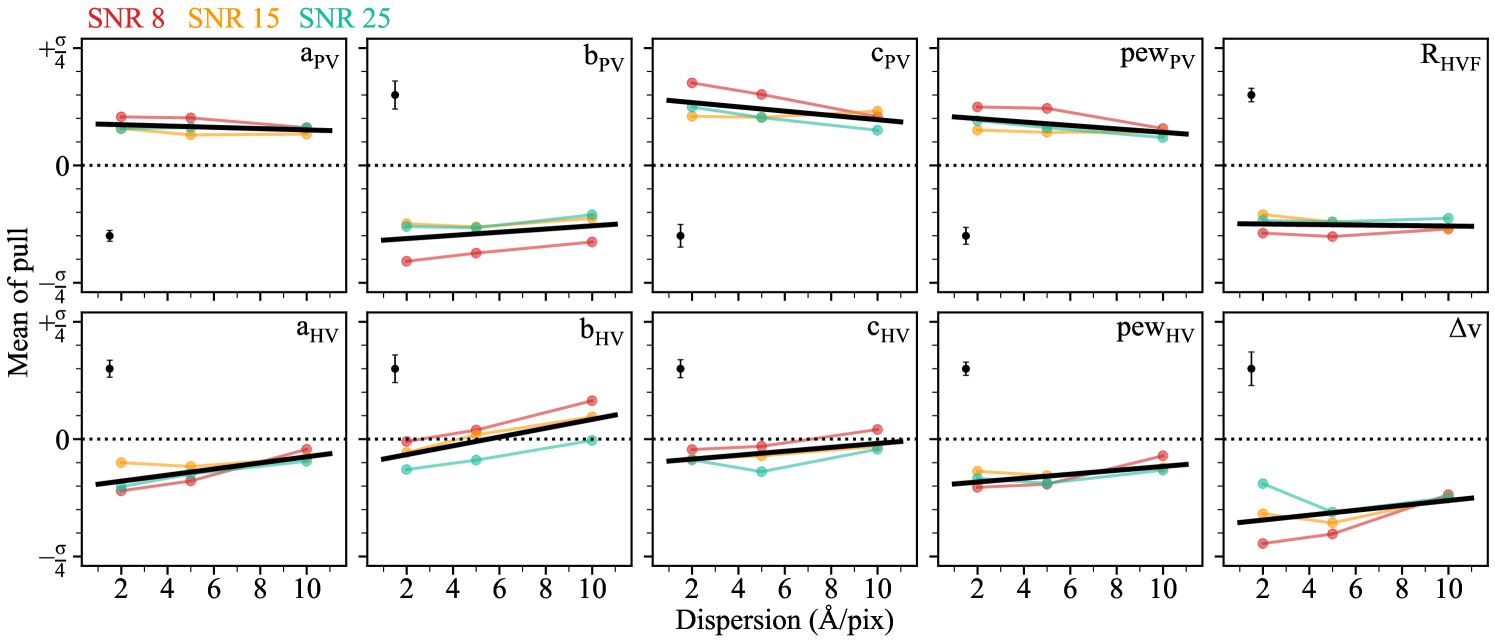
In a similar fashion, we can analyse how closely the means of these pull distributions lie to zero to identify any biases in the measurements. In Fig. 6 we plot the means of the pull distributions for each of the simulations as a function of dispersion, after having applied the uncertainty corrections discussed above. We observe slight biases that are consistent between the different SNR and dispersion pairings and appear relatively flat with changing dispersion. We correct for these trends using a linear regression as a function of dispersion. The same investigation was performed for the single component fits to the simulated features with no HV components. While we find the means to be centered upon zero – indicating no bias in the measurements – the standard deviations of these distributions fell in the range 1 – 1.3 and therefore, small corrections were made to the uncertainties using the same method as for the two-component fits above.
4 Results
With the cuts informed by the simulations (dispersion 10 Å/pix and SNR 8), we arrive at our final sample of 329 spectra (see Table 1) for which we can study the presence of high-velocity features in the Si ii . With the MCMC/BIC classification method outlined in Section 3.1, we fit our sample, taking all those classified as HVF with km s-1 and km s-1 as our HVF subsample. Of the 329 spectra we identify 85 as possessing both PV and HV components, corresponding to 26% of the sample. The HVF spectral sample comprises spectra from 75 SNe, including 8 objects for which we find these HV components in multiple epochs. In the sample there exists one object (ZTF18abauprj) for which we have both HVF spectra, and a final epoch showing no sign of a HV component, providing a glimpse at the full evolution of these features as time evolves. In our sample, we also have 10 pairs of spectra from the same object coming from different instruments with phase separations of a day or less. In all these cases the classifications are consistent between these spectra with 6 pairs as PVF and 4 as HVF. The measured values for velocity for all these components are consistent within the uncertainties, as are the feature widths and the majority of the feature depths. Any differences in the depth parameters - which are all 0.05 in size - are likely predominantly the result of changing line profiles over the hours elapsed between the spectra, although there may be small systematic differences.
In Section 4.1, we describe how the observed SN measurements were used to validate the priors used in the simulations. In Section 4.2 we explore the phase evolution of the HVFs. We then define and analyse a reduced low-bias sample to draw conclusions about the properties of HVFs in Section 4.3, and correlations with light curve and host parameters in Section 4.5.
4.1 Validation of simulation priors
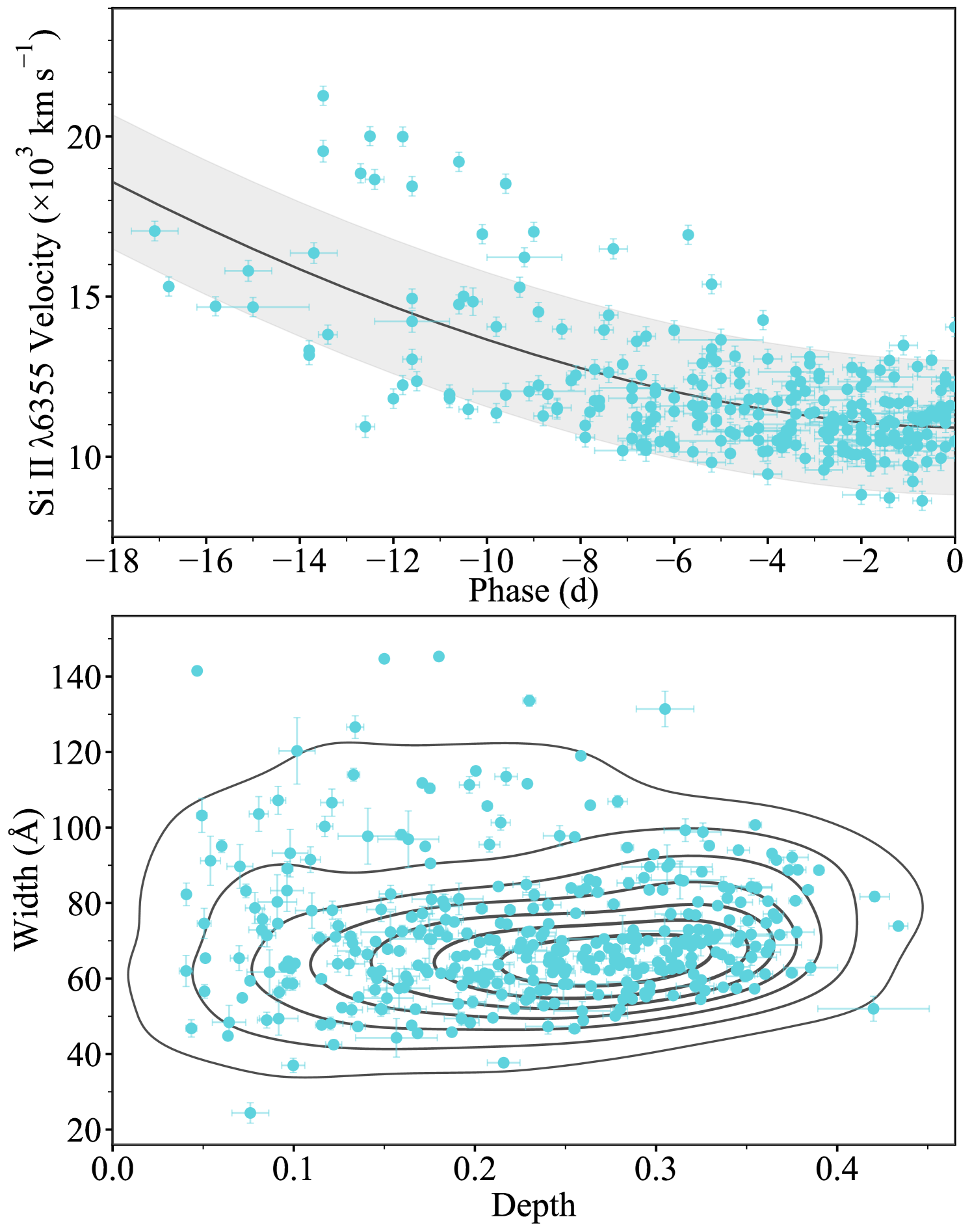
The top panel of Fig. 7 displays the measured velocity evolution for the 329 spectra from our 307 SNe Ia, split into the photospheric components, and high-velocity components where classified. Power-law fits were performed to the velocities as a function of phase for the HV components, as well as three samples of the PV velocities, i) all the PV components, ii) just the PV components with HV counterparts, and iii) just the singular PV components. These three fits are consistent from around 10 d onwards, with the PV velocities in objects possessing HV components drifting to higher velocities at early phases. This agrees with the findings of Silverman et al. (2015) in that HVFs tend to be accompanied by higher velocity PVFs. We also plot in grey the velocity evolution from the PTF sample (Maguire et al., 2014) that was used as reference for our Si ii feature generation in the simulations. These PTF measurements were performed on the overall Si ii features without distinction between PV and HV components. The PTF velocity evolution therefore likely has some level of contamination from HVFs, and would be expected to lie somewhere between our measured PVF (blue) and HVF (pink) evolution curves, as it does.
In the bottom panel of Fig. 7 we present the measured depths and widths of the singlet lines making up the PV and HV components. As for the velocity evolution we plot the comparison PTF data as grey contours to show how our final measurements align with the distributions chosen to inform the feature generation in the simulations. As expected, the distribution of PVF measurements lie in the same parameter space as the PTF data, but our measurements are slightly more compact in both dimensions which, as with the velocity, is likely due to HVF contamination in the PTF dataset inflating the depths and widths in some cases. For the generation of the HVF components in the simulations, we made the assumption that the widths and depths of the HV components followed the same distribution. However, as clearly visible in Fig. 7, these components tend to cluster more towards shallower depths and narrower widths. While some false positive classifications may be contaminating the HVF cluster, there remains a clear distinction between the HVF and PVF distributions. To evaluate the effect that this discrepancy has upon the calculated detection efficiencies we recalculated the true-positive rates from the simulations, excluding any simulated spectra from the calculations with or Å so has to be more in agreement with the measurements from the observations. The residuals between the true positive rates these updated simulations and the original simulations are presented in Figure 8. In most cases, the true-positive rate increases with the cut to only focus on the observed region of the parameter space. This implies that we are less sensitive to finding HV components with similar widths and depths to their PV counterparts - likely due to increased degeneracy in the fit. Therefore, we updated the detection efficiencies with a GP interpolation (following the method of Section 3.2.2) to these new values.
4.2 Phase evolution
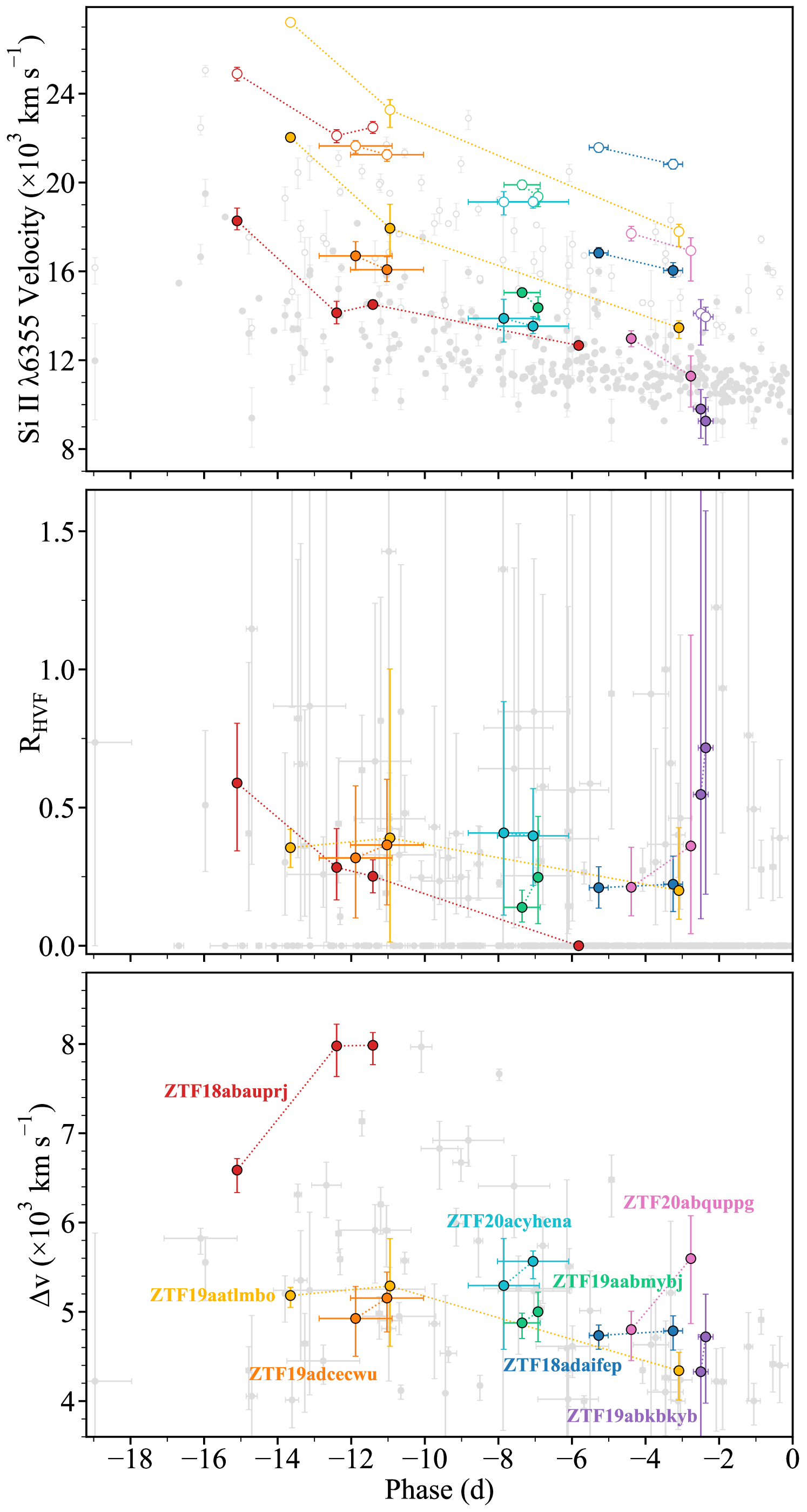
The evolution of the ratio of pEW/pEW (R) is seen for our observed sample in the middle panel of Fig. 9. In general, the uncertainties on the measured R values are large as many of the two-component fits exhibit high levels of degeneracy and posteriors of the numerator and denominator in the ratio (pEW and pEW) are inversely correlated.
The SNe with multiple spectra allow us to probe the evolution of this ratio within individual objects, with the overall sample - including single-epoch objects - giving a more global view of how the distribution of R changes with phase. For most of our multi-phase objects, we possess only two spectral epochs, separated by less than 2.5 d, leading to very little evolution in R which appears to remain approximately constant on such small timescales. However, for ZTF19aatlmbo (SN 2019ein) and ZTF18abauprj (SN 2018cnw), we have three and four spectra spanning 9.3 d and 10.6 d, respectively. ZTF18abauprj displays a clear decrease in this ratio with time, with the HV component fading away completely somewhere between and d, whereas ZTF19aatlmbo exhibits a far flatter evolution; albeit with large uncertainties on the spectrum at d. The R evolution for these multi-spectra objects is consistent with previous studies showing a decline with phase, with HV components starting out strong and fading away over time (Silverman et al., 2015). As clear from these two objects, while we see a decrease in R with time in individual SNe, this decay occurs at different phases, and we see many multi-spectra targets still exhibiting HVFs after the HV component in ZTF18abauprj had faded away completely. When combining the multi-spectra and single-spectra objects to get a global view of how R varies with phase, we find no clear evolution, with some large and small measurements of this ratio and early and late phases, further supporting the idea that the fading away of HV components occurs at different phases in different objects.
The bottom panel of Fig. 9 presents the evolution of the velocity separation, , with phase. As for R, the multi-epoch spectra with small temporal differences do not shed much light upon the phase evolution of . For ZTF18abauprj, we see an upwards evolution and the converse for ZTF19aatlmbo, implying that there is not a singular strict evolutionary trend for such features. However, when looking at the global evolution of the sample, we observe a dearth in the higher velocity separation spectra as we approach maximum light, with all the separations from HVF spectra after d clustering below 5000 km s-1. This indicates more separated HV components tend to fade away at earlier phases compared to those that are more entangled with their PV counterpart.
4.3 Defining a low-bias sample
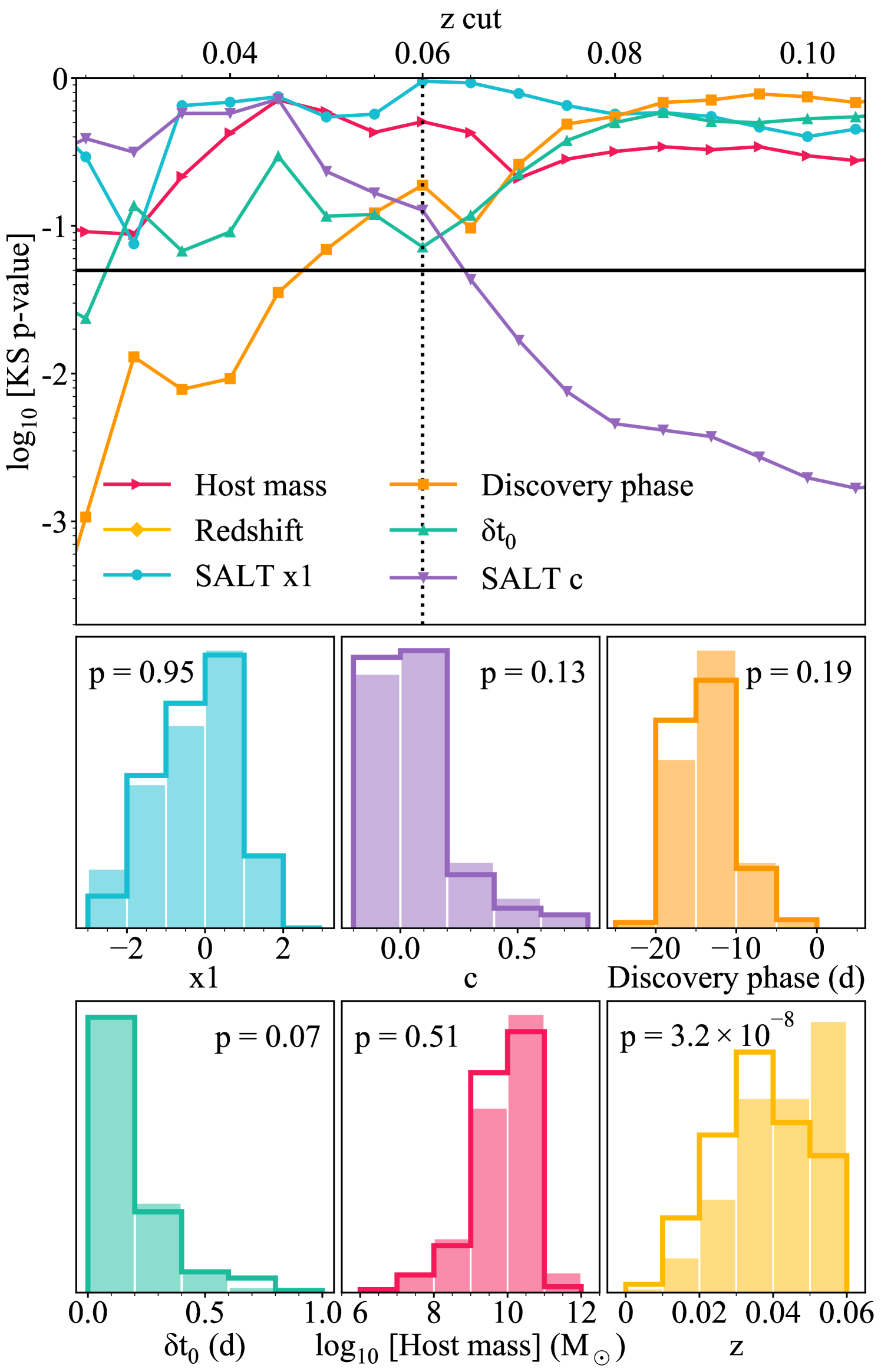
In order to analyse global properties of SNe Ia containing Si ii HVFs, we are required to understand and mitigate the potential biases present in our sample that make it unrepresentative of the global SN Ia population. To this end we define a ‘control sample’ as the 994 SNe Ia from the DR2 volume-limited (z 0.06) sample presented in Rigault et al. (2024). At this point we also remove any objects from our sample of 307 SNe that did not pass the initial suggested cuts outlined in Sect. 2.1 (fit probability , , , d), reducing our ‘base sample’ to 261 SNe Ia. Through Kolmogorov-Smirnov (KS) tests between this base sample and the control sample, we can identify parameters in which our sample exhibits a significant level of bias and then eliminate these by way of a redshift-based cut. KS p-values below the threshold of 0.05 signify that the difference between the two samples is statistically unlikely to have occurred simply by chance, and points to them coming from separation populations.
The top panel of Fig. 10 presents these KS-test results for a number of measurements between the control sample and the base 261 SNe sample after imposing different redshift cuts, e.g., the data point at , corresponds to the KS-test between the base sample limited to SNe Ia with and the full control sample. The parameters investigated here are the SALT2 stretch and colours parameters, and , the phase of first photometric detection, the uncertainty in the date of maximum light (), the host galaxy mass (measurements from Smith et al. in prep), and the host galaxy redshift (not shown on plot). Our base sample of 261 SNe compared to the control sample has KS p-values that are greater than our bias threshold of 0.05 in all parameters for all redshift cut values, except and host redshift. As we introduce more restrictive redshift cuts to our sample, we see the KS p-values for rise, until it crosses our threshold to be considered low bias at a redshift cut of z = 0.06.
The comparison of the redshift distribution between the base and control samples exhibits such small p-values - for all potential redshift cuts - that it falls below the y-axis scaling of the plot in Fig. 10. This difference is not surprising at redshift cuts either far above or far below that of the control sample (z = 0.06). With a redshift cut equal to that of the control sample we see that the difference between the populations is that our sample peaks at lower redshifts, most likely due to the apparent brightness required to obtain a high enough SNR spectrum pre-peak to enter our sample. The redshift distribution describes the geometric distribution of our objects in space, with the intrinsic physics of the objects described by the other parameters. Therefore, the bias in the redshift distribution should not impact our results given that we observe no statistically significant bias in the other parameters. We consequently place a cut at z = 0.06, leaving us with 210 spectra from 190 SNe from which to investigate global HVF properties. The distributions of these parameters in this low-bias cut sample can be seen as step plots in the bottom panels of Fig. 10 along with the control sample as the bars.
4.4 Parameter distributions
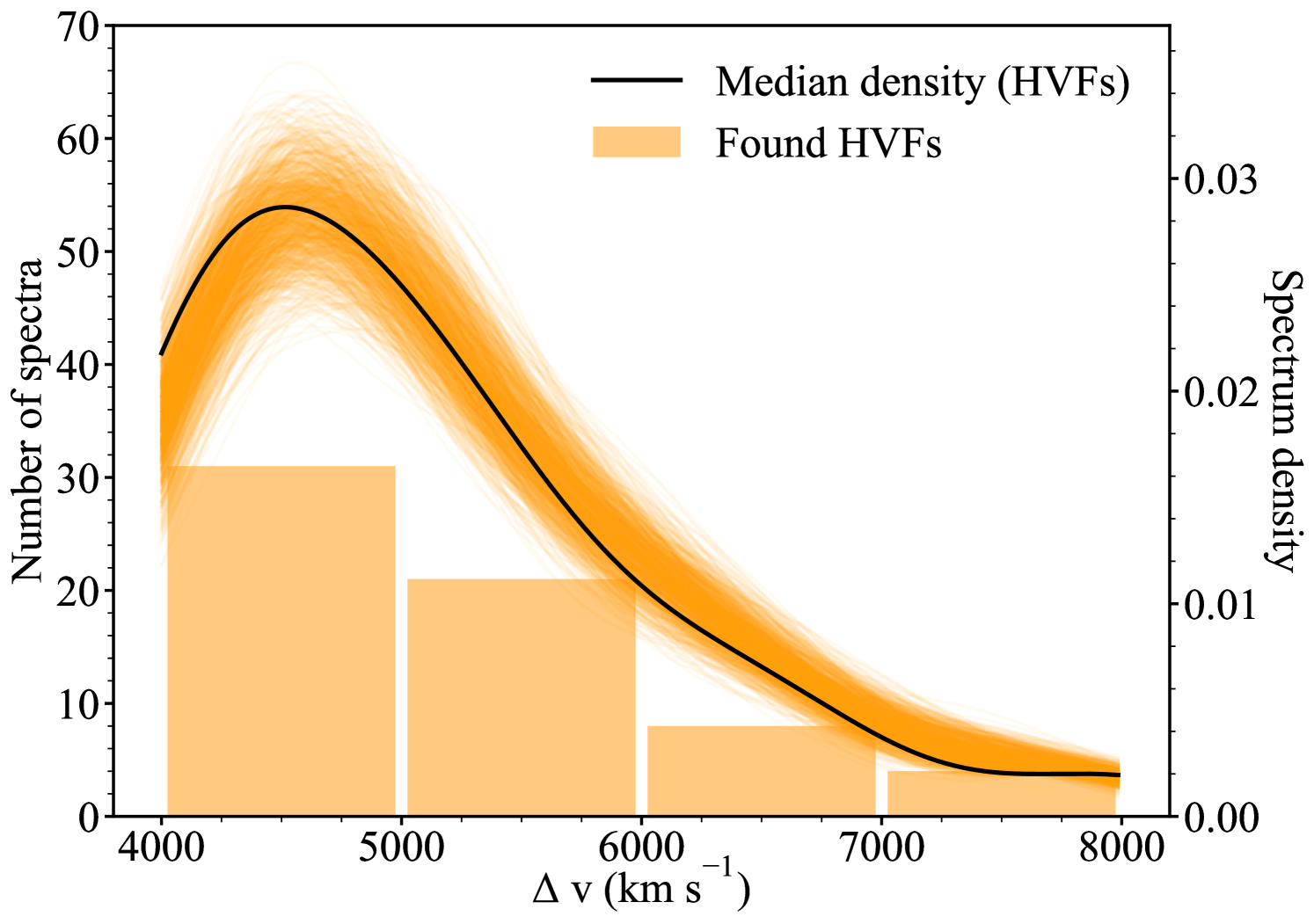
In Fig. 11 we present the distribution of velocity separations found in the 64 HVF spectra of the low-bias sample as the solid bar histogram. In general we observe a distribution skewed towards smaller velocity separations with very few spectra showing the extreme separations of 8000 km s-1. As seen in Fig. 3 our classification method is very sensitive to the larger velocity separations, however its detection efficiency drops off as the features encroach on one another and become increasingly entangled. As an example, we have a true-positive rate of 25% for features with SNR 8 and dispersion 2 Å/pix that possess a velocity separation of 4000 km s-1, implying that for every one spectrum that we identify with this parameter set, we miss three others; the true value is the number of identified targets divided by the fractional true-positive rate. Therefore, we can draw efficiency values from our 3D GP interpolation of the true-positive rates to scale the distribution of velocity separations on a spectrum-by-spectrum basis. This is first performed using the measured values of velocity separation, for which a Gaussian KDE of the probability density function (PDF) can be seen in Fig. 11 as the black solid line. In order to probe the potential variation of this distribution we employ a Monte-Carlo method, sampling each of the velocity separations in the sample from their individual distributions - described by their measured medians and upper and lower uncertainties - before then performing the detection efficiency scaling with the resulting values. This procedure is repeated 1000 times with each of these PDFs plotted as a faint orange line in Fig. 11. These PDFs are all multiplied by the number of spectra that they represent and therefore, represent spectrum densities instead of probabilities.
In order to probe the potential variation of this distribution we employ a Monte-Carlo method, sampling each of the velocity separations in the sample from their individual distributions - described by their measured medians and upper and lower uncertainties - before then performing the detection efficiency scaling with the resulting values. This procedure is repeated 1000 times with each of these PDFs plotted as a faint orange line in Fig. 11. In each iteration we account for the variation due to false positives by randomly reclassifying some HVF spectra with km s-1 as non-HVF in accordance with our adopted conservative false positive rate of 2%. These final PDFs are all multiplied by the number of spectra that they represent and therefore, represent spectrum densities instead of probabilities.
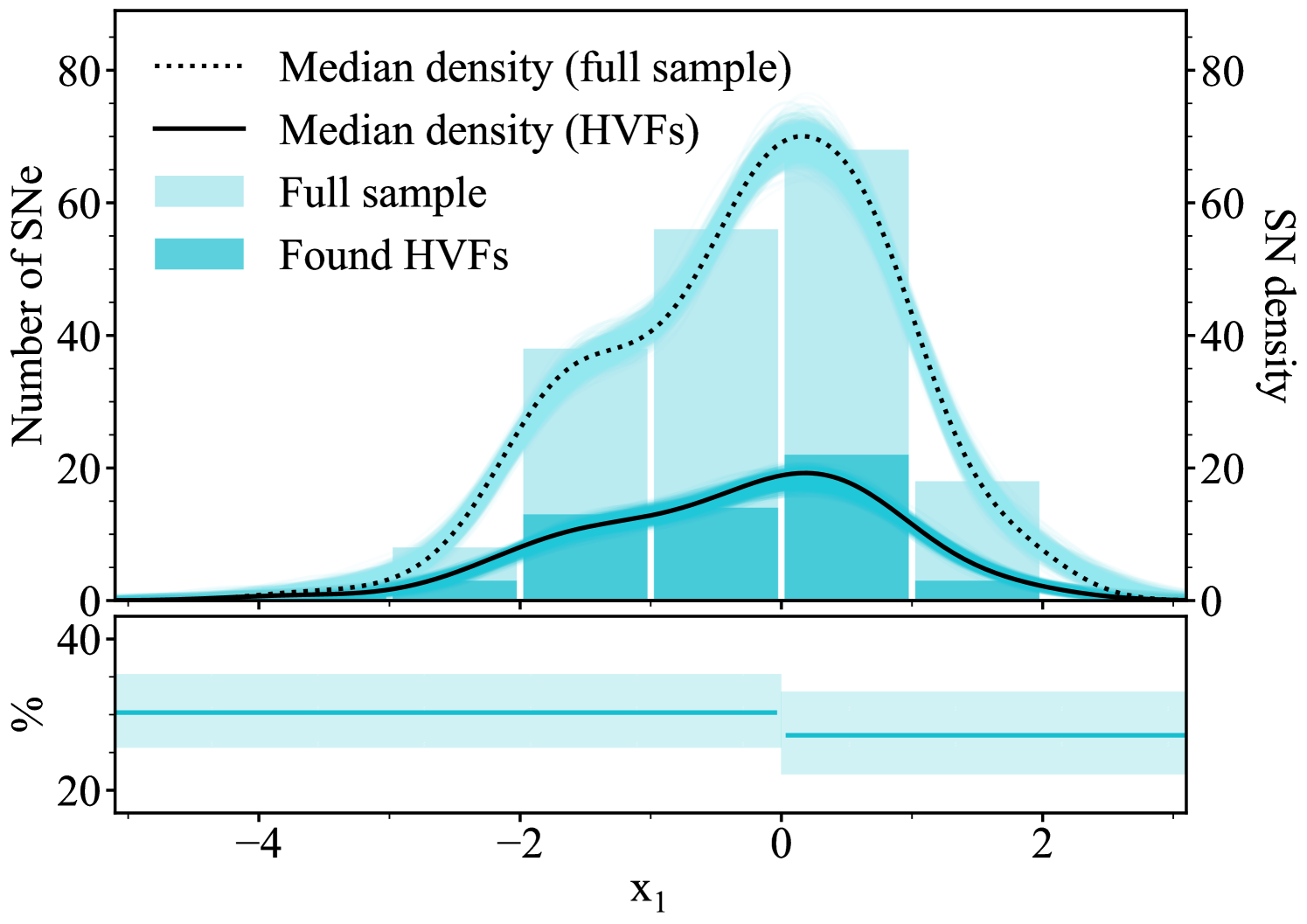
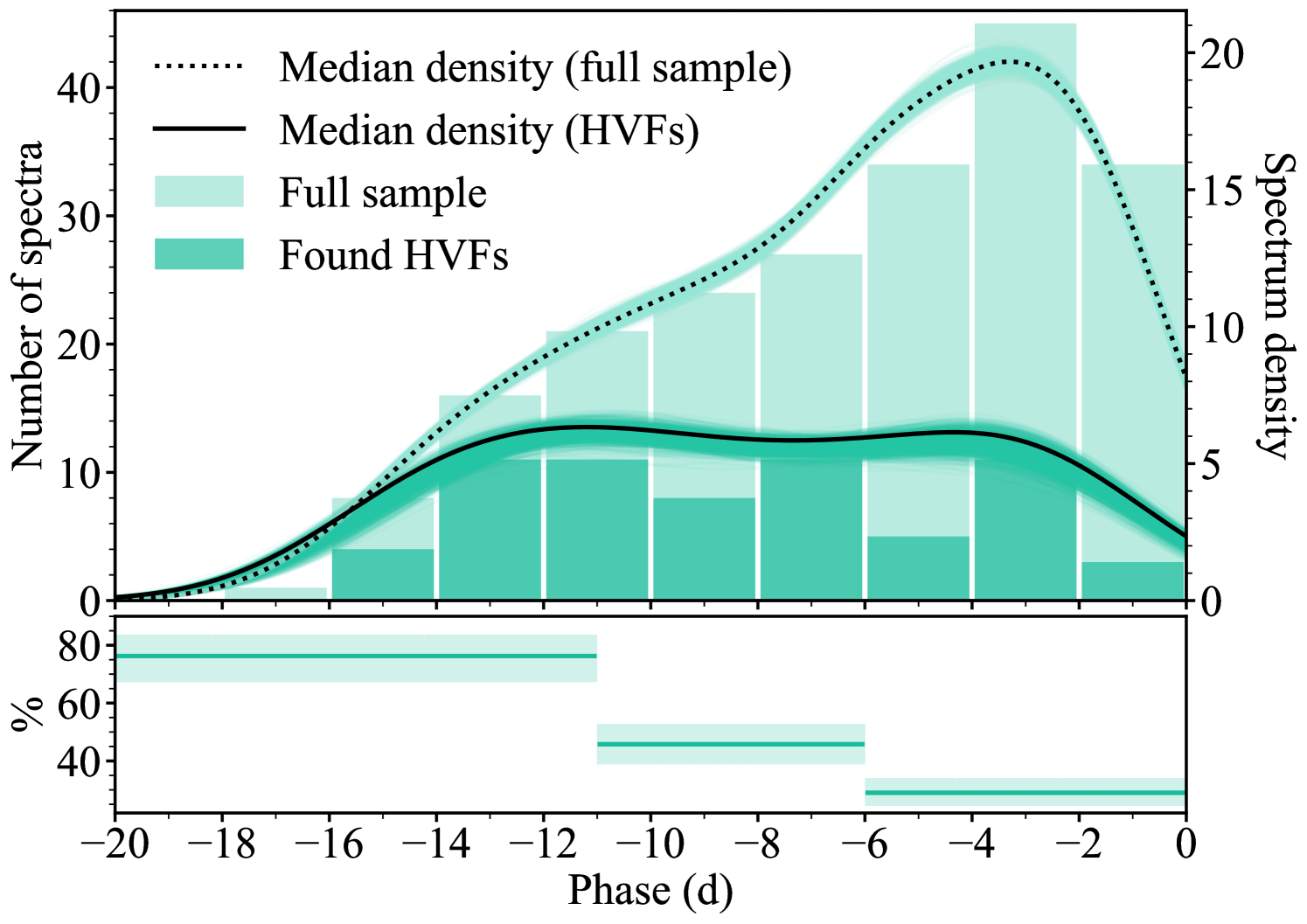
Figure 12 presents the phase distribution of the spectra displaying HVF against our full low-bias sample. The full sample is presented as the faint bars with the HVF spectra as the solid bars. As before, we perform the detection efficiency scaling on a spectrum-by-spectrum basis and plot the resulting density function from the velocity separation values as the solid black curve. The spectrum density function of the full phase distribution is plotted as the dotted black line. As for the velocity separation analysis, we perform Monte-Carlo sampling for these two phase distributions, randomly reclassifying some HVF spectra with km s-1 as non-HVF in accordance with the false positive rate and drawing velocity separations and phases from the corresponding individual distributions to calculate new PDFs. In each of these 1000 iterations we also integrate over three phase bins to calculate the percentage of spectra exhibiting a Si ii HV component. These three regions are divided up to each hold 1/3 of the 64 HVF spectra from the low-bias sample, giving bins for 11 d, to d and 6 d. The percentages of HVF spectra for these three phase ranges are shown in the bottom panel of Fig. 12 along with the shaded regions representing 68% confidence intervals calculated via the Clopper-Pearson method. These calculations indicate that we find Si ii HV components in 76% of spectra before d, 46% of spectra between and d, and 29% of spectra between d and maximum light. If we were to use the original detection efficiencies before introducing the cuts to only consider simulations with and Å (see Section 4.1), we calculate slightly higher percentages of 83%, 49%, and 32% for these three phase intervals. Therefore, Si ii HV components are close to 2.5 times more common at early phases, but still appear in approximately one third of spectra in the week before maximum light.
4.5 Light curve observables and host measurements
In Fig. 13 we present the distributions of the SALT2 light curve parameter for the SNe Ia in our full low-bias sample and only those showing evidence of HVFs as the faint and solid histograms, respectively. This information is then displayed in the form of SN density functions for the full sample (dotted) and those for which we have a spectrum with an identified HVF (solid). As for the and phase parameters before, we perform a Monte-Carlo sampling of the individual measurements over 1000 iterations to assess the amount of variation in these density curves accounting for the estimated false positive rate and uncertainties in the values. For each of these iterations, we integrate under the two density curves over two regions ( and ) and calculate the percentage of SNe exhibiting HV components in the Si ii . As visible in the bottom panel of Fig. 13, these two percentages (30% and 27%) are consistent with one another and support the idea of HVFs being ubiquitous across the SN Ia population. As before for the phase percentages, these uncertainties represent 68% confidence intervals.
As seen in Fig. 12, Si ii HVFs are more prevalent at earlier phases and there is a significant decrease in the percentage of SN Ia spectra displaying HVF features as the phase approaches maximum light. By cutting the sample and repeating these percentage calculations with only the earliest phases, we can test the impact of this phase dependence on any potential trend with . We introduce a phase cut at d - the median HVF spectral phase - and recalculate the rates of occurrence in HVF in low and high SNe Ia at these earlier phases as 43% () and 56% ( ). While the difference between these two percentages is slightly larger than before (and in the opposite direction), they still overlap in the 1 uncertainty region and therefore support the idea of HVF ubiquity.
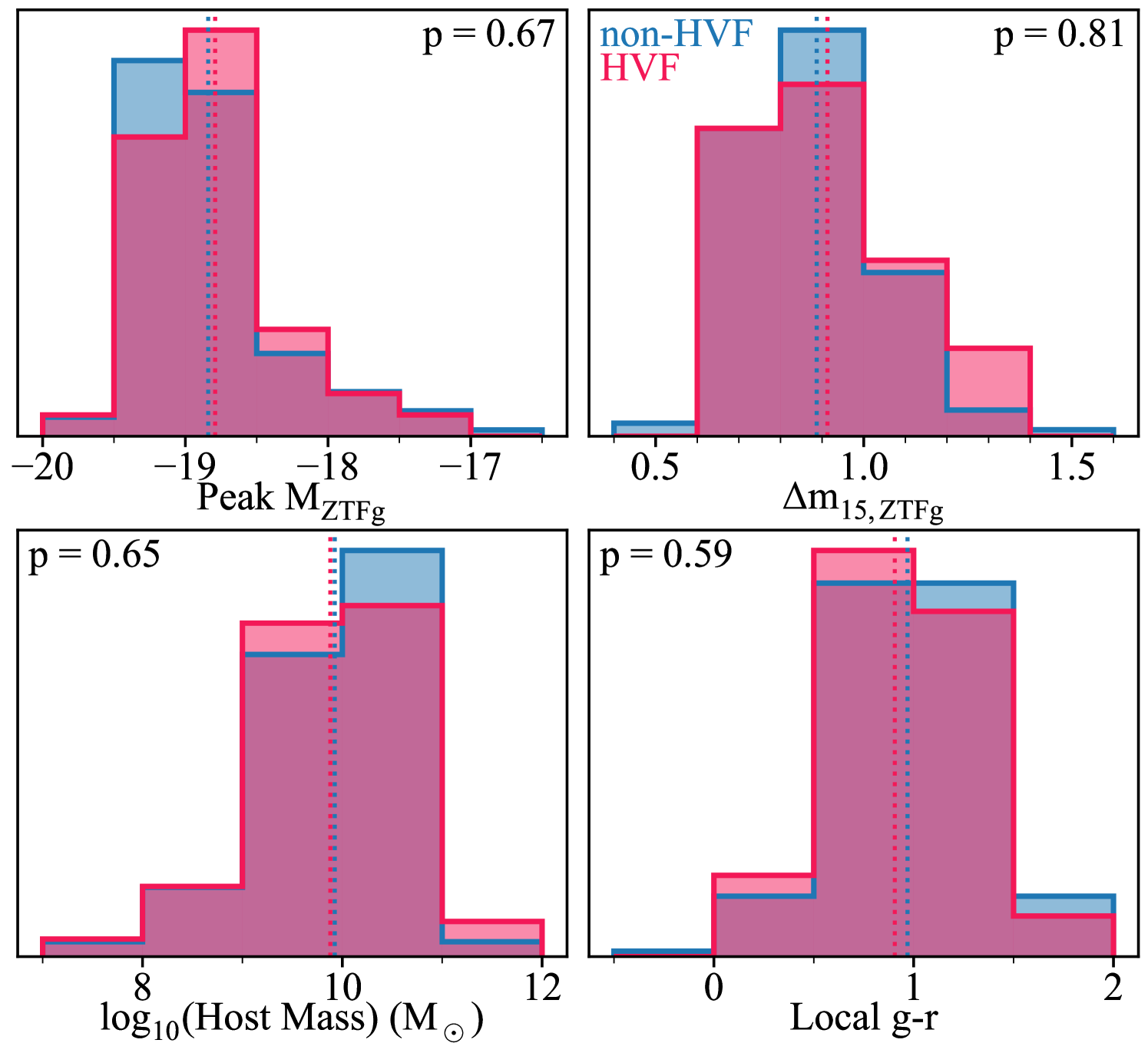
We also investigated the relationship between the presence of HVFs and light-curve parameters (peak absolute ZTFg-band magnitude, the g-band decline rate in 15 days post maximum, m15,ZTFg) measured from GP fitting in Dimitriadis et al. (2024). These are shown in the top panels of Fig. 14. We employ KS tests to quantify the likelihood of the two populations hailing from the same parent population. Resulting p-values that fall below the threshold of 0.05 indicate that the difference between the two samples for a given measurement is unlikely to have occurred simply by chance, and may point to a physical underlying distinction. We observe no significant difference between the HVF and non-HVF populations in terms of the peak ZTFg-band absolute magnitude and m15 parameters with the p values as 0.67 and 0.81 respectively. This again supports the ubiquity of these features across the Ia population.
The host galaxy mass and local g-r colour (Smith et al. in prep.) are shown in the bottom panels of Fig. 14. The p values for the host mass and local colour distributions of the HVF and non-HVF samples are large relative to the 0.05 threshold, with values of 0.65 and 0.59, respectively, again consistent with a lack of a difference in the local environment between SNe Ia with and without a Si ii HVF.
As before for investigating trends with , we repeated these statistical tests exclusively with spectra before d. We once again find large p-values for peak absolute magnitude and m15 in the ZTFg-band (0.91 and 0.52) as well as for the host galaxy mass and local g-r colour (1.0 and 0.94), indicating no difference between the HVF and non-HVF populations in these observables.
5 Discussion
In Section 5.1, we discuss our results in the context of the results of the literature, particularly those of Silverman et al. (2015). In Section 5.2 we investigate the potential false classification rates of the ‘Wang’ (Wang et al., 2009) and the ‘Branch’ (Branch et al., 2006, 2009), classification schemes if HVFs are not taken into account. Finally, we compare our velocity distributions to hydrodynamical explosion models in Section 5.3.
5.1 Comparison to literature
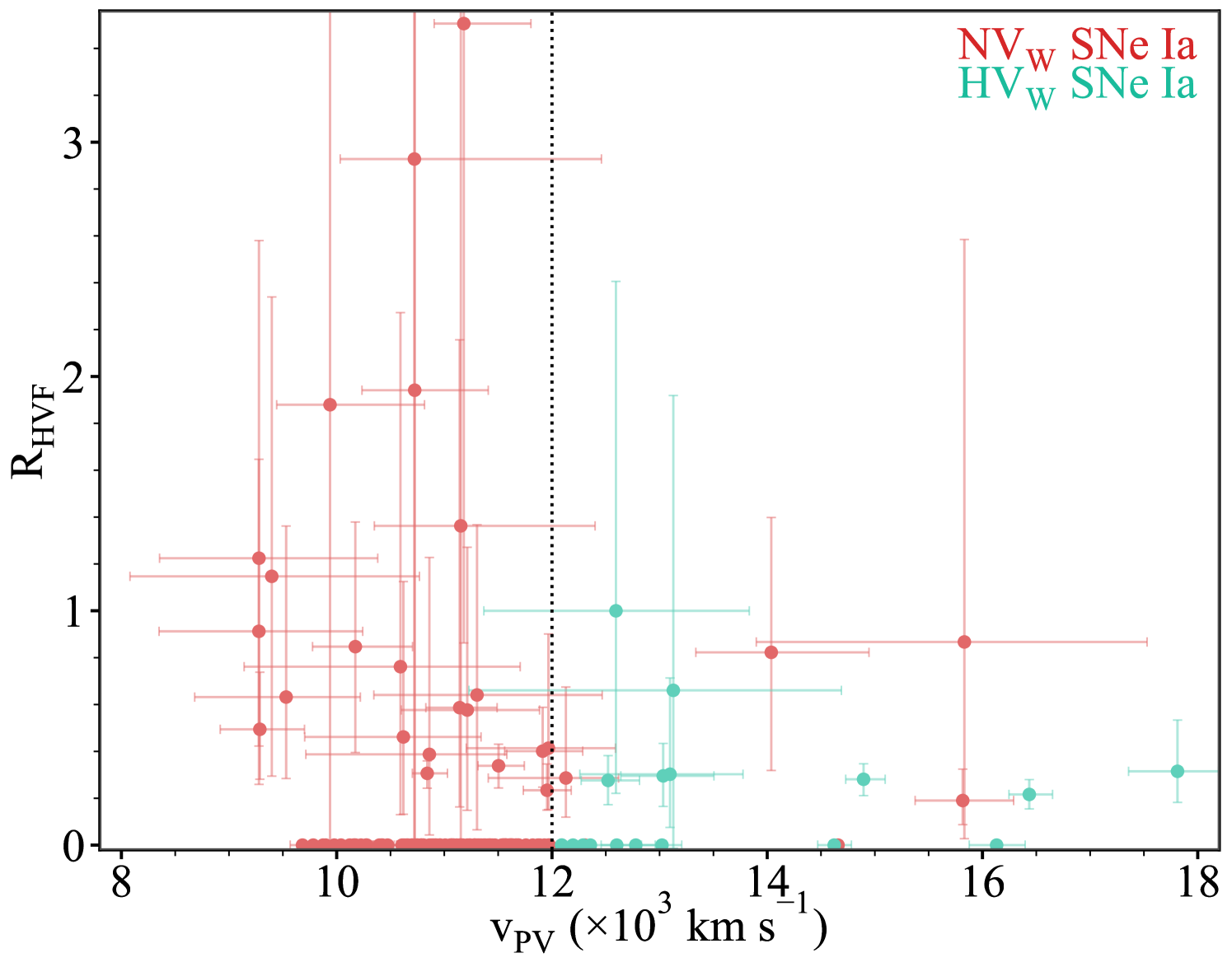
Silverman et al. (2015) investigated the properties of SNe Ia both with and without HVF in the context of the velocity-based classification scheme of Wang et al. (2009). The ‘Wang classification scheme’ divides objects into normal velocity (NV) and high velocity (HV) subclasses depending on whether the photospheric velocity (measured from the Si ii feature) is less than or greater than 11800 km s-1 around peak (5 to 5 d), respectively. We chose to add the ‘W’ subscript here to differentiate between the high-velocity Wang subclass (HV) and the high-velocity components (HV). While the cutoff of 11800 km s-1 was employed by Silverman et al. (2015), we chose to adopt a cutoff of 12000 km s-1 for consistency with other ZTF DR2 studies (Burgaz et al., 2024). Our Wang classifications are drawn from the latest spectrum we have for each object. In the case of the HV class, only spectra later that 5 d were used. However, for any object for which the latest pre-peak spectrum has PV km s-1, regardless of phase, we denote it as NV as the photospheric velocity is not expected to increase and the objects will still have PV km s-1 around peak. These classifications are then augmented by classifications from (Burgaz et al., 2024) for which they examined a slightly later phase range of 5 to 5 d with respect to peak brightness.
Figure 15 presents the pEW ratio, R, against the photospheric velocity of the Si ii feature for the low-bias sample of 190 SNe Ia. When investigating the same parameters, Silverman et al. (2015) found a dearth of NV SNe (PV km s-1) exhibiting HVFs in the Si ii (R 0), with these features found more predominantly in HV SNe. Contrary to this, we find HVFs in 26 of the NV classified objects in our low-bias sample (36 in the full sample), largely populating the empty region of the parameter space seen by Silverman et al. (2015). An increase in R with increasing photospheric velocity was also observed by Silverman et al. (2015). While this correlation makes intuitive sense for the evolution of individual objects, with R and photospheric velocity both decreasing over time, we observe no such global correlation in Fig. 15. As before with the lack of a global downwards trend in the middle panel of Fig. 9, this indicates that the onset of the R evolution begins at different phases for different objects.
5.2 Wang and Branch reclassifications
As described above, Wang classifications (NV vs. HV) are generally measured using the Si ii photospheric velocity in the phase range 5 to 5 d with respect to peak. However, the specific measurement of the photospheric velocity will change depending upon whether we employ a single- or a double-velocity component model. Historically this feature has been treated as a single component around peak, believed to be free of any HV components. However, our study, as well as the results from Silverman et al. (2015), suggests that HV components might be more common at these phases (later than 5 d) than previously thought, with one third of SN Ia spectra between 5 d and peak displaying a HVF. Therefore, we pose the question, if in these large spectroscopic studies we were to consider and account for HV Si ii absorption close to maximum light, what percentage of the HV classifications would be overturned in favour of a NV subtype?
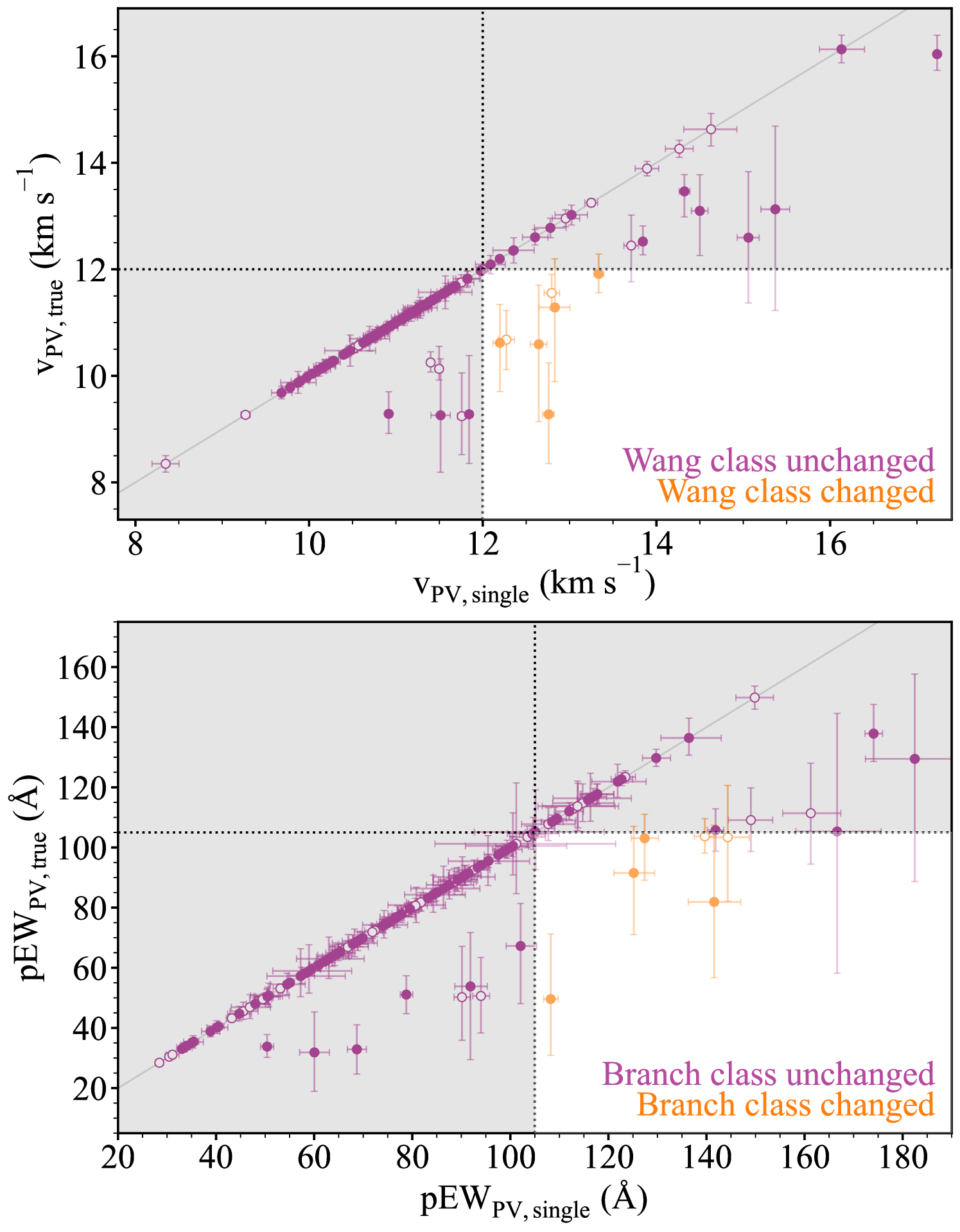
In the top panel of Fig. 16, we compare the photospheric velocity from the single component fits against the ‘true’ photospheric velocities (i.e. single component fits for spectra without a HVF, and double component fits for spectra with a HVF). All spectra identified to have a HV component exhibit lower photospheric velocities in their two-component fits as would be expected. We indicate the Wang classification cut off velocity of 12000 km s-1 by the vertical and horizontal dotted lines, highlighting the region in the bottom right in which the objects would be classified as HV with the single component model, but as NV by the double-component model (orange points). When considering the 85 objects from the low-bias sample which possess a spectrum later than 5 d, there are five SNe Ia (seven of the 150 SNe from the full sample with a spectrum later than 5 d), indicating that % of HV classifications (% for the full sample) before peak would be incorrect if we were to not consider HV components. These uncertainties represent 68% confidence intervals and are calculated as binomial with the Clopper-Pearson interval. Such large uncertainties are the result of low number statistics and while this leaves the percentages fairly unconstrained, this suggests that HVF components could cause a significant rate of false HV classifications in the 5 d before maximum light.
We similarly perform this analysis with respect to the Branch classification scheme (Branch et al., 2006, 2009), which divides up the SN Ia population based upon the equivalent widths of the Si ii and Si ii lines. Broad line SNe Ia (BL) exhibit pEW Å with a pEW Å. While we have no information on the Si ii , we can examine the effects of HV components upon the measured Si ii pEW. The bottom panel of Fig. 16 displays the measured photospheric pEW coming from the single component fits against the ‘true’ photospheric pEWs (as above for the Wang analysis). The cutoff width at 105 Å is indicated by the dotted lines, with the orange points once again corresponding to those spectra that would receive an incorrect classification if we were to not consider the HV components. In the Branch scheme parameter space there are four SNe that are misclassified (six for the full sample), resulting in % of incorrect BL classifications (% for the full sample) with respect to the Si ii line. In their sample of BL SNe Ia, Yarbrough et al. (2023) also found the BL population to have higher Si ii velocities than their CN counterparts, further supporting this idea as the HV components would also cause an offset in measured single component velocities to higher values. These uncertainties represent 68% intervals as before for the Wang reclassifications, and once again the low number of datapoints results in loosely constrained percentages.
With generally smaller velocity separations in this phase range around peak, false positives are more probable and could have the inverse effect in both these cases. Incorrectly employing a double-component model to a Si ii feature with no HVF would artificially decrease the photospheric velocity and width, potentially resulting in HV SNe being classified as NV and Branch BL SNe being missed. Therefore, the misclassification rates calculated here represent upper limits.
5.3 HVF origins
While the specific origins and formation channels of these HV components of the Si ii feature remain unclear, they provide clear evidence of intermediate-mass element material in the upper ejecta of the majority of SNe Ia. Regardless of the explosion mechanism or progenitor channel, any model aiming to reproduce these features will require some fraction of silicon at the corresponding high velocities.
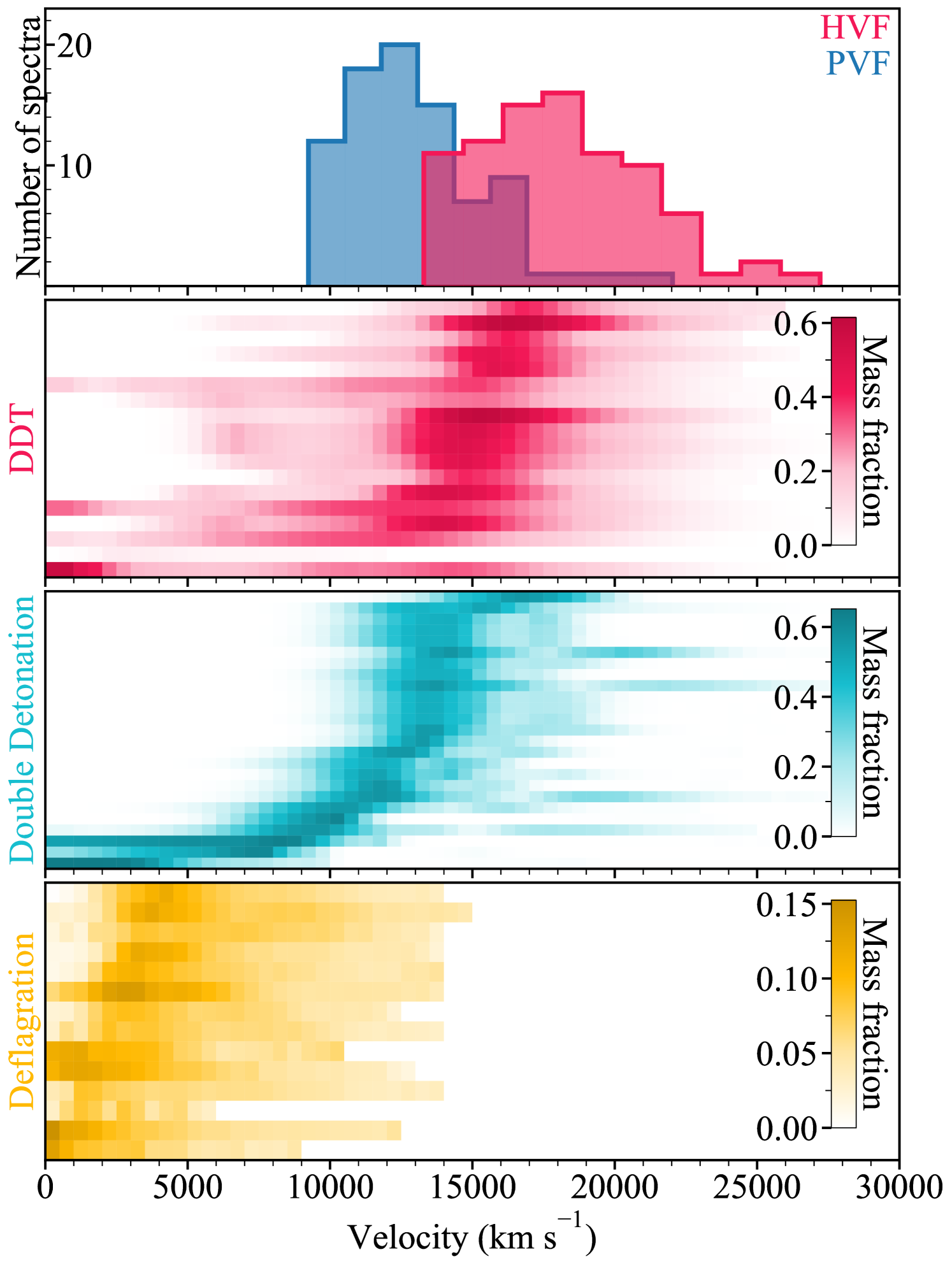
In Fig. 17 we present the measured velocity distributions for the PV and HV components for the HVF classified spectra in our sample, with the Si-abundance profiles from a number of explosion models from the Heidelberg Supernova Model Archive (HESMA; Kromer et al., 2017), arising from three different explosion mechanisms. In pink we plot the delayed-detonation (DDT) models (Röpke et al. 2012; Seitenzahl et al. 2013; Ohlmann et al. 2014) arising from an initial subsonic deflagration that later transitions to a supersonic detonation. In blue, we plot the double-detonation models (Sim et al. 2012; Gronow et al. 2020; Gronow et al. 2021), which involves a detonation in a helium shell atop the white dwarf, sending a shock-wave inwards which converges in - and subsequently detonates - the core. Finally, in yellow we show the silicon abundances from the pure subsonic deflagration models (Fink et al. 2014; Kromer et al. 2015).
As expected, the pure deflagration models are very homogeneous in nature, possessing very flat distributions of the elements in the model. As a result of the low energy they also do not produce material moving as velocities faster than around 15000 km s-1, and therefore, are incapable of producing the HV - and many of the PV - components that we see in the DR2. The DDT and double-detonation models possess more layered ejecta structures, with peaks in the silicon abundance profiles in the 10000 to 15000 km s-1 range. The majority of these models also exhibit silicon at velocities covering the full HVF velocity distribution. The formation of such HVFs is dependant upon the ionisation profile, which in turn is dependant upon not only the abundances, but also the density profile of the plasma. This will be the focus of a follow-up modelling study with a handful of well-sampled HVF objects (Harvey et al. in prep.).
We also note here that the models presented in Fig. 17 are designed to reproduce the overall SN Ia photometric and spectroscopic evolution coming from the primary white dwarf itself. These HVFs may instead be the result of environmental components such as CSM, which are not included in the models. Through the spectroscopic modelling of the HVFs exhibited by SN 1999ee, Mazzali et al. (2005b) explored the ejecta conditions needed to recreate the evolution. In terms of an abundance enhancement, they required a region of the upper ejecta to be dominated by silicon and calcium (90 and 10 per cent respectively), which is hard to justify in terms of nuclear burning. Therefore, they concluded that the density enhancements in these regions to be a more plausible reason for the HVFs. In Mazzali et al. (2005a) they suggested the sweeping up of surrounding CSM to be responsible for the line-forming region higher up in the ejecta, pointing to a thick disk and/or high density CSM environment produced by a companion wind. They also proposed angular fluctuations as a potential cause of density enhancement, with HVFs being the result of three-dimensional effects. This was further supported by Tanaka et al. (2006) who investigated various density enhancement geometries and degrees of photospheric coverage to produce the observed HVF population. This multidimensional requirement is supported by the observed polarisation difference between the HV and PV components of the Ca NIR triplet in SN 2001el (Wang et al. 2003; Kasen et al. 2003) and in the Si ii of SN 2019ein/ZTF19aatlmbo (Patra et al., 2022)
6 Conclusions
In this work we conducted a thorough search for Si ii high-velocity components within the ZTF Cosmology Data Release 2 by way of MCMC fitting and model selection with the Bayesian Information Criterion. Through simulations, we quantified the detection efficiency over the spectral quality (SNR and dispersion), as well as for simulated velocity separation between the two components. These simulations were also employed to test the accuracy of the estimated uncertainties and identify and correct the biases in the model parameters. Within our sample of 329 spectra we identified 85 Si ii HV components. We subsequently defined a low-bias subsample with a redshift cut at 0.06 (210 spectra from 190 SNe) which was then used to calculate rates. Conclusions from the analysis are as follows:
-
1.
76% of spectra before 11 d exhibit HVF in the Si ii feature. This percentage drops as we approach maximum light with 29% of spectra showing HVFs after d.
-
2.
For individual objects, we observe a decrease in the HVF strength ratio R with time, corresponding to the fading away of the HV component to leave just the PV absorption. This evolution occurs at different phases for different objects and therefore, globally we see a relatively uniform distribution of R with phase.
-
3.
HV components with larger separations from their PV counterparts fade at earlier epochs, leaving just the smaller separations as we approach maximum light. We do not observe consistent evolution from object to object, with some increasing, others decreasing, and some remaining constant.
-
4.
We see no tendency of Si ii HVFs to occur in objects with high or low SALT values, supporting the proposed ubiquity of HVFs across the SN Ia class.
-
5.
Comparison of a low-bias subsample of our targets with the volume-limited DR2 sample (defined as a control sample) shows no statistical difference between the HVF and non-HVF populations in ZTFg-band peak magnitude and (ZTFg), host mass, or local host g-r colour.
-
6.
We do not reproduce the finding from Silverman et al. (2015) that Wang classification scheme HV objects are more likely to exhibit Si ii HVFs, with a fairly significant portion of our HVF spectra coming from NV objects.
-
7.
The fitting of Si ii profiles without consideration of contributions from potential HV components may cause a number of false HV classifications. We calculate an upper limit for the false HV classification rate of % in the phase range 5 to 0 d.
-
8.
Similarly for the Branch classification scheme, we find that up to % of broad line (BL) classifications drawn from spectra in the phase range 5 to 0 d are the result of HV components making for broader line profiles.
Acknowledgements.
The research conducted in this publication was funded by the Irish Research Council under grant number GOIPG/2020/1387. K.M., U.B., G.D., M.D., and J.T. acknowledge support from EU H2020 ERC grant no. 758638. L.G. acknowledges financial support from the Spanish Ministerio de Ciencia e Innovación (MCIN), the Agencia Estatal de Investigación (AEI) 10.13039/501100011033, and the European Social Fund (ESF) ”Investing in your future” under the 2019 Ramón y Cajal program RYC2019-027683-I and the PID2020-115253GA-I00 HOSTFLOWS project, from Centro Superior de Investigaciones Científicas (CSIC) under the PIE project 20215AT016, and the program Unidad de Excelencia María de Maeztu CEX2020-001058-M. Y.-L.K. has received funding from the Science and Technology Facilities Council [grant number ST/V000713/1]. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement n°759194 - USNAC). This work has been supported by the research project grant “Understanding the Dynamic Universe” funded by the Knut and Alice Wallenberg Foundation under Dnr KAW 2018.0067, Vetenskapsrådet, the Swedish Research Council, project 2020-03444. Based on observations obtained with the Samuel Oschin Telescope 48-inch and the 60-inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project. ZTF is supported by the National Science Foundation under Grant No. AST-1440341 and a collaboration including Caltech, IPAC, the Weizmann Institute of Science, the Oskar Klein Center at Stockholm University, the University of Maryland, the University of Washington, Deutsches Elektronen-Synchrotron and Humboldt University, Los Alamos National Laboratories, the TANGO Consortium of Taiwan, the University of Wisconsin at Milwaukee, and Lawrence Berkeley National Laboratories. Operations are conducted by COO, IPAC, and UW. This work was supported by the GROWTH project (Kasliwal et al., 2019) funded by the National Science Foundation under Grant No 1545949. The SALT classification spectra of SN 2020lil and SN 2020pst were obtained through Rutgers University program 2020-1-MLT-007 (PI: S. W. Jha). Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programmes 199.D-0143, 1103.D-0328, and 106.216C.009. The authors thank Michael Tucker for advising in the quality and inclusion of SNIFS/UH-88 spectra from the SCAT survey. Based on observations collected at Copernico 1.82m telescope (Asiago Mount Ekar, Italy) INAF - Osservatorio Astronomico di Padova. The data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOT. Some of the data presented herein were obtained at Keck Observatory, which is a private 501(c)3 non-profit organization operated as a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the Native Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. Based on observations obtained with the Apache Point Observatory 3.5-meter telescope, which is owned and operated by the Astrophysical Research Consortium. This article is based on observations made with the Gran Telescopio Canarias operated by the Instituto de Astrofisica de Canarias, the Isaac Newton Telescope, and the William Herschel Telescope operated by the Isaac Newton Group of Telescopes, the Italian Telescopio Nazionale Galileo operated by the Fundacion Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica), and the Liverpool Telescope operated by Liverpool John Moores University with financial support from the UK Science and Technology Facilities Council. All these facilities are located at the Spanish Roque de los Muchachos Observatory of the Instituto de Astrofisica de Canarias on the island of La Palma. Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere. This work makes use of observations from the Las Cumbres Observatory global telescope network. Based on observations obtained at the international Gemini Observatory, a program of NSF’s NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation on behalf of the Gemini Observatory partnership: the National Science Foundation (United States), National Research Council (Canada), Agencia Nacional de Investigación y Desarrollo (Chile), Ministerio de Ciencia, Tecnología e Innovación (Argentina), Ministério da Ciência, Tecnologia, Inovações e Comunicações (Brazil), and Korea Astronomy and Space Science Institute (Republic of Korea). Based on observations obtained at the Southern Astrophysical Research (SOAR) telescope, which is a joint project of the Ministério da Ciência, Tecnologia e Inovações (MCTI/LNA) do Brasil, the US National Science Foundation’s NOIRLab, the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU). This paper includes data gathered with the 6.5 meter Magellan Telescopes located at Las Campanas Observatory, Chile. These results made use of the Lowell Discovery Telescope (LDT) at Lowell Observatory. Lowell is a private, non-profit institution dedicated to astrophysical research and public appreciation of astronomy and operates the LDT in partnership with Boston University, the University of Maryland, the University of Toledo, Northern Arizona University and Yale University. The Large Monolithic Imager was built by Lowell Observatory using funds provided by the National Science Foundation (AST-1005313). The upgrade of the DeVeny optical spectrograph has been funded by a generous grant from John and Ginger Giovale and by a grant from the Mt. Cuba Astronomical Foundation. Some of the observations reported in this paper were obtained with the Southern African Large Telescope (SALT). This work made use of the Heidelberg Supernova Model Archive (HESMA), https://hesma.h-its.org.References
- Aldering et al. (2002) Aldering, G., Adam, G., Antilogus, P., et al. 2002, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 4836, Survey and Other Telescope Technologies and Discoveries, ed. J. A. Tyson & S. Wolff, 61–72
- Allington-Smith et al. (2002) Allington-Smith, J., Murray, G., Content, R., et al. 2002, PASP, 114, 892
- Barnsley et al. (2012) Barnsley, R., Smith, R., & Steele, I. 2012, in Astronomical Society of the Pacific Conference Series, Vol. 461, Astronomical Data Analysis Software and Systems XXI, ed. P. Ballester, D. Egret, & N. P. F. Lorente, 517
- Bellm et al. (2019) Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002
- Bellm & Sesar (2016) Bellm, E. C. & Sesar, B. 2016, pyraf-dbsp: Reduction pipeline for the Palomar Double Beam Spectrograph, Astrophysics Source Code Library, record ascl:1602.002
- Benetti et al. (2005) Benetti, S., Cappellaro, E., Mazzali, P. A., et al. 2005, ApJ, 623, 1011
- Benn et al. (2008) Benn, C., Dee, K., & Agócs, T. 2008, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 7014, Ground-based and Airborne Instrumentation for Astronomy II, ed. I. S. McLean & M. M. Casali, 70146X
- Blagorodnova et al. (2018) Blagorodnova, N., Neill, J. D., Walters, R., et al. 2018, PASP, 130, 035003
- Blondin et al. (2011) Blondin, S., Mandel, K. S., & Kirshner, R. P. 2011, A&A, 526, A81
- Branch et al. (2009) Branch, D., Chau Dang, L., & Baron, E. 2009, PASP, 121, 238
- Branch et al. (2006) Branch, D., Dang, L. C., Hall, N., et al. 2006, PASP, 118, 560
- Brown et al. (2013) Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031
- Buckley et al. (2006) Buckley, D. A. H., Swart, G. P., & Meiring, J. G. 2006, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 6267, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed. L. M. Stepp, 62670Z
- Burgaz et al. (2024) Burgaz, U., Maguire, K., Dimitriadis, G., et al. 2024, arXiv e-prints, arXiv:2407.06828
- Buzzoni et al. (1984) Buzzoni, B., Delabre, B., Dekker, H., et al. 1984, The Messenger, 38, 9
- Cenko et al. (2006) Cenko, S. B., Fox, D. B., Moon, D.-S., et al. 2006, PASP, 118, 1396
- Cepa et al. (2000) Cepa, J., Aguiar, M., Escalera, V. G., et al. 2000, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 4008, Optical and IR Telescope Instrumentation and Detectors, ed. M. Iye & A. F. Moorwood, 623–631
- Childress et al. (2014) Childress, M. J., Filippenko, A. V., Ganeshalingam, M., & Schmidt, B. P. 2014, MNRAS, 437, 338
- Childress et al. (2013) Childress, M. J., Scalzo, R. A., Sim, S. A., et al. 2013, ApJ, 770, 29
- Clemens et al. (2004) Clemens, J. C., Crain, J. A., & Anderson, R. 2004, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 5492, Ground-based Instrumentation for Astronomy, ed. A. F. M. Moorwood & M. Iye, 331–340
- Crawford et al. (2010) Crawford, S. M., Still, M., Schellart, P., et al. 2010, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 7737, Observatory Operations: Strategies, Processes, and Systems III, ed. D. R. Silva, A. B. Peck, & B. T. Soifer, 773725
- Das et al. (2023) Das, K. K., Kasliwal, M. M., Fremling, C., et al. 2023, ApJ, 959, 12
- Dekany et al. (2020) Dekany, R., Smith, R. M., Riddle, R., et al. 2020, PASP, 132, 038001
- Dimitriadis et al. (2024) Dimitriadis, G., Burgaz, U., Deckers, M., et al. 2024, arXiv e-prints, arXiv:2409.04200
- Dimitriadis et al. (2022) Dimitriadis, G., Foley, R. J., Arendse, N., et al. 2022, ApJ, 927, 78
- Dressler et al. (2011) Dressler, A., Bigelow, B., Hare, T., et al. 2011, PASP, 123, 288
- Fink et al. (2014) Fink, M., Kromer, M., Seitenzahl, I. R., et al. 2014, MNRAS, 438, 1762
- Foreman-Mackey et al. (2013) Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306
- Gerardy et al. (2004) Gerardy, C. L., Höflich, P., Fesen, R. A., et al. 2004, ApJ, 607, 391
- Gobat (2022) Gobat, C. 2022, Asymmetric Uncertainty: Handling nonstandard numerical uncertainties, Astrophysics Source Code Library, record ascl:2208.005
- Graham et al. (2019) Graham, M. J., Kulkarni, S. R., Bellm, E. C., et al. 2019, PASP, 131, 078001
- Gronow et al. (2020) Gronow, S., Collins, C., Ohlmann, S. T., et al. 2020, A&A, 635, A169
- Gronow et al. (2021) Gronow, S., Collins, C. E., Sim, S. A., & Röpke, F. K. 2021, A&A, 649, A155
- Guy et al. (2007) Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11
- Hamuy et al. (2006) Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2
- Hatano et al. (1999) Hatano, K., Branch, D., Fisher, A., Baron, E., & Filippenko, A. V. 1999, ApJ, 525, 881
- Hook et al. (2004) Hook, I. M., Jørgensen, I., Allington-Smith, J. R., et al. 2004, PASP, 116, 425
- Hung et al. (2017) Hung, T., Gezari, S., Blagorodnova, N., et al. 2017, ApJ, 842, 29
- Kasen et al. (2003) Kasen, D., Nugent, P., Wang, L., et al. 2003, ApJ, 593, 788
- Kasliwal et al. (2019) Kasliwal, M. M., Cannella, C., Bagdasaryan, A., et al. 2019, PASP, 131, 038003
- Kim et al. (2022) Kim, Y. L., Rigault, M., Neill, J. D., et al. 2022, PASP, 134, 024505
- Kobulnicky et al. (2003) Kobulnicky, H. A., Nordsieck, K. H., Burgh, E. B., et al. 2003, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 4841, Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, ed. M. Iye & A. F. M. Moorwood, 1634–1644
- Kochanek et al. (2017) Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502
- Kromer et al. (2017) Kromer, M., Ohlmann, S., & Röpke, F. K. 2017, Mem. Soc. Astron. Italiana, 88, 312
- Kromer et al. (2015) Kromer, M., Ohlmann, S. T., Pakmor, R., et al. 2015, MNRAS, 450, 3045
- Lezmy et al. (2022) Lezmy, J., Copin, Y., Rigault, M., Smith, M., & Neill, J. D. 2022, A&A, 668, A43
- Maguire et al. (2014) Maguire, K., Sullivan, M., Pan, Y. C., et al. 2014, MNRAS, 444, 3258
- Marion et al. (2013) Marion, G. H., Vinko, J., Wheeler, J. C., et al. 2013, ApJ, 777, 40
- Masci et al. (2019) Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003
- Mazzali et al. (2005a) Mazzali, P. A., Benetti, S., Altavilla, G., et al. 2005a, ApJ, 623, L37
- Mazzali et al. (2005b) Mazzali, P. A., Benetti, S., Stehle, M., et al. 2005b, MNRAS, 357, 200
- McCarthy et al. (1998) McCarthy, J. K., Cohen, J. G., Butcher, B., et al. 1998, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 3355, Optical Astronomical Instrumentation, ed. S. D’Odorico, 81–92
- Miller & Stone (1993) Miller, J. S. & Stone, R. P. S. 1993, in , Santa Cruz, CA, Lick Observatory
- Nordin et al. (2011) Nordin, J., Östman, L., Goobar, A., et al. 2011, A&A, 526, A119
- Ohlmann et al. (2014) Ohlmann, S. T., Kromer, M., Fink, M., et al. 2014, A&A, 572, A57
- Oke et al. (1995) Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375
- Patra et al. (2022) Patra, K. C., Yang, Y., Brink, T. G., et al. 2022, MNRAS, 509, 4058
- Pedregosa et al. (2011) Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, Journal of Machine Learning Research, 12, 2825
- Perley (2019) Perley, D. A. 2019, PASP, 131, 084503
- Perlmutter et al. (1999) Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565
- Phillips (1993) Phillips, M. M. 1993, ApJ, 413, L105
- Piascik et al. (2014) Piascik, A. S., Steele, I. A., Bates, S. D., et al. 2014, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 9147, Ground-based and Airborne Instrumentation for Astronomy V, ed. S. K. Ramsay, I. S. McLean, & H. Takami, 91478H
- Prentice et al. (2018) Prentice, S. J., Maguire, K., Smartt, S. J., et al. 2018, ApJ, 865, L3
- Prochaska et al. (2020) Prochaska, J., Hennawi, J., Westfall, K., et al. 2020, The Journal of Open Source Software, 5, 2308
- Pskovskii (1977) Pskovskii, I. P. 1977, Sov. Ast., 21, 675
- Quimby et al. (2006) Quimby, R., Höflich, P., Kannappan, S. J., et al. 2006, ApJ, 636, 400
- Riess et al. (1998) Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009
- Rigault et al. (2019) Rigault, M., Neill, J. D., Blagorodnova, N., et al. 2019, A&A, 627, A115
- Rigault et al. (2024) Rigault, M., Smith, M., Goobar, A., et al. 2024, arXiv e-prints, arXiv:2409.04346
- Rockosi et al. (2010) Rockosi, C., Stover, R., Kibrick, R., et al. 2010, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 7735, Ground-based and Airborne Instrumentation for Astronomy III, ed. I. S. McLean, S. K. Ramsay, & H. Takami, 77350R
- Röpke et al. (2012) Röpke, F. K., Kromer, M., Seitenzahl, I. R., et al. 2012, ApJ, 750, L19
- Seitenzahl et al. (2013) Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013, MNRAS, 429, 1156
- Sharma et al. (2023) Sharma, Y., Sollerman, J., Fremling, C., et al. 2023, ApJ, 948, 52
- Silverman et al. (2012) Silverman, J. M., Kong, J. J., & Filippenko, A. V. 2012, MNRAS, 425, 1819
- Silverman et al. (2015) Silverman, J. M., Vinkó, J., Marion, G. H., et al. 2015, MNRAS, 451, 1973
- Sim et al. (2012) Sim, S. A., Fink, M., Kromer, M., et al. 2012, MNRAS, 420, 3003
- Smartt et al. (2015) Smartt, S. J., Valenti, S., Fraser, M., et al. 2015, A&A, 579, A40
- Smith et al. (2020) Smith, K. W., Smartt, S. J., Young, D. R., et al. 2020, PASP, 132, 085002
- Steele et al. (2004) Steele, I. A., Smith, R. J., Rees, P. C., et al. 2004, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 5489, Ground-based Telescopes, ed. J. Oschmann, Jacobus M., 679–692
- Stevenson et al. (2016) Stevenson, K. B., Bean, J. L., Seifahrt, A., et al. 2016, ApJ, 817, 141
- Tanaka et al. (2006) Tanaka, M., Mazzali, P. A., Maeda, K., & Nomoto, K. 2006, ApJ, 645, 470
- Taubenberger (2017) Taubenberger, S. 2017, in Handbook of Supernovae, ed. A. W. Alsabti & P. Murdin, 317
- Thomas et al. (2004) Thomas, R. C., Branch, D., Baron, E., et al. 2004, ApJ, 601, 1019
- Tonry et al. (2018) Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505
- Tucker et al. (2022) Tucker, M. A., Shappee, B. J., Huber, M. E., et al. 2022, PASP, 134, 124502
- Valenti et al. (2014) Valenti, S., Sand, D., Pastorello, A., et al. 2014, MNRAS, 438, L101
- Wang et al. (2003) Wang, L., Baade, D., Höflich, P., et al. 2003, ApJ, 591, 1110
- Wang et al. (2009) Wang, X., Filippenko, A. V., Ganeshalingam, M., et al. 2009, ApJ, 699, L139
- Yarbrough et al. (2023) Yarbrough, Z., Baron, E., DerKacy, J. M., et al. 2023, MNRAS, 521, 3873
Appendix A Supplementary photometry
Our initial light curve quality cut was employed as a general guideline to remove any supernovae from our sample with a poor corresponding SALT fit. A total of 2954 supernovae from the 3585 met this criteria. For completeness, these 2954 light curves were visually inspected, leading to the identification of 13 poorly sampled light curves which resulted in spectral phase estimates that were unrealistically early ( d). Supplementary forced photometry for these objects was obtained from the Asteroid Terrestrial-impact Last Alert System (ATLAS; Tonry et al. 2018; Smith et al. 2020), leading to more reliable estimates of .
Of the 631 objects which do not meet the initial criteria, there are a number which have acceptable enough SALT fits with respect to from which we can accurately estimate a spectral phase. Through visual inspection we identified 255 such objects which were then added to the sample.
For the remaining 376 targets, we scraped as many forced photometry light curves as possible from ATLAS. If an ATLAS light curve could not be located, we instead attempted to scrape photometry from the All-Sky Automated Survey for Supernovae (ASAS-SN; Kochanek et al. 2017). In total this search returned 197 light curves from ATLAS and 2 from ASAS-SN. We fit these supplementary light curves with SALT and inspected the fits by eye. In the case of a successful SALT fit to this additional data which produces a well constrained estimate of maximum light we ‘accept’ the supplementary SALT fit. In total we accept the updated values for 84 of these objects (82 from ATLAS and 2 from ASAS-SN).
We set an errorfloor of 1.0 d on the value for any object that required supplementary photometry and/or did not meet the initial criteria laid out in Sect. 2. We note here that while these objects are included in the sample at this point, the corresponding spectra may be removed subject to one of the various cuts that follow. Any spectra in the final sample corresponding to objects with these updated phases are excluded from any plots and analyses relating to light curve fit parameters other than (, ). All updated peak MJD values coming from supplementary photometry can be found in Table 2.
| ZTF Name | Updated MJD t0 | Photometry source |
|---|---|---|
| ZTF18aagrebu | 58178.71.0 | ATLAS18mgm |
| ZTF18aaqfkqh | 58198.91.0 | ATLAS18mtr |
| ZTF18aaqgadq | 58249.71.0 | ATLAS18oin |
| ZTF18abiirfq | 58331.51.0 | ATLAS18sqq |
| ZTF18abywcnl | 58400.31.0 | ATLAS18vui |
| ZTF18acbwiic | 58426.81.0 | ATLAS18ycb |
| ZTF18accdxpa | 58420.61.0 | ATLAS18xaz |
| ZTF18accpjrx | 58412.31.0 | ATLAS18xlz |
| ZTF18acdfpne | 58312.61.0 | ATLAS18rvf |
| ZTF18acdnjqh | 58423.11.0 | ATLAS18znr |
| ZTF18acefgoc | 58406.31.0 | ATLAS18xlv |
| ZTF18achaqmd | 58450.41.0 | ATLAS18zek |
| ZTF18acswtoq | 58463.91.0 | ATLAS18zmv |
| ZTF18acwzawt | 58188.51.0 | ATLAS18mis |
| ZTF18acybqhe | 58335.11.0 | ATLAS18sss |
| ZTF18aczddnw | 58454.81.0 | ATLAS18zvg |
| ZTF18aczzrkn | 58488.21.0 | ATLAS18bcfl |
| ZTF18adazgdh | 58489.61.0 | ATLAS19acw |
| ZTF19aajwhse | 58526.01.0 | ATLAS19kkz |
| ZTF19aakpmoy | 58539.41.0 | ATLAS19dhw |
| ZTF19aalahqe | 58538.91.0 | ATLAS19dqu |
| ZTF19aanjvqr | 58222.31.0 | ATLAS18mzf |
| ZTF19aarnqzw | 58610.31.0 | ATLAS19hun |
| ZTF19aawlnlq | 58613.71.0 | ATLAS19jrk |
| ZTF19aawscnp | 58636.11.0 | ATLAS19lqt |
| ZTF19aaxpjwk | 58595.51.0 | ATLAS19emj |
| ZTF19aaydpru | 58635.31.0 | ATLAS19lgf |
| ZTF19abcttsc | 58677.21.0 | ATLAS19omd |
| ZTF19abdsntm | 58676.41.0 | ATLAS19oif |
| ZTF19abjkfrf | 58301.11.0 | ATLAS17odb |
| ZTF19abqgwuy | 58654.01.0 | ASASSN-19ol |
| ZTF19abxdtew | 58746.11.0 | ATLAS19uro |
| ZTF19acchtyp | 58775.11.0 | ATLAS19ynq |
| ZTF19aceeexa | 58779.11.0 | ATLAS19ykk |
| ZTF19acmyljb | 58786.41.0 | ATLAS19ztf |
| ZTF19acnwvuw | 58800.81.0 | ATLAS19zjy |
| ZTF19acrddcz | 58813.61.0 | ATLAS19balj |
| ZTF19acrmmpq | 58810.61.0 | ATLAS19bfsx |
| ZTF19actfpmy | 58814.11.0 | ATLAS19bapx |
| ZTF19acuymeu | 58826.01.0 | ATLAS19bbnc |
| ZTF19acxngol | 58823.91.0 | ASASSN-19acx |
| ZTF19acxolhu | 58832.91.0 | ATLAS19bcxj |
| ZTF19acyftrs | 58829.11.0 | ATLAS19bcjz |
| ZTF19acygbye | 58827.91.0 | ATLAS19bced |
| ZTF19acymuae | 58835.61.0 | ATLAS19bcub |
| ZTF19aczjsdy | 58822.81.0 | ATLAS19bbhj |
| ZTF19aczjyre | 58819.21.0 | ATLAS19bbhw |
| ZTF19adcecwu | 58863.21.0 | ATLAS19bfni |
| ZTF19adcghbt | 58845.11.0 | ATLAS19benj |
| ZTF20aacciep | 58850.81.0 | ATLAS19bfrh |
| ZTF20aaflngq | 58877.81.0 | ATLAS20bkl |
| ZTF20aagmrid | 58868.91.1 | ATLAS20avi |
| ZTF20aakzezp | 58862.81.0 | ATLAS20hfd |
| ZTF20aalkcea | 58895.41.0 | ATLAS20fde |
| ZTF20aamifit | 58891.41.0 | ATLAS20fsi |
| ZTF20aasmueu | 58916.51.0 | ATLAS20hwj |
| ZTF20aasoarv | 58916.31.0 | ATLAS20hzz |
| ZTF20aasxfcd | 58924.21.0 | ATLAS20ikg |
| ZTF20aatpoef | 58941.81.0 | ATLAS20iwi |
| ZTF20aaublmd | 58931.81.0 | ATLAS20ibe |
| ZTF20aaubntq | 58937.81.0 | ATLAS20ibk |
| ZTF20aaukudw | 58953.51.0 | ATLAS20jsc |
| ZTF20aavxraf | 58928.31.0 | ATLAS20hmy |
| ZTF20aawfnro | 58937.91.0 | ATLAS20ibn |
| ZTF Name | Updated MJD t0 | Photometry source |
|---|---|---|
| ZTF20aayngca | 58985.81.0 | ATLAS20lvx |
| ZTF20aazlvht | 58994.81.0 | ATLAS20mcj |
| ZTF20aazppkz | 58922.81.0 | ATLAS20hid |
| ZTF20abahpah | 58992.91.0 | ATLAS20mfn |
| ZTF20abkhhjn | 59024.81.0 | ATLAS20pld |
| ZTF20abkhibz | 59019.61.0 | ATLAS20pli |
| ZTF20abmmymj | 59061.91.0 | ATLAS20tia |
| ZTF20abpsdmr | 58265.51.0 | ATLAS18pje |
| ZTF20abqqwui | 59077.41.0 | ATLAS20xbd |
| ZTF20abvyauy | 59091.81.0 | ATLAS20xni |
| ZTF20abxyajd | 59070.01.0 | ATLAS20ugl |
| ZTF20acduffd | 59125.71.0 | ATLAS20bcef |
| ZTF20acedqji | 59131.91.0 | ATLAS20bcms |
| ZTF20acogywb | 58993.11.0 | ATLAS20lti |
| ZTF20acqhysq | 59175.51.0 | ATLAS20bfpg |
| ZTF20acuhjpn | 59185.01.0 | ATLAS20bgfa |
| ZTF20acwvmms | 59197.21.0 | ATLAS20bhkh |
| ZTF20acxnxbh | 59212.51.0 | ATLAS20bihi |
| ZTF20acyhena | 59175.41.0 | ATLAS20bfgx |
| ZTF20acyonmr | 59139.71.0 | ATLAS20bcmf |
Figure 18 illustrates one such example of an updated estimate. As visible in the plot, there are only three ZTF photometry points for ZTF19abjkfrf, in a single band, post-peak. Due to the poor phase coverage of the light curve, this object will be excluded from almost all studies, especially those concerning cosmological measurements. As we possess a good quality pre-peak spectrum however, updating the phase estimate in this fashion allows us to avoid cutting otherwise acceptable data. For this object the phase estimate has changed from 35.9 to 12.5 d. The updated estimates for for the 92 supernovae in Table 2 were subsequently used to as initial constraints in refitting the corresponding light curves for the DR2.
Appendix B Data
We present the feature measurements for all 329 spectra in Tables 4-9. For other measurements presented in this paper - lightcurve properties, Branch and Wang classifications, host galaxy properties - we refer the reader to the source papers (Dimitriadis et al. 2024; Burgaz et al. 2024, Smith et al. in prep.).
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | pEW (Å) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|
| ZTF19abyzuos | 2019qdj | 58753.4 | ARC-DIS | |||||
| ZTF18abadjhx | 2018cro | 58289.4 | ARC-DIS | |||||
| ZTF19acewotx | 2019sql | 58779.4 | ARC-DIS | |||||
| ZTF19aaywlmi | 2019hqg | 58658.3 | ARC-DIS | |||||
| ZTF20absvtnc | 2020rpn | 59086.3 | ARC-DIS | |||||
| ZTF18aazsabq | 2018crn | 58288.3 | ARC-DIS | |||||
| ZTF18aauizcr | 2018btb | 58257.3 | ARC-DIS | |||||
| ZTF18acbxsge | 2018huw | 58438.3 | ARC-DIS | |||||
| ZTF18acurmpd | 2018awn | 58228.8 | Copernico-AFOSC | |||||
| ZTF20acowddo | 2020yyg | 59161.8 | Copernico-AFOSC | |||||
| ZTF19acftfst | 2019suj | 58778.9 | Copernico-AFOSC | |||||
| ZTF19aakzwao | 2019bkh | 58547.2 | Copernico-AFOSC | |||||
| ZTF18abosdwf | 2018fcw | 58347.0 | Copernico-AFOSC | |||||
| ZTF20acuhjpn | 2020aavb | 59177.2 | Copernico-AFOSC | |||||
| ZTF19aaksrlb | 2019bdz | 58543.1 | Copernico-AFOSC | |||||
| ZTF19aajxwnz | 2019bek | 58543.1 | Copernico-AFOSC | |||||
| ZTF19aakoasy | 2019baq | 58543.1 | Copernico-AFOSC | |||||
| ZTF18adaslwa | 2018kyi | 58480.9 | Copernico-AFOSC | |||||
| ZTF19aalcyfd | 2019bic | 58543.9 | Copernico-AFOSC | |||||
| ZTF19aakykjl | 2019bjw | 58544.8 | Copernico-AFOSC | |||||
| ZTF20abapyxl | 2020kku | 58988.1 | GTC-OSIRIS | |||||
| ZTF20abbhyxu | 2020kyx | 58994.2 | GTC-OSIRIS | |||||
| ZTF18aahvndq | 2020jhf | 58978.9 | GTC-OSIRIS | |||||
| ZTF20abtctgr | 2020rlj | 59078.2 | GTC-OSIRIS | |||||
| ZTF20abmddts | 2020pwu | 59052.6 | Gemini N-GMOS | |||||
| ZTF18acxyarg | 2018kij | 58470.5 | Gemini N-GMOS | |||||
| ZTF18acqsfxh | 2018izc | 58453.5 | Keck I-LRIS | |||||
| ZTF18aaqqhis | 2018ccy | 58252.2 | Keck I-LRIS | |||||
| ZTF19abasxkg | 2019ibb | 58664.6 | Keck I-LRIS | |||||
| ZTF20abmdfcy | 2020psv | 59054.6 | Keck I-LRIS | |||||
| ZTF20acinaeq | 2020wfg | 59136.6 | Keck I-LRIS | |||||
| ZTF20acwilfu | 2020acbc | 59194.5 | Keck I-LRIS | |||||
| ZTF19actldas | 2019vdg | 58813.6 | Keck I-LRIS | |||||
| ZTF19aczjyre | 2019vnj | 58813.7 | Keck I-LRIS | |||||
| ZTF20abtzhfc | 2020rmy | 59084.4 | Keck I-LRIS | |||||
| ZTF19aacgslb | 2019np | 58493.6 | FTN-FLOYDS | |||||
| ZTF19aapszzy | 2019dkx | 58587.6 | FTN-FLOYDS | |||||
| ZTF20abyptpc | 2020ssf | 59101.5 | FTN-FLOYDS | |||||
| ZTF19aamrdmm | 2019btp | 58558.6 | FTN-FLOYDS | |||||
| ZTF20aatvdwr | 2020esm | 58941.5 | FTN-FLOYDS | |||||
| ZTF18abfhryc | 2018dhw | 58318.5 | FTN-FLOYDS | |||||
| ZTF20acuoclk | 2020abqd | 59191.4 | FTN-FLOYDS | |||||
| ZTF18aahfbqp | 2020acua | 59207.4 | FTN-FLOYDS | |||||
| ZTF19aczjyuf | 2019vju | 58814.7 | FTS-FLOYDS | |||||
| ZTF19aarnqzw | 2019dwq | 58598.5 | FTN-FLOYDS | |||||
| ZTF20aakyoez | 2020bpi | 58883.6 | FTN-FLOYDS | |||||
| ZTF20acpylns | 2020zlc | 59169.5 | FTN-FLOYDS | |||||
| ZTF20aavxraf | 2020ees | 58918.6 | FTN-FLOYDS | |||||
| ZTF18aaslhxt | 2018btk | 58261.0 | LT-SPRAT | |||||
| ZTF19acrdqej | 2019ulw | 58804.0 | LT-SPRAT | |||||
| ZTF20abyptpc | 2020ssf | 59112.0 | LT-SPRAT | |||||
| ZTF20aaaxacu | 2019zjh | 58850.2 | LT-SPRAT | |||||
| ZTF20abegate | 2020mby | 59020.9 | LT-SPRAT | |||||
| ZTF20acxncha | 2020adfe | 59212.9 | LT-SPRAT | |||||
| ZTF19acynije | 2019wup | 58837.8 | LT-SPRAT | |||||
| ZTF20aayuyak | 2020jht | 58988.9 | LT-SPRAT | |||||
| ZTF19ackjmge | 2019tqr | 58788.2 | LT-SPRAT | |||||
| ZTF19aanyuyh | 2020pkj | 59058.1 | LT-SPRAT | |||||
| ZTF19acxyumq | 2019wvc | 58835.2 | LT-SPRAT | |||||
| ZTF19adcdtyy | 2019zho | 58848.2 | LT-SPRAT | |||||
| ZTF19acyiqnw | 2019wwa | 58836.3 | LT-SPRAT |
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | pEW (Å) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|
| ZTF18aczdetm | 2018khg | 58480.1 | LT-SPRAT | |||||
| ZTF20abjbiqf | 2020nxh | 59042.9 | LT-SPRAT | |||||
| ZTF20abeywdn | 2020mon | 59028.9 | LT-SPRAT | |||||
| ZTF18aaxdrjn | 2018cdt | 58272.9 | LT-SPRAT | |||||
| ZTF20aawmlfq | 2020igy | 58973.1 | LT-SPRAT | |||||
| ZTF20abciflj | 2020lhe | 59008.9 | LT-SPRAT | |||||
| ZTF20aalbjpf | 2020bpy | 58888.9 | LT-SPRAT | |||||
| ZTF19acxyumq | 2019wvc | 58837.2 | LT-SPRAT | |||||
| ZTF19aartuli | 2019dzo | 58610.9 | LT-SPRAT | |||||
| ZTF19aaobwpx | 2019czy | 58581.0 | LT-SPRAT | |||||
| ZTF19acxndsk | 2019wiq | 58836.2 | LT-SPRAT | |||||
| ZTF19acxyfkf | 2019wuz | 58832.0 | LT-SPRAT | |||||
| ZTF20acpgnej | 2020yzg | 59174.2 | LT-SPRAT | |||||
| ZTF19aawlnlq | 2019euw | 58612.2 | LT-SPRAT | |||||
| ZTF18acqxcga | 2018izd | 58460.2 | LT-SPRAT | |||||
| ZTF18aahheaj | 2018avp | 58222.1 | LT-SPRAT | |||||
| ZTF19aafwrhf | 2019wis | 58836.1 | LT-SPRAT | |||||
| ZTF20aaupolv | 2020fyt | 58959.9 | LT-SPRAT | |||||
| ZTF19aaraxhh | 2019duf | 58600.2 | LT-SPRAT | |||||
| ZTF19adcfsdr | 2019zcq | 58849.3 | LT-SPRAT | |||||
| ZTF18aaupmks | 2018bsr | 58256.0 | LT-SPRAT | |||||
| ZTF20acduffd | 2020uea | 59122.0 | LT-SPRAT | |||||
| ZTF18abwkczr | 2018grc | 58382.2 | LT-SPRAT | |||||
| ZTF20aaeuxqk | 2020ut | 58869.2 | LT-SPRAT | |||||
| ZTF18acqqyah | 2018iuu | 58452.2 | LT-SPRAT | |||||
| ZTF18acatuts | 2018hcr | 58406.9 | LT-SPRAT | |||||
| ZTF20aazppkz | 2020dxa | 58913.2 | LT-SPRAT | |||||
| ZTF18acaszeh | 2018hju | 58408.9 | LT-SPRAT | |||||
| ZTF19aantarc | 2019crb | 58582.0 | LT-SPRAT | |||||
| ZTF19aailsfh | 2019amp | 58526.1 | LT-SPRAT | |||||
| ZTF18aczddnw | 2018jeo | 58452.2 | LT-SPRAT | |||||
| ZTF20acgrjqt | 2019xhk | 58846.2 | LT-SPRAT | |||||
| ZTF19aamrdmm | 2019btp | 58558.5 | Shane-KAST | |||||
| ZTF20acxzqyp | 2020aczg | 59203.5 | Shane-KAST | |||||
| ZTF18adalarn | 2018las | 58486.5 | Shane-KAST | |||||
| ZTF19abdsntm | 2019kcx | 58670.2 | Shane-KAST | |||||
| ZTF18abtfrbf | 2018gdg | 58376.3 | Shane-KAST | |||||
| ZTF19acazbqm | 2019roz | 58762.2 | Shane-KAST | |||||
| ZTF19abaosan | 2019igg | 58667.5 | Shane-KAST | |||||
| ZTF18abuhzfc | 2018ggx | 58376.3 | Shane-KAST | |||||
| ZTF18abdfaqi | 2018cxm | 58307.3 | Shane-KAST | |||||
| ZTF19aaklqod | 2020ctr | 58898.7 | Shane-KAST | |||||
| ZTF19aalvaxt | 2019bpc | 58558.3 | Shane-KAST | |||||
| ZTF20acpkpla | 2020zgc | 59168.3 | Shane-KAST | |||||
| ZTF20acpiywu | 2020zmi | 59168.2 | Shane-KAST | |||||
| ZTF19abqmpsr | 2019oml | 58721.5 | Shane-KAST | |||||
| ZTF19aanyuyh | 2020pkj | 59057.5 | Shane-KAST | |||||
| ZTF20abxyajd | 2020qdl | 59057.5 | Shane-KAST | |||||
| ZTF20acuxpwz | 2020abpt | 59190.0 | Magellan-Baade-IMACS | |||||
| ZTF19aadoocn | 2019xa | 58511.3 | Magellan-Clay-LDSS-3 | |||||
| ZTF20abptxls | 2020qln | 59073.2 | NOT-ALFOSC | |||||
| ZTF18abosdwf | 2018fcw | 58347.1 | NOT-ALFOSC | |||||
| ZTF20abixkhh | 2020nqw | 59038.0 | NOT-ALFOSC | |||||
| ZTF20aayvymx | 2020jjf | 58981.0 | NOT-ALFOSC | |||||
| ZTF20acriwfa | 2020urj | 59131.2 | NOT-ALFOSC | |||||
| ZTF18abauprj | 2018cnw | 58296.1 | NOT-ALFOSC | |||||
| ZTF19aadnxat | 2019vu | 58509.2 | NOT-ALFOSC | |||||
| ZTF20actrwym | 2020aazr | 59189.8 | NOT-ALFOSC | |||||
| ZTF18aaovbiy | 2018bdo | 58239.0 | NOT-ALFOSC | |||||
| ZTF18abrlupd | 2018fry | 58365.9 | NOT-ALFOSC | |||||
| ZTF20aayhacx | 2020jgb | 58982.1 | NOT-ALFOSC |
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | pEW (Å) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|
| ZTF20acwujgz | 2020acrz | 59205.3 | NTT-EFOSC2 | |||||
| ZTF18adazeua | 2018lef | 58483.3 | NTT-EFOSC2 | |||||
| ZTF18acurmpd | 2018awn | 58229.1 | NTT-EFOSC2 | |||||
| ZTF18acwzawt | 2018aby | 58186.3 | NTT-EFOSC2 | |||||
| ZTF18acyymoy | 2018but | 58260.3 | NTT-EFOSC2 | |||||
| ZTF19aaxibby | 2019hbs | 58644.4 | NTT-EFOSC2 | |||||
| ZTF19abywqza | 2019pil | 58730.3 | NTT-EFOSC2 | |||||
| ZTF19abqlrtb | 2019nwf | 58716.4 | NTT-EFOSC2 | |||||
| ZTF18aavjnfx | 2018bsq | 58258.3 | NTT-EFOSC2 | |||||
| ZTF20acwmpsj | 2020acdo | 59200.3 | NTT-EFOSC2 | |||||
| ZTF19abkbkxy | 2018ebs | 58334.2 | NTT-EFOSC2 | |||||
| ZTF19adbpulv | 2019yzi | 58852.1 | NTT-EFOSC2 | |||||
| ZTF19acuymeu | 2019vsm | 58824.2 | NTT-EFOSC2 | |||||
| ZTF19aafmwhv | 2019aof | 58524.4 | NTT-EFOSC2 | |||||
| ZTF19aacxrzt | 2019qe | 58498.2 | NTT-EFOSC2 | |||||
| ZTF20aaghnxd | 2020alf | 58872.3 | NTT-EFOSC2 | |||||
| ZTF18acswtoq | 2018jao | 58455.0 | NTT-EFOSC2 | |||||
| ZTF20aaifsri | 2020akj | 58872.4 | NTT-EFOSC2 | |||||
| ZTF18accpubd | 2018evb | 58342.3 | NTT-EFOSC2 | |||||
| ZTF19abjarnh | 2019moe | 58702.3 | NTT-EFOSC2 | |||||
| ZTF19abidfxd | 2019lsg | 58693.3 | NTT-EFOSC2 | |||||
| ZTF19abeggfi | 2018fvq | 58369.1 | NTT-EFOSC2 | |||||
| ZTF19acxovyh | 2019vro | 58823.4 | NTT-EFOSC2 | |||||
| ZTF19abmolyr | 2019mrw | 58701.3 | NTT-EFOSC2 | |||||
| ZTF19acxolhu | 2019wew | 58826.3 | NTT-EFOSC2 | |||||
| ZTF19aaycomi | 2019hbb | 58643.4 | NTT-EFOSC2 | |||||
| ZTF19abmpoxa | 2019mtp | 58702.2 | NTT-EFOSC2 | |||||
| ZTF18abtgtpn | 2018enk | 58334.4 | NTT-EFOSC2 | |||||
| ZTF20acogesf | 2020ykj | 59158.4 | NTT-EFOSC2 | |||||
| ZTF19aaairqh | 2019bp | 58491.2 | NTT-EFOSC2 | |||||
| ZTF18abjrfqx | 2018elj | 58334.3 | NTT-EFOSC2 | |||||
| ZTF20acqzjqz | 2020aabz | 59174.2 | NTT-EFOSC2 | |||||
| ZTF19aavhxby | 2019fzm | 58635.2 | NTT-EFOSC2 | |||||
| ZTF18acsynfy | 2018ihs | 58437.1 | NTT-EFOSC2 | |||||
| ZTF20aanvpzo | 2020cpt | 58900.3 | NTT-EFOSC2 | |||||
| ZTF19aceeexa | 2019suf | 58777.1 | NTT-EFOSC2 | |||||
| ZTF20acizliy | 2020wob | 59146.2 | NTT-EFOSC2 | |||||
| ZTF19aaydpru | 2019ftd | 58627.0 | NTT-EFOSC2 | |||||
| ZTF20aaporoa | 2020cyx | 58905.2 | NTT-EFOSC2 | |||||
| ZTF20acojxtb | 2020ymu | 59158.2 | NTT-EFOSC2 | |||||
| ZTF19aacilht | 2019qo | 58497.3 | NTT-EFOSC2 | |||||
| ZTF20acumcrz | 2020abln | 59190.1 | NTT-EFOSC2 | |||||
| ZTF19aaeicsm | 2019aba | 58515.2 | NTT-EFOSC2 | |||||
| ZTF18abspszv | 2018exv | 58342.3 | NTT-EFOSC2 | |||||
| ZTF20aafgbrf | 2020xr | 58864.2 | NTT-EFOSC2 | |||||
| ZTF20aaiawlj | 2020avg | 58881.4 | NTT-EFOSC2 | |||||
| ZTF20acxnxbh | 2020acqx | 59199.1 | NTT-EFOSC2 | |||||
| ZTF20aarbget | 2020dko | 58906.3 | NTT-EFOSC2 | |||||
| ZTF18aazxdyy | 2018aly | 58202.3 | NTT-EFOSC2 | |||||
| ZTF19ablovot | 2019mga | 58701.3 | NTT-EFOSC2 | |||||
| ZTF19acylgic | 2019wku | 58835.2 | NTT-EFOSC2 | |||||
| ZTF19aaynsyd | 2019gfb | 58635.4 | NTT-EFOSC2 | |||||
| ZTF18aahfzea | 2018aqh | 58216.2 | NTT-EFOSC2 | |||||
| ZTF19adcbxkw | 2019yzx | 58850.2 | NTT-EFOSC2 | |||||
| ZTF18aalurka | 2018awj | 58230.1 | NTT-EFOSC2 | |||||
| ZTF20acqhysq | 2020aagw | 59174.3 | NTT-EFOSC2 | |||||
| ZTF20aakzezp | 2020dp | 58852.3 | NTT-EFOSC2 | |||||
| ZTF19aaywyug | 2019hch | 58644.1 | NTT-EFOSC2 | |||||
| ZTF18acsxvrp | 2018jfv | 58454.1 | NTT-EFOSC2 | |||||
| ZTF18abcscfv | 2018akb | 58204.4 | NTT-EFOSC2 | |||||
| ZTF19abkdrir | 2019mfv | 58704.4 | NTT-EFOSC2 |
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | pEW (Å) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|
| ZTF19abtsrup | 2019owu | 58733.4 | NTT-EFOSC2 | |||||
| ZTF20aapadwx | 2020ddr | 58905.4 | NTT-EFOSC2 | |||||
| ZTF19abucvhz | 2019nzo | 58718.4 | NTT-EFOSC2 | |||||
| ZTF19ablfaey | 2019mon | 58702.2 | NTT-EFOSC2 | |||||
| ZTF18adbhrjs | 2018ldw | 58483.3 | NTT-EFOSC2 | |||||
| ZTF19aabvfwn | 2019jf | 58492.2 | NTT-EFOSC2 | |||||
| ZTF18acsovsw | 2018jny | 58462.3 | NTT-EFOSC2 | |||||
| ZTF19aaddzpk | 2019qr | 58497.3 | NTT-EFOSC2 | |||||
| ZTF19aacgslb | 2019np | 58495.3 | P200-DBSP | |||||
| ZTF19aakzwao | 2019bkh | 58546.3 | P200-DBSP | |||||
| ZTF18abmjvuf | 2018fio | 58351.2 | P200-DBSP | |||||
| ZTF19aadnxat | 2019vu | 58509.4 | P200-DBSP | |||||
| ZTF18acxyarg | 2018kij | 58479.2 | P200-DBSP | |||||
| ZTF18abupgql | 2018gjr | 58374.4 | P200-DBSP | |||||
| ZTF19aadmjtn | 2019rx | 58509.2 | P200-DBSP | |||||
| ZTF18aahfxnn | 2018bau | 58218.0 | P200-DBSP | |||||
| ZTF19aabvfwn | 2019jf | 58495.5 | P200-DBSP | |||||
| ZTF20abmudrv | 2020pst | 59049.1 | SALT-RSS | |||||
| ZTF19aatgznl | 2019ekb | 58614.4 | UH88-SNIFS | |||||
| ZTF19aanuhox | 2019cqd | 58579.5 | UH88-SNIFS | |||||
| ZTF19acnwvuw | 2019tym | 58791.2 | UH88-SNIFS | |||||
| ZTF20acovrzx | 2020yzs | 59161.3 | UH88-SNIFS | |||||
| ZTF20aawfnro | 2020ery | 58931.5 | UH88-SNIFS | |||||
| ZTF20acyvzbr | 2020adld | 59205.6 | UH88-SNIFS | |||||
| ZTF20aaubntq | 2020err | 58931.4 | UH88-SNIFS | |||||
| ZTF20adadshh | 2020adqy | 59219.5 | UH88-SNIFS | |||||
| ZTF19abajuqh | 2019ibd | 58663.6 | UH88-SNIFS | |||||
| ZTF19acbpnii | 2019rwt | 58763.3 | UH88-SNIFS | |||||
| ZTF19aatgrxl | 2019enu | 58614.3 | UH88-SNIFS | |||||
| ZTF20aaublmd | 2020erg | 58931.4 | UH88-SNIFS | |||||
| ZTF20aasdibr | 2020eeb | 58917.3 | UH88-SNIFS | |||||
| ZTF19abuejud | 2019pig | 58732.2 | UH88-SNIFS | |||||
| ZTF19acjfhom | 2019tpg | 58791.4 | UH88-SNIFS | |||||
| ZTF19aamhjlk | 2019bsr | 58559.3 | UH88-SNIFS | |||||
| ZTF20acxvvnf | 2020adle | 59205.5 | UH88-SNIFS | |||||
| ZTF18abwuqcw | 2018eoy | 58335.9 | UH88-SNIFS | |||||
| ZTF19aatzlmw | 2019eow | 58614.5 | UH88-SNIFS | |||||
| ZTF18abosrco | 2018epx | 58336.0 | UH88-SNIFS | |||||
| ZTF19abuhlxk | 2019pdx | 58728.9 | UH88-SNIFS | |||||
| ZTF19aaaajtq | 2019ir | 58496.7 | UH88-SNIFS | |||||
| ZTF20acyvzef | 2020admd | 59205.6 | UH88-SNIFS | |||||
| ZTF19adaiyrd | 2019xbf | 58844.6 | UH88-SNIFS | |||||
| ZTF19acjerzj | 2019ubh | 58790.5 | UH88-SNIFS | |||||
| ZTF19aaapnxn | 2018jdq | 58455.6 | UH88-SNIFS | |||||
| ZTF19aacijie | 2019qb | 58496.0 | UH88-SNIFS | |||||
| ZTF19aathcvn | 2019eok | 58614.5 | UH88-SNIFS | |||||
| ZTF19aanjjhk | 2019cew | 58573.3 | UH88-SNIFS | |||||
| ZTF19abrogbl | 2019omi | 58727.5 | UH88-SNIFS | |||||
| ZTF20acumxrh | 2020abjl | 59191.2 | SOAR-Goodman | |||||
| ZTF18abtsuqv | 2018ddi | 58309.4 | SOAR-Goodman | |||||
| ZTF20acwijiy | 2020acca | 59201.2 | SOAR-Goodman | |||||
| ZTF18acbxhua | 2018how | 58419.1 | SOAR-Goodman | |||||
| ZTF20achadaa | 2020var | 59131.1 | SOAR-Goodman | |||||
| ZTF19aainjqn | 2019aox | 58525.1 | SOAR-Goodman | |||||
| ZTF20acxiyyp | 2020acod | 59200.3 | VLT-FORS2 | |||||
| ZTF20acwpfvq | 2020acei | 59199.3 | VLT-FORS2 | |||||
| ZTF20acwcqnv | 2020acae | 59195.3 | VLT-FORS2 | |||||
| ZTF20achptde | 2020ver | 59136.1 | VLT-FORS2 | |||||
| ZTF19ababmsi | 2019hxe | 58656.2 | WHT-ACAM | |||||
| ZTF18adasopt | 2018lfb | 58484.0 | WHT-ISIS | |||||
| ZTF18adbckox | 2018lem | 58484.9 | WHT-ISIS |
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | a | b (Å) | c (Å) | pEW (Å) | pEW (Å) | R | (km s-1) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ZTF19acgdfjt | 2019sup | 58779.4 | ARC-DIS | |||||||||||
| ZTF20aafsnpp | 2020zi | 58872.4 | ARC-DIS | |||||||||||
| ZTF18adaifep | 2018koy | 58485.3 | ARC-DIS | |||||||||||
| ZTF18aahjafd | 2018loz | 58229.3 | ARC-DIS | |||||||||||
| ZTF18abauprj | 2018cnw | 58289.3 | ARC-DIS | |||||||||||
| ZTF18abauprj | 2018cnw | 58290.3 | DCT-DeVeny | |||||||||||
| ZTF18aamigmk | 2018aye | 58230.0 | Copernico-AFOSC | |||||||||||
| ZTF19abkcpxe | 2019mqn | 58702.1 | NTT-EFOSC2 | |||||||||||
| ZTF20acogywb | 2020jgl | 58976.9 | GTC-OSIRIS | |||||||||||
| ZTF19aagmsrr | 2019aik | 58515.5 | Gemini N-GMOS | |||||||||||
| ZTF19aaplpaa | 2019cxx | 58582.4 | Gemini N-GMOS | |||||||||||
| ZTF19aallvor | 2019bit | 58546.6 | Keck I-LRIS | |||||||||||
| ZTF20abjfufv | 2020tfc | 59109.4 | Keck I-LRIS | |||||||||||
| ZTF18abauprj | 2018cnw | 58286.6 | Keck I-LRIS | |||||||||||
| ZTF20abvyauy | 2020rmg | 59084.6 | Keck I-LRIS | |||||||||||
| ZTF20abkacis | 2020orf | 59047.4 | Keck II-DEIMOS | |||||||||||
| ZTF18acusegd | 2018jov | 58462.5 | FTN-FLOYDS | |||||||||||
| ZTF19aatlmbo | 2019ein | 58605.3 | FTN-FLOYDS | |||||||||||
| ZTF20abzbfct | 2020tkp | 59113.5 | FTN-FLOYDS | |||||||||||
| ZTF18acsyzca | 2018jky | 58458.5 | FTS-FLOYDS | |||||||||||
| ZTF20abpsdmr | 2018btj | 58257.6 | FTN-FLOYDS | |||||||||||
| ZTF19aampyum | 2019bse | 58556.4 | FTN-FLOYDS | |||||||||||
| ZTF20acynlkj | 2020aden | 59209.3 | FTN-FLOYDS | |||||||||||
| ZTF19abxjimu | 2019pxo | 58737.5 | FTN-FLOYDS | |||||||||||
| ZTF20abmcxct | 2020pna | 59051.1 | LT-SPRAT | |||||||||||
| ZTF19aatgrxv | 2019ens | 58613.1 | LT-SPRAT | |||||||||||
| ZTF19adcecwu | 2019yvq | 58851.2 | LT-SPRAT | |||||||||||
| ZTF19aatlmbo | 2019ein | 58608.0 | LT-SPRAT | |||||||||||
| ZTF19aajwhse | 2019ahi | 58518.2 | LT-SPRAT | |||||||||||
| ZTF20aaodkvl | 2020csx | 58896.2 | LT-SPRAT | |||||||||||
| ZTF19adcecwu | 2019yvq | 58852.1 | LT-SPRAT | |||||||||||
| ZTF20abquppg | 2020ram | 59077.1 | LT-SPRAT | |||||||||||
| ZTF19aabmybj | 2019on | 58496.0 | LT-SPRAT | |||||||||||
| ZTF18acusbyf | 2018jmo | 58463.0 | LT-SPRAT | |||||||||||
| ZTF20aatwonv | 2020euz | 58938.9 | LT-SPRAT | |||||||||||
| ZTF20abijfqq | 2020nlb | 59025.8 | LT-SPRAT | |||||||||||
| ZTF19acmdpyr | 2019ugu | 58793.1 | Shane-KAST | |||||||||||
| ZTF19abkbkyb | 2018enb | 58335.4 | Shane-KAST | |||||||||||
| ZTF19abauzma | 2019iln | 58668.5 | Shane-KAST | |||||||||||
| ZTF20aammhli | 2020cdj | 58892.5 | Shane-KAST | |||||||||||
| ZTF20acpcuwx | 2020yxd | 59158.5 | Shane-KAST | |||||||||||
| ZTF20actddoh | 2020aatc | 59177.0 | Magellan-Baade-IMACS | |||||||||||
| ZTF19aatlmbo | 2019ein | 58615.9 | NOT-ALFOSC |
| ZTF Name | IAU | MJD | Phase (d) | a | b (Å) | c (Å) | a | b (Å) | c (Å) | pEW (Å) | pEW (Å) | R | (km s-1) | Telescope-Instrument |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ZTF20abrjmgi | 2020qxp | 59075.9 | NOT-ALFOSC | |||||||||||
| ZTF18aaqcozd | 2018bjc | 58249.1 | NOT-ALFOSC | |||||||||||
| ZTF20acikuon | 2020wcj | 59147.3 | NTT-EFOSC2 | |||||||||||
| ZTF19abkbkyb | 2018enb | 58335.2 | NTT-EFOSC2 | |||||||||||
| ZTF19abqgwuy | 2019has | 58642.4 | NTT-EFOSC2 | |||||||||||
| ZTF20acyhena | 2020zem | 59168.1 | NTT-EFOSC2 | |||||||||||
| ZTF20aclkuqh | 2020xpk | 59152.2 | NTT-EFOSC2 | |||||||||||
| ZTF18adaifep | 2018koy | 58483.2 | NTT-EFOSC2 | |||||||||||
| ZTF19aanjvqr | 2018aqi | 58216.2 | NTT-EFOSC2 | |||||||||||
| ZTF20acpknjk | 2020zgh | 59168.1 | NTT-EFOSC2 | |||||||||||
| ZTF20acxkxxr | 2020acol | 59198.0 | NTT-EFOSC2 | |||||||||||
| ZTF19aacwljg | 2019qc | 58498.2 | NTT-EFOSC2 | |||||||||||
| ZTF20acqksdi | 2020zpi | 59170.2 | NTT-EFOSC2 | |||||||||||
| ZTF19aavsyhq | 2019gis | 58643.3 | NTT-EFOSC2 | |||||||||||
| ZTF18achaqmd | 2018ilu | 58437.0 | NTT-EFOSC2 | |||||||||||
| ZTF18abmxahs | 2018feb | 58349.1 | NTT-EFOSC2 | |||||||||||
| ZTF18abncsdn | 2018evf | 58343.3 | NTT-EFOSC2 | |||||||||||
| ZTF20aagfjlj | 2020aai | 58871.2 | NTT-EFOSC2 | |||||||||||
| ZTF19aakizps | 2019amo | 58523.3 | NTT-EFOSC2 | |||||||||||
| ZTF20acpmgdz | 2020zhh | 59168.2 | NTT-EFOSC2 | |||||||||||
| ZTF19aabyheu | 2019kf | 58492.2 | NTT-EFOSC2 | |||||||||||
| ZTF18aasdted | 2018big | 58254.4 | P200-DBSP | |||||||||||
| ZTF18aarldnh | 2018lpd | 58255.3 | P200-DBSP | |||||||||||
| ZTF20abquppg | 2020ram | 59075.4 | P200-DBSP | |||||||||||
| ZTF19aavnwyt | 2019gcj | 58638.3 | P200-DBSP | |||||||||||
| ZTF18acusrws | 2018kdx | 58465.4 | P200-DBSP | |||||||||||
| ZTF19abvalfd | 2019pfe | 58728.2 | P200-DBSP | |||||||||||
| ZTF18acuixmb | 2018jsy | 58466.2 | P200-DBSP | |||||||||||
| ZTF18aaxsioa | 2018cfa | 58277.4 | P200-DBSP | |||||||||||
| ZTF19acnjwgm | 2019ubs | 58792.3 | P200-DBSP | |||||||||||
| ZTF19aabmybj | 2019on | 58495.5 | P200-DBSP | |||||||||||
| ZTF20abcsjtx | 2020lil | 59000.8 | SALT-RSS | |||||||||||
| ZTF19acapeun | 2019qym | 58754.9 | UH88-SNIFS | |||||||||||
| ZTF20acyhena | 2020zem | 59167.3 | UH88-SNIFS | |||||||||||
| ZTF20acoyfpk | 2020yvu | 59160.3 | UH88-SNIFS | |||||||||||
| ZTF19aawfcgp | 2019gcd | 58636.6 | UH88-SNIFS | |||||||||||
| ZTF19aaljcsu | 2019bgn | 58545.9 | UH88-SNIFS | |||||||||||
| ZTF19aakpmoy | 2019awq | 58528.0 | SOAR-Goodman | |||||||||||
| ZTF19abjkfrf | 2018cqw | 58288.2 | SOAR-Goodman | |||||||||||
| ZTF19aaumvig | 2019fdf | 58619.2 | SOAR-Goodman | |||||||||||
| ZTF20absyium | 2020rqk | 59077.9 | TNG-DOLORES | |||||||||||
| ZTF20acbovrt | 2020tug | 59114.2 | VLT-FORS2 |