Zwicky Transient Facility and Globular Clusters: The Period-Luminosity and Period-Wesenheit Relations for Anomalous Cepheids Supplemented with Large Magellanic Cloud Sample

Chow-Choong Ngeow Graduate Institute of Astronomy, National Central University, 300 Jhongda Road, 32001 Jhongli, Taiwan Anupam Bhardwaj INAF-Osservatorio astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy Matthew J. Graham Division of Physics, Mathematics, and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA Steven L. Groom IPAC, California Institute of Technology, 1200 E. California Blvd, Pasadena, CA 91125, USA Frank J. Masci IPAC, California Institute of Technology, 1200 E. California Blvd, Pasadena, CA 91125, USA Reed Riddle Caltech Optical Observatories, California Institute of Technology, Pasadena, CA 91125, USA

Abstract

We present the first $gri$ -band period-luminosity (PL) and period-Wesenheit (PW) relations for the fundamental mode anomalous Cepheids. These PL and PW relations were derived from a combined sample of five anomalous Cepheids in globular cluster M92 and the Large Magellanic Cloud, both of which have distance accurate to $\sim 1\%$ available from literature. Our $g$ -band PL relation is similar to the $B$ -band PL relation as reported in previous study. We applied our PL and PW relations to anomalous Cepheids discovered in dwarf galaxy Crater II, and found a larger but consistent distance modulus than the recent measurements based on RR Lyrae. Our calibrations of $gri$ -band PL and PW relations, even though less precise due to small number of anomalous Cepheids, will be useful for distance measurements to dwarf galaxies.

^†^†software: astropy (Astropy Collaboration et al., 2013, 2018), dustmaps (Green, 2018), gatspy (VanderPlas & Ivezić, 2015), Matplotlib (Hunter, 2007), NumPy (Harris et al., 2020), SciPy (Virtanen et al., 2020).

1 Introduction

Anomalous Cepheids (hereafter ACep; also known as BLBOO type variable stars) are evolved core-helium burning stars that cross the instability strip with masses of $\sim 1$ to $\sim 2\ M_{\odot}$ and pulsation periods in between $\sim 0.5$ and $\sim 2.5$ days. Some of the theoretical work and recent reviews on ACep can be found in Cox & Proffitt (1988), Bono et al. (1997), Marconi et al. (2004), Fiorentino et al. (2006), Sandage & Tammann (2006), and Monelli & Fiorentino (2022). Similar to classical Cepheids and RR Lyrae, ACep can pulsate in fundamental mode or first-overtone mode, and follow period-luminosity (PL) relations. On the PL plane, ACep are fainter than classical Cepheids but brighter than Type II Cepheids at a given period (for example, see Figure 5 in Soszyński et al., 2015).

The earliest optical PL(Z, where Z represents metallicity) relations for ACep in $B$ - and/or $V$ -band were derived by Nemec et al. (1988), Nemec et al. (1994), Bono et al. (1997), Pritzl et al. (2002), and Marconi et al. (2004). Later, ACep PL relations were extended to include other filters, such as $I$ - and $K$ -band, as well as the period-Wesenheit (PW) relations,¹¹1By construction, Wesenheit index is extinction-free (Madore, 1982; Madore & Freedman, 1991). in Marconi et al. (2004), Ripepi et al. (2014), Soszyński et al. (2015), Groenewegen & Jurkovic (2017), and Iwanek et al. (2018). Recently, Ripepi et al. (2019) and Ripepi et al. (2022) derived the PL and PW relations in the Gaia filters using ACep located in both the Large and Small Magellanic Cloud (LMC and SMC, respectively).

Refer to caption — Figure 1: ZTF light curves for the two ACep in GC. The numbers of data points in the $gri$ -band light curves are 410, 630, and 180, respectively, for NGC5466 V19, and 1433, 1402, and 432, respectively, for M92 V7. The black crosses are rejected outliers based on a two-step process as described in the text (see also Ngeow et al., 2022b). The black curves are the fitted low-order Fourier expansion to the remaining data points on the light curves.

To date, empirical ACep PL and PW relations in the optical band are only available in the Johnson-Cousin $BVI$ filters and Gaia $GB_{p}R_{p}$ filters. On the other hand, the Sloan Digital Sky Survey (SDSS) and the SDSS-variant $ugriz$ filters (or a subset of them) are now becoming more popular in a number of time-series synoptic sky surveys, such as the representative Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST, Ivezić et al., 2019). Similar to our previous work on contact binaries (Ngeow et al., 2021), RR Lyrae (Ngeow et al., 2022a) and Type II Cepheids (Ngeow et al., 2022b), we aimed to derive the $gri$ -band PL and PW relations for ACep using homogeneous $gri$ -band data obtained from the Zwicky Transient Facility (ZTF, Bellm & Kulkarni, 2017; Bellm et al., 2019; Graham et al., 2019; Dekany et al., 2020). ZTF repeatedly observes the northern sky in customized $gri$ filters with a dedicated $47$ -squared-degree wide-field mosaic CCD camera mounted on the Palomar 48-inch Samuel Oschin Schmidt telescope. The high-level surveys carried out by ZTF can be divided into public surveys, partner surveys, and California Institute of Technology (Caltech) surveys. All ZTF imaging data, regardless of the surveys, were processed via the same dedicated reduction pipeline (Masci et al., 2019), and the final catalog products were calibrated to the Pan-STARRS1 (Panoramic Survey Telescope and Rapid Response System 1, Chambers et al., 2016; Magnier et al., 2020) AB magnitude system.

ACep are very rare in globular clusters (hereafter GC) but there are a number of known ACep in nearby dwarf galaxies (for example, see Nemec et al., 1994; Marconi et al., 2004; Monelli & Fiorentino, 2022) including LMC and SMC. Therefore, the empirical PL and PW relations derived in the literature are exclusively based on dwarf galaxies and/or Magellanic Clouds. However, with exceptions of a few cases, dwarf galaxies in general are more distant than GC which limits the accurate calibration of ACep PL and PW relations. The absolute calibration of $gri$ -band PL and PW relations for ACep will be useful to obtain independent distances to ACep host dwarf galaxies in the era of LSST. Since there are only a few ACep in the GC (Section 2.1), we also utilized the LMC sample (Section 2.2) to derive PL and PW relations in Section 3. Note that very accurate distances to nearby GCs are now known from Baumgardt & Vasiliev (2021) and a percent level precise distance to the LMC is available based on late-type eclipsing binaries (Pietrzyński et al., 2019). We test our relations to a dwarf galaxy in Section 4, followed by discussion and conclusion of this work in Section 5.

2 Sample and Data

2.1 GC Samples with ZTF Data

We searched the literature for ACep in GC that are located north of $-30^{\circ}$ declination (i.e. within the footprint of ZTF), and identified four such ACep. For M9 V12, even though Arellano Ferro et al. (2013) argued it is an ACep, later Soszyński et al. (2020) re-classified this cluster variable star as a Type II Cepheid. Hence, we discarded this variable star, which leave three GC ACep in our sample. ZTF light curves for these three ACep were extracted from the PSF (point-spread function) catalogs using a matching radius of $1\arcsec$ . These ZTF PSF catalogs include the ZTF partner surveys data until 31 May 2022 and the ZTF Public Data Release 11.²²2See https://www.ztf.caltech.edu/ztf-public-releases.html

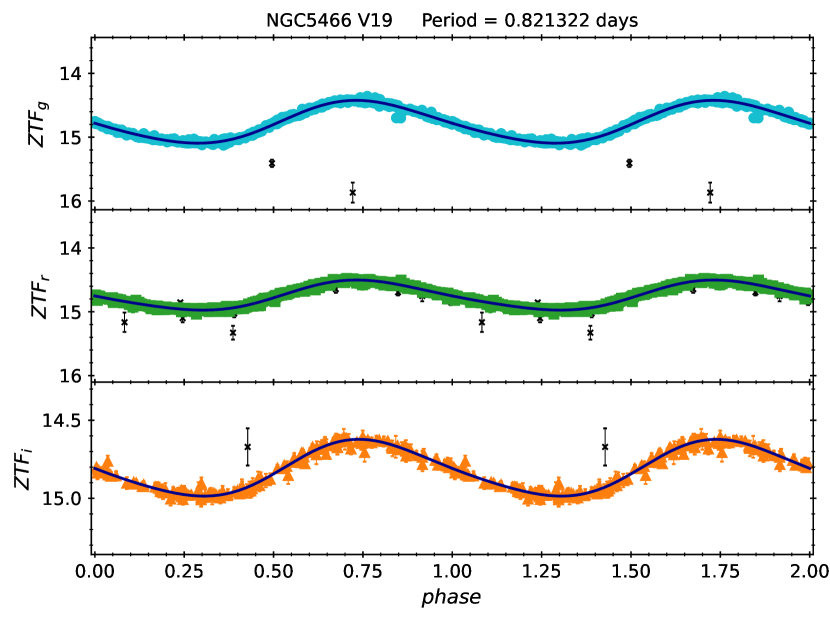
NGC5466 V19 (Zinn & Dahn, 1976; McCarthy & Nemec, 1997), a.k.a. BL BOO (the prototype of the BLBOO type variable stars), is a well-known ACep which has been classified as a first-overtone variable star (Nemec et al., 1988, 1994). We first used the LombScargleMultiband module from the astroML/gatspy³³3https://github.com/astroML/gatspy, also see VanderPlas (2016). package (VanderPlas & Ivezić, 2015) to search the period of this ACep on the ZTF $gri$ -band light curves. A low-order Fourier expansion was used to fit the folded light curves (for more details, see Ngeow et al., 2022b, and reference therein), and outliers beyond $3s$ from the fitted light curves were identified and removed (where $s$ is the dispersion of the fitted light curve). We then ran the second pass of the LombScargleMultiband module to determined the final adopted period, $P=0.821322$ days, for NGC5466 V19. The low-order Fourier expansion was fitted to the folded light curves (with outliers removed) for the second time, determining the following $gri$ -band intensity mean magnitudes: $14.748$ , $14.738$ , and $14.806$ mag, respectively. Due to large number of available data points per light curves (see Figure 1), we estimated negligible errors on these mean magnitudes. We note that this two-step process is identical to the one adopted for the Type II Cepheids studied in Ngeow et al. (2022b). The left panel of Figure 1 presents the folded ZTF light curves for this ACep.

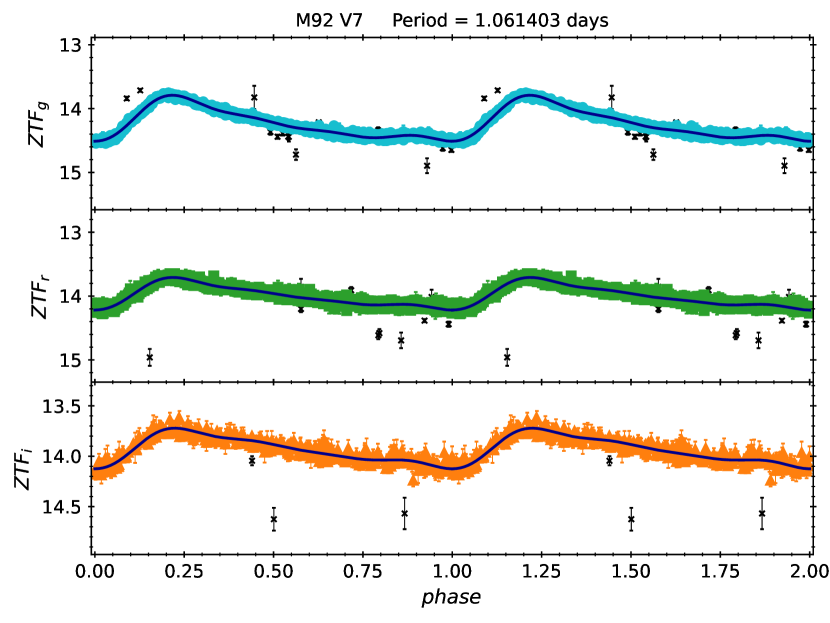
M92 V7 is another bona fide ACep located in the GC (Osborn et al., 2012; Yepez et al., 2020), which pulsates in the fundamental mode. Based on the same two-step process as in the case of NGC5466 V19, we determined a period of $1.061403$ days for M92 V7, and the intensity mean magnitudes of $14.214$ , $13.989$ , and $13.929$ mag in the $gri$ -band, respectively. The ZTF light curves for this ACep are shown in the right panel of Figure 1.

M15 V142 was re-classified as an ACep in Bhardwaj et al. (2021). However, ZTF light curves for this ACep exhibit strong evidence of blending (i.e. the light curves are “flat”), therefore we removed this ACep from our sample.

2.2 LMC Samples with Archival Data

Table 1: Mean magnitudes and extinction for the five LMC ACep

OGLE-IV ID	ID in Sebo et al. (2002)	Period (days)^a^aPeriods adopted from the OGLE-IV LMC ACep catalog (Soszyński et al., 2015).	$B$	$V$	$I$	$g$	$r$	$i$	$E(V-I)$ ^b^bExtinction retrieved from Skowron et al. (2021).	$\Delta$ ^c^c $\Delta=(V-I)_{SEBO}-(V-I)_{OGLE}$ are the difference of the colors between Sebo et al. (2002) and Soszyński et al. (2015).
OGLE-LMC-ACEP-019	Ogle114046	0.9094064	18.15	17.83	17.33	17.88	17.77	17.72	$0.08\pm 0.07$	$\cdots$
OGLE-LMC-ACEP-021	Ogle194404	1.2958507	18.11	17.85	17.25	17.87	17.81	17.63	$0.10\pm 0.07$	$-0.00$
OGLE-LMC-ACEP-026	Ogle132771	1.7387480	18.13	17.61	16.94	17.76	17.46	17.35	$0.11\pm 0.08$	$+0.03$
OGLE-LMC-ACEP-046	Ogle272276	1.2637156	18.48	17.98	17.37	18.12	17.84	17.78	$0.09\pm 0.08$	$+0.03$
OGLE-LMC-ACEP-050	Ogle243639	1.0446956	17.60	16.95	16.61	17.16	16.75	17.04	$0.10\pm 0.09$	$-0.12$

The forth phase of Optical Gravitational Lensing Experiment (OGLE-IV) found 141 ACep in the LMC (Soszyński et al., 2015). The $(B-V)$ colors are required to transform the Johnson-Cousin $BVI$ -band photometry to the Pan-STARRS1 $gri$ -band photometry (Tonry et al., 2012). Hence, we cannot use OGLE-IV data which only covers $V$ - and $I$ -bands. Therefore, we cross-matched the OGLE-IV LMC ACep catalog with the sample of $BVI$ photometry presented in Sebo et al. (2002). In total, we found four common fundamental mode ACep (OGLE-LMC-ACEP-019, 021, 026, and 046) and one first-overtone ACep (OGLE-LMC-ACEP-050). The $BVI$ -band mean magnitudes of these five LMC ACep were then transformed to the $gri$ -band using the relations provided in Tonry et al. (2012). Both $BVI$ -band mean magnitudes and the transformed $gri$ -band mean magnitudes for these LMC ACep are provided in Table 1.

3 The PL and PW Relations

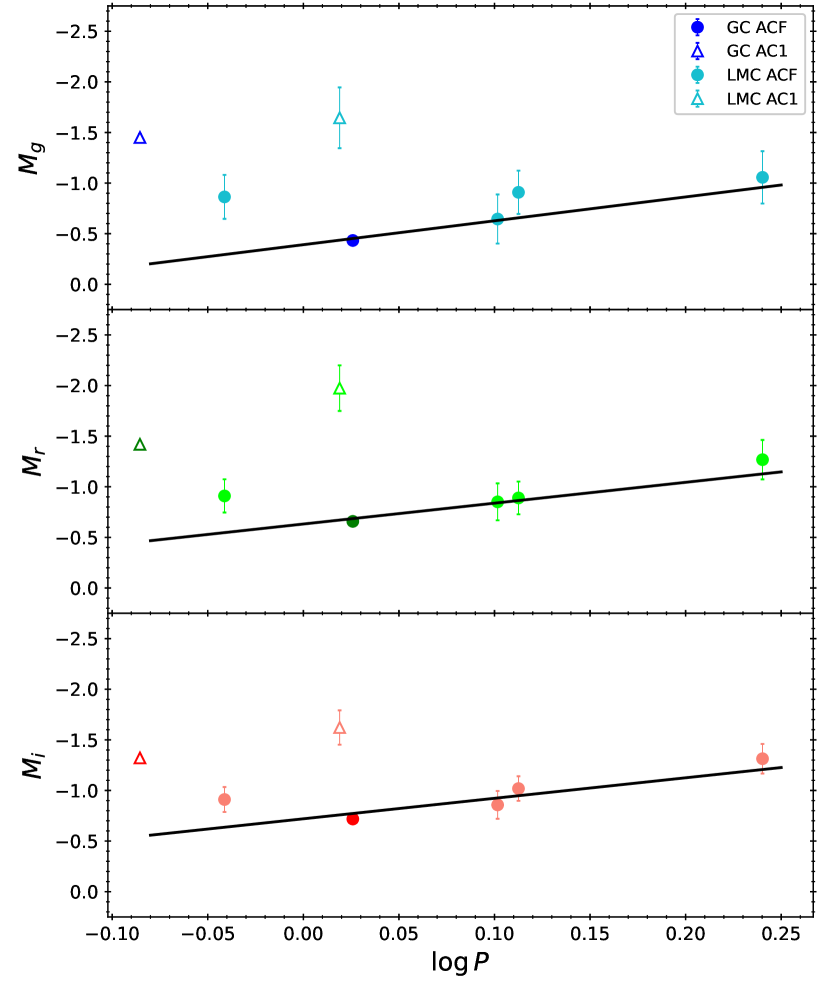
Mean magnitudes of the two GC ACep were converted to absolute magnitudes by adopting the GC distances presented in Baumgardt & Vasiliev (2021), together with the extinction corrections based on the Bayerstar2019 3D reddening map (Green et al., 2019).⁴⁴4See http://argonaut.skymaps.info/usage, the reddening values were queried via the dustmaps package (Green, 2018) available at https://dustmaps.readthedocs.io/en/latest/. Similarly, we adopted the most precise LMC distance from Pietrzyński et al. (2019) and the LMC extinction map of Skowron et al. (2021) to convert the mean magnitudes of five LMC ACep to absolute magnitudes. We note that accuracy of the adopted distance to NGC5466, M92, and LMC is at the $\sim 1\%$ level. As there are only two first-overtone ACep in our sample, we only fit the four LMC and one GC fundamental mode ACep (hereafter collectively referred as calibrating ACep) and obtain the following PL relations:

$\displaystyle M_{g}$	$\displaystyle=$	$\displaystyle-2.36[\pm 0.99]\log P-0.39[\pm 0.04],\sigma=0.36,$	(1)
$\displaystyle M_{r}$	$\displaystyle=$	$\displaystyle-2.06[\pm 0.76]\log P-0.63[\pm 0.04],\sigma=0.23,$	(2)
$\displaystyle M_{i}$	$\displaystyle=$	$\displaystyle-2.03[\pm 0.59]\log P-0.72[\pm 0.05],\sigma=0.18,$	(3)

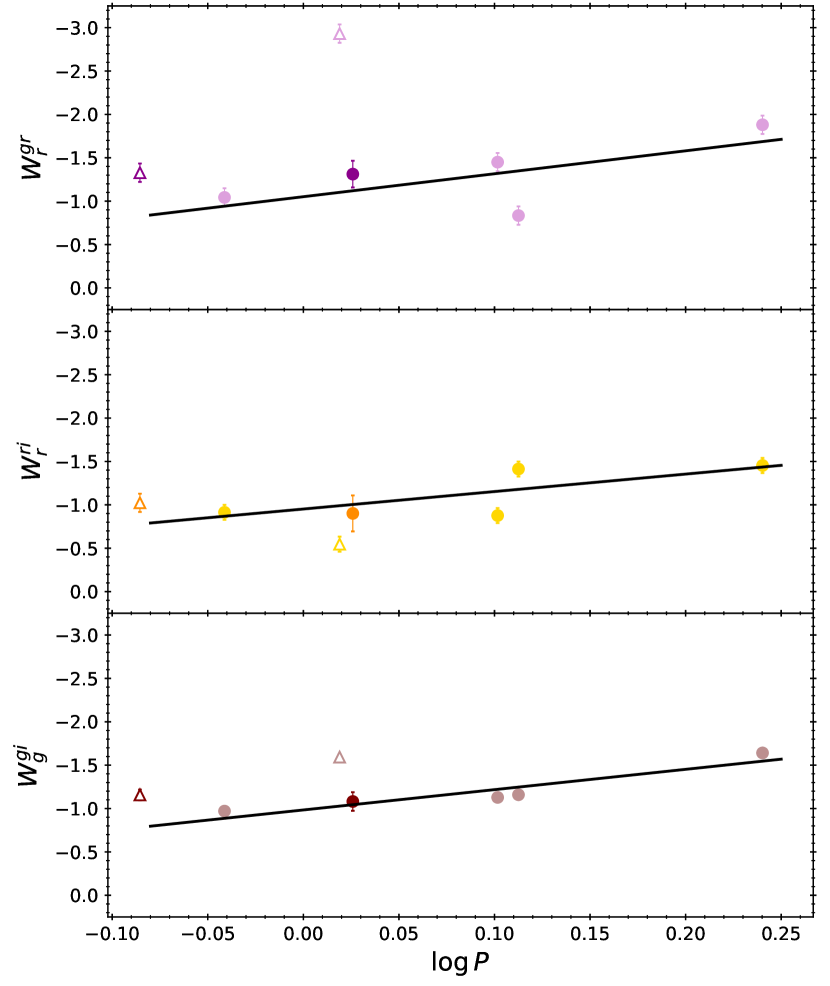
where $\sigma$ is the dispersion of the fitted PL relations. Similar, we obtained the following PW relations (see Ngeow et al., 2021) based on the calibrating ACep:

$\displaystyle W^{gr}_{r}$	$\displaystyle=$	$\displaystyle r-2.905(g-r),$	(4)
	$\displaystyle=$	$\displaystyle-2.64[\pm 0.51]\log P-1.05[\pm 0.07],\sigma=0.35,$	(4)
$\displaystyle W^{ri}_{r}$	$\displaystyle=$	$\displaystyle r-4.051(r-i),$	(5)
	$\displaystyle=$	$\displaystyle-2.01[\pm 0.43]\log P-0.95[\pm 0.06],\sigma=0.22,$	(5)
$\displaystyle W^{gi}_{g}$	$\displaystyle=$	$\displaystyle g-2.274(g-i),$	(6)
	$\displaystyle=$	$\displaystyle-2.34[\pm 0.17]\log P-0.08[\pm 0.02],\sigma=0.11.$	(6)

Figure 2 presents the $gri$ -band PL (left panel) and PW (right panel) relations derived in this work.

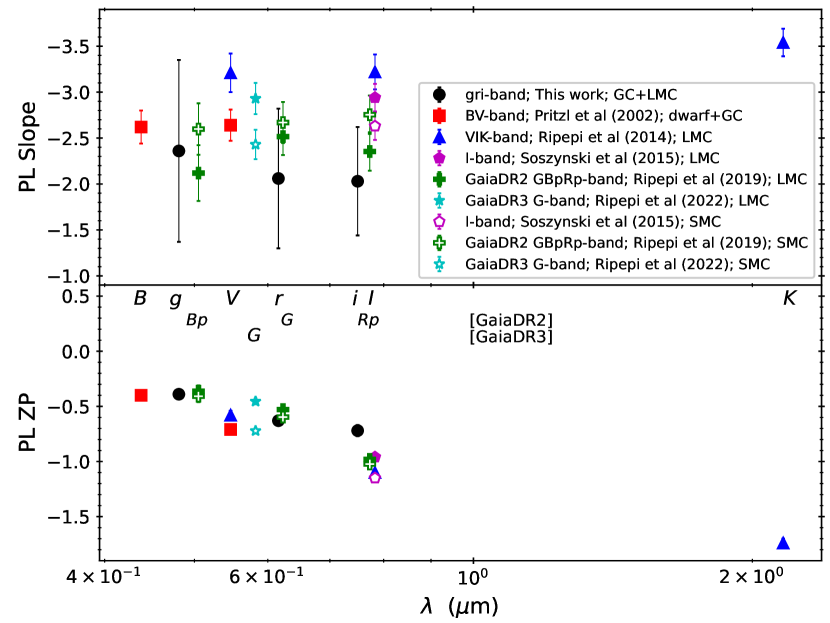
Since in general PW relations are expected to exhibit a smaller dispersion than the PL relations, the large dispersions seen in equation (4) and (5) could due to the less accurate colors for some of the LMC ACep derived in Sebo et al. (2002). Last column in Table 1 compares the $(V-I)$ colors listed in the OGLE-IV catalog (Soszyński et al., 2015) and those derived from the mean magnitudes given in Sebo et al. (2002). The color difference for OGLE-LMC-ACEP-050 is $\sim 4$ times larger than other ACep listed in Table 1, suggesting the less accurate colors might cause this ACep to be brighter in the $W^{gr}_{r}$ PW relation but fainter than the fitted relations in the $W^{ri}_{r}$ PW relations (see the right panels of Figure 2, where OGLE-LMC-ACEP-050 is labeled as LMC AC1).

In Figure 3, we compared the empirical PL relations, for fundamental mode ACep, in various filters to equation (1) – (3). In case of the PL slopes, we notice that: (a) in contrast to other pulsating stars (classical Cepheids, Type II Cepheids, and RR Lyrae), there is no clear trends for the PL slopes as a function of wavelengths (i.e. filters), which could due to large uncertainties in the slopes determined in most studies; (b) for a given filter, the PL slopes can be either in agreement (such as in Gaia filters) or disagreement (such as in $V$ -band) among different studies; and (c) PL relations from Ripepi et al. (2014) have the steepest slopes, and disagreed with previous works, for the reasons discussed in their study. Despite the large errors due to small number statistics, our $g$ -band slopes agree well with the $B$ -band PL slope from Pritzl et al. (2002). The PL zero-points (ZP) were found to be more consistent between different studies and follow the expected trend with wavelength.

4 An Example of Application: Distance to Crater II

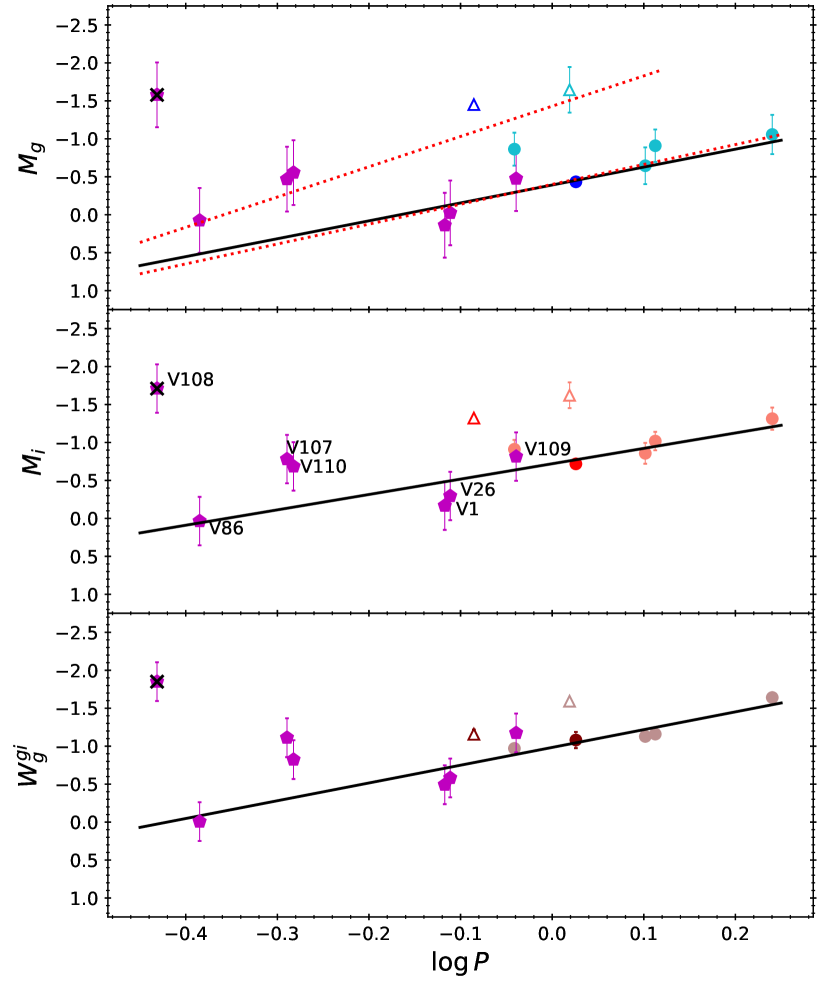
Vivas et al. (2020) reported a discovery of seven ACep in a dwarf galaxy Crater II, providing us an opportunity to test our derived PL and PW relations. As shown in Figure 4, V108 (with the shortest period) is much brighter than the rest of the ACep in Crater II, suggesting this ACep could either be a foreground object or mis-classified as an ACep. Nevertheless, it is clear that V108 should not be used to derive the distance to Crater II. In the top panel of Figure 4, we overlaid the $B$ -band PL relations adopted from Pritzl et al. (2002, without any photometric transformation) together with the $g$ -band PL relation derived in equation (1). It is clear that the three longest period ACep (V1, V26, and V109) can be fit well with either the $B$ - or $g$ -band fundamental mode ACep PL relation, hence they are most likely pulsating in the fundamental mode. Similarly, the three shortest period ACep (V86,⁵⁵5V86 is located on the $i$ -band PL relation and $W^{gi}_{g}$ PW relation (see middle and bottom panel of Figure 4) based on the fundamental mode ACep, implying it could be a fundamental mode pulsator. However, as pointed out by the referee, the pulsation period for this ACep is very short and it is unlikely pulsating in the fundamental mode. Unless the PL (and PW) relations for fundamental and first-overtone ACep are in parallel, using locations of the ACep on PL (and PW) plane might not be a reliable method to determine the pulsation mode of ACep, because the un-parallel PL (and PW) relations for both pulsation modes could intersect at short period. V107 and V110) should be first-overtone pulsators.

The mean magnitudes provided in Vivas et al. (2020) are in the SDSS photometric system. Therefore, following the procedures described in Ngeow et al. (2022a), we transformed our $gi$ -band PL relations to the SDSS system by adding a small correction term to our PL relations. These correction terms were determined using a subset of calibrating ACep with the same mean $(g-i)_{SDSS}$ colors as the fundamental mode ACep in Crater II. Similarly, we transformed our $W^{gi}_{g}$ PW relation to the SDSS system and using $W^{gi}_{SDSS}=g_{SDSS}-2.058(g_{SDSS}-i_{SDSS})$ . We fit the three longest period fundamental mode ACep with our derived PL and PW relations, and obtained $\mu_{g}=20.45\pm 0.25$ , $\mu_{i}=20.55\pm 0.29$ , and $\mu_{W}=20.54\pm 0.30$ mag. Errors on these distance moduli $\mu$ were based on the small number statistics (Dean & Dixon, 1951; Keeping, 1962, p. 202) for only three ACep. Extinction corrections were applied to the $g$ - and $i$ -band mean magnitudes by using the Bayerstar2019 3D reddening map (Green et al., 2019) when deriving the distance moduli for these ACep.

Using RR Lyrae and a theoretical PL relation, Vivas et al. (2020) derived a distance modulus of $20.33\pm 0.01$ mag to Crater II. On the other hand, based on the same RR Lyrae sample but with the latest empirical PL relations, Ngeow et al. (2022a) argued that the distance modulus of Crater II should be (slightly) larger. Albeit with a larger error (due to small number of samples), the distance modulus derived from ACep is consistent with RR Lyrae-based distance modulus, and supports a farther distance to Crater II.

5 Discussions and Conclusions

Despite the small number of calibrating ACep, we derived for the first time the fundamental mode ACep PL and PW relations in the $gri$ -band based on the most precise distances to date to GC and LMC available in the literature. Though the errors on the slopes of our derived PL relations are large, our PL relations fairly agree with published PL relations in other optical filters, especially our $g$ -band PL relation is similar to the $B$ -band PL relation. Comparison of the PL slopes from various studies also revealed that these PL slopes did not “converge” to a trend, implying more data are needed to improve the ACep PL relations in the future. We applied our PL and PW relations to ACep found in dwarf galaxy Crater II, and found that half of the ACep in Crater II are pulsating in fundamental mode. Based on these fundamental mode ACep, we derived a distance to Crater II which agrees with those reported in the literature.

Monelli & Fiorentino (2022) compiled a list of nearby dwarf galaxies with number of pulsating stars found in these galaxies. As can be seen from their list, almost all nearby dwarf galaxies host at least one RR Lyrae, and about half of them also host ACep. Certainly, for a dwarf galaxy with both RR Lyrae and ACep, RR Lyrae is the preferred distance indicator because in general RR Lyrae are more abundant than ACep and the RR Lyre PL and PW relations are well-developed. On the other hand, ACep are in general brighter, by $\sim 0.4$ to $\sim 2.5$ mag above the horizontal branch (Vivas et al., 2020, and reference therein), than RR Lyrae because they are more massive. This implies that newly discovered but distant dwarf galaxies near the detection limit of a synoptic sky survey (such as LSST) could miss RR Lyrae but still detecting ACep. In such cases, ACep can provide an independent distance to these dwarf galaxies, and a test for cross-validation for other distance measurements such as using the tip of the red-giant branch (TRGB) method.

We are thankful for the useful discussions and comments from an anonymous referee that improved the manuscript. We are thankful for funding from the Ministry of Science and Technology (Taiwan) under the contracts 107-2119-M-008-014-MY2, 107-2119-M-008-012, 108-2628-M-007-005-RSP and 109-2112-M-008-014-MY3. Based on observations obtained with the Samuel Oschin Telescope 48-inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project. ZTF is supported by the National Science Foundation under Grants No. AST-1440341 and AST-2034437 and a collaboration including current partners Caltech, IPAC, the Weizmann Institute of Science, the Oskar Klein Center at Stockholm University, the University of Maryland, Deutsches Elektronen-Synchrotron and Humboldt University, the TANGO Consortium of Taiwan, the University of Wisconsin at Milwaukee, Trinity College Dublin, Lawrence Livermore National Laboratories, IN2P3, University of Warwick, Ruhr University Bochum, Northwestern University and former partners the University of Washington, Los Alamos National Laboratories, and Lawrence Berkeley National Laboratories. Operations are conducted by COO, IPAC, and UW. This research has made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. This research made use of Astropy,⁶⁶6http://www.astropy.org a community-developed core Python package for Astronomy (Astropy Collaboration et al., 2013, 2018). This research has made use of the Spanish Virtual Observatory⁷⁷7https://svo.cab.inta-csic.es project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00. PO:1.2m

References

Arellano Ferro et al. (2013) Arellano Ferro, A., Bramich, D. M., Figuera Jaimes, R., et al. 2013, MNRAS, 434, 1220
Astropy Collaboration et al. (2013) Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33
Astropy Collaboration et al. (2018) Astropy Collaboration, Price-Whelan, A. M., Sipőcz, B. M., et al. 2018, AJ, 156, 123
Baumgardt & Vasiliev (2021) Baumgardt, H. & Vasiliev, E. 2021, MNRAS, 505, 5957
Bhardwaj et al. (2021) Bhardwaj, A., Rejkuba, M., Sloan, G. C., et al. 2021, ApJ, 922, 20
Bellm & Kulkarni (2017) Bellm, E. & Kulkarni, S. 2017, Nature Astronomy, 1, 0071
Bellm et al. (2019) Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002
Bono et al. (1997) Bono, G., Caputo, F., Santolamazza, P., et al. 1997, AJ, 113, 2209
Chambers et al. (2016) Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, arXiv:1612.05560
Cox & Proffitt (1988) Cox, A. N. & Proffitt, C. R. 1988, ApJ, 324, 1042
Dean & Dixon (1951) Dean, R. B. & Dixon, W. J. 1951, Anal. Chem., 23, 636
Dekany et al. (2020) Dekany, R., Smith, R. M., Riddle, R., et al. 2020, PASP, 132, 038001
Fiorentino et al. (2006) Fiorentino, G., Limongi, M., Caputo, F., et al. 2006, A&A, 460, 155
Graczyk et al. (2020) Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2020, ApJ, 904, 13
Graham et al. (2019) Graham, M. J., Kulkarni, S. R., Bellm, E. C., et al. 2019, PASP, 131, 078001
Green (2018) Green, G. M. 2018, The Journal of Open Source Software, 3, 695
Green et al. (2019) Green, G. M., Schlafly, E., Zucker, C., et al. 2019, ApJ, 887, 93
Groenewegen & Jurkovic (2017) Groenewegen, M. A. T. & Jurkovic, M. I. 2017, A&A, 604, A29
Harris et al. (2020) Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357
Hunter (2007) Hunter, J. D. 2007, Computing in Science and Engineering, 9, 90
Ivezić et al. (2019) Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111
Iwanek et al. (2018) Iwanek, P., Soszyński, I., Skowron, D., et al. 2018, Acta Astronomica, 68, 213
Keeping (1962) Keeping, E. S. 1962, Introduction to Statistical Inference (Princeton, NJ: Van Nostrand-Reinhold)
Madore (1982) Madore, B. F. 1982, ApJ, 253, 575
Madore & Freedman (1991) Madore, B. F. & Freedman, W. L. 1991, PASP, 103, 933
Magnier et al. (2020) Magnier, E. A., Sweeney, W. E., Chambers, K. C., et al. 2020, ApJS, 251, 5
Marconi et al. (2004) Marconi, M., Fiorentino, G., & Caputo, F. 2004, A&A, 417, 1101
Masci et al. (2019) Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003
McCarthy & Nemec (1997) McCarthy, J. K. & Nemec, J. M. 1997, ApJ, 482, 203
Monelli & Fiorentino (2022) Monelli, M. & Fiorentino, G. 2022, Universe, 8, 191
Nemec et al. (1988) Nemec, J. M., Wehlau, A., & Mendes de Oliveira, C. 1988, AJ, 96, 528
Nemec et al. (1994) Nemec, J. M., Nemec, A. F. L., & Lutz, T. E. 1994, AJ, 108, 222
Ngeow et al. (2021) Ngeow, C.-C., Liao, S.-H., Bellm, E. C., et al. 2021, AJ, 162, 63
Ngeow et al. (2022a) Ngeow, C.-C., Bhardwaj, A., Dekany, R. et al. 2022a, AJ, 163, 239
Ngeow et al. (2022b) Ngeow, C.-C., Bhardwaj, A., Henderson, J.-Y. et al. 2022b, arXiv:2208.03404
Osborn et al. (2012) Osborn, W., Kopacki, G., & Haberstroh, J. 2012, Acta Astronomica, 62, 377
Pietrzyński et al. (2019) Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200
Pritzl et al. (2002) Pritzl, B. J., Armandroff, T. E., Jacoby, G. H., et al. 2002, AJ, 124, 1464
Ripepi et al. (2014) Ripepi, V., Marconi, M., Moretti, M. I., et al. 2014, MNRAS, 437, 2307
Ripepi et al. (2019) Ripepi, V., Molinaro, R., Musella, I., et al. 2019, A&A, 625, A14
Ripepi et al. (2022) Ripepi, V., Clementini, G., Molinaro, R., et al. 2022, arXiv:2206.06212
Rodrigo & Solano (2020) Rodrigo, C. & Solano, E. 2020, in Contributions to the XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society (Barcelona: Spanish Astronomical Society), 182
Rodrigo et al. (2012) Rodrigo, C., Solano, E., & Bayo, A. 2012, IVOA Working Draft
Sandage & Tammann (2006) Sandage, A. & Tammann, G. A. 2006, ARA&A, 44, 93
Sebo et al. (2002) Sebo, K. M., Rawson, D., Mould, J., et al. 2002, ApJS, 142, 71
Skowron et al. (2021) Skowron, D. M., Skowron, J., Udalski, A., et al. 2021, ApJS, 252, 23
Soszyński et al. (2015) Soszyński, I., Udalski, A., Szymański, M. K., et al. 2015, Acta Astronomica, 65, 233
Soszyński et al. (2020) Soszyński, I., Udalski, A., Szymański, M. K., et al. 2020, Acta Astronomica, 70, 101
Tonry et al. (2012) Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99
VanderPlas & Ivezić (2015) VanderPlas, J. T., & Ivezić, Ž. 2015, ApJ, 812, 18
VanderPlas (2016) VanderPlas, J. 2016, gatspy: General tools for Astronomical Time Series in Python, ascl:1610.007
Virtanen et al. (2020) Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261
Vivas et al. (2020) Vivas, A. K., Walker, A. R., Martínez-Vázquez, C. E., et al. 2020, MNRAS, 492, 1061
Yepez et al. (2020) Yepez, M. A., Arellano Ferro, A., & Deras, D. 2020, MNRAS, 494, 3212
Zinn & Dahn (1976) Zinn, R. & Dahn, C. C. 1976, AJ, 81, 527